Figure 1.
Details of the cable-driven transmission, disc and masses. (a) steel cable, (b) capstan system, (c) pulley system, (d) masses and (e) perforated disc.
Figure 1.
Details of the cable-driven transmission, disc and masses. (a) steel cable, (b) capstan system, (c) pulley system, (d) masses and (e) perforated disc.
Figure 2.
Details of the assembly of type S load cells.
Figure 2.
Details of the assembly of type S load cells.
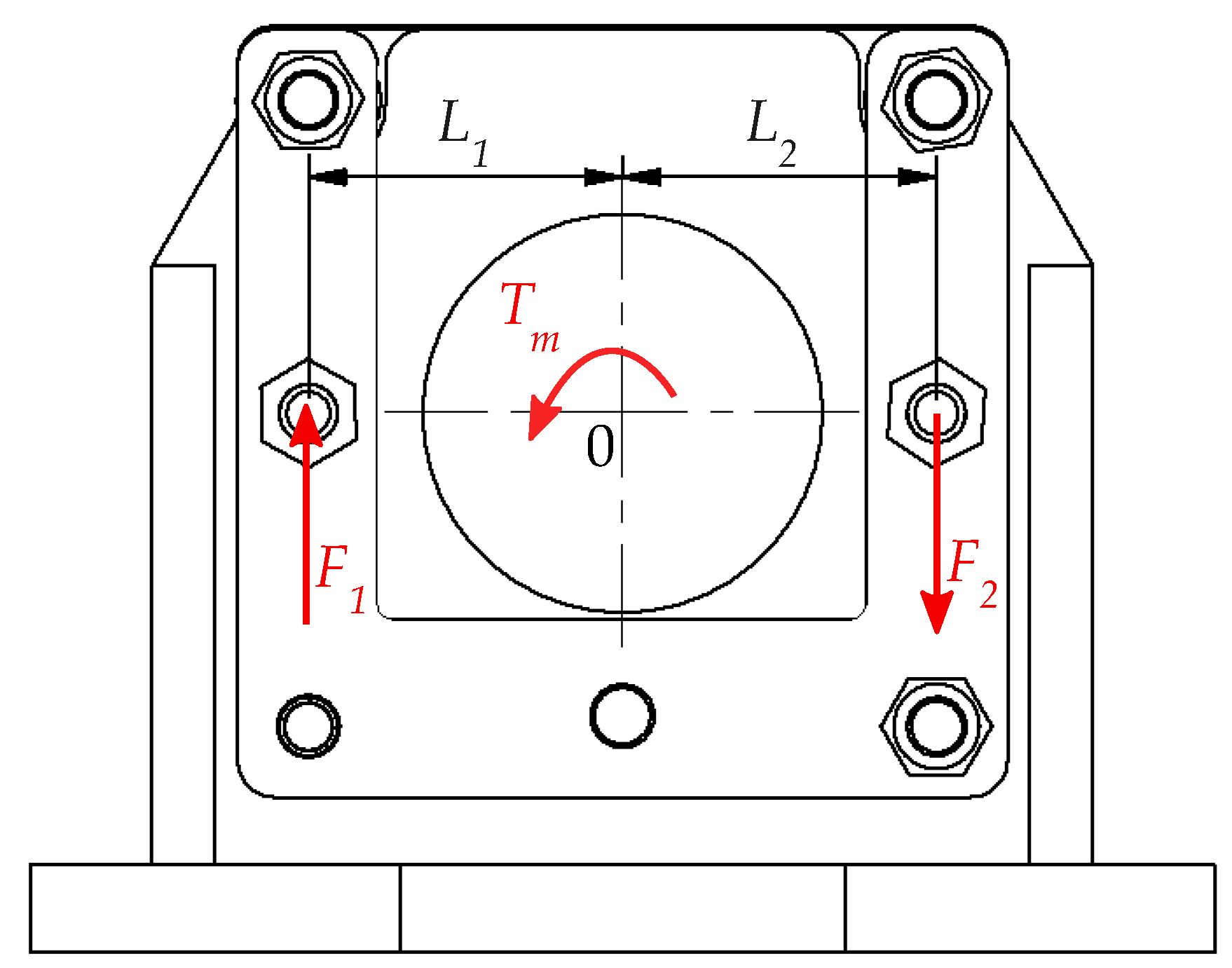
Figure 3.
The free-body diagram for mounting the swing arm motor.
Figure 3.
The free-body diagram for mounting the swing arm motor.
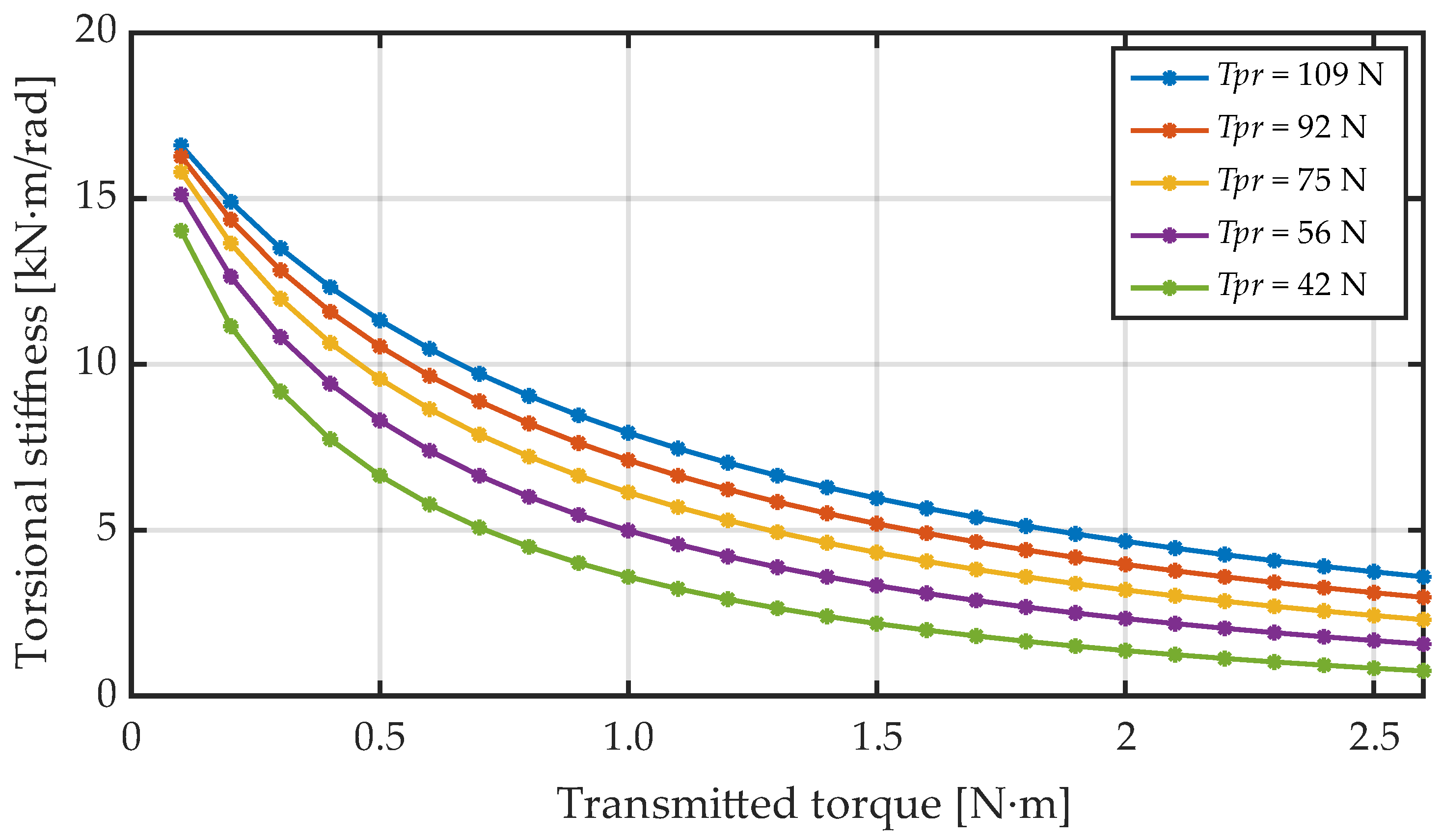
Figure 4.
Effect of transmitted torque on transmission torsional stiffness.
Figure 4.
Effect of transmitted torque on transmission torsional stiffness.
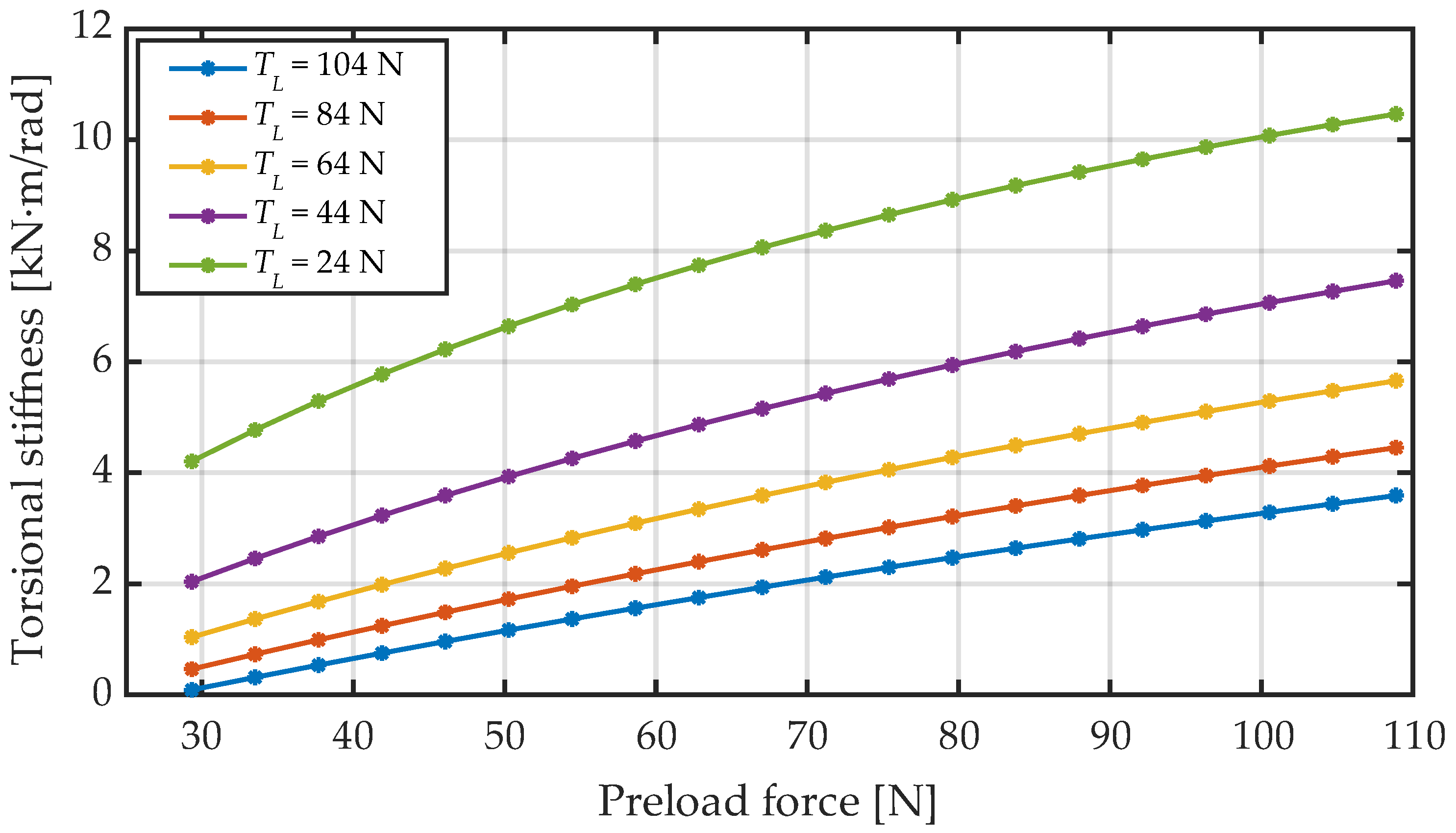
Figure 5.
Effect of preload tension on transmission torsional stiffness.
Figure 5.
Effect of preload tension on transmission torsional stiffness.
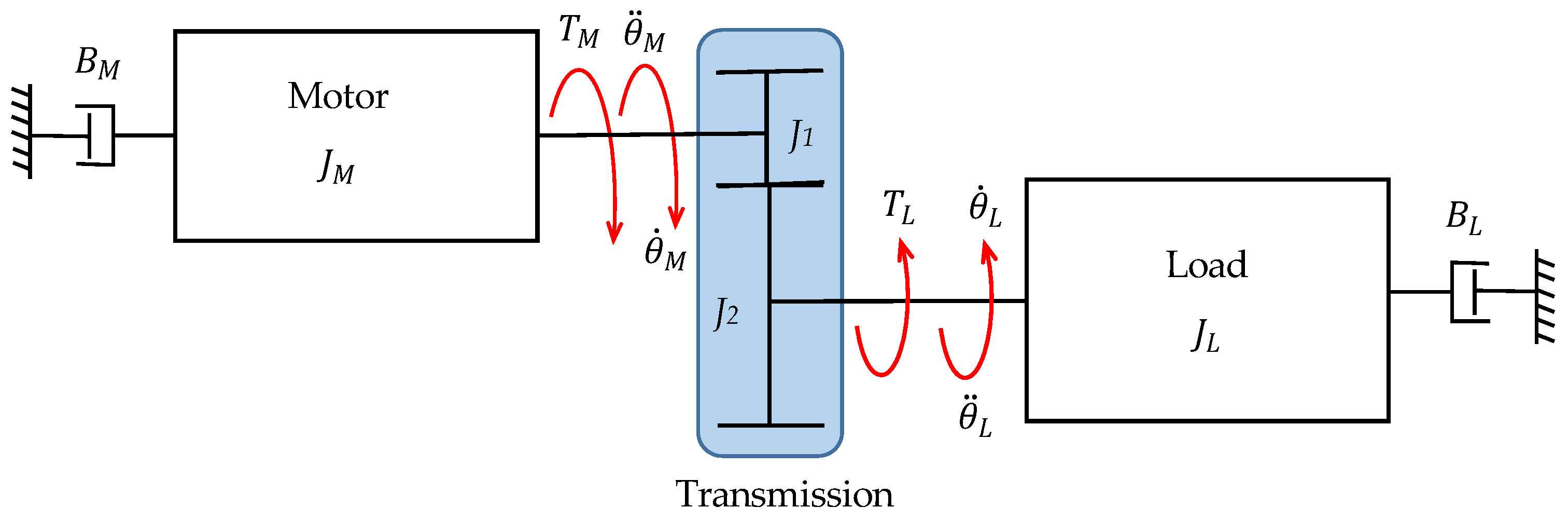
Figure 6.
Schematic of the simplified model of the cable-driven transmission.
Figure 6.
Schematic of the simplified model of the cable-driven transmission.
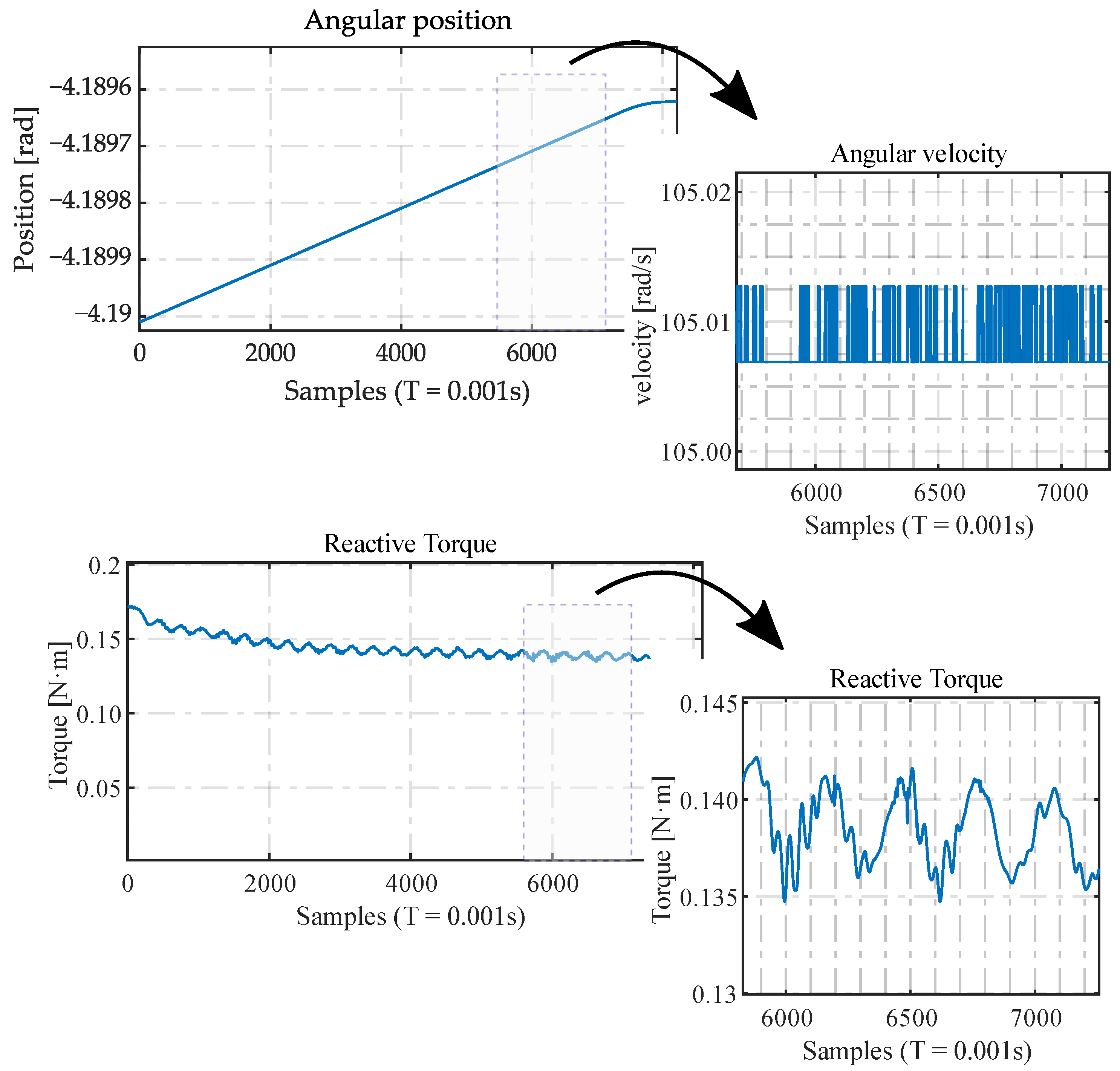
Figure 7.
Measurement of the position and reactive torque in the transmission without external load, for a speed of 1000 rpm (105 rad/s) in the motor.
Figure 7.
Measurement of the position and reactive torque in the transmission without external load, for a speed of 1000 rpm (105 rad/s) in the motor.
Figure 8.
Free-body diagram of the transmission pulleys of the test bench: (A), (B) bearings position, (cg) center of gravity, (D) point of application of the cable force, (E) external force application point, and (a–e) shaft dimensions.
Figure 8.
Free-body diagram of the transmission pulleys of the test bench: (A), (B) bearings position, (cg) center of gravity, (D) point of application of the cable force, (E) external force application point, and (a–e) shaft dimensions.
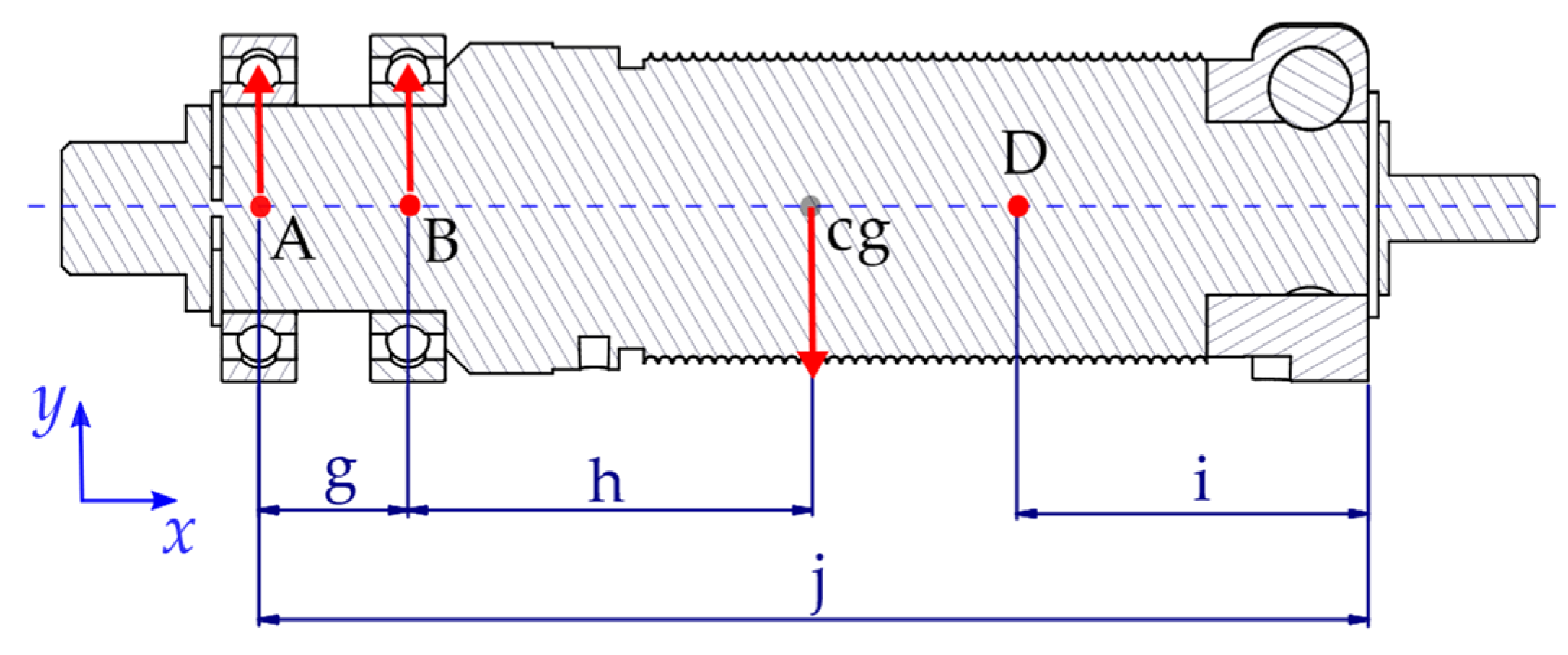
Figure 9.
Free-Body Diagram of the Test Bench Transmission capstans: (A), (B) bearings position, (cg) center of gravity, (D) point of application of the cable force, and (g–j) shaft dimensions.
Figure 9.
Free-Body Diagram of the Test Bench Transmission capstans: (A), (B) bearings position, (cg) center of gravity, (D) point of application of the cable force, and (g–j) shaft dimensions.
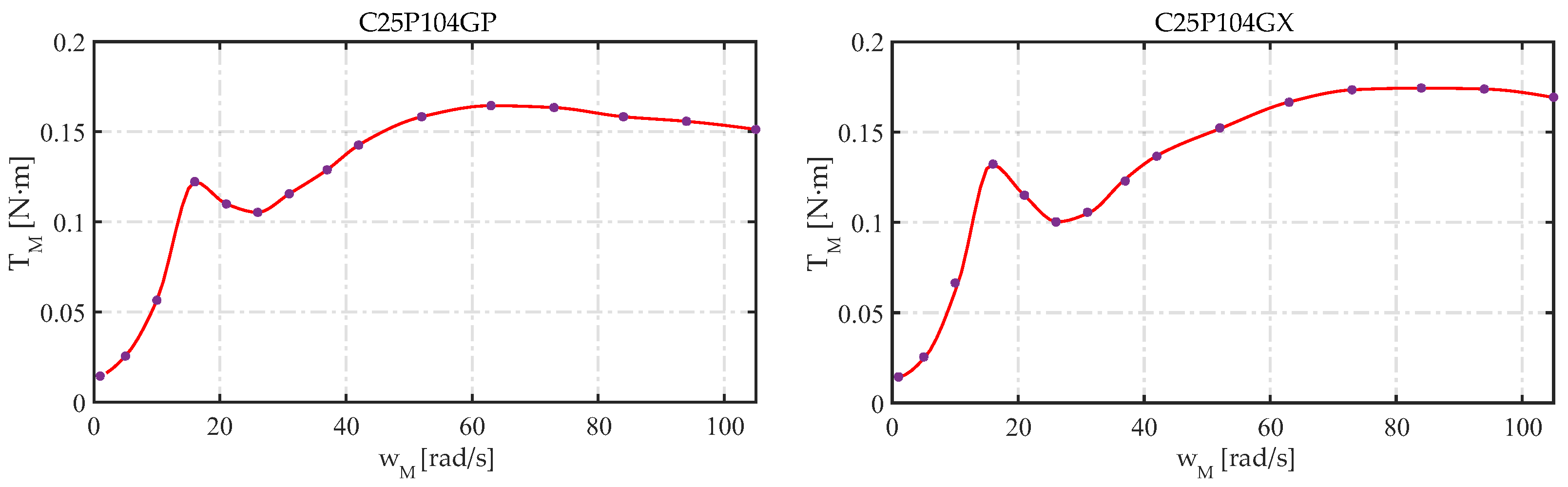
Figure 10.
Speed−torque curves for the C25P104GP and C25P104GX configurations.
Figure 10.
Speed−torque curves for the C25P104GP and C25P104GX configurations.
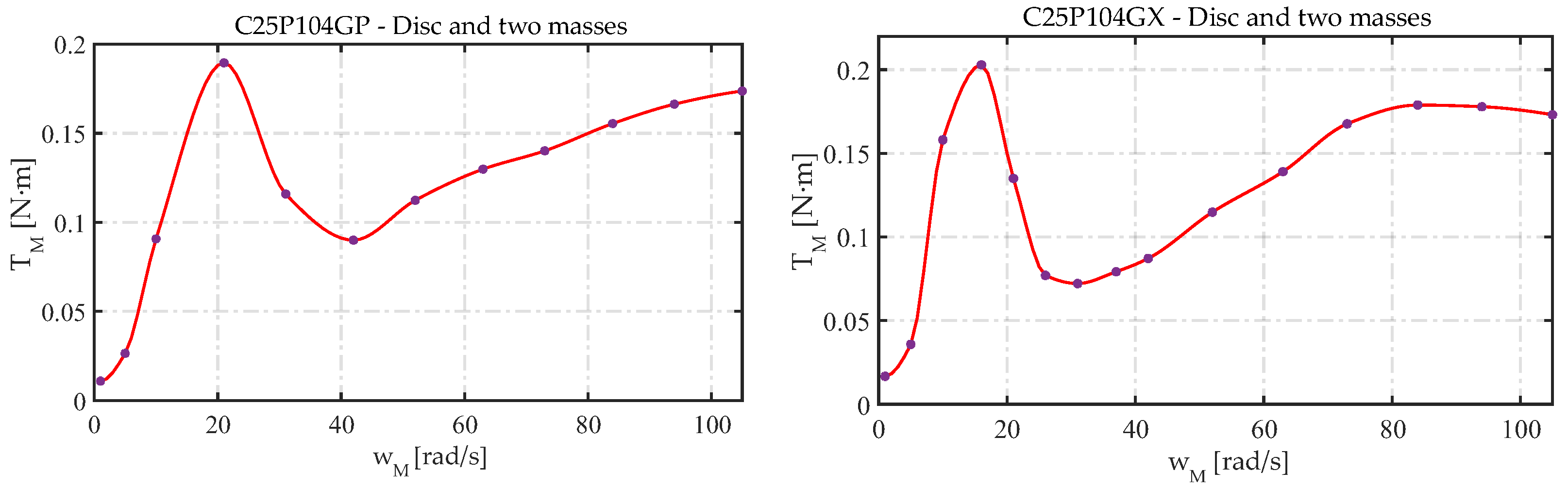
Figure 11.
Speed−torque curves for the C25P104GP-D2M and C25P104GX-D2M configurations.
Figure 11.
Speed−torque curves for the C25P104GP-D2M and C25P104GX-D2M configurations.
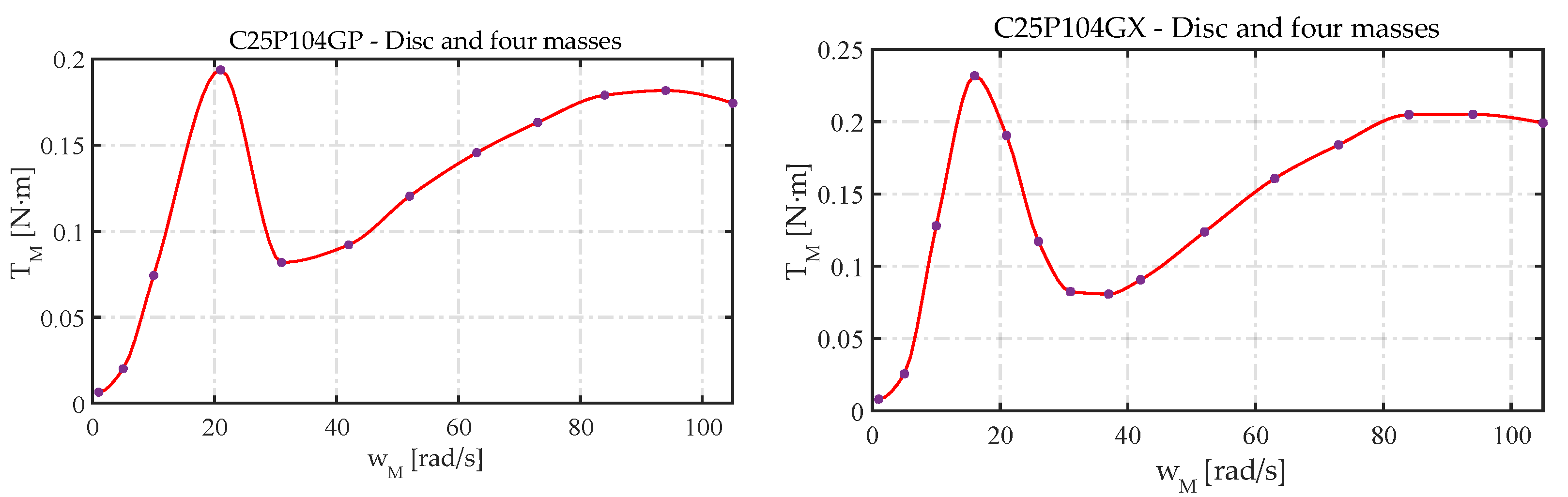
Figure 12.
Speed−torque curves for the C25P104GP-D4M and C25P104GX-D4M configurations.
Figure 12.
Speed−torque curves for the C25P104GP-D4M and C25P104GX-D4M configurations.
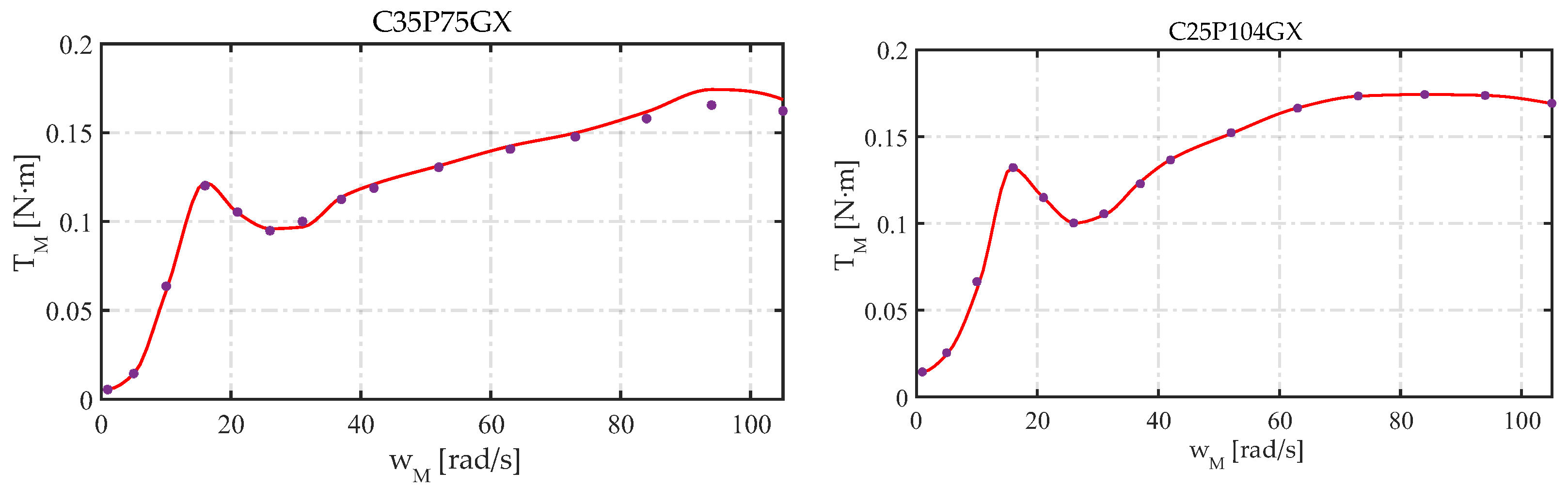
Figure 13.
Speed−torque curves for the C35P75GX and C25P104GX configurations.
Figure 13.
Speed−torque curves for the C35P75GX and C25P104GX configurations.
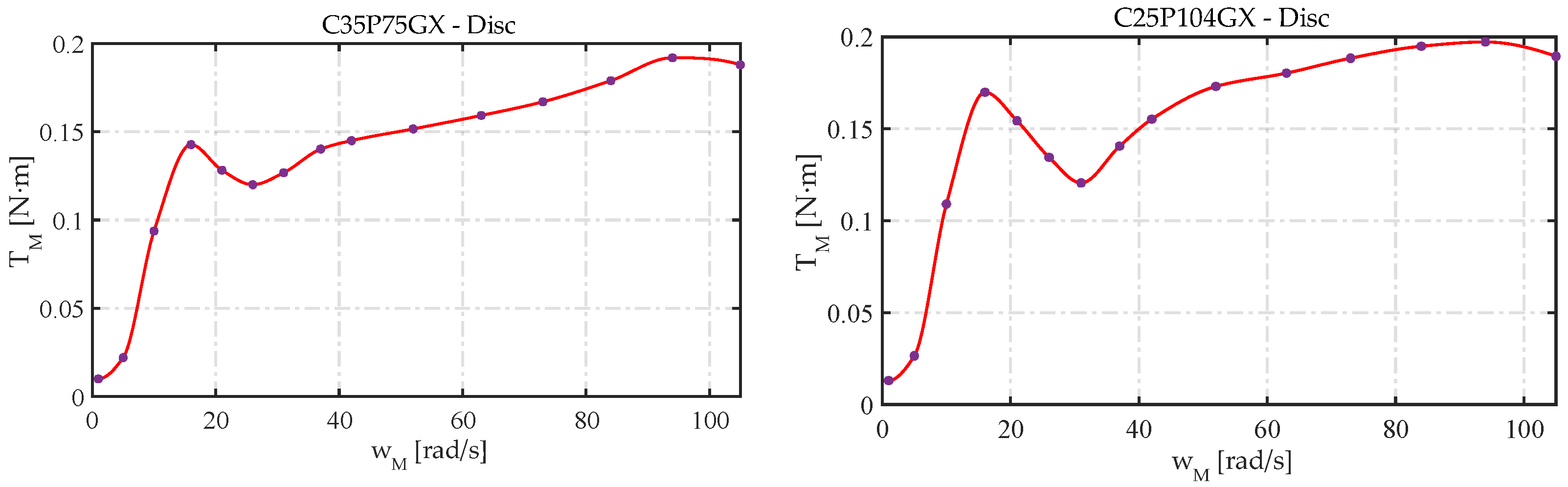
Figure 14.
Speed−torque curves for the C35P75GX-D and C25P104GX-D configurations.
Figure 14.
Speed−torque curves for the C35P75GX-D and C25P104GX-D configurations.
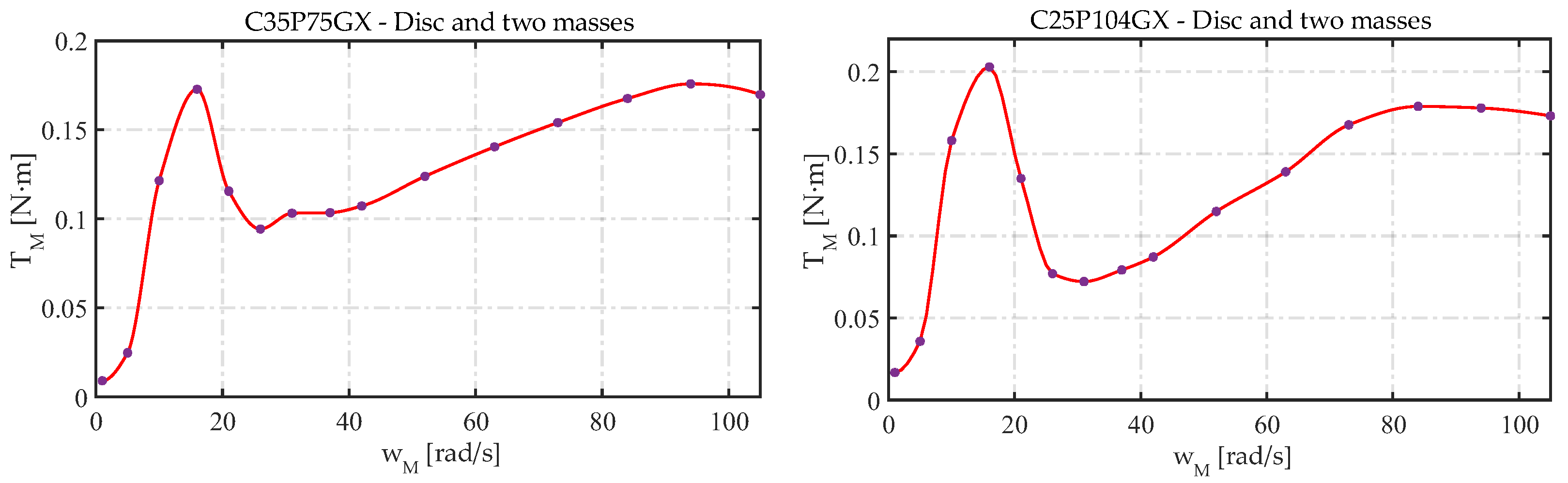
Figure 15.
Speed−torque curves for the C35P75GX-D2M and C25P104GX-D2M configurations.
Figure 15.
Speed−torque curves for the C35P75GX-D2M and C25P104GX-D2M configurations.
Figure 16.
Speed−torque curves for the C35P75GX-D4M and C25P104GX-D4M configurations.
Figure 16.
Speed−torque curves for the C35P75GX-D4M and C25P104GX-D4M configurations.
Figure 17.
Friction torque variation as a function of speed and external load for the C35P75GX configuration.
Figure 17.
Friction torque variation as a function of speed and external load for the C35P75GX configuration.
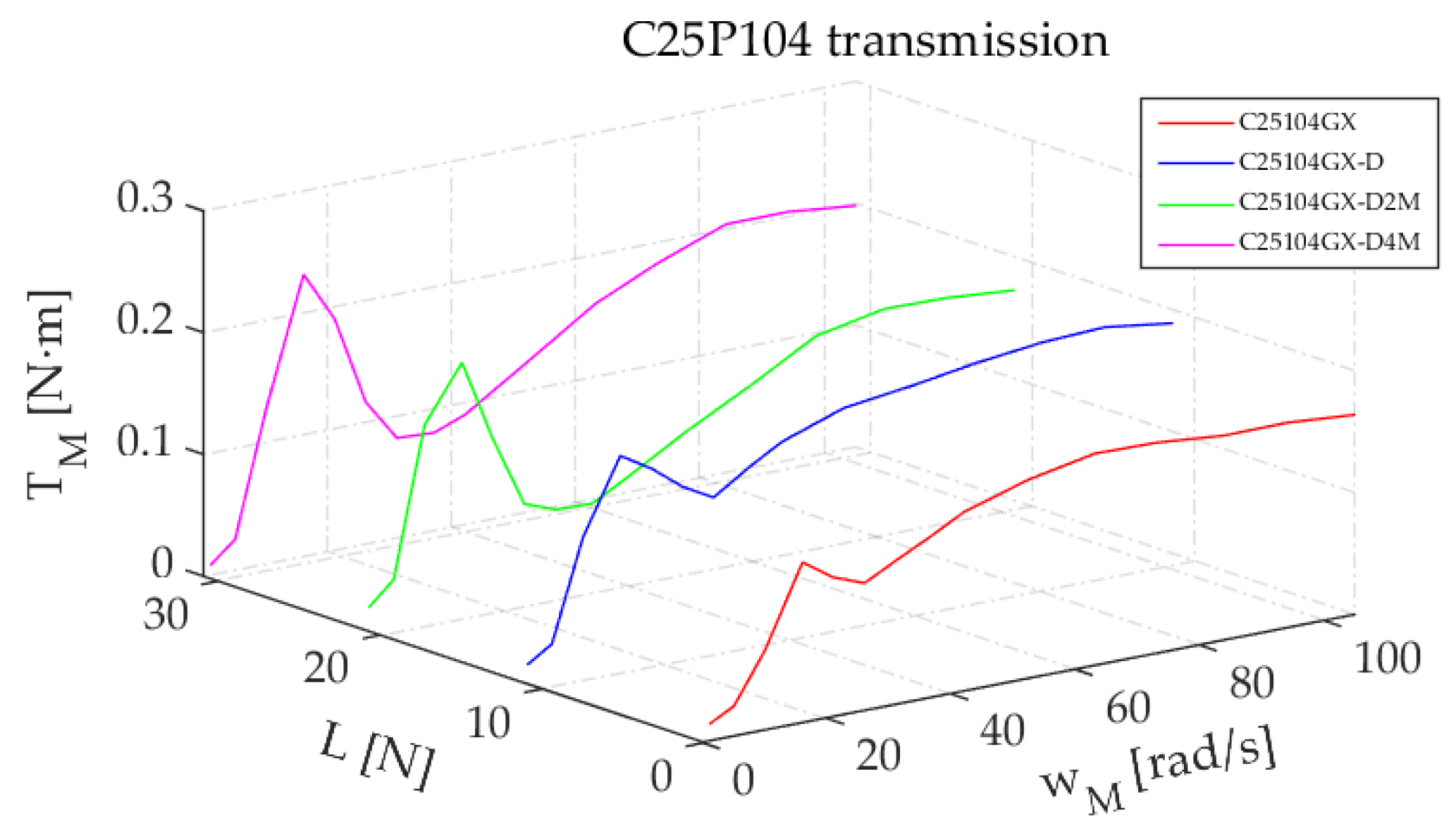
Figure 18.
Friction torque variation as a function of speed and external load for the C25P104GX configuration.
Figure 18.
Friction torque variation as a function of speed and external load for the C25P104GX configuration.
Figure 19.
Static friction torque estimated using the LuGre model for the C35P75GX-D4M configuration.
Figure 19.
Static friction torque estimated using the LuGre model for the C35P75GX-D4M configuration.
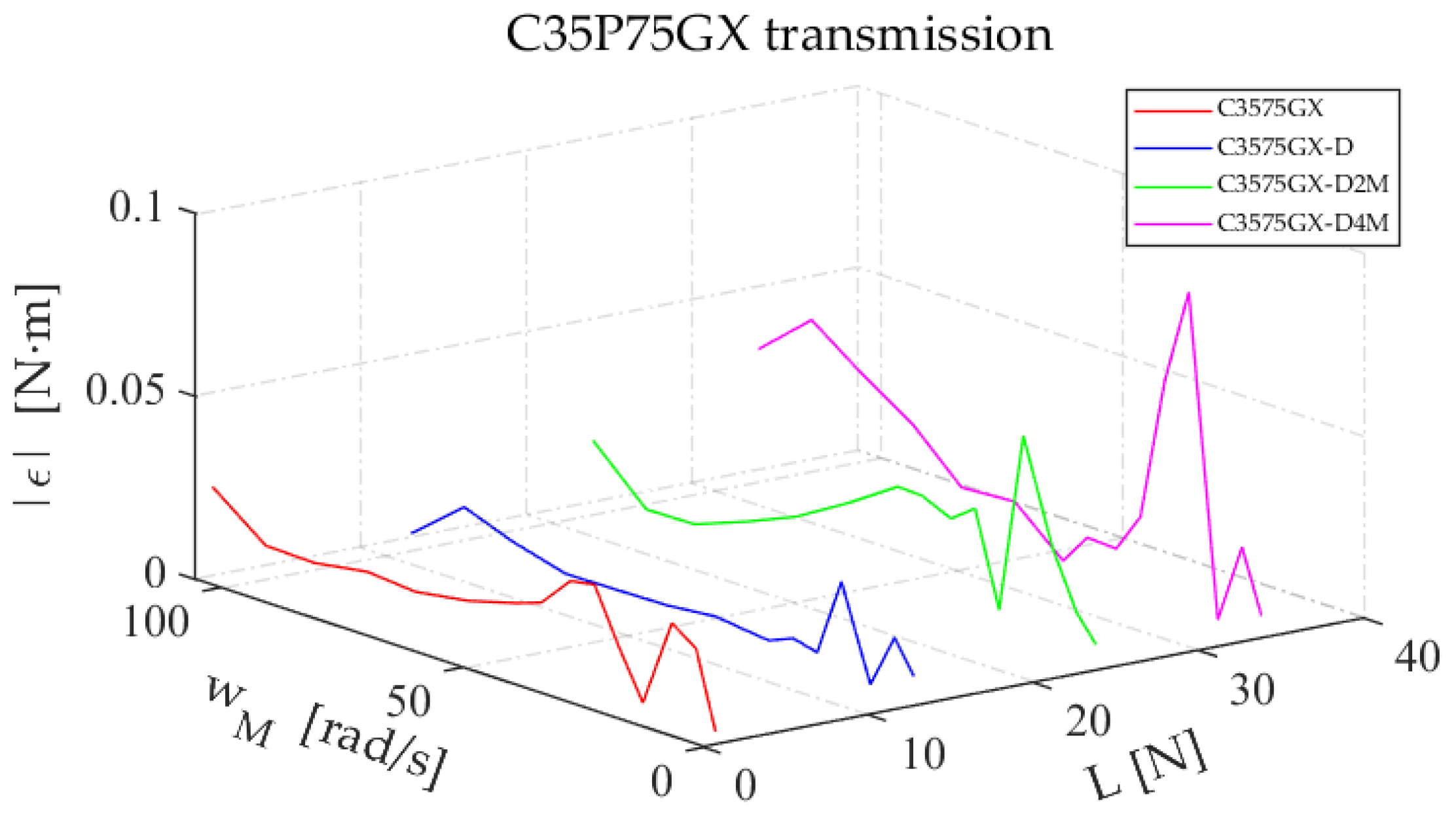
Figure 20.
Absolute error when using static LuGre model for C35P75GX configurations.
Figure 20.
Absolute error when using static LuGre model for C35P75GX configurations.
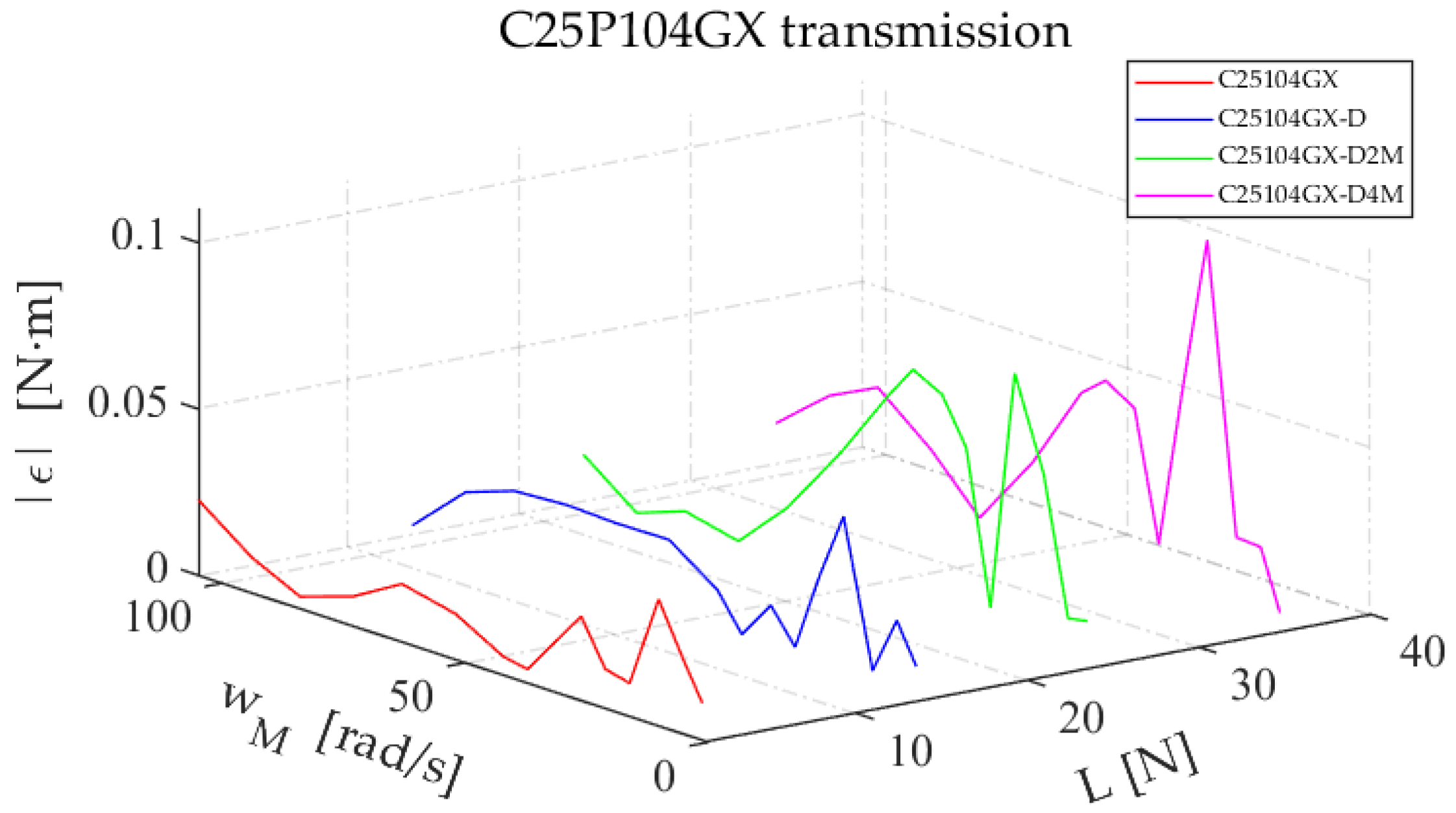
Figure 21.
Absolute error when using static LuGre model for C25P104GX configurations.
Figure 21.
Absolute error when using static LuGre model for C25P104GX configurations.
Figure 22.
Static friction torque estimated using the model proposed for the C25P104GX-D4M configuration.
Figure 22.
Static friction torque estimated using the model proposed for the C25P104GX-D4M configuration.
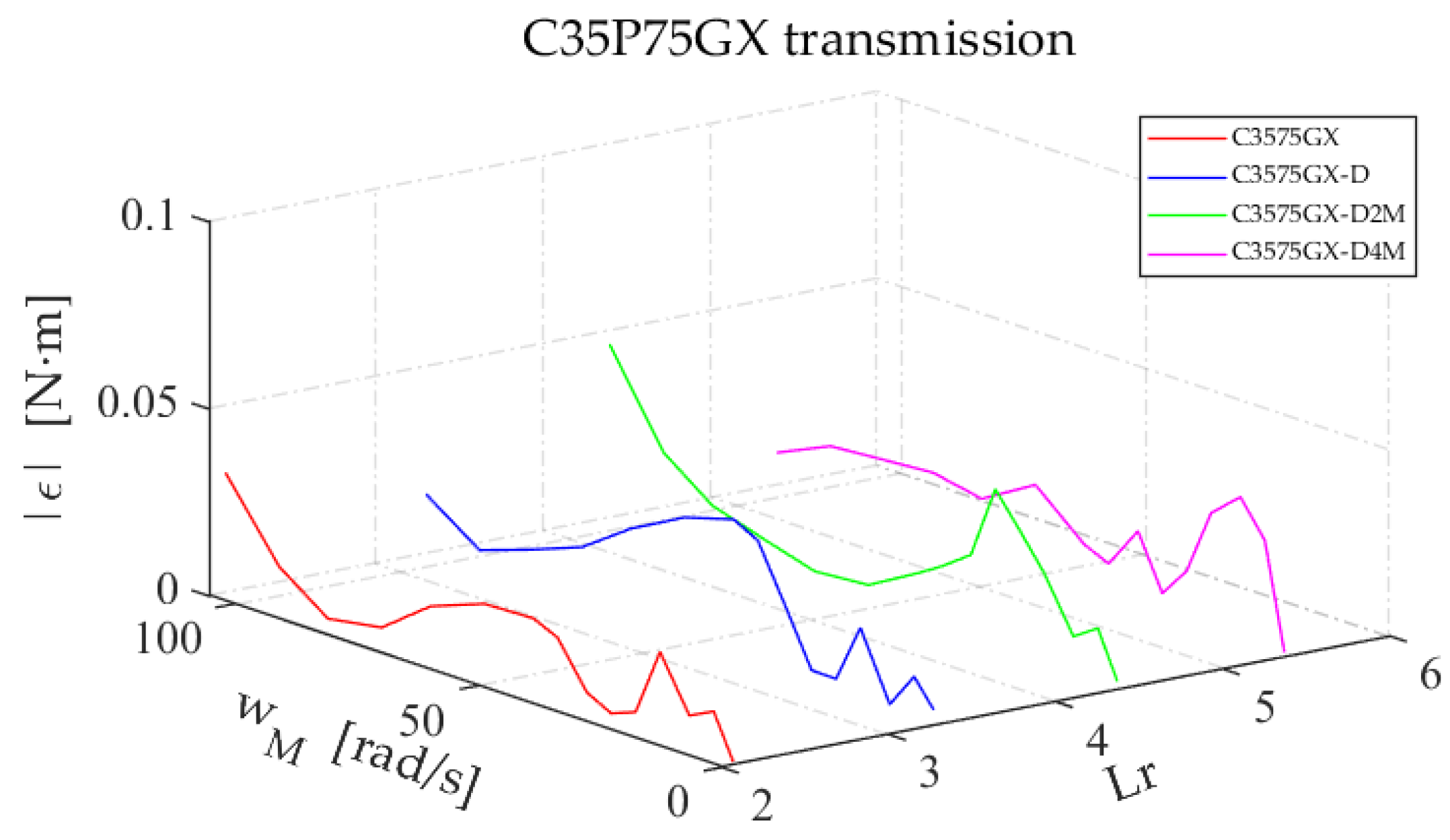
Figure 23.
Absolute error when using the model proposed for the C35P75GX configurations.
Figure 23.
Absolute error when using the model proposed for the C35P75GX configurations.
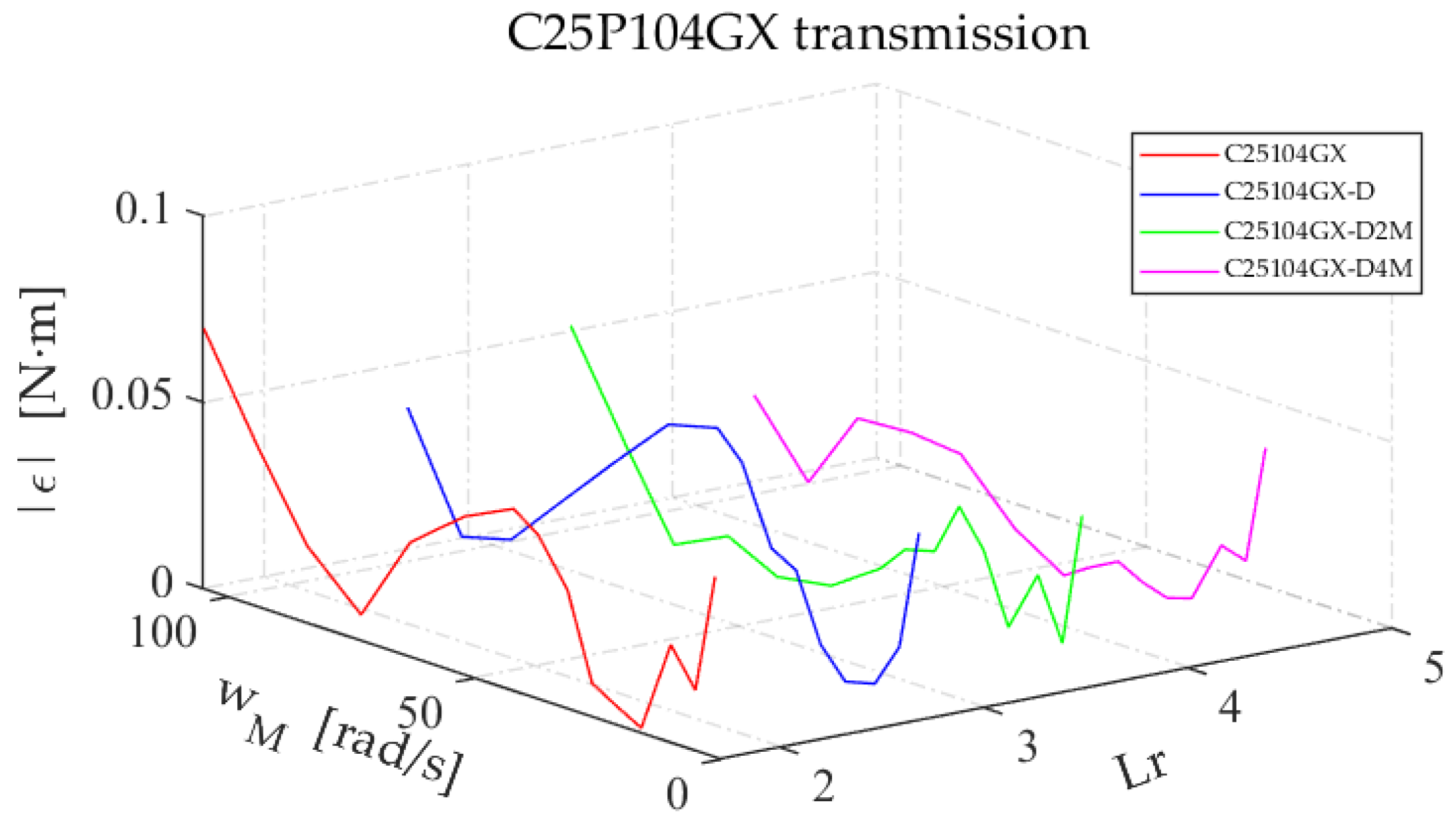
Figure 24.
Absolute error when using the model proposed for the C25P104GX configurations.
Figure 24.
Absolute error when using the model proposed for the C25P104GX configurations.
Table 1.
LuGre model parameters.
Table 1.
LuGre model parameters.
| Static Parameters |
| Coulomb friction |
| Static friction (stiction) |
| Viscous friction coefficient |
| Shape factor |
| Stribeck velocity |
| Dynamic Parameters |
| Stiffness of the bristles |
| Damping of the bristles |
Table 2.
Physical specifications of the transmission elements.
Table 2.
Physical specifications of the transmission elements.
| | Useful Length | Diameter | Weight | Inertia |
|---|
| | [mm] | [mm] | [N] | [kg·mm2] |
|---|
| Capstan 25 | 140 | 25 | 7.95 | 65.39 |
| Capstan 35 | 100 | 35 | 9.62 | 145.72 |
| Pulley 75 | 105 | 75 | 25.46 | 1769.15 |
| Pulley 104 | 140 | 104 | 23.49 | 4024.90 |
Table 3.
Transmission configurations evaluated.
Table 3.
Transmission configurations evaluated.
| Configuration | Capstan | Pulley | Thread | Disc | Masses |
|---|
| C25P104GP | 25 mm | 104 mm | P | No | 0 |
| C25P104GP-D | 25 mm | 104 mm | P | Yes | 0 |
| C25P104GP-D2M | 25 mm | 104 mm | P | Yes | 2 |
| C25P104GP-D4M | 25 mm | 104 mm | P | Yes | 4 |
| C25P104GX | 25 mm | 104 mm | X | No | 0 |
| C25P104GX-D | 25 mm | 104 mm | X | Yes | 0 |
| C25P104GX-D2M | 25 mm | 104 mm | X | Yes | 2 |
| C25P104GX-D4M | 25 mm | 104 mm | X | Yes | 4 |
| C35P75GX | 35 mm | 75 mm | X | No | 0 |
| C35P75GX-D | 35 mm | 75 mm | X | Yes | 0 |
| C35P75GX-D2M | 35 mm | 75 mm | X | Yes | 2 |
| C35P75GX-D4M | 35 mm | 75 mm | X | Yes | 4 |
Table 4.
Inertial specifications of the perforated disc and the additional masses.
Table 4.
Inertial specifications of the perforated disc and the additional masses.
| | Weight | Inertia |
|---|
| | [N] | [kg·mm2] |
|---|
| Perforated disc | 11.28 | 3790.2 |
| Disc and one pair of masses | 21.09 | 12,910.6 |
| Disc and two pairs of masses | 30.90 | 22,031.1 |
Table 5.
Dimensions of the capstans and pulleys.
Table 5.
Dimensions of the capstans and pulleys.
| Element | Dimensions [mm] |
| g | h | i | j | |
| Capstan 35 mm | 18 | 52 | 41 | 134 | |
| Capstan 25 mm | 18 | 80 | 60 | 195 | |
| | a | b | c | d | e |
| Pulley 75 mm | 30 | 31 | 31 | 32 | 139 |
| Pulley 104 mm | 30 | 70 | 46 | 20 | 190 |
Table 6.
Static parameters identified for the LuGre model (C35P75GX).
Table 6.
Static parameters identified for the LuGre model (C35P75GX).
| | | | α |
|---|
| 0.107 | 3.367·10−7 | 8.422 | 7.596·10−4 | 2 |
Table 7.
Static parameters identified for the LuGre model (C25P104GX).
Table 7.
Static parameters identified for the LuGre model (C25P104GX).
| | | | α |
|---|
| 0.112 | 1.405·10−4 | 7.360 | 7.161·10−4 | 2 |
Table 8.
Summary of errors of the proposed friction model compared to the LuGre model.
Table 8.
Summary of errors of the proposed friction model compared to the LuGre model.
| | Friction Moment (N·m) |
|---|
| Transmission | Measured | Proposed | | LuGre | |
|---|
| | Value | Model | Error | Model | Error |
|---|
| C35P75GXD | 0.1427 | 0.1268 | 11.1% | 0.1185 | 17.0% |
| C35P75GXD2m | 0.1728 | 0.1507 | 12.8% | 0.1168 | 32.4% |
| C35P75GXD4m | 0.2023 | 0.1740 | 14.0% | 0.1167 | 42.3% |
| C25P104GXD | 0.1700 | 0.1679 | 1.2% | 0.1226 | 27.9% |
| C25P104GX2m | 0.2030 | 0.1951 | 3.9% | 0.1226 | 39.6% |
| C25P104GXD4m | 0.2318 | 0.2260 | 2.5% | 0.1226 | 47.1% |