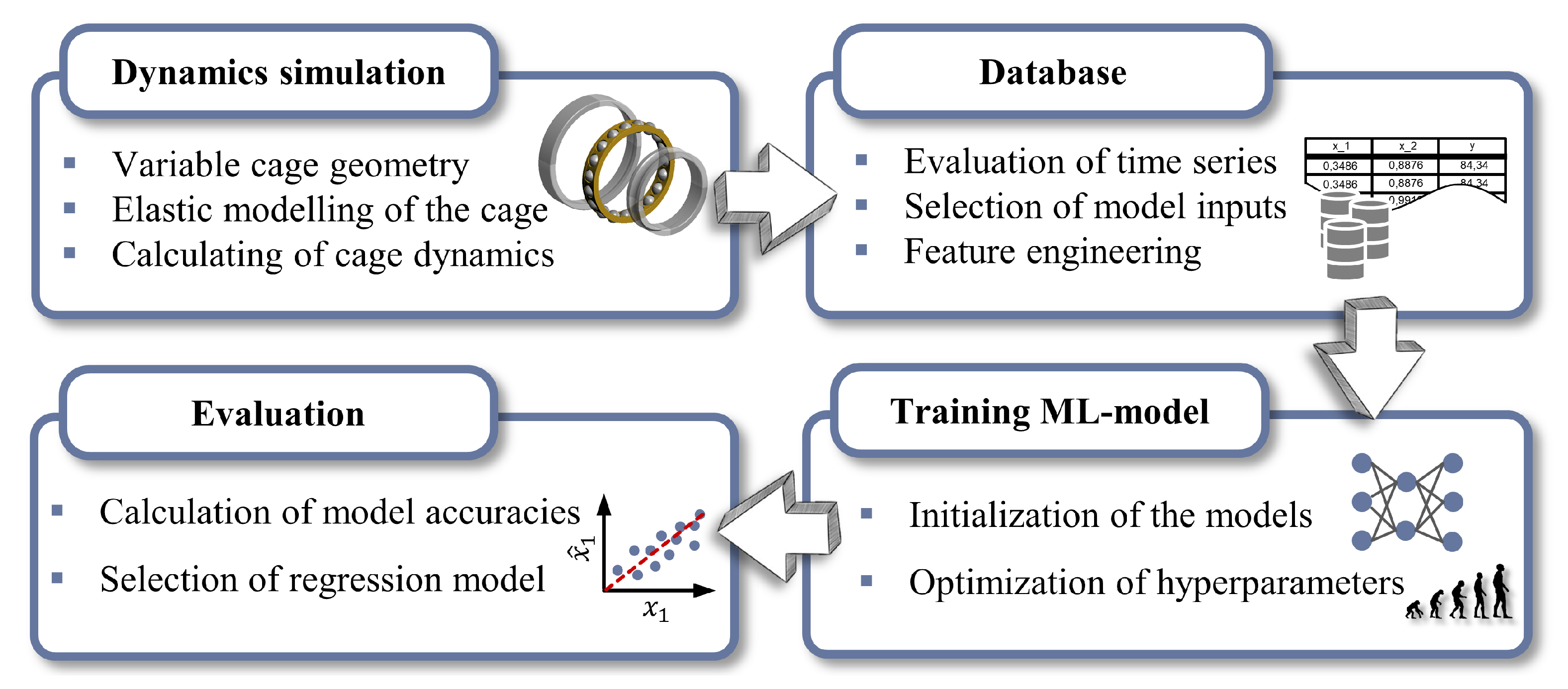
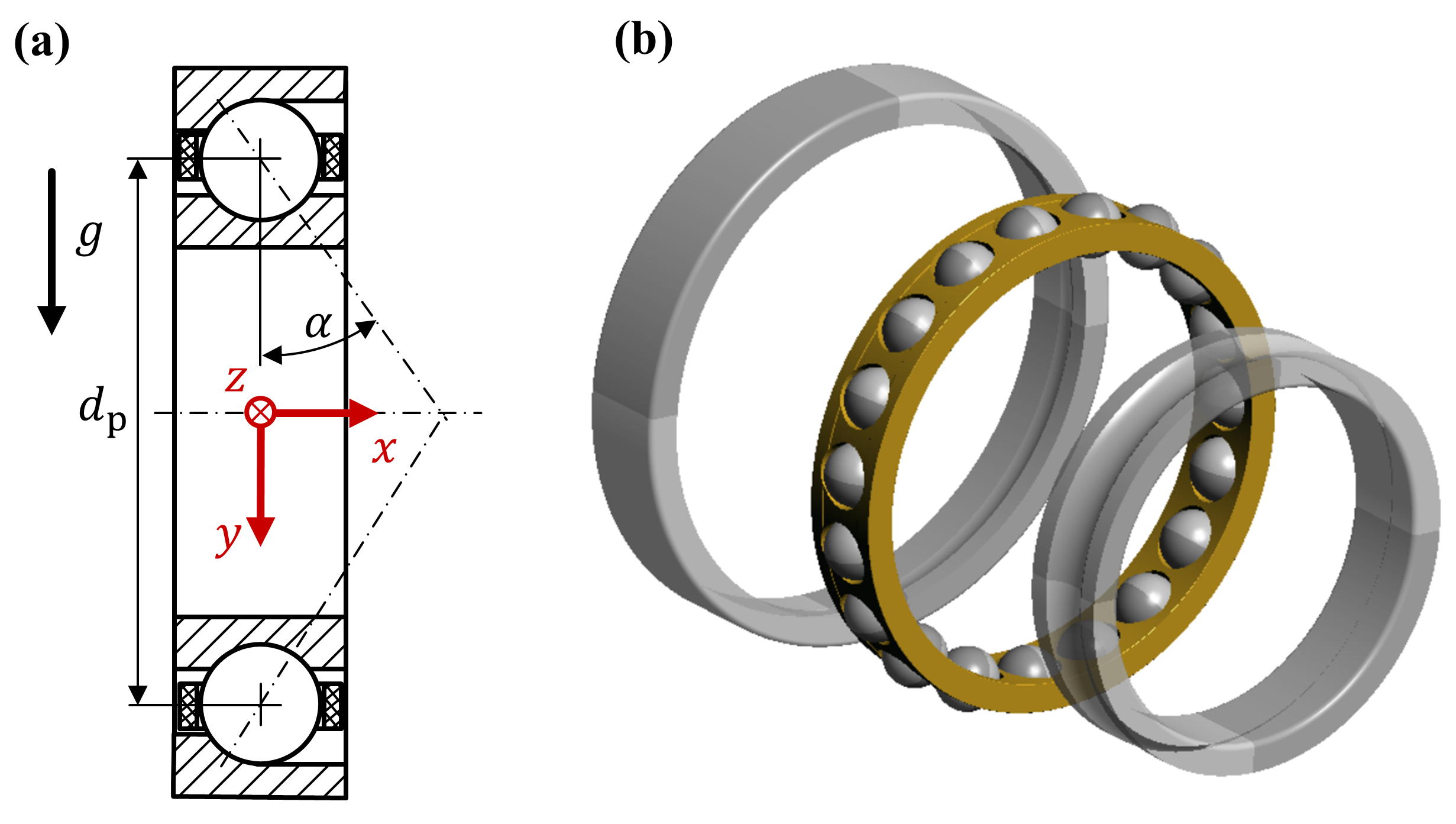
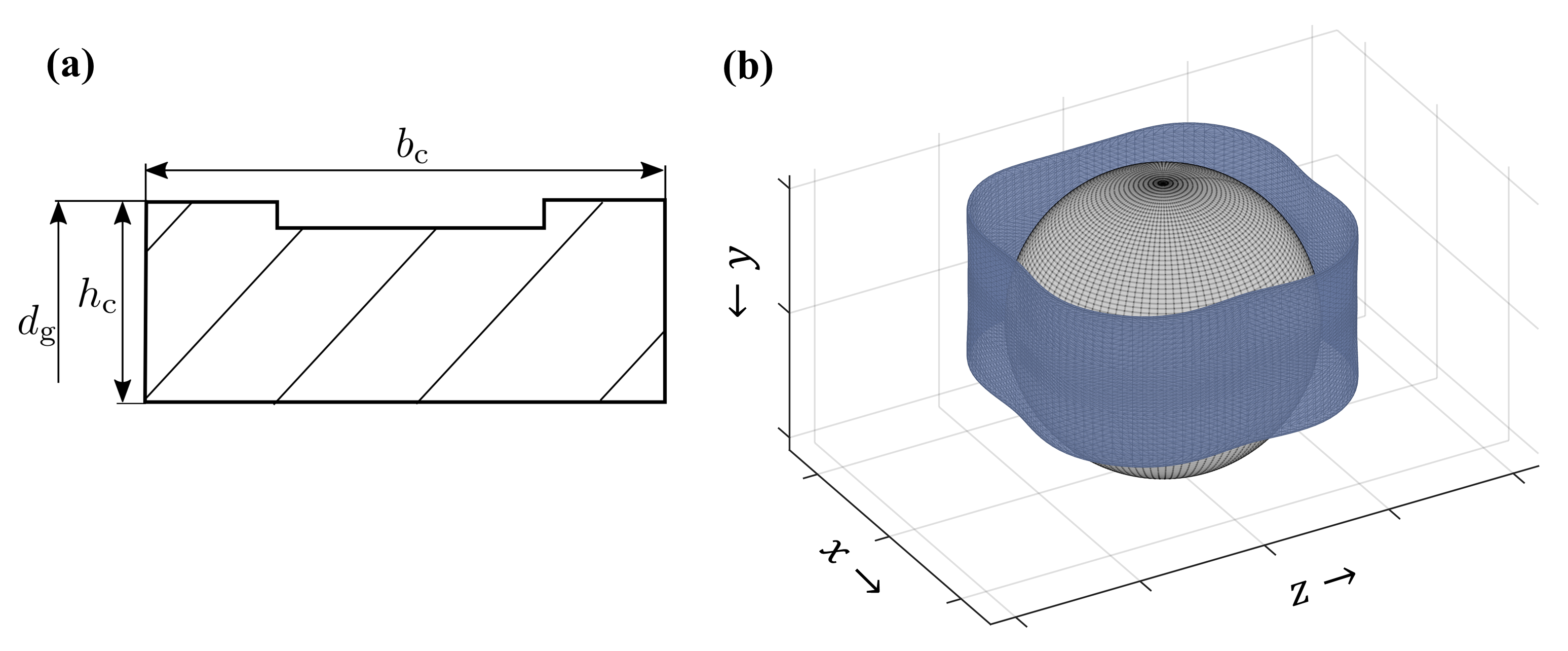
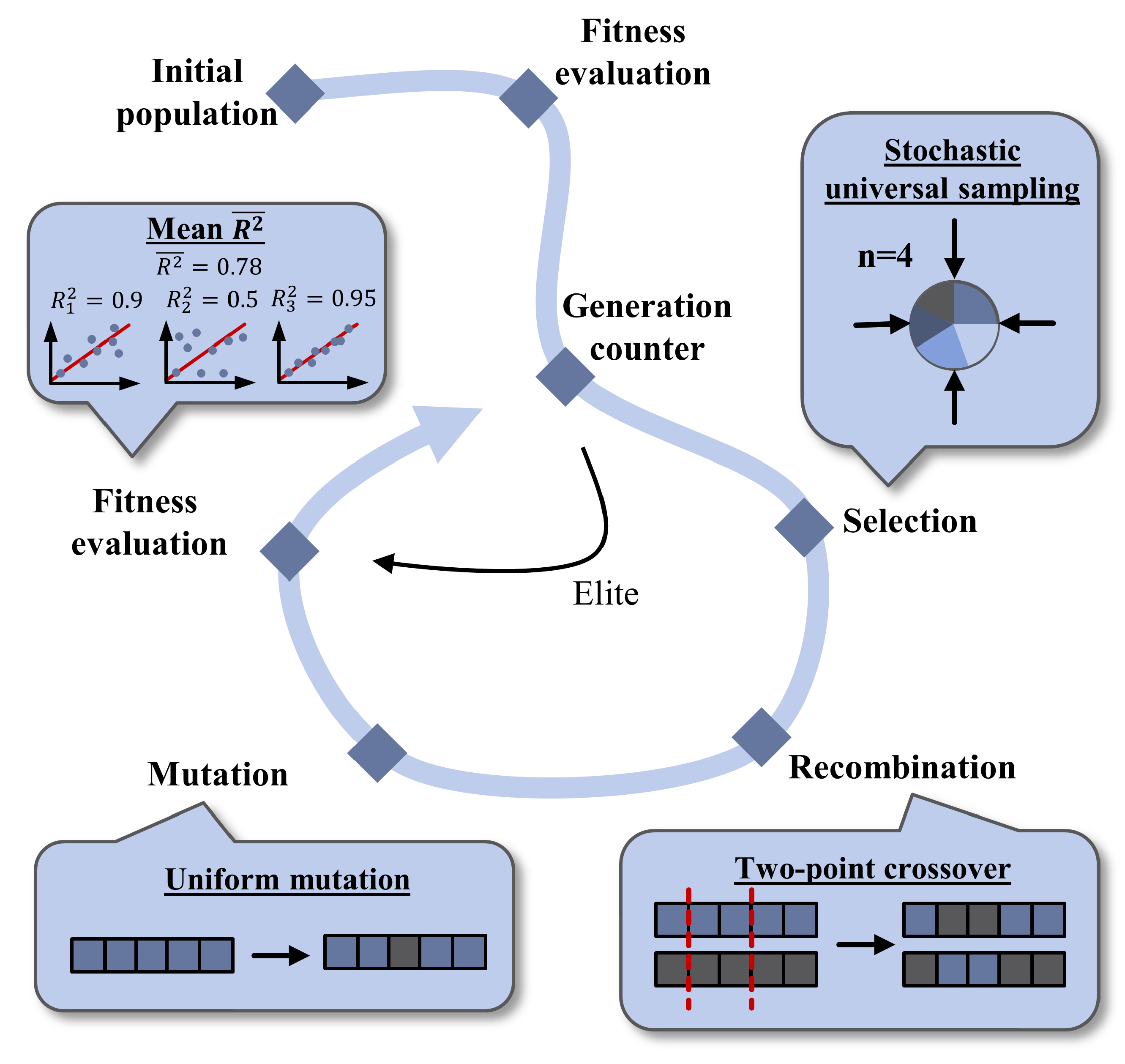
1. Introduction
The use of dynamics and noise behavior as criteria to assess the performance of a rolling bearing are coming into increasing focus besides the lifetime and energy efficiency. In addition to potentially negative health consequences of noise pollution [
1], one reason for this is the increasing electrification of passenger cars and the associated sensitivity regarding disturbing and unpleasant noise of all machine elements contained in the technical system [
2]. Besides unpleasant noise caused by bearing dynamics, in precision applications such as the bearing assembly of the main spindle of machine tools, vibration of the bearing can lead to a negative influence on manufacturing accuracy [
3].
The vibrations emitted by a rolling bearing may have various causes. Due to the rotation of the rolling element set, the force transmitting points between the inner and outer ring differ. This leads to a changing stiffness and to unavoidable vibrations of the rolling bearing caused by the design itself and is known as variable compliance [
4]. The characteristics of these vibrations differ depending on the rolling bearing type (geometry, number of rolling elements, and pitch diameter) and load conditions (operating contact angle and load zone). In addition to the geometry-related causes of vibrations in rolling bearings, production-related geometric deviations of the bearing rings or rolling elements, such as roughness, waviness, or surface damage (scratches and inclusions in the material), influence the radial displacement of the rings and can cause undesired vibrations [
5]. Thus, depending on the frequency of vibration occurring, isolated surface deviations can be assigned to the inner or outer bearing part based on the respective ball-pass frequency [
6].
The cage of the rolling bearing can also be a source of vibrations and noise. An example are highly dynamic cage movements, which are called “cage rattling” or “cage instability” in the literature and are associated with strong noise generation [
7,
8,
9]. The normal and frictional forces at the guiding surfaces accelerate the cage, so that certain operating conditions lead to a high-frequency motion and severe deformation of the cage [
10,
11]. These cage dynamics lead to a sharp increase in frictional torque [
8,
9,
12] and temperature in the rolling bearing [
8] and can have a negative effect on cage life due to severe deformations and component stresses. Cage dynamics depend on many influencing factors; an overview of previous research papers is provided in
Table 1.
The dynamic behavior of the cage depends on the bearing and cage properties as well as the operating conditions of the bearing. As the cage is (besides the rib contact) accelerated by the rolling elements contact, the dynamic behavior of the rolling elements has an influence on the cage motion. The kinematics of the rolling elements is affected by various factors, such as the bearing load and speed, the friction in the contact to the raceway, the rolling element geometry and the bearing clearance. However, these parameters are determined depending on the intended application with focus on bearing lifetime and accuracy of shaft guidance. The influence of the bearing design and load on the cage dynamics during the application is not usually in the focus in the bearing selection. Therefore, the cage dynamics must be adjusted by adapting the cage geometry in the available design space of the selected bearing. By varying the cage geometry, properties such as the pocket and guidance clearance, the mass inertia and stiffness, and the shape of the cage pocket are affected. By defining the cage properties, the dynamics can be adjusted, for example, to avoid unstable cage movements or to minimize the friction loss caused by the cage as well as the robustness against shock loads.
The influencing parameters on the resulting cage dynamics can be named in general, but the quantification of their effects is only partially known so far. There are two primary reasons for this. First, the calculation using numerical computer simulations or the measurement of the cage dynamics (motion, forces, or deformation) on a test rig are time consuming and complicated. In particular for experimental tests, the range of influencing parameters that can be investigated is usually limited. Second, the interaction of the influencing variables is complex, so that it is not possible to determine the influence of the individual effects directly on the basis of the observed dynamics. Cage instability, for example, is caused by high frictional forces in the cage contacts and high rotational speeds of the bearing [
14]. If one of the two parameters is low, the probability that highly dynamic movements will be excited is reduced. In addition to this example, other interactions can be found, making it more difficult to determine the cage dynamics depending of the influencing factors such as cage geometry and bearing load.
Machine learning methods are suitable for identifying complex patterns and relationships in the data provided. The application of machine learning algorithms in the field of tribological problems is increasing, especially in recent years. A comprehensive overview of the use of machine learning for tribological problems was provided by Marian and Tremmel [
20]. Based on experimental test results, calculations, or information collected from the literature, regression methods are used to predict typical tribological behavior in the form of temperature, specific wear, or coefficient of friction. In addition to applications at the nano or micro scale, machine learning methods are also used at the macro scale, such as in bearing technology. Schwarz et al. used an ensemble classification model to determine the dependence between geometric parameters and load of a rolling bearing and the resulting dynamics of a cage. The result of the classification was one of the classes “unstable”, “stable”, or “circling” that were used to assess the qualitative behavior of the cage [
21]. By extending this approach with a regression algorithm, not only the cage motion class but also the resulting forces on the cage or the acceleration of the cage can be estimated.
In previous research investigations [
21], it was possible to quantify the dynamics of the cage for different operating conditions, but this was usually completed in isolated cases within the framework of complex numerical calculations or tests. A method for the time-efficient estimation of the quantitative dynamic behavior of rolling bearing cages for certain cage properties and rolling bearing loads is not yet available. The aim of this paper is to present a procedure for predicting the dynamics of a rolling bearing cage in an angular contact ball bearing using dynamics simulations and regression machine learning algorithms. This enables time-efficient estimation of the dynamics for the intended application during the development and selection of rolling bearing cages and also for operating conditions that are not directly included in the training data.
3. Results
3.1. Dynamics Simulation Results
The results of the dynamics simulations contain time series that include dynamics of the cage as well as the rolling elements.
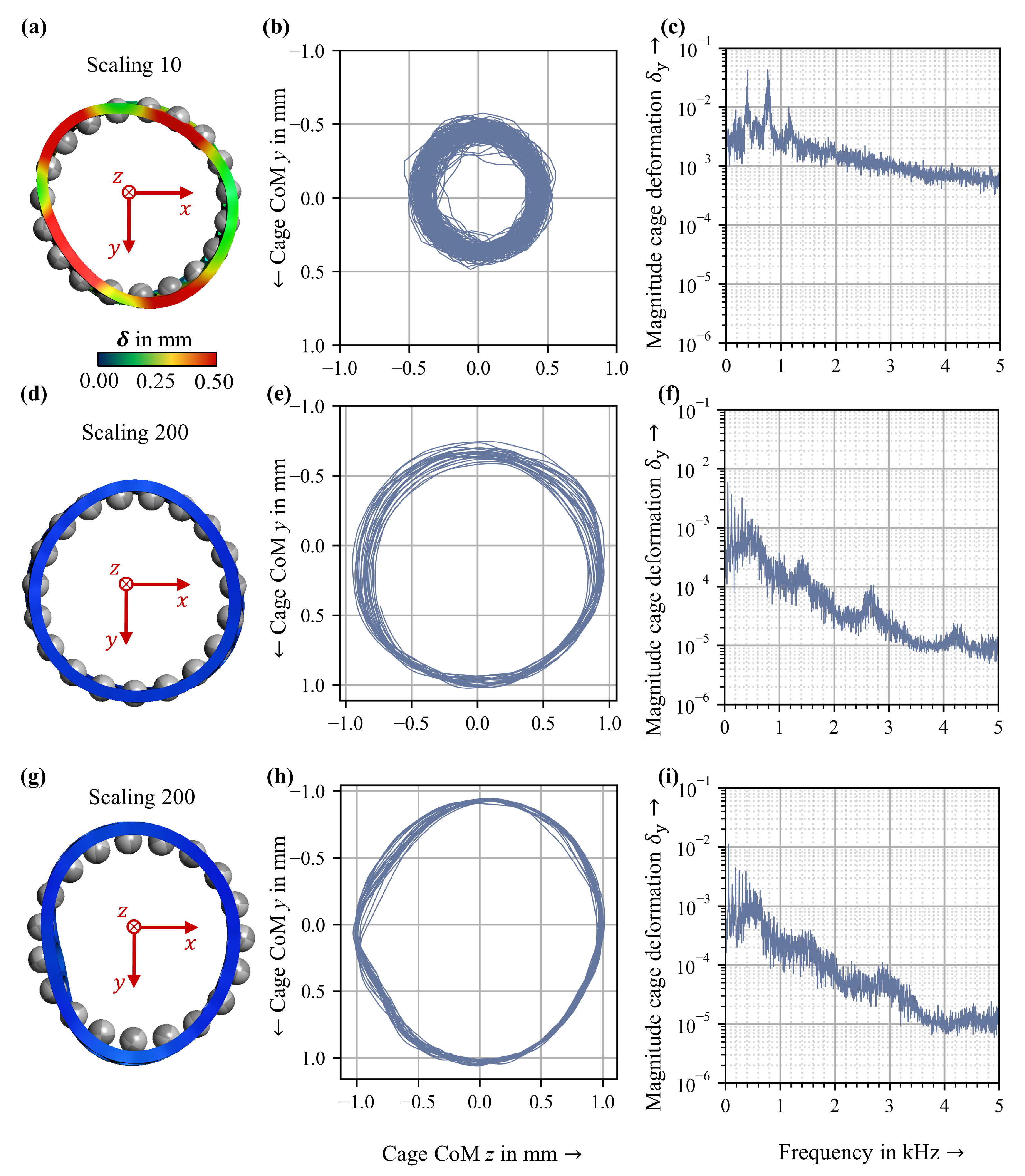
Figure 5 shows an example of the dynamic behavior of a cage for different operating conditions of the bearing. In the qualitative assessment of cage dynamics, a fundamental differentiation is made between “unstable”, “stable”, and “circling” cage motions [
21,
34]. These types of movements could also be observed for the cages investigated.
Figure 5a–c illustrates an example of an unstable cage motion (loading conditions
,
N,
N,
rpm
Nm), that is characterized by high dynamics as well as severe and high-frequency cage deformations. The cage was pressed against the outer ring and strongly deformed. This led to the diameter of the circular center of gravity trajectory being significantly larger than in the other two calculations. In addition, high contact forces caused frictional losses, which significantly impair the energy efficiency of the rolling bearing. In the case of stable cage motion (loading conditions
,
N,
N,
rpm
Nm), no significant deformations occurred and the dynamics of the cage were generally low, see
Figure 5d–f. The contact forces between the cage and the rolling element and outer ring were also significantly reduced compared to an unstable motion, and therefore the frictional losses were also lower. The circling cage motion (loading conditions
,
N,
N,
rpm
Nm) is characterized by a circular motion of the cage center of mass that exhibits small variations in the rotational speed. The rotational speed of the cage center of mass corresponds to the speed of the rolling element set. The cage is pressed in a radial direction due to the centrifugal force acting, so that the number of contacts to the guidance rib and the contact force acting in the contact increase.
In addition to the load on the bearing, the geometry of the cage can also influence the dynamic response of the bearing.
Figure 6 shows the cage dynamics for a load situation (
,
N,
N,
rpm
Nm) and three different cage geometries. The first cage variant performed a highly dynamic cage motion with severe deformations and a high rotational speed of the cage center of mass, see
Figure 6a–c. A modification of the cage geometry (cross-section and shape of the cage pocket) for the other two variants and the same operating conditions led to circling cage motions in both cases. The amplitudes of the deformations were significantly smaller compared to the first cage variant and the larger amplitudes were shifted to the low frequency range, see
Figure 6d–i.
An overview of the simulations performed and the resulting cage motion types is shown in
Figure 7. Certain cage geometries (ID 02 or 05) had a high proportion of unstable cage motions, while other cage variants exhibited a much lower tendency to unstable cage motions (ID 14 or 10). In addition, differences in the proportion of circumferential and stable cage movements were also evident for the different cage variants. The dynamic behavior of the cage variants illustrates the potential of the geometry parameters to positively influence the dynamics of the cage. A clear influence could also be identified in the loading conditions, as was found, for example, by Schwarz et al. [
14]. However, as the operating conditions often cannot be influenced, these serve only as a reference for comparing the dynamic behavior of the cage geometries.
The simulation results were further processed so that the influence of cage geometry and bearing load was represented by a database consisting of input and target variables and could be used for machine learning.
3.2. Preprocessing of Calculation Results and Data Analysis
The calculated time series were the starting point for determining the targets for machine learning. For the evaluation of the cage dynamics, the time range s was analyzed to avoid unrepresentative cage motions due to the initial conditions at the beginning of the calculation.
In addition it was checked whether the simulation results are suitable to be integrated into the database. Especially for simulations with high friction coefficients, a severe deformation of the cage occurred, which led to a termination of the simulation. Nonphysical results as the automatically generated inputs are out of a reasonable range for this application and were removed from the database. Using the density-based LOF approach, outliers in the database could be identified and removed. The LOF approach was applied to each of the classes “unstable”, “stable” and “circling”. Outliers with respect to the dynamic behavior typical for the respective classes were thereby identified.
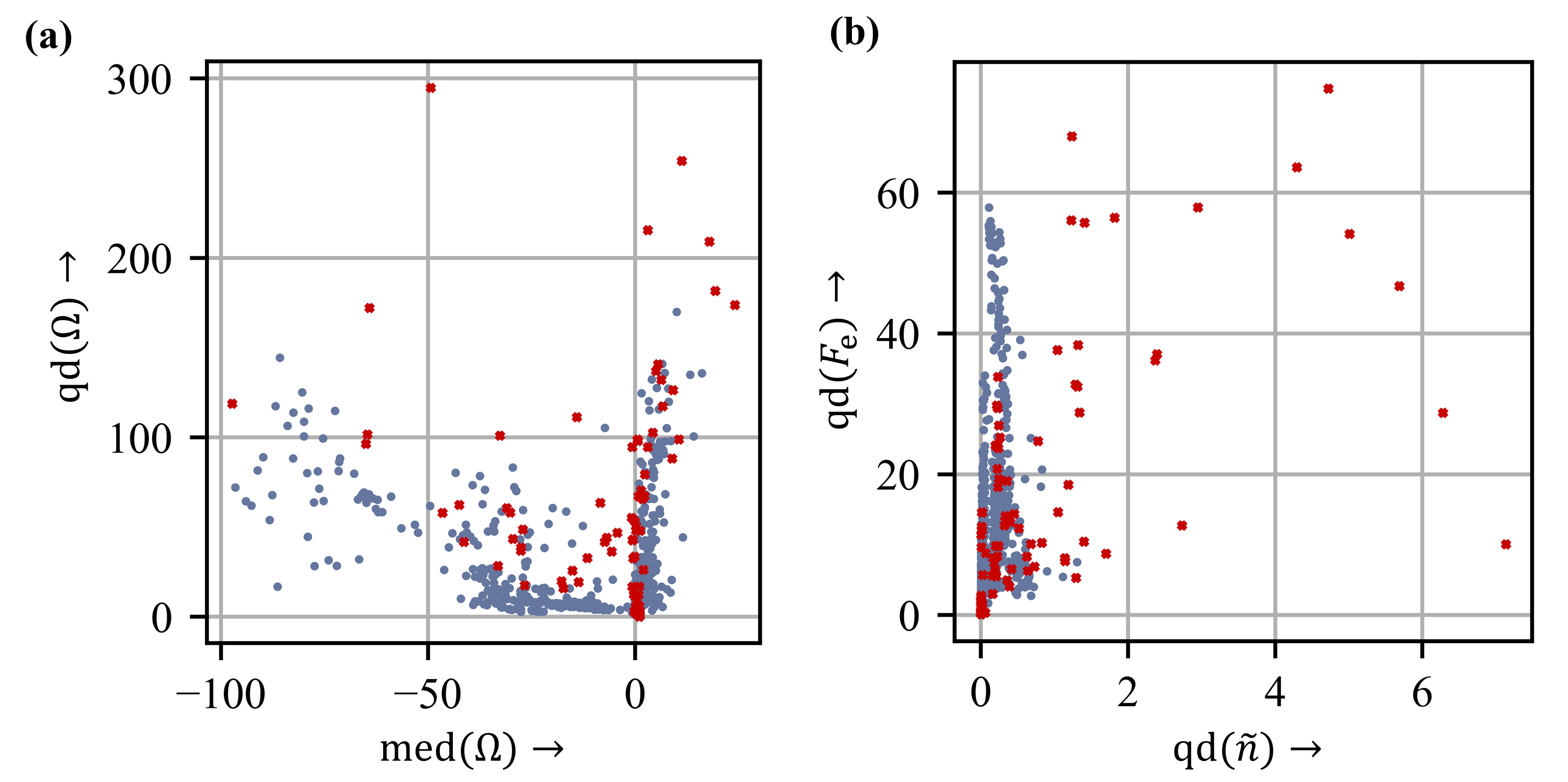
Figure 8 illustrates the outliers (red) and the remaining datasets (blue). Outlier detection reliably removed atypical cage movements, ensuring a high-quality database for machine learning. After preparing the simulation results, the database for machine learning contained a total of 1362 data sets.
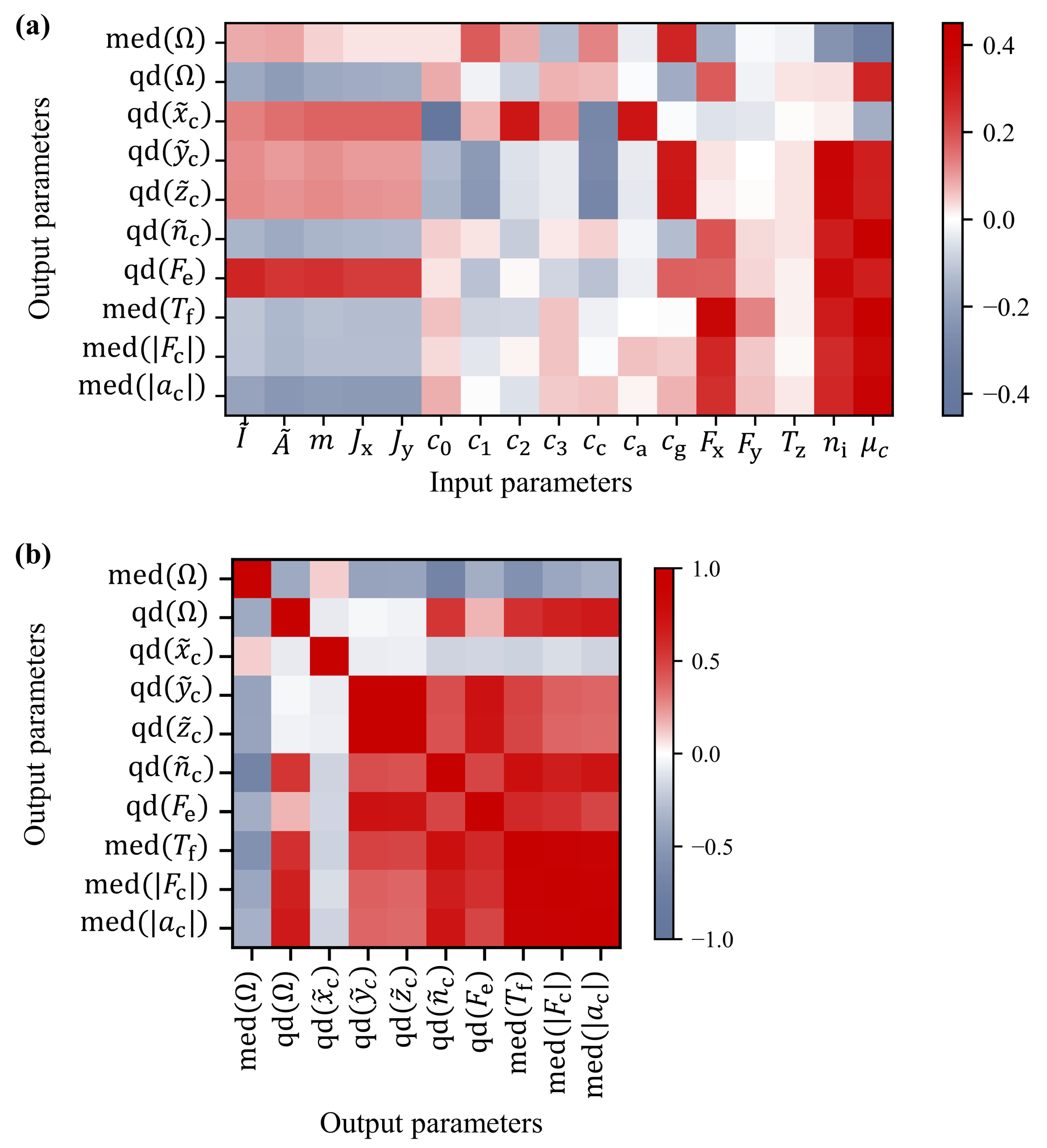
Figure 9 shows the correlation matrix for determining the qualitative relationship between input and output parameters. The mechanical properties of the cage (area moment of inertia
, mass
m, area cross section
, and moment of inertia
J) had similar values for the correlation coefficient and thus a related influence on the target parameters, see
Figure 9a. A mathematical negative correlation existed between the mechanical properties and the center of mass acceleration of the cage
. Accordingly, lower accelerations occur at higher masses of the cage, which can be justified by the inertia of the geometry. There is also a positive correlation between the cage mass and the equivalent force
representing the deformation of the cage. Thus, for the cages with larger masses, the equivalent deformation force tend to be larger. With respect to the bearing speed
and friction coefficient
, a mathematical positive correlation to cage acceleration, contact forces, and finally a highly-dynamic cage movement could be clearly determined. This is due to the increased relative velocity and frictional force in the contact between the cage and the other components, which leads to a stronger excitation of the cage and an increased tendency to highly dynamic movements.
Based on the matrix in
Figure 9b, a mutual correlation of the output parameters was also evident. Highly dynamic cage movements are characterized by strong deformations of the cage, high accelerations, and a high frictional torque, for which reason these parameters exhibited a strong correlation. Due to the opposite movement of the center of mass in the case of unstable cage dynamics, there is a mathematical negative relationship between the median of the
-ratio and the other parameters. The weak relationship of the normalized
-coordinate of the cage to the other target quantities is also noticeable. The contact forces between the cage and the rolling element/rib point primarily in radial direction, which is the direction of the resulting acceleration. Therefore, the correlation between the quantile distance of the two non-axial coordinates is more significant, especially in the case of an unstable cage motion. The quantile distance of the
-ratio also indicates a slightly lower correlation to the other parameters, but still stronger than the quantile distance of the
-coordinate of the cage center of mass.
Although there were trends based on the correlation matrix that suggest the resulting dynamic behavior of the cage, the relationship is highly nonlinear due to interactions between the parameters. Therefore, the regression algorithms are trained in the following to learn the relationship between input and output parameters.
3.3. Evaluating Optimization and Regression Results
The EA determined the hyperparameters of the models to maximize the average coefficient of determination for the validation data sets. The best individuals or parameter combinations are shown in
Table 7. A large number of neurons, or many estimators in the ensemble methods, increase the adjustable model parameters, the risk of overfitting to the training data, and poor prediction accuracy for test data. However, the hyperparameters causing overfitting were not chosen by the optimization to maximize the number of model parameters to reach high values for the prediction accuracy based on the training data. In general, this is a first indication that a generalization capable model was created by the training and optimization.
The hyperparameters optimized by the EA were used for training the algorithms. Afterwards, the models were evaluated using the coefficient of determination
for test and training data, see
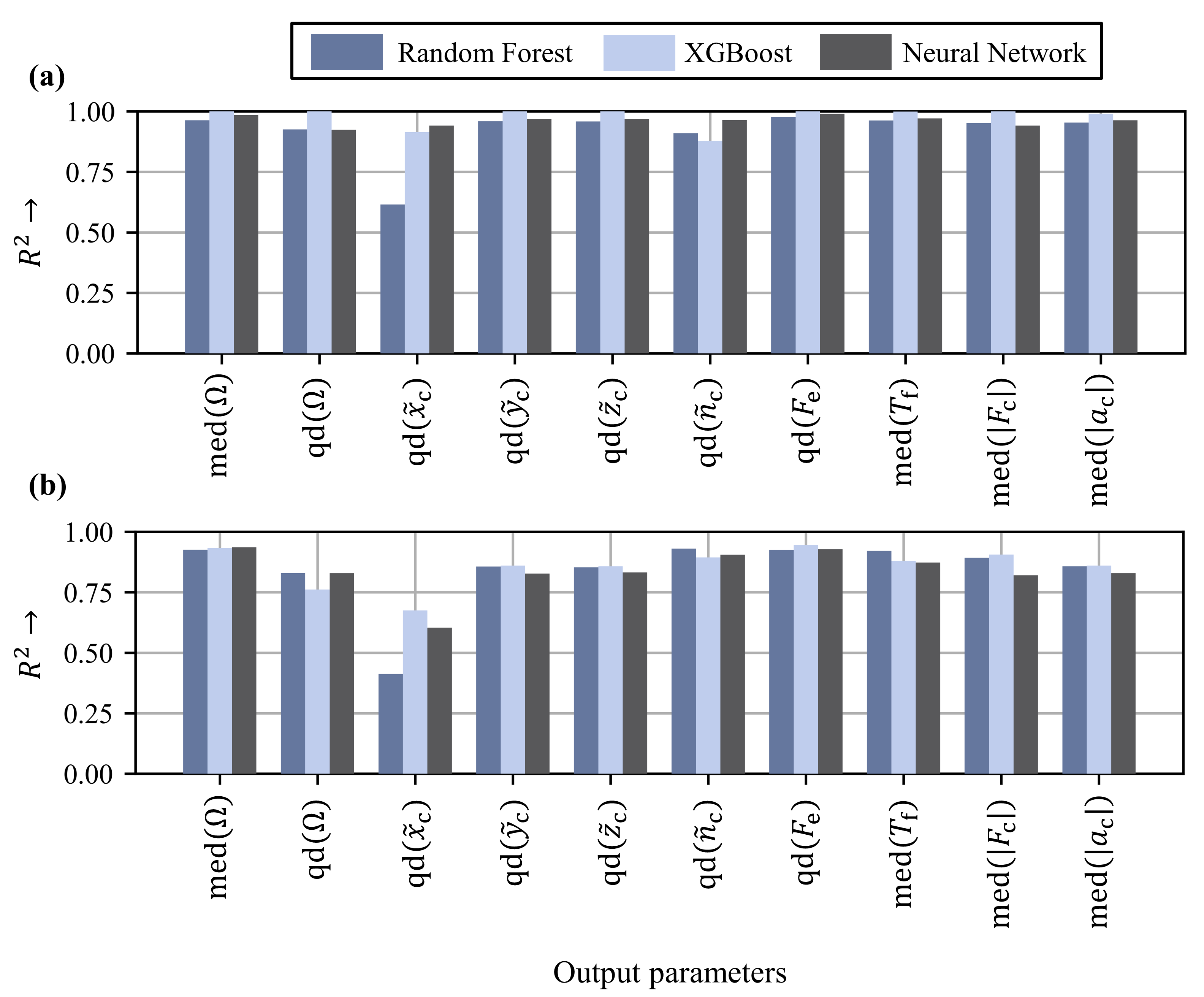
Figure 10. For the training data, acceptable values for
were obtained for all algorithms. The quantile distance for the normalized
-coordinate of the cage reached
in the case of the random forest regressor, which is to be assessed as a medium correlation. The excitation of the cage, as well as the translational center of mass movement, occurs both for the contact of the cage to the rolling elements and to the rib in the radial direction. The relationship between the geometry and load parameters as well as the axial center of mass movement and finally the
of the predictions were therefore lower compared to the other center of mass coordinates. Random forest regressor predicted very well for all target values, but reached a slightly lower
compared to XGboost and the neural network for training data. The random components in the random forest algorithm (e.g., feature selection) prevent possible overfitting to the training data and led to slightly inferior prediction. The coefficients of determination
for XGBoost were very high and indicate a significant fit to the data sets.
The test datasets generally showed a lower coefficient of determination than the training datasets but were within an acceptable range apart from the quantile distance of the normalized coordinate of the cage. qd() exhibited the worst values of for the random forest and the ANN. Thus, while qd() is suitable for assessing cage dynamics when derived from calculated time series, there is no strong correlation to bearing load or cage geometry. The difference in prediction accuracy for training and test data was lowest for random forest, which indicates a generalization of the model. However, the difference for XGBoost and the ANN was also in an acceptable range, which is also a sufficient generalization capability. All models reached comparable values for the coefficient of determination based on the test data sets and thus can be used equally for the prediction of cage dynamics. The best prediction values for based on the test data sets were obtained for the quantile distance of the equivalent deformation force , the median of the -ratio and the median of the friction torque in the range of . For the remaining target parameters, with the exception of qd(), at least one of the models investigated achieved a coefficient of determination and sufficient prediction accuracy.
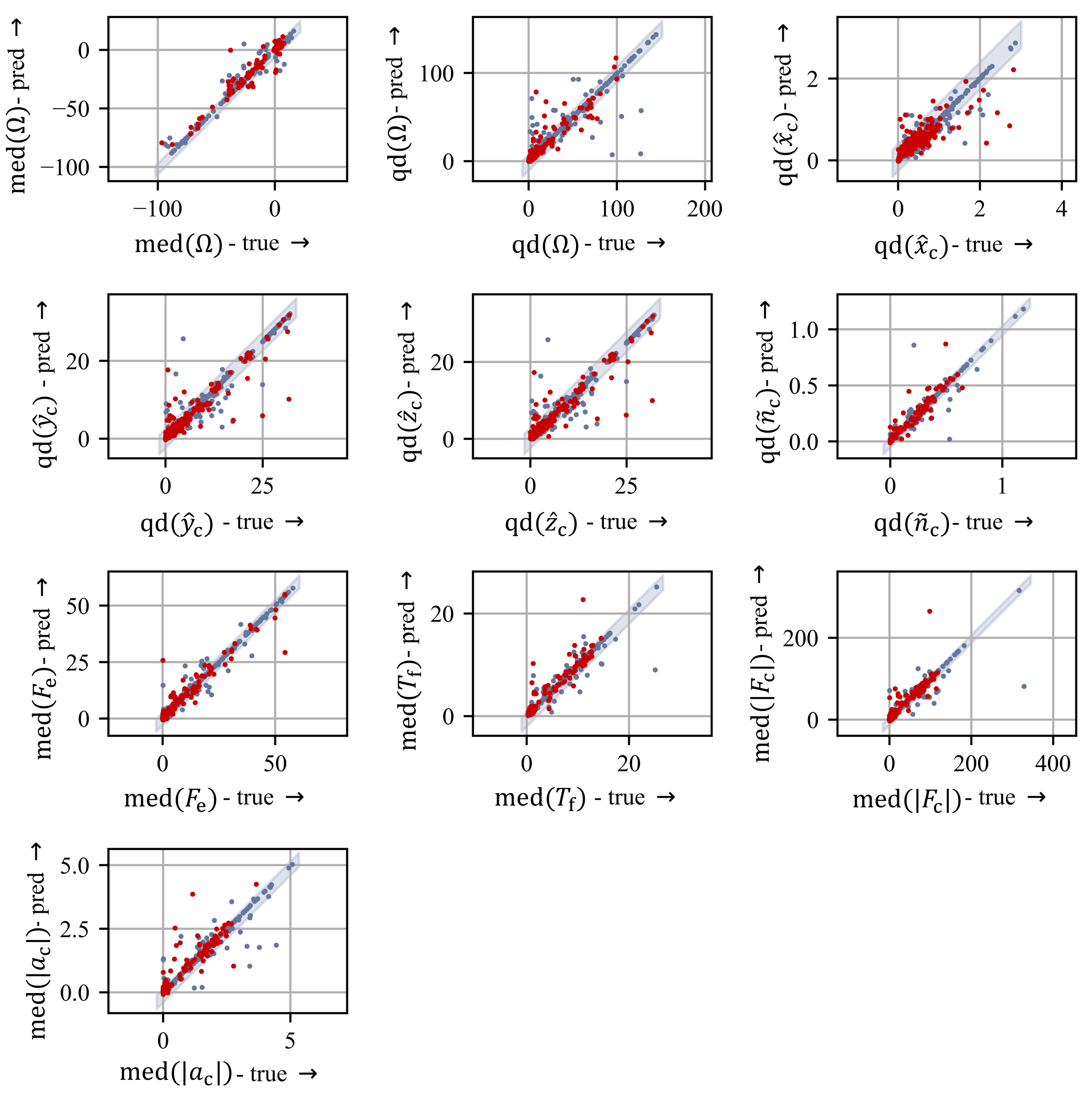
The scatter plot in
Figure 11 shows, representative of the trained models, the predictions of the ANN compared to the true values in the training (blue) and test (red) data. As can be seen from the correlation matrix and the coefficient of determination, the predictions for the quantile distance of the axial coordinate of the cage qd(
) were considerably more scattered than the other target variables. For the quantile distance of the omega ratio, the deviation of the predictions from the test data sets was smaller, but a stronger, though still acceptable, scatter was also present here. For the remaining parameters, a good correlation was present, analogous to the
. The deviations are within a tolerable range, as can be seen by the intervals containing 90% of the errors determined for the test data (blue area).
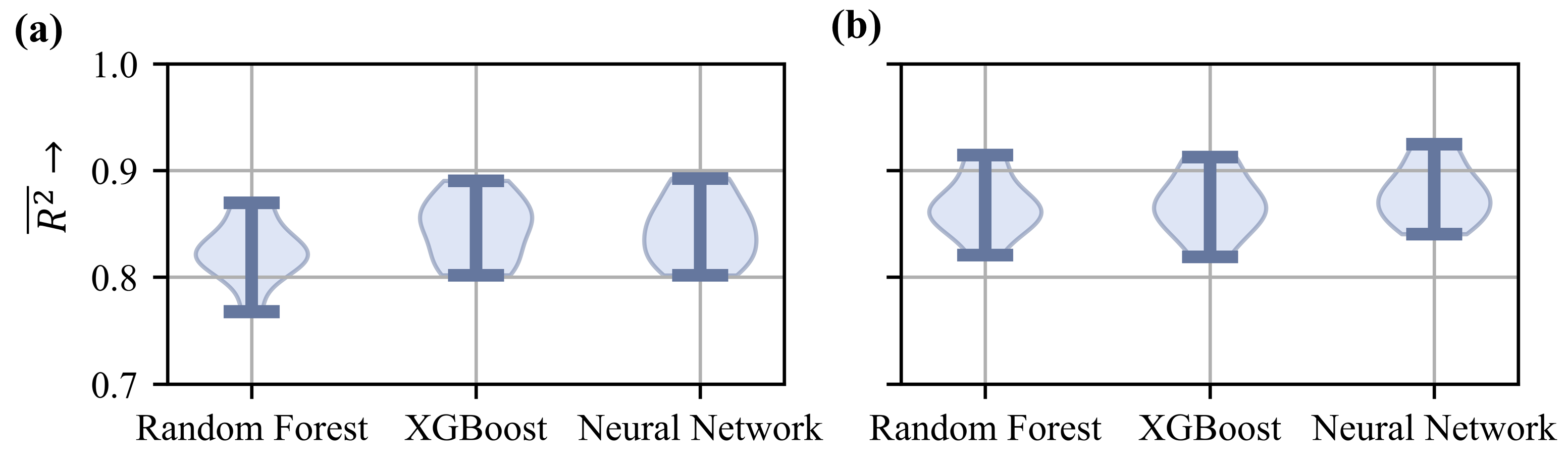
The hyperparameters obtained from the optimization by the EA were used to perform a 10-fold cross-validation. This allowed us to determine how strong the predictions of the algorithm differ depending on the used training and test data set, see
Figure 12. Based on this, the sensitivity of the prediction results for different training and test data sets could be investigated.
Figure 12 exhibits the distribution of the average prediction of the target values for the training data and a 10-fold cross-validation including (a) and excluding (b) the quantile distance of the cage coordinate
as regression target. For all three models, omitting the normalized coordinate improves the average prediction quality, as lower
values are obtained for qd(
) than for the other values in all iterations of the cross-validation. The minima and maxima of
for the three models without considering
in the cross-validation were very similar and differ only slightly. As no obvious favorite could be identified based on the prediction accuracies, all three algorithms were suitable for predicting the cage dynamics with a comparable error tolerance.
4. Discussion
The results of the dynamics simulation illustrate the strong influence of the bearing load and cage geometry on the resulting cage dynamics, see
Figure 7. Depending on the geometry, the tendency of a cage to highly dynamic and unstable cage movements varies significantly. However, the relationship between the geometry parameters and the resulting cage dynamics is very complex and difficult to determine using conventional methods of descriptive statistics, as can be seen from the covariance matrix in
Figure 9. The complex relationship between the input and output parameters can basically be determined with the help of the investigated algorithms. Analyzing the prediction results for test data, it can be seen that for the quantile distance of the normalized center of mass coordinate
of the cage, mediocre prediction values could be obtained. As the frictional forces acting in contact between the cage and the other components accelerate the cage primarily in the bearing plane, the physical relationship between the input parameters of the model and the resulting axial cage motion is less than for the other parameters. The normalized
coordinate of the cage is thus less suitable for predicting the cage dynamics. Though, as a component of the multivariate metric CDI, which can be derived from calculated time series representing cage dynamics,
is a contribution to improve the classification performance.
The algorithms Random Forest, XGBoost, and ANN achieved similar values for the
of the different target variables for the test data sets, see
Figure 10. A 10-fold cross-validation exhibited that the differences between the models are small, and thus all algorithms are suitable for the prediction of the cage dynamics. The robustness of the predicted targets for a given cage geometry with respect to deviations from the true values can be improved by a large number of predictions by the regression algorithm with a subsequent statistical analysis. This reduces the influence of single incorrect predictions and improves the comparability of the dynamic behavior of different cage variants.
A transfer of the predictions to other rolling bearing sizes is possible in general. For this purpose, new training data must be generated and the existing database expanded. However, a similar effect on the cage dynamics can be expected, especially for the load conditions as shown, for example, by Schwarz et al. for various bearings [
14,
21]. Therefore, the amount of training data for the same bearing type and similar cage shapes can probably be lower than for the investigated angular contact ball bearing. In addition to the extension to other bearing types, other parameters can also be added as input variables, so that depending on the existing application, the model can also be designed flexibly. As with the geometry parameters, new data sets must be created for the training, but the database established so far serves as an initial starting point for further investigations.