Abstract
The primary task of rotary shaft seals is to prevent an unwanted fluid transfer between two areas. In shaft passages of gearboxes, for example, rotary shaft seals avoid the leakage of transmission oil to ambient air. This means the flow in the lubricant film in the sealing gap between the sealing edge and the shaft surface consists of at least two phases. Taking the phenomenon of cavitation into account, the flow consists of three phases. This study aims to provide an in-depth understanding of the multiphase flow in the lubricant film of rotary shaft seals. As experimental studies of the flow processes on a microscale have proven to be quite difficult, a simulation-based approach is applied. Computational fluid dynamics (CFD) serves to compute the transient multiphase flows in the lubricant film in the sealing gap. The computational domain is a three-dimensional microscale model of the lubricant film. The results show the transient hydrodynamic pressure buildup and the dynamic phase interactions during operation. This study provides far-reaching insights into the multiphase flow processes in the lubricant film in the sealing gap and simulation-based evidence of the lubrication and sealing mechanism of rotary shaft seals.
1. Introduction
Rotary shaft seals, according to [1,2], are widely used sealing systems in many technical applications. As summarized in [3], the basic task of sealing systems is to separate two areas to prevent a free exchange between the fluid to be sealed and the ambient fluid. Thus, according to [4], they represent a tribological system consisting of the sealing element, the counter body, the fluid to be sealed, and the ambient fluid. Figure 1 shows the basic structure of the tribological system rotary shaft seal. The sealing element is the elastomeric sealing ring, the counter body is the sealing counter face on the shaft, the fluid to be sealed is commonly oil, and the ambient fluid is air. In the dynamic state, the rotary shaft seal forms an active sealing mechanism. More detailed descriptions of the physical operating principles and operating hypotheses explaining the active sealing mechanism can be found among others in [5,6].
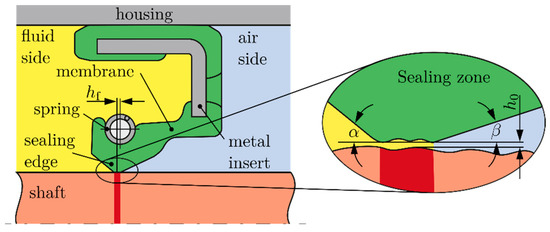
Figure 1.
Elastomeric sealing ring in the sealing system of a rotary shaft seal.
When the shaft rotates, the sealing edge lifts in the sealing zone, causing a thin lubricant film to be built up in the sealing gap between the sealing edge and the shaft surface. As a result, there is no solid boundary between the fluid to be sealed and the ambient fluid, leading to a phase interaction. Assuming that the fluid to be sealed is oil and the ambient fluid is air, and taking the phenomenon of cavitation into account, this results in a multiphase flow in the sealing gap consisting of oil, oil vapor, and air.
To date, there is a lack of studies dealing with the transient multiphase flow of rotary shaft seals. In [7,8,9] models for the prediction of the position of the oil meniscus on the air side, the film height, the cavitation zones, and the pressure distribution are presented. The transient formulation of the Reynolds equation is applied here to solve the hydrodynamic behavior of the lubricant. The Jakobsson–Floberg–Olsson (JFO) model, according to [10,11], provides a solution to the cavitation phenomenon. The fluid properties of the secondary phase air are neglected. Simplified models serve to consider the surface roughness. The Reynolds equation is usually used to solve the fluid dynamics of rotary shaft seals. This is opposed by studies [12,13] which question the general validity of the Reynolds equation to these tribological problems. With increasing computational performance, the complete solution for the Navier–Stokes equations becomes even more common in the computation of the fluid dynamics of rotary shaft seals. For example, Yang et al. [14] used computational fluid dynamics (CFD) to analyze the flow field around a ribbed helix lip seal. Keller et al. [15] optimized the microstructures on rotary shaft seals by applying CFD.
This paper deals with the numerical implementation of and solution to the transient laminar multiphase flow in the lubricant film in the sealing gap of rotary shaft seals. CFD is used for this purpose. The inputs are fluid properties that depend on various operating conditions and surface measurement data of sealing edge surfaces. This will provide a detailed insight into the flow processes in the sealing gap and lead to an in-depth understanding of the active sealing mechanism.
2. Methods and Materials
In this study, CFD is used to analyze the multiphase flow in the lubricant film in the sealing gap of rotary shaft seals. The commercial software ANSYS Fluent 2021 R2 provides the numerical implementation of and solution to the multiphase flow. The computational domain is limited to the sealing zone. Three representative segments are used to approximate the lubricant film over the circumference of a rotary shaft seal. Data from microscopic scans provide the consideration of the rough elastomer surface. The sealing counter face is assumed to be ideally smooth. The sealing gap height is predicted via lubricant film thickness equations. This means an indirect coupling of the structure and the fluid. The computational model relies on the assumption of a laminar flow. The model considers the three fluid phases: oil, oil vapor, and air. The material properties of oil are defined in indirect dependence on the temperature. Oil vapor and air are assumed to be constant. The energy equation and heat transfers are neglected. A pressure-based solver with absolute velocity formulation is employed.
2.1. Gorvening Equations
The conservation laws for mass, momentum, and energy provide a description of the fluid flows. Assuming an isothermal flow, the conservation law for energy can be neglected. This study employs the mixture model to describe multiphase flow. A detailed description of the mixture model can be found in [16,17]. Considering a flow with phases, the continuity equation for the mixture is given by the following equation:
where
is the mass-averaged velocity vector and
is the mixture density. Here, and are the volume fraction and the density of the th phase and is the velocity vector of the th phase. The momentum equation for the mixture model is as follows:
where represents the body forces and represents the gravity vector. The viscosity of the mixture model is based on the following equation:
where is the viscosity of the corresponding phase . The drift velocity, i.e., the relative velocity of phase to the center of mass of the mixture, is given by the following equation:
As described in [18], local pressure that drops below the saturation pressure of the fluid can occur in a fluid flow in micro irregularities, such as on the asperities of a rough surface. This causes the fluid to go from the liquid phase to the vapor phase. The unsteady mass transfer between the phases in vapor cavitation can be described using the model of Schnerr and Sauer [19]. The vapor transport equation
allows the description of the mass transfer between the two phases in cavitation, where and are the volume fraction and the density of the vapor phase. The velocity of the vapor is represented by . The mass transfer rates for evaporation and for condensation provide a description of the mass transfer between the two phases depending on the local pressure via the following equations:
and
Here, is the radius of the vapor bubbles, is the density of the liquid phase, and the local density.
2.2. CFD Modeling
The modeling represents a decisive step in CFD. This includes the definition of the geometry of the computational domain, the specification of the material parameters, the discretization of the computational domain into a discrete computational grid, and the setting of boundary conditions.
2.2.1. Geometry
The first step in CFD modeling is to define the geometry of the computational domain. This includes the setting of reasonable borders, relevant to the problem. As shown in Figure 2, the fluid domain in the sealing gap is bounded by the shaft surface and the sealing edge surface. In addition, it is necessary to define an air side and an oil side border of the computational domain. This study focuses on the hydrodynamic effects of the rough elastomer sealing edge surface, so the shaft surface is assumed to be ideally smooth in a first approximation. The deformed rough sealing edge surface results from previous finite element analyses (FEA) according to [20,21]. The limit gap height provides the definition for the air side and the oil side border of the fluid domain.
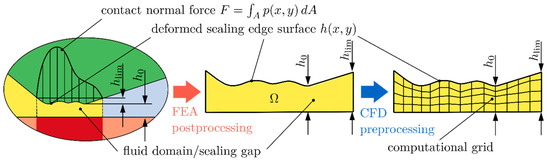
Figure 2.
CFD modeling of the lubricant film in the sealing gap of rotary shaft seals.
In addition to the sealing edge surface , the minimum gap height defines the computational domain. An estimation of the lubricant film thickness is based on the equation proposed by [22,23]. Marx et al. [22] used an optical interferometry to measure the lubricant film thickness under soft elastohydrodynamic lubrication (EHL) conditions and obtained the film thickness equation as follows:
Here, the dimensionless elasticity parameter, according to [24],
represents the relation between the load parameter
and the velocity parameter
according to [25,26]. is the normal force, the dynamic viscosity, and the effective velocity. The reduced Young’s modulus is given by
with the respective Young’s moduli and and Poisson’s ratios and of the contact bodies. According to [27], the radius of curvature in and direction is
with the effective wavelengths
according to [28], and the root mean square roughness slopes . is the root mean square height. The reduced radius of curvature results in
Sperka et al. [23] provide the analytical equation
for determining the ratio between the central lubricant film thickness and the minimum lubricant film thickness . Here,
and
represent dimensionless parameters according to [29], and is the pressure viscosity coefficient.
By setting the minimum lubricant film thickness equal to the minimum sealing gap height ,
is obtained as the upper boundary surface of the computational domain. Hence, the lower boundary surface of the computational domain is smooth, like the left and right boundary surfaces.
2.2.2. Fluid Properties
The multiphase flow considered in this study is composed of three phases: lubricant (oil), lubricant vapor (oil vapor), and air. The lubricant properties are considered to be dependent on the operating conditions of the fluid to be sealed. The fluid properties of the other two phases, oil vapor and air, are assumed to be constant.
The lubricant properties decisively determine the lubrication and sealing mechanism of rotary shaft seals. They affect the flow behavior and the friction condition during operation. The lubricant properties change considerably depending on the temperature. Rotary shaft seals are subjected to a wide range of operating conditions and, thus, undergo a wide range of temperatures. A method for estimating the contact temperature in the sealing gap and, thus, the temperature of the lubricant is presented in [30]. Based on the given operating conditions, friction conditions, fluid data, and process-related settings, this tool allows the estimation of the temperature in the sealing gap. The determination of the lubricant properties is performed analogously to [31]. The lubricant adopted in this study is a mineral oil without additives (FVA 3 reference oil, ISO VG 100, Weber Reference Oils, Oberhausen–Rheinhausen, Germany), according to [32]. Rotational speeds in a range of () are considered. The sealing ring has a nominal inner diameter of . The shaft is half in the oil sump with a lubricant temperature in the sump of . Table 1 shows a list of the adopted lubricant properties. The properties of the lubricant vapor are taken from [10]. The vaporization pressure and the bubble number density of are applied as input for the cavitation model. The properties of the secondary phases, air and oil vapor, are listed in Table 2.

Table 1.
Lubricant properties in the sealing gap under different operating conditions.

Table 2.
Fluid properties of oil vapor and air.
2.2.3. Geometric and Structural Parameters
The computation of the sealing gap height with the lubricant film thickness equation involves the input of geometrical and structural mechanical parameters in addition to the fluid properties.
The compressed sealing edge surface segments considered in this study are shown in Figure 3. These three representative surface segments originate from a total of measuring fields on different sealing rings. The selection is based on the root mean square height in the unmounted state. Across all considered measurement fields, values in a range of are obtained. The surface segment in Figure 3 has a root mean square height of in the unmounted state. That in Figure 3 is and that in Figure 3 is . Preliminary FEA, according to [20,21], are used to determine the deformation of the sealing edge surfaces in operation. The color bar represents the deformed surface . The limit gap height is set as . The axis corresponds to the circumferential direction and the axis to the axial direction. The arrow indicates the main direction of motion with the circumferential speed . Table 3 lists the corresponding geometric surface parameters in the deformed state. The reduced Young’s modulus is for all segments.

Figure 3.
Deformed rough sealing edge surface segments: (a) seg 1; (b) seg 2; and (c) seg 3.

Table 3.
Geometrical and structural mechanical parameters of the considered deformed sealing edge surface segments.
2.2.4. Discretization of the Computational Domain and Boundary Conditions
Since there is no exact analytical solution to the system conservation equations, a numerical approximation is required. The finite volume method (FVM) allows the discretization of the continuous conservation equations given in (1) and (4) into a discontinuous integral formulation. The meshing algorithm given in [31] is used for the discretization. The algorithm provides an automatic meshing of the computational domain by specifying the minimum gap height , the number of grid points and in and directions, and the number of cell layers in direction. This enables the generation of structured hexahedral CFD grids for various lubricant films. According to [33], hexahedral grids provide more accurate flow field solutions than tetrahedral ones with the same number of edges.
In order to minimize the discretization error, grid refinement studies, as in [34,35,36], were performed in advance. For the grid refinement study, a steady state was assumed. The Grid Convergence Index (GCI) method, according to [37], was proposed by [38] to quantify the discretization error. In order to obtain a suitable computational grid, an initial computational grid was systematically refined. Figure 4 shows an example of two computational grids with different fine discretization. The discretization error estimation was performed using the lubricant film segment for the surface segment seg 1 of Figure 3a. The computations were performed at a circumferential speed of . The critical variable in this study represents the mass flow rate on the fluid side . For the evaluation, the dimensionless mass flow rate is calculated based on the following equation:
where corresponds to the area of the bottom surface (shaft surface). The results of the grid refinement study are presented in Table 4. From the presented example, a could be achieved with the first refinement level. Based on this, a grid of cells is selected for further studies.

Figure 4.
Computational grid of the sealing edge surface segment seg 1 from Figure 3a: initial coarse discretization (number of cells (a) and finer discretization (number of cells ) (b).

Table 4.
Grid study.
Figure 4a shows the six bounding surfaces of the computational domain. To solve the problem, boundary conditions need to be defined there. As marked in blue in Figure 4a, the surface with coordinates is coupled to the hidden surface with coordinates via a translational periodicity. Pressure outlets are defined at the area marked in red on the air side and on the hidden opposite fluid side. The gauge pressure on the two sides is . On the air side, the initial air volume fraction is and on the fluid side . The two remaining white surfaces in Figure 4a are defined as walls. The upper rough sealing edge surface is stationary, whereas the lower shaft surface is subjected to the circumferential speed . The computational domain is initialized at the beginning of the analysis () with an oil volume fraction of and an air and oil vapor fraction of . Only the right boundary surface on the air side is initialized with an air volume fraction of . Figure 4a also indicates the minimum gap height .
2.3. Solver Settings and Solution Control
The Semi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm, as proposed by [39], is applied to solve the given transient multiphase problem. This is implemented in the applied commercial software ANSYS Fluent 2021 R2. It is a pressure-based solver with absolute velocity formulation and is suitable for both steady-state and transient problems. The under-relaxation factors decisively determine the stability and the convergence of the solver. Table 5 lists the under-relaxation factors employed for the solution control. These settings ensure a convergent and stable solution for all cases considered here. The residual criteria proved to be appropriate for the present problem are for the continuity, for the velocities, and for the volume fractions of the secondary phases. Preliminary investigations proved that with time steps by a time step size of , a sufficiently fine time discretization can be achieved at reasonable computational effort. Furthermore, it was found that a stable state occurs in the resulting total time of for all investigated operating conditions.

Table 5.
Solution controls.
3. Results
3.1. Sealing Gap Heights
As previously introduced, the minimum sealing gap height corresponds to the minimum lubricant film thickness in this study. Thus, the sealing gap height depends on the parameters from Table 1 and Table 3. Figure 5 shows the curve of the sealing gap height versus the circumferential speed . The markers represent the estimated values for the sealing edge surface segments shown in Figure 3. The corresponding lines show the general profile. The sealing gap heights according to Wollesen [40] and Dakov [41] are compared. Wollesen estimated the sealing gap height based on measured friction torques and lubricant film temperatures of typical rotary shaft seals. Dakov adopted a numerical approach and computed the minimal gap height of rotary shaft seals with hydrodynamic sealing aids based on a fully coupled soft elastohydrodynamic analysis (EHL).
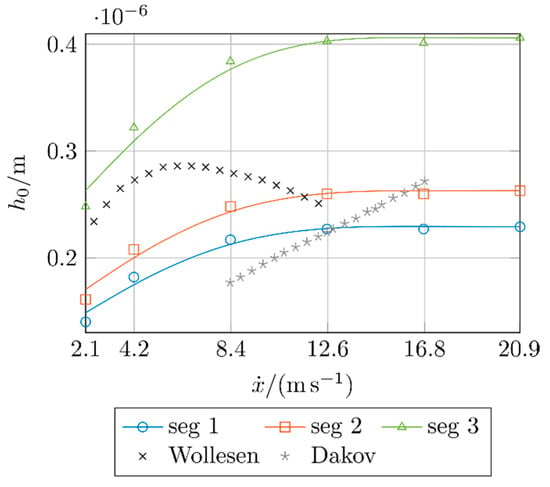
Figure 5.
Sealing gap height versus circumferential speed .
The results for the gap heights are in the same order of magnitude regardless of the applied model. The minimum gap heights for all surface segments considered in the present study lie in a range of . The gap height increases up to a circumferential speed of and remains approximately constant beyond this. The sealing gap heights from [40] show the same trend, up to a circumferential speed of but drop slightly as the speed increases. The gap height curve in [41] shows a linear increase over the circumferential speed.
3.2. Pumping Rates
The measured data from back-pumping rate tests out of [31] according to [42] serve to validate the computational results. The sealing ring is mounted inversely to its original mounting orientation, meaning that oil is constantly provided on the original air side. When the shaft is rotating, the rotary shaft seal pumps oil from the air side to the fluid side. There, the pumping rate of the rotary shaft seal can be determined from the oil pumped through the sealing gap.
In order to compare the computed results with the measured values, the pumping rate of each examined sealing edge segment is extrapolated to the circumference. Figure 6a shows the computed pumping rates plotted against the circumferential speed for the sealing ring segments examined. The computed points are linearly fitted. Segment 1 and segment 2 show a linear increase with increasing velocity. Segment 3 is an exception here. The values for the pumping rate are very low or even negative, regardless of the velocity. However, negative values do not mean leakage of the rotary shaft seal, but rather that, in this segment, oil enters the fluid domain via the fluid boundary on the fluid side. This effect is essential for the lubrication mechanism of rotary shaft seals. If the sealing ring pumps fluid out of the sealing gap over the entire circumference, the sealing ring runs dry, becomes thermally damaged, and finally fails. It is, therefore, necessary that fluid enters the sealing gap in areas around the circumference to ensure fluid exchange during operation. Furthermore, it is not critical for the rotary shaft seal to show leakage in certain areas, as long as the back-pumping effect of the remaining areas compensates this.
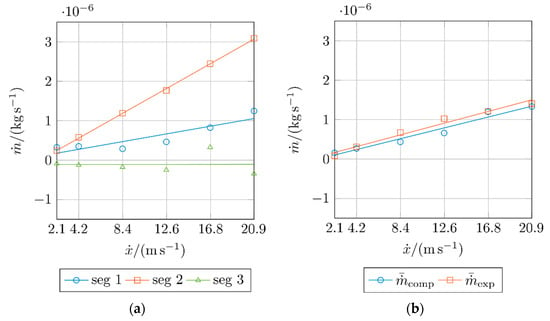
Figure 6.
Pumping rate against the circumferential speed: extrapolated mass flow rates of the evaluated sealing edge segments (a), and average values of the computed results and the measured data from the back-pumping rate tests [31] (b).
Figure 6b compares the computed pumping rates with the measured pumping rates . Here, the computed values represent the average values of the results obtained for the three surface segments. The experimental results show the average values of a total of values. The trend lines show a linear course. The computed trend line matches the trend line of the measured data quite closely. Thus, the presented model provides valid results for the fluid flows in the lubricant film in the sealing gap of rotary shaft seals.
3.3. Phase Interactions and Flow Features
In operation, the sealing edge lifts up and there is no solid boundary between the fluid to be sealed (oil) and the ambient fluid (air). A phase interaction occurs between oil and air. In addition, high pressure gradients in the fluid domain lead to cavitation.
Figure 7 shows the volume fractions of the two phases, oil and air , at different times at a circumferential speed of . The results obtained are for seg 1 of Figure 3a. The color bars represent the volume fraction of the respective phase. Figure 7a shows the air and oil fractions in the fluid domain at a time of . The air fraction increases rapidly starting from the air side while the oil fraction decreases. After a time of , only a small fraction of oil remains on the air side, see Figure 7b. Over time, the oil fraction decreases further until a continuous air film forms on the air side after a time of , see Figure 7d. Beyond this time, the phase transition between air and oil does not change its position. The phase transition between oil and air is also known as the oil meniscus. There are areas that are approximately from the center of the fluid domain to the oil side where neither oil nor air are present. Here, cavitation occurs, resulting in oil vapor. These cavitation zones vary slightly over time.

Figure 7.
Volume fractions of oil and air in the fluid film segment seg 1 at different times at a circumferential speed of : (a) ; (b) ; (c) ; and (d) .
Figure 8 shows the volume fractions at different circumferential speeds in seg 1. The position of the phase transition between oil and air does not vary with increasing circumferential speed. However, the velocity affects the fraction of oil vapor in the fluid domain. As the velocity increases, the cavitation zones expand and more oil vapor occurs.

Figure 8.
Volume fractions of oil and air in the fluid film segment speeds after a time of : (a) ; (b) ; (c) ; and (d) .
Figure 9 shows the oil and air volume fractions in the other two lubricant film segments examined, each at the circumferential speeds and . Some of the results are very different from those for seg 1. The phase boundary between oil and air extends to the air side for seg 2. In seg 3, there is a distinct phase boundary between oil and air in the fluid region. Compared to the results for seg 1, this is closer to the air side. Moreover, seg 3 shows a relatively large mixed area where oil and air are present.
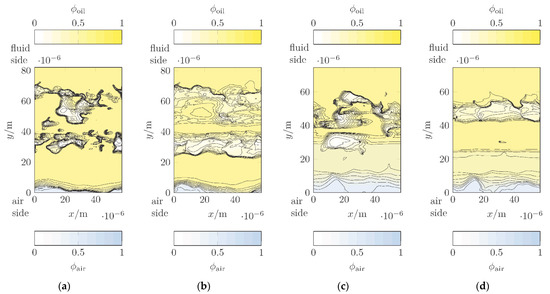
Figure 9.
Volume fractions of oil and air in the fluid film segments seg 2 and seg 3 at different circumferential speeds after a time of : (a) seg 2 at ; (b) seg 2 at ; (c) seg 3 at ; and (d) seg 3 at .
The flow features in the different lubricant film segments are shown in Figure 10. Following [43], the streamlines and the distribution of the -vorticity are presented. The values are obtained from a transformed surface with an ISO distance of to the upper surface (sealing edge surface). The presented flow features result at a circumferential speeds of after a time of . In general, the fluid film segments show a similar flow characteristic. Three regions can be distinguished. In the middle of the domain, where the lubricant film thickness is lowest, the streamlines indicate straight lines in the circumferential direction. Here, the -vorticity is low, which implies that the tangential flow component in the circumferential direction is dominant. In the regions on the fluid side and the air side, the -vorticity is stronger, and the streamlines show significantly higher proportions of the flow component in the axial direction. On the fluid side, a stronger z-vortex intensity is apparent than on the air side. In conclusion, a major proportion of the fluid is dragged along in the sealing gap and, thus, lubricates the sealing edge. Axial flow components appear on the fluid side and the air side, which provide the basis for the active sealing mechanism of rotary shaft seals.

Figure 10.
Streamlines and distribution of the -vorticity at a circumferential speed of after a time of : (a) seg 1; (b) seg 2; and (c) seg 3.
3.4. Cavitation and Hydrodynamic Pressure
It appears that the effect of cavitation and, thus, the formation of oil vapor in the lubricant film in the sealing gap of rotary shaft seals depends on the circumferential speed. A significant deviation over time cannot be established. A nearly steady state is reached after a short period of time. The phenomenon of cavitation depends on the pressures in the flow. The cavitation number serves to characterize the tendency of a fluid flow to cavitate. The cavitation number, according to [44,45,46], is calculated as follows:
It is assumed in the following that if the cavitation number is , the fluid tends to cavitate. If the cavitation number is , the evaporation of the liquid is not expected. This does not represent an exact cutoff value, but it gives an indication of the tendency of a fluid to cavitate under specific operating parameters.
Figure 11 shows the development of hydrodynamic pressure and the tendency toward cavitation versus the circumferential speed for seg 1. Here, the median value of the total pressure in the fluid domain and the fraction of the area in the fluid region where are plotted. The volume fraction of oil vapor and the total hydrodynamic pressure for the lubricant film seg 1 at different circumferential speeds are shown in Figure 12. The hydrodynamic pressure first drops over the circumferential speed and then increases sharply. The median value of the total pressure in the fluid domain is at a circumferential speed of in Figure 12a, drops to a value of at a circumferential speed of in Figure 12b, and then increases continuously to a value of for a circumferential speed of in Figure 12d. The fraction of areas in the fluid domain is shown in Figure 12a where is . With increasing circumferential speed, this fraction increases and is for the fluid region in Figure 12d at a circumferential speed of . At the lower circumferential speeds in Figure 12a,b, high oil vapor fractions appear especially in the low-pressure regions. At the high circumferential speeds in Figure 12c,d, oil vapor volume fractions also appear in the regions with higher pressures. Continuous stripes in the circumferential direction with oil vapor appear in the lubricant film segment. This is consistent with the visual observations in [18], where the so-called cavitation streamers could be found in the sealing gap of a transparent seal.
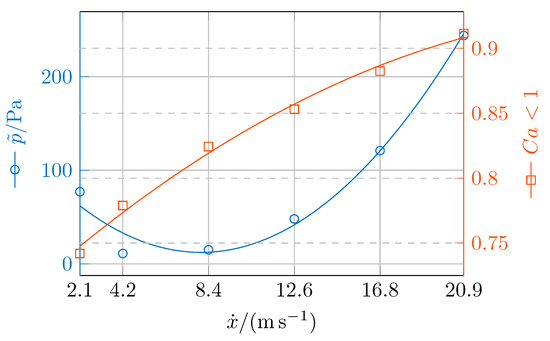
Figure 11.
Median value of total hydrodynamic pressure and the fraction of areas in the fluid domain tending toward cavitation where .

Figure 12.
Volume fractions of oil vapor and hydrodynamic pressure in the sealing edge surface segment seg 1 at different speeds after a time of : (a) ; (b) ; (c) ; and (d) .
Figure 13 shows the oil vapor fraction and the total hydrodynamic pressure in the lubricant film segments seg 2 and seg 3 at circumferential speeds of and . In seg 2, the median value in Figure 13a increases to a value of in Figure 13b. The fraction of areas in the fluid domain tending toward cavitation increases from to . The median hydrodynamic pressure values for seg 3 range from in Figure 13c to in Figure 13d. The fraction of areas tending toward cavitation increases from to . Thus, all examined lubricant film segments show qualitatively the same behavior.

Figure 13.
Volume fractions of oil vapor and hydrodynamic pressure in the fluid film segments seg 2 and seg 3 at different speeds after a time of : (a) seg 2 at ; (b) seg 2 at ; (c) seg 3 at ; and (d) seg 3 at .
4. Conclusions
The present study deals with the computation of the transient multiphase flow in the lubricant film in the sealing gap of rotary shaft seals. In conclusion, the following points can be stated:
- Computational fluid dynamics (CFD) is suitable for the computation of transient flow processes of rotary shaft seals.
- The presented method allows the implementation of surface measurement data for this purpose.
- The lubricant film thickness equations according to [22,23] provide plausible sealing gap heights with the presented input parameters comparable to those from [40,41].
- The results of three selected sealing edge segments show different flow processes. This means that the dynamic sealing gap of a rotary shaft seal may not be assumed to be constant but varies over the entire circumference.
- On average, the computed mass flow rates show high agreement with the measured data. Consequently, the presented model provides physically reasonable and valid results.
- The computed phase interaction provides an in-depth insight into the sealing and lubrication mechanism of rotary shaft seals. The results show that a steady state is established after a period of . This is in agreement with the results from [7], where at a time of , the motion of the oil meniscus stops and reaches a stable position. A variation of the position of the phase interface depending on the circumferential speed cannot be found.
- The flow features show a dominant tangential flow in the lubricant film with axial flow components on the fluid side and on the air side. This provides explanations for the lubrication and sealing mechanism of rotary shaft seals.
- The analyses of the hydrodynamic pressure and cavitation show that there is almost no noticeable variation over time. However, as the circumferential speed increases, the cavitation zone fraction increases and the pressure increases after a slight drop. The obtained cavitation zone fraction corresponds to the values given in [8].
In conclusion, this numerical study provides an in-depth insight into the multiphase flow processes in the lubricant film in the sealing gap of rotary shaft seals. In addition, the presented modeling enables a variety of extension possibilities. Fluid–solid interfaces offer the possibility to consider heat transitions in the system. Dynamic mesh models allow the coupling of elastic deformations during operation. The implementation in ANSYS Fluent 2021 R2 offers a variety of extensions with the help of the so-called user-defined functions (UDF). Thus, the present paper forms the basis for far-reaching investigations on various problems in sealing technology and tribology.
Author Contributions
Conceptualization, J.G.; methodology, J.G.; investigation, J.G.; writing—original draft preparation, J.G.; writing—review and editing, J.G., S.F. and F.B.; visualization, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Area of the bottom surface of the fluid domain | |
| Cavitation number | |
| Nominal diameter | |
| Reduced Young’s modulus | |
| Young’s modulus of the sealing ring | |
| Young’s modulus of the shaft | |
| Normal force | |
| Body forces | |
| Gravity vector | |
| Central film thickness | |
| Sealing gap height | |
| Minimum gap height | |
| Central film thickness | |
| Spring lever arm | |
| Limit gap height | |
| Minimum film thickness | |
| Moe’s parameter | |
| Moe’s parameter | |
| Mass transfer rate for condensation | |
| Mass transfer rate for evaporation | |
| Mass flow rate on the fluid side | |
| Dimensionless mass flow rate on the fluid side | |
| Rotational speed | |
| Number of cells | |
| Number of time steps | |
| Number of grid points in circumferential direction | |
| Number of grid points in axial direction | |
| Number of cell layers in radial direction | |
| Local pressure | |
| Median pressure | |
| Vaporization pressure | |
| Radius of the vapor bubbles | |
| Reduced radius of curvature in circumferential direction | |
| Reduced radius of curvature in axial direction | |
| Root mean square height | |
| Time | |
| Time step size | |
| Velocity parameter | |
| Effective velocity | |
| Velocity vector of the th phase | |
| Mass-averaged velocity vector of the mixture | |
| Drift velocity vector | |
| Velocity vector of the vapor phase | |
| Load parameter | |
| ISO distance | |
| Circumferential direction | |
| Circumferential speed | |
| Axial direction | |
| Radial direction | |
| Fluid side contact surface angle | |
| Under-relaxation factor for body forces | |
| Under-relaxation factor for momentum | |
| Under-relaxation factor for pressure | |
| Pressure viscosity coefficient | |
| Under-relaxation factor for vaporization mass | |
| Under-relaxation factor for vaporization mass | |
| Under-relaxation factor for density | |
| Under-relaxation factor for vaporization mass | |
| Air side contact surface angle | |
| Residual criterion of air volume fraction | |
| Residual criterion of continuity | |
| Residual criterion of vapor volume fraction | |
| Residual criterion of circumferential velocity | |
| Residual criterion of axial velocity | |
| Residual criterion of radial velocity | |
| Viscosity of the th phase | |
| Dynamic viscosity of the liquid phase | |
| Viscosity of the mixture | |
| Contact temperature | |
| Oil sump temperature | |
| Effective wavelength in circumferential direction | |
| Effective wavelength in axial direction | |
| Poisson’s ratio of the shaft | |
| Poisson’s ratio of the sealing ring | |
| Local density | |
| Bubble number density | |
| Density of the th phase | |
| Density of the liquid phase | |
| Density of the mixture | |
| Density of the vapor phase | |
| Root mean square slope in circumferential direction | |
| Root mean square slope in axial direction | |
| Volume fraction of the air phase | |
| Volume fraction of the th phase | |
| Volume fraction of the oil phase | |
| Volume fraction of the vapor phase | |
| -vorticity |
Abbreviations
| CFD | Computational fluid dynamics |
| FEA | Grid convergence index |
| GCI | Finite element analyses |
| JFO | Jakobsson–Floberg–Olsson cavitation model |
| UDF | User-defined functions |
References
- DIN 3760:1996-09; Radial-Wellendichtringe. DIN: Berlin, Germany, 1996.
- ISO 6194-1:2007-09; Rotary Shaft Lip-Type Seals Incorporating Elastomeric Sealing Elements—Part 1: Nominal Dimensions and Tolerances. ISO: Geneva, Switzerland, 2007.
- Bauer, F. Federvorgespannte-Elastomer-Radial-Wellendichtungen; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021; ISBN 978-3-658-32921-1. [Google Scholar]
- Bauer, F. Tribologie; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021; ISBN 978-3-658-32919-8. [Google Scholar]
- Kammüller, M. Zur Abdichtwirkung von Radial-Wellendichtringen; Universität Stuttgart: Stuttgart, Germany, 1986. [Google Scholar]
- Müller, H.K. Concepts of Sealing Mechanism of Rubber Lip Type Rotary Shaft Seals. In Proceedings of the 11th International Conference on Fluid Sealing, Cannes, France, 8–10 April 1987; pp. 698–709. [Google Scholar]
- Salant, R.F. Analysis of the Transient Behavior of Rotary Lip Seals-Fluid Mechanics and Bulk Deformation. Tribol. Trans. 1998, 41, 471–480. [Google Scholar] [CrossRef]
- Shen, D.; Salant, R.F. A Transient Mixed Lubrication Model of a Rotary Lip Seal with a Rough Shaft. Tribol. Trans. 2006, 49, 621–634. [Google Scholar] [CrossRef]
- Hajjam, M.; Bonneau, D. A Transient Finite Element Cavitation Algorithm with Application to Radial Lip Seals. Tribol. Int. 2007, 40, 1258–1269. [Google Scholar] [CrossRef]
- Jakobsson, B.; Floberg, L. The Finite Journal Bearing Considering Vaporization, (Das Gleitlager von Endlicher Breite Mit Verdampfung); Chalmers Tekniska Högskolas handlingar; Avd. Maskinteknik; Report from the Institute of Machine Elements, Chalmers University of Technology; Gumpert: Göteborg, Sweden, 1957; Volume 190. [Google Scholar]
- Olsson, K.-O. Cavitation in Dynamically Loaded Bearings; Chalmers Tekniska Högskolas handlingar; Gumperts: Göteborg, Sweden, 1965; Volume 34. [Google Scholar]
- Almqvist, T.; Larsson, R. Some Remarks on the Validity of Reynolds Equation in the Modeling of Lubricant Film Flows on the Surface Roughness Scale. J. Tribol. 2004, 126, 703–710. [Google Scholar] [CrossRef]
- Dobrica, M.B.; Fillon, M. About the Validity of Reynolds Equation and Inertia Effects in Textured Sliders of Infinite Width. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2009, 223, 69–78. [Google Scholar] [CrossRef]
- Yang, A.-S.; Wen, C.-Y.; Tseng, C.-S. Analysis of Flow Field around a Ribbed Helix Lip Seal. Tribol. Int. 2009, 42, 649–656. [Google Scholar] [CrossRef]
- Keller, D.; Jacobs, G.; Neumann, S. Development of a Low-Friction Radial Shaft Seal: Using CFD Simulations to Optimise the Microstructured Sealing Lip. Lubricants 2020, 8, 41. [Google Scholar] [CrossRef]
- Ungarish, M. Hydrodynamics of Suspensions: Fundamentals of Centrifugal and Gravity Separation; Springer: Berlin, Germany; New York, NY, USA, 1993; ISBN 978-3-540-54762-4. [Google Scholar]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Boston, MA, USA, 1994; ISBN 978-0-12-282470-8. [Google Scholar]
- Hamilton, D.B.; Walowit, J.A.; Allen, C.M. A Theory of Lubrication by Microirregularities. J. Basic Eng. 1966, 88, 177–185. [Google Scholar] [CrossRef]
- Schnerr, G.H.; Sauer, J. Physical and Numerical Modeling of Unsteady Cavitation Dynamics; ICMF New Orleans: New Orleans, LO, USA, 2001; p. 12. [Google Scholar]
- Grün, J.; Feldmeth, S.; Bauer, F. Wear on Radial Lip Seals: A Numerical Study of the Influence on the Sealing Mechanism. Wear 2021, 476, 203674. [Google Scholar] [CrossRef]
- Grün, J.; Feldmeth, S.; Bauer, F. The Sealing Mechanism of Radial Lip Seals: A Numerical Study of the Tangential Distortion of the Sealing Edge. Tribol. Mater. 2022, 1, 1–10. [Google Scholar] [CrossRef]
- Marx, N.; Guegan, J.; Spikes, H.A. Elastohydrodynamic Film Thickness of Soft EHL Contacts Using Optical Interferometry. Tribol. Int. 2016, 99, 267–277. [Google Scholar] [CrossRef]
- Sperka, P.; Krupka, I.; Hartl, M. Analytical Formula for the Ratio of Central to Minimum Film Thickness in a Circular EHL Contact. Lubricants 2018, 6, 80. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Brewe, D. Simplified Solution for Stresses and Deformations. J. Lubr. Technol. 1983, 105, 171–177. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R. The Effect of Material Properties on the Lubrication of Elastic Rollers. J. Mech. Eng. Sci. 1960, 2, 188–194. [Google Scholar] [CrossRef]
- Dowson, D.; Higginson, G.R.; Whitaker, A.V. Elasto-Hydrodynamic Lubrication: A Survey of Isothermal Solutions. J. Mech. Eng. Sci. 1962, 4, 121–126. [Google Scholar] [CrossRef]
- Karami, G.; Evans, H.P.; Snidle, R.W. Elastohydrodynamic Lubrication of Circumferentially Finished Rollers Having Sinusoidal Roughness. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1987, 201, 29–36. [Google Scholar] [CrossRef]
- Griffiths, B. Manufacturing Surface Technology; Elsevier: Amsterdam, The Netherlands, 2001; ISBN 978-1-85718-029-9. [Google Scholar]
- Moes, H. Communications. In Proceedings of the Symposium on Elastohydrodynamic Lubrication, London, UK, 21–23 September 1965; Volume 180, pp. 244–245. [Google Scholar]
- Feldmeth, S.; Bauer, F.; Haas, W. Abschätzung der Kontakttemperatur bei Radial-Wellendichtungen mit der Selbstentwickelten Open-Source-Software InsECT. In Proceedings of the KISSsoft AG (Hg.) 2016—Tagungsband Schweizer Maschinenelemente Kolloquium SMK, Stuttgart, Germany, 12–13 October 2016; pp. 233–248. [Google Scholar]
- Grün, J.; Feldmeth, S.; Bauer, F. Computational Fluid Dynamics of the Lubricant Flow in the Sealing Gap of Rotary Shaft Seals. In Proceedings of the M2D2022—9th International Conference on Mechanics and Materials in Design, Funchal, Portugal, 26–30 June 2022; pp. 1035–1050. [Google Scholar]
- Forschungsvereinigung Antriebstechnik, e.V. Referenzöle Für Wälz-und Gleitlager-, Zahnrad-und Kupplungsversuche; Forschungsvereinigung Antriebstechnik e.V.: Hesse, Germany, 1985; Volume 180. [Google Scholar]
- Biswas, R.; Strawn, R.C. Tetrahedral and Hexahedral Mesh Adaptation for CFD Problems. Appl. Numer. Math. 1998, 26, 135–151. [Google Scholar] [CrossRef]
- Gao, R.; Kirk, G. CFD Study on Stepped and Drum Balance Labyrinth Seal. Tribol. Trans. 2013, 56, 663–671. [Google Scholar] [CrossRef]
- Adjemout, M.; Brunetiere, N.; Bouyer, J. Optimization of Mesh Density for Numerical Simulations of Hydrodynamic Lubrication Considering Textured Surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 1132–1144. [Google Scholar] [CrossRef]
- Snyder, T.; Braun, M. Comparison of Perturbed Reynolds Equation and CFD Models for the Prediction of Dynamic Coefficients of Sliding Bearings. Lubricants 2018, 6, 5. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A Calculation Procedure for Heat, Mass and Momentum Transfer in Three-Dimensional Parabolic Flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Wollesen, V. Temperaturbestimmung in der Dichtzone von Radialwellendichtringen als Randbedingung für die Modellierung des Dichtvorganges; Technische Universität Hamburg-Harburg: Hamburg, Germany, 1993. [Google Scholar]
- Dakov, N. Elastohydrodynamic Lubrication Analysis of a Radial Oil Seal with Hydrodynamic Features. Tribol. Int. 2022, 173, 107653. [Google Scholar] [CrossRef]
- Merkle, L.; Baumann, M.; Bauer, F. Back-Pumping Rate Measurement of Elastomeric Radial Lip Seals in Converse Installation: Basics, Wear Formation and Long-Term Tests. In Proceedings of the M2D2022—9th International Conference on MECHANICS and Materials in Design, Funchal, Portugal, 26–30 June 2022; pp. 363–374. [Google Scholar]
- Galletti, C.; Mariotti, A.; Siconolfi, L.; Mauri, R.; Brunazzi, E. Numerical Investigation of Flow Regimes in T-Shaped Micromixers: Benchmark between Finite Volume and Spectral Element Methods. Can. J. Chem. Eng. 2019, 97, 528–541. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics, 1st ed.; Cambridge University Press: New York, NY, USA, 2000; ISBN 978-0-521-66396-0. [Google Scholar]
- Arndt, R.E.A. Cavitation in Fluid Machinery and Hydraulic Structures. Annu. Rev. Fluid Mech. 1981, 13, 273–326. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: New York, NY, USA, 2014; ISBN 978-1-107-64476-2. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).