Abstract
The active control of hydrodynamic bearings is beginning to receive more attention in the pursuit of lower power losses and reduced maintenance. This paper presents a method by which, from simple measurements, rich information can be deduced from a running bearing that can used to modify the operating parameters of the unit. The bearing is a line-pivot, unidirectional, steadily loaded, directly lubricated tilting pad thrust bearing. This control is achieved by designing an Observer whose inputs include the output measurement(s) from the bearing. The Observer is, in some ways, an inverse model of the bearing (or Plant) that runs in parallel to the bearing and estimates the states of the bearing, such as the applied load, pivot height, minimum film thickness, maximum temperature, effective temperature and power loss. These estimated parameters can then be used in a control algorithm to modify bearing parameters such as inlet temperature or pivot location. It is demonstrated that disturbances in the load on the bearing can be detected simply by measuring a representative temperature in the bearing or changes in pivot height. Appropriate corrective action can then be employed. Whilst only steady-state operation is considered, the method could be developed to study time-varying situations.
1. Introduction
Active control of hydrodynamic journal bearings has been studied in order to improve their damping and stiffness coefficients. Probably the earliest example is the work by Ulbrich and Althaus [1] in 1986, who controlled the pads in a tilting-pad, hydrodynamic journal bearing with piezo-actuators. Santos et al. [2] developed this further using a hydraulic chamber fed by proportional and servo valves. Theoretical modelling was also undertaken, and good agreement was obtained between the experimental and predicted damping and rotor stabilisation. Deckler et al. [3,4] developed a model of an actively controlled, time-dependent journal bearing that enabled the pads to be moved radially under the action of piezo-actuators by a control algorithm. Vivaros and Nicoletti [5] employed electromagnetic actuators in a tilting-pad journal bearing with a proportional-derivative control feedback algorithm. Shaft-vibration amplitudes were reduced by between 11 and 18% depending on the shaft speed, and good agreement was obtained with a mathematical model. Further work has been pursued on hydrodynamic, hydrostatic, aerostatic and magnetic journal bearings by many authors [6,7,8] examining the dynamic performance of such contacts, and Santos presents a useful review [9].
The active control of tilting-pad thrust bearings has received less attention, probably because they do not normally present the time-dependent stability problems of their journal bearing counterparts. However, modern measurement, actuator and control systems provide an opportunity to tune these bearings to produce optimum performance under varying conditions. Such an approach is often called tribotronics. Sanadgol and Maslen [10] modelled a magnetic thrust bearing whose stiffness was altered to control the vibration of a compressor when undergoing surge. Riaz et al. [11] employed a low-cost, digital controller to provide closed-loop control of film height using a pulse-width-modulated pressure supply. They demonstrated that film height could be maintained when step changes in load were applied, with the response time appearing to be in the order of 1 s (based on an assumed sampling rate of 490 Hz).
The method employed in this paper is informed by the Observer principle developed by Luenberger [12]. Such state Observers are widely used in control systems [13,14,15]. The basic principle is that a modified model of the system to be controlled (the ‘Observer’) is run in parallel to the actual system (the ‘Plant’). All the inputs to the Plant are also input to the Observer, and the Observer also receives the output(s) of the Plant. In this way, the Observer’s state eventually converges, over time, to the state of the Plant. The state variables of the Observer can then be used to control the Plant in real time. Chen et al. [16] theoretically studied a magnetic journal bearing on a vertical shaft and used a Luenberger observer to estimate unbalanced forces so that these could be counteracted by the bearing. They demonstrated that the method could satisfactorily deal with rotational disturbances. Ur Rehman et al. [17] developed an observer-based control system for a hydrostatic bearing. Experimental difficulties prevented the researchers from comparing predictions with experiments and thus the validity of their approach could not be established, although their model produced some extremely promising predictions. To the author’s knowledge, an observer-based control approach has not yet been developed for hydrodynamic thrust bearings, and this paper seeks to address this. As temporal variations are unlikely to be important, a steady-state approach is adopted that reduces the complexity of the observer design. Heat generation and dissipation are major issues in hydrodynamic bearings and thus a thermo-hydrodynamic approach is adopted when modelling the bearings.
Illustrated in Figure 1 is a block diagram of the Plant, Observer and feedback system. The Plant is supplied with lubricant at a particular temperature (hence viscosity) along with the load and speed. The load can be altered by a disturbance, which will then alter the operating conditions of the bearing. This paper demonstrates that commercial design programs can be employed to characterise the performance of a specific bearing in its operating environment. Two programs are employed ESDU 83004 [18] and a finite-element, thermo-hydrodynamic analysis package [19]. The bearing is designed, or modelled, with these systems and performance equations are then obtained that can be used to design the Observers. The aim is to obtain the full state of the bearing by measuring a limited number of variables and running an Observer without the need to have the design programs running alongside the real bearing. For the FE model, a series of operating conditions are considered, and multiple regression is employed to produce performance equations. No attempt is made to produce non-dimensional analyses since each bearing arrangement will have its own characteristics. The FE model of the bearing can be calibrated against the real bearing before installation, as discussed by Almqvist et al. [20].
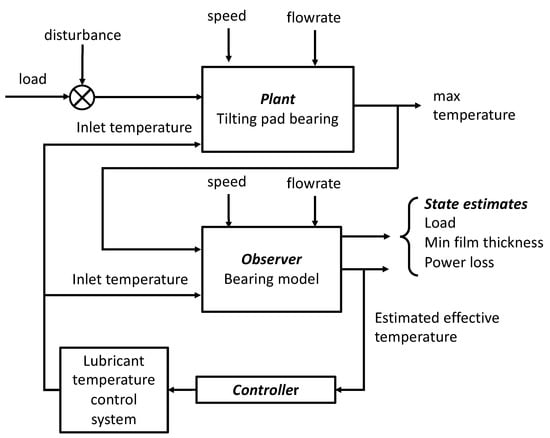
Figure 1.
Block Diagram for an Observer-based control system using an Observer based on ESDU 83004.
To demonstrate how the Observer system operates, a simulation of a bearing is employed rather than data from a real bearing. It is argued that this in no way diminishes the validity of the approach.
2. Observer Design
To design an Observer, one needs an accurate model of the real system. In what follows two approached are adopted. Firstly, the design procedure of EDSU 83004 [18] is employed, and secondly a thermo-hydrodynamic model is developed with a finite-element package [19]. In the former case, equations predicting bearing performance are provided in the design guide and they can be manipulated to provide an Observer. In the latter case, the bearing is modelled in finite elements, and then characteristic performance equations are developed so that the package is not required when operating in real time.
2.1. Observer Design Based on ESDU 83004
This code provides design criteria for a line-pivot, uni-directional, steadily loaded, directly lubricated, tilting-pad, thrust bearing. In this study, the maximum temperature in the contact and the inlet temperature are measured, as shown in Figure 1. For the purposes of a system description of the arrangement, the Plant is considered to have the two fixed inputs: shaft speed and lubricant flowrate. Two potentially variable inputs are the applied load and the inlet temperature of the lubricant. The Plant’s output is designated as the maximum temperature of the lubricant (or pad). This output acts as an input to the Observer (based in a computer system that can be remote from the Plant). The Observer is also supplied with the inlet temperature of the lubricant, and the same speed and flowrate information as in the real bearing. The Observer provides estimates of the state of the bearing such as the applied load, minimum film thickness, pivot height and power loss. In this case, the estimated mean temperature, Te, is used by the controller to heat or cool the lubricant and thus change its inlet temperature.
The ESDU guide suggests that the effective temperature, Te, is linked to the inlet and maximum temperatures according to the following:
where s2 is a constant that can be obtained from a curve-fit equation of data provided in the guide, as follows:
where N is the rotational speed in Hz.
Once the effective temperature is determined, the effective viscosity can be deduced, and the minimum film thickness obtained from an equation in the guide, as follows:
where is the effective viscosity (Pa-s), dm is the mean diameter (m), l the pad length (m), the lubricant density (kg m−3), the specific heat of the lubricant (J kg−1K−1) and .
(See Appendix A for the proof)
An estimate of the applied load can be obtained from the following (see Appendix A):
where b is the pad radial width
The power loss per pad can then be evaluated from the following ESDU equation:
Equations (1)–(5) provide estimates of the state of the bearing, based simply on a single measurement in the real bearing. The bearing studied employed a directed lubrication system and consisted of eight pads. A sketch of one of the pads is shown in Figure 2, with more details of the geometry presented in Table 1.
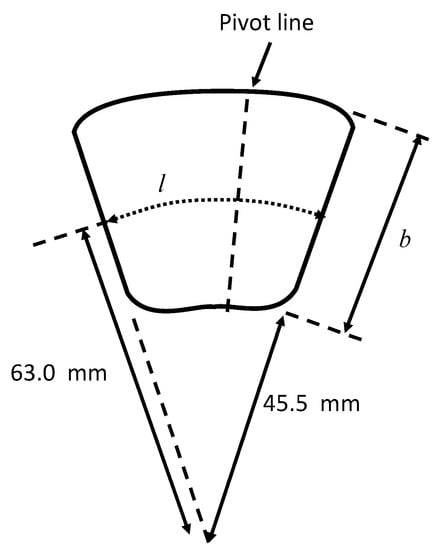
Figure 2.
Dimensions of a pad for the ‘ESDU’ bearing.

Table 1.
Line-pivot, tilting-pad thrust bearing characteristics for the ESDU Observer.
2.2. Observer Design Based on FE Modelling
The process involved here is to model the real bearing offline, characterise the performance so that these characteristics can be employed in real time. To achieve this, an example bearing was chosen with the specifications listed in Table 2.

Table 2.
Line-pivot, tilting-pad thrust bearing characteristics for the FE simulation.
The bearing and its meshing are illustrated in Figure 3. A thermo-hydrodynamic analysis was undertaken, with all surfaces losing heat through radiation only, with the surfaces having an assumed emissivity of 0.8. Heat was generated through viscous dissipation and heat flow was modelled using the steady-state Fourier equation. In the case of the collar, translational effects were included in the heat flow equation to allow for the collar’s rotation. The bearing model was run for inlet temperatures of 50, 60, 70 and 80 °C, and pivot heights of 40 and . The resulting FE predictions are listed in Appendix B. Multiple regression was employed to produce the following relationships:
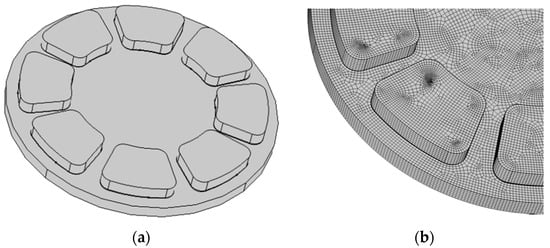
Figure 3.
The 8-pad, tilting-pad bearing and its FE mesh: (a) The 8-pad, tilting-pad bearing; (b) The FE mesh.
(The validity of these equations when compared with the predictions from the CFD program are discussed later. The data upon which these equations are based are presented in Appendix B). Thus, the states of the bearing can be estimated by the Observer if the maximum temperature of the pad (or the fluid) and the inlet temperature are measured. Equation (6) will generate the pivot height, which can then be employed in Equation (7) to generate the minimum film thickness and Equation (8) to yield the effective temperature. The effective temperature enables the effective viscosity to be determined, which allows the applied load to be evaluated from Equation (9). Finally, the power loss can be generated from Equation (10). The block diagram of the system is shown in Figure 3.
3. Running the Observers
3.1. The ESDU-Based System
In this bearing, the maximum temperature, Tmax, was monitored. The simulation of the plant produced a value of 72.6 °C. (Whilst the minimum film thickness would not be available to the Observer, for checking purposes, it can be noted that it was 19.5 ) When the value of Tmax, was fed into the Observer, the following state was estimated:
| Load | 2739 N |
| Power loss per pad | 547 W |
The estimated load is only 0.04% less than the actual load, and the estimated film thickness is the same as the actual. Thus, the Observer can be trusted to accurately estimate the state variables of the bearing.
Now consider that a 25% increase in load to 3438 N occurs (i.e., a disturbance as shown in Figure 1 with no change in the inlet flow rate. It is assumed that this load change is unknown and the only indication that something has changed is a rise in the maximum temperature from 72.6 to 77.6 ℃. When fed into the Observer, the estimations are as follows:
| Load | 3424 N (+25%) |
| (−15%) | |
| Power loss per pad | 583 W (+7%) |
Clearly, the Observer is correctly indicating that the load has increased by 25% and the minimum film thickness has dropped, but it is not below the minimum acceptable level of 15 μm. No correction is required, but there is an opportunity to reduce the power loss.
This can be achieved by increasing the inlet temperature to 59 °C. The Observer then estimates the following:
| Load | 3424 N |
| Power loss per pad | 525 W |
The power loss has been reduced by 10% and is now 4% less than the value pertaining to when the load was at its original level. This raises another useful aspect of employing an observer in that the bearing can be tuned to give minimum power loss whilst still maintaining an acceptable film thickness.
3.2. The FE-Based System
Details of the bearing examined were presented in Table 3 and a block diagram of the system is shown in Figure 4. The FE simulation of the bearing indicated that the maximum temperature of the pad was 68.6 °C. (i.e., if the real bearing was running, this would be the temperature that was measured). Using Equations (6)–(10) leads to the estimates in Table 3. The calculations from the FE package are also presented in this table, and the Observer’s accuracy is seen to be good. This confirms the validity of the multiple regression equations noted earlier.

Table 3.
FE Observer estimates and comparison with actual values–inlet temperature controlled.
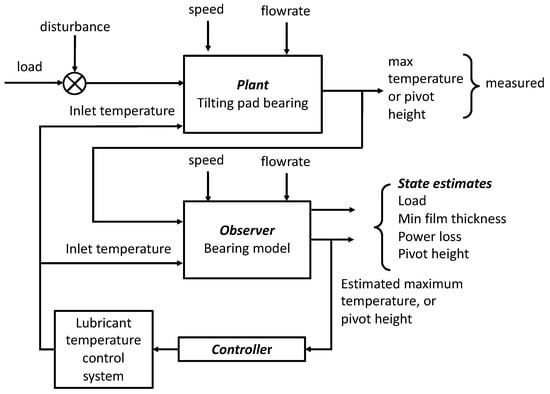
Figure 4.
Block Diagram for a control system using an Observer based on the finite-element model.
If we now consider that the maximum pad temperature rises to 71 °C, then the following are estimated:
| a pivot height of 49.2 | (a decrease of 18%) |
| a min. film thickness of 20.0 | (a decrease of 20%) |
| an effective temperature of 56.6 °C | (an increase of 3%) |
| an applied load of 4881 N | (an increase of 72%) |
| power loss of 218 W | (an increase of 22%) |
If it is required to reduce this power loss, then the inlet temperature will have to be increased. This would be increased gradually, monitoring the maximum pad temperature and using Equations (6)–(10) to estimate the state of the bearing. It is interesting to note that large changes in load are generating only small changes in maximum pad temperature, but large changes in pivot height. This suggests that measuring the pivot height may offer a more useful means of monitoring bearing performance. This can be accomplished as follows. The measured values of inlet temperature and pivot height are fed directly into Equations (7)–(10), and the maximum temperature is obtained from the following rearranged version of Equation (6):
Under normal running conditions, the Observer’s estimates (based now upon the pivot height as a measured input) compared with the actual state are shown in Table 4.

Table 4.
FE Observer estimates and comparison with actual values–pivot height controlled.
Again, good agreement is obtained. If we now consider that an increase in load occurs, which reduces the pivot height by 3.3% to 58 , then the Observer estimates the following:
| a min. film thickness of 24.1 μm | (a decrease of 4.4%) |
| a maximum temperature of 69.0 °C | (an increase of 0.7%) |
| an effective temperature of 55.8 °C | (an increase of 0.3%) |
| an applied load of 3787 N | (an increase of 4.9%) |
| a power loss of 198 W | (an increase of 0.4%) |
Thus, an increase in load of 4.9% can be detected as a 3.3% decrease in pivot height, whereas the maximum temperature only changes by 0.7%. Pivot height, therefore, is a more sensitive indicator than maximum temperature and is a better parameter to monitor.
The above approach is a steady-state one. If a time-dependent Observer is required, then the time-dependent heat flow equations in the fluid and the surrounding solids must be solved. This is likely to be expensive in computer time and may not merit the additional cost and complexity.
4. Conclusions
This paper presented a method by which measurements can be captured from a running, tilting-pad thrust bearing (the Plant) and used to modify the operating parameters of the unit. Control is achieved by designing an Observer whose inputs are either the maximum temperature in the bearing or the pivot height.
The Observer is, in some ways, an inverse model of the bearing that runs in parallel to it and estimates the states of the bearing, such as the applied load, pivot height, minimum film thickness, maximum temperature, effective temperature and power loss. These estimated parameters are then used in a control algorithm to modify bearing parameters such as inlet temperature or pivot location. The following two approaches to Observer design are employed: one using the design guide ESDU 83004, and the other an FE, thermo-hydrodynamic simulation. The latter Observer employed performance equations derived from multiple regression analyses of the output from an FE model. Hence, the FE model itself, once validated against the real bearing, only had to be run once to produce the data for the regression analysis. When the estimates from both Observers were compared with the simulations of the real bearing, it was shown that the Observers produce quality estimates of the bearing’ states. An appropriate controller can then be designed to modify the inlet temperature of the lubricant to achieve the required performance of the Observer, and hence the bearing itself. Whilst only a steady-state operation is considered, the method could be developed to study time-varying situations, although the cost of this may be prohibitive. It is likely that this overall approach could be adopted in many tribological environments to obtain more detail about their states without the requirement of extensive instrumentation.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Disclaimer
Ethical review and approval were waived for this study because neither humnans nor animals were involved in the research study.
Appendix A
ESDU 83004 proposes the following equations:
where pmean is the mean pressure (Pa),
And
where . Substituting Equation (A3) into Equation (A1) produces the following:
Additionally, Equation (A2) can be rearranged to yield the following:
Substituting Equation (A5) into Equation (A4) results in the following:
Rearranging produces the following:
From Equation (A2),
which can be manipulated to produce the following:
Appendix B

Table A1.
Data from the runs of the FE model used in the multiple regression analysis.
Table A1.
Data from the runs of the FE model used in the multiple regression analysis.
| Inlet Temperature Tin (degC) | Pivot Height hp (μm) | Tilt (rad) | Force per Pad, w (N), | Mean Viscosity, | Max_pad_temp, Tmax (°C) | Minimum Film Thickness hmin (μm) | Mean Fluid Temp, Te (°C) | Power Loss per Pad z (W) |
|---|---|---|---|---|---|---|---|---|
| 50 | 40 | 0.0012240 | 6226.5 | 0.078142 | 75.19 | 15.948 | 59.134 | 228.5 |
| 50 | 50 | 0.0015175 | 4679.8 | 0.089024 | 71.562 | 20.18 | 56.495 | 214.72 |
| 50 | 60 | 0.0017955 | 3585.1 | 0.096495 | 68.593 | 24.718 | 54.869 | 199.05 |
| 50 | 70 | 0.0020635 | 2806 | 0.10178 | 66.107 | 29.451 | 53.793 | 183.79 |
| 50 | 80 | 0.0023210 | 2246.5 | 0.10583 | 64.014 | 34.391 | 53.008 | 170.05 |
| 60 | 40 | 0.0011610 | 4284.7 | 0.05216 | 78.43 | 17.186 | 66.371 | 162.35 |
| 60 | 50 | 0.0014460 | 3081.5 | 0.057505 | 74.984 | 21.585 | 64.308 | 145.83 |
| 60 | 60 | 0.0017180 | 2297.8 | 0.061058 | 72.41 | 26.241 | 63.101 | 131.27 |
| 60 | 70 | 0.0019810 | 1763.5 | 0.063473 | 70.426 | 31.072 | 62.34 | 118.53 |
| 60 | 80 | 0.0022410 | 1390.4 | 0.065169 | 68.884 | 35.963 | 61.831 | 107.6 |
| 70 | 40 | 0.0011060 | 3070.6 | 0.036353 | 83.94 | 18.267 | 74.583 | 120.18 |
| 70 | 50 | 0.0013700 | 2075.5 | 0.038194 | 80.64 | 23.079 | 72.907 | 101.74 |
| 70 | 60 | 0.0016380 | 1492.5 | 0.039374 | 78.394 | 27.813 | 72.002 | 87.978 |
| 70 | 70 | 0.0019030 | 1121.7 | 0.040156 | 76.806 | 32.605 | 71.462 | 77.347 |
| 70 | 80 | 0.0021650 | 871.44 | 0.040695 | 75.643 | 37.457 | 71.113 | 68.895 |
| 80 | 40 | 0.0010990 | 2428.3 | 0.028603 | 90.811 | 18.404 | 83.485 | 95.223 |
| 80 | 50 | 0.0013620 | 1625.2 | 0.029739 | 88.199 | 23.236 | 82.181 | 80.052 |
| 80 | 60 | 0.0016220 | 1155 | 0.03037 | 86.4 | 28.127 | 81.479 | 68.599 |
References
- Ulbrich, H.; Althaus, J. Actuator Design for Rotor Control. In Proceedings of the 12th Biennial Conference on Vibration and Noise, Montreal, QC, Canada, 17–21 September 1989; pp. 17–22. [Google Scholar]
- Santos, I.F. Design and Evaluation of Two Types of Active Tilting Pad Journal Bearings. In Active Control of Vibration; Burrows, C.R., Keogh, P.S., Eds.; Mech. Eng. Publication Ltd.: London, UK, 1994; pp. 79–87. [Google Scholar]
- Deckler, D.C.; Veillette, R.J.; Cho, F.K.; Braun, M.J. Modelling of a Controllable Tilting Pad Bearing. In Proceedings of the American Control Conference, Albuquerque, NM, USA, 4–6 June 1997. [Google Scholar]
- Deckler, D.C.; Veillette, R.J.; Braun, M.J.; Cho, F.K. Simulation and Control of an Active Tilting-Pad Journal Bearing. Tribol. Trans. 2004, 47, 440–458. [Google Scholar] [CrossRef]
- Vivaros, H.P.; Nicoletti, R. Lateral Vibration Attenuation of Shafts Supported by Tilting-Pad Journal Bearing With Embedded Electromagnetic Actuators. J. Eng. Gas Turbines Power 2014, 136, 042503. [Google Scholar] [CrossRef]
- Wu, M.F.; Cavalva, K.L. Experimental validation and comparison between different active control methods applied to a journal bearing supported rotor. Struct. Control. Health Monit. 2019, 26, e2446. [Google Scholar] [CrossRef]
- Morosi, S.; Santos, I.F. Experimental Investigations of Active Air Bearings. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition. Volume 7: Structures and Dynamics, Parts A and B, Copenhagen, Denmark, 11–15 June 2012; ASME. pp. 901–910. [Google Scholar] [CrossRef]
- Babin, A.; Kornaev, A.; Rodichev, A.; Savin, L. Active thrust fluid-film bearings: Theoretical and experimental studies. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 261–273. [Google Scholar] [CrossRef]
- Santos, I.F. Trends in Controllable Oil Film Bearings. In IUTAM Symposium on Emerging Trends in Rotor Dynamics; Gupta, K., Ed.; IUTAM Bookseries; Springer: Dordrecht, The Netherlands, 2011; Volume 1011. [Google Scholar] [CrossRef]
- Sanadgol, D.; Maslen, E. Effects of actuator dynamics in active control of surge with magnetic thrust bearing actuation. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; pp. 1091–1096. [Google Scholar] [CrossRef]
- Riaz, M.T.; Rehman, W.U.; Ali, H.; Husnain, S.; Jiang, G.; Lodhi, E.; Aaqib, S.M.; Qureshi, M.M. Design and Experimental Validation of a Small-Scale Prototype Active Aerostatic Thrust Bearing. In Proceedings of the 2021 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 26–27 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Luenberger, D. An Introduction to Observers. IEEE Trans Autom. Control. 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Smith, E.H.; Gill, K.F. Controlling the attitude and two flexure-modes of a flexible satellite. Aeronaut. J. 1977, 81, 41–44. [Google Scholar] [CrossRef]
- Banghu, B.; Bingham, C. Nonlinear state-observer techniques for sensorless control of automotive PMSM’s, including load-torque estimation and saliency. In Proceedings of the European Power Electronics and Drives Conference EPE 2003, Toulouse, France, 2–4 September 2003. [Google Scholar] [CrossRef]
- Eissa, M.A.; Sali, A.; Hassan, M.K.; Bassiuny, A.M.; Darwish, R.R. Observer-Based Fault Detection With Fuzzy Variable Gains and Its Application to Industrial Servo System. IEEE Access 2020, 8, 131224–131238. [Google Scholar] [CrossRef]
- Chen, X.; Su, C.-Y.; Fukuda, T. A nonlinear disturbance observer for multivariable systems and its application to magnetic bearing systems. IEEE Trans. Control. Syst. Technol. 2004, 12, 569–577. [Google Scholar] [CrossRef]
- Rehman, W.U.; Guiyun, J.; Yuan Xin, L.; Yongqin, W.; Iqbal, N.; UrRehman, S.; Bibi, S. Linear extended state observer-based control of active lubrication for active hydrostatic journal bearing by monitoring bearing clearance. Ind. Lubr. Tribol. 2019, 71, 869–884. [Google Scholar] [CrossRef]
- Calculation Methods for Steadily Loaded, Off-Set Pivot, Tilting-Pad Thrust Bearings. ESDU 83004. 1983. pub. IHS EDSDU. Available online: https://www.esdu.com/cgi-bin/ps.pl?sess=unlicensed_1220115034725fdk&t=doc&p=esdu_83004 (accessed on 25 November 2021).
- Comsol Multiphysics, Version 5; COMSOL, Inc.: Avenue Burlington, MA, USA. Available online: https://cn.comsol.com/ (accessed on 25 November 2021).
- Almqvist, T.; Glavatskikh, S.B.; Larsson, R. (June 22, 1999) THD Analysis of Tilting Pad Thrust Bearings—Comparison Between Theory and Experiments. ASME J. Tribol. 2000, 122, 412–417. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).