Third-Generation Calibrations for MeerKAT Observation
Abstract
1. Introduction
2. MeerKAT Observations of the Saraswati Supercluster
3. Third-Generation Calibrations
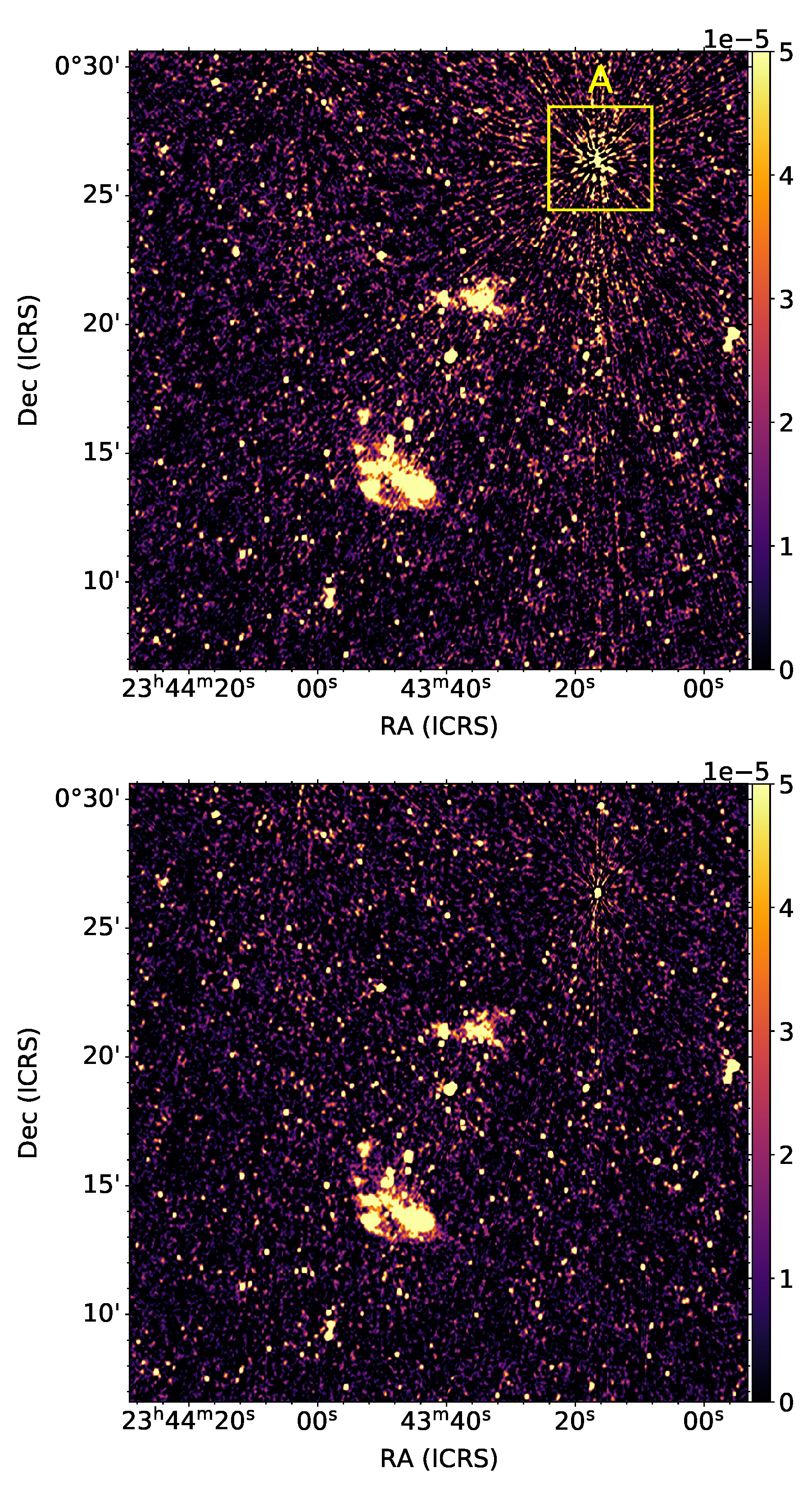
3.1. Source Peeling with CubiCal
3.2. Facet-Based Calibration with killMS
3.3. Applications of the DDE to MeerKAT Data
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://github.com/Athanaseus/aimfast, accessed on 1 October 2021. |
| 2 |
References
- Tempel, E.; Stoica, R.S.; Martínez, V.J.; Liivamägi, L.J.; Castellan, G.; Saar, E. Detecting filamentary pattern in the cosmic web: A catalogue of filaments for the SDSS. Mon. Not. R. Astron. Soc. 2014, 438, 3465–3482. [Google Scholar] [CrossRef]
- Jasche, J.; Leclercq, F.; Wandelt, B.D. Past and present cosmic structure in the SDSS DR7 main sample. J. Cosmol. Astropart. Phys. 2015, 1, 036. [Google Scholar] [CrossRef]
- Vazza, F.; Ferrari, C.; Brüggen, M.; Bonafede, A.; Gheller, C.; Wang, P. Forecasts for the detection of the magnetised cosmic web from cosmological simulations. Astron. Astrophys. 2015, 580, A119. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef]
- Camilo, F.; Scholz, P.; Serylak, M.; Buchner, S.; Merryfield, M.; Kaspi, V.M.; Archibald, R.F.; Bailes, M.; Jameson, A.; van Straten, W.; et al. Revival of the Magnetar PSR J1622-4950: Observations with MeerKAT, Parkes, XMM-Newton, Swift, Chandra, and NuSTAR. Astrophys. J. 2018, 856, 180. [Google Scholar] [CrossRef]
- van Haarlem, M.P.; Wise, M.W.; Gunst, A.W.; Heald, G.; McKean, J.P.; Hessels, J.W.T.; de Bruyn, A.G.; Nijboer, R.; Swinbank, J.; Fallows, R.; et al. LOFAR: The LOw-Frequency ARray. Astron. Astrophys. 2013, 556, A2. [Google Scholar] [CrossRef]
- Gupta, Y.; Ajithkumar, B.; Kale, H.S.; Nayak, S.; Sabhapathy, S.; Sureshkumar, S.; Swami, R.V.; Chengalur, J.N.; Ghosh, S.K.; Ishwara-Chandra, C.H.; et al. The upgraded GMRT: Opening new windows on the radio Universe. Curr. Sci. 2017, 113, 707–714. [Google Scholar] [CrossRef]
- McConnell, D.; Allison, J.R.; Bannister, K.; Bell, M.E.; Bignall, H.E.; Chippendale, A.P.; Edwards, P.G.; Harvey-Smith, L.; Hegarty, S.; Heywood, I.; et al. The Australian Square Kilometre Array Pathfinder: Performance of the Boolardy Engineering Test Array. Publ. Astron. Soc. Aust. 2016, 33, e042. [Google Scholar] [CrossRef]
- van Weeren, R.J.; de Gasperin, F.; Akamatsu, H.; Brüggen, M.; Feretti, L.; Kang, H.; Stroe, A.; Zandanel, F. Diffuse Radio Emission from Galaxy Clusters. Space Sci. Rev. 2019, 215, 16. [Google Scholar] [CrossRef]
- Govoni, F.; Orrù, E.; Bonafede, A.; Iacobelli, M.; Paladino, R.; Vazza, F.; Murgia, M.; Vacca, V.; Giovannini, G.; Feretti, L.; et al. A radio ridge connecting two galaxy clusters in a filament of the cosmic web. Science 2019, 364, 981–984. [Google Scholar] [CrossRef]
- Noordam, J.E.; Smirnov, O.M. The MeqTrees software system and its use for third-generation calibration of radio interferometers. Astron. Astrophys. 2010, 524, A61. [Google Scholar] [CrossRef]
- Bagchi, J.; Sankhyayan, S.; Sarkar, P.; Raychaudhury, S.; Jacob, J.; Dabhade, P. Saraswati: An Extremely Massive 200 Megaparsec Scale Supercluster. Astrophys. J. 2017, 844, 25. [Google Scholar] [CrossRef]
- Pearson, T.J.; Readhead, A.C.S. Image Formation by Self-Calibration in Radio Astronomy. Annu. Rev. Astron. Astrophys. 1984, 22, 97–130. [Google Scholar] [CrossRef]
- van Weeren, R.J.; Williams, W.L.; Hardcastle, M.J.; Shimwell, T.W.; Rafferty, D.A.; Sabater, J.; Heald, G.; Sridhar, S.S.; Dijkema, T.J.; Brunetti, G.; et al. LOFAR Facet Calibration. Astrophys. J. Suppl. Ser. 2016, 223, 2. [Google Scholar] [CrossRef]
- Shimwell, T.W.; Tasse, C.; Hardcastle, M.J.; Mechev, A.P.; Williams, W.L.; Best, P.N.; Röttgering, H.J.A.; Callingham, J.R.; Dijkema, T.J.; de Gasperin, F.; et al. The LOFAR Two-metre Sky Survey. II. First data release. Astron. Astrophys. 2019, 622, A1. [Google Scholar] [CrossRef]
- Tasse, C.; Shimwell, T.; Hardcastle, M.J.; O’Sullivan, S.P.; van Weeren, R.; Best, P.N.; Bester, L.; Hugo, B.; Smirnov, O.; Sabater, J.; et al. The LOFAR Two-meter Sky Survey: Deep Fields Data Release 1. I. Direction-dependent calibration and imaging. Astron. Astrophys. 2021, 648, A1. [Google Scholar] [CrossRef]
- Jonas, J.L. MeerKAT - The South African Array With Composite Dishes and Wide-Band Single Pixel Feeds. IEEE Proc. 2009, 97, 1522–1530. [Google Scholar] [CrossRef]
- Bagchi, J.; Enßlin, T.A.; Miniati, F.; Stalin, C.S.; Singh, M.; Raychaudhury, S.; Humeshkar, N.B. Evidence for shock acceleration and intergalactic magnetic fields in a large-scale filament of galaxies ZwCl 2341.1+0000. New Astron. 2002, 7, 249–277. [Google Scholar] [CrossRef][Green Version]
- van Weeren, R.J.; Röttgering, H.J.A.; Bagchi, J.; Raychaudhury, S.; Intema, H.T.; Miniati, F.; Enßlin, T.A.; Markevitch, M.; Erben, T. Radio observations of ZwCl 2341.1+0000: A double radio relic cluster. Astron. Astrophys. 2009, 506, 1083–1094. [Google Scholar] [CrossRef]
- Józsa, G.I.G.; White, S.V.; Thorat, K.; Smirnov, O.M.; Serra, P.; Ramatsoku, M.; Ramaila, A.J.T.; Perkins, S.J.; Molnár, D.C.; Makhathini, S.; et al. MeerKATHI—An end-to-end data reduction pipeline for MeerKAT and other radio telescopes. arXiv 2020, arXiv:2006.02955. [Google Scholar]
- Tasse, C. Applying Wirtinger derivatives to the radio interferometry calibration problem. arXiv 2014, arXiv:1410.8706. [Google Scholar]
- Tasse, C. Nonlinear Kalman filters for calibration in radio interferometry. Astron. Astrophys. 2014, 566, A127. [Google Scholar] [CrossRef]
- Kenyon, J.S.; Smirnov, O.M.; Grobler, T.L.; Perkins, S.J. CUBICAL-fast radio interferometric calibration suite exploiting complex optimization. Mon. Not. R. Astron. Soc. 2018, 478, 2399–2415. [Google Scholar] [CrossRef]
- Tasse, C.; Hugo, B.; Mirmont, M.; Smirnov, O.; Atemkeng, M.; Bester, L.; Hardcastle, M.J.; Lakhoo, R.; Perkins, S.; Shimwell, T. Faceting for direction-dependent spectral deconvolution. Astron. Astrophys. 2018, 611, A87. [Google Scholar] [CrossRef]
- Parekh, V.; Kincaid, R.; Thorat, K.; Hugo, B.; Sankhyayan, S.; Kale, R.; Oozeer, N.; Smirnov, O.; Heywood, I.; Makhathini, S.; et al. MOSS I: Double radio relics in the Saraswati supercluster. arXiv 2021, arXiv:2110.07713. [Google Scholar]
- Smirnov, O.M. Revisiting the radio interferometer measurement equation. I. A full-sky Jones formalism. Astron. Astrophys. 2011, 527, A106. [Google Scholar] [CrossRef]
- Williams, P.K.G.; Allers, K.N.; Biller, B.A.; Vos, J. A Tool and Workflow for Radio Astronomical “Peeling” in CASA. Res. Notes Am. Astron. Soc. 2019, 3, 110. [Google Scholar] [CrossRef]
- Smirnov, O.M. Revisiting the radio interferometer measurement equation. II. Calibration and direction-dependent effects. Astron. Astrophys. 2011, 527, A107. [Google Scholar] [CrossRef]
- Smirnov, O.M.; Tasse, C. Radio interferometric gain calibration as a complex optimization problem. Mon. Not. R. Astron. Soc. 2015, 449, 2668–2684. [Google Scholar] [CrossRef]





| Source | RMS | DR1 | DR2 | DR3 | MAD | MIN | MAX | SUM NEG | SKEW | KURT | NORM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Jy beam | Jy beam | mJy beam | mJy beam | mJy beam | |||||||
| A | |||||||||||
| DI | 37.0 | 2288.95 | 66.77 | 4282.69 | 15.0 | −1.27 | 84.61 | −1170.39 | −6.59 | 175.62 | 132,287.84 |
| DD (CubiCal) | 16.0 | 5384.67 | 521.17 | 6011.81 | 9.0 | −0.16 | 1.93 | −642.60 | 1.2 | 12.53 | 32,982.4 |
| DD (killMS) | 18.0 | 4819.0 | 207.25 | 6728.32 | 8.0 | −0.41 | 84.35 | −648.68 | −2.19 | 61.92 | 68,730.32 |
| B | |||||||||||
| DI | 23.0 | 1452.71 | 89.54 | 1703.88 | 11.0 | −0.38 | 33.66 | −780.03 | 1.26 | 41.87 | 48,327.62 |
| DD | 17.0 | 1948.45 | 203.95 | 2391.82 | 9.0 | −0.17 | 1.11 | −640.55 | 1.53 | 13.83 | 40,406.3 |
| DD | 19.0 | 1729.23 | 89.72 | 2616.98 | 8.0 | −0.37 | 32.80 | −525.23 | 0.78 | 63.84 | 43,861.46 |
| C | |||||||||||
| DI | 37.0 | 859.03 | 35.10 | 1587.62 | 12.0 | −0.89 | 31.37 | −974.88 | 2.47 | 161.56 | 81,404.9 |
| DD | 18.0 | 1786.54 | 123.52 | 2228.62 | 9.0 | −0.25 | 3.19 | −683.07 | 0.56 | 23.3 | 29,623.6 |
| DD | 23.0 | 1329.44 | 39.44 | 2416.91 | 9.0 | −0.77 | 30.30 | −647.93 | −6.74 | 207.55 | 134,959.27 |
| D | |||||||||||
| DI | 38.0 | 823.34 | 39.83 | 1596.63 | 15.0 | −0.79 | 31.54 | −1009.09 | −1.06 | 91.05 | 52,000.85 |
| DD | 24.0 | 1335.30 | 57.60 | 2241.26 | 10.0 | −0.55 | 2.09 | −668.20 | −3.96 | 86.19 | 97,598.32 |
| DD | 23.0 | 1293.42 | 52.52 | 2414.77 | 9.0 | −0.58 | 30.27 | −672.90 | −4.67 | 102.88 | 107,886.23 |
| E | |||||||||||
| DI | 201.0 | 903.81 | 31.46 | 9191.59 | 47.0 | −5.77 | 181.59 | −4077.27 | −5.1 | 196.17 | 117,774.02 |
| DD | 30.0 | 6097.83 | 237.53 | 12,902.67 | 14.0 | −0.76 | 2.60 | −895.05 | 0.29 | 76.61 | 38,640.5 |
| DD | 36.0 | 4446.85 | 233.40 | 12,927.69 | 17.0 | −0.69 | 162.08 | −1178.32 | −1.13 | 33.72 | 43,613.94 |
| Full image | |||||||||||
| DI | 20.0 | - | 31.46 | 9191.59 | 9.0 | −5.77 | 181.59 | −196,953.75 | −15.45 | 5995.31 | 75,889,133.95 |
| DD | 14.0 | - | 115.12 | 12,902.67 | 7.0 | −1.58 | 42.21 | −154,531.51 | −1.59 | 636.36 | 26,984,110.13 |
| DD | 12.0 | - | 122.20 | 12,927.69 | 7.0 | −1.33 | 162.08 | −154,750.56 | −4.86 | 531.9 | 43,647,231.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parekh, V.; Kincaid, R.; Hugo, B.; Ramaila, A.; Oozeer, N. Third-Generation Calibrations for MeerKAT Observation. Galaxies 2021, 9, 90. https://doi.org/10.3390/galaxies9040090
Parekh V, Kincaid R, Hugo B, Ramaila A, Oozeer N. Third-Generation Calibrations for MeerKAT Observation. Galaxies. 2021; 9(4):90. https://doi.org/10.3390/galaxies9040090
Chicago/Turabian StyleParekh, Viral, Robert Kincaid, Benjamin Hugo, Athanaseus Ramaila, and Nadeem Oozeer. 2021. "Third-Generation Calibrations for MeerKAT Observation" Galaxies 9, no. 4: 90. https://doi.org/10.3390/galaxies9040090
APA StyleParekh, V., Kincaid, R., Hugo, B., Ramaila, A., & Oozeer, N. (2021). Third-Generation Calibrations for MeerKAT Observation. Galaxies, 9(4), 90. https://doi.org/10.3390/galaxies9040090






