Abstract
This review aims at proposing to the field an overview of the Cusp-core problem, including a discussion of its advocated solutions, assessing how each can satisfactorily provide a description of central densities. Whether the Cusp-core problem reflects our insufficient grasp on the nature of dark matter, of gravity, on the impact of baryonic interactions with dark matter at those scales, as included in semi-analytical models or fully numerical codes, the solutions to it can point either to the need for a paradigm change in cosmology, or to to our lack of success in ironing out the finer details of the ΛCDM paradigm.
1. Introduction
Notwithstanding the many successes of the concordance cosmology model, also known as the CDM model, fundamental issues remain open. Most of the cosmology community considers the CDM paradigm to accurately describe the Universe’s large scale structure formation and evolution, its early state and the proportions of its content in matter and energy [1,2,3,4,5]. This view has been reinforced with each new discovery, such as the kinetic Sunyaev-Zel’Dovich (SZ) effect, the Cosmic Microwave Background (CMB) B-mode polarisation [6], or its lensing [7,8]... Among its most famous resisting issues, the questions of the nature, “fine tuning” and “cosmic coincidence” problems of the cosmological constant remain open [9,10].
The “cosmological constant fine tuning problem” emerges from the large discrepancy between the observed value of and the huge values predicted by quantum field theories for the present quantum vacuum energy, the latter exceeding the former by more than 100 orders of magnitude [9,10,11]: the cosmological observation upper bounds are limited to , while the naive theoretical expectations obtain . This is the most extreme fine tuning problem known to physics. As is constant, the concordance model also presents a strong fine tuning of the dark energy (DE) initial conditions. The “cosmic coincidence problem” questions the relative coincidence of the orders of magnitude at present of dark matter (DM) and DE energy densities [12].
Further issues of the CDM paradigm revolve around observations of the CMB or of smaller scales structures. Unexplained statistical anomalies in the CMB large-angle fluctuations contradict the CDM CMB multipoles statistical independence, which reflects the assumption that the content of our Universe should realise a Gaussian and statistically isotropic random field. These anomalies comprise detection in the CMB of a power hemispherical asymmetry [13,14,15,16,17,18], of a cold spot, marking an underdense region [19,20,21], and of a quadrupole-octupole alignment [22,23,24,25,26]. Such anomalies could either mark new physics, be caused by statistical effects [27], or reflect unknown systematics.
Furthermore, puzzling tensions have been found between the cosmological fluctuations parameters measured by cluster number counts and weak lensing, compared with the 2013 Planck results [28], as well as between the 2013 Planck Hubble parameter, compared with SNIa data. Those tensions have persisted between the Planck 2015 data and the growth rate [29], as well as with the CFHTLenS weak lensing [30].
In addition to those CMB issues, the description of small scale structures in the CDM model also raise problems e.g., [31,32,33,34,35,36]. They count the “missing satellite problem” MSP [32,37], the “Too Big To Fail” problem TBTF [34,35], the angular momentum catastrophe AMC [38,39], the satellites planes problem [40], and the baryonic Tully-Fisher relation reproduction problem [41]. Among those small-scale problems, the so called Cusp-core problem CC [31,42] retains a central role. The CC coins the gap between the flat central slopes of density profiles in dwarf galaxies (i.e., dwarfs), Low Surface Brightness (LSBs), and Irregulars galaxies on one hand, while they all are DM dominated, and on the other hand, the cuspy central slopes of dissipationless N-body simulations density profile predictions [43,44,45].
Besides the aforementioned issues, further problems of the CDM paradigm [46,47,48,49,50] are left out of this review, as we focus here on the CC problem. Note however that the formation of cusps and issues of satellites in CDM are tightly connected, as shown through the mechanism in some unified models [51,52,53] that can turn cusps into cores as well as alleviate the MSP, since the shape of the parent halo determines strongly its tidal effect on satellites e.g., [54,55,56], with cored profiles even capable of stripping the satellite out of existence [56].
We organise the discussion as follows: starting with a short exposition of the initial discussions on the CC problem, Section 2 will summarise its issues, while early solutions involving baryons, DM matter type changes or gravity modifications will be presented in Section 3. A review of the baryonic solutions to SPH simulations collapse models through gas heating feedback effects from dynamical friction of baryonic clumps will be discussed in Section 4, including a discussion in Section 4.1, where the supernovae explosions [57] solutions of core heating will be presented, a Section 4.2 that will discuss both baryonic approaches and a unified baryonic solution [53] and a presentation of the resulting mass dependent density profile in Section 4.3. Finally, Section 5 will review and discuss solutions modifying the DM nature, before to conclude in Section 6.
2. Exposition of the Cusp/Core Problem
The CC problem emerged after Flores & Primack [42] and Moore [31] showed DDO galaxies’ rotation curves could be better fitted with cored (or pseudo-)isothermal density profiles, ruling out cuspy profiles. As dissipationless CDM model simulations persisted to produce cuspy profiles (see Figure 1), this was coined as the CC problem.
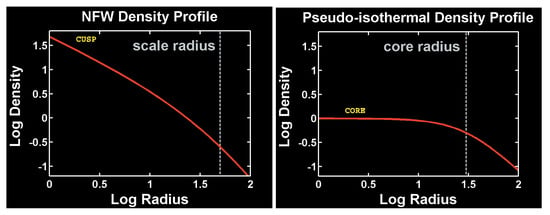
Figure 1.
Illustration of the CC problem. The cuspy NFW profile is displayed on the left panel, with the dotted vertical line representing the profile’s scale radius. The right panel exemplifies the cored profile, with the dotted vertical line marking the profile’s core radius.
Indeed, such cuspy DM profile was obtained in the dissipationless N-body simulations of Navarro, Frenk, & White [43,58], yielding inner density , for the power index . Moreover, they found such profile (thus coined NFW profile) to emerge universally, thus independently of cosmology and scale, from dissipationless simulations. This universality was challenged by the obtaining of a steeper profile at [59,60], or even by studies observing dependence of the inner slope on the nature of the object and/or on its mass [61,62,63,64,65,66,67,68,69]. Finally (see Figure 2), the so-called Einasto profile, yielding a central flattening down to [70], tend to better fit more recent N-body dissipationless simulations [71]. Nevertheless, the CC problem persists, and has been strongly debated for two decades, as even this smallest predicted inner slope from dissipationless N-body simulations exceeds slopes outputted from SPH simulations [72,73], semi-analytical models [74,75,76,77,78,79,80] or even observations [36,81,82,83,84,85].
Historically, the first contradicting results originated from dwarf and LSB observation in HI: their rotation curves (RCs) did not match the NFW halo [86,87,88]. Fueling the debate, steep profiles could not be excluded for several objects studied by van den Bosch & Swaters [89]. However evidence against steep profiles further mounted through H data, in de Blok & Bosma [90], in the inner slopes measured by de Blok et al. [82], and obtained by Spekkens et al. [91], although contradicted by RCs agreeing with cusply profiles produced by Hayashi et al. [92]. Nevertheless, flat profiles were usually in agreement with high resolution observations [93,94,95,96,97], etc.
Understanding of the construction of RCs was refined with their decomposition for some spiral galaxies into their components in terms of stars, gas and DM, fitted with various models in Gentile et al. [98,99,100]. The results favoured constant density core profiles over cuspy models, in the same way as the THINGS (The HI Nearby Galaxy Survey) 7 dwarf galaxies processed by Oh et al. [36]. Figure 3 compares the RCs of the latter, among others, with those of NFW and pseudo-isothermal (ISO) profiles, clearly showing the ISO fits them best. The LITTLE THINGS survey also produced similar results [101].
However, as the previous results emanate mainly from low brightness objects such as dwarfs or LSBs, while large galaxies or high-surface brightness objects inner structure determination is more complex, general statements on inner density profiles of all galaxies, in particular on their cored or cuspy nature, are far from settled. Indeed, while the high-surface brightness galaxies studied by [102] present cored centres, their analysis by e.g., [68,78,103,104,105] disagree. Other surveys contain a mix of cored and cuspy objects. In particular, in the THING sample, galaxies with low luminosity, , tend to follow a cored ISO profile, while luminous galaxies, , are equally well fitted by cored or cuspy profiles.
Such confused picture is reinforced by the lack of systematically flat slopes in dwarf galaxies: in Simon et al. [103], a large scatter in the inner slopes of the low mass spirals NGC2976, NGC4605, NGC5949, NGC5963 and NGC6689, was obtained, with a cored profile for NGC2976, a cuspy slope for NGC5963, while for NGC4605, for NGC5949 and for NGC6689. We illustrate this in Figure 4: its top left panel confronts NGC5963’s DM halo RC (black dots with error-bars) to RCs computed from (a) the [74] model that accounts for baryonic physics (yellow dashed line), (b) a fitted NFW profile (cyan line), (c) a fitted pseudo-isothermal profile (ISO, shortdashed magenta line), while its top right panel confronts the same kinds of fits to the RC from NGC5949, and the bottom panel only displays NGC2976’s RC with a flat power law (black line) and model (a) (dashed line). The NGC5963 RC is well fitted by the cuspy NFW profile’s. The NGC5949 RC is equally well approximated by RCs from a cuspy NFW or ISO cored profiles. Finally, the NGC2976 RC reflects a very flat inner profile (). The three RCs displayed in Figure 4 all agree with the [76] model.
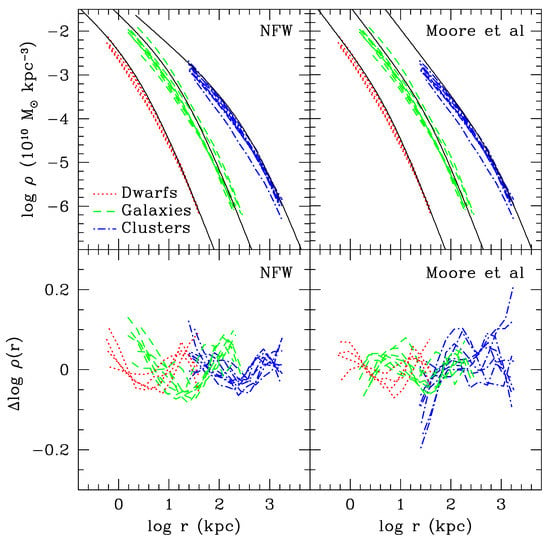

Figure 2.
Comparison of density profiles with simulations. The NFW profile (solid lines) is compared in the top left panel with simulations from Ref. [106]. Note that the Einasto profile fits also well those simulations [44]. The same comparison for the Moore profile is displayed in the top right panel, and each panel represents simulations of dwarfs galaxies (red line), medium size galaxies (green line), and galaxy clusters (blue line). The bottom left and right panels focus on the residuals between the corresponding theoretical profiles and the compared simulations this figure is reproduced from Figure 1 in [106].
It appears then that if a cored profile agrees with RCs of many dwarfs, some remain clearly cuspy.
In addition, opposite conclusions on the core/cusp question have been drawn from the same objects with similar techniques by different studies: Ref. [107] analysed NGC2976’s DM inner profile to lie within , when the same object yielded sometimes incompatible profiles in [108], traced either by gas, , or stars, .
In agreement with the preceding considerations, galaxies’ observed RCs were recognised by [109] to exhibit much more diversity than what simulations produced.
The conclusion this brings emphasizes the difficulty of galaxies’ inner slope assessment, including for dwarfs. This moreover calls for a redefinition of the CC problem in terms of inner mass, rather than inner slope of galaxies density or RCs. Indeed, as shown by several studies, including those mentioned here, and despite kinematic maps recent improvements, there exists no agreement on DM slope distributions correlated with morphologies [36,103,108], but rather a range of profiles.
This lack of agreement appears even more obvious for the extreme ends of the mass spectrum of galaxies: for larger masses, dominated by stars, as in spiral galaxies, and for lighter galaxies, such as dwarf spheroidals (dSphs), which models require the account of biases, that result in opposite consequences.
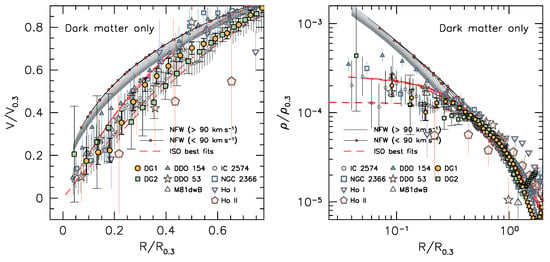

Figure 3.
Confrontations between RCs (left panel) or density profiles (right panel) from the pseudo-isothermal (ISO, red dashed line) and the NFW (solid lines) profiles, to thoses from (a) the [72] simulated galaxies marked DG1 and DG2, and (b) 7 dwarf galaxies selected from THINGS. The small red dots emphasize the NFW RCs for [10–90] km/s. RCs are normalised to the rotation velocity V at the distance where , noted this figure is reproduced from Figure 6 in [36].
To interpret and assess these results on dSphs, a range of approaches have been tried. As stellar orbit anisotropy and mass are degenerate in the spherical Jeans equation [110], its results highly vary with assumptions. Similar degeneracies also hinder the approach applying parameter space maximum likelihood to Jeans modelling [111,112,113]. With Schwarzschild modelling, cored profiles are found [114,115,116,117], for, e.g., Sculptor or Fornax dSphs. More recently a study by [118] has found that the majority of dSPhs favor cuspy profiles. Multiple stellar populations methods also obtained cored profile [119,120,121,122] for Fornax (measuring its slope at kpc) and Sculptor (for its slope at pc). Nevertheless, the lack of agreement on a single inner distribution for dSphs still remains, with contradictory results such as the cusp obtained from Schwarzschild modelling for Draco [117].
Such scatter preventing a unified understanding occurs as well for galaxy clusters scales. In clusters MACS1206, MS2137-23, RXJ1133, A383, A1201, A963 and RXJ1133, studies with a combination of BCG’s (Brightest Central Galaxy) stars velocity dispersion, weak and strong lensing, Sand et al. [123] found cores, and only the RXJ1133 profile could be compatible with the NFW model. Such flatter profiles were also obtained, in similar studies (see also [124]), for A611 by Newman et al. [125], 2009, for A383 by Newman et al. [126], 2011 and for MS2137, A963, A383, A611, A2537, A2667, A2390 by Newman et al. [127], 2013. This contradicts other studies such as the cuspy profile in the strong lensing and X-ray observations of A611, among seven cuspy or flat profiles of relaxed massive clusters with average slope , by Donnaruma et al. [128].
More generally, conflicting estimates with simulations are common with gravitational lensing [128,129,130], although much shallower slopes (0.5) can also result from that technique [123,125,126,127,131,132,133]. A similar wide slopes spanning can stem from X-ray analyses, ranging from cores at 0.6 [134], to NFW-like 1.2 [135], up to very cuspy profiles 1.9 [136]. However, NFW also agrees with some X-ray profiles [137].
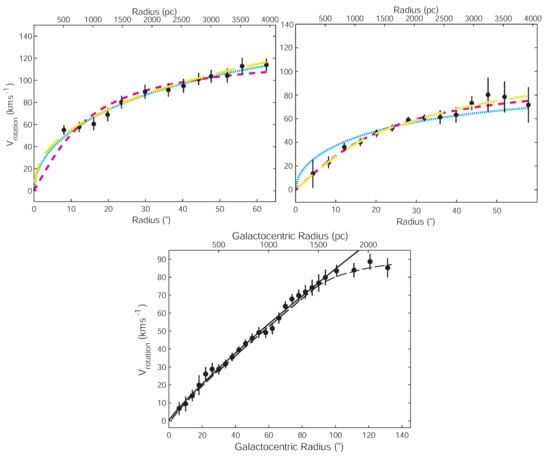

Figure 4.
Presentation of the DM halo RCs (error-barred, black dots) for the galaxies NGC5963, NGC5949 and NGC2976, provided in Ref. [103]. In the two top panels showing resp. NGC5963, on top left, and NGC5949, on top right, are represented NFW profile fitted RCs (dotted cyan lines), pseudo-isothermal profile fitted RCs (ISO, short-dashed magenta lines) and the RCs from Ref. [76]’s model (yellow dashed lines). The bottom panel, displaying NGC2976, compares its observations with a density power-law fit model (slope , solid line) and with Ref. [76]’s model (dashed line; this figure is adapted from Figures 4 and 5 in Ref. [76]).
Although the situation improved with more recent, higher resolution, observations, as they agree on flatter-than-NFW profiles on average, compared with the early data’s conflicting density profiles inner structures, such high resolution pictures still display galaxy to galaxy inner structure diversity, reflected in [109] simulations.
Despite the agreement of the IC2574 galaxy’s RC with the simulations from Ref. [109] (presented in Figure 5, shaded green band) for radii > 6 kpc, the galaxy’s inner region behaviour differs completely from their simulations. Such divergence emphasizes that correct RC slope predictions for some inner regime doesn’t entail that the successful simulation remains accurate in all regimes of the RC. As the main characteristic of the CC problem resides in the inner galaxy’s mass deficit [109], the focus should lie in the DM excess in the central distribution produced by CDM rather than on the density profile shape. The observation vs prediction discrepancy already appears where the asymptotic value of the circular velocity is reached [138].
It is therefore unfortunate that practically no observational papers in the field depart from the inner slope estimation method using α. A notable exception can be found in the inner slope estimation via the integrated indicator performed by [120] in the cases of the Fornax and Sculptor galaxy clusters. As Γ is integrated, contrary to the local α, its evaluation is easier, but provides a lesser constraint on the inner slopes.
Finally, an alternate probe of the DM inner profile flattening to rotation curves consists in the dynamical friction timing (DFT) technique, that is assessing the time an object like a globular clusters (GC) requires to move inside the distribution of mass. It clearly represents an indirect method to obtain the DM inner slope, however it presents the advantage of directly probing the density, rather that the integrated mass furnished by rotation curves. Thanks to the presence of GCs in dwarf galaxies, like Sagittarius or Fornax, Ref. [86] was able to show analytically that the inner density profile must be cored. This behaviour focused on GCs was confirmed by several simulations [139,140,141,142]. The key interests of the DFT technique are twofold: (1) it concentrates on smallest scale galactic systems like dwarf galaxies, on which the proposed solutions to the CC problem show their main drawbacks, and (2) its method is independent from that of rotation curves, giving information on the structure of the mass distribution in the studied systems. Recently, DFT studies have shifted their focus from GCs to DF on stars. Using analytical approaches, as in Hernandez [143], or numerical techniques, in Inoue [144], on ultra-faint satellite galaxies of our galaxy, was shown that DM fractions imply DFT for the stars themselves and are incompatible with cusped dark matter haloes, at these tiny scales, out of reach of SNF models, and even maybe of DFBC solutions.
Since smaller mass objects are more likely to harbour inner profiles in agreement with predictions of dissipationless, N-body, codes (cuspy), a definite verdict on the nature of the inner slope, cored or cuspy, of the smaller end of the mass spectrum, i.e., dSphs, is critical.
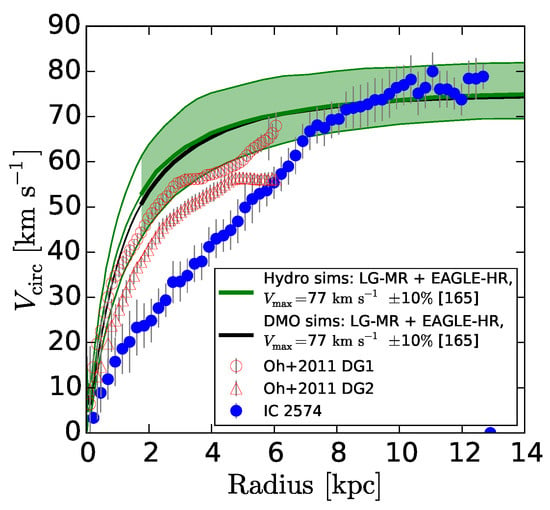

Figure 5.
Observed RC from galaxy IC2574 (filled blue circles with error bars) compared with the DG1 (open red circles) and DG2 (open red triangles) simulated galaxies from [72]. The green shaded region and line, as well as the black line, respectively stands for the scatter of one and both median RCs for simulated galaxies from which this figure, Figure 1 is extracted from Ref. [109].
3. Initially Proposed CC Problem Solutions
In the wealth of propositions to solve the CC problem, the initial attempts were determined by the limited state of knowledge and observations. Systematic effect and poor resolution were first invoked as the origin for the CC inconsistencies e.g., [89,145]: they blamed beam smearing, slit-misplacement, non-circular motions or beam off-centering, as they are sources of systematically lowering slopes.
For instance, finite HI emission beam size tends to smear the HI observations, inducing a larger measured disk, depending on the HI distribution, beam size, intrinsic velocity gradients and galaxy inclination angle. With modern high spatial resolution (<1 kpc, see below), the smear can be resolved.
The slit misplacement for an H emitting galaxy can entail missing the galaxy’s dynamic centre, inducing a flatter measured profile. One of the solutions to avoid this slope underestimate have used 3d spectroscopy [94,102]. As H observations assume circular motions for the gas, any non-circular orbits underestimate the slope. Some have found [97] that those departures from circular velocity remain within the order of a few km/s. Current high resolution rotation curve data are able to discriminate cuspy from cored haloes with asymptotic inner slopes [84].
Projection effects were put forward by several papers [92,106,146] to explain the discrepancy of their simulations with observations, despite their claims of good agreement of their profiles, becoming shallower in the range the virial radius towards the centre. Their argument lies on the practice of representing the 3D DM haloes motion with a spherically averaged circular velocity, traced by the gas disk rotation speeds. Their claim is to blame the disagreement with data on the correspondence fitting formulae rather than their simulations [92]. Current DM-only high resolution simulations clearly reject this explanation, as their inner profiles cannot reach shallower slope than ≃−0.8 [70], compared with high resolution galaxy observations revealing much smaller values.
More generally, simulations limitations, such as over-merging or lack of relaxation or resolution, have been blamed to source the CDM model’s failure [82,147,148]. This was already questioned then by Ref. [149]’s convergence tests proving the dissipationless N-body simulations of the time were adequate to properly obtain the CDM density profiles, despite their neglecting the galaxies inner kpc regions effects of baryons. Such effects were shown to dominate the DM generated profiles in clusters’ central 10 kpc regions [123,125,126,127]. Modern simulations no longer suffer from the blamed limitations and hydrodynamic cosmological high resolution models now account for baryons, as will be discussed in the next section on baryonic resolutions of the CC Problem.
Questioning of the very paradigm of CDM opened the door to speculations on the nature of DM, such as warm WDM [150], fluid [151], repulsive [152], fuzzy [153], decaying [154], self-annihilating [155], or self-interacting [156] DM. More fundamental questioning led to altered small scale DM power spectrum e.g., [157] or modifications of gravity itself, such as the so-called [158,159] or [160,161,162,163] theories, or the so-called Modified Newton Dynamics MOND, [164,165]1. Such paradigmatic modifications, whether touching DM nature, initial conditions or the nature of gravity, will hereafter be denoted, in their impact the CC problem, as “cosmological solutions“, and developed in Section 5.
4. Baryonic Resolutions of the CC Problem
Before resorting to the above mentioned “cosmological solutions” to deal with the CC problem, a thorough check, whether neglected or poorly understood local physics could explain it, would be wise. Indeed, discarding the concordance, i.e., CDM, model would risk to significantly alter the otherwise very successful predictions CDM provided, thus loosing the explanations for many observations of our Universe. This is the aim of the current section.
Keeping the framework of the CDM model, “astrophysical solutions” alter the results of pure CDM structure formation with some “heating” mechanism applied to inner DM distribution, originated in the effects of baryons. The inner density profile gets then flatter than for pure CDM evolution. Such “heating” mechanism could be provided by
- accounting for the action, in structure formation, of angular momentum;
- the induced dynamics from a central black hole, claimed to shallow the DM cusp [170,171,172];
- the modification of equilibrium from the presence of a rotating bar;
- the mechanism of dynamical friction that induces baryons-DM transfer of angular momentum [74,173,174];
- the supernova (SN) explosions-generated bulk motions in gas, dubbed AGN feedback [54,55,72].
Larger angular momentum acquired by a proto-structure has been correlated to flatter inner density profile by many contributors within the framework of spherical [175,176,177,178,179,180,181,182,183,184,185,186], or even elliptic [187], infall models.2 Such models were able to produce RCs agreeing with those of dwarf galaxies [179], which profile builds flatter than giant galaxies’ because structure’s density peak height3 anticorrelate with the angular momentum they get during their formation.
Dynamical friction was shown to flatten, and even erase, the DM formed cusps in both galaxy clusters and dwarfs by transferring energy from baryon clumps to DM [173,174]. Conversely, DM adiabatic contraction (AC) in haloes steepens their density profiles [193,194].4
The above effects see also [196] were all combined in the model from Del Popolo [74], including:
- -
- tidal torques caused ordered angular momentum acquired during the structure formation;
- -
- its obtained random angular momentum;
- -
- its dynamical friction induced baryons-DM energy and angular momentum exchanges;
- -
- and the effects of its DM adiabatic contraction (hereafter, AC).
In addition to inducing flatter density profiles in the center of galaxies and clusters, dynamical friction and angular momentum also tend to modify their overall internal structure [197,198,199,200]. The simple confrontation of real structures, including baryons, with the outputs of dissipationless simulations is demonstrably incorrect [74]: the non-negligible action of baryons in the inner regions of structures explains the failures of N-body simulations to reproduce observed density profiles. This is illustrated in Figure 6, showing halo evolution for two masses, and , modeled using the “Dynamical Friction from Baryonic Clumps” scenario (hereafter DFBC scenario) from Ref. [74] and discussed below.
The impact of baryons content, environment and formation history on dwarf galaxies density profiles was demonstrated with the Del Popolo DFBC model [76].
The “heating” mechanism 5 was first put forward by Navarro et al. [201], flattening the inner profile from the feedback of SN explosion into the medium, as discussed below.
In the present state of the field, the discussion on astrophysical solutions to the CC problem have narrowed down to the following mechanisms
- the cusp reduction through “supernovae feedback flattening” (SNFF) [54,55,72,73,201,202,203], and
- the cusp flattening via the “Dynamical Friction from Baryonic Clumps” (DFBC) [74,173,174,204,205,206,207,208,209,210].
They will be discussed in more details in Section 4.1 and Section 4.2, and are put in context below.
In general, baryons and DM usually “interact” in smooth distributions via AC, that can be counterbalanced by transferring energy back from baryons to DM. AC leads DM to collapse towards the centre of the halo, steepens its profile and increase its central density. The counteracting transfer has the opposite effect. It can occur via
- Dynamical friction transfer of incoming clumps orbital energy to DM.This leads DM particles to drift towards the halo edges and thus to flatten the DM density profile [74,173,174,204,205,206,207,208,209,210], see also the review of [211].
- DM particles “heating” from galactic internal energy sources [211].Such source expelling from, or relocating baryons in, the halo (for instance, bulk motions induced from SN explosions, [54,55]) can temporarily flatten the gravitational potential, shift DM particles outwards, and flatten the cusp.
We will now discuss the two favoured “heating” mechanisms in the CC problem solution, and how those solutions are synthesised into the proposal of a mass dependent density profile for DM haloes with baryons.
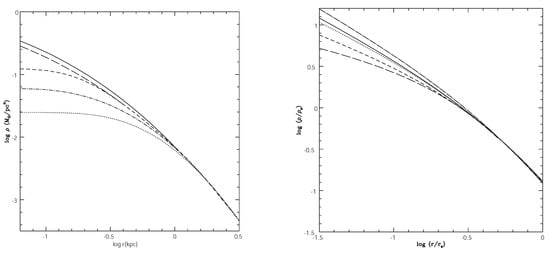

Figure 6.
Halo densityprofile evolutions with redshift following the DFBC scenario of [74]. The evolution for a halo yields profiles at , and 0, characterised resp. by the solid, long-dashed, short-dashed, dot-dashed and dotted lines, and presented in the left panel. The profile evolution, ending at with the total (DM + Baryons) mass density profile of a halo and marked by the dot-dashed line, is reproduced in the right panel. That DM profile is characterised at 1 and 0 resp. by the solid, dotted, short-dashed, and long-dashed lines this figure is extracted from Figures 3 and 5 in [74].
4.1. Discussion on Supernovae Feedback Flattening
Historically, the first solution proposed to the CC problem while accounting for the effects of baryons, as initially suggested in Ref. [42] and confirmed by many efforts, employed SNF [54,55,72,73,201,202,203,212,213].
Profile flattening by a single sudden baryons expulsion into the halo was first shown by Ref. [201], and found to be most effective in dwarfs and other shallow potential structures. However, energy from a single explosion was shown [214] to remain insufficient to drive the profile to a core, while repeated moderately violent explosive events would be required see [215] for a different point of view.
A more detailed study of the [201] approach, focused on evolving from NFW profiles to DDO154’s RC via a gas outflow event modeled from an abrupt change in the disk potential, by Gelato and Sommer-Larsen [202], established that at least 75% of the disk mass should be expelled that way to generate this RC.
In the case of larger galaxies and deeper potential structures, a core was shown by Read and Gilmore [203] to result from repeated and alternate outflows and re-accretions of gas.
In primordial galaxies, a core was determined to follow from SN-explosions-driven gas random bulk motions [54,55], as confirmed in [72] simulations. The average slope of the latter simulations were compared with observations of THINGS dwarfs in Refs. [36,85]. Producing simulations for larger galaxies than [72], and comparing them with observations [73], correlation between the stellar mass and the inner slope were obtained for galaxies were obtained. These results were obtained from simulated galaxies thanks to the N-Body+SPH code GASOLINE [216]. With an 86 kpc softening, gas particles and DM particles resolution were reduced to and , reps., thanks to the “zoom” technique of Ref. [217]. Two realisations were produced, distinguished by their star formation thresholds: a High Threshold run (HT), with star forming hydrogen cloud densities >cm, and a Low Threshold run (LT), with hydrogen densities >cm. Both SNF blast wave mechanism [218] and/or early stellar feedback [219] were implemented in those simulations, as later by [69] in the same way. The Governato simulations resulting energy feedback to the interstellar medium (ISM) amounted to ergs from >8 stars, while the ISM gas ejecting energy was coupled to the SN expelled energy via the coefficient . The fiducial was selected for the MaGICC simulations [219].
Comparably, a combination of bursty star formation and SNF, inducing inner (1 kpc) halo potential fast oscillations and expanding gas bubbles when the central cold gas density reaches >100/cm and stars start to form5, was shown to flatten the cusp [221]. However in this model, no noticeable modifications of the DM inner density profiles are induced for smaller densities (e.g., 0.1/cm). The case of larger mass galaxies was treated by Governato et al. [73] with the same method (also see Figure 7 top panels). Agreement with the results of [221] (Figure 7 bottom left panel) was obtained from introducing a new SNF scheme in the RAMSES adaptive mesh refinement code by Teyssier et al. [212], showing flat galaxies inner profile for . Similar outcomes with a lower threshold at were produced by Onorbe et al. [222] (Figure 7 bottom right panel)6.
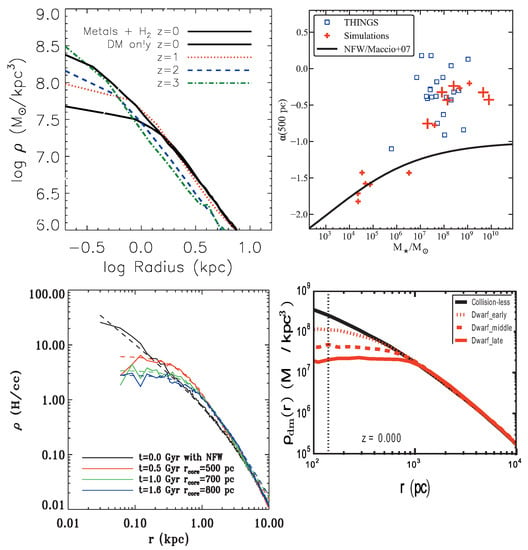
Figure 7.
Density profiles including baryonic effect. The Figure 1 in Ref. [73]’s hydrodynamic simulations present density profile evolution (top left panel) reflected on their inner logarithmic slopes (at 0.5 kpc). The Ref. [73]’s results (red crosses) are compared, in the top right panel, for different stellar mass galaxies, with THINGS galaxies’ results (open squares), and with DM-only N-body simulation reproduced from Figure 3 in [73], shown as a solid line. Results from hydrodynamic simulations are presented in the bottom panels: density profile evolution from Figure 5 in Ref. [212] are shown on the bottom left panel, while the bottom right presents hydrodynamic evolution for three different types of dwarfs, where stars all form either in early times, in medium or in late times in Figure 6 of [222].
Since their simulations found little effect of baryons on rotation curves of galaxies with km/s, even in their inner regions, this perspective was denounced by [109]. They argued that the cores obtained by [221], since no evidence of core formation was detected in their [109] work, were inherently reflecting an ad hoc choice of parameters.
Such understanding agrees with the findings of Ref. [223], which 7 high-resolution dwarfs simulations, included in halos with 1-2 and following different assembly history, could not reveal any inner core flattening. A very extended assembly history dwarf, thus also having an extended star formation rate (SFR) history, exhibits their lowest detected inner slope: they measured it to reach, at 0.01–0.02 , up to −0.8. It also remains consistent with the core-less simulated realistic galaxies of Ref. [224].
In addition to those contradictions in core formation between various high resolution hydrodynamical simulations, several criticisms have arisen on the methods and assumptions used in simulation models of the types of [72,225], as they obtain faulty
- core formation energetics: the number of stars, obtained in their galaxies, generates an insufficient energy to flatten the galaxies cusp [226]. Moreover, their required core-forming baryonic mass marginally exceeds the dSphs observed baryon content [215]. That problem in Penarrubia [226] is illustrated in Figure 8’s left panel. However, the right panel displays the opposite results from Maxwell’s study. In addition, the SNFF solution they propose for the CC problem, requiring the formation of numerous SNs, entails a star formation efficiency (SFE) constraint towards larger values, opposite to the SFE constraint induced by the complementary solution to the Too-Big-To-Fail (TBTF) problem [34,35]7;
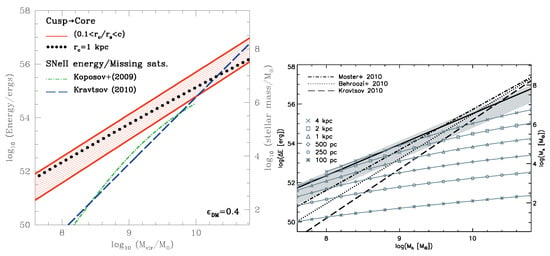 Figure 8. Minimal SN energy/mass output, , needed to convert a DM cusp into a core as a function of halo mass, , measured at virial mass, , in the left panel. The constraints on the minimal amount of energy as a function of mass can also be expressed in terms of stellar mass, standing for luminosity, shown in the right axes of each panel. Conversion from stellar mass proceeds, in the left panel, from a luminous MW satellites constrained star formation efficiency , the resulting luminosities converting into SNeII energy output via Ref. [226]’s Equation (6) with strong energy coupling , while it assumes, in the right panel, 100% efficiency (). The left panel, reproduced from Figure 2 in [226], presents: (a) the range of minimum SN explosions energy required to obtain a core of size given within , with c and , respectively being the concentration parameter and the scale radius of the NFW profile at given virial mass , as the red shaded area; (b) for a fixed core size kpc, the dotted black line is obtained; (c) the SN explosion energy outputs, indicated from two different studies [227,228] as dot-dashed green and dashed blue lines, denote those compatible with the “missing satellite” [32,37] problem and reveal, for haloes with , the tension with the “core/cusp” problem. The right panel, extracted from Figure 3 in [229], shows: (a) the left panel red shaded area of Penarrubia et al. [226]’s energy estimates, as shaded grey area; (b) solid lines with symbols for the conversion energy of cuspy to pseudo-isothermal density profiles at fixed core sizes, indicated in the legend by the symbol types; (c) the solid black line for the scaling with halo mass , while the ratio of the cusp mass redistribution limit radius, , over the halo radius, , is fixed; (d) the dotted, dashed, and dot-dashed lines, respectively, for the Behroozi et al. [230], Kravtsov [228], and Moster et al. [231] relations.
Figure 8. Minimal SN energy/mass output, , needed to convert a DM cusp into a core as a function of halo mass, , measured at virial mass, , in the left panel. The constraints on the minimal amount of energy as a function of mass can also be expressed in terms of stellar mass, standing for luminosity, shown in the right axes of each panel. Conversion from stellar mass proceeds, in the left panel, from a luminous MW satellites constrained star formation efficiency , the resulting luminosities converting into SNeII energy output via Ref. [226]’s Equation (6) with strong energy coupling , while it assumes, in the right panel, 100% efficiency (). The left panel, reproduced from Figure 2 in [226], presents: (a) the range of minimum SN explosions energy required to obtain a core of size given within , with c and , respectively being the concentration parameter and the scale radius of the NFW profile at given virial mass , as the red shaded area; (b) for a fixed core size kpc, the dotted black line is obtained; (c) the SN explosion energy outputs, indicated from two different studies [227,228] as dot-dashed green and dashed blue lines, denote those compatible with the “missing satellite” [32,37] problem and reveal, for haloes with , the tension with the “core/cusp” problem. The right panel, extracted from Figure 3 in [229], shows: (a) the left panel red shaded area of Penarrubia et al. [226]’s energy estimates, as shaded grey area; (b) solid lines with symbols for the conversion energy of cuspy to pseudo-isothermal density profiles at fixed core sizes, indicated in the legend by the symbol types; (c) the solid black line for the scaling with halo mass , while the ratio of the cusp mass redistribution limit radius, , over the halo radius, , is fixed; (d) the dotted, dashed, and dot-dashed lines, respectively, for the Behroozi et al. [230], Kravtsov [228], and Moster et al. [231] relations. - energy coupling: their exceeds the 0.05 coupling that studies such as [232] deduced;
- star formation threshold: the [72] results have been found in [109,233] to require a very high star formation threshold;
- tensions with TBTF solution: those models simply encounter adverse conditions [215,234,235] when trying to solve the TBTF problem;
- feedback resolution: accurately describing the cusp transformation into a core via their feedback processes would require better resolution than they present [236,237,238,239].
Despite the SNF limitations,8for , correlations between and galaxies inner slope have been found, comparing THINGS dwarves average slopes with [72]’s simulations in Refs. [36,85], and similarly in [73] for larger objects.
Inversely, hydrodynamic simulations for produce cuspy profiles, in contradiction with the Fornax and Sculptor cored inner structure found by Ref. [120] thanks to their more reliable DM haloes’ slopes from mass profiles . Only with 50% more SN energy injections could Ref. [240] claim agreement with [120]’s cores.
Assuming SN feedback and other specific assumptions, a Semi-Analytic model from Gnedin and Zhao [214] claimed impossibility to obtain cores. As, among details of stellar feedback, the core formation impact of baryonic clumps, such as in Ref. [74], is ignored, such objection is weakened.
However, there exists one core-forming SNF dwarf galaxies simulation for masses : with the P-SPH mode in the GIZMO code, Ref. [222] obtained cores in a much less natural way than in the DFBC scenario, discussed in the next section.
4.2. Discussion of Gas Clumps Dynamical Friction
As discussed in the introduction of the present Section 4, Refs. [173,174] proposed an alternate path from SNF for the turning of cusps into cores: baryon clumps with mass ratios to the system above can transfer, through dynamical friction (DF), clumps orbital energy to DM. Such heating induces similar effects to SNF without the need to wait for a full massive stellar cycle, moving to outer orbits the central DM particles and thus flattening the inner DM density profile. It is more efficient on earliest, smallest haloes of the hierarchical structure formation.
DFBC was first shown to function in galaxies [173], then in clusters [174]. Cluster C0337-2522 evolution with such model [205] showed the BCG generation precedes DFBC inner slope formation, resulting in flatter than NFW inner profiles with .
Implemented in a hybrid N-body/SPH simulation, DFBC galaxy evolution showed heated up cusps by baryons subhalos into a core of ≃1 kpc, and was compared with DM-only systems and mixed DM/baryons systems [206].
Refs. [208,209,210]’s simulations confirmed such outcomes.
The main steps of the DFBC can be outlined in the following:
- the linear phase develops from initial DM and diffuse gas proto-structures.
- DM gravitational collapse first form non-linear potential wells, attracting then the baryons.
- Unstable accreting gas then fragment into clumpy structures e.g., [241,242,243,244,245,246,247,248,249], leading to highly gas-rich discs.
- Further instability in the rotating discs, triggered by their surface density, , exceeding a threshold at [250], with , the disc’s 1-D vertical velocity dispersion and , its angular velocity, while Q is related with the instability of the vertical kinetic to gravitational balance to the excess of centrifugal angular velocity, fragment it into clumps, which largest can reach mass ratios with the disc of a few percent and 1 kpc radii e.g., [251]. Typical clumps, in galaxies with baryon mass –, range within – see [246,248,249], are rotationally supported, in Jeans equilibrium [248] and stable for long periods ( Myr).
- As in local star-generating systems and following the Kennicutt-Schmidt law, a few percents of those clumps’ gas converts to stars [251], while DF migrates them to the DM halo (galactic) center.
- The first collapse phase’s AC compressed baryons [193,194] and e.g., galaxy at in our Figure 6, reenforcing the DM cusp.
- The previous effect is countered by DF-induced migration of clumps to galaxy center, as DF transfers energy and angular momentum from baryons to DM, heating up the cusp into a core.
- SNF only intervenes later (e.g., around ), when SN explosions expel gas, decreasing surrounding stellar density. Moreover, such feedback destroys the smallest gas clumps as soon as a small fraction of their mass turns to stars.9
Although sharing some common features (e.g., clumps to DM energy transfer via gravitational interaction), leading some to consider SNFF and DFBC as the same idea implemented differently, they fundamentally differ on two crucial points:
- their respective profile flattening epochs differ markedly: while pure SNFF DM profile does not depart noticeably from NFW at [222,225,252], DFBC flattening initiate at higher redshifts (, see Figure 6);
- their clumps moving energy sources diverge in nature: in Refs. [54,55]’s definition, while clumps motion is driven, in the SNFF model, by SN explosions energy, the DFBC views them to just “passively” infall to the halo centre.
The two competing scenarios predictions for the central density slope vs. stellar mass and vs. circular velocity relationships were confronted in Refs. [253,254] with a series of high resolution data predictions from the Milky Way, Sculptor, Fornax, LITTLE THINGS [101], THINGS dwarfs [36,85] and Refs. [103,108]. Such confrontation showed slightly better performance from the DFBC model compared with the SNFF scenario, as the former predicts core emergence at smaller stellar masses than , limiting the latter. Although very small dwarfs () cannot produce cores in DFBC, this nevertheless agrees with results from Ref. [255].
Both competing model face the same caveats in their resolution of the CC problem: galaxies containing a bulge have been demonstrably able to reconstitute their cusp [79]. This effect can even been found in dwarf galaxies [237].
4.3. Mass Dependent DM Density Profiles
Assuming that baryons are indeed responsible for some cored DM haloes, while allowing some others to be cuspy, and using the results of SPH simulations, the SNFF or DFBC models, some authors synthesised the diversity of DM density profiles and generalized the usual density profiles, giving the mass dependent empirical law that would solve the CC problem. For example, Ref. [256] generalized the Einasto profile into a mass dependent parameterised profile, encompassing both cuspy and cored cases, while [257] obtained such mass dependent profile by modifying the Zhao [258] profile. In the following we will give the details concerning the works of [257,259].
In previous discussions, we saw that the DM density profile is well approximated by the NFW law, and even better fitted by the Einasto profile. Those two profiles are obtained by DM-only simulations. There, the hydrodynamical processes, fundamental in the determination of the structure of the density profile, are neglected. For example AC [193,194] produced by gas cooling, which strengthens cusps, is not taken into account by N-body, DM-only simulations. At the same time, the presence of baryons can expand haloes. As discussed in Section 4.1 and Section 4.2, stellar feedback and DFBC can produce a halo expansion and a flattening of the inner density profile. As discussed there, Ref. [69] showed how the inner slope is modified by SNF. The results of this paper were used to obtain a DM halo whose slope depends from the ratio between stellar and DM masses, .
The generalised NFW profile (gNFW) is a specific form of a law depending on three parameters :
being the scale radius and the scale density. and , are the logarithmic slopes of the inner and outer regions respectively, while the sharpness of the transition from inner to outer region is specified by . The peculiar case corresponds to the NFW profile. The goal of [259] was that of making the profile given in Equation (1) mass dependent, in the sense that its three parameters would depend on the ratio , using haloes obtained, in [69] from SPH simulations. The density profile of the haloes were fitted, using Equation (1). The behavior of the three parameters was captured using fitting laws as a function of . The outer slope was modeled with a parabola. In the cases of the inner slope, , and of the transition parameter, , double power law model were used.
The best fits for these parameters to the values for SPH galaxies are shown as dotted lines in Figure 9. The functional forms of the fits are:
where .
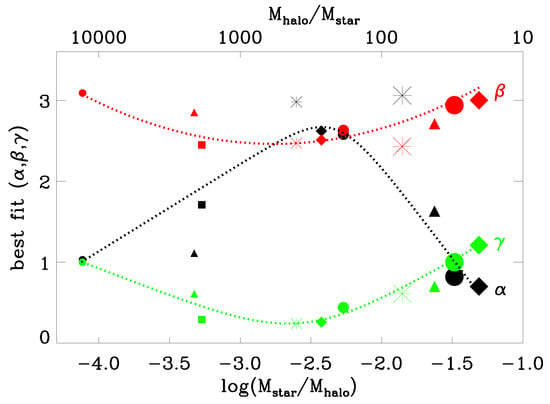
Figure 9.
Best fits to the generalised NFW parameters (green), (red), and (black) plotted in terms of . The symbols mark various SPH simulated galaxies Figure reproduced from Figure 1 in [259].
Given the stellar-to-halo mass ratio of a galaxy, by means of Equations (1) and (2), it is possible to compute the entire DM profiles.
Ref. [259] also showed that the concentration parameter is dependent on . The dependence of the concentration parameter on is shown in Figure 10. Each simulation is represented by its symbol and size as described in Table 1 of [259]. The dependence of the ratio between concentration parameters obtained from SPH and pure DM N-body simulations, , on is nearly exponential. Its best fit is:
where .
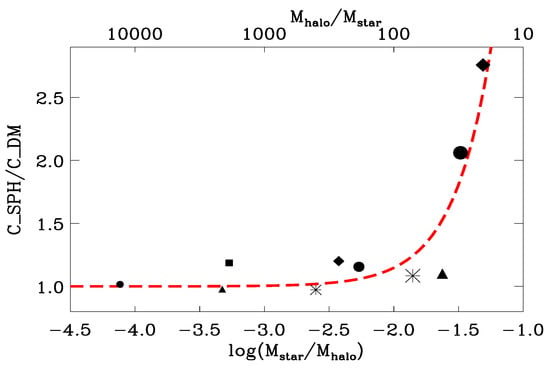
Figure 10.
Ratio, for a given halo, between concentration parameters of its models, in the SPH simulation and in the DM-only simulation, as a function of . The best fit to is represented by the dashed red line Figure reproduced from Figure 4 in [259].
has been derived fitting a NFW profile to the DM-only version of each galaxy, while has been obtained from hydrodynamical runs where their galaxies DM halo model profile had their scale radius correspondence converted between into .
A comparison of the model with simulated data of the density profiles, and rotation velocities gives a good agreement.
The mass dependent density profile idea from Ref. [259] was applied by several other authors. As mentioned above, it was applied by Lazar et al. [256] to the Einasto profile and by Freundlich et al. [257] to the so-called Dekel-Zhao density profile, a peculiar case of Equation (1). We now focus on another popular profile, similar in performance to the Einasto profile, the modified NFW model, adopted by Freundlich et al. [257] in the form from Zhao [258]
where the radial dependence is encoded in , with respect to the characteristic radius , and the density scale is set by the typical density . It is equivalent to the generalised NFW profile, noting the parameters , and . Note that, for any natural numbers n and k, setting and , it is possible to integrate the mass and obtain the corresponding equilibrium velocity dispersion and gravitational potential analytically. Some choices of integers actually yield very good DM simulations fits, and are even able to accommodate baryons’ presence, as well as cusps or core.
The profile referred to as the Dekel-Zhao (DZ) profile, found for and , which corresponds in Equation (4) to and , and leaves two free parameters, a and a concentration parameter c, have been found, using the NIHAO suite of simulations [260], particularly efficient at representing cored profiles [261], but also cuspy profiles.
Following Equation (4), it takes the form
using and defining the concentration from the virial equilibirum radius of the spherical mass distribution , where the average density at that radius computes as , while the shape factor is involved in the profile mass integration, yielding the average critical density , and thus relating the density scale to the shape parameters, c and the central slope a, as .
As measurements are made at fixed given resolution, the central slope is actually an integrated slope with respect to the actual profile. Freundlich et al. [257] explicits, for a fixed resolution , an inner logarithmic slope
and the corresponding averaged concentration parameter
The physically motivated restrictions to positive density and inner slope result in the conditions and , respectively. One can reobtain the intrinsic parameters , employed in analytic expressions, from the observed , usually bestowed to numerical tests, by inverting Equations (6) and (7), as
and
Equations (18) and (21) and Section 2.3 in Freundlich et al. [257] respectively provided analytic expressions for the DZ profile’s gravitational potential, velocity dispersion and lensing properties, as well as, using some NiHAO SPH simulations suite’s profiles (see their Figure 3), compared the DZ, gNFW and Einasto profiles through fits, assuming their parameters free, and finally finding the DZ profile performs significantly better than Einasto’s and marginally better than the gNFW on NiHAO.
In this context, the mass dependent, DZ-based profile from Freundlich et al. [257], was constructed, as in Di Cintio et al. [259], from the NIHAO simulations suite [260], to set the DZ parameters functional forms. SPH simulations were fitted by Di Cintio et al. [69] with a similar profile to Equation (4), to set the free parameters forms as a function of , as did Lazar et al. [256] with the Einasto profile and Freundlich et al. [257] with the DZ profile. However, the mass dependence introduced, similarly to Equations (2) by Di Cintio et al. [259], to improve galaxies and clusters density profiles fits, such as in the modified Einasto profile from Lazar et al. [256] or in the modified NFW from [262], does not allow to keep any analytic form for the mass, as detected through lensing, velocity dispersion or gravitational potential. On the contrary, the DZ profile keeps that possibility intact.
This is the advantage of the DZ profile fit by Freundlich et al. [257], applied to simulated NIHAO haloes’ density profile logarithms, optimising the parameters, spacing the grid profile radii r in the range 0.01 -, through a least-square minimization. Setting the virial mass , the profile can set the scale by extracting the corresponding , leaving the remaining free parameters a and c. The star distribution can be samely fitted to get the star mass at virial radius and obtain the corresponding . The theoretical slope and concentration are related to the integrated (observed) ones through Equations (6)–(9), respectively, as shown in Figure 11.
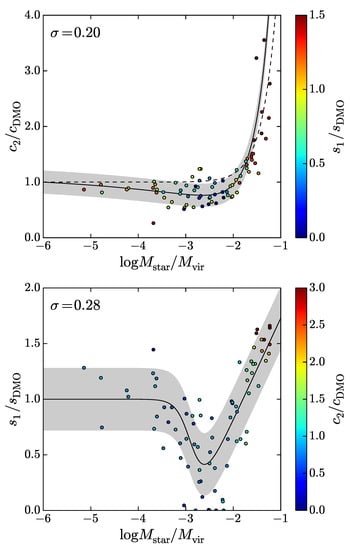
Figure 11.
Ratios, for integrated slopes and concentrations (lower panel) and (upper panel), between the DZ model parameters and their DM-only NFW profiles counterparts, as a function of mass ratios . The NFW integrated parameters, and , were obtained from the Dutton and Macciò [263] relation Equations (47) and (48) of [257] and their best fits, Equations (45) and (49) on their Figure 9, here marked as plain black lines. The best fit residual rms is shown in gray. The dashed black line in the panel represents the best-fit function from Di Cintio et al. [259]. Color coding, indicated on the right side in each panel, for each halo compounds the information of the other panel.
This fitting procedure allowed to obtain, for each NIHAO haloes, their and as a function of , as seen Figure 8, black dots in Freundlich et al. [257].
The obtained and behaviour were synthesised in two parameterised functions of , where , , , and are ajustable and which used values were given in Table 1 of Freundlich et al. [257]
while the parameter is introduced for
The resulting mass-dependent profile presents the advantages, over the Di Cintio et al. [259] approach, to require less free parameters as well as to allow integration into analytic expressions for lensing properties, dispersion velocity and gravitational potential.
5. Cosmological Solutions to the CC Problem
The CC problem, together with the other small scale problems encountered by the CDM model, open the question of a more general failure of the CDM’s paradigm. This justifies models in which the nature of DM or gravity itself are modified. Such models encountered various degrees of success in their already widely checked instances. We will here focus on alternate models of DM. Several approaches have been used and we will detail the two main avenues, before discussing other possibilities.
5.1. Warm DM
Warm DM (WDM) presents the simplest departure from CDM, endowing DM with a small velocity dispersion ( m/s nowadays), also linked, for thermally produced DM, to a small DM relic mass [150,264]. Since velocity dispersion is expected to decrease with time, it should be more important in the past and thus smear small scale structure formation. Such smear induces similar DM “heating” as the baryonic solutions of Section 4: in this case the WDM particles higher velocity than for CDM smears the haloes to flatter profiles as well as produce fewer low mass haloes. These effects of WDM on structure formation have been copiously simulated e.g., [252,265,266,267].
Despite solving the CC problem for haloes with their corresponding scales on a case by case basis by tuning its particle mass, WDM does not manage to solve it with one mass for all galaxies, nor in the entire CC problem mass range [268]. As shown in Ref. [269], neither WDM or pure collisionless CDM models can match observed disk galaxies rotation curves, while they can agree with hydrodynamical simulations including baryons (see Section 2’s discussion).
In addition, Ref. [265], for a keV thermal relic, and several other authors e.g., [270,271,272], shown that, for instance, the strong-lensing subhalo fraction is too high compared with WDM produced subhaloes. Furthermore, WDM thermal mass displays tensions between expected core size (1 kpc core corresponding to 0.1 keV) and large scale structure 1–2 keV leads to 10–20 pc cores, see Figure 12 and Ref. [273]. In conclusion, because its power spectrum falls off too sharply, WDM does not improve on CDM [274]. Finally, since WDM structure formation is also shown to modify the Lyman- forest [275], the situation is even worse, as WDM solution to the CC problem in our vicinity cannot, at the same time, be consistent with observed high redshift Lyman- forest.
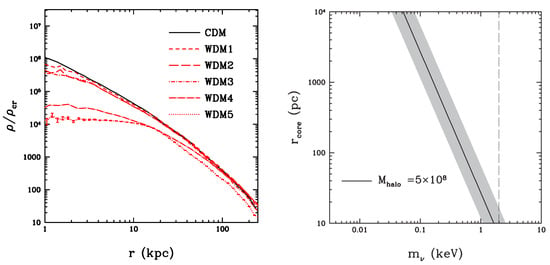
Figure 12.
WDM effect on the CC problem, reproduced from Figures 2 and 8 in [273]. The WDM core formation is illustrated against the CDM density profile (solid black line) by showing profiles from a range of five WDM particle masses, from keV (WDM1, as per the legend) to 0.05 keV (WDM5), in the left panel. The right panel synthesises the WDM core radius obtained for its given particle mass with other constraints: while the solid black line marks the core size dependence at fixed halo mass, the shaded area limits the plane to the cosmological constraints for and the vertical dashed line sets the upper limit from large scale observations.
5.2. Self-Interacting DM
The second simplest variation away from CDM, coined Self-interacting DM hereafter SIDM [156], consists in granting to DM a self-interaction cross-section, within the same magnitude of nucleon-nucleon interactions (≃(m/g)cm).10 The resulting elastic scattering in regions of highest density (inner galactic regions) redistributes energy and angular momentum so that tri-axiality is reduces and a Burkert profile core forms [276].
The CC problem has been claimed to be solved in dwarfs, MW-sized galaxies, and galaxy clusters by SIDM from some cosmological simulations [127,277,278,279] consistent with merging galaxy clusters observations [280,281,282], 0.1–0.5 cm/g cross sections. Figure 13 presents simulations of haloes from galaxies to clusters masses, with set within two values, in the case of Ref. [278]. Although SIDM appears to solve the CC problem, since its cored subhaloes are more sensitive to disruption and tidal stripping than CDM’s, and to improve on WDM [278,279], as enough subhaloes survive, a different point of view still remains [268].
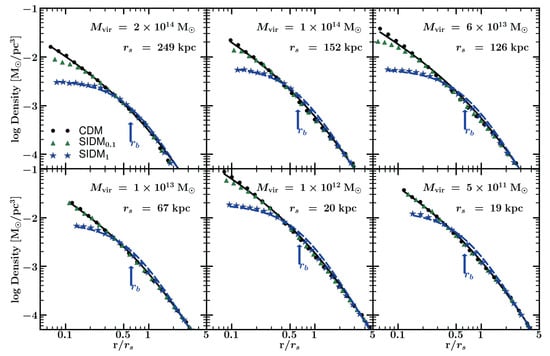
Figure 13.
SIDM simulations compared with CDM, indicated by black dots, in density profiles, reproducing a figure from Figure 4 in Ref. [278]. Two SIDM models, designated in the legend as and , are shown, using DM particle masses , marked with blue stars, and , characterised with green triangles, respectively. They are ovelayed with the NFW, plotted as a black line, and the Burkert, traced in blue, density profiles. The core radii of Burkert’s profiles are located with arrows.
The SIDM’s attraction does not entirely resides in its structure formation effects. As “hidden sector” particle models naturally produce them e.g., [156,283,284], it also retains appeal from the particle theory point of view.
5.3. Other DM Models
Other proposals to change from the CDM model are more or less loose declinations altering around the SIDM concept. Here is a list of the main variations:
- RDM switching interaction to negative scattering results in repulsive DM RDM, Ref. [152].
The next two variations from SIDM are very commonly related to indirect DM detection:
- SADM if self-interaction produces a DM particles annihilation, the result is coined Self-Annihilating DM SADM, Ref. [155] proposing cross section-velocity (m/GeV) cm. Such annihilation decreases the dense regions’ particle numbers, in particular in the halo’s centre, reducing central gravity, therefore allowing to expand central particles’ orbits and thus to flatten the central profile. At the same time, annihilation results in radiation emissions that are possibly detectable.
- DDM Alternately, self-interaction can result in DM decay into relativistic particles, designated as Decaying DM DDM, Ref. [154]. Their gravitational effect on structures is similar to SADM, as they equally deplete galaxies’ central density, since the relativistic particles escape away, while larger scales structures behaviour remain similar to CDM. Similarly, the relativistic decay products produce radiations that can also be detected.
The last main variations are more loosely related to SIDM:
- BCDM Superfluid behaviour of non-relativistic, massive boson condensates in haloes centre can also result in smoothing down their profiles from cusp to cored [285]. Recent structure formation simulations [286] demonstrated that the Bose condensate DM (BCDM) small scale gravity vs. uncertainty principle opposition reduced substructures and flattened the density profile at those scales, while producing larger scale structures indistinguishable from CDM outputs.
- SFDM As scalar field condensation also forms a Bose condensate, similar flat galaxies inner profiles were obtained from such implementation of the BCDM [287], that was called Scalar Field Dark Matter (SFDM)
- FDM Further implementation of the gravity vs. uncertainty principle exploited the wave-particle duality to obtain Fuzzy DM FDM, Ref. [153], using galactic core sized Compton wavelength, ultra-light ( eV) scalar particles. As they cannot be “squeezed” below their Compton wavelength, they also develop flatter profiles and form less substructures.
6. Conclusions
Since the first assessment by Öpik of the amount of matter surrounding our solar system through vertical star motion with respect to the plane of the ecliptic more than a century ago [288], current data indicates a dominant amount of matter should be in the form of DM. However, such dynamics and geometric data has still not been confirmed, to date, by direct or indirect DM particles detection [4,5].
Grasping the essence of DM from a gravitational point of view should privilege the study of galaxy satellites, dwarf galaxies and other small scale structures, dominated by DM, all the more as they present significant departures from the CDM model predictions. In this review, we focused on the departure constituted by the CC problem, formulated more than twenty years ago. Although we now have some competing explanations, there is no concensus on the CC problem’s cause.
In this review, we have discussed the focus on baryonic effects on small scale structures. We recalled that the DFBC model can explain cores in dwarfs from baryon clumps interactions with DM, while cusps form in MW-type galaxies [253]. Although the SNFF model gets similar results, its prediction cover structures in a more restricted range [73]. Note that both models, by depleting the DM density in central halo regions, also explain other small scale problems such as the TBTF or the subhaloes abundance problems. However, baryonic solutions to the CC and other small scale problems are still debated, as some issues remain, such as with the SNFF in classical MW dwarfs [215,226], or the possible future discovery of dwarfs with flat inner profiles which would drive the SNFF model to conclude that DM is actually not cold11, or even that no baryonic physics solutions clearly appear for the TBTF problem in isolated galaxies. Escaping this debate would entail understanding how the SIDM model or one its variants, as we have discussed, could solve the CC problem. Future surveys, including measurements of star velocities, would anyhow be required to further our understanding of the CC problem and other small scale issues.
From an observational point of view, as discriminating cores from cusps in dSphs remains delicate, the discussion on their structure persists see the introduction and, e.g., [289]. Although the Subaru Hyper-Supreme-Camera [290] and GAIA [291] were foreseen as providing possible resolution for the question, their abilities would not exceed larger dwarf galaxies, of the size of Sagittarius [292]. Based on Jeans equations, their determination of density profile using stars line of sight velocity and 2D projection radius are plagued with degeneracy with the anisotropy parameter. Notwithstanding the challenges GAIA faces from it [292], improvements to measure dwarfs’s stars proper motions of the [293], that yield density slope at half-light radius, were recommended, that focused on only one component out of the three velocities and on just two components out of three positions see [294]. However successful these efforts may be, understanding dwarfs inner structure will be crucial. In contrast, the difficulties of the SNFF tensions do not appear fundamental: baryons, through the more efficient DFBC model, can still turn cusps into cores sooner than gas turns into stars. Consequently, should cored dwarfs with be discovered, despite their inconsistency with the SNFF, provided , the CDM model correct with baryonic effects of the DFBC model would remain consistent with observations.
Beyond the CC problem and the other documented issues in small scales of the CDM model, further testing could involve
- checking the predicted large subhaloes number within galaxies’ virial radius, barely agreeing with anomalies in the gravitational lensing fluxes [295];
- measuring subhaloes perturbations of the MW’s cold tidal streams see [296].
Finally, the nature and existence of DM would find a definitive solution in detection of DM particles, whether in colliders, direct or indirect means. Despite the hopes raised by a diphoton excess decay at 750 GeV at 3.9 significance in the LHC, as it was later ruled out as a statistical fluctuation, no evidence of super-symmetry (SUSY), that would allow WIMPS particles DM, have so far emerged and collider detection of DM is yet elusive. Although controversial, the annual modulation claimed in DAMA/LIBRA/CoGeNT remains the only possible direct DM particle detection. To date, no incontrovertible direct, indirect or collider evidence for the nature or existence of DM has been announced.
Author Contributions
All authors have contributed equally in this work. All authors have read and agreed to the published version of the manuscript.
Funding
MLeD acknowledges the financial support by the Lanzhou University starting fund, the Fundamental Research Funds for the Central Universities (Grant No. lzujbky-2019-25), National Science Foundation of China (grant No. 12047501) and the 111 Project under Grant No. B20063.
Institutional Review Board Statement
N/A.
Informed Consent Statement
N/A.
Data Availability Statement
N/A.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | Generalisations of Einstein’s General Relativity, , and theories modify gravity in distinct ways. Replacing, in their Lagrangian, the Ricci scalar by a function , the first type dates from the Buchdahl [158] introduction in 1970 but picked up interest with Starobinsky [159] a decade later. Developed from the Teleparallel Equivalent of GR, theories also modify their Lagrangian from the torsion scalar to a function. On one hand, both types were introduced to absorb the origin of cosmic acceleration into gravity and dispense from the need for DE [160]. On the other hand, MOND, introduced to fit galaxies rotation curves by Milgrom in 1983 [164,165], purports to replace DM. The DM effects of the MOND Newtonian modification also lead to other GR generalisations with the same aim [166,167,168,169]. |
| 2 | A General Relativistic version of secondary infall models is at the root of works by a group including Mimoso and Le Delliou [188,189,190,191]. |
| 3 | A proto-structure’s peak height measures the ratio of its central peak overdensity to its mass variance see [192], as . More massive objects are characterised by larger . |
| 4 | As computed with iterative methods e.g., [195]. |
| 5 | This process agrees with the assumptions from Ref. [72]; the bulk gas flows start beyond >10/cm [220]. |
| 6 | Essentially, galaxies are not able to turn cusps into cores under the SNF mechanism. |
| 7 | “Too Big to Fail” is used in the context of Milky Way (MW) satellite simulations producing bigger objects than observed MW satellites without any mechanism explaining why such object would fail to be detected. |
| 8 | Recall footnote 11. |
| 9 | Star formation is not an efficient process. |
| 10 | Note that 1 cm/g ≃ 1 barn/GeV, so multiplying by the DM particle mass yields the cross-section. |
| 11 | Note that such conclusion is not true for the DFBC model. |
References
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Supp. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Supp. 2011, 192, 18. [Google Scholar] [CrossRef]
- Del Popolo, A. Dark matter, density perturbations, and structure formation. Astron. Rep. 2007, 51, 169–196. [Google Scholar] [CrossRef]
- Del Popolo, A. Non-baryonic dark matter in cosmology. In American Institute of Physics Conference Series; Ureña-López, L.A., Becerril-Bárcenas, R., Linares-Romero, R., Eds.; American Institute of Physics: University Park, MD, USA, 2013; Volume 1548, pp. 2–63. [Google Scholar] [CrossRef]
- Del Popolo, A. Nonbaryonic Dark Matter in Cosmology. Int. J. Mod. Phys. D 2014, 23, 1430005. [Google Scholar] [CrossRef]
- Hanson, D.; Hoover, S.; Crites, A.; Ade, P.A.R.; Aird, K.A.; Austermann, J.E.; Beall, J.A.; Bender, A.N.; Benson, B.A.; Bleem, L.E.; et al. Detection of B-Mode Polarization in the Cosmic Microwave Background with Data from the South Pole Telescope. Phys. Rev. Lett. 2013, 111, 141301. [Google Scholar] [CrossRef]
- Smith, K.M.; Zahn, O.; Doré, O. Detection of gravitational lensing in the cosmic microwave background. Phys. Rev. D 2007, 76, 043510. [Google Scholar] [CrossRef]
- Das, S.; Sherwin, B.D.; Aguirre, P.; Appel, J.W.; Bond, J.R.; Carvalho, C.S.; Devlin, M.J.; Dunkley, J.; Dünner, R.; Essinger-Hileman, T.; et al. Detection of the Power Spectrum of Cosmic Microwave Background Lensing by the Atacama Cosmology Telescope. Phys. Rev. Lett. 2011, 107, 021301. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Astashenok, A.V.; del Popolo, A. Cosmological measure with volume averaging and the vacuum energy problem. Class. Quantum Gravity 2012, 29, 085014. [Google Scholar] [CrossRef]
- Martin, J. Everything You Always Wanted To Know About The Cosmological Constant Problem (But Were Afraid To Ask). Comptes Rendus Phys. 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Sivanandam, N. Is the Cosmological Coincidence a Problem? Phys. Rev. 2013, D87, 083514. [Google Scholar] [CrossRef]
- Eriksen, H.K.; Hansen, F.K.; Banday, A.J.; Górski, K.M.; Lilje, P.B. Asymmetries in the Cosmic Microwave Background Anisotropy Field. Astrophys. J. 2004, 605, 14–20. [Google Scholar] [CrossRef]
- Hansen, F.K.; Banday, A.J.; Górski, K.M. Testing the cosmological principle of isotropy: Local power-spectrum estimates of the WMAP data. Mon. Not. R. Astron. Soc. 2004, 354, 641–665. [Google Scholar] [CrossRef]
- Jaffe, T.R.; Banday, A.J.; Eriksen, H.K.; Górski, K.M.; Hansen, F.K. Evidence of Vorticity and Shear at Large Angular Scales in the WMAP Data: A Violation of Cosmological Isotropy? Astrophys. J. Lett. 2005, 629, L1–L4. [Google Scholar] [CrossRef]
- Hoftuft, J.; Eriksen, H.K.; Banday, A.J.; Górski, K.M.; Hansen, F.K.; Lilje, P.B. Increasing Evidence for Hemispherical Power Asymmetry in the Five-Year WMAP Data. Astrophys. J. 2009, 699, 985–989. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XXIII. Isotropy and statistics of the CMB. Astron. Astrophys. 2014, 571, A23. [Google Scholar] [CrossRef]
- Akrami, Y.; Fantaye, Y.; Shafieloo, A.; Eriksen, H.K.; Hansen, F.K.; Banday, A.J.; Górski, K.M. Power Asymmetry in WMAP and Planck Temperature Sky Maps as Measured by a Local Variance Estimator. Astrophys. J. Lett. 2014, 784, L42. [Google Scholar] [CrossRef]
- Cruz, M.; Martínez-González, E.; Vielva, P.; Cayón, L. Detection of a non-Gaussian spot in WMAP. Mon. Not. R. Astron. Soc. 2005, 356, 29–40. [Google Scholar] [CrossRef]
- Cruz, M.; Tucci, M.; Martínez-González, E.; Vielva, P. The non-Gaussian cold spot in WilkinsonMicrowaveAnisotropyProbe: Significance, morphology and foreground contribution. Mon. Not. R. Astron. Soc. 2006, 369, 57–67. [Google Scholar] [CrossRef]
- Cruz, M.; Cayón, L.; Martínez-González, E.; Vielva, P.; Jin, J. The Non-Gaussian Cold Spot in the 3 Year Wilkinson Microwave Anisotropy Probe Data. Astrophys. J. 2007, 655, 11–20. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Starkman, G.D.; Huterer, D.; Copi, C.J. Is the Low-l Microwave Background Cosmic? Phys. Rev. Lett. 2004, 93, 221301. [Google Scholar] [CrossRef] [PubMed]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. On the large-angle anomalies of the microwave sky. Mon. Not. R. Astron. Soc. 2006, 367, 79–102. [Google Scholar] [CrossRef]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. Uncorrelated universe: Statistical anisotropy and the vanishing angular correlation function in WMAP years 13. Phys. Rev. D 2007, 75, 023507. [Google Scholar] [CrossRef]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. Large-Angle Anomalies in the CMB. Adv. Astron. 2010, 2010, 847541. [Google Scholar] [CrossRef]
- Copi, C.J.; Huterer, D.; Schwarz, D.J.; Starkman, G.D. Large-scale alignments from WMAP and Planck. Mon. Not. R. Astron. Soc. 2015, 449, 3458–3470. [Google Scholar] [CrossRef]
- Bennett, C.L.; Hill, R.S.; Hinshaw, G.; Larson, D.; Smith, K.M.; Dunkley, J.; Gold, B.; Halpern, M.; Jarosik, N.; Kogut, A.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Are There Cosmic Microwave Background Anomalies? Astrophys. J. Supp. 2011, 192, 17. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Macaulay, E.; Wehus, I.K.; Eriksen, H.K. Lower Growth Rate from Recent Redshift Space Distortion Measurements than Expected from Planck. Phys. Rev. Lett. 2013, 111, 161301. [Google Scholar] [CrossRef] [PubMed]
- Raveri, M. Is there concordance within the concordance ΛCDM model? arXiv 2015, arXiv:1510.00688. [Google Scholar]
- Moore, B. Evidence against dissipation-less dark matter from observations of galaxy haloes. Nature 1994, 370, 629–631. [Google Scholar] [CrossRef]
- Moore, B.; Quinn, T.; Governato, F.; Stadel, J.; Lake, G. Cold collapse and the core catastrophe. Mon. Not. R. Astron. Soc. 1999, 310, 1147–1152. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Steinhardt, P. New Light on Dark Matter. Science 2003, 300, 1909–1914. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. Too big to fail? The puzzling darkness of massive Milky Way subhaloes. Mon. Not. R. Astron. Soc. 2011, 415, L40–L44. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. The Milky Way’s bright satellites as an apparent failure of ΛCDM. Mon. Not. R. Astron. Soc. 2012, 422, 1203–1218. [Google Scholar] [CrossRef]
- Oh, S.H.; Brook, C.; Governato, F.; Brinks, E.; Mayer, L.; de Blok, W.J.G.; Brooks, A.; Walter, F. The Central Slope of Dark Matter Cores in Dwarf Galaxies: Simulations versus THINGS. Astron. J. 2011, 142, 24. [Google Scholar] [CrossRef]
- Klypin, A.A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where are the missing Galactic satellites? Astrophys. J. 1999, 522, 82–92. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Burkert, A.; Swaters, R.A. The angular momentum content of dwarf galaxies: New challenges for the theory of galaxy formation. Mon. Not. R. Astron. Soc. 2001, 326, 1205–1215. [Google Scholar] [CrossRef]
- Cardone, V.F.; Del Popolo, A.; Kroupa, P. Angular momentum transfer and the size—mass relation in early—type galaxies. Mon. Not. R. Astron. Soc. 2009, 400, 766. [Google Scholar] [CrossRef][Green Version]
- Pawlowski, M.S.; Famaey, B.; Jerjen, H.; Merritt, D.; Kroupa, P.; Dabringhausen, J.; Lüghausen, F.; Forbes, D.A.; Hensler, G.; Hammer, F.; et al. Co-orbiting satellite galaxy structures are still in conflict with the distribution of primordial dwarf galaxies. Mon. Not. R. Astron. Soc. 2014, 442, 2362–2380. [Google Scholar] [CrossRef]
- McGaugh, S.S. Novel Test of Modified Newtonian Dynamics with Gas Rich Galaxies. Phys. Rev. Lett. 2011, 106, 121303. [Google Scholar] [CrossRef]
- Flores, R.A.; Primack, J.R. Observational and theoretical constraints on singular dark matter halos. Astrophys. J. Lett. 1994, 427, L1–L4. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Navarro, J.F.; Ludlow, A.; Springel, V.; Wang, J.; Vogelsberger, M.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Helmi, A. The diversity and similarity of simulated cold dark matter haloes. Mon. Not. R. Astron. Soc. 2010, 402, 21–34. [Google Scholar] [CrossRef]
- Saburova, A.; Del Popolo, A. On the surface density of dark matter haloes. Mon. Not. R. Astron. Soc. 2014, 445, 3512–3524. [Google Scholar] [CrossRef]
- Kroupa, P.; Theis, C.; Boily, C.M. The Great disk of Milky Way satellites and cosmological sub-structures. Astron. Astrophys. 2005, 431, 517–521. [Google Scholar] [CrossRef]
- Kroupa, P.; Famaey, B.; de Boer, K.S.; Dabringhausen, J.; Pawlowski, M.S.; Boily, C.M.; Jerjen, H.; Forbes, D.; Hensler, G.; Metz, M. Local-Group tests of dark-matter Concordance Cosmology: Towards a new paradigm for structure formation? Astron. Astrophys. 2010, 523, A32. [Google Scholar] [CrossRef]
- Kroupa, P. The dark matter crisis: Falsification of the current standard model of cosmology. Publ. Astron. Soc. Austral. 2012, 29, 395–433. [Google Scholar] [CrossRef]
- Kroupa, P.; Pawlowski, M.; Milgrom, M. The failures of the standard model of cosmology require a new paradigm. Int. J. Mod. Phys. 2012, D21, 1230003. [Google Scholar] [CrossRef]
- Kroupa, P. Galaxies as simple dynamical systems: Observational data disfavor dark matter and stochastic star formation. Can. J. Phys. 2015, 93, 169–202. [Google Scholar] [CrossRef]
- Zolotov, A.; Brooks, A.M.; Willman, B.; Governato, F.; Pontzen, A.; Christensen, C.; Dekel, A.; Quinn, T.; Shen, S.; Wadsley, J. Baryons Matter: Why Luminous Satellite Galaxies have Reduced Central Masses. Astrophys. J. 2012, 761, 71. [Google Scholar] [CrossRef]
- Brooks, A.M.; Zolotov, A. Why Baryons Matter: The Kinematics of Dwarf Spheroidal Satellites. Astrophys. J. 2014, 786, 87. [Google Scholar] [CrossRef]
- Del Popolo, A.; Lima, J.A.S.; Fabris, J.C.; Rodrigues, D.C. A unified solution to the small scale problems of the ΛCDM model. J. Cosmo. Astrop. Phys. 2014, 4, 021. [Google Scholar] [CrossRef]
- Mashchenko, S.; Couchman, H.M.P.; Wadsley, J. The removal of cusps from galaxy centres by stellar feedback in the early Universe. Nature 2006, 442, 539–542. [Google Scholar] [CrossRef]
- Mashchenko, S.; Wadsley, J.; Couchman, H.M.P. Stellar Feedback in Dwarf Galaxy Formation. Science 2008, 319, 174. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Benson, A.J.; Walker, M.G.; Gilmore, G.; McConnachie, A.W.; Mayer, L. The impact of dark matter cusps and cores on the satellite galaxy population around spiral galaxies. Mon. Not. R. Astron. Soc. 2010, 406, 1290–1305. [Google Scholar] [CrossRef]
- Sommer-Larsen, J.; Gelato, S.; Vedel, H. Formation of Disk Galaxies: Feedback and the Angular Momentum Problem. Astrophys. J. 1999, 519, 501–512. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Moore, B.; Governato, F.; Quinn, T.; Stadel, J.; Lake, G. Resolving the Structure of Cold Dark Matter Halos. Astrophys. J. Lett. 1998, 499, L5–L8. [Google Scholar] [CrossRef]
- Fukushige, T.; Makino, J. Structure of Dark Matter Halos from Hierarchical Clustering. Astrophys. J. 2001, 557, 533–545. [Google Scholar] [CrossRef]
- Jing, Y.P.; Suto, Y. The Density Profiles of the Dark Matter Halo Are Not Universal. Astrophys. J. Lett. 2000, 529, L69–L72. [Google Scholar] [CrossRef] [PubMed]
- Ricotti, M. Dependence of the inner dark matter profile on the halo mass. Mon. Not. R. Astron. Soc. 2003, 344, 1237–1249. [Google Scholar] [CrossRef]
- Ricotti, M.; Wilkinson, M.I. On the origin of dark matter cores in dwarf galaxies. Mon. Not. R. Astron. Soc. 2004, 353, 867–873. [Google Scholar] [CrossRef][Green Version]
- Ricotti, M.; Pontzen, A.; Viel, M. Is the Concentration of Dark Matter Halos at Virialization Universal? Astrophys. J. Lett. 2007, 663, L53–L56. [Google Scholar] [CrossRef]
- Del Popolo, A. On the universality of density profiles. Mon. Not. R. Astron. Soc. 2010, 408, 1808–1817. [Google Scholar] [CrossRef]
- Cardone, V.F.; Del Popolo, A.; Tortora, C.; Napolitano, N.R. Secondary infall model and dark matter scaling relations in intermediate-redshift early-type galaxies. Mon. Not. R. Astron. Soc. 2011, 416, 1822–1835. [Google Scholar] [CrossRef]
- Del Popolo, A. Non-power law behavior of the radial profile of phase-space density of halos. J. Cosmo. Astrop. Phys. 2011, 7, 014. [Google Scholar] [CrossRef]
- Del Popolo, A.; Cardone, V.F.; Belvedere, G. Surface density of dark matter haloes on galactic and cluster scales. Mon. Not. R. Astron. Soc. 2013, 429, 1080–1087. [Google Scholar] [CrossRef]
- Di Cintio, A.; Brook, C.B.; Macciò, A.V.; Stinson, G.S.; Knebe, A.; Dutton, A.A.; Wadsley, J. The dependence of dark matter profiles on the stellar-to-halo mass ratio: A prediction for cusps versus cores. Mon. Not. R. Astron. Soc. 2014, 437, 415–423. [Google Scholar] [CrossRef]
- Stadel, J.; Potter, D.; Moore, B.; Diemand, J.; Madau, P.; Zemp, M.; Kuhlen, M.; Quilis, V. Quantifying the heart of darkness with GHALO—A multibillion particle simulation of a galactic halo. Mon. Not. R. Astron. Soc. 2009, 398, L21–L25. [Google Scholar] [CrossRef]
- Gao, L.; Navarro, J.F.; Cole, S.; Frenk, C.S.; White, S.D.M.; Springel, V.; Jenkins, A.; Neto, A.F. The redshift dependence of the structure of massive Λ cold dark matter haloes. Mon. Not. R. Astron. Soc. 2008, 387, 536–544. [Google Scholar] [CrossRef]
- Governato, F.; Brook, C.; Mayer, L.; Brooks, A.; Rhee, G.; Wadsley, J.; Jonsson, P.; Willman, B.; Stinson, G.; Quinn, T.; et al. Bulgeless dwarf galaxies and dark matter cores from supernova-driven outflows. Nature 2010, 463, 203–206. [Google Scholar] [CrossRef]
- Governato, F.; Zolotov, A.; Pontzen, A.; Christensen, C.; Oh, S.H.; Brooks, A.M.; Quinn, T.; Shen, S.; Wadsley, J. Cuspy no more: How outflows affect the central dark matter and baryon distribution in Λ cold dark matter galaxies. Mon. Not. R. Astron. Soc. 2012, 422, 1231–1240. [Google Scholar] [CrossRef]
- Del Popolo, A. The Cusp/Core Problem and the Secondary Infall Model. Astrophys. J. 2009, 698, 2093–2113. [Google Scholar] [CrossRef]
- Cardone, V.F.; Del Popolo, A. Newtonian acceleration scales in spiral galaxies. Mon. Not. R. Astron. Soc. 2012, 427, 3176–3187. [Google Scholar] [CrossRef]
- Del Popolo, A. Density profile slopes of dwarf galaxies and their environment. Mon. Not. R. Astron. Soc. 2012, 419, 971–984. [Google Scholar] [CrossRef]
- Del Popolo, A. On the density-profile slope of clusters of galaxies. Mon. Not. R. Astron. Soc. 2012, 424, 38–51. [Google Scholar] [CrossRef]
- Del Popolo, A.; Cardone, V.F. Statistical properties of the dark matter haloes of dwarf galaxies and correlations with the environment. Mon. Not. R. Astron. Soc. 2012, 423, 1060–1072. [Google Scholar] [CrossRef]
- Del Popolo, A.; Hiotelis, N. Cusps and cores in the presence of galactic bulges. J. Cosmo. Astrop. Phys. 2014, 1, 047. [Google Scholar] [CrossRef]
- Popolo, A.D. Profiles of dark-matter haloes at high redshift. Mon. Not. R. Astron. Soc. 2001, 325, 1190. [Google Scholar] [CrossRef][Green Version]
- Burkert, A. The Structure of Dark Matter Halos in Dwarf Galaxies. Astrophys. J. Lett. 1995, 447, L25. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Bosma, A.; McGaugh, S. Simulating observations of dark matter dominated galaxies: Towards the optimal halo profile. Mon. Not. R. Astron. Soc. 2003, 340, 657–678. [Google Scholar] [CrossRef]
- Swaters, R.A.; Madore, B.F.; van den Bosch, F.C.; Balcells, M. The Central Mass Distribution in Dwarf and Low Surface Brightness Galaxies. Astrophys. J. 2003, 583, 732–751. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; Kaufmann, T. Recovering cores and cusps in dark matter haloes using mock velocity field observations. Mon. Not. R. Astron. Soc. 2011, 414, 3617–3626. [Google Scholar] [CrossRef]
- Oh, S.H.; de Blok, W.J.G.; Brinks, E.; Walter, F.; Kennicutt, R.C., Jr. Dark and Luminous Matter in THINGS Dwarf Galaxies. Astron. J. 2011, 141, 193. [Google Scholar] [CrossRef]
- Hernandez, X.; Gilmore, G. Dynamical friction in dwarf galaxies. Mon. Not. R. Astron. Soc. 1998, 297, 517. [Google Scholar] [CrossRef]
- McGaugh, S.S.; de Blok, W.J.G. Testing the Dark Matter Hypothesis with Low Surface Brightness Galaxies and Other Evidence. Astrophys. J. 1998, 499, 41–65. [Google Scholar] [CrossRef]
- Côté, S.; Carignan, C.; Freeman, K.C. The Various Kinematics of Dwarf Irregular Galaxies in Nearby Groups and Their Dark Matter Distributions. Astron. J. 2000, 120, 3027–3059. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Swaters, R.A. Dwarf galaxy rotation curves and the core problem of dark matter haloes. Mon. Not. R. Astron. Soc. 2001, 325, 1017–1038. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Bosma, A. High-resolution rotation curves of low surface brightness galaxies. Astron. Astrophys. 2002, 385, 816–846. [Google Scholar] [CrossRef]
- Spekkens, K.; Giovanelli, R.; Haynes, M.P. The Cusp/Core Problem in Galactic Halos: Long-Slit Spectra for a Large Dwarf Galaxy Sample. Astron. J. 2005, 129, 2119–2137. [Google Scholar] [CrossRef]
- Hayashi, E.; Navarro, J.F.; Power, C.; Jenkins, A.; Frenk, C.S.; White, S.D.M.; Springel, V.; Stadel, J.; Quinn, T.R. The inner structure of ΛCDM haloes - II. Halo mass profiles and low surface brightness galaxy rotation curves. Mon. Not. R. Astron. Soc. 2004, 355, 794–812. [Google Scholar] [CrossRef]
- Blais-Ouellette, S.; Amram, P.; Carignan, C. Accurate Determination of the Mass Distribution in Spiral Galaxies. II. Testing the Shape of Dark Halos. Astron. J. 2001, 121, 1952–1964. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; McGaugh, S.S.; de Blok, W.J.G. Mass Models for Low Surface Brightness Galaxies with High-Resolution Optical Velocity Fields. Astrophys. J. 2008, 676, 920–943. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; McGaugh, S.S.; Mihos, J.C. Constraining the NFW Potential with Observations and Modeling of Low Surface Brightness Galaxy Velocity Fields. Astrophys. J. 2009, 692, 1321–1332. [Google Scholar] [CrossRef]
- Weldrake, D.T.F.; de Blok, W.J.G.; Walter, F. A high-resolution rotation curve of NGC 6822: A test-case for cold dark matter. Mon. Not. R. Astron. Soc. 2003, 340, 12–28. [Google Scholar] [CrossRef]
- Trachternach, C.; de Blok, W.J.G.; Walter, F.; Brinks, E.; Kennicutt, R.C., Jr. Dynamical Centers and Noncircular Motions in THINGS Galaxies: Implications for Dark Matter Halos. Astron. J. 2008, 136, 2720–2760. [Google Scholar] [CrossRef]
- Gentile, G.; Salucci, P.; Klein, U.; Vergani, D.; Kalberla, P. The cored distribution of dark matter in spiral galaxies. Mon. Not. R. Astron. Soc. 2004, 351, 903–922. [Google Scholar] [CrossRef]
- Gentile, G.; Salucci, P.; Klein, U.; Granato, G.L. NGC 3741: The dark halo profile from the most extended rotation curve. Mon. Not. R. Astron. Soc. 2007, 375, 199–212. [Google Scholar] [CrossRef]
- Salucci, P.; Lapi, A.; Tonini, C.; Gentile, G.; Yegorova, I.; Klein, U. The universal rotation curve of spiral galaxies—II. The dark matter distribution out to the virial radius. Mon. Not. R. Astron. Soc. 2007, 378, 41–47. [Google Scholar] [CrossRef]
- Oh, S.H.; Hunter, D.A.; Brinks, E.; Elmegreen, B.G.; Schruba, A.; Walter, F.; Rupen, M.P.; Young, L.M.; Simpson, C.E.; Johnson, M.C.; et al. High-resolution Mass Models of Dwarf Galaxies from LITTLE THINGS. Astron. J. 2015, 149, 180. [Google Scholar] [CrossRef]
- Spano, M.; Marcelin, M.; Amram, P.; Carignan, C.; Epinat, B.; Hernandez, O. GHASP: An Hα kinematic survey of spiral and irregular galaxies—V. Dark matter distribution in 36 nearby spiral galaxies. Mon. Not. R. Astron. Soc. 2008, 383, 297–316. [Google Scholar] [CrossRef]
- Simon, J.D.; Bolatto, A.D.; Leroy, A.; Blitz, L.; Gates, E.L. High-Resolution Measurements of the Halos of Four Dark Matter-Dominated Galaxies: Deviations from a Universal Density Profile. Astrophys. J. 2005, 621, 757–776. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- Martinsson, T.P.K.; Verheijen, M.A.W.; Westfall, K.B.; Bershady, M.A.; Andersen, D.R.; Swaters, R.A. The DiskMass Survey. VII. The distribution of luminous and dark matter in spiral galaxies. Astron. Astrophys. 2013, 557, A131. [Google Scholar] [CrossRef]
- Navarro, J.F.; Hayashi, E.; Power, C.; Jenkins, A.R.; Frenk, C.S.; White, S.D.M.; Springel, V.; Stadel, J.; Quinn, T.R. The inner structure of ΛCDM haloes—III. Universality and asymptotic slopes. Mon. Not. R. Astron. Soc. 2004, 349, 1039–1051. [Google Scholar] [CrossRef]
- Simon, J.D.; Bolatto, A.D.; Leroy, A.; Blitz, L. High-Resolution Measurements of the Dark Matter Halo of NGC 2976: Evidence for a Shallow Density Profile. Astrophys. J. 2003, 596, 957–981. [Google Scholar] [CrossRef]
- Adams, J.J.; Simon, J.D.; Fabricius, M.H.; van den Bosch, R.C.E.; Barentine, J.C.; Bender, R.; Gebhardt, K.; Hill, G.J.; Murphy, J.D.; Swaters, R.A.; et al. Dwarf Galaxy Dark Matter Density Profiles Inferred from Stellar and Gas Kinematics. Astrophys. J. 2014, 789, 63. [Google Scholar] [CrossRef]
- Oman, K.A.; Navarro, J.F.; Fattahi, A.; Frenk, C.S.; Sawala, T.; White, S.D.M.; Bower, R.; Crain, R.A.; Furlong, M.; Schaller, M.; et al. The unexpected diversity of dwarf galaxy rotation curves. Mon. Not. R. Astron. Soc. 2015, 452, 3650–3665. [Google Scholar] [CrossRef]
- Evans, N.W.; An, J.; Walker, M.G. Cores and cusps in the dwarf spheroidals. Mon. Not. R. Astron. Soc. 2009, 393, L50–L54. [Google Scholar] [CrossRef]
- Wolf, J.; Bullock, J.S. Dark matter concentrations and a search for cores in Milky Way dwarf satellites. arXiv 2012, arXiv:astro-ph.CO/1203.4240. [Google Scholar]
- Hayashi, K.; Chiba, M. Probing Non-spherical Dark Halos in the Galactic Dwarf Galaxies. Astrophys. J. 2012, 755, 145. [Google Scholar] [CrossRef]
- Richardson, T.; Fairbairn, M. Analytical solutions to the mass-anisotropy degeneracy with higher order Jeans analysis: A general method. Mon. Not. R. Astron. Soc. 2013, 432, 3361–3380. [Google Scholar] [CrossRef]
- Jardel, J.R.; Gebhardt, K. The Dark Matter Density Profile of the Fornax Dwarf. Astrophys. J. 2012, 746, 89. [Google Scholar] [CrossRef]
- Breddels, M.A.; Helmi, A.; van den Bosch, R.C.E.; van de Ven, G.; Battaglia, G. Orbit-based dynamical models of the Sculptor dSph galaxy. Mon. Not. R. Astron. Soc. 2013, 433, 3173–3189. [Google Scholar] [CrossRef]
- Jardel, J.R.; Gebhardt, K. Variations in a Universal Dark Matter Profile for Dwarf Spheroidals. Astrophys. J. Lett. 2013, 775, L30. [Google Scholar] [CrossRef]
- Jardel, J.R.; Gebhardt, K.; Fabricius, M.H.; Drory, N.; Williams, M.J. Measuring Dark Matter Profiles Non-Parametrically in Dwarf Spheroidals: An Application to Draco. Astrophys. J. 2013, 763, 91. [Google Scholar] [CrossRef]
- Hayashi, K.; Chiba, M.; Ishiyama, T. Diversity of Dark Matter Density Profiles in the Galactic Dwarf Spheroidal Satellites. Astrophys. J. 2020, 904, 45. [Google Scholar] [CrossRef]
- Battaglia, G.; Helmi, A.; Tolstoy, E.; Irwin, M.; Hill, V.; Jablonka, P. The Kinematic Status and Mass Content of the Sculptor Dwarf Spheroidal Galaxy. Astrophys. J. Lett. 2008, 681, L13. [Google Scholar] [CrossRef]
- Walker, M.G.; Peñarrubia, J. A Method for Measuring (Slopes of) the Mass Profiles of Dwarf Spheroidal Galaxies. Astrophys. J. 2011, 742, 20. [Google Scholar] [CrossRef]
- Agnello, A.; Evans, N.W. A Virial Core in the Sculptor Dwarf Spheroidal Galaxy. Astrophys. J. Lett. 2012, 754, L39. [Google Scholar] [CrossRef]
- Amorisco, N.C.; Evans, N.W. Dark matter cores and cusps: The case of multiple stellar populations in dwarf spheroidals. Mon. Not. R. Astron. Soc. 2012, 419, 184–196. [Google Scholar] [CrossRef]
- Sand, D.J.; Treu, T.; Smith, G.P.; Ellis, R.S. The Dark Matter Distribution in the Central Regions of Galaxy Clusters: Implications for Cold Dark Matter. Astrophys. J. 2004, 604, 88–107. [Google Scholar] [CrossRef]
- Del Popolo, A. The flat density profiles of massive, and relaxed galaxy clusters. J. Cosmo. Astrop. Phys. 2014, 7, 019. [Google Scholar] [CrossRef]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J.; Richard, J.; Marshall, P.J.; Capak, P.; Miyazaki, S. The Distribution of Dark Matter Over Three Decades in Radius in the Lensing Cluster Abell 611. Astrophys. J. 2009, 706, 1078–1094. [Google Scholar] [CrossRef]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J. The Dark Matter Distribution in A383: Evidence for a Shallow Density Cusp from Improved Lensing, Stellar Kinematic, and X-ray Data. Astrophys. J. Lett. 2011, 728, L39. [Google Scholar] [CrossRef]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J. The Density Profiles of Massive, Relaxed Galaxy Clusters. II. Separating Luminous and Dark Matter in Cluster Cores. Astrophys. J. 2013, 765, 25. [Google Scholar] [CrossRef]
- Donnarumma, A.; Ettori, S.; Meneghetti, M.; Gavazzi, R.; Fort, B.; Moscardini, L.; Romano, A.; Fu, L.; Giordano, F.; Radovich, M.; et al. Abell 611. II. X-ray and strong lensing analyses. Astron. Astrophys. 2011, 528, A73. [Google Scholar] [CrossRef]
- Dahle, H.; Hannestad, S.; Sommer-Larsen, J. The Density Profile of Cluster-Scale Dark Matter Halos. Astrophys. J. Lett. 2003, 588, L73–L76. [Google Scholar] [CrossRef]
- Gavazzi, R.; Fort, B.; Mellier, Y.; Pelló, R.; Dantel-Fort, M. A radial mass profile analysis of the lensing cluster MS 2137.3-2353. Astron. Astrophys. 2003, 403, 11–27. [Google Scholar] [CrossRef]
- Sand, D.J.; Treu, T.; Ellis, R.S. The Dark Matter Density Profile of the Lensing Cluster MS 2137-23: A Test of the Cold Dark Matter Paradigm. Astrophys. J. Lett. 2002, 574, L129–L133. [Google Scholar] [CrossRef]
- Del Popolo, A. The Mass and temperature functions in a moving barrier model. Mon. Not. R. Astron. Soc. 2002, 337, 529. [Google Scholar] [CrossRef]
- Del Popolo, A.; Hiotelis, N.; Penarrubia, J. A theoretical study of the luminosity temperature relation for clusters of galaxies. Astrophys. J. 2005, 628, 76. [Google Scholar] [CrossRef][Green Version]
- Ettori, S.; Fabian, A.C.; Allen, S.W.; Johnstone, R.M. Deep inside the core of Abell 1795: The Chandra view. Mon. Not. R. Astron. Soc. 2002, 331, 635–648. [Google Scholar] [CrossRef]
- Lewis, A.D.; Buote, D.A.; Stocke, J.T. Chandra Observations of A2029: The Dark Matter Profile Down to below 0.01rvir in an Unusually Relaxed Cluster. Astrophys. J. 2003, 586, 135–142. [Google Scholar] [CrossRef]
- Arabadjis, J.S.; Bautz, M.W.; Garmire, G.P. Chandra Observations of the Lensing Cluster EMSS 1358+6245: Implications for Self-interacting Dark Matter. Astrophys. J. 2002, 572, 66–78. [Google Scholar] [CrossRef][Green Version]
- Schmidt, R.W.; Allen, S.W. The dark matter haloes of massive, relaxed galaxy clusters observed with Chandra. Mon. Not. R. Astron. Soc. 2007, 379, 209–221. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; Spekkens, K. Do Baryons Alter the Halos of Low Surface Brightness Galaxies? Astrophys. J. Lett. 2011, 741, L29. [Google Scholar] [CrossRef]
- Sánchez-Salcedo, F.J.; Reyes-Iturbide, J.; Hernandez, X. An extensive study of dynamical friction in dwarf galaxies: The role of stars, dark matter, halo profiles and MOND. Mon. Not. R. Astron. Soc. 2006, 370, 1829–1840. [Google Scholar] [CrossRef]
- Read, J.I.; Goerdt, T.; Moore, B.; Pontzen, A.P.; Stadel, J.; Lake, G. Dynamical friction in constant density cores: A failure of the Chandrasekhar formula. Mon. Not. R. Astron. Soc. 2006, 373, 1451–1460. [Google Scholar] [CrossRef]
- Inoue, S. The test for suppressed dynamical friction in a constant density core of dwarf galaxies. Mon. Not. R. Astron. Soc. 2009, 397, 709–716. [Google Scholar] [CrossRef]
- Dutta Chowdhury, D.; van den Bosch, F.C.; van Dokkum, P. On the Evolution of the Globular Cluster System in NGC 1052-DF2: Dynamical Friction, Globular-Globular Interactions, and Galactic Tides. Astrophys. J. 2020, 903, 149. [Google Scholar] [CrossRef]
- Hernandez, X. Theoretical lower limits on sizes of ultrafaint dwarf galaxies from dynamical friction. Mon. Not. R. Astron. Soc. 2016, 462, 2734–2738. [Google Scholar] [CrossRef][Green Version]
- Inoue, S. Emergence of a stellar cusp by a dark matter cusp in a low-mass compact ultrafaint dwarf galaxy. Mon. Not. R. Astron. Soc. 2017, 467, 4491–4500. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Robertson, B.E.; Dalcanton, J.J.; de Blok, W.J.G. Constraints on the Structure of Dark Matter Halos from the Rotation Curves of Low Surface Brightness Galaxies. Astron. J. 2000, 119, 1579–1591. [Google Scholar] [CrossRef]
- Power, C.; Navarro, J.F.; Jenkins, A.; Frenk, C.S.; White, S.D.M.; Springel, V.; Stadel, J.; Quinn, T. The inner structure of ΛCDM haloes - I. A numerical convergence study. Mon. Not. R. Astron. Soc. 2003, 338, 14–34. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S.; Bosma, A.; Rubin, V.C. Mass Density Profiles of Low Surface Brightness Galaxies. Astrophys. J. Lett. 2001, 552, L23–L26. [Google Scholar] [CrossRef]
- Borriello, A.; Salucci, P. The dark matter distribution in disc galaxies. Mon. Not. R. Astron. Soc. 2001, 323, 285–292. [Google Scholar] [CrossRef]
- Diemand, J.; Moore, B.; Stadel, J. Convergence and scatter of cluster density profiles. Mon. Not. R. Astron. Soc. 2004, 353, 624–632. [Google Scholar] [CrossRef][Green Version]
- Sommer-Larsen, J.; Dolgov, A. Formation of Disk Galaxies: Warm Dark Matter and the Angular Momentum Problem. Astrophys. J. 2001, 551, 608–623. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Fluid Dark Matter. Astrophys. J. Lett. 2000, 534, L127–L129. [Google Scholar] [CrossRef]
- Goodman, J. Repulsive dark matter. New Astron. 2000, 5, 103–107. [Google Scholar] [CrossRef]
- Hu, W.; Barkana, R.; Gruzinov, A. Fuzzy Cold Dark Matter: The Wave Properties of Ultralight Particles. Phys. Rev. Lett. 2000, 85, 1158–1161. [Google Scholar] [CrossRef]
- Cen, R. Decaying Cold Dark Matter Model and Small-Scale Power. Astrophys. J. Lett. 2001, 546, L77–L80. [Google Scholar] [CrossRef]
- Kaplinghat, M.; Knox, L.; Turner, M.S. Annihilating Cold Dark Matter. Phys. Rev. Lett. 2000, 85, 3335–3338. [Google Scholar] [CrossRef]
- Spergel, D.N.; Steinhardt, P.J. Observational Evidence for Self-Interacting Cold Dark Matter. Phys. Rev. Lett. 2000, 84, 3760–3763. [Google Scholar] [CrossRef]
- Zentner, A.R.; Bullock, J.S. Halo Substructure and the Power Spectrum. Astrophys. J. 2003, 598, 49–72. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s other gravity and the acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Dent, J.B.; Dutta, S.; Saridakis, E.N. f(T) gravity mimicking dynamical dark energy. Background and perturbation analysis. J. Cosmo. Astrop. Phys. 2011, 1, 9. [Google Scholar] [CrossRef]
- Zheng, R.; Huang, Q.G. Growth factor in f(T) gravity. J. Cosmo. Astrop. Phys. 2011, 3, 2. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics—Implications for galaxies. Astrophys. J. 1983, 270, 371–389. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Mendoza, S.; Bernal, T.; Hernandez, X.; Hidalgo, J.C.; Torres, L.A. Gravitational lensing with f(χ)=χ3/2 gravity in accordance with astrophysical observations. Mon. Not. R. Astron. Soc. 2013, 433, 1802–1812. [Google Scholar] [CrossRef]
- Campigotto, M.C.; Diaferio, A.; Hernandez, X.; Fatibene, L. Strong gravitational lensing in f(χ)=χ3/2 gravity. JCAP 2017, 6, 57. [Google Scholar] [CrossRef]
- Barrientos, E.; Lobo, F.S.N.; Mendoza, S.; Olmo, G.J.; Rubiera-Garcia, D. Metric-affine f(R,T) theories of gravity and their applications. Phys. Rev. D 2018, 97, 104041. [Google Scholar] [CrossRef]
- Barrientos, E.; Mendoza, S. MOND as the weak field limit of an extended metric theory of gravity with a matter-curvature coupling. Phys. Rev. D 2018, 98, 084033. [Google Scholar] [CrossRef]
- Le Delliou, M.; Henriksen, R.N.; MacMillan, J.D. Black holes and galactic density cusps—I. Radial orbit cusps and bulges. Mon. Not. R. Astron. Soc. 2011, 413, 1633–1642. [Google Scholar] [CrossRef]
- Le Delliou, M.; Henriksen, R.N.; MacMillan, J.D. Black holes and galactic density cusps. Spherically symmetric anisotropic cusps. Astron. Astrophys. 2010, 522, A28. [Google Scholar] [CrossRef]
- Le Delliou, M.; Henriksen, R.N.; MacMillan, J.D. Black holes and galactic density cusps. From black hole to bulge. Astron. Astrophys. 2011, 526, A13. [Google Scholar] [CrossRef]
- El-Zant, A.; Shlosman, I.; Hoffman, Y. Dark Halos: The Flattening of the Density Cusp by Dynamical Friction. Astrophys. J. 2001, 560, 636–643. [Google Scholar] [CrossRef]
- El-Zant, A.A.; Hoffman, Y.; Primack, J.; Combes, F.; Shlosman, I. Flat-cored Dark Matter in Cuspy Clusters of Galaxies. Astrophys. J. Lett. 2004, 607, L75–L78. [Google Scholar] [CrossRef]
- Nusser, A. Self-similar spherical collapse with non-radial motions. Mon. Not. R. Astron. Soc. 2001, 325, 1397–1401. [Google Scholar] [CrossRef]
- Hiotelis, N. Density profiles in a spherical infall model with non-radial motions. Astron. Astrophys. 2002, 382, 84–91. [Google Scholar] [CrossRef][Green Version]
- Le Delliou, M.; Henriksen, R.N. Non-radial motion and the NFW profile. Astron. Astrophys. 2003, 408, 27–38. [Google Scholar] [CrossRef]
- Ascasibar, Y.; Yepes, G.; Gottlöber, S.; Müller, V. On the physical origin of dark matter density profiles. Mon. Not. R. Astron. Soc. 2004, 352, 1109–1120. [Google Scholar] [CrossRef]
- Williams, L.L.R.; Babul, A.; Dalcanton, J.J. Investigating the Origins of Dark Matter Halo Density Profiles. Astrophys. J. 2004, 604, 18–39. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Lima, J.A.S. Extended Spherical Collapse and the Accelerating Universe. Int. J. Mod. Phys. D 2013, 22, 1350038. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Lima, J.A.S. Spherical collapse model with shear and angular momentum in dark energy cosmologies. Mon. Not. R. Astron. Soc. 2013, 430, 628–637. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F.; Maydanyuk, S.P.; Lima, J.A.S.; Jesus, J.F. Shear and rotation in Chaplygin cosmology. Phys. Rev. D 2013, 87, 043527. [Google Scholar] [CrossRef]
- Del Popolo, A.; Ercan, E.N.; Xia, Z. Ellipsoidal Collapse and Previrialization. Astron. J. 2001, 122, 487–495. [Google Scholar] [CrossRef]
- Del Popolo, A.; Gambera, M. Substructure effects on the collapse of density perturbations. Astron. Astrophys. 1997, 321, 691–695. [Google Scholar]
- Cardone, V.F.; Leubner, M.P.; Del Popolo, A. Spherical galaxy models as equilibrium configurations in non-extensive statistics. Mon. Not. R. Astron. Soc. 2011, 414, 2265–2274. [Google Scholar] [CrossRef]
- Del Popolo, A. Some improvements to the spherical collapse model. Astron. Astrophys. 2006, 454, 17–26. [Google Scholar] [CrossRef]
- Popolo, A.D. On the evolution of aspherical perturbations in the universe: An analytical model. Astron. Astrophys. 2002, 387, 759. [Google Scholar] [CrossRef]
- Mimoso, J.P.; Le Delliou, M.; Mena, F.C. Separating expansion from contraction in spherically symmetric models with a perfect fluid: Generalization of the Tolman-Oppenheimer-Volkoff condition and application to models with a cosmological constant. Phys. Rev. D 2010, 81, 123514. [Google Scholar] [CrossRef]
- Mimoso, J.P.; Le Delliou, M.; Mena, F.C. Local conditions separating expansion from collapse in spherically symmetric models with anisotropic pressures. Phys. Rev. D 2013, 88, 043501. [Google Scholar] [CrossRef]
- Le Delliou, M.; Mena, F.C.; Mimoso, J.P. Role of shell crossing on the existence and stability of trapped matter shells in spherical inhomogeneous Λ-CDM models. Phys. Rev. D 2011, 83, 103528. [Google Scholar] [CrossRef]
- Le Delliou, M.; Mimoso, J.P.; Mena, F.C.; Fontanini, M.; Guariento, D.C.; Abdalla, E. Separating expansion and collapse in general fluid models with heat flux. Phys. Rev. D 2013, 88, 027301. [Google Scholar] [CrossRef]
- Del Popolo, A.; Gambera, M. Peak mass in large-scale structure and dynamical friction. Astron. Astrophys. 1996, 308, 373–375. [Google Scholar]
- Blumenthal, G.R.; Faber, S.M.; Flores, R.; Primack, J.R. Contraction of dark matter galactic halos due to baryonic infall. Astrophys. J. 1986, 301, 27–34. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Kravtsov, A.V.; Klypin, A.A.; Nagai, D. Response of Dark Matter Halos to Condensation of Baryons: Cosmological Simulations and Improved Adiabatic Contraction Model. Astrophys. J. 2004, 616, 16–26. [Google Scholar] [CrossRef]
- Spedicato, E.; Bodon, E.; Del Popolo, A.; Mahdavi-Amiri, N. ABS Methods and ABSPACK for Linear Systems and Optimization, a Review. Q. J. Belg. Fr. Ital. Oper. Res. Soc. 2002, 1, 51–66. [Google Scholar] [CrossRef]
- Del Popolo, A.; Kroupa, P. Density profiles of dark matter haloes on galactic and cluster scales. Astron. Astrophys. 2009, 502, 733–747. [Google Scholar] [CrossRef]
- Del Popolo, A. A theoretical study of the mass-temperature relation for clusters of galaxies. Mon. Not. R. Astron. Soc. 2002, 336, 81–90. [Google Scholar] [CrossRef]
- Del Popolo, A.; Gambera, M. Non radial motions and the shapes and the abundance of clusters of galaxies. Astron. Astrophys. 2000, 357, 809–815. [Google Scholar]
- Colafrancesco, S.; Antonuccio-Delogu, V.; Del Popolo, A. On the Dynamical Origin of Bias in Clusters of Galaxies. Astrophys. J. 1995, 455, 32. [Google Scholar] [CrossRef]
- Del Popolo, A. Numerical tests of dynamical friction in gravitational inhomogeneous systems. Astron. Astrophys. 2003, 406, 1–6. [Google Scholar] [CrossRef]
- Navarro, J.F.; Eke, V.R.; Frenk, C.S. The cores of dwarf galaxy haloes. Mon. Not. R. Astron. Soc. 1996, 283, L72–L78. [Google Scholar] [CrossRef]
- Gelato, S.; Sommer-Larsen, J. On DDO 154 and cold dark matter halo profiles. Mon. Not. R. Astron. Soc. 1999, 303, 321–328. [Google Scholar] [CrossRef][Green Version]
- Read, J.I.; Gilmore, G. Mass loss from dwarf spheroidal galaxies: The origins of shallow dark matter cores and exponential surface brightness profiles. Mon. Not. R. Astron. Soc. 2005, 356, 107–124. [Google Scholar] [CrossRef]
- Ma, C.P.; Boylan-Kolchin, M. Are Halos of Collisionless Cold Dark Matter Collisionless? Phys. Rev. Lett. 2004, 93, 021301. [Google Scholar] [CrossRef] [PubMed]
- Nipoti, C.; Treu, T.; Ciotti, L.; Stiavelli, M. Galactic cannibalism and cold dark matter density profiles. Mon. Not. R. Astron. Soc. 2004, 355, 1119–1124. [Google Scholar] [CrossRef]
- Romano-Díaz, E.; Shlosman, I.; Hoffman, Y.; Heller, C. Erasing Dark Matter Cusps in Cosmological Galactic Halos with Baryons. Astrophys. J. Lett. 2008, 685, L105. [Google Scholar] [CrossRef]
- Romano-Díaz, E.; Shlosman, I.; Heller, C.; Hoffman, Y. Dissecting Galaxy Formation. I. Comparison Between Pure Dark Matter and Baryonic Models. Astrophys. J. 2009, 702, 1250–1267. [Google Scholar] [CrossRef]
- Cole, D.R.; Dehnen, W.; Wilkinson, M.I. Weakening dark matter cusps by clumpy baryonic infall. Mon. Not. R. Astron. Soc. 2011, 416, 1118–1134. [Google Scholar] [CrossRef]
- Inoue, S.; Saitoh, T.R. Cores and revived cusps of dark matter haloes in disc galaxy formation through clump clusters. Mon. Not. R. Astron. Soc. 2011, 418, 2527–2531. [Google Scholar] [CrossRef]
- Nipoti, C.; Binney, J. Early flattening of dark matter cusps in dwarf spheroidal galaxies. Mon. Not. R. Astron. Soc. 2015, 446, 1820–1828. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. Cold dark matter heats up. Nature 2014, 506, 171–178. [Google Scholar] [CrossRef]
- Teyssier, R.; Pontzen, A.; Dubois, Y.; Read, J.I. Cusp-core transformations in dwarf galaxies: Observational predictions. Mon. Not. R. Astron. Soc. 2013, 429, 3068–3078. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.S.; Fattahi, A.; Navarro, J.F.; Bower, R.G.; Crain, R.A.; Dalla Vecchia, C.; Furlong, M.; Helly, J.C.; Jenkins, A.; et al. The APOSTLE simulations: Solutions to the Local Group’s cosmic puzzles. Mon. Not. R. Astron. Soc. 2016, 457, 1931–1943. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Zhao, H. Maximum feedback and dark matter profiles of dwarf galaxies. Mon. Not. R. Astron. Soc. 2002, 333, 299–306. [Google Scholar] [CrossRef]
- Garrison-Kimmel, S.; Rocha, M.; Boylan-Kolchin, M.; Bullock, J.S.; Lally, J. Can feedback solve the too-big-to-fail problem? Mon. Not. R. Astron. Soc. 2013, 433, 3539–3546. [Google Scholar] [CrossRef]
- Wadsley, J.W.; Stadel, J.; Quinn, T. Gasoline: A flexible, parallel implementation of TreeSPH. New Astron. 2004, 9, 137–158. [Google Scholar] [CrossRef]
- Katz, N.; White, S.D.M. Hierarchical galaxy formation—Overmerging and the formation of an X-ray cluster. Astrophys. J. 1993, 412, 455–478. [Google Scholar] [CrossRef]
- Stinson, G.; Seth, A.; Katz, N.; Wadsley, J.; Governato, F.; Quinn, T. Star formation and feedback in smoothed particle hydrodynamic simulations—I. Isolated galaxies. Mon. Not. R. Astron. Soc. 2006, 373, 1074–1090. [Google Scholar] [CrossRef]
- Stinson, G.S.; Brook, C.; Macciò, A.V.; Wadsley, J.; Quinn, T.R.; Couchman, H.M.P. Making Galaxies In a Cosmological Context: The need for early stellar feedback. Mon. Not. R. Astron. Soc. 2013, 428, 129–140. [Google Scholar] [CrossRef]
- Ceverino, D.; Klypin, A. The Role of Stellar Feedback in the Formation of Galaxies. Astrophys. J. 2009, 695, 292–309. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. How supernova feedback turns dark matter cusps into cores. Mon. Not. R. Astron. Soc. 2012, 421, 3464–3471. [Google Scholar] [CrossRef]
- Oñorbe, J.; Boylan-Kolchin, M.; Bullock, J.S.; Hopkins, P.F.; Kereš, D.; Faucher-Giguère, C.A.; Quataert, E.; Murray, N. Forged in FIRE: Cusps, cores and baryons in low-mass dwarf galaxies. Mon. Not. R. Astron. Soc. 2015, 454, 2092–2106. [Google Scholar] [CrossRef]
- González-Samaniego, A.; Colín, P.; Avila-Reese, V.; Rodríguez-Puebla, A.; Valenzuela, O. Simulations of Isolated Dwarf Galaxies Formed in Dark Matter Halos with Different Mass Assembly Histories. Astrophys. J. 2014, 785, 58. [Google Scholar] [CrossRef]
- Schaller, M.; Frenk, C.S.; Bower, R.G.; Theuns, T.; Jenkins, A.; Schaye, J.; Crain, R.A.; Furlong, M.; Dalla Vecchia, C.; McCarthy, I.G. Baryon effects on the internal structure of ΛCDM haloes in the EAGLE simulations. Mon. Not. R. Astron. Soc. 2015, 451, 1247–1267. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. Flattening Dark Matter Cusps with Supernova Feedback: A Physical Model. 2011, p. 12. Galaxy Formation. Available online: https://ui.adsabs.harvard.edu/abs/2011gafo.confE..12P/abstract (accessed on 17 November 2021).
- Peñarrubia, J.; Pontzen, A.; Walker, M.G.; Koposov, S.E. The Coupling between the Core/Cusp and Missing Satellite Problems. Astrophys. J. Lett. 2012, 759, L42. [Google Scholar] [CrossRef]
- Koposov, S.E.; Yoo, J.; Rix, H.W.; Weinberg, D.H.; Macciò, A.V.; Escudé, J.M. A Quantitative Explanation of the Observed Population of Milky Way Satellite Galaxies. Astrophys. J. 2009, 696, 2179–2194. [Google Scholar] [CrossRef]
- Kravtsov, A. Dark Matter Substructure and Dwarf Galactic Satellites. Adv. Astron. 2010, 2010, 281913. [Google Scholar] [CrossRef]
- Maxwell, A.J.; Wadsley, J.; Couchman, H.M.P. The Energetics of Cusp Destruction. Astrophys. J. 2015, 806, 229. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Conroy, C.; Wechsler, R.H. A Comprehensive Analysis of Uncertainties Affecting the Stellar Mass-Halo Mass Relation for 0 < z < 4. Astrophys. J. 2010, 717, 379–403. [Google Scholar] [CrossRef]
- Moster, B.P.; Somerville, R.S.; Maulbetsch, C.; van den Bosch, F.C.; Macciò, A.V.; Naab, T.; Oser, L. Constraints on the Relationship between Stellar Mass and Halo Mass at Low and High Redshift. Astrophys. J. 2010, 710, 903–923. [Google Scholar] [CrossRef]
- Revaz, Y.; Jablonka, P. The dynamical and chemical evolution of dwarf spheroidal galaxies with GEAR. Astron. Astrophys. 2012, 538, A82. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.S.; Fattahi, A.; Navarro, J.F.; Bower, R.G.; Crain, R.A.; Dalla Vecchia, C.; Furlong, M.; Helly, J.C.; Jenkins, A.; et al. Local Group galaxies emerge from the dark. arXiv 2014, arXiv:1412.2748. [Google Scholar]
- Ferrero, I.; Abadi, M.G.; Navarro, J.F.; Sales, L.V.; Gurovich, S. The dark matter haloes of dwarf galaxies: A challenge for the Λ cold dark matter paradigm? Mon. Not. R. Astron. Soc. 2012, 425, 2817–2823. [Google Scholar] [CrossRef]
- Papastergis, E.; Giovanelli, R.; Haynes, M.P.; Shankar, F. Is there a “too big to fail” problem in the field? Astron. Astrophys. 2015, 574, A113. [Google Scholar] [CrossRef]
- Choi, E.; Ostriker, J.P.; Naab, T.; Oser, L.; Moster, B.P. The impact of mechanical AGN feedback on the formation of massive early-type galaxies. Mon. Not. R. Astron. Soc. 2015, 449, 4105–4116. [Google Scholar] [CrossRef]
- Laporte, C.F.P.; Peñarrubia, J. Under the sword of Damocles: Plausible regeneration of dark matter cusps at the smallest galactic scales. Mon. Not. R. Astron. Soc. 2015, 449, L90–L94. [Google Scholar] [CrossRef]
- Laporte, C.F.P.; White, S.D.M. The redistribution of matter in the cores of galaxy clusters. Mon. Not. R. Astron. Soc. 2015, 451, 1177–1189. [Google Scholar] [CrossRef][Green Version]
- Marinacci, F.; Pakmor, R.; Springel, V. The formation of disc galaxies in high-resolution moving-mesh cosmological simulations. Mon. Not. R. Astron. Soc. 2014, 437, 1750–1775. [Google Scholar] [CrossRef]
- Madau, P.; Shen, S.; Governato, F. Dark Matter Heating and Early Core Formation in Dwarf Galaxies. Astrophys. J. Lett. 2014, 789, L17. [Google Scholar] [CrossRef]
- Noguchi, M. Clumpy star-forming regions as the origin of the peculiar morphology of high-redshift galaxies. Nature 1998, 392, 253. [Google Scholar] [CrossRef]
- Noguchi, M. Early Evolution of Disk Galaxies: Formation of Bulges in Clumpy Young Galactic Disks. Astrophys. J. 1999, 514, 77–95. [Google Scholar] [CrossRef]
- Immeli, A.; Samland, M.; Westera, P.; Gerhard, O. Subgalactic Clumps at High Redshift: A Fragmentation Origin? Astrophys. J. 2004, 611, 20–25. [Google Scholar] [CrossRef]
- Immeli, A.; Samland, M.; Gerhard, O.; Westera, P. Gas physics, disk fragmentation, and bulge formation in young galaxies. Astron. Astrophys. 2004, 413, 547–561. [Google Scholar] [CrossRef]
- Bournaud, F.; Elmegreen, B.G.; Elmegreen, D.M. Rapid Formation of Exponential Disks and Bulges at High Redshift from the Dynamical Evolution of Clump-Cluster and Chain Galaxies. Astrophys. J. 2007, 670, 237–248. [Google Scholar] [CrossRef]
- Agertz, O.; Teyssier, R.; Moore, B. Disc formation and the origin of clumpy galaxies at high redshift. Mon. Not. R. Astron. Soc. 2009, 397, L64–L68. [Google Scholar] [CrossRef]
- Aumer, M.; Burkert, A.; Johansson, P.H.; Genzel, R. The Structure of Gravitationally Unstable Gas-rich Disk Galaxies. Astrophys. J. 2010, 719, 1230–1243. [Google Scholar] [CrossRef]
- Ceverino, D.; Dekel, A.; Bournaud, F. High-redshift clumpy discs and bulges in cosmological simulations. Mon. Not. R. Astron. Soc. 2010, 404, 2151–2169. [Google Scholar] [CrossRef]
- Ceverino, D.; Dekel, A.; Mandelker, N.; Bournaud, F.; Burkert, A.; Genzel, R.; Primack, J. Rotational support of giant clumps in high-z disc galaxies. Mon. Not. R. Astron. Soc. 2012, 420, 3490–3520. [Google Scholar] [CrossRef]
- Toomre, A. On the gravitational stability of a disk of stars. Astrophys. J. 1964, 139, 1217–1238. [Google Scholar] [CrossRef]
- Krumholz, M.R.; Dekel, A. Survival of star-forming giant clumps in high-redshift galaxies. Mon. Not. R. Astron. Soc. 2010, 406, 112–120. [Google Scholar] [CrossRef]
- Macciò, A.V.; Stinson, G.; Brook, C.B.; Wadsley, J.; Couchman, H.M.P.; Shen, S.; Gibson, B.K.; Quinn, T. Halo Expansion in Cosmological Hydro Simulations: Toward a Baryonic Solution of the Cusp/Core Problem in Massive Spirals. Astrophys. J. Lett. 2012, 744, L9. [Google Scholar] [CrossRef]
- Del Popolo, A.; Pace, F. The Cusp/Core problem: Supernovae feedback versus the baryonic clumps and dynamical friction model. Astrophys. Space Sci. 2016, 361, 162. [Google Scholar] [CrossRef]
- Del Popolo, A. On the dark matter haloes inner structure and galaxy morphology. Astrophys. Space Sci. 2016, 361, 222. [Google Scholar] [CrossRef]
- Weidner, C.; Kroupa, P.; Pflamm-Altenburg, J.; Vazdekis, A. The galaxy-wide IMF of dwarf late-type to massive early-type galaxies. Mon. Not. R. Astron. Soc. 2013, 436, 3309. [Google Scholar] [CrossRef]
- Lazar, A.; Bullock, J.S.; Boylan-Kolchin, M.; Chan, T.K.; Hopkins, P.F.; Graus, A.S.; Wetzel, A.; El-Badry, K.; Wheeler, C.; Straight, M.C.; et al. A dark matter profile to model diverse feedback-induced core sizes of ΛCDM haloes. Mon. Not. R. Astron. Soc. 2020, 497, 2393–2417. [Google Scholar] [CrossRef]
- Freundlich, J.; Jiang, F.; Dekel, A.; Cornuault, N.; Ginzburg, O.; Koskas, R.; Lapiner, S.; Dutton, A.; Macciò, A.V. The Dekel-Zhao profile: A mass-dependent dark-matter density profile with flexible inner slope and analytic potential, velocity dispersion, and lensing properties. Mon. Not. R. Astron. Soc. 2020, 499, 2912–2933. [Google Scholar] [CrossRef]
- Zhao, H. Analytical models for galactic nuclei. Mon. Not. R. Astron. Soc. 1996, 278, 488–496. [Google Scholar] [CrossRef]
- Di Cintio, A.; Brook, C.B.; Dutton, A.A.; Macciò, A.V.; Stinson, G.S.; Knebe, A. A mass-dependent density profile for dark matter haloes including the influence of galaxy formation. Mon. Not. R. Astron. Soc. 2014, 441, 2986–2995. [Google Scholar] [CrossRef]
- Wang, L.; Dutton, A.A.; Stinson, G.S.; Macciò, A.V.; Penzo, C.; Kang, X.; Keller, B.W.; Wadsley, J. NIHAO project—I. Reproducing the inefficiency of galaxy formation across cosmic time with a large sample of cosmological hydrodynamical simulations. Mon. Not. R. Astron. Soc. 2015, 454, 83–94. [Google Scholar] [CrossRef]
- Dekel, A.; Ishai, G.; Dutton, A.A.; Maccio, A.V. Dark-matter halo profiles of a general cusp/core with analytic velocity and potential. Mon. Not. R. Astron. Soc. 2017, 468, 1005–1022. [Google Scholar] [CrossRef]
- Read, J.I.; Agertz, O.; Collins, M.L.M. Dark matter cores all the way down. Mon. Not. R. Astron. Soc. 2016, 459, 2573–2590. [Google Scholar] [CrossRef]
- Dutton, A.A.; Macciò, A.V. Cold dark matter haloes in the Planck era: Evolution of structural parameters for Einasto and NFW profiles. Mon. Not. R. Astron. Soc. 2014, 441, 3359–3374. [Google Scholar] [CrossRef]
- Colín, P.; Avila-Reese, V.; Valenzuela, O. Substructure and Halo Density Profiles in a Warm Dark Matter Cosmology. Astrophys. J. 2000, 542, 622–630. [Google Scholar] [CrossRef]
- Polisensky, E.; Ricotti, M. Constraints on the Dark Matter Particle Mass from the Number of Milky Way Satellites. Phys. Rev. 2011, D83, 043506. [Google Scholar] [CrossRef]
- Lovell, M.R.; Eke, V.; Frenk, C.S.; Gao, L.; Jenkins, A.; Theuns, T.; Wang, J.; White, S.D.M.; Boyarsky, A.; Ruchayskiy, O. The haloes of bright satellite galaxies in a warm dark matter universe. Mon. Not. R. Astron. Soc. 2012, 420, 2318–2324. [Google Scholar] [CrossRef]
- Angulo, R.E.; Hahn, O.; Abel, T. The warm dark matter halo mass function below the cut-off scale. Mon. Not. R. Astron. Soc. 2013, 434, 3337–3347. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; Martinez, G.D.; Bullock, J.S.; Kaplinghat, M. The Case Against Warm or Self-Interacting Dark Matter as Explanations for Cores in Low Surface Brightness Galaxies. Astrophys. J. Lett. 2010, 710, L161–L166. [Google Scholar] [CrossRef]
- Wu, X.; Kroupa, P. Galactic rotation curves, the baryon-to-dark-halo-mass relation and space—Time scale invariance. Mon. Not. R. Astron. Soc. 2015, 446, 330–344. [Google Scholar] [CrossRef]
- Dalal, N.; Kochanek, C.S. Direct Detection of Cold Dark Matter Substructure. Astrophys. J. 2002, 572, 25–33. [Google Scholar] [CrossRef]
- Fadely, R.; Keeton, C.R. Near-infrared K and L’ Flux Ratios in Six Lensed Quasars. Astron. J. 2011, 141, 101. [Google Scholar] [CrossRef]
- Fadely, R.; Keeton, C.R. Substructure in the lens HE 0435-1223. Mon. Not. R. Astron. Soc. 2012, 419, 936–951. [Google Scholar] [CrossRef][Green Version]
- Macciò, A.V.; Paduroiu, S.; Anderhalden, D.; Schneider, A.; Moore, B. Cores in warm dark matter haloes: A Catch 22 problem. Mon. Not. R. Astron. Soc. 2012, 424, 1105–1112. [Google Scholar] [CrossRef]
- Schneider, A.; Anderhalden, D.; Macciò, A.V.; Diemand, J. Warm dark matter does not do better than cold dark matter in solving small-scale inconsistencies. Mon. Not. R. Astron. Soc. 2014, 441, L6–L10. [Google Scholar] [CrossRef]
- Narayanan, V.K.; Spergel, D.N.; Davé, R.; Ma, C.P. Constraints on the Mass of Warm Dark Matter Particles and the Shape of the Linear Power Spectrum from the Lyα Forest. Astrophys. J. Lett. 2000, 543, L103–L106. [Google Scholar] [CrossRef]
- Burkert, A. The Structure and Evolution of Weakly Self-interacting Cold Dark Matter Halos. Astrophys. J. Lett. 2000, 534, L143–L146. [Google Scholar] [CrossRef] [PubMed]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J.; Nipoti, C.; Richard, J.; Jullo, E. The Density Profiles of Massive, Relaxed Galaxy Clusters. I. The Total Density Over Three Decades in Radius. Astrophys. J. 2013, 765, 24. [Google Scholar] [CrossRef]
- Rocha, M.; Peter, A.H.G.; Bullock, J.S.; Kaplinghat, M.; Garrison-Kimmel, S.; Oñorbe, J.; Moustakas, L.A. Cosmological simulations with self-interacting dark matter—I. Constant-density cores and substructure. Mon. Not. R. Astron. Soc. 2013, 430, 81–104. [Google Scholar] [CrossRef]
- Peter, A.H.G.; Rocha, M.; Bullock, J.S.; Kaplinghat, M. Cosmological simulations with self-interacting dark matter—II. Halo shapes versus observations. Mon. Not. R. Astron. Soc. 2013, 430, 105–120. [Google Scholar] [CrossRef]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A Direct Empirical Proof of the Existence of Dark Matter. Astrophys. J. Lett. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Randall, S.W.; Markevitch, M.; Clowe, D.; Gonzalez, A.H.; Bradač, M. Constraints on the Self-Interaction Cross Section of Dark Matter from Numerical Simulations of the Merging Galaxy Cluster 1E 0657-56. Astrophys. J. 2008, 679, 1173–1180. [Google Scholar] [CrossRef]
- Dawson, W.A.; Wittman, D.; Jee, M.J.; Gee, P.; Hughes, J.P.; Tyson, J.A.; Schmidt, S.; Thorman, P.; Bradač, M.; Miyazaki, S.; et al. Discovery of a Dissociative Galaxy Cluster Merger with Large Physical Separation. Astrophys. J. Lett. 2012, 747, L42. [Google Scholar] [CrossRef]
- Yoshida, N.; Springel, V.; White, S.D.M.; Tormen, G. Weakly Self-interacting Dark Matter and the Structure of Dark Halos. Astrophys. J. Lett. 2000, 544, L87–L90. [Google Scholar] [CrossRef]
- Davé, R.; Spergel, D.N.; Steinhardt, P.J.; Wandelt, B.D. Halo Properties in Cosmological Simulations of Self-interacting Cold Dark Matter. Astrophys. J. 2001, 547, 574–589. [Google Scholar] [CrossRef]
- Harko, T. Bose-Einstein condensation of dark matter solves the core/cusp problem. J. Cosmo. Astrop. Phys. 2011, 5, 22. [Google Scholar] [CrossRef]
- Schive, H.Y.; Chiueh, T.; Broadhurst, T. Cosmic structure as the quantum interference of a coherent dark wave. Nat. Phys. 2014, 10, 496–499. [Google Scholar] [CrossRef]
- Robles, V.H.; Matos, T. Flat central density profile and constant dark matter surface density in galaxies from scalar field dark matter. Mon. Not. R. Astron. Soc. 2012, 422, 282–289. [Google Scholar] [CrossRef]
- Öpik, E. Selective absorption of light in space, and the dynamics of the Universe. Bull. De La Soc. Astr. De Russ. 1915, 21, 150. [Google Scholar]
- Strigari, L.E.; Frenk, C.S.; White, S.D.M. Dynamical models for the Sculptor dwarf spheroidal in a Lambda CDM universe. arXiv 2014, arXiv:1406.6079. [Google Scholar]
- Takada, M. Subaru Hyper Suprime-Cam Project. In American Institute of Physics Conference Series; Kawai, N., Nagataki, S., Eds.; American Institute of Physics: University Park, MD, USA, 2010; Volume 1279, pp. 120–127. [Google Scholar] [CrossRef]
- de Bruijne, J.H.J. Science performance of Gaia, ESA’s space-astrometry mission. Astrophys. Space Sci. 2012, 341, 31–41. [Google Scholar] [CrossRef]
- Richardson, T.D.; Spolyar, D.; Lehnert, M.D. Plan β: Core or cusp? Mon. Not. R. Astron. Soc. 2014, 440, 1680–1689. [Google Scholar] [CrossRef]
- Strigari, L.E.; Bullock, J.S.; Kaplinghat, M.; Diemand, J.; Kuhlen, M.; Madau, P. Redefining the Missing Satellites Problem. Astrophys. J. 2007, 669, 676–683. [Google Scholar] [CrossRef]
- Battaglia, G.; Helmi, A.; Breddels, M. Internal kinematics and dynamical models of dwarf spheroidal galaxies around the Milky Way. New Astron. Rev. 2013, 57, 52–79. [Google Scholar] [CrossRef]
- Metcalf, R.B.; Amara, A. Small-scale structures of dark matter and flux anomalies in quasar gravitational lenses. Mon. Not. R. Astron. Soc. 2012, 419, 3414–3425. [Google Scholar] [CrossRef]
- Carlberg, R.G.; Grillmair, C.J. Gaps in the GD-1 Star Stream. Astrophys. J. 2013, 768, 171. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).