Abstract
The detection of the radio signal from filaments in the cosmic web is crucial to distinguish possible magnetogenesis scenarios. We review the status of the different attempts to detect the cosmic web at radio wavelengths. This is put into the context of the advanced simulations of cosmic magnetism carried out in the last few years by our MAGCOW project. While first attempts of imaging the cosmic web with the MWA and LOFAR have been encouraging and could discard some magnetogenesis models, the complexity behind such observations makes a definitive answer still uncertain. A combination of total intensity and polarimetric data at low radio frequencies that the SKA and LOFAR2.0 will achieve is key to removing the existing uncertainties related to the contribution of many possible sources of signal along deep lines of sight. This will make it possible to isolate the contribution from filaments, and expose its deep physical connection with the origin of extragalactic magnetism.
1. Introduction
1.1. The Puzzling Origin of Cosmic Magnetism
Understanding how the observed magnetic fields in the largest structures in the Universe emerged is an important open issue in modern astrophysics.
Theoretical and numerical work has shown that the microgauss (μG) magnetic fields inferred from radio observations e.g., [1,2,3,4] could be produced by small-scale turbulent dynamo amplification, provided that the magnetic Reynolds number in the intracluster medium (ICM1) is large enough e.g., [5,6,7,8]. In typical ICM conditions (density [cm−3], temperature – K and plasma beta ), a dynamo can bring the magnetic energy density close to equipartition with the turbulent plasma kinetic energy in galaxy clusters. A small-scale dynamo also erases the memory of the initial magnetic field level, as verified by direct numerical simulations e.g., [9,10,11,12,13,14,15,16,17]. While all previous results are based on ideal magneto-hydrodynamical (MHD) simulations, kinetic simulations have recently started to explore the more realistic situation of weakly collisional plasmas. They confirmed the action of a dynamo but also highlighted the important role of Prandtl number variations on the initial magnetisation value and of kinetic instabilities e.g., [18,19,20].
Regardless of the exact nature of the small-scale dynamo process in the ICM, a non-zero seed magnetic field is necessary for the dynamo to start. Then, different sources and mechanisms to generate and amplify magnetic fields in diluted cosmic plasmas are viable. At present, we still do not know whether the observed fields have mostly a “primordial” origin (meaning they are the result of processes that happened soon after the Big Bang) or are connected to the evolution of galaxies and of their black holes.
Several processes might have created truly primordial seed fields, either during inflation by breaking the conformal invariance for the electromagnetic field, or by coupling it to other light fields and generating helicity e.g., [21,22,23]. In the post-inflationary epoch, a causal process could lead to the production of large amplitudes and small (below the size of the Hubble radius at the generation time) coherence lengths [24,25,26]. Recently, the first pilot cosmological simulations for the evolution of helical magnetic fields have been presented by [27]. Assessing whether primordial magnetic fields were present at the epoch of the Cosmic Microwave Background (CMB) is important as they impact the Big Bang Nucleosynthesis, alter CMB anisotropies patterns and affect angular power spectra in temperature and polarisation e.g., [28,29,30].
Alternatively, or in addition, magnetic field seeds may have been injected by feedback events following the overcooling of gas onto the massive halos as well as the formation of stellar populations and supermassive black holes (SMBH). Such astrophysical sources can seed magnetic fields in cosmic structures at low redshift (), in an inside-out fashion which starts from galaxies: star formation drives winds of magnetised plasma into the circumgalactic medium e.g., [31,32,33,34,35] as well as into voids [36]. Jets and winds from active galactic nuclei (AGN) can magnetise the central regions of clusters and groups e.g., [37,38] and affect the transport of heat, entropy, metals and cosmic rays during the formation of cosmic structures e.g., [39].
Somewhat in between primordial and astrophysical scenarios, additional processes such as the “Biermann-battery” mechanism [40], aperiodic plasma fluctuations in the inter-galactic plasma [41], resistive mechanisms [42], ionization fronts around the first stars [43,44] or even the accretion of magnetic monopoles at the formation of primordial black holes [45] might provide additional seed magnetic fields.
Overall, it is fair to say that the present uncertainty in the amplitude of seed fields in the Universe, based on theory, is uncomfortably large. Basically, it allows for primordial fields with amplitudes in the range of ~– G e.g., [22,46,47]. A recent survey of astrophysical seeding scenarios, with state-of-the-art cosmological MHD simulations, has inferred a lower limit of for the magnetisation of voids [48]. Other limits have been suggested by modelling magnetic effects on CMB anisotropies from magnetically induced perturbations on post-recombination heating e.g., [49]. Such very low bounds seem to be incompatible with the absence of detected Inverse Compton Cascade emission from blazars e.g., [50,51,52,53,54], which yields limits of ∼ G2. Other stringent limits have been suggested by modelling magnetic effects on post-recombination heating e.g., [57,58,59] or by the small-scale baryonic density fluctuation induced by primordial magnetic fields, which would alter CMB anisotropies by promoting to inhomogeneous recombination and heating e.g., [60,61,62]. Recent limits for the average present-day magnetisation of the Universe have also been derived by the level of excess in diffuse radio emission detected by ARCADE2 and EDGES 21cm line experiments, yielding ≤– nG depending on the unknown spectral index of primordial seed fields [63].
1.2. The Magnetic Cosmic Web and Its Radio Observations
In the present situation, any significant detection of, or constraints on, magnetic fields beyond the scale of galaxies and galaxy clusters will have the potential of discriminating between different hypotheses for the origin of cosmic magnetism. Previous work has shown that the radio signatures of drastically different magnetic field scenarios would leave very different imprints in Faraday Rotation and/or synchrotron emission from the magnetised cosmic web [33,64,65], in regions where small-scale dynamo is not expected to operate, due to the different local plasma conditions there e.g., [66,67].
In the (numerically) simple scenario in which magnetic fields were already in place at very early cosmic epochs, and got later advected, compressed and amplified up to the observed values within galaxy clusters and groups, we expect that the three-dimensional distribution of the magnetic cosmic web pretty much follows that of the matter cosmic web.
Figure 1 shows a volume rendering3 of baryon gas density and magnetic fields in one of the largest MAGCOW simulations (and cosmological MHD simulations in general), i.e., a comoving Mpc3 volume simulated with cells and dark matter particles, for a constant spatial comoving resolution of kpc and assuming a simple uniform seed magnetic field of nG comoving, seeded at the beginning of the run (). For further analysis of this simulation, see [68,69,70,71]. Spectacular threads of magnetic fields that trace the underlying matter distribution of the cosmic web are clearly seen in the image. These fields are the result of an initially uniform magnetic field distribution that has been compressed by the matter field. Given that the isotropic adiabatic compression of magnetic field lines increases the strength by (where is the gas density and is the gas mean density) in the absence of dynamo amplification the range of amplitude in magnetic field strength is smaller than the range of gas densities across the cosmic web. We anticipate that, in astrophysical scenarios, on the other hand, the distribution of magnetic fields is much more confined closer to the high density peaks of the cosmic web e.g., [65].
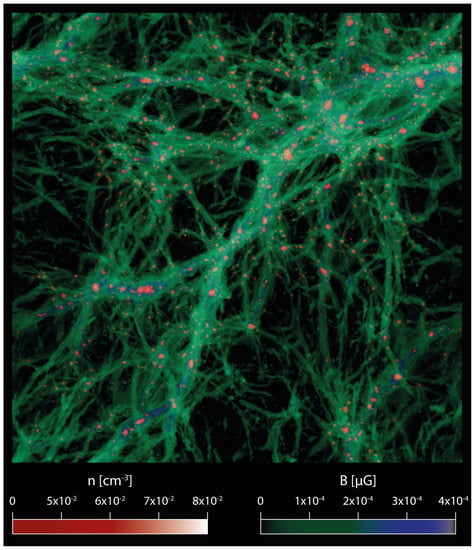
Figure 1.
Three-dimensional volume rendering of the gas density and of the magnetic field strength in one of the largest MAGCOW simulations of a primordial seed field ( comoving) evolved in a 1003 Mpc3 volume using simulated with 24003 cells and dark matter particles.
The diffuse gas in the cosmic web, especially in the low redshift Universe (), has not been imaged in X-ray, owing to the scarcity of detectable X-ray photons from the warm-hot intergalactic medium e.g., [72,73]. The exceptions are attempts involving massive galaxy clusters [74,75], or stacking techniques [76]. In the radio band, the situation may be less challenging because cosmic filaments are surrounded by strong accretion shocks e.g., [77,78], which may also accelerate cosmic rays and produce synchrotron emission e.g., [64,79,80,81].
In the last few years, a new low-frequency radio telescope have detected magnetic fields beyond the scale of galaxy clusters. In several cases, our MAGCOW simulations were used to quantify the implications of such limits, and turn them into constraints on the different models of cosmic magnetism. Table 1 gives an (incomplete) overview of relevant estimates or limits on the magnetisation of the cosmic web at different scales, for a very heterogeneous collection of observations.

Table 1.
(Incomplete) list of recent and relevant measures or upper limits that attempted to detect magnetic fields on extragalactic scales, together with the estimated overdensity range they refer to.
First, a few short (≤) and overdense () filaments between pre-merging clusters were detected by LOFAR-High Band Antenna (HBA): in Abell 399-Abell 401 [82] and Abell 1758A and B [83]. The modelling of the steep spectrum (, where ) emission in Abell 399-Abell 401, which currently prefers a scenario based on turbulent re-acceleration of fossil relativistic electrons, suggested volume-filling ∼ μG magnetic fields [84]. A similar case, albeit more internal to the cluster volume, appears to be the bridge connecting the halo and relic region in the Coma cluster, whose recent LOFAR-HBA observation has also been modelled with our simulations [85].
On the other hand, LOFAR-HBA observations of two clusters connected by longer filaments (∼10–20 Mpc, which are expected to enclose a – gas overdensity) could not detect diffuse radio emission, suggesting a μG upper limit for the magnetisation of such extended filaments, under the hypothesis that relativistic electrons are accelerated by structure formation shocks here [86].
On even larger scales, upper limits on the amplitude of magnetic fields have been statistically derived from the lack of detection of the cross-correlated signal between the large-scale distribution of galaxies in optical and IR surveys, and MWA surveys, which was used to suggest a μG upper limit on the average magnetisation of the cosmic web surrounding halos, i.e., [87,88].
Finally, Ref. [70] have made a statistical detection of the diffuse radio emission between pairs of halos separated by ≤, with the stacking of 390,808 pairs of luminous red galaxies identified in the Sloan Digital Sky Survey Data Release 5 and observed at four different radio frequencies (from 50 to 120 MHz) using the the GLEAM survey with MWA and with the Owens Valley Radio Observatory Long Wavelength Array. The reported detection is at the ∼ level, has a spectral index of and appears difficult to explain with any known population of radio galaxies and AGN. Based on the analysis of our MAGCOW simulations, the emission was suggested to be compatible with a diffuse magnetic field in filaments, in the ∼10–20 nG ballpark for a typical expected gas density in the – range.
However, building a consistent mock statistical analysis with simulations is far from trivial, and more recent work using the same MAGCOW simulations has suggested that it is difficult to reproduce the same excess signal from cluster pairs, if all outliers are removed [89].
A way to overcome sensitivity limitations of total intensity in radio observations is to use the Faraday Rotation Measure (RM) along the line-of-sight to a polarised background radio source. This can be used to perform a tomography of the cosmic web, with a fine grid of background sources e.g., [90,91]. Fully exploiting this method currently suffers from the lack of large and dense grids of polarised sources, which should become available with the SKA [67]. Early attempts to constrain extragalactic magnetic fields statistically have set very high upper limits at the level of 0.3–7 μG e.g., [91,92,93]. Later work by [94] used the (lack of) evolution of RM in sources observed with the NRAO VLA Sky Survey (NVSS) to infer much lower, 0.65–1.7 nG limits for the extragalactic magnetic fields. More recently, Ref. [95] claimed the detection of the RM contribution by filaments overlapping the polarised emission by a giant radio galaxy using LOFAR-HBA.
By cross-correlating the RM signal of 1742 radio galaxies in the NVSS [96] with the distribution of optical and IR galaxies, Ref. [97] recently measured a upper bound to the RM contribution of the magnetised cosmic web, which may suggest a upper limit on the magnetisation of the cosmic web on 1– scales (–).
The excess RM between random pairs of extended radio galaxies can be used to constrain the amplitude of intergalactic magnetic fields. This is done by comparing the difference, as a function of angular scale, between physically related pairs of extended radio galaxies, and random associations of radio lobes [98,99]. In particular, Ref. [100] found that the RM difference between random and physical pairs of 349 radio galaxies observed with LOFAR-HBA was . Such a difference constrains the magnetisation of cosmic matter to ≤ for field with a coherence length , and –.
Finally, more indirect constraints on the amplitude of magnetic fields on the largest scales have been inferred from the Cosmic Microwave Background (see Section 1.1). These can be turned into an estimate on the current magnetisation of voids, under the reasonable hypothesis of ideal MHD and lack of other sources of magnetisation in the very low density Universe (–). See Table 2 for a summary of observational limits on cosmic magnetic fields.

Table 2.
Main parameters of MAGCOW runs employed in this work. All quantities given are comoving. For more details, see Section 2 and Appendix A.
In Section 3, we will attempt to translate such measurements into constraints on extragalactic magnetic fields on different scales, with the strong caveat that each different measurement comes from very different selection functions, class of sources and redshift selection. They are also very differently affected by cosmic foregrounds, background and observational limitations. In Section 4, we present our conclusions and put them in the broader context of the aim to find the origin of cosmic magnetism.
2. Methods and Materials: Cosmological Simulations of the Cosmic Web
The MAGCOW project, funded by a Starting Grant from the European Research Council4, is built around the idea of exploring the origin of cosmic magnetism, through the combination of radio observations capable of probing the most rarefied cosmic regions of the Universe, and advanced numerical simulations.
Over the latest few years, we produced large simulations for the co-evolution of dark matter (DM), gas matter, supermassive black holes and stellar populations, together with their associated magnetic fields, in an expanding space-time, with customized versions of the ENZO code [101].
This paper is not meant to be too detailed on the numerical subtleties of our simulations, which have been documented elsewhere [102,103,104,105]. Here, we review the most relevant physical aspects of the models examined in our old and new runs, and refer to the Appendix A for a more complete overview of the numerical details and code implementation specifics.
A first large set of (25) simulations has been already described in detail in [65]. In this contribution, we also include the results from more recent re-simulations, tailored to improve the comparison with new observational results.
All models use some prescription for the seeding of magnetic fields, either at the start of the simulation, mimicking primordial mechanisms, or during the simulation, mimicking astrophysical generation of magnetic fields.
The older simulations included in this paper are (for consistency, we keep the same naming given in previous papers):
- P: a baseline primordial model in which we initialised a spatially uniform seed field at the start of the simulation;
- DYN5: a run starting from a negligible and spatially uniform seed field, in which we used a sub-grid model for turbulent dynamo amplification (see Appendix A), for cells with a gas density , i.e., basically already within filaments;
- CSF2: a run including radiative cooling, star formation and feedback, starting from a negligible and spatially uniform seed field. Magnetic fields are released at every episode of thermal feedback from star formation (with a fixed small conversion efficiency per event, ≤10%), to reproduce an astrophysical seeding scenario in which winds from supernova remnant magnetise the large-scale structures.
- CSFBH2: similar to CSF2, but also including the formation, growth, merger and feedback events of supermassive black holes. In addition, in this case, magnetic energy is released by SMBH feedback events (∼10% of the feedback energy) mimicking an astrophysical seeding scenario in which active galactic nuclei magnetise large-scale structures. The model parameters for baryon physics were tuned in previous work to reproduce cosmic star formation history and galaxy groups/clusters scaling relations (see Appendix A).
The new runs are introduced here for the first time:
- P01: a simple primordial model in which we initialised a spatially uniform seed field at the start of the simulation, and in which we allowed for the sub-grid dynamo amplification of magnetic fields only for cells with a gas density , which approximately marks region within the virial radius of halos, where turbulence is predicted to be well developed and mostly solenoidal [106]. As a further relevant difference with the “old” DYN5, the amplification efficiency is increased by a factor 10 for , leading to more realistic magnetic fields in low-redshift clusters and groups.
- CMB2, CMB3, and CMB4: we simulated primordial magnetic fields derived from the constraints by the Cosmic Microwave Background observations following our recent work [105]. In detail, the fields scale dependence is described by a power law spectrum: characterised by a constant spectral index and an amplitude, commonly referred by smoothing the fields within a scale , and therefore in the remainder of the paper we will use to refer to the smoothed magnetic field amplitude. In this work, we used the three models outlined in [105], which resulted as the least challenged by low-redshift radio observations of the cosmic web: we assumed (CMB2), (CMB3) and (CMB4) and , and (comoving), respectively. All runs also adopted the same run-time sub-grid model for dynamo amplification, as in the P01 model.
Table 2 summarises all relevant parameters of our runs and more information is given in the Appendix A.
All runs assumed a CDM cosmological model, with density parameters , , , and a Hubble constant km/s/Mpc [107]. Runs were started at and have the constant spatial resolution of (comoving) and the constant mass resolution for DM of per particle.
Our simulations are limited to the ideal MHD scenario, meaning that the resistive dissipation of magnetic fields, kinetic plasma effects and other features connected with the departure from the single fluid model cannot be accounted for. Although it is fair to say that these phenomena have been scarcely studied in the very low-density regime which we are mostly concerned with here. The numerical work that investigated non-ideal MHD effects reported negligible differences compared to ideal MHD in the periphery of galaxy clusters, or in even more rarefied environments e.g., [108,109].
3. Results
We start by looking at the statistical distribution of magnetic field strength as a function of gas overdensity, . This was measured at in the old MAGCOW runs presented in Section 2, which are the first four panels in Figure 2. Each pixel in the phase diagram is weighted by the relative gas mass fraction. We overlay onto the various phase distributions the approximate constraints that can be derived from observations, according to our best estimate of the gas overdensity along the line-of-sight which is mostly probed by each observation, as in Section 1.2.
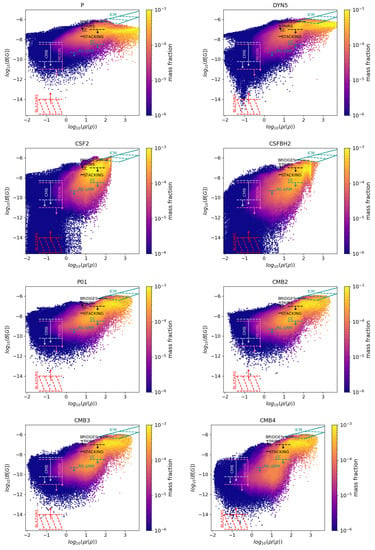
Figure 2.
Phase diagrams for all MAGCOW runs discussed in this paper, at . The contribution to each pixel is weighted by the gas mass fraction within a 853 Mpc3 volume. We additionally overlay the approximate range of detections and limits by current observations, as in Table 2. The dark cyan colors represent Faraday Rotation observations, the black lines synchrotron total intensity observations, the light grey lines are measurements of CMB multipoles, the pink lines are for estimates based on reionisation, and the red lines are from blazars observations. Solid lines refer to detections and dashed lines refer to non-detections.
As expected, most cosmic environments carry the memory of magnetic seeding and show very different trends. For example, in sheets and low-density filaments, , most of gas matter in the P model carries memory of the seed field, having . This is significantly lower in the DYN5 model owing to the partial effect of dynamo amplification here, which is assumed to operate even in very low density regimes. In the astrophysical scenarios (CSF2 and CSFBH2), the average magnetisation is much lower (≤) and there is a ∼6 order of magnitude spread in the possible values of . The latter depends on the proximity of cells to a nearby source of magnetisation. Such differences persist in the denser environment of cluster outskirts, where the magnetic field strengths are better approximated by the adiabatic relation.
On densities larger than the typical density enclosed by virialised halos, all models struggle to match the magnetisation observed in real clusters and groups (which we show using the latest compilation of RM results in galaxy clusters by [110,111]). This is due to both the lack of resolution (which is only partially compensated by the subgrid dynamo model in DYN5) and of the scarcity of big clusters of galaxies that can form in our volume. The comparison with the approximate magnetic field constraints that can be derived from the observations listed in Section 1.2 suggested first important trends:
- none of these simulations is optimal to simulate the ICM or intracluster bridges in detail because their modest resolution prevents us from properly resolving the “MHD scale” which is key for the development of a small-scale dynamo e.g., [14]. Hence, the comparison is not very informative here.
- in the very low-density Universe, the P and the DYN5 models have some tension with CMB limits. This problem is not as severe for astrophysical models. Vice versa, both CSF2 and CSFBH2 models produce a too low magnetisation in very low-density regions, in disagreement with blazar limits [54].
- the non-detection of diffuse emission in cluster–cluster filaments with LOFAR-HBA [86] is consistent with all models. The non-detection of the galaxy-synchrotron cross-correlation [88] is in disagreement with the primordial model as well as on the DYN5 model because an excess cross-correlated signal is to be expected, as we discussed in [104].
- likewise, the upper limits on Faraday Rotation by [97], and even more the RM difference between pairs of giant radio galaxies by [100], appear hard to reconcile with the large primordial seed field of the P model, as well as with the widespread amplification of magnetic fields in filaments included in the DYN5 model.
- the stacking detection of flat spectrum synchrotron emission between pairs of halos by [70] is only apparently consistent with all models. However, in that work, the detailed analysis of these simulations also showed that the DYN5 and CSFBH2 models are incapable of producing enough radio emission compatible with the observed extend of the stacking excess. In all astrophysical scenarios, some patches of high magnetic field can be found within filaments. These are typically confined to the active galaxies, from which they were released, and cannot efficiently fill the most peripheral layers of filaments, where most of the emission from the shocked gas comes from in our models.
Based on the work mentioned above, it may be tempting to conclude that a primordial model with a seed field of ∼ (i.e., a primordial model similar to the P, but with initial amplitude down scaled by a factor ∼2) is presently favoured by the observational data. However, there are a number of caveats:
The statistical detections or limits to the radio signature of the cosmic web always come jointly with the complex removal of fore- and backgrounds, which are always present (and sometimes even dominant) on the large angular scales (≥) at which most of these observations are taken. For example, the contamination by the magnetised screen of the Milky Way is always present, and can produce artefacts e.g., [112]. The removal of radio galaxies is also particularly difficult, and assessing the contribution from the background of faint or/and unresolved sources is non-trivial e.g., [70], as well as very challenging to properly include in simulations e.g., [71,113]. Finally, estimates coming from synchrotron emission needs a guess on the quantity of accelerated electrons to derive the amplitude of magnetic fields, but the acceleration efficiency by cosmic shocks is largely unknown e.g., [114,115,116], also based on the modelling of real radio observations of cluster radio shocks e.g., [117,118,119]. Moreover, the possible additional contribution from turbulent re-acceleration operating on scales larger than cluster “bridges” is largely unconstrained [84].
Motivated by the above comparison with observational constraints, to improve the simulated amplification of magnetic fields in halos, as well as to incorporate more realistic primordial seed fields as in [105], we produced our new P01, CMB2, CMB3 and CMB4 runs. Their phase diagrams are given in the last four panels of Figure 2. Overall, these models match the boundaries of observations better than the original P model. In particular, the “blue” CMB4 model gives the most conservative (and low) average magnetic field on the scale of voids, making this model compatible at least with some of the existing limits from CMB analysis and reionization, and at the same time with limits from blazars. To better illustrate the different volumetric properties of these models, we give in Figure 3 an example of the maps of Faraday Rotation and synchrotron radio emission at 120 MHz from shock accelerated relativistic electrons (based on the same diffusive shock acceleration model used in [68]) at and integrated along a line-of-sight of , for our most realistic primordial model (P01, CMB2, CMB3 and CMB4) and for the most complete astrophysical scenario (CSFBH2).
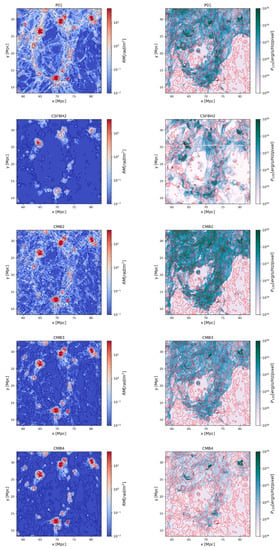
Figure 3.
Maps of Faraday Rotation (left) and synchrotron radio emission at 120 MHz (right), for a small portion (focusing on a few long filaments) for all our runs at . The contours approximately mark the projected location of ordinary matter distribution.
The P01, CMB2 and CMB3 models show a very diffuse RM signal (≥) on most scales, while the CSFBH2 and CMB4 models show signatures mostly correlated with halos. The synchrotron emission in the CSFBH2 model is patchier than in all other models, which have instead more uniform and volume filling emission patterns associated with filaments, with up to several Megaparsec from the halo they contain. It shall be noticed that the gas density structure underlying the synchrotron and RM signals (in contours) is not exactly the same in all runs. The presence (or absence) of feedback from galaxies and, to a lesser extent, the dynamical impact of different large-scale magnetic fields influence the gas distribution in filaments, as tested in our work [102,103].
Since several detection attempts are relying on stacking or statistical techniques, it is useful to use a sample of simulated filaments to predict the typical Faraday Rotation and synchrotron signal from the average population.
Here, we limit to low redshift data (, i.e., ∼200 Mpc) and focus on the population of filaments with three-dimensional length between 5–20 Mpc, which is abundant also in the small simulated volume at our disposal e.g., [120], and which is typically targeted by direct or stacking observations of cluster-cluster pairs e.g., [70,86].
First, we extract from each three-dimensional volume a catalog of filaments in the given range of lengths, using the algorithm developed in [121] for our simulations. By construction, all detected filaments are delimited by halos, and are filled with gas with an average temperature. The RM and synchrotron emission maps are finally rescaled to the same projected angular size of ≈, i.e., of the order of the maximum angular scale sample by the recent stacking observation by [70], and corresponding to a projected linear size of 10 Mpc at . Finally, we produced the average of both observables over the entire population of extracted filaments. For each of the ∼50 filaments extracted with this procedure, we computed the average profile along a narrow stripe connecting the two nearest halos (corresponding to kpc at the reference distance) and averaged the profile with the rest of the population. All ≤ of halos identified in the simulation are masked out from the analysis, to mimic the masking of galaxies and halos which is typically done in real observations.
As in real observations, we also need to compare this signal with the sort of “baseline emission level” produced by the average cosmic web along the line-of-sight. We followed two approaches here: first, we generate a control set of profiles in the same 5–20 Mpc length range, by extracting pairs of halos with a projected distance in this range, which gives only a ≤30% chance of having a true filament in between such halos [86]. In a second approach, we randomly drew segments in the same length range over our projected sky model, with the contribution from halos masked out (a procedure which most often selects fields without large filaments, as it can be guessed from Figure 1).
Figure 4 gives the average profiles of Faraday Rotation and synchrotron emission for our simulated population of filaments, random pairs of halos or random empty fields. This attempts to quantify the realistic level of difference between magnetised filaments and control samples in a selection of our most realistic scenarios.
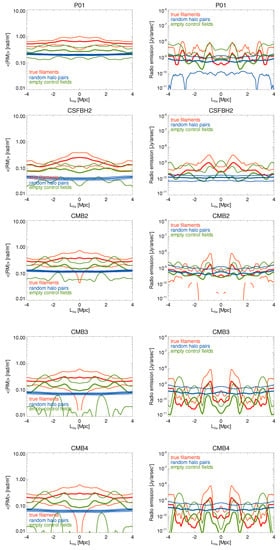
Figure 4.
Simulated average Faraday Rotation and radio emission from true filaments in the 5–20 Mpc range of length (red), for the region between random pairs of clusters in the same range of length (blue), or for random empty control fields (green), for all our runs. We assumed the simulated volume at the distance of 200 Mpc, and we include no other foregrounds or backgrounds. In addition, we remove the contribution from all virial spheres of halos identified in the volume. For each model, we give the sample mean and variance.
In all cases, the true filaments give a higher RM and a higher synchrotron emission profile than both control samples (halo pairs and empty fields). However, the RM signal is affected by less scatter raising the chances of detection. The middle region of filaments has an RM signal which is typically ≥2– above our control samples. However, the amplitude of the RM is here very low, ∼–, which makes detection a real challenge for existing radio polarimetric observations.
Even for targets at high galactic latitude, the RM fluctuations of the Galactic foreground can be as large as on a ∼ angular scale [122]. On the other hand, the typical intrinsic RM contribution from polarised background sources is –, depending on whether the source is a compact AGN or a star forming galaxy e.g., [123,124]. Finally, a representative RM sensitivity that can be presently reached with the JVLA is for wide total bandwidth GHz observations of bright polarised sources. Future SKA-MID-like observations are expected to reach see, e.g., [67] for a more detailed discussion. On the other hand, the sample-averaged synchrotron emission presents a larger scatter, both for true filaments and for the control samples, which causes the latter to statistically overlap with the signature of true filaments within our control sample, within the scatter. Interestingly, all profiles for true filaments show a peak of emission at a distance of ∼3–4 Mpc from their surrounding halos, which may mark the presence of substructures and shocks within such filaments, a feature which has been already noticed by [89]. These features appear more pronounced when the average background magnetic field level is lower, as visible by the sequence of our CMB2-3–4 runs, and they are also related to some level of magnetic field amplification around the subhalos present in these large regions. Even if the virial volume of (sub)halos is masked out in our analysis, patches of magnetised gas can stream out of them and mix with the surrounding intergalactic medium here, increasing the scatter in the synchrotron profile. In any case, the average amplitude of the signal is very low, and about a factor ∼10–102 below what can be reached with current instruments.
The difference between the simple uniform P01 model and the astrophysical scenario is of a factor ∼2 in RM and ∼5–10 in emission for such objects, while a range of values is predicted for the different spectral models of the CMB2, CMB3 and CMB4 models. All the latter models show a large variance in the profile, the highest being associated with the “blue” CMB4 model. This variance is caused by the large magnetic field fluctuations present in the initial conditions, which are mostly also present in the evolved filament population [105].
However, here we only showed the average signal of the populations, which is faint and nearly impossible to detect. Current observations can still hope to detect ∼3– positive fluctuations, which can bring the previous quantities to ∼ and ∼ in primordial models, e.g., at the edge of detection with present instruments, also via stacking techniques. This is more clearly seen in the full distribution of RM and synchrotron emission across the selected sample of filaments and control fields in the various models, shown in Figure 5. Assessing the contribution of such large fluctuations in real stacking experiments [70], as well as defining strategies to build observational samples which can maximise their presence, is still a non-trivial task.
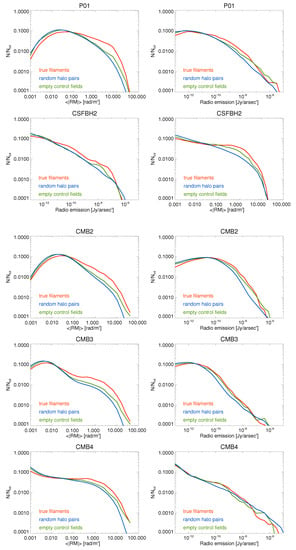
Figure 5.
Distribution of the Faraday Rotation and radio emission for the ensemble of filaments in the 5–20 Mpc range of length (red), the region between random pairs of clusters in the same range of length (blue), or in random empty control fields (green), for all our runs, measured in the same data of Figure 4.
As a final remark, it is worth stressing that the signal in all profiles shown here is a signature of the magnetic cosmic web. The latter represents a ubiquitous foreground and background (depending on where the main targets are located): by definition, only gas and magnetic fields in the cosmic web contribute to the RM and synchrotron emission in our models. While it makes a clear detection of the radio signature of filaments only more difficult in practice e.g., [89], any detection of the radio signal from the matter distribution of the cosmic web (provided that other contaminants and foregrounds are removed) would be a powerful probe of cosmic magnetism [86].
4. Discussion and Conclusions
The origin of extragalactic magnetism is still unknown. Studies of the low-density cosmic web, outside of galaxies and clusters of galaxies, have the potential of discovering this origin because most possible scenarios for the origin of magnetic fields observed in self-gravitating halos would predict very different amplitudes and topologies of magnetic fields on the scale of filaments and voids. Therefore, the chance of detecting an unambiguous radio signature from cosmic filaments has recently triggered many exciting observational attempts, which mostly involved low-frequency radio surveys, with LOFAR and MWA. Given the complexity of observations (which can be variously contaminated by astrophysical backgrounds, foregrounds, outliers and contaminants) and their often statistical nature, advanced numerical simulations, such as the MAGCOW ones presented here, are often essential to turn a radio measurement into a realistic constraint on three-dimensional magnetic fields.
At present, the non-detection of the inverse Compton cascade signal from blazars, as well as detection of the stacked signal from halo pairs, seem to exclude purely astrophysical scenarios. In addition, primordial scenarios in which magnetic fields are maximally amplified in filaments and halos can be discarded as they would overpredict the cross-correlation between synchrotron emission and galaxies, as well as the typical RM difference between pairs of extended polarised sources. Clearly, astrophysical sources of magnetic fields related to galaxy evolution exist and are observed. However, the existing hints for large-scale signature of magnetic fields are found to require a primordial and volume-distributed seeding mechanism.
Inflationary primordial models, such as our latest simulation with tangled initial magnetic fields, are least constrained by existing observational bounds and detections. In particular, the bluest primordial spectrum, explored here, (, CMB4) yields the best match with observational constraints. This match would have profound implications for the physics of the early Universe and the dynamics of inflation. More work is necessary to explore this intriguing possibility.
To conclude, it is worth stressing that a few more observable astrophysical effects are suitable to constrain the distribution of cosmic magnetic fields. We did not include them here explicitly because recent works, including our MAGCOW simulations too, have exposed many additional uncertainties related to their use.
The first example charged cosmic rays with energies ≥ (aka Ultra High Energy Cosmic Rays, UHECR) are believed to have a predominantly extra-galactic origin, and their propagation towards Earth is affected by the Lorentz force e.g., [125,126]. Large deflection angles will hamper the possibility of locating the real sources of UHECRs at the highest energies, yet the amplitude of these deflections can greatly vary depending on model assumptions, ranging from ≤ to ∼ e.g., [126,127,128]. With MAGCOW simulations, we tackled the propagation of such high energy cosmic rays, reporting the observed level of isotropy of ≥ event can in principle be used to rule out primordial models with a uniform magnetic field larger than ∼ [129] in addition to very red or very blue primordial spectra [105], yet the present uncertainties in the distribution and duty cycle of sources and on the composition of cosmic rays make such estimates still too model dependent, and degenerate with other model uncertainties [130,131].
Second, the RM of Fast Radio Bursts (FRB), e.g., [132], together with their often detected Dispersion Measure, can be used to derive the average magnetic field along the line-of-sight e.g., [133,134,135]. However, the limited amount of FRBs with an observed RM, and the large existing uncertainties on the physical conditions at the progenitor, its location in the host galaxy, and the additional Faraday screen of our Galaxy, make it presently impossible to use FRBs as a reliable proxy of cosmic magnetism [130,136], even if big progresses are also expected from the SKA here e.g., [137,138].
Finally, also the puzzling lack of infrared absorption in the observed spectra of distant blazars e.g., [139,140] can be explained by the oscillation of high energy photons into axion-like particles, mediated by large scale magnetic fields [141]. We tested that a realistic distribution of ∼0.1–1 nG magnetic fields in voids and filaments can account for the observed spectra [142]. However, such a possibility remains speculative.
To summarise, the combination of total intensity and polarimetric data at low frequencies with existing (e.g., LOFAR and MWA) and future (SKA, LOFAR2.0) large surveys is the best way to remove the existing uncertainties coming from different sources along deep cosmic lines of sight. Finally, low frequency observations are the best tool to detect cosmic filaments and to measure both their magnetic content and their deep physical connection with the origin of magnetism in the Universe.
Author Contributions
F.V. prepared the manuscript and all the numerical simulations analysed in this article. C.G. contributed to the production of numerical simulations used in this work. G.I. produced the volume rendering used in Figure 1. S.B. produced the filament catalog used in the Section 3. D.P. produced the analytic model predictions for the CMB models simulated in this paper. All coauthors contributed in the drafting, editing and literature review of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
F.V., N.L., K.R., S.B., P.D.F., D.W., G.I. and M.B. acknowledge financial support from the Horizon 2020 program under the ERC Starting Grant MAGCOW, no. 714196. S.E. acknowledges financial contribution from the contracts ASI-INAF Athena 2019-27-HH.0, “Attività di Studio per la comunità scientifica di Astrofisica delle Alte Energie e Fisica Astroparticellare” (Accordo Attuativo ASI-INAF n. 2017-14-H.0), INAF mainstream project 1.05.01.86.10, and from the European Union’s Horizon 2020 Programme under the AHEAD2020 project (grant agreement n. 871158). P.D.F. was partially supported by the National Research Foundation (NRF) of Korea through grants 2016R1A5A1013277 and 2020R1A2C2102800. D.W. is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)-441694982. G.B. acknowledges partial support from mainstream PRIN INAF “Galaxy cluster science with LOFAR”. A.B. and C.S. acknowledge support from the ERC-StG DRANOEL, no. 714245, and from the MIUR grant FARE SMS. MB acknowledges support from the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy-EXC 2121 “Quantum Universe”-390833306. DP and FF acknowledge financial support by the agreement n. 2020-9-HH.0 ASI-UniRM2 “Partecipazione italiana alla fase A della missione LiteBIRD”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
In this work we used the ENZO code (http://enzo-project.org), the product of a collaborative effort of scientists at many universities and national laboratories. Samples of our simulations are available at https://cosmosimfrazza.myfreesites.net/the_magnetic_cosmic_web. A collection of codes used in this work can be found at https://github.com/FrancoVazza/JULIA.
Acknowledgments
This study was presented by F.V. at the “A new window on the radio emission from galaxies, clusters and cosmic web” virtual conference on 10 March 2021, during the Covid-19 pandemic. We thank our anonymous reviewers for their helpful feedback on this manuscript. Our simulations were run on the Piz Daint supercomputer at CSCS-ETH (Lugano), on the JUWELS cluster at Juelich Superc omputing Centre (JSC), under projects “stressicm” and “radgalicm” and on the Marconi100 clusters at CINECA (Bologna), under project INA21. We acknowledge the computing centre of Cineca and INAF, under the coordination of the “Accordo Quadro MoU per lo svolgimento di attività congiunta di ricerca Nuove frontiere in Astrofisica: HPC e Data Exploration di nuova generazione”, for the availability of computing resources and support. For the creation of scientific visualizations such as Figure 1, G.I. acknowledges the assistance of the Visit Lab of A. Guidazzoli of CINECA under the project FIBER OF THE UNIVERSE (http://visitlab.cineca.it/index.php/portfolio/fiber-of-the-universe/). F.V. acknowledges fruitful collaboration and scientific discussion with Torrance Hodgson, Tessa Vernstrom, Eleni Vardoulaki, Shane O’Sullivan and Valentin Pomakov.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGN | Active Galactic Nucleus |
| AMR | Adaptive Mesh Refinement |
| CMB | Cosmic Microwave Background |
| FRB | Fast Radio Bursts |
| GLEAM | The Galactic and Extra Galactic All Sky MWA Survey |
| GPU | Graphics Processing Unit |
| HBA | High Band Antenna |
| HLL | Harten-Lax van Leer |
| ICM | Intra Cluster Medium |
| IGM | Inter Galactic Medium |
| IR | Infa Red |
| JVLA | Karl G. Jansky Very Large Array |
| KAT | Karoo Array Telescope |
| LOFAR | Low Frequency Array |
| LOS | Line-of-Sight |
| MAGOCW | The Magnetised Cosmic Web |
| MeerKAT | MeerKAT |
| MHD | Magneto Hydro Dynamics |
| MWA | Murchison Widefield Array |
| PLM | Piecewise Linear Method |
| RK | Runge–Kutta |
| RM | Rotation Measure |
| SDSS | Sloan Digital Sky Survey |
| SKA | Square Kilometer Array |
| SMBH | Super Massive Black Hole |
| TVD | Total Variation Dininishing |
| UHECR | Ultra High Energy Cosmic Rays |
| WHIM | Warm Hot Interagalactic Medium |
| CDM | Lambda Cold Dark Matter |
Appendix A. Numerical Simulations
All runs presented in this paper solve ideal magneto-hydrodynamics on an expanding comoving volume, using a customised version of the cosmological grid code ENZO. The MHD scheme of preference is the Dedner formulation [143], i.e., a hyperbolic divergence cleaning to keep the term as small as possible. The MHD solver adopts the PLM (Piecewise Linear Method) reconstruction, fluxes at cell interfaces are calculated using the Harten–Lax–van Leer (HLL) approximate Riemann solver. Time integration is performed using the total variation diminishing (TVD) second-order Runge–Kutta (RK) scheme [144]. Other work has shown that this approach is robust and competitive compared to other MHD solvers [145,146,147]. In most runs (produced either with Piz-Daint at CSCS or with Marconi100 at CINECA), we relied on the GPU-accelerated MHD version of ENZO, by [148].
Although the use of adaptive mesh refinement is crucial to resolve the turbulent flow inside forming structures and its related dynamo amplification e.g., [12,16], for the goal of this investigation, we only used a uniform grid approach on large volumes, as they are overall more suitable to model strong accretion shocks in low density regions, and to follow the topology of magnetic fields in voids e.g., [103].
Our main text already includes a basic description of all important adopted physical modules, but here we wish to add a few more technical details on the sub-grid dynamo model, and on our prescriptions to couple star formation and the growth of supermassive black holes to the release of magnetic fields.
- Sub-grid dynamo amplification: in most runs, we estimated at run-time the unresolvable amplification of magnetic fields with an approximate sub-grid approach to incorporate small-scale dynamo amplification and overcome the impossibility of employing adaptive mesh refinement everywhere in the simulation. This is done by measuring the gas vorticity at run-time and using it to guess the dissipation rate of solenoidal turbulence into magnetic field amplification. We assume that a small fraction, , of such kinetic power gets channeled into the amplification of magnetic fields, , where L is the stencil of cells to compute the vorticity. The fraction of turbulent kinetic power that gets converted into magnetic energy, , sets the amplified magnetic energy as . For a reasonable guess on , we followed the fitting formulas given by [149], and set the saturation level and the typical growth time of magnetic fields as a function of the local Mach number of the flow (), and set , where is the ratio between magnetic and kinetic energy at saturation, and is the growth rate, taken from [149]. The topology of the newly created magnetic fields is for simplicity taken to be parallel to the local gas vorticity. Manifestly, this procedure is much simpler than more sophisticated subgrid models [150]. However, this simplistic method reproduced the results obtained by other methods e.g., [7,65,130]. In these runs, we adopt the same amplification efficiency calibrated in [65] for the DYN5 run, but in all other new runs (P, CMB2, CMB3, CMB4), we allowed the sub-grid model to be activated only for , i.e., only within the virial radius of halos, where turbulence is predicted to be well developed and mostly solenoidal, and we increased by a factor 10 the amplification for , where the virialisation of halos is also expected to maximise the amplification of magnetic fields via small-scale dynamo e.g., [16,151].
- Astrophysical sources of magnetisation: in runs including radiative (equilibrium) cooling, gas undergoes collapse and can form stars, or supermassive black holes. We resorted here to the numerical recipes in the public version of ENZO [101] to further release of magnetic dipoles, with a total magnetic energy per event which is a fixed fraction of the feedback energy. The injection of additional magnetic energy via bipolar jets happens with an efficiency with respect to the feedback energy, the latter being times the energy accreted by star forming particles. Likewise, we use the prescriptions by ENZO [152] to inject and grow SMBH and attach magnetic feedback to their thermal feedback. We assume accretion for SMBH following from the spherical Bondi–Hoyle formula with a fixed accretion rate, and a fixed “boost” factor to the mass growth rate of SMBH () to balance the effect of coarse resolution, properly resolving the mass accretion rate onto our simulated SMBH particles. The injection of additional magnetic energy via bipolar jets happens with an efficiency and efficiency with respect to the thermal feedback energy, which is set to be . The only run presented here which features magnetisation by stars and supermassive black hole feedback is CSFBH2, which was shown to yield the most realistic results on the cosmic star formation history, as well as on scaling relations of galaxy clusters and groups in earlier work [65,104]. We also showed results from the CSF2 run, which only contains feedback from the star forming phase.
The typical time needed to complete these runs is ∼100,000 core hours for each non-radiative run and ∼400,000 core hours (on average) for our runs with cooling, chemistry, star formation and SMBH particles.
Notes
| 1 | The full list of acronyms used in this work is given in the Abbreviations section at the end of the paper. |
| 2 | See [55,56] for advanced discussions on the physical interpretations of such limits. |
| 3 | The volume rendering was realised using the CG Animation Software Blender in which we imported the ENZO simulation data previously converted in the openVDB format. This data format is optimised to maximise the shading of the volume rendering (and so the resolution and contrast of quantities’ small details) using light tracing not reachable with standard scientific visualisation tools such as Paraview. |
| 4 | https://cosmosimfrazza.myfreesites.net/erc-magcow, accessed on 12 November 2021. |
References
- Kempner, J.C.; Sarazin, C.L. Radio Halo and Relic Candidates from the Westerbork Northern Sky Survey. ApJ 2001, 548, 639–651. [Google Scholar] [CrossRef]
- Feretti, L.; Giovannini, G.; Govoni, F.; Murgia, M. Clusters of galaxies: Observational properties of the diffuse radio emission. Astron. Astrophys. Rev. 2012, 20, 54. [Google Scholar] [CrossRef]
- Brunetti, G.; Jones, T.W. Cosmic Rays in Galaxy Clusters and Their Nonthermal Emission. Int. J. Mod. Phys. D 2014, 23, 1430007. [Google Scholar] [CrossRef]
- Van Weeren, R.J.; de Gasperin, F.; Akamatsu, H.; Brüggen, M.; Feretti, L.; Kang, H.; Stroe, A.; Zandanel, F. Diffuse Radio Emission from Galaxy Clusters. Sci. Space Rev. 2019, 215, 16. [Google Scholar] [CrossRef]
- Cho, J.; Vishniac, E.T. The Generation of Magnetic Fields through Driven Turbulence. ApJ 2000, 538, 217–225. [Google Scholar] [CrossRef]
- Schekochihin, A.A.; Cowley, S.C.; Taylor, S.F.; Maron, J.L.; McWilliams, J.C. Simulations of the Small-Scale Turbulent Dynamo. ApJ 2004, 612, 276–307. [Google Scholar] [CrossRef]
- Ryu, D.; Kang, H.; Cho, J.; Das, S. Turbulence and Magnetic Fields in the Large-Scale Structure of the Universe. Science 2008, 320, 909–912. [Google Scholar] [CrossRef]
- Rincon, F. Dynamo theories. J. Plasma Phys. 2019, 85, 205850401. [Google Scholar] [CrossRef]
- Dolag, K.; Bartelmann, M.; Lesch, H. SPH simulations of magnetic fields in galaxy clusters. A&A 1999, 348, 351–363. [Google Scholar]
- Schober, J.; Schleicher, D.; Federrath, C.; Klessen, R.; Banerjee, R. Magnetic field amplification by small-scale dynamo action: Dependence on turbulence models and Reynolds and Prandtl numbers. Phys. Rev. Lett. E 2012, 85, 026303. [Google Scholar] [CrossRef]
- Cho, J. Origin of Magnetic Field in the Intracluster Medium: Primordial or Astrophysical? ApJ 2014, 797, 133. [Google Scholar] [CrossRef]
- Vazza, F.; Brunetti, G.; Brüggen, M.; Bonafede, A. Resolved magnetic dynamo action in the simulated intracluster medium. Mon. Not. R. Astron. Soc. 2018, 474, 1672–1687. [Google Scholar] [CrossRef]
- Donnert, J.; Vazza, F.; Brüggen, M.; ZuHone, J. Magnetic Field Amplification in Galaxy Clusters and its Simulation. arXiv 2018, arXiv:1810.09783. [Google Scholar] [CrossRef]
- Domínguez-Fernández, P.; Vazza, F.; Brüggen, M.; Brunetti, G. Dynamical evolution of magnetic fields in the intracluster medium. Mon. Not. R. Astron. Soc. 2019, 486, 623–638. [Google Scholar] [CrossRef]
- Roh, S.; Ryu, D.; Kang, H.; Ha, S.; Jang, H. Turbulence Dynamo in the Stratified Medium of Galaxy Clusters. ApJ 2019, 883, 138. [Google Scholar] [CrossRef]
- Quilis, V.; Martí, J.M.; Planelles, S. Cosmic magnetic fields with masclet: An application to galaxy clusters. Mon. Not. R. Astron. Soc. 2020, 494, 2706–2717. [Google Scholar] [CrossRef]
- Steinwandel, U.P.; Boess, L.M.; Dolag, K.; Lesch, H. On the small scale turbulent dynamo in the intracluster medium: A comparison to dynamo theory. arXiv 2021, arXiv:2108.07822. [Google Scholar]
- Mogavero, F.; Schekochihin, A.A. Models of magnetic field evolution and effective viscosity in weakly collisional extragalactic plasmas. Mon. Not. R. Astron. Soc. 2014, 440, 3226–3242. [Google Scholar] [CrossRef]
- Rincon, F.; Califano, F.; Schekochihin, A.A.; Valentini, F. Turbulent dynamo in a collisionless plasma. Proc. Natl. Acad. Sci. USA 2016, 113, 3950–3953. [Google Scholar] [CrossRef]
- St-Onge, D.A.; Kunz, M.W.; Squire, J.; Schekochihin, A.A. Fluctuation dynamo in a weakly collisional plasma. J. Plasma Phys. 2020, 86, 905860503. [Google Scholar] [CrossRef]
- Turner, M.S.; Widrow, L.M. Inflation-produced, large-scale magnetic fields. Phys. Rev. Lett. 1988, 37, 2743–2754. [Google Scholar] [CrossRef]
- Widrow, L.M.; Ryu, D.; Schleicher, D.R.G.; Subramanian, K.; Tsagas, C.G.; Treumann, R.A. The First Magnetic Fields. Sci. Space Rev. 2012, 166, 37–70. [Google Scholar] [CrossRef]
- Hutschenreuter, S.; Dorn, S.; Jasche, J.; Vazza, F.; Paoletti, D.; Lavaux, G.; Enßlin, T.A. The primordial magnetic field in our cosmic backyard. Class. Quantum Gravity 2018, 35, 154001. [Google Scholar] [CrossRef]
- Vachaspati, T. Magnetic fields from cosmological phase transitions. Phys. Lett. 1991, B265, 258–261. [Google Scholar] [CrossRef]
- Caprini, C.; Durrer, R.; Servant, G. The stochastic gravitational wave background from turbulence and magnetic fields generated by a first-order phase transition. JCAP 2009, 2009, 024. [Google Scholar] [CrossRef]
- Ellis, J.; Fairbairn, M.; Lewicki, M.; Vaskonen, V.; Wickens, A. Intergalactic Magnetic Fields from First-Order Phase Transitions. J. Cosmol. Astropart. Phys. 2019, 2019, 019. [Google Scholar] [CrossRef]
- Mtchedlidze, S.; Domínguez-Fernández, P.; Du, X.; Brandenburg, A.; Kahniashvili, T.; O’Sullivan, S.; Schmidt, W.; Brüggen, M. Evolution of primordial magnetic fields during large-scale structure formation. arXiv 2021, arXiv:2109.13520. [Google Scholar]
- Paoletti, D.; Finelli, F.; Paci, F. The full contribution of a stochastic background of magnetic fields to CMB anisotropies. Mon. Not. R. Astron. Soc. 2009, 396, 523–534. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalup, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XIX. Constraints on primordial magnetic fields. Astron. Astrophys. 2016, 594, A19. [Google Scholar]
- Shaw, J.; Lewis, A. Massive Neutrinos and Magnetic Fields in the Early Universe. Phys. Rev. D 2010, 81, 043517. [Google Scholar] [CrossRef]
- Kronberg, P.P.; Lesch, H.; Hopp, U. Magnetization of the Intergalactic Medium by Primeval Galaxies. ApJ 1999, 511, 56–64. [Google Scholar] [CrossRef]
- Völk, H.J.; Atoyan, A.M. Early Starbursts and Magnetic Field Generation in Galaxy Clusters. ApJ 2000, 541, 88–94. [Google Scholar] [CrossRef][Green Version]
- Donnert, J.; Dolag, K.; Lesch, H.; Müller, E. Cluster magnetic fields from galactic outflows. Mon. Not. R. Astron. Soc. 2009, 392, 1008–1021. [Google Scholar] [CrossRef]
- Bertone, S.; Vogt, C.; Enßlin, T. Magnetic field seeding by galactic winds. Mon. Not. R. Astron. Soc. 2006, 370, 319–330. [Google Scholar] [CrossRef]
- Samui, S.; Subramanian, K.; Srianand, R. Efficient cold outflows driven by cosmic rays in high redshift galaxies and their global effects on the IGM. arXiv 2017, arXiv:1706.01890. [Google Scholar] [CrossRef]
- Beck, A.M.; Hanasz, M.; Lesch, H.; Remus, R.S.; Stasyszyn, F.A. On the magnetic fields in voids. Mon. Not. R. Astron. Soc. 2013, 429, L60–L64. [Google Scholar] [CrossRef]
- Dubois, Y.; Teyssier, R. Cosmological MHD simulation of a cooling flow cluster. A&A 2008, 482, L13–L16. [Google Scholar]
- Xu, H.; Li, H.; Collins, D.C.; Li, S.; Norman, M.L. Turbulence and Dynamo in Galaxy Cluster Medium: Implications on the Origin of Cluster Magnetic Fields. ApJ Lett. 2009, 698, L14–L17. [Google Scholar] [CrossRef]
- Planelles, S.; Schleicher, D.R.G.; Bykov, A.M. Large-Scale Structure Formation: From the First Nonlinear Objects to Massive Galaxy Clusters. In Multi-Scale Structure Formation and Dynamics in Cosmic Plasmas: Space Sciences Series of ISSI; Balogh, A., Bykov, A., Eastwood, J., Kaastra, J., Eds.; Springer Science+Business Media: New York, USA, USA, 2016; Volume 51, pp. 93–139. ISBN 978-1-4939-3546-8. [Google Scholar] [CrossRef]
- Kulsrud, R.M.; Cen, R.; Ostriker, J.P.; Ryu, D. The Protogalactic Origin for Cosmic Magnetic Fields. ApJ 1997, 480, 481–491. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Ibscher, D.; Supsar, M. Plasma Effects on Fast Pair Beams in Cosmic Voids. ApJ 2012, 758, 102. [Google Scholar] [CrossRef]
- Miniati, F.; Bell, A.R. Resistive Magnetic Field Generation at Cosmic Dawn. ApJ 2011, 729, 73. [Google Scholar] [CrossRef]
- Langer, M.; Aghanim, N.; Puget, J.L. Magnetic fields from reionisation. A&A 2005, 443, 367–372. [Google Scholar]
- Durrive, J.B.; Tashiro, H.; Langer, M.; Sugiyama, N. Mean energy density of photogenerated magnetic fields throughout the Epoch of Reionization. Mon. Not. R. Astron. Soc. 2017, 472, 1649–1658. [Google Scholar] [CrossRef]
- Araya, I.J.; Rubio, M.E.; San Martín, M.; Stasyszyn, F.A.; Padilla, N.D.; Magaña, J.; Sureda, J. Magnetic field generation from PBH distributions. Mon. Not. R. Astron. Soc. 2021, 503, 4387–4399. [Google Scholar] [CrossRef]
- Subramanian, K. The origin, evolution and signatures of primordial magnetic fields. Rep. Prog. Phys. 2016, 79, 076901. [Google Scholar] [CrossRef] [PubMed]
- Vachaspati, T. Progress on cosmological magnetic fields. Rep. Prog. Phys. 2021, 84, 074901. [Google Scholar] [CrossRef]
- Garaldi, E.; Pakmor, R.; Springel, V. Magnetogenesis around the first galaxies: The impact of different field seeding processes on galaxy formation. Mon. Not. R. Astron. Soc. 2021, 502, 5726–5744. [Google Scholar] [CrossRef]
- Paoletti, D.; Finelli, F. Constraints on primordial magnetic fields from magnetically-induced perturbations: Current status and future perspectives with LiteBIRD and future ground based experiments. J. Cosmol. Astropart. Phys. 2019, 2019, 028. [Google Scholar] [CrossRef]
- Dolag, K.; Kachelrieß, M.; Ostapchenko, S.; Tomàs, R. Blazar Halos as Probe for Extragalactic Magnetic Fields and Maximal Acceleration Energy. ApJ 2009, 703, 1078–1085. [Google Scholar] [CrossRef]
- Neronov, A.; Vovk, I. Evidence for Strong Extragalactic Magnetic Fields from Fermi Observations of TeV Blazars. Science 2010, 328, 73–75. [Google Scholar] [CrossRef]
- Caprini, C.; Gabici, S. Gamma-ray observations of blazars and the intergalactic magnetic field spectrum. Phys. Rev. Lett. 2015, 91, 123514. [Google Scholar] [CrossRef]
- Chen, W.; Buckley, J.H.; Ferrer, F. Search for GeV γ-Ray Pair Halos Around Low Redshift Blazars. Phys. Rev. Lett. 2015, 115, 211103. [Google Scholar] [CrossRef]
- Alves Batista, R.; Saveliev, A. The Gamma-Ray Window to Intergalactic Magnetism. Universe 2021, 7, 223. [Google Scholar] [CrossRef]
- Broderick, A.E.; Chang, P.; Pfrommer, C. The Cosmological Impact of Luminous TeV Blazars. I. Implications of Plasma Instabilities for the Intergalactic Magnetic Field and Extragalactic Gamma-Ray Background. ApJ 2012, 752, 22. [Google Scholar] [CrossRef]
- Miniati, F.; Elyiv, A. Relaxation of Blazar-induced Pair Beams in Cosmic Voids. ApJ 2013, 770, 54. [Google Scholar] [CrossRef]
- Kunze, K.E.; Komatsu, E. Constraints on primordial magnetic fields from the optical depth of the cosmic microwave background. J. Cosmol. Astropart. Phys. 2015, 2015, 027. [Google Scholar] [CrossRef]
- Chluba, J.; Paoletti, D.; Finelli, F.; Rubiño-Martín, J.A. Effect of primordial magnetic fields on the ionization history. Mon. Not. R. Astron. Soc. 2015, 451, 2244–2250. [Google Scholar] [CrossRef]
- Paoletti, D.; Chluba, J.; Finelli, F.; Rubino-Martin, J.A. Improved CMB anisotropy constraints on primordial magnetic fields from the post-recombination ionization history. Mon. Not. R. Astron. Soc. 2019, 484, 185–195. [Google Scholar] [CrossRef]
- Trivedi, P.; Reppin, J.; Chluba, J.; Banerjee, R. Magnetic heating across the cosmological recombination era: Results from 3D MHD simulations. Mon. Not. R. Astron. Soc. 2018, 481, 3401–3422. [Google Scholar] [CrossRef]
- Jedamzik, K.; Saveliev, A. Stringent Limit on Primordial Magnetic Fields from the Cosmic Microwave Background Radiation. Phys. Rev. Lett. 2019, 123, 021301. [Google Scholar] [CrossRef]
- Galli, S.; Pogosian, L.; Jedamzik, K.; Balkenhol, L. Consistency of Planck, ACT and SPT constraints on magnetically assisted recombination and forecasts for future experiments. arXiv 2021, arXiv:2109.03816. [Google Scholar]
- Natwariya, P.K. Constraint on primordial magnetic fields in the light of ARCADE 2 and EDGES observations. Eur. Phys. J. C 2021, 81, 394. [Google Scholar] [CrossRef]
- Vazza, F.; Ferrari, C.; Brüggen, M.; Bonafede, A.; Gheller, C.; Wang, P. Forecasts for the detection of the magnetised cosmic web from cosmological simulations. A&A 2015, 580, A119. [Google Scholar]
- Vazza, F.; Brueggen, M.; Gheller, C.; Hackstein, S.; Wittor, D.; Hinz, P.M. Simulations of extragalactic magnetic fields and of their observables. Class. Quantum Gravity 2017, 34, 234001. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Gheller, C.; Wang, P. On the amplification of magnetic fields in cosmic filaments and galaxy clusters. Mon. Not. R. Astron. Soc. 2014, 445, 3706–3722. [Google Scholar] [CrossRef]
- Locatelli, N.; Vazza, F.; Domínguez-Fernández, P. The Challenge of Detecting Intracluster Filaments with Faraday Rotation. Galaxies 2018, 6, 128. [Google Scholar] [CrossRef]
- Vazza, F.; Ettori, S.; Roncarelli, M.; Angelinelli, M.; Brüggen, M.; Gheller, C. Detecting shocked intergalactic gas with X-ray and radio observations. A&A 2019, 627, A5. [Google Scholar]
- Vazza, F.; Feletti, A. The quantitative comparison between the neuronal network and the cosmic web. Front. Phys. 2020, 8, 491. [Google Scholar] [CrossRef]
- Vernstrom, T.; Heald, G.; Vazza, F.; Galvin, T.J.; West, J.L.; Locatelli, N.; Fornengo, N.; Pinetti, E. Discovery of magnetic fields along stacked cosmic filaments as revealed by radio and X-ray emission. Mon. Not. R. Astron. Soc. 2021, 505, 4178–4196. [Google Scholar] [CrossRef]
- Hodgson, T.; Vazza, F.; Johnston-Hollitt, M.; McKinley, B. FIGARO Simulation: FIlaments & GAlactic RadiO Simulation. arXiv 2021, arXiv:2106.07901. [Google Scholar]
- Simionescu, A.; Ettori, S.; Werner, N.; Nagai, D.; Vazza, F.; Akamatsu, H.; Pinto, C.; de Plaa, J.; Wijers, N.; Nelson, D.; et al. Voyage through the hidden physics of the cosmic web. Exp. Astron. 2021, 51, 1043–1079. [Google Scholar] [CrossRef]
- Angelinelli, M.; Ettori, S.; Vazza, F.; Jones, T.W. Properties of clumps and filaments around galaxy clusters. arXiv 2021, arXiv:2102.01096. [Google Scholar]
- Eckert, D.; Jauzac, M.; Shan, H.; Kneib, J.P.; Erben, T.; Israel, H.; Jullo, E.; Klein, M.; Massey, R.; Richard, J.; et al. Warm–hot baryons comprise 5–10 per cent of filaments in the cosmic web. Nature 2015, 528, 105–107. [Google Scholar] [CrossRef]
- Reiprich, T.H.; Veronica, A.; Pacaud, F.; Ramos-Ceja, M.E.; Ota, N.; Sanders, J.; Kara, M.; Erben, T.; Klein, M.; Erler, J.; et al. The Abell 3391/95 galaxy cluster system. A 15 Mpc intergalactic medium emission filament, a warm gas bridge, infalling matter clumps, and (re-) accelerated plasma discovered by combining SRG/eROSITA data with ASKAP/EMU and DECam data. A&A 2021, 647, A2. [Google Scholar]
- Tanimura, H.; Aghanim, N.; Kolodzig, A.; Douspis, M.; Malavasi, N. First detection of stacked X-ray emission from cosmic web filaments. A&A 2020, 643, L2. [Google Scholar]
- Ryu, D.; Kang, H.; Hallman, E.; Jones, T.W. Cosmological Shock Waves and Their Role in the Large-Scale Structure of the Universe. ApJ 2003, 593, 599–610. [Google Scholar] [CrossRef]
- Pfrommer, C.; Springel, V.; Enßlin, T.A.; Jubelgas, M. Detecting shock waves in cosmological smoothed particle hydrodynamics simulations. Mon. Not. R. Astron. Soc. 2006, 367, 113–131. [Google Scholar] [CrossRef]
- Keshet, U.; Waxman, E.; Loeb, A. Imprint of Intergalactic Shocks on the Radio Sky. ApJ 2004, 617, 281–302. [Google Scholar] [CrossRef]
- Brown, S.D. Synchrotron Emission on the Largest Scales: Radio Detection of the Cosmic-Web. J. Astrophys. Astron. 2011, 32, 577–584. [Google Scholar] [CrossRef]
- Araya-Melo, P.A.; Aragón-Calvo, M.A.; Brüggen, M.; Hoeft, M. Radio emission in the cosmic web. Mon. Not. R. Astron. Soc. 2012, 423, 2325–2341. [Google Scholar] [CrossRef][Green Version]
- Govoni, F.; Orrù, E.; Bonafede, A.; Iacobelli, M.; Paladino, R.; Vazza, F.; Murgia, M.; Vacca, V.; Giovannini, G.; Feretti, L.; et al. A radio ridge connecting two galaxy clusters in a filament of the cosmic web. Science 2019, 364, 981–984. [Google Scholar] [CrossRef]
- Botteon, A.; van Weeren, R.J.; Brunetti, G.; de Gasperin, F.; Intema, H.T.; Osinga, E.; Di Gennaro, G.; Shimwell, T.W.; Bonafede, A.; Brüggen, M.; et al. A giant radio bridge connecting two galaxy clusters in Abell 1758. Mon. Not. R. Astron. Soc. 2020, 499, L11–L15. [Google Scholar]
- Brunetti, G.; Vazza, F. Second-order Fermi Reacceleration Mechanisms and Large-Scale Synchrotron Radio Emission in Intracluster Bridges. Phys. Rev. Lett. 2020, 124, 051101. [Google Scholar] [CrossRef]
- Bonafede, A.; Brunetti, G.; Vazza, F.; Simionescu, A.; Giovannini, G.; Bonnassieux, E.; Shimwell, T.W.; Brüggen, M.; van Weeren, R.J.; Botteon, A.; et al. The Coma Cluster at LOw Frequency ARray Frequencies. I. Insights into Particle Acceleration Mechanisms in the Radio Bridge. ApJ 2021, 907, 32. [Google Scholar] [CrossRef]
- Locatelli, N.; Vazza, F.; Bonafede, A.; Banfi, S.; Bernardi, G.; Gheller, C.; Botteon, A.; Shimwell, T. New constraints on the magnetic field in cosmic web filaments. A&A 2021, 652, A80. [Google Scholar] [CrossRef]
- Brown, S.; Vernstrom, T.; Carretti, E.; Dolag, K.; Gaensler, B.M.; Staveley-Smith, L.; Bernardi, G.; Haverkorn, M.; Kesteven, M.; Poppi, S. Limiting magnetic fields in the cosmic web with diffuse radio emission. Mon. Not. R. Astron. Soc. 2017, 468, 4246–4253. [Google Scholar] [CrossRef]
- Vernstrom, T.; Gaensler, B.M.; Brown, S.; Lenc, E.; Norris, R.P. Low-frequency radio constraints on the synchrotron cosmic web. Mon. Not. R. Astron. Soc. 2017, 467, 4914–4936. [Google Scholar] [CrossRef]
- Hodgson, T.; Vazza, F.; Johnston-Hollitt, M.; Duchesne, S.W.; McKinley, B. Stacking the Synchrotron Cosmic Web with FIGARO. arXiv 2021, arXiv:2108.13682. [Google Scholar]
- Akahori, T.; Gaensler, B.M.; Ryu, D. Statistical Techniques for Detecting the Intergalactic Magnetic Field from Large Samples of Extragalactic Faraday Rotation Data. ApJ 2014, 790, 123. [Google Scholar] [CrossRef]
- Vacca, V.; Oppermann, N.; Enßlin, T.; Jasche, J.; Selig, M.; Greiner, M.; Junklewitz, H.; Reinecke, M.; Brüggen, M.; Carretti, E.; et al. Using rotation measure grids to detect cosmological magnetic fields: A Bayesian approach. A&A 2016, 591, A13. [Google Scholar]
- Blasi, P.; Burles, S.; Olinto, A.V. Cosmological Magnetic Field Limits in an Inhomogeneous Universe. ApJ Lett. 1999, 514, L79–L82. [Google Scholar] [CrossRef]
- Xu, Y.; Kronberg, P.P.; Habib, S.; Dufton, Q.W. A Faraday Rotation Search for Magnetic Fields in Large-scale Structure. ApJ 2006, 637, 19–26. [Google Scholar] [CrossRef]
- Pshirkov, M.S.; Tinyakov, P.G.; Urban, F.R. New Limits on Extragalactic Magnetic Fields from Rotation Measures. Phys. Rev. Lett. 2016, 116, 191302. [Google Scholar] [CrossRef] [PubMed]
- O’Sullivan, S.P.; Machalski, J.; Van Eck, C.L.; Heald, G.; Brüggen, M.; Fynbo, J.P.U.; Heintz, K.E.; Lara-Lopez, M.A.; Vacca, V.; Hardcastle, M.J.; et al. The intergalactic magnetic field probed by a giant radio galaxy. A&A 2019, 622, A16. [Google Scholar]
- Taylor, A.R.; Stil, J.M.; Sunstrum, C. A Rotation Measure Image of the Sky. ApJ 2009, 702, 1230–1236. [Google Scholar] [CrossRef]
- Amaral, A.D.; Vernstrom, T.; Gaensler, B.M. Constraints on large-scale magnetic fields in the intergalactic medium using cross-correlation methods. Mon. Not. R. Astron. Soc. 2021, 503, 2913–2926. [Google Scholar] [CrossRef]
- Vernstrom, T.; Gaensler, B.M.; Rudnick, L.; Andernach, H. Differences in Faraday Rotation between Adjacent Extragalactic Radio Sources as a Probe of Cosmic Magnetic Fields. ApJ 2019, 878, 92. [Google Scholar] [CrossRef]
- Stuardi, C.; O’Sullivan, S.P.; Bonafede, A.; Brüggen, M.; Dabhade, P.; Horellou, C.; Morganti, R.; Carretti, E.; Heald, G.; Iacobelli, M.; et al. The LOFAR view of intergalactic magnetic fields with giant radio galaxies. A&A 2020, 638, A48. [Google Scholar]
- O’Sullivan, S.P.; Brüggen, M.; Vazza, F.; Carretti, E.; Locatelli, N.T.; Stuardi, C.; Vacca, V.; Vernstrom, T.; Heald, G.; Horellou, C.; et al. New constraints on the magnetization of the cosmic web using LOFAR Faraday rotation observations. Mon. Not. R. Astron. Soc. 2020, 495, 2607–2619. [Google Scholar] [CrossRef]
- Bryan, G.L.; Norman, M.L.; O’Shea, B.W.; Abel, T.; Wise, J.H.; Turk, M.J.; Reynolds, D.R.; Collins, D.C.; Wang, P.; Skillman, S.W.; et al. ENZO: An Adaptive Mesh Refinement Code for Astrophysics. ApJS 2014, 211, 19. [Google Scholar] [CrossRef]
- Gheller, C.; Vazza, F. A survey of the thermal and non-thermal properties of cosmic filaments. Mon. Not. R. Astron. Soc. 2019, 486, 981–1002. [Google Scholar] [CrossRef]
- Banfi, S.; Vazza, F.; Wittor, D. Shock waves in the magnetized cosmic web: The role of obliquity and cosmic-ray acceleration. arXiv 2020, arXiv:2006.10063. [Google Scholar] [CrossRef]
- Gheller, C.; Vazza, F. Multiwavelength cross-correlation analysis of the simulated cosmic web. Mon. Not. R. Astron. Soc. 2020, 494, 5603–5618. [Google Scholar] [CrossRef]
- Vazza, F.; Paoletti, D.; Banfi, S.; Finelli, F.; Gheller, C.; O’Sullivan, S.P.; Brüggen, M. Simulations and observational tests of primordial magnetic fields from Cosmic Microwave Background constraintsok. Mon. Not. R. Astron. Soc. 2021, 500, 5350–5368. [Google Scholar] [CrossRef]
- Miniati, F. The Matryoshka Run: A Eulerian Refinement Strategy to Study the Statistics of Turbulence in Virialized Cosmic Structures. ApJ 2014, 782, 21. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; et al. Planck 2015 results. XIII. Cosmological parameters. A&A 2016, 594, A13. [Google Scholar]
- Bonafede, A.; Dolag, K.; Stasyszyn, F.; Murante, G.; Borgani, S. A non-ideal magnetohydrodynamic GADGET: Simulating massive galaxy clusters. Mon. Not. R. Astron. Soc. 2011, 418, 2234–2250. [Google Scholar] [CrossRef]
- Ruszkowski, M.; Lee, D.; Brüggen, M.; Parrish, I.; Oh, S.P. Cosmological Magnetohydrodynamic Simulations of Cluster Formation with Anisotropic Thermal Conduction. ApJ 2011, 740, 81. [Google Scholar] [CrossRef]
- Govoni, F.; Murgia, M.; Vacca, V.; Loi, F.; Girardi, M.; Gastaldello, F.; Giovannini, G.; Feretti, L.; Paladino, R.; Carretti, E.; et al. Sardinia Radio Telescope observations of Abell 194. The intra-cluster magnetic field power spectrum. A&A 2017, 603, A122. [Google Scholar]
- Stuardi, C.; Bonafede, A.; Lovisari, L.; Domínguez-Fernández, P.; Vazza, F.; Brüggen, M.; van Weeren, R.J.; de Gasperin, F. The intracluster magnetic field in the double relic galaxy cluster Abell 2345. Mon. Not. R. Astron. Soc. 2021, 502, 2518–2535. [Google Scholar] [CrossRef]
- Hodgson, T.; Johnston-Hollitt, M.; McKinley, B.; Vernstrom, T.; Vacca, V. Low(er) frequency follow-up of 28 candidate, large-scale synchrotron sources. Publ. Astron. Soc. Aust. 2020, 37, e032. [Google Scholar] [CrossRef]
- Loi, F.; Murgia, M.; Govoni, F.; Vacca, V.; Prandoni, I.; Bonafede, A.; Feretti, L. Simulations of the polarized radio sky and predictions on the confusion limit in polarization for future radio surveys. Mon. Not. R. Astron. Soc. 2019, 485, 5285–5293. [Google Scholar] [CrossRef]
- Bykov, A.M.; Vazza, F.; Kropotina, J.A.; Levenfish, K.P.; Paerels, F.B.S. Shocks and Non-thermal Particles in Clusters of Galaxies. Sci. Space Rev. 2019, 215, 14. [Google Scholar] [CrossRef]
- Kang, H.; Ryu, D.; Ha, J.H. Electron Preacceleration in Weak Quasi-perpendicular Shocks in High-beta Intracluster Medium. ApJ 2019, 876, 79. [Google Scholar] [CrossRef]
- Xu, R.; Spitkovsky, A.; Caprioli, D. Electron Acceleration in One-dimensional Nonrelativistic Quasi-perpendicular Collisionless Shocks. ApJ Lett. 2020, 897, L41. [Google Scholar]
- Botteon, A.; Brunetti, G.; Ryu, D.; Roh, S. Shock acceleration efficiency in radio relics. A&A 2020, 634, A64. [Google Scholar]
- Rajpurohit, K.; Hoeft, M.; Vazza, F.; Rudnick, L.; van Weeren, R.J.; Wittor, D.; Drabent, A.; Brienza, M.; Bonnassieux, E.; Locatelli, N.; et al. New mysteries and challenges from the Toothbrush relic: Wideband observations from 550 MHz to 8 GHz. A&A 2020, 636, A30. [Google Scholar]
- Locatelli, N.T.; Rajpurohit, K.; Vazza, F.; Gastaldello, F.; Dallacasa, D.; Bonafede, A.; Rossetti, M.; Stuardi, C.; Bonassieux, E.; Brunetti, G.; et al. Discovering the most elusive radio relic in the sky: Diffuse shock acceleration caught in the act? Mon. Not. R. Astron. Soc. 2020, 496, L48–L53. [Google Scholar] [CrossRef]
- Gheller, C.; Vazza, F.; Favre, J.; Brüggen, M. Properties of cosmological filaments extracted from Eulerian simulations. Mon. Not. R. Astron. Soc. 2015, 453, 1164–1185. [Google Scholar] [CrossRef]
- Banfi, S.; Vazza, F.; Gheller, C. On the alignment of haloes, filaments and magnetic fields in the simulated cosmic web. Mon. Not. R. Astron. Soc. 2021, 503, 4016–4031. [Google Scholar] [CrossRef]
- Oppermann, N.; Junklewitz, H.; Greiner, M.; Enßlin, T.A.; Akahori, T.; Carretti, E.; Gaensler, B.M.; Goobar, A.; Harvey-Smith, L.; Johnston-Hollitt, M.; et al. Estimating extragalactic Faraday rotation. A&A 2015, 575, A118. [Google Scholar]
- Schnitzeler, D.H.F.M. The latitude dependence of the rotation measures of NVSS sources. Mon. Not. R. Astron. Soc. 2010, 409, L99–L103. [Google Scholar] [CrossRef]
- Banfield, J.K.; Schnitzeler, D.H.F.M.; George, S.J.; Norris, R.P.; Jarrett, T.H.; Taylor, A.R.; Stil, J.M. Radio galaxies and their magnetic fields out to z ≤ 3. Mon. Not. R. Astron. Soc. 2014, 444, 700–710. [Google Scholar]
- Sigl, G.; Miniati, F.; Ensslin, T.A. Ultra-high energy cosmic rays in a structured and magnetized universe. Phys. Rev. 2003, D68, 043002. [Google Scholar]
- Dolag, K.; Grasso, D.; Springel, V.; Tkachev, I. Constrained simulations of the magnetic field in the local Universe and the propagation of ultrahigh energy cosmic rays. J. Cosmol. Astropart. Phys. 2005, 2005, 009. [Google Scholar] [CrossRef]
- Berezinsky, V. Extragalactic cosmic rays and their signatures. Astropart. Phys. 2014, 53, 120–129. [Google Scholar] [CrossRef][Green Version]
- Alves Batista, R.; Sigl, G. Diffusion of cosmic rays at EeV energies in inhomogeneous extragalactic magnetic fields. J. Cosmol. Astropart. Phys. 2014, 2014, 031. [Google Scholar] [CrossRef][Green Version]
- Hackstein, S.; Vazza, F.; Brüggen, M.; Sigl, G.; Dundovic, A. Propagation of ultrahigh energy cosmic rays in extragalactic magnetic fields: A view from cosmological simulations. Mon. Not. R. Astron. Soc. 2016, 462, 3660–3671. [Google Scholar] [CrossRef]
- Hackstein, S.; Brüggen, M.; Vazza, F.; Gaensler, B.M.; Heesen, V. Fast radio burst dispersion measures and rotation measures and the origin of intergalactic magnetic fields. Mon. Not. R. Astron. Soc. 2019, 488, 4220–4238. [Google Scholar] [CrossRef]
- Globus, N.; Piran, T.; Hoffman, Y.; Carlesi, E.; Pomarède, D. Cosmic ray anisotropy from large-scale structure and the effect of magnetic horizons. Mon. Not. R. Astron. Soc. 2019, 484, 4167–4173. [Google Scholar] [CrossRef]
- Petroff, E.; Hessels, J.W.T.; Lorimer, D.R. Fast radio bursts. Astron. Astrophys. Rev. 2019, 27, 4. [Google Scholar] [CrossRef]
- Dolag, K.; Gaensler, B.M.; Beck, A.M.; Beck, M.C. Constraints on the distribution and energetics of fast radio bursts using cosmological hydrodynamic simulations. Mon. Not. R. Astron. Soc. 2015, 451, 4277–4289. [Google Scholar] [CrossRef]
- Petroff, E.; Burke-Spolaor, S.; Keane, E.F.; McLaughlin, M.A.; Miller, R.; Andreoni, I.; Bailes, M.; Barr, E.D.; Bernard, S.R.; Bhandari, S.; et al. A polarized fast radio burst at low Galactic latitude. Mon. Not. R. Astron. Soc. 2017, 469, 4465–4482. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Hinz, P.M.; Wittor, D.; Locatelli, N.; Gheller, C. Probing the origin of extragalactic magnetic fields with Fast Radio Bursts. Mon. Not. R. Astron. Soc. 2018, 480, 3907–3915. [Google Scholar] [CrossRef]
- Hackstein, S.; Brüggen, M.; Vazza, F.; Rodrigues, L.F.S. Redshift estimates for fast radio bursts and implications on intergalactic magnetic fields. Mon. Not. R. Astron. Soc. 2020, 498, 4811–4829. [Google Scholar] [CrossRef]
- Johnston-Hollitt, M.; Govoni, F.; Beck, R.; Dehghan, S.; Pratley, L.; Akahori, T.; Heald, G.; Agudo, I.; Bonafede, A.; Carretti, E.; et al. Using SKA Rotation Measures to Reveal the Mysteries of the Magnetised Universe. In Proceedings of the Advancing Astrophysics with the Square Kilometre Array (AASKA14), Giardini Naxos, Italy, 8–13 June 2014; p. 92. [Google Scholar]
- Taylor, R.; Agudo, I.; Akahori, T.; Beck, R.; Gaensler, B.; Heald, G.; Johnston-Hollitt, M.; Langer, M.; Rudnick, L.; Scaife, A.; et al. SKA Deep Polarization and Cosmic Magnetism. In Proceedings of the Advancing Astrophysics with the Square Kilometre Array (AASKA14), Giardini Naxos, Italy, 8–13 June 2014; p. 113. [Google Scholar]
- Tavecchio, F.; Roncadelli, M.; Galanti, G.; Bonnoli, G. Evidence for an axion-like particle from PKS 1222+216? Phys. Rev. Lett. 2012, 86, 085036. [Google Scholar]
- Horns, D.; Maccione, L.; Meyer, M.; Mirizzi, A.; Montanino, D.; Roncadelli, M. Hardening of TeV gamma spectrum of active galactic nuclei in galaxy clusters by conversions of photons into axionlike particles. Phys. Rev. Lett. 2012, 86, 075024. [Google Scholar] [CrossRef]
- Mirizzi, A.; Raffelt1, G.G.; Serpico, P.D. Photon-Axion Conversion in Intergalactic Magnetic Fields and Cosmological Consequences. In Axions; Lecture Notes in Physics; Kuster, M., Raffelt, G., Beltrán, B., Eds.; Springer: Berlin, Germany, 2008; Volume 741, p. 115. [Google Scholar]
- Montanino, D.; Vazza, F.; Mirizzi, A.; Viel, M. Enhancing the Spectral Hardening of Cosmic TeV Photons by Mixing with Axionlike Particles in the Magnetized Cosmic Web. Phys. Rev. Lett. 2017, 119, 101101. [Google Scholar] [CrossRef]
- Dedner, A.; Kemm, F.; Kröner, D.; Munz, C.D.; Schnitzer, T.; Wesenberg, M. Hyperbolic Divergence Cleaning for the MHD Equations. J. Comput. Phys. 2002, 175, 645–673. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient Implementation of Essentially Non-oscillatory Shock-Capturing Schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Kritsuk, A.G.; Nordlund, Å.; Collins, D.; Padoan, P.; Norman, M.L.; Abel, T.; Banerjee, R.; Federrath, C.; Flock, M.; Lee, D.; et al. Comparing Numerical Methods for Isothermal Magnetized Supersonic Turbulence. ApJ 2011, 737, 13. [Google Scholar] [CrossRef]
- Pakmor, R.; Marinacci, F.; Springel, V. Magnetic Fields in Cosmological Simulations of Disk Galaxies. ApJ Lett. 2014, 783, L20. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Raives, M.J. Accurate, meshless methods for magnetohydrodynamics. Mon. Not. R. Astron. Soc. 2016, 455, 51–88. [Google Scholar] [CrossRef]
- Wang, P.; Abel, T.; Kaehler, R. Adaptive mesh fluid simulations on GPU. New Astron. 2010, 15, 581–589. [Google Scholar] [CrossRef]
- Federrath, C.; Schober, J.; Bovino, S.; Schleicher, D.R.G. The Turbulent Dynamo in Highly Compressible Supersonic Plasmas. ApJ Lett. 2014, 797, L19. [Google Scholar] [CrossRef]
- Grete, P.; Vlaykov, D.G.; Schmidt, W.; Schleicher, D.R.G. A nonlinear structural subgrid-scale closure for compressible MHD. II. A priori comparison on turbulence simulation data. Phys. Plasmas 2016, 23, 062317. [Google Scholar] [CrossRef]
- Beresnyak, A.; Miniati, F. Turbulent Amplification and Structure of the Intracluster Magnetic Field. ApJ 2016, 817, 127. [Google Scholar] [CrossRef]
- Kim, J.H.; Wise, J.H.; Alvarez, M.A.; Abel, T. Galaxy Formation with Self-consistently Modeled Stars and Massive Black Holes. I. Feedback-regulated Star Formation and Black Hole Growth. ApJ 2011, 738, 54. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).