Modelling the Energy Spectra of Radio Relics
Abstract
1. Introduction
2. Materials and Methods
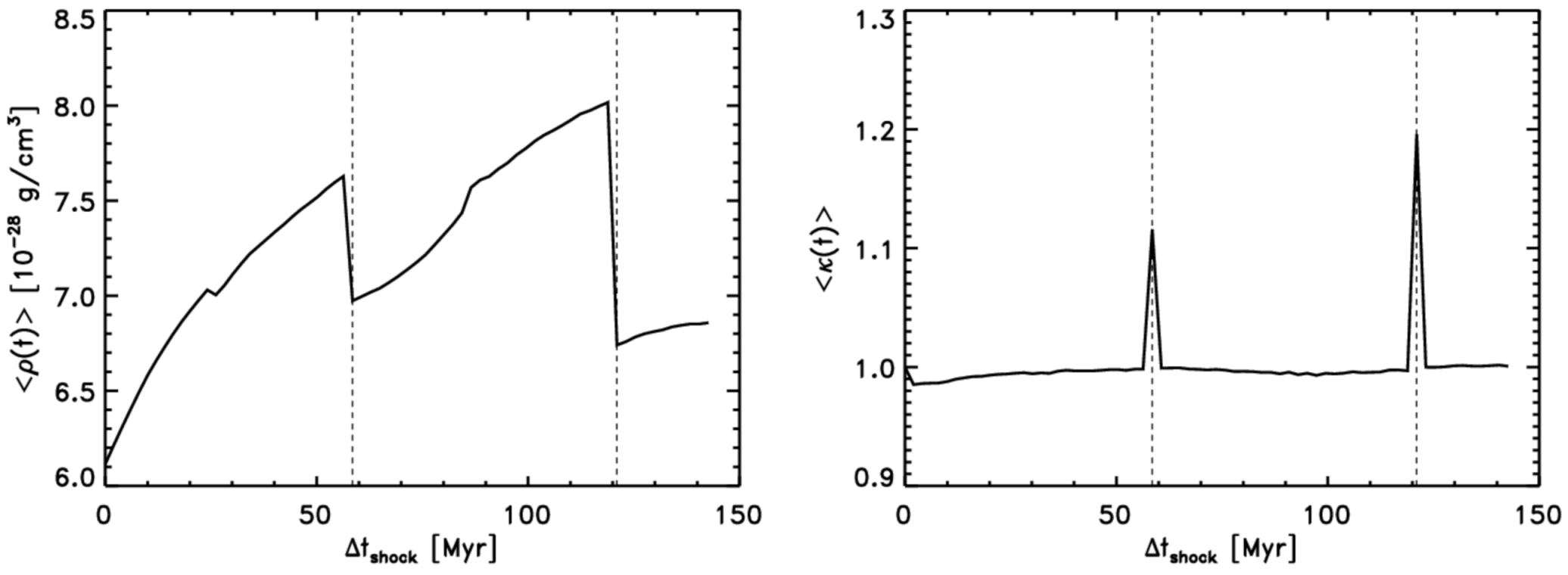
2.1. Modelling of the Cosmic-Ray Spectra
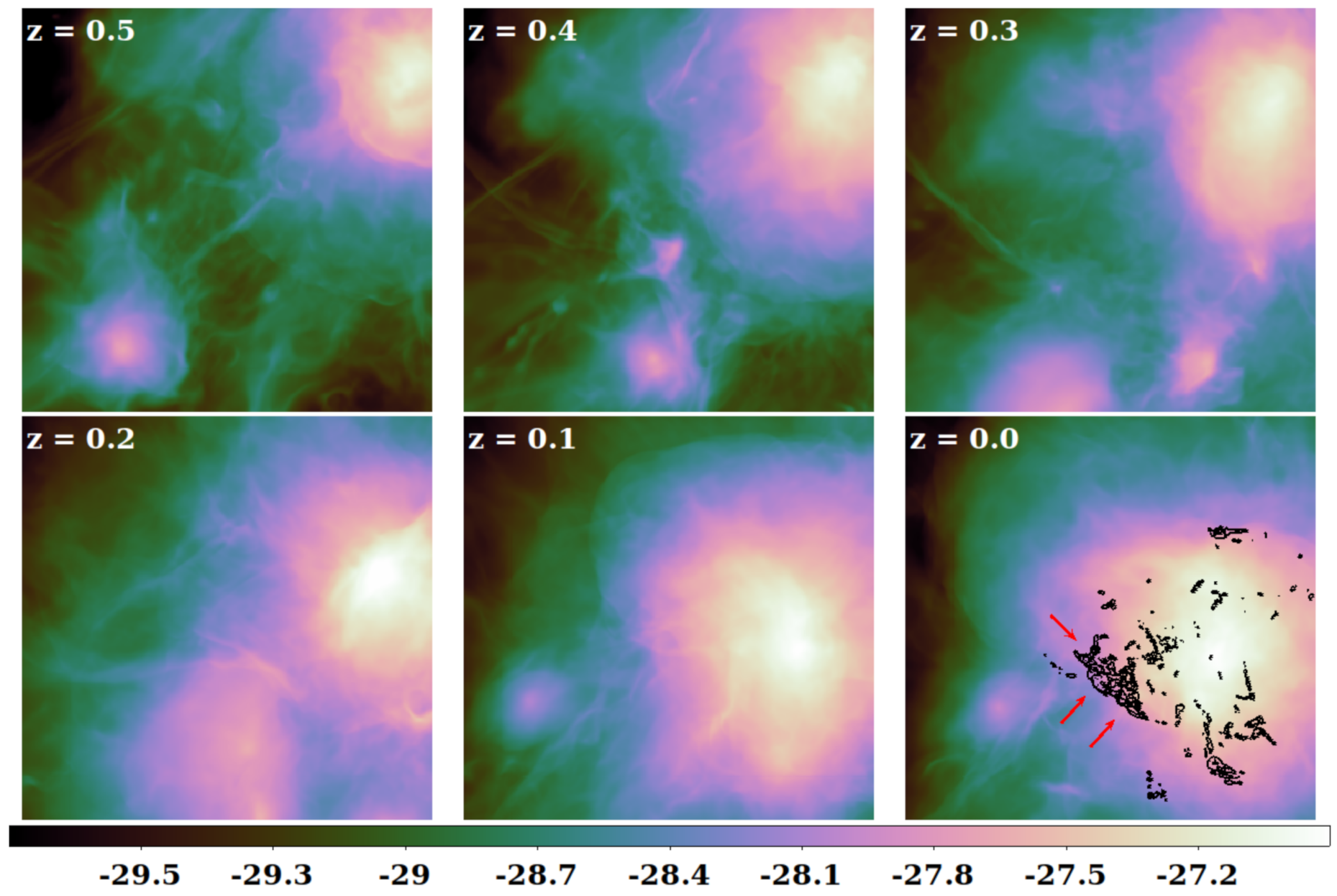
2.2. Cluster Simulation
3. Results
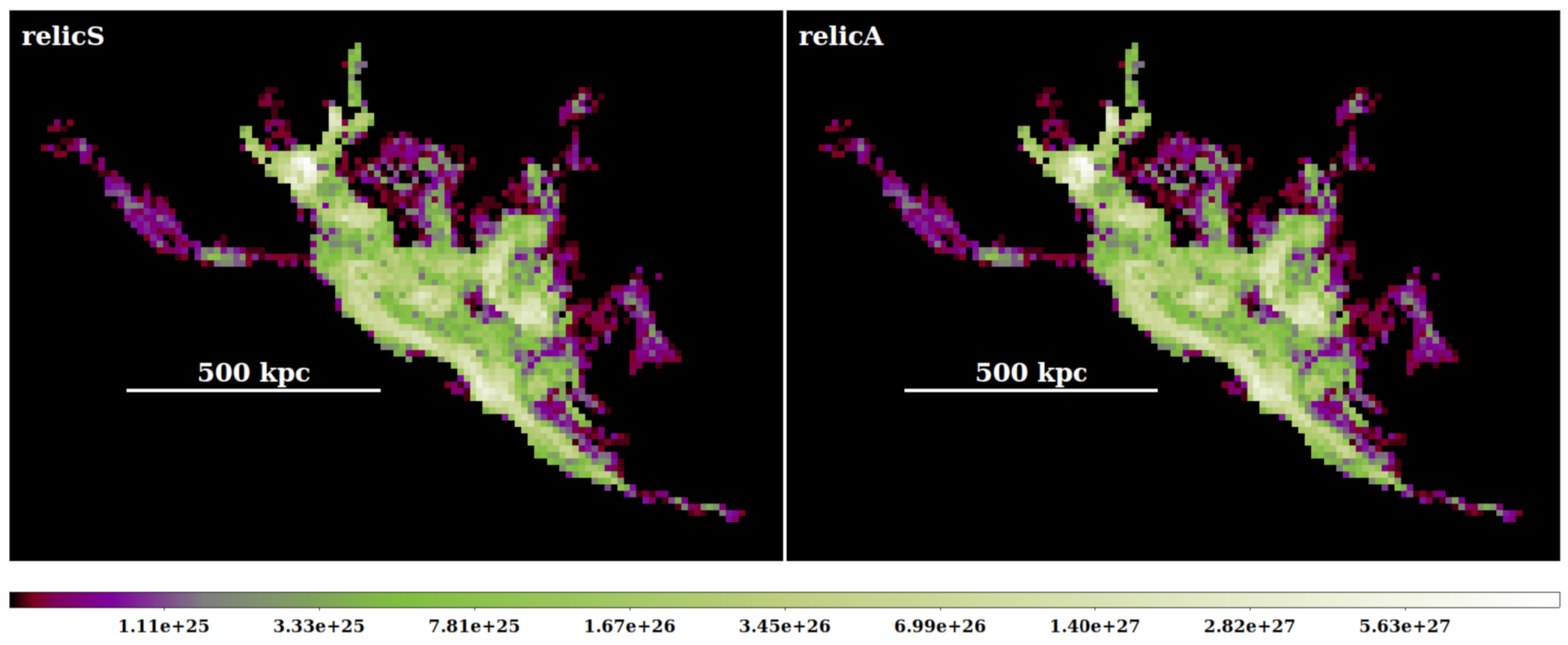
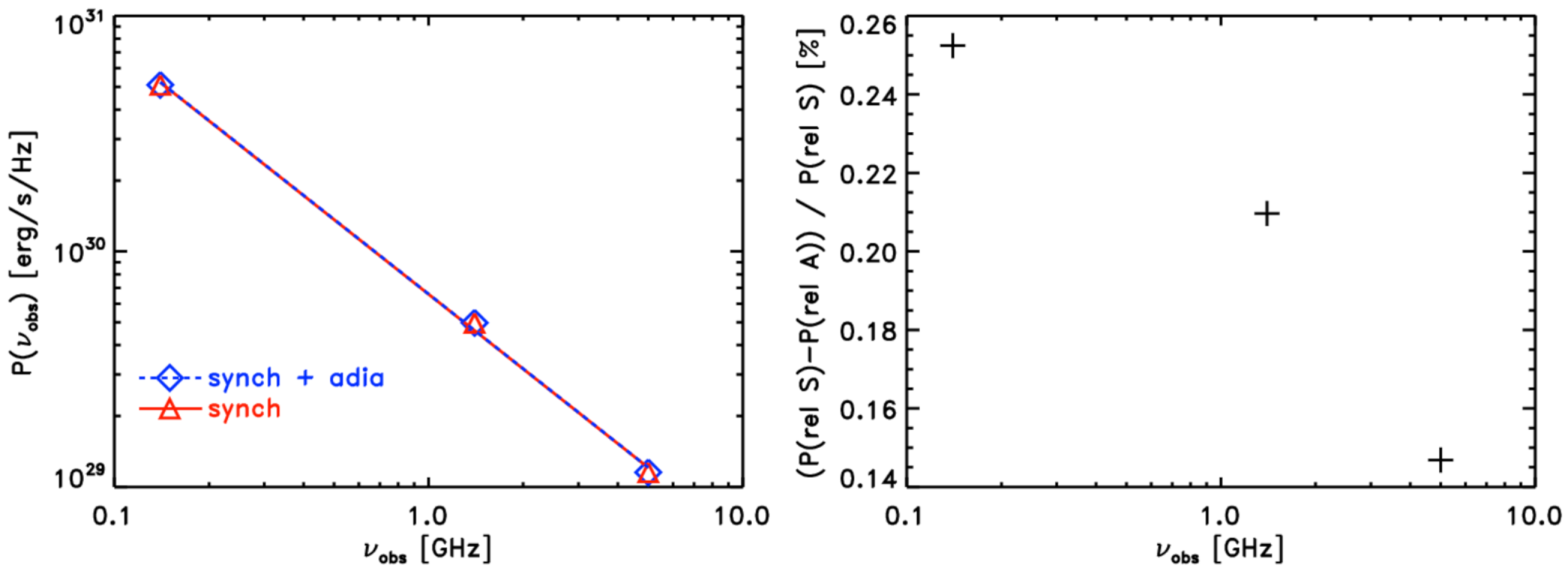
3.1. Radio Power
3.2. Integrated Radio Spectra
3.3. Numerical Caveats
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brunetti, G.; Jones, T.W. Cosmic Rays in Galaxy Clusters and Their Nonthermal Emission. Int. J. Mod. Phys. D 2014, 23, 1430007. [Google Scholar] [CrossRef]
- van Weeren, R.J.; de Gasperin, F.; Akamatsu, H.; Brüggen, M.; Feretti, L.; Kang, H.; Stroe, A.; Zandanel, F. Diffuse Radio Emission from Galaxy Clusters. Sci. Space Rev. 2019, 215, 16. [Google Scholar] [CrossRef]
- Bykov, A.M.; Vazza, F.; Kropotina, J.A.; Levenfish, K.P.; Paerels, F.B.S. Shocks and Non-thermal Particles in Clusters of Galaxies. Sci. Space Rev. 2019, 215, 14. [Google Scholar] [CrossRef]
- Drury, L.O. An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 1983, 46, 973–1027. [Google Scholar] [CrossRef]
- Ensslin, T.A.; Biermann, P.L.; Klein, U.; Kohle, S. Cluster radio relics as a tracer of shock waves of the large-scale structure formation. Astron. Astrophys. 1998, 332, 395–409. [Google Scholar]
- Rajpurohit, K.; Wittor, D.; van Weeren, R.J.; Vazza, F.; Hoeft, M.; Rudnick, L.; Locatelli, N.; Eilek, J.; Forman, W.R.; Bonafede, A.; et al. Understanding the radio relic emission in the galaxy cluster MACS J0717.5+3745: Spectral analysis. Astron. Astrophys. 2021, 646, A56. [Google Scholar] [CrossRef]
- Rajpurohit, K.; Vazza, F.; van Weeren, R.J.; Hoeft, M.; Brienza, M.; Bonnassieux, E.; Riseley, C.J.; Brunetti, G.; Bonafede, A.; Brüggen, M.; et al. Dissecting nonthermal emission in the complex multiple-merger galaxy cluster Abell 2744: Radio and X-ray analysis. arXiv 2021, arXiv:2104.05690. [Google Scholar] [CrossRef]
- Hoeft, M.; Brüggen, M. Radio signature of cosmological structure formation shocks. Mon. Not. R. Astron. Soc. 2007, 375, 77–91. [Google Scholar] [CrossRef]
- Nuza, S.E.; Hoeft, M.; van Weeren, R.J.; Gottlöber, S.; Yepes, G. How many radio relics await discovery? Mon. Not. R. Astron. Soc. 2012, 420, 2006–2019. [Google Scholar] [CrossRef]
- Nuza, S.E.; Gelszinnis, J.; Hoeft, M.; Yepes, G. Can cluster merger shocks reproduce the luminosity and shape distribution of radio relics? Mon. Not. R. Astron. Soc. 2017, 470, 240–263. [Google Scholar] [CrossRef]
- Wittor, D.; Hoeft, M.; Vazza, F.; Brüggen, M.; Domínguez-Fernández, P. Polarization of radio relics in galaxy clusters. Mon. Not. R. Astron. Soc. 2019, 490, 3987–4006. [Google Scholar] [CrossRef]
- Wittor, D.; Ettori, S.; Vazza, F.; Rajpurohit, K.; Hoeft, M.; Domínguez-Fernández, P. Exploring the spectral properties of radio relics—I: Integrated spectral index and Mach number. Mon. Not. R. Astron. Soc. 2021, 506, 396–414. [Google Scholar] [CrossRef]
- Dominguez-Fernandez, P.; Bruggen, M.; Vazza, F.; Banda-Barragan, W.E.; Rajpurohit, K.; Mignone, A.; Mukherjee, D.; Vaidya, B. Morphology of radio relics—I. What causes the substructure of synchrotron emission? Mon. Not. R. Astron. Soc. 2021, 500, 795–816. [Google Scholar] [CrossRef]
- Domínguez-Fernández, P.; Brüggen, M.; Vazza, F.; Hoeft, M.; Banda-Barragán, W.E.; Rajpurohit, K.; Wittor, D.; Mignone, A.; Mukherjee, D.; Vaidya, B. Morphology of radio relics—II. Properties of polarized emission. Mon. Not. R. Astron. Soc. 2021, 507, 2714–2734. [Google Scholar] [CrossRef]
- Shklovskii, I.S. Secular Variation of the Flux and Intensity of Radio Emission from Discrete Sources. Astron. Zhurnal 1960, 37, 256. [Google Scholar]
- Kardashev, N.S. Nonstationarity of Spectra of Young Sources of Nonthermal Radio Emission. Sov. Astron. 1962, 6, 317. [Google Scholar]
- Longair, M.S. High Energy Astrophysics. An Informal Introduction for Students of Physics and Astronomy; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Enßlin, T.A.; Gopal-Krishna. Reviving fossil radio plasma in clusters of galaxies by adiabatic compression in environmental shock waves. Astron. Astrophys. 2001, 366, 26–34. [Google Scholar] [CrossRef]
- Bryan, G.L.; Norman, M.L.; O’Shea, B.W.; Abel, T.; Wise, J.H.; Turk, M.J.; Reynolds, D.R.; Collins, D.C.; Wang, P.; Skillman, S.W.; et al. ENZO: An Adaptive Mesh Refinement Code for Astrophysics. ApJS 2014, 211, 19. [Google Scholar] [CrossRef]
- Wittor, D.; Vazza, F.; Brüggen, M. Testing cosmic ray acceleration with radio relics: A high-resolution study using MHD and tracers. Mon. Not. R. Astron. Soc. 2017, 464, 4448–4462. [Google Scholar] [CrossRef]
- Banfi, S.; Vazza, F.; Wittor, D. Shock waves in the magnetized cosmic web: The role of obliquity and cosmic ray acceleration. Mon. Not. R. Astron. Soc. 2020, 496, 3648–3667. [Google Scholar] [CrossRef]
- Wittor, D.; Vazza, F.; Ryu, D.; Kang, H. Limiting the shock acceleration of cosmic ray protons in the ICM. Mon. Not. R. Astron. Soc. 2020, 495, L112–L117. [Google Scholar] [CrossRef]
- Wittor, D.; Vazza, F.; Brüggen, M. Studying the Effect of Shock Obliquity on the γ-ray and Diffuse Radio Emission in Galaxy Clusters. Galaxies 2016, 4, 71. [Google Scholar] [CrossRef]
- Wittor, D.; Jones, T.; Vazza, F.; Brüggen, M. Evolution of vorticity and enstrophy in the intracluster medium. Mon. Not. R. Astron. Soc. 2017, 471, 3212–3225. [Google Scholar] [CrossRef]
- Wittor, D. Origin and Effects of the Non-Thermal Components in Large-Scale Structures of the Universe. Ph.D. Thesis, Universität Hamburg, Hamburg, Germany, 2017. [Google Scholar]
- Loi, F.; Murgia, M.; Vacca, V.; Govoni, F.; Melis, A.; Wittor, D.; Kierdorf, M.; Bonafede, A.; Boschin, W.; Brienza, M.; et al. Spectropolarimetric observations of the CIZA J2242.8+5301 northern radio relic: No evidence of high-frequency steepening. Mon. Not. R. Astron. Soc. 2020, 498, 1628–1637. [Google Scholar] [CrossRef]
- Rajpurohit, K.; Vazza, F.; Hoeft, M.; Loi, F.; Beck, R.; Vacca, V.; Kierdorf, M.; van Weeren, R.J.; Wittor, D.; Govoni, F.; et al. A perfect power-law spectrum even at the highest frequencies: The Toothbrush relic. Astron. Astrophys. 2020, 642, L13. [Google Scholar] [CrossRef]
- Rajpurohit, K.; Hoeft, M.; Vazza, F.; Rudnick, L.; van Weeren, R.J.; Wittor, D.; Drabent, A.; Brienza, M.; Bonnassieux, E.; Locatelli, N.; et al. New mysteries and challenges from the Toothbrush relic: Wideband observations from 550 MHz to 8 GHz. Astron. Astrophys. 2020, 636, A30. [Google Scholar] [CrossRef]
- Enßlin, T.A.; Brüggen, M. On the formation of cluster radio relics. Mon. Not. R. Astron. Soc. 2002, 331, 1011–1019. [Google Scholar] [CrossRef]
- de Gasperin, F.; Ogrean, G.A.; van Weeren, R.J.; Dawson, W.A.; Brüggen, M.; Bonafede, A.; Simionescu, A. Abell 1033: Birth of a radio phoenix. Mon. Not. R. Astron. Soc. 2015, 448, 2197–2209. [Google Scholar] [CrossRef][Green Version]
- Mandal, S.; Intema, H.T.; van Weeren, R.J.; Shimwell, T.W.; Botteon, A.; Brunetti, G.; de Gasperin, F.; Brüggen, M.; Di Gennaro, G.; Kraft, R.; et al. Revived fossil plasma sources in galaxy clusters. Astron. Astrophys. 2020, 634, A4. [Google Scholar] [CrossRef]
- Hahn, O.; Abel, T. Multi-scale initial conditions for cosmological simulations. Mon. Not. R. Astron. Soc. 2011, 415, 2101–2121. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wittor, D.; Hoeft, M.; Brüggen, M. Modelling the Energy Spectra of Radio Relics. Galaxies 2021, 9, 111. https://doi.org/10.3390/galaxies9040111
Wittor D, Hoeft M, Brüggen M. Modelling the Energy Spectra of Radio Relics. Galaxies. 2021; 9(4):111. https://doi.org/10.3390/galaxies9040111
Chicago/Turabian StyleWittor, Denis, Matthias Hoeft, and Marcus Brüggen. 2021. "Modelling the Energy Spectra of Radio Relics" Galaxies 9, no. 4: 111. https://doi.org/10.3390/galaxies9040111
APA StyleWittor, D., Hoeft, M., & Brüggen, M. (2021). Modelling the Energy Spectra of Radio Relics. Galaxies, 9(4), 111. https://doi.org/10.3390/galaxies9040111




