The Low-Energy Spectral Index of Gamma-ray Burst Prompt Emission from Internal Shocks
Abstract
1. Introduction
2. Dynamics of Two-Shell Collision
3. Synchrotron Radiation with a Decaying Magnetic Field and a Variable Electron Injection Rate
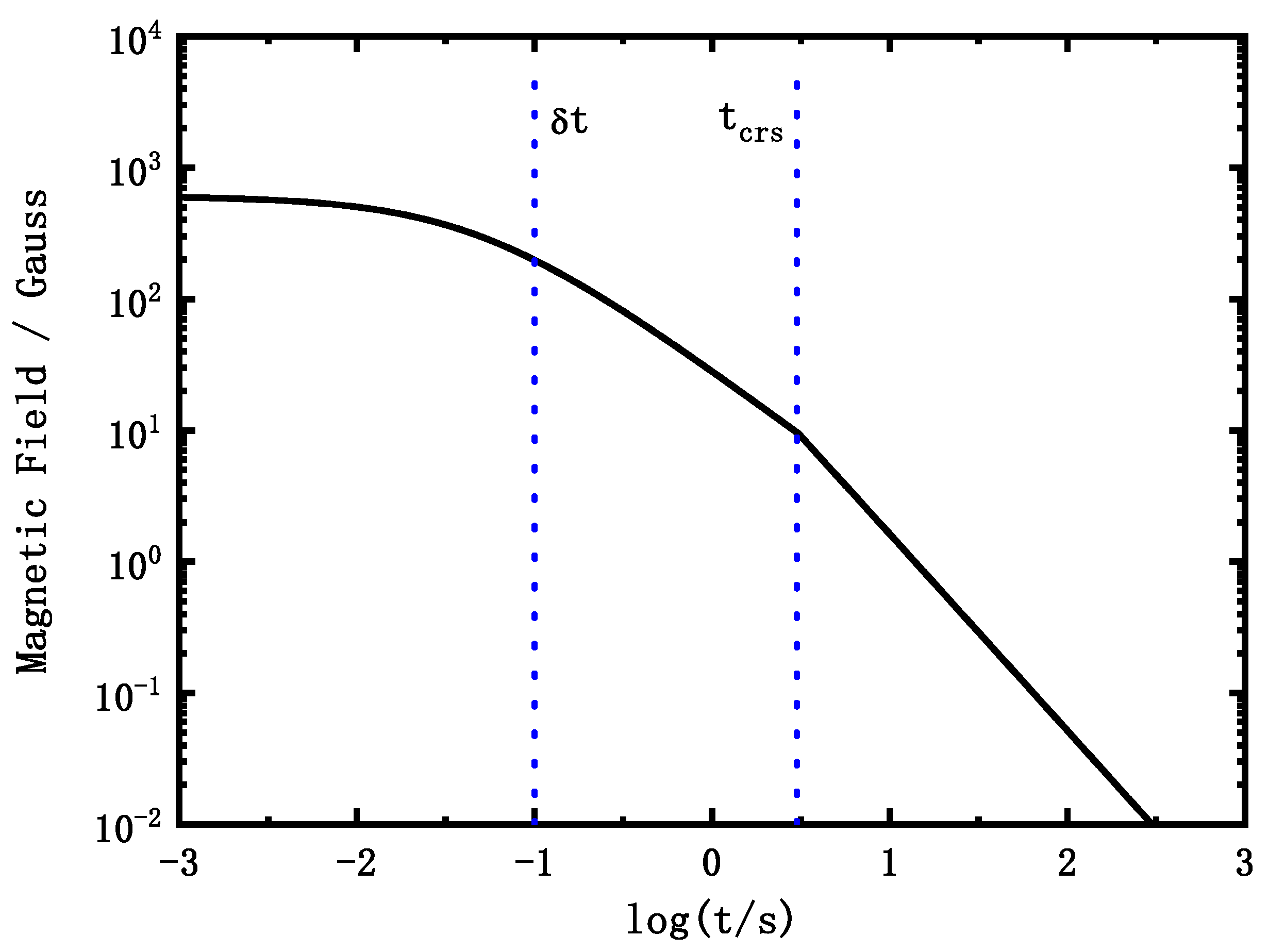
3.1. Synchrotron Radiation with a Decaying Magnetic Field
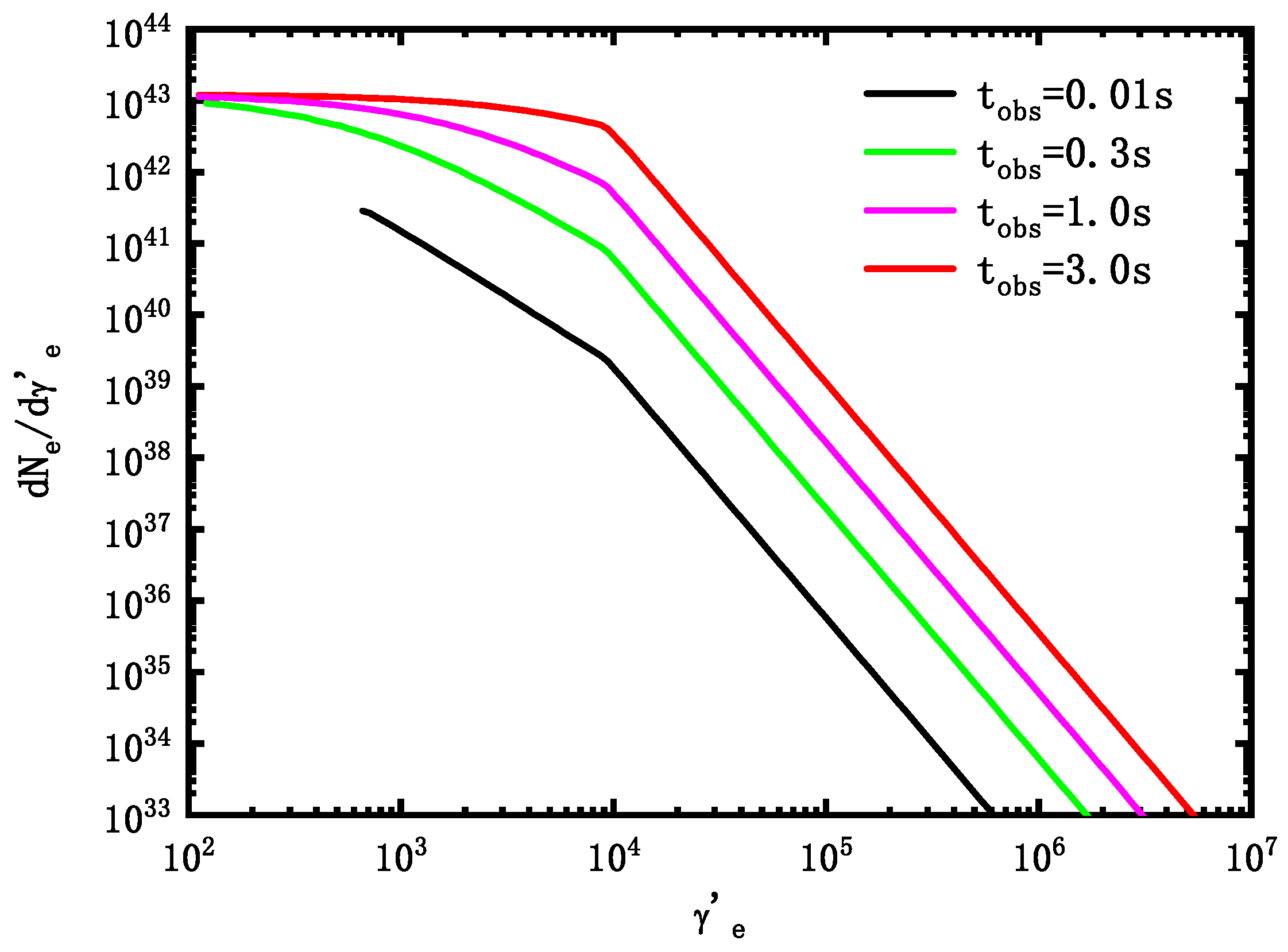
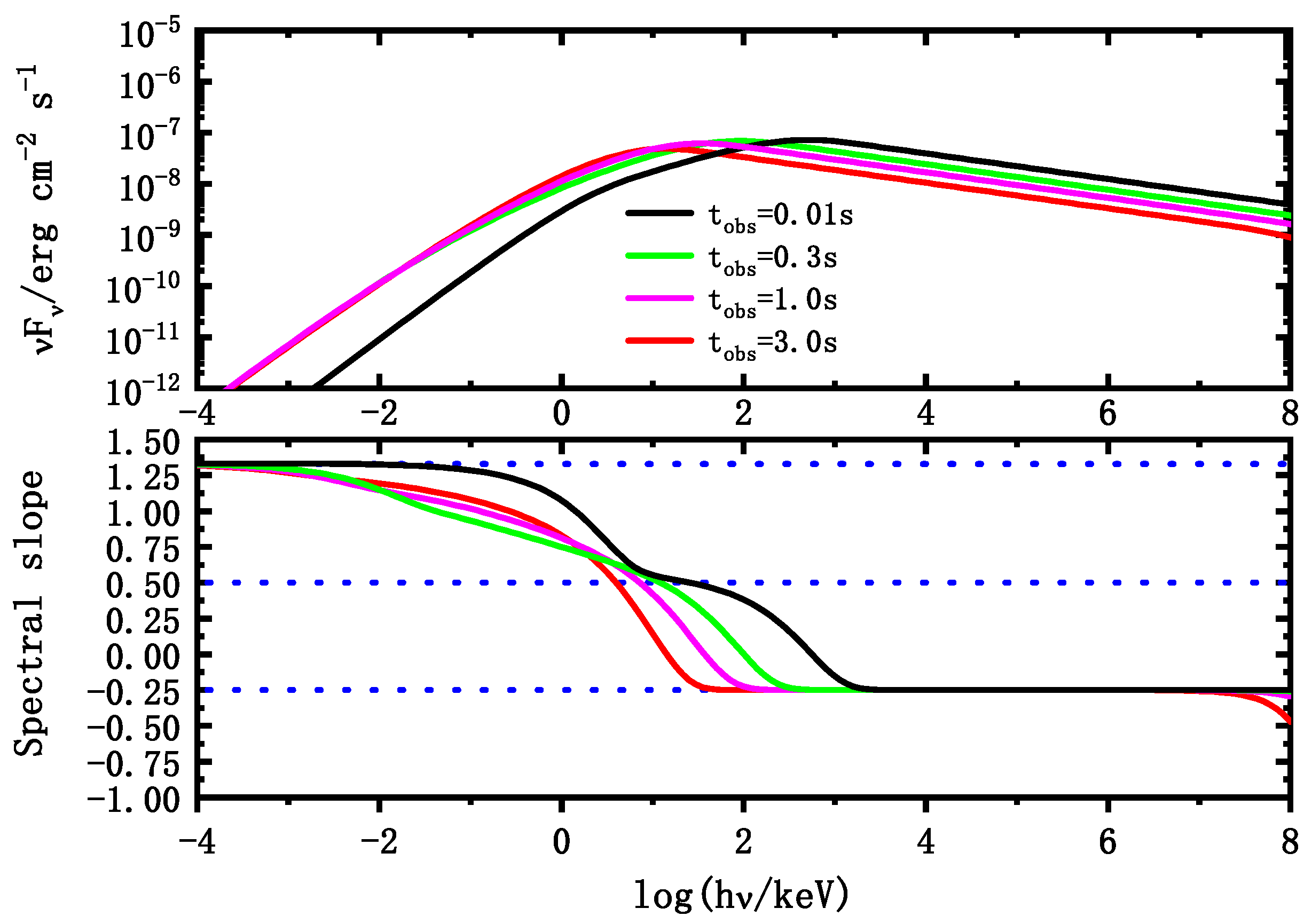
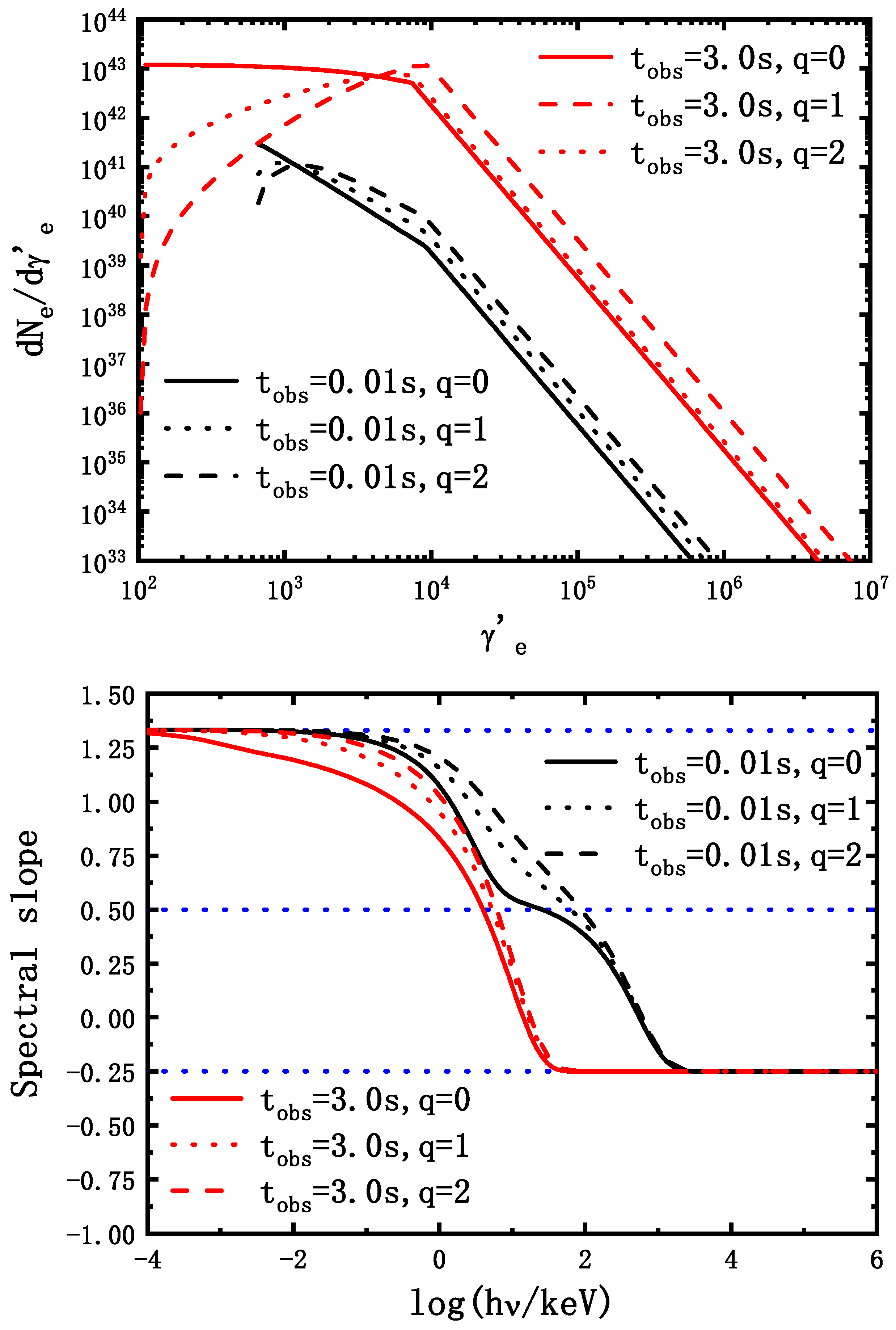
3.2. The Effect of the Variable Electron Injection Rate
4. Application to the Actual GRB Spectra
5. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | The high-energy electron distribution above the break electron energy is . |
References
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE Observations of Gamma-Ray Burst Spectra. I. Spectral Diversity. Astrophys. J. 1993, 413, 281. [Google Scholar] [CrossRef]
- Gruber, D.; Goldstein, A.; von Ahlefeld, V.W.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Byrne, D.; Clevel, W.H.; Connaughton, V.; Diehl, R.; et al. The Fermi GBM Gamma-Ray Burst Spectral Catalog: Four Years of Data. Astrophys. J. Suppl. 2014, 211, 12. [Google Scholar] [CrossRef]
- Preece, R.D.; Briggs, M.S.; Mallozzi, R.S.; Pendleton, G.N.; Paciesas, W.S.; Band, D.L. The BATSE Gamma-Ray Burst Spectral Catalog. I. High Time Resolution Spectroscopy of Bright Bursts Using High Energy Resolution Data. Astrophys. J. 2000, 126, 19. [Google Scholar] [CrossRef]
- Zhang, B. Gamma-ray Burst Prompt Emission. IJMPD 2014, 23, 1430002. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The Physics of Gamma-Ray Bursts and Relativistic Jets. Phys. Rep. 2014, 561, 1. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Collisional Mechanism for Gamma-Ray Burst Emission. Mon. Not. R. Astron. Soc. 2010, 407, 1033. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, B. Cosmological Implications of Fast Radio Burst/Gamma-Ray Burst Associations. Astrophys. J. 2014, 783, 35. [Google Scholar] [CrossRef]
- Giannios, D. Prompt GRB emission from gradual energy dissipation. Astron. Astrophys. 2008, 480, 305. [Google Scholar] [CrossRef]
- Lazzati, D.; Begelman, M.C. Non-Thermal Emission from the Photospheres of Gamma-Ray Burst Outflows. I. High-Frequency Tails. Astrophys. J. 2010, 725, 1137. [Google Scholar] [CrossRef]
- Lazzati, D.; Morsony, B.J.; Margutti, R.; Begelman, M.C. Photospheric Emission As the Dominant Radiation Mechanism in Long-Duration Gamma-Ray Bursts. Astrophys. J. 2013, 765, 103. [Google Scholar] [CrossRef]
- Lundman, C.; Pe’er, A.; Ryde, F. A Theory of Photospheric Emission from Relativistic, Collimated Outflows. Mon. Not. R. Astron. Soc. 2013, 428, 2430. [Google Scholar] [CrossRef]
- Meszaros, P.; Ramirez-ruiz, E.; Rees, M.J.; Zhang, B. X-Ray-rich Gamma-Ray Bursts, Photospheres, and Variability. Astrophys. J. 2002, 578, 812. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Steep Slopes and Preferred Breaks in Gamma-Ray Burst Spectra: The Role of Photospheres and Comptonization. Astrophys. J. 2000, 530, 292. [Google Scholar] [CrossRef]
- Pe’er, A. Temporal Evolution of Thermal Emission from Relativistically Expanding Plasma. Astrophys. J. 2008, 682, 463. [Google Scholar] [CrossRef]
- Pe’er, A.; Meszaros, P.; Rees, M.J. The Observable Effects of a Photospheric Component on GRB and XRF Prompt Emission Spectrum. Astrophys. J. 2006, 642, 995. [Google Scholar] [CrossRef]
- Pe’er, A.; Ryde, F. A Theory of Multicolor Blackbody Emission from Relativistically Expanding Plasmas. Astrophys. J. 2011, 732, 49. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Dissipative Photosphere Models of Gamma-Ray Bursts and X-Ray Flashes. Astrophys. J. 2005, 628, 847. [Google Scholar] [CrossRef]
- Thompson, C. A Model of Gamma-Ray Bursts. Mon. Not. R. Astron. Soc. 1994, 270, 480. [Google Scholar] [CrossRef]
- Thompson, C.; Meszaros, P.; Rees, M.J. Thermalization in Relativistic Outflows and the Correlation between Spectral Hardness and Apparent Luminosity in Gamma-Ray Bursts. Astrophys. J. 2007, 666, 1012. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, B. Low Energy Spectral Index and Ep Evolution of Quasi-thermal Photosphere Emission of Gamma-Ray Bursts. Astrophys. J. 2014, 785, 112. [Google Scholar] [CrossRef]
- Pe’er, A.; Zhang, B. Synchrotron Emission in Small-Scale Magnetic Fields as a Possible Explanation for Prompt Emission Spectra of Gamma-Ray Bursts. Astrophys. J. 2006, 653, 454. [Google Scholar] [CrossRef]
- Uhm, Z.L.; Zhang, B. Fast-Cooling Synchrotron Radiation in a Decaying Magnetic Field and Γ-Ray Burst Emission Mechanism. Nat. Phys. 2014, 10, 351. [Google Scholar] [CrossRef]
- Zhang, B.B.; Uhm, Z.L.; Connaughton, V.; Briggs, M.S.; Zhang, B. Synchrotron Origin of the Typical GRB Band Function—A Case Study of GRB 130606B. Astrophys. J. 2016, 816, 72. [Google Scholar] [CrossRef]
- Geng, J.J.; Huang, Y.F.; Wu, X.F.; Zhang, B.; Zong, H.S. Low-energy Spectra of Gamma-Ray Bursts from Cooling Electrons. Astrophys. J. 2018, 234, 3. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Z.; Liu, X.; Zhang, B.B.; Bai, J.; Meszaros, P. Gamma-Ray Burst Spectrum with Decaying Magnetic Field. Astrophys. J. 2014, 780, 12. [Google Scholar] [CrossRef]
- Daigne, F.; Bosnjak, Z.; Dubus, G. Reconciling observed gamma-ray burst prompt spectra with synchrotron radiation? Astron. Astrophys. 2011, 526, 110. [Google Scholar] [CrossRef]
- Wang, X.Y.; Li, Z.; Dai, Z.G.; Meszaros, P. GRB 080916C: On the Radiation Origin of the Prompt Emission from keV/MeV TO GeV. Astrophys. J. 2009, 698, 98. [Google Scholar] [CrossRef][Green Version]
- Lloyd, N.M.; Petrosian, V. Synchrotron Radiation as the Source of Gamma-Ray Burst Spectra. Astrophys. J. 2000, 543, 722. [Google Scholar] [CrossRef]
- Shen, R.F.; Zhang, B. Prompt Optical Emission and Synchrotron Self-Absorption Constraints on Emission Site of GRBs. Mon. Not. R. Astron. Soc. 2009, 398, 1936. [Google Scholar] [CrossRef][Green Version]
- Xu, S.Y.; Yang, Y.P.; Zhang, B. On the Synchrotron Spectrum of GRB Prompt Emission. Astrophys. J. 2018, 853, 43. [Google Scholar] [CrossRef]
- Bosnjak, Z.; Daigne, F. Spectral Evolution in Gamma-Ray Bursts: Predictions of the Internal Shock Model and Comparison to Observations. Astron. Astrophys. 2014, 568, A45. [Google Scholar] [CrossRef]
- Burgess, J.M. Time-resolved Analysis of Fermi Gamma-Ray Bursts with Fast- and Slow-cooled Synchrotron Photon Models. Astrophys. J. 2014, 784, 17. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, H. The Internal-collision-induced Magnetic Reconnection and Turbulence (ICMART) Model of Gamma-ray Bursts. Astrophys. J. 2011, 726, 90. [Google Scholar] [CrossRef]
- Panaitescu, A.; Meszaros, P. Gamma-Ray Bursts from Upscattered Self-absorbed Synchrotron Emission. Astrophys. J. 2000, 544, 17. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 497, L17. [Google Scholar] [CrossRef]
- Wang, K.; Dai, Z.G. GeV Emission during X-Ray Flares from Late Internal Shocks: Application to GRB 100728A. Astrophys. J. 2013, 772, 152. [Google Scholar] [CrossRef][Green Version]
- Yu, Y.W.; Dai, Z.G. X-Ray and High Energy Flares from Late Internal Shocks of Gamma-Ray Bursts. Astrophys. J. 2009, 692, 133. [Google Scholar] [CrossRef]
- Dai, Z.G.; Lu, T. Hydrodynamics of Relativistic Blast Waves in a Density-Jump Medium and Their Emission Signature. Astrophys. J. 2002, 565, L87. [Google Scholar] [CrossRef]
- Kumar, P.; Piran, T. Some Observational Consequences of Gamma-Ray Burst Shock Models. Astrophys. J. 2000, 532, 286. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Hydrodynamic Timescales and Temporal Structure of Gamma-Ray Bursts. Astrophys. J. 1995, 455, L143. [Google Scholar] [CrossRef]
- Blandford, R.; McKee, C. Fluid Dynamics of Relativistic Blast Waves. Phys. Fluids 1976, 19, 1130. [Google Scholar] [CrossRef]
- Sari, R.; Esin, A.A. On The Synchrotron Self-Compton Emission from Relativistic Shocks and Its Implications for Gamma-Ray Burst Afterglows. Astrophys. J. 2001, 548, 787. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Arimoto, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. Fermi Observations of High-Energy Gamma-Ray Emission from GRB 080916C. Science 2009, 323, 1688. [Google Scholar] [PubMed]
- Abdo, A.A.; Ackermann, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; Bastieri, D.; et al. Fermi observations of high-energy gamma-ray emission from GRB 080825C. Astrophys. J. 2009, 707, 580. [Google Scholar] [CrossRef][Green Version]
- Zhang, B. Open Questions in GRB Physics. Comptes Rendus Phys. 2011, 12, 206. [Google Scholar] [CrossRef]
- Derishev, E.V.; Kocharovsky, V.V.; Kocharovsky, V.V. Physical Parameters and Emission Mechanism in Gamma-Ray Bursts. Astron. Astrophys. 2011, 372, 1071. [Google Scholar] [CrossRef]
- Piran, T.; Sari, R.; Zou, Y.C. Observational Limits on Inverse Compton Processes in Gamma-Ray Bursts. Mon. Not. R. Astron. Soc. 2009, 393, 1107. [Google Scholar] [CrossRef]
- Racusin, J.L.; Oates, S.R.; Schady, P.; Burrows, D.N.; De Pasquale, M.; Donato, D.; Gehrels, N.; Koch, S.; McEnery, J.; Piran, T.; et al. Fermi and Swift Gamma-ray Burst Afterglow Population Studies. Astrophys. J. 2011, 738, 138. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Nakamura, T.; Yamazaki, R.; Inoue, A.K.; Ioka, K. Gamma-Ray Burst Formation Rate Inferred from the Spectral Peak Energy-Peak Luminosity Relation. Astrophys. J. 2004, 609, 935. [Google Scholar] [CrossRef]
- Amati, L.; Frontera, F.; Tavani, M.; Antonelli, A.; Costa, E.; Feroci, M.; Guidorzi, C.; Heise, J.; Masetti, N.; Montanari, E.; et al. Intrinsic Spectra and Energetics of BeppoSAX Gamma–Ray Bursts with Known Redshifts. Astron. Astrophys. 2002, 390, 81. [Google Scholar] [CrossRef]
- Yu, H.F.; Van Eerten, H.J.; Greiner, J.; Sari, R.E.; Bhat, P.N.; Von Kienlin, A.; Paciesas, W.S.; Preece, R.D. The Sharpness of Gamma-Ray Burst Prompt Emission Spectra. Astron. Astrophys. 2015, 583, 129. [Google Scholar] [CrossRef][Green Version]
- Guiriec, S.; Connaughton, V.; Briggs, M.S.; Burgess, M.; Ryde, F.; Daigne, F.; Meszaros, P.; Goldstein, A.; McEnery, J.; Omodei, N.; et al. Detection of a Thermal Spectral Component in the Prompt Emission of GRB 100724B. Astrophys. J. Lett. 2011, 727, L33. [Google Scholar] [CrossRef]
- Oganesyan, G.; Nava, L.; Ghirlanda, G.; Celotti, A. Detection of Low-energy Breaks in Gamma-Ray Burst Prompt Emission Spectra. Astrophys. J. 2017, 846, 137. [Google Scholar] [CrossRef]
- Daigne, F. Mochkovitch, R.The Expected Thermal Precursors of Gamma-Ray Bursts in the Internal Shock Model. Mon. Not. R. Astron. Soc. 2002, 336, 1271. [Google Scholar] [CrossRef]
- Ryde, F. Is Thermal Emission in Gamma-Ray Bursts Ubiquitous? Astrophys. J. Lett. 2005, 625, L95. [Google Scholar] [CrossRef]
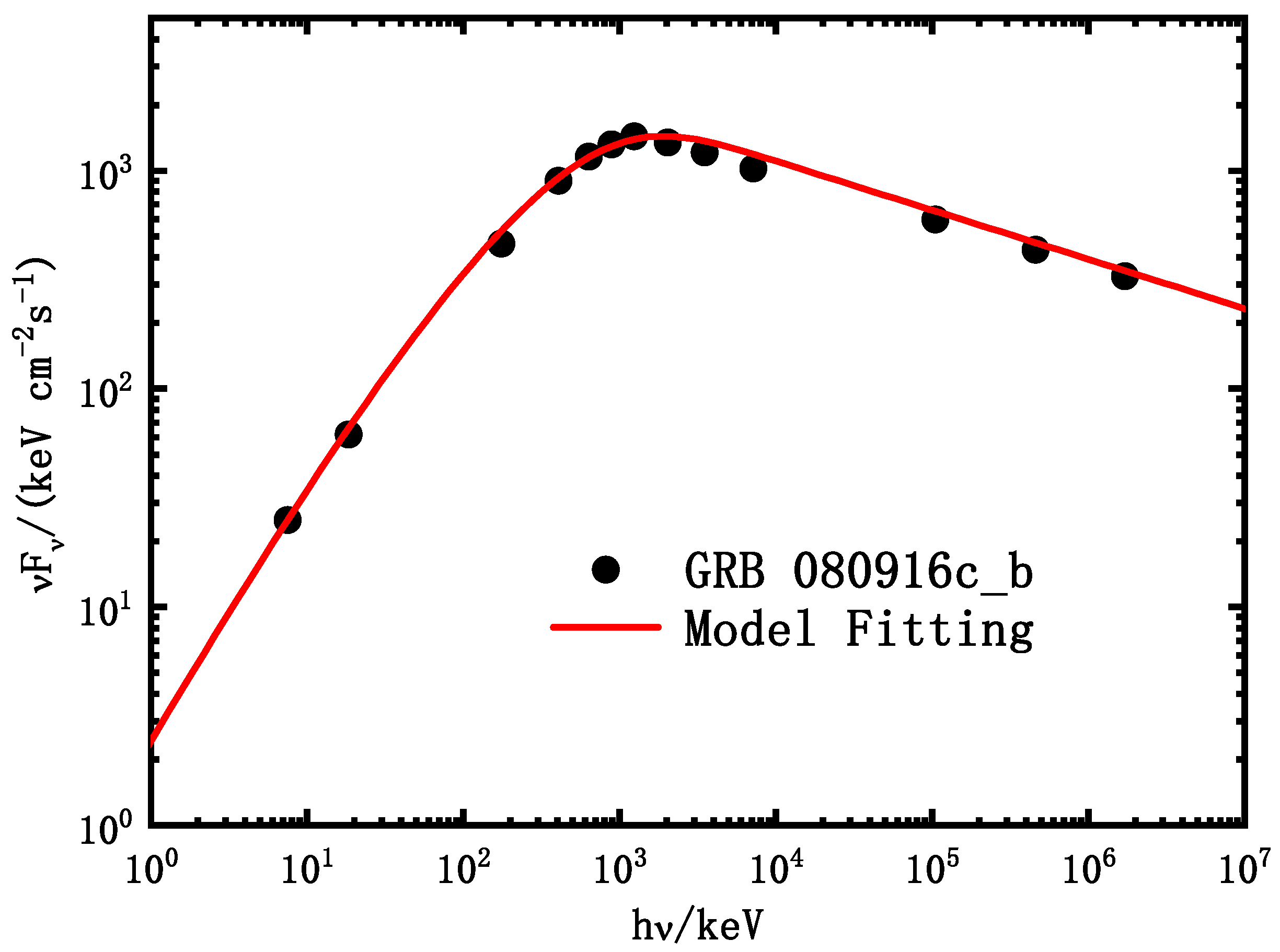
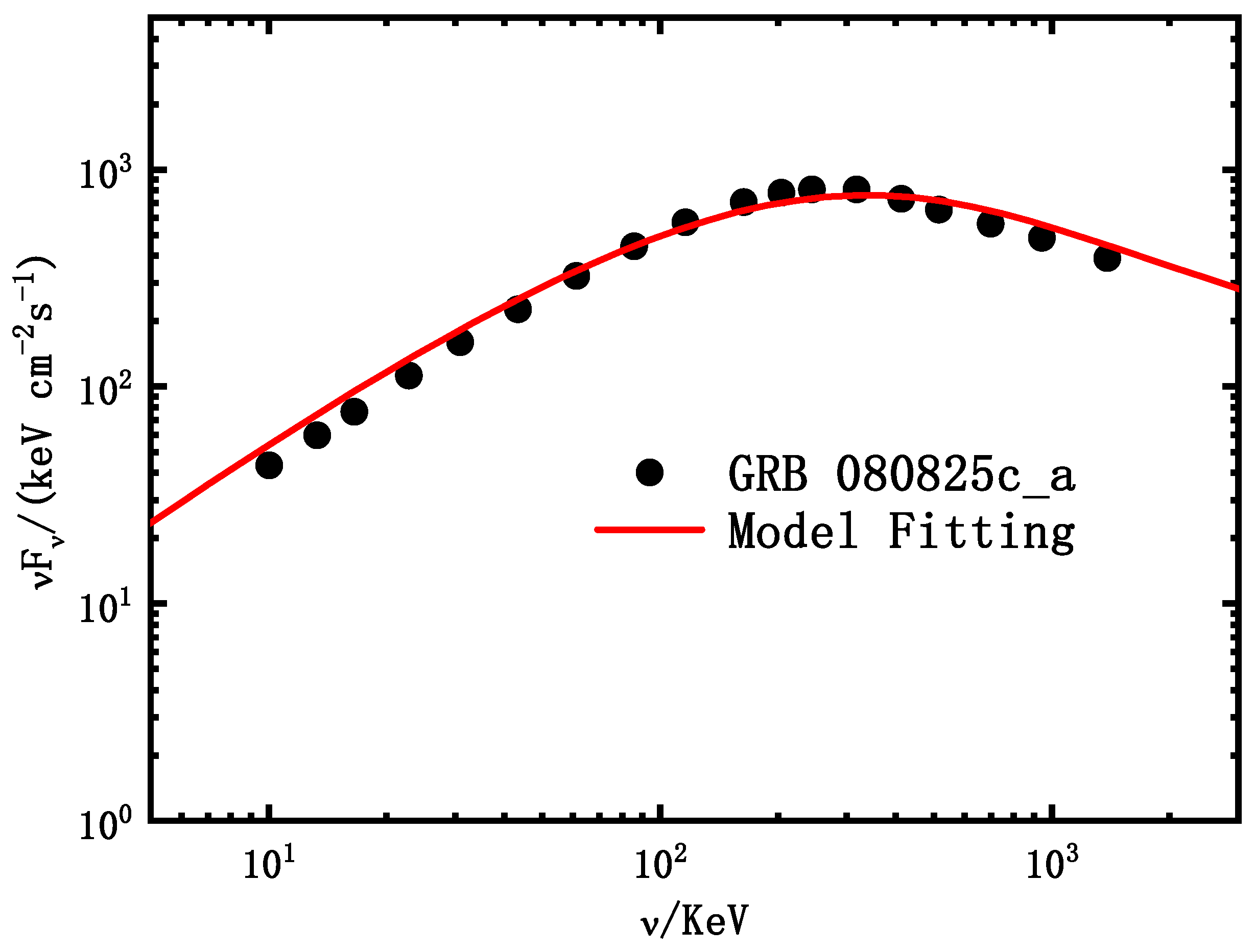
| Parameters | Symbol | GRB 080916c | GRB 080825c |
|---|---|---|---|
| Redshift | z | 4.35 | 1 |
| Index of electron injection rate | q | 0 | 2 |
| redefined time interval (s) | 0.1 | 0.1 | |
| Shock cross time (s) | 3 | 3 | |
| Kenetic luminosity (erg/s) | 3.3 | 1.2 | |
| Bulk Lorentz factor of region 1 | 146 | 255 | |
| Bulk Lorentz factor of region 2 | |||
| Electron injection index | p | 2.5 | 3.2 |
| Electron equipartition factor | 0.3 | 0.3 | |
| Magnetic equipartition factor | 0.3 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Dai, Z.-G. The Low-Energy Spectral Index of Gamma-ray Burst Prompt Emission from Internal Shocks. Galaxies 2021, 9, 68. https://doi.org/10.3390/galaxies9030068
Wang K, Dai Z-G. The Low-Energy Spectral Index of Gamma-ray Burst Prompt Emission from Internal Shocks. Galaxies. 2021; 9(3):68. https://doi.org/10.3390/galaxies9030068
Chicago/Turabian StyleWang, Kai, and Zi-Gao Dai. 2021. "The Low-Energy Spectral Index of Gamma-ray Burst Prompt Emission from Internal Shocks" Galaxies 9, no. 3: 68. https://doi.org/10.3390/galaxies9030068
APA StyleWang, K., & Dai, Z.-G. (2021). The Low-Energy Spectral Index of Gamma-ray Burst Prompt Emission from Internal Shocks. Galaxies, 9(3), 68. https://doi.org/10.3390/galaxies9030068







