Abstract
Recently, microquasar jets have aroused the interest of many researchers focusing on the astrophysical plasma outflows and various jet ejections. In this work, we concentrate on the investigation of electromagnetic radiation and particle emissions from the jets of stellar black hole binary systems characterized by the hadronic content in their jets. Such emissions are reliably described within the context of relativistic magneto-hydrodynamics. Our model calculations are based on the Fermi acceleration mechanism through which the primary particles (mainly protons and electrons) of the jet are accelerated. As a result, a small portion of thermal protons of the jet acquire relativistic energies, through shock-waves generated into the jet plasma. From the inelastic collisions of fast (non-thermal) protons with the thermal (cold) ones, secondary charged and neutral particles (pions, kaons, muons, -particles, etc.) are created, as well as electromagnetic radiation from the radio wavelength band to X-rays and even very high energy gamma-rays. One of our main goals is, through the appropriate solution of the transport equation and taking into account the various mechanisms that cause energy losses to the particles, to study the secondary particle concentrations within hadronic astrophysical jets. After assessing the suitability and sensitivity of the derived (for this purpose) algorithms on the Galactic MQs SS 433 and Cyg X-1, as a concrete extragalactic binary system, we examine the LMC X-1 located in the Large Magellanic Cloud, a satellite galaxy of our Milky Way Galaxy. It is worth mentioning that, for the companion O star (and its extended nebula structure) of the LMC X-1 system, new observations using spectroscopic data from VLT/UVES have been published a few years ago.
1. Introduction
In recent years, astrophysical magnetohydrodynamical flows in Galactic, extragalactic microquasars (MQs), and X-ray binary systems (XRBs) have been modelled with the purpose of studying their multi-messenger emissions, for example, neutrinos, gamma-rays, and so forth. [1,2,3]. For the detection of such emissions, extremely sensitive detector tools are in operation for recording their signals reaching the Earth like IceCube, ANTARES, KM3NeT [4,5,6], and so forth. Modelling offers good support for future attempts to detect radiative multiwavelength emissions and neutrino emission, while in parallel, several numerical simulations may be performed towards this aim [7,8,9].
Microquasars (or generally XRBs) are binary systems consisting of a compact stellar object (usually a black hole or a neutron star) and a donor (companion) star [10]. Mass from the companion star overflows through the system’s Langrangian points to the equatorial region of the compact object gaining angular momentum and, thus, forming an accretion disc of very high temperature gas and matter. This mass expelling could be mainly due to a concentrated stellar wind [11,12,13]. Consequently, a portion of the disc’s matter is being collimated by the system’s magnetic field (initially it is attached to the rotating disc) and is ejected perpendicular to the disc in two opposite directions [14] forming the system’s jets. The jets are detectable from the Earth even when the system’s distance is too large which is due to the relativistic velocities they acquire [15,16,17] combined with Doppler effects when they are headed towards the Earth. It has been shown that the kinetic luminosity coming from astrophysical microquasar jets constitutes a substantially large part of the total galactic cosmic radiation [18]. Moreover, it has been proved that microquasar binary systems that do not produce thermal jets are more likely to be neutrino and gamma-ray emission sources [19].
The most well-studied microquasar systems include the Galactic X-ray binaries SS 433, Cyg X-1, Cyg X-3, and so forth. [20,21,22], while from the extragalactic systems we mention the LMC X-1, LMC X-3 located in the neighbouring galaxy of the Large Magellanic Cloud [23], and the Messier X-7 in the Messier 33 galaxy [24]. Their respective relativistic jets are emission sources in various wavelength bands and high-energy neutrinos. In this work, we focus our study on the extragalactic binary system LMC X-1 with the purpose to determine its gamma-ray and neutrino emissions produced through the processes and mechanisms that are about to be discussed below. Concerning the LMC X-1 system, new observational results have been recorded, shedding more light on its unique spectral and environmental characteristics [25,26] and thus providing a more solid base for LMC X-1 microquasar a fact that motivated our present study which furthermore aims to compare them with simulated emissions from the Galactic SS 433 and Cyg X-1 systems.
The SS 433 microquasar has definitely hadronic content in its jets verified from observations of various spectra. For detailed studies of this system based on hadronic modelling of its jets, the reader is referred to the Refs. [7,8,9] and references therein. Radiative transfer calculations may be performed at every point inside the jet for a range of frequencies (energies), at every location [27] providing the relevant emission and absorption coefficients. Line-of-sight integration, afterwards, provides synthetic images of -ray emission, at the energy-window of interest [27,28].
In the present work, we adopt as main mechanisms producing high energy gamma-rays and neutrinos in MQs jets the proton-proton (p-p) and the proton-photon (p-) interactions taking place within the hadronic jets, see [3] and the references therein. Furthermore, it is worth mentioning that, a photon field emanating from the companion star in many X-ray binaries may cause -ray absorption of photons with energies in the same range of those emitted from the donor star [29,30,31]. This absorption becomes important when the distance from the central object of the gamma-ray production region is of the same order with the binary system’s separation, that is, the distance between the two stellar objects [29,30].
Studies of the concentrations of jet particles whose interactions lead to neutrino and gamma-ray production need to take into account various energy loss and decay mechanisms that occur due to several hadronic processes, particle acceleration and particle scattering [1,2]. In the known fluid approximation, macroscopically the jet matter behaves as a fluid collimated by the magnetic field. At a smaller scale, consideration of the kinematics of the jet plasma becomes necessary for treating shock acceleration effects. In the model employed in this work [1,2], the jets are considered to be conic along the z-axis (ejection axis) with a radius , where is its half-opening angle [32]. The jet radius at its base, , is given by , where is the distance of the jet’s base to the central compact object.
In the rest of the paper, after a brief description (Section 2) of the interaction chains leading to neutrino and gamma-ray emission, we solve the steady-state transfer equation (Section 3) to determine the energy distributions of the primary and secondary jet particles. Then (Section 4), the obtained predictions for high-energy neutrino and gamma-ray production, for the LMC X-1 MQ system, are presented and compared with those obtained for the Galactic SS 433 and Cyg X-1 systems. Finally (Section 5), we summarize the main conclusions extracted from the present study.
2. Interaction Mechanisms Inside the Jet
According to the jet-accretion speculation, only 10% of the system’s Eddington luminosity [33] , M in solar masses, is transferred to the jet for acceleration and collimation through the magnetic field B given by the equipartition of magnetic and kinetic energy density of the jet as [1,2,27,28].
By assuming the one-zone approximation [34], we consider a small portion of the hadrons (mainly protons) equal to to be accelerated in a zone from to with the rate [35] according to the second-order Fermi acceleration mechanism, where c denotes the speed of light, e the electron’s charge, the proton’s energy, and the acceleration efficiency. The particles are accelerated to nearly relativistic velocities [36] resulting in a power-law distribution given in the jet’s rest frame by [GeVcm], where is a normalization constant. Model parameters, such as the length of the acceleration zone, and system parameters for SS 433, Cygnus X-1 and LMC X-1, are tabulated in Table 1.

Table 1.
Parameters describing geometric characteristics of the well-studied SS 433, Cygnus X-1 and the extragalactic LMC X-1 binary systems.
In general, the main interactions of the relativistic protons include those with the stellar winds [29,30,37,38], the radiation fields composed of internal and external emission sources [29,30,39], as well as the cold hadronic matter of the jet. In this work, we consider the last two cases of interactions because they are the most important. In other words, we assume that neutrino and gamma-ray emissions are products of reaction chains that are caused by the p-p and p- interactions inside the jet. The KM3NeT, ANTARES, and IceCube are prominent examples of undersea water and under-ice detectors that are able to detect those neutrinos that reach the Earth [4,5,6].
The first of the aforementioned reaction chains begins with the inelastic p-p collisions of the relativistic protons with the cold ones inside the jet, which generate neutral pions () and charged pions () according to the following reactions
with and being the particle multiplicities that depend on the proton energy [40].
Besides p-p interactions, pions are generated due to proton-photon (p-) interaction through photo-pion production
In these p- interactions, photons originate from the accretion disc or they are products of the synchrotron mechanism. In the reaction chains (1) and (2), the neutral pions decay into gamma-ray photons as
while the charged pions decay into muons and neutrinos in one or two steps as
Thus, the produced muons subsequently decay to electrons (or positrons ) and anti-neutrinos (or neutrinos). These are the main reactions feeding the neutrino and gamma-ray production channels in the p-p and p- mechanisms employed in our model.
All particles that take part in the neutrino and gamma-ray production processes lose energy while travelling along the acceleration zone, which could be due to different mechanisms, as it is illustrated in Figure 1, Figure 2 and Figure 3 for the systems SS 433, Cyg. X-1 and LMC X-1. At first, the particles (p, , , etc.) can be subjected to adiabatic energy losses due to jet expansion along the ejection axis with a rate depending linearly on the jet’s bulk velocity [41]. Another important cooling mechanism, that depends on the cold proton density inside the jet, is due to inelastic collisions of the accelerated particles with the cold ones. The inelastic cross section for the p-p scattering is given by [7,8,9,42]
where , with in GeV and GeV being the threshold for the production of a single neutral pion. Respectively, for pion-proton inelastic scattering, it holds that [43]
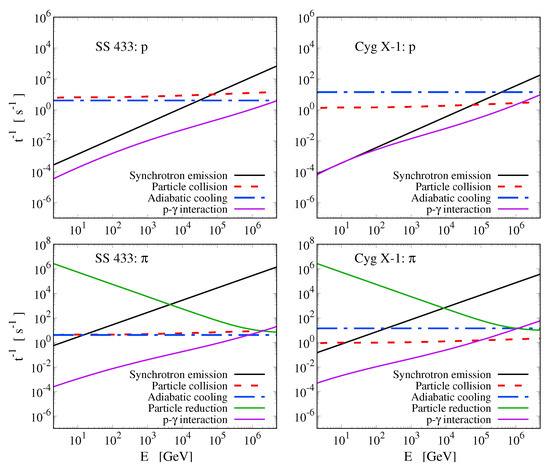
Figure 1.
Cooling rates for relativistic protons and pions () produced at the base of the jet after the p-p and p- collision processes take place in SS 433 (first column) and Cygnus X-1 (second column). Those mechanisms include synchrotron emission (solid lines), particle collision (dashed lines), adiabatic cooling (dotted lines), p- interactions, as well as the particle reduction rate which includes the decay and escape rate of the particles (dotted-dashed lines).
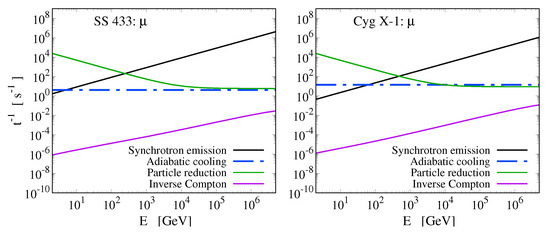
Figure 2.
Cooling rates for muons () produced in the jets of the systems SS 433 and Cygnus X-1. Similarly to the electron case and because of their size, muons also lose energy due to Inverse Compton scattering.
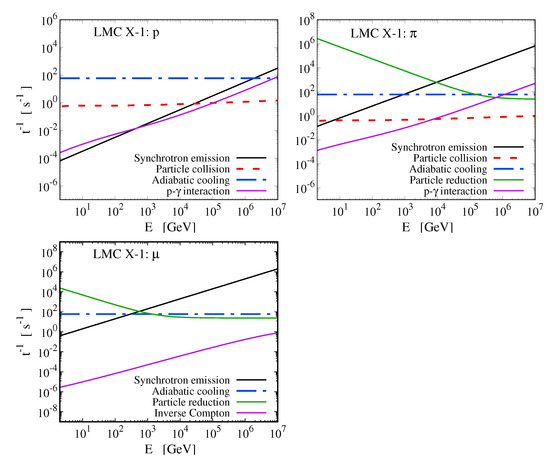
Figure 3.
Respective cooling rates for the system of our interest LMC X-1.
In addition, the particles that are accelerated by the magnetic fields emit synchrotron radiation. Thus, they gradually lose part of their energy with a rate that strongly depends on the magnetic field and the particle’s energy.
Furthermore, protons and pions interact with radiation fields coming from internal or external regions of the jet, such as the system’s accretion disc [44], as well as the synchrotron-emitting particles themselves, which leads to partial energy loss. Lighter particles, mainly electrons, transfer part of their energy to low-energy photons via Inverse Compton scattering [45]. In this work, we consider that muons may also be subjected to an Inverse Compton energy loss mechanism due to their size and leptonic nature. This assumption has been made in previous studies as well [2]. However, such contributions can be ignored compared to those mentioned above.
3. Solution of the Transfer Equation
The steady-state transfer equation, which fulfills the conditions mentioned above, is given by [8,37,51]
where denotes the particle distribution in units of GeVcm, while is the particle source (or injection) function giving the respective production rate (in GeVcms). Concerning the energy loss rate , all the cooling mechanisms discussed are being represented as it is evident from the definition .
For each particle, the decay rate is added to the particle escape rate from the jet according to the relation: . The escape rate is approximated by , where stands for the ending of the acceleration zone. It is worth mentioning that, inside the jet the particle distributions are rather independent of time, so that the steady-state approximation usually applied in the transfer equation and leads to Equation (8) is a good approximation. This is also the case for the purposes of our present work, while contributions of other terms of the full transfer equation are planned to be examined in future works.
The general solution of the differential Equation (8) is given by [52,53,54]
where
In Figure 4, we plot the calculated distributions of relativistic electrons and protons accelerated by shock-waves through the Fermi mechanism for three different values of the proton-to-lepton ratio in the electron case and three different values of the distance to the central object in the proton case. The model with corresponds to purely hadronic jet. Obviously, the electron energy distributions decrease as increases. Moreover, in the case of LMC X-1 system are significantly larger compared to those of the Cygnus X-1 MQ. Evidently, in order to calculate the neutrino and gamma-ray emissivities, one needs to calculate first the energy distributions of all particles involved in the reaction chain (see Section 2). These distributions are obtained in the next subsection.
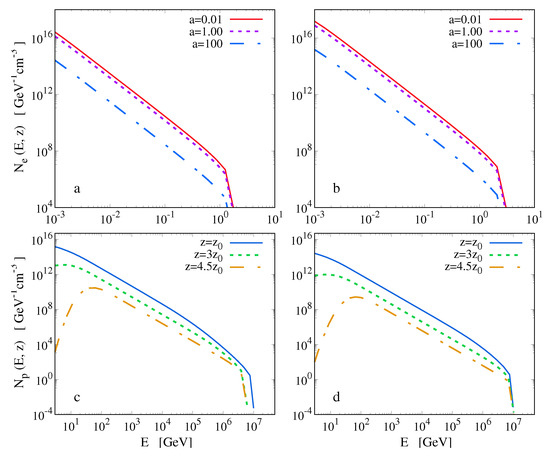
Figure 4.
Energy distributions for relativistic electrons and protons produced in Cygnus X-1 (a,c) and LMC X-1 (b,d). In the electrons’ case, the solid lines refer to the proton-to-electron ratio , the dashed lines to , and the dashed-dotted ones describe electron distributions assuming that (i.e., they correspond to a purely hadronic model). For protons, the solid lines refer to particle production at the jet’s base , while the dashed or dotted-dashed ones refer to different distances to the central object, covering the length of the acceleration zone.
3.1. Particle Injection Functions
3.1.1. Relativistic Protons Injection Function
In previous works [1,38,55], the appropriate injection function for the relativistic protons produced by the Fermi acceleration mechanism was assumed to be of power-law type with exponent [56,57]. In the jet’s rest frame, this power-law translates to the following expression
where is a normalization constant calculated through the total luminosity that is carried by the protons (or electrons) inside the jet (see Appendix A), where GeV is the minimum proton energy that is sufficient and necessary for the Fermi mechanism to occur. The maximum energy is calculated by equating the particle acceleration rate with the total energy loss rate, namely, . For the binary systems of our interest, this is approximated as GeV. The dependence on z is due to particle conservation enforced on the respective current density [58]. Transformation of the source function of Equation (10) to the observer’s reference frame gives [8,9,59]
where responds to the jet’s Lorentz factor and is the angle between the jet’s ejection axis and the line of sight.
3.1.2. Pion Energy Distribution
The pion source function calculation requires the fast proton distribution, as well as the p-p collision rate along with the pion spectra produced by each one of these collisions as
where . In the latter integral, denotes the pion mean number produced per p-p collision given by [42]
where , , , and . Additionally, is the cold proton density of the jet written as
where is the cold proton Lorentz factor.
In the case of the p- interaction mechanism, for the produced pions, we have
where is the p- collision frequency (see Appendix B). In addition, is the mean number of positive or negative pions produced per p- collision. We have , where the mean inelasticity, , and .
3.1.3. Muon Spectra from Pion Decay
For the muon energy distribution, both the mean right-handed and the mean left-handed muon numbers per pion decay are required for obtaining the total injection function. According to the CP invariance and provided that , it holds that [60]
where and represent the positive and negative right (or correspondingly left) handed muon spectra, respectively (see Appendix C). In Equation (16), we have used , , and the Heaviside function. Additionally, the pion decay rate is given by s, which implies that the pion distribution is important for the muon distribution calculation.
4. Results and Discussion
4.1. Neutrino Energy-Spectra from Pion and Muon Decay
After obtaining the energy distributions of the particles discussed above, one is able to estimate the total number of neutrinos produced directly from pion decay, as well as from muon decay. Thus, the total emissivity contains both contributions, as
The first term represents the neutrino injection originating from pion decay as
where , while the second term gives
with . In the latter equation, the muon decay rate depends on their energy as follows s. In addition, . From the four different integrals of the latter summation, the first and second represent the left-handed muons of positive and negative charge, respectively, while the third and fourth stand for the corresponding right-handed ones.
4.2. Gamma-Ray Emissivity for GeV
In this work, we assumed that gamma-ray production is mainly due to neutral pions decay, which in turn are mainly products of p-p inelastic collisions. The respective gamma-ray spectra have been calculated for photons of energy through the expression [42]
where , , and . In addition, we have TeV). These results are consistent with proton energies in the range TeV TeV. Besides , Equation (20) considers also the contribution of mesons decay, which represents approximately the 25% when .
In the energy range of our interest GeV, the gamma-ray emissivity, produced at a distance z from the compact object along the jet’s ejection axis, is given by
(in units of GeVcms). For GeV, the delta-function approximation is employed.
4.3. Neutrino and -ray Intensity Calculations
By introducing the calculated rates for the cooling mechanisms of particles that lead to neutrino and gamma-ray production into the transfer equation discussed previously, see Equation (8), along with the corresponding injection functions, where we are able to calculate the particle energy distributions. These results are shown in Figure 5 which includes graphs corresponding to the charged pions produced by the p-p and p- interactions and the muons that result from the pion decays.
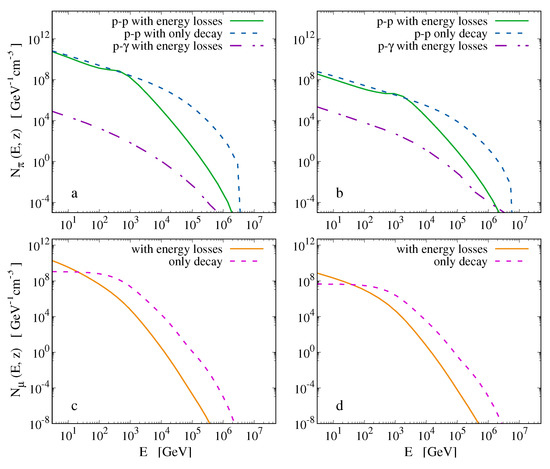
Figure 5.
Energy distributions for pions () (a,b) and muons () (c,d) produced in Cygnus X-1 (a,c) and LMC X-1 (b,d). Particle production takes place at , where evident is the effect of the energy-loss interactions to the particle distributions (solid lines) in comparison to the case where only decay occurs (dashed lines).
We consider the aforementioned mechanisms and interactions taking place inside the hadronic relativistic jets of the extragalactic binary system LMC X-1 located in our galaxy-neighbor LMC (Large Magellanic Cloud) at a large distance from the Earth (about 48 kpc) [23]. The energy spectra of the produced high-energy neutrinos and gamma-rays are, then, numerically calculated. For the sake of comparison, in Figure 5, the corresponding results for the galactic Cygnus X-1 system are also shown.
In the next stage, integration over the acceleration zone gives the total intensity as [1,2]
All the calculations were performed through the development of a C-code (that employs Gauss-Legendre numerical integration of the GSL library) and the use of the parameter values listed in Table 1 mostly describing geometric characteristics of the systems of interest.
As we mentioned, firstly we calculated the fast proton distributions for three different distances z from the central object for the binary systems Cygnus X-1 and LMC X-1 as illustrated in the graphs c and d, respectively, of Figure 4. It is evident that the total particle density production decreases as we move closer to the ending of the acceleration zone even though the (average) particle energy increases.
In Figure 5 graphs a and b, we show the energy distributions for pions that have suffered energy losses caused by various mechanisms, such as synchrotron radiation emission, collisions with the rest of the jet matter, and so forth [1,2,55]. For comparison, we also plot the respective distributions of particles that do not lose energy at all. We notice that, in the energy range – GeV, the particle distributions (pions in this case) appeared reduced by (99.720–99.999)%, for the system Cygnus X-1, and by (95.390–99.997)% for LMC X-1, due to energy loss mechanisms. This indicates the significant effect caused by the cooling mechanisms on the total particle distributions.
Furthermore, the cooling processes may affect the shape of the power-law distributions which become somewhat steeper (the index of the power-law changes) if the energy losses are significant enough [61]. In addition, we notice the dominant contribution of the p-p process compared to the p- one. The same conclusion may be extracted from the graphs c and d of Figure 5 for the muon distributions. We furthermore observe that the cooling rate characteristics are reflected upon the particle distributions as is implied from the deviation of the two curves in the pion and muon case. The starting point of the deviation coincides with the beginning of the dominance of the synchrotron mechanism over the particle decay. Further, the solid curve (with energy losses) compared to the dashed one (only decay) shows faster decrease [1,2,55].
Moreover, in Figure 4 and Figure 5, we see that there are no significant differences between results obtained for these two binary systems. This is due to the fact that their black hole masses have similar magnitudes. The parameter, however, that has the strongest impact is the jet’s half-opening angle , which, roughly speaking, describes the degree of the jet’s collimation. This is directly connected with the system’s magnetic field, which is responsible for the collimation represented by the angle .
After calculating all the necessary distributions, the neutrino and gamma-ray emissivities and the corresponding intensities and fluxes (weighted by the energy squared) are readily obtained. These results are illustrated in Figure 6 and Figure 7 along with the sensitivities of the most prominent detectors suited for such high-energy observations. It should be mentioned that gamma-ray fluxes from the LMC X-1 have not been detected yet, but the sensitivities of the next-generation detectors (like the IceCube-Gen2, CTA, etc.) are quite promising for performing relevant measurements in the near future.
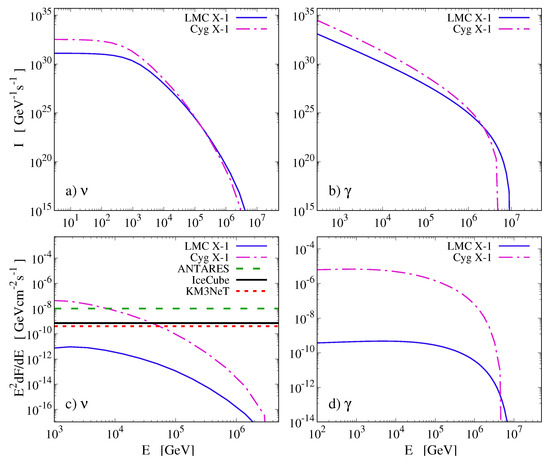
Figure 6.
Neutrino (a,c) and gamma-ray (b,d) intensities and their respective differential fluxes produced by pion () decay taking place at the base of the jet of the binary system LMC X-1 (solid lines), as well as the well-studied system Cygnus X-1 (dashed lines). Additionally, the sensitivities of detectors ANTARES [64], IceCube [65] and KM3NeT [66] are presented in graph c, and the respective sensitivities of MAGIC, HESS, and the foreseen sensitivity of the next-generation Cherenkov Telescope Array (CTA) [67] are also presented in graph d. In graph d, the differential gamma-ray flux points for Cyg X-1, as observed by the MAGIC telescope, are also presented for the sake of comparison with the calculations.
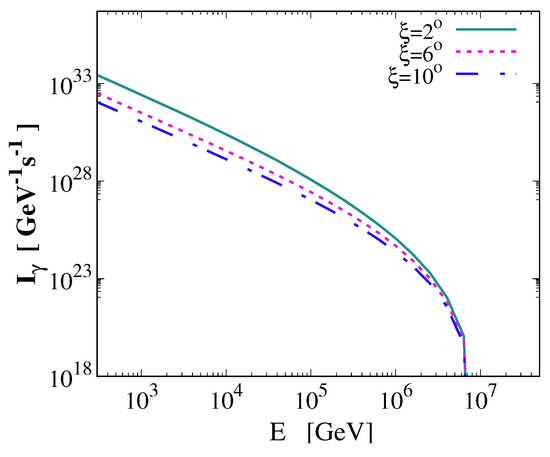
Figure 7.
Calculated gamma-ray intensity emanating from the LMC X-1 (for ) for three different values of the jet’s half-opening angle (for details see the text).
Concerning Cygnus X-1, in Figure 6 (graph d), we compare our results with the observational data coming from the MAGIC telescope [17,62] and conclude that for – GeV, the differential gamma-ray flux is of the order of – GeVcms (i.e., about two to three orders of magnitude smaller). One of the possible reasons of this discrepancy could be the gamma-ray absorption of photons with an energy in this range caused by a strong photon field emanated by the system’s companion star (not taking into account in our present calculations) that will also be featured in future studies through the calculation of the pair-production optical depth of Equation (A.1) in [30]. This absorption becomes important when the distance from the gamma-ray production region up to the central object is smaller (or about equal) to the system’s binary separation (distance between the two stellar objects) [29,30].
For the LMC X-1 system, our results show that the increase of the half-opening angle leads to a decrease in the gamma-ray production, which is an expected result since the p-p collision rate drops with the jet’s expansion, as shown in Figure 7.
Before closing, it is worth noting that, even though high-energy neutrinos coming from binary system LMC X-1 has not been detected yet, our present calculations may guide planned next-generation detectors as, for example, the observatory detector IceCube-Gen2, an IceCube expansion that is 10 times larger and has five times the effective area of the latter. Such a tool may make source identification and neutrino detection much more promising [63].
Finally, because our theoretical results are the first of this type, they would be useful for comparisons with future calculations that may come out within the context of other models and microquasar jet’s scenarios.
5. Summary and Conclusions
During the last few decades, the structure and evolution of relativistic astrophysical plasma outflows (jets), and specifically those connected to compact cosmic structures, became research subjects of intense interest. Towards this aim, a great research effort, experimental, theoretical, and phenomenological is absorbed by various high-energy phenomena, including production and terrestrial detection of high-energy cosmic radiation and neutrinos, originating from Galactic and extragalactic sources heading towards the Earth. In particular, we mentioned the jets of very large scale ejected from the galaxy’s quasar systems involving supermassive black holes at the central region (AGN) and those of much smaller scale involving stellar mass black holes and a companion star, known as micro-quasars and X-ray binary systems.
In this work, we concentrated on the latter class, the two-body systems consisting of a central object (usually a stellar mass black hole) and a companion star often of O-type or B-type main sequence stars. The former absorbs mass from the latter, forming an accretion disc of gas and matter which emits X-ray radiation due to very high temperatures prevailing in the area of the accretion disk and black hole. The jets are formed when the system’s magnetic field collects matter that is ejected away from the system in a collimated and accelerated bulk-like plasma flow.
The mass outflow can acquire relativistic velocities and is expelled perpendicular to the disc’s surface. In many models, these jets are treated magnetohydrodynamically by assuming various reliable approximations. In the present work, we considered the jet’s matter to be mainly hadronic, with a portion of it accelerated through shock-waves to relativistic velocities. From the inelastic collision of relativistic protons on the cold ones (p-p interactions mechanism), secondary neutral and charged particles (pions, kaons, muons, etc.) are produced. Such secondary particles are also produced through the proton-photon inelastic collisions channel (photopion production mechanism). These pions decay leading to high-energy neutrino and gamma-ray emissions.
One of our main goals was the calculation of the energy-spectra of high energy neutrino and gamma-ray produced inside such astrophysical jets. As concrete examples, we have chosen the Galactic X-ray binaries Cygnus X-1 and SS 433 system, as well as the extragalactic LMC X-1 binary system in order to simulate their neutrino and gamma-ray intensities emitted. For the observation of such high-energy cosmic radiations and particle (neutrino) emissions, extremely sensitive detection instruments are operating at the Earth like the IceCube detector (deep under the ice at South Pole), the ANTARES, KM3NeT (underwater in the Mediterranean sea), the CTA, and so forth, and next-generation detectors have been designed as the IceCube-Gen2. The reliable theoretical predictions of the present work for the LMC X-1 system, like the primary and secondary particles’ distributions inside its jets, the estimation of the produced intensities as functions of the energy for different half-opening angle values of its jets, as well as the other findings may offer guidance and support to the aforementioned high-energy cosmic gamma-ray and neutrino detectors.
Author Contributions
Conceptualization, O.K. and I.S.; methodology, O.K.; software, T.P.; validation, O.K. and I.S.; formal analysis, T.P.; investigation, T.P. and O.K.; writing—original draft preparation, T.P. and O.K.; writing—review and editing, O.K. and I.S.; visualization, T.P. and O.K.; supervision, O.K. and I.S.; project administration, O.K. and I.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
There is no data used in this paper.
Acknowledgments
This research is co-financed (O.T.K) by Greece and the European Union (European Social Fund-ESF) through the Operational Programme “Human Resources Development, Education, and Lifelong Learning 2014–2020” in the context of the project (MIS5047635). Th.V.P wishes to thank T.S. Kosmas for fruitful discussions during my stay in the Dept. of Physics, University of Ioannina.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Normalization Constant
The normalization constant for the relativistic proton source function depends on the lower and upper limit of their energy as follows
The above result is calculated through the total luminocity carried by the protons that is given by
Appendix B. p-γ Collision Frequency
The p- collision frequency is given by
where and the respective cross-section
The radiation density consists of the synchrotron photons produced by both the relativistic electrons as well as the protons and an X-ray distribution for 2 keV 100 keV originated in a corona that surrounds the inner accretion disc. It holds
Appendix C. Right and Left-Handed Muon Spectra
The right-handed positive and negative muon spectra produced by pion decay are
where and . According to CP invariance, the number of produced by the decay is the same as the produced by the decay. Therefore, as the pion energy distribution refers to the sum of both and distributions, it is . Similarly, it holds the same for the negative right-handed muons.
References
- Reynoso, M.M.; Romero, G.E.; Christiansen, H.R. Production of gamma rays and neutrinos in the dark jets of the microquasar SS433. Mon. Not. R. Astron. Soc. 2008, 387, 1745–1754. [Google Scholar] [CrossRef][Green Version]
- Reynoso, M.M.; Romero, G.E. Magnetic field effects on neutrino production in microquasars. Astron. Astrophys. 2009, 493, 1–11. [Google Scholar] [CrossRef]
- Romero, G.E.; Boettcher, M.; Markoff, S.; Tavecchio, F. Relativistic Jets in Active Galactic Nuclei and Microquasars. Space Sci. Rev. 2017, 207, 5–61. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Searches for Sterile Neutrinos with the IceCube Detector. Phys. Rev. Lett. 2016, 117, 071801. [Google Scholar] [CrossRef]
- Aartsen, M.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Al Samarai, I.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Neutrino emission from the direction of the blazar TXS 0506+056 prior to the IceCube-170922A alert. Science 2018, 361, 147–151. [Google Scholar] [CrossRef]
- Adrián-Martínez, S.; Ageron, M.; Aharonian, F.; Aiello, S.; Albert, A.; Ameli, F.; Anassontzis, E.; Andre, M.; Androulakis, G.; Anghinolfi, M.; et al. Letter of intent for KM3NeT 2.0. J. Phys. G Nucl. Part Phys. 2016, 43, 084001. [Google Scholar] [CrossRef]
- Smponias, T.; Kosmas, O.T. High Energy Neutrino Emission from Astrophysical Jets in the Galaxy. Adv. High Energy Phys. 2015, 2015, 921757. [Google Scholar] [CrossRef]
- Smponias, T.; Kosmas, O.T. Neutrino Emission from Magnetized Microquasar Jets. Adv. High Energy Phys. 2017, 2017, 4962741. [Google Scholar] [CrossRef]
- Kosmas, O.; Smponias, T. Simulations of Gamma-Ray Emission from Magnetized Microquasar Jets. Adv. High Energy Phys. 2018, 2018, 9602960. [Google Scholar] [CrossRef]
- Mirabel, I.F.; Rodríguez, L.F. Sources of Relativistic Jets in the Galaxy. Annu. Rev. Astron. Astrophys. 1999, 37, 409–443. [Google Scholar] [CrossRef]
- Friend, D.B.; Castor, J.I. Radiation driven winds in X-ray binaries. Astrophys. J. 1982, 261, 293–300. [Google Scholar] [CrossRef]
- Hanke, M.; Wilms, J.; Nowak, M.A.; Pottschmidt, K.; Schulz, N.S.; Lee, J.C. Chandrax-ray spectroscopy of the focused wind in the cygnus X-1 system. I. the nondip spectrum in the low/hard state. Astrophys. J. 2008, 690, 330–346. [Google Scholar] [CrossRef]
- Hell, N.; Miškovičová, I.; Brown, G.V.; Wilms, J.; Clementson, J.; Hanke, M.; Beiersdorfer, P.; Liedahl, D.; Pottschmidt, K.; Porter, F.S.; et al. Low charge states of Si and S in Cygnus X-1. Phys. Scr. 2013, T156, 014008. [Google Scholar] [CrossRef]
- Falcke, H.; Biermann, P. The jet-disk symbiosis. 1. Radio to X-ray emission models for quasars. Astron. Astrophys. 1994, 293, 665–682. [Google Scholar]
- Aharonian, F.; Akhperjanian, A.G.; Aye, K.M.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Berghaus, P.; Bernlöhr, K.; Boisson, C.; et al. Discovery of Very High Energy Gamma Rays Associated with an X-ray Binary. Science 2005, 309, 746–749. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Asensio, M.; Baixeras, C.; Barrio, J.A.; Bartelt, M.; Bartko, H.; et al. Variable Very-High-Energy Gamma-Ray Emission from the Microquasar LS I +61 303. Science 2006, 312, 1771–1773. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Very High Energy Gamma-Ray Radiation from the Stellar Mass Black Hole Binary Cygnus X–1. Astrophys. J. 2007, 665, L51–L54. [Google Scholar] [CrossRef]
- Heinz, S.; Sunyaev, R. Cosmic rays from microquasars: A narrow component to the CR spectrum? Astron. Astrophys. 2002, 390, 751–766. [Google Scholar] [CrossRef]
- Levinson, A.; Waxman, E. Probing Microquasars with TeV Neutrinos. Phys. Rev. Lett. 2001, 87, 171101. [Google Scholar] [CrossRef]
- Romney, J.D.; Schilizzi, R.T.; Fejes, I.; Spencer, R.E. The Inner Beams of SS 433. Astrophys. J. 1987, 321, 822. [Google Scholar] [CrossRef]
- Reid, M.J.; McClintock, J.E.; Narayan, R.; Gou, L.; Remillard, R.A.; Orosz, J.A. The trigonometric parallax of cygnus X-1. Astrophys. J. 2011, 742, 83. [Google Scholar] [CrossRef]
- Kantzas, D.; Markoff, S.; Beuchert, T.; Lucchini, M.; Chhotray, A.; Ceccobello, C.; Tetarenko, A.J.; Miller-Jones, J.C.A.; Bremer, M.; Garcia, J.A.; et al. A new lepto-hadronic model applied to the first simultaneous multiwavelength data set for Cygnus X–1. Mon. Not. R. Astron. Soc. 2020, 500, 2112–2126. [Google Scholar] [CrossRef]
- Di Benedetto, G.P. The Cepheid distance to the Large Magellanic Cloud and NGC 4258 by the surface brightness technique and improved calibration of the cosmic distance scale. Mon. Not. R. Astron. Soc. 2008, 390, 1762–1776. [Google Scholar] [CrossRef]
- Orosz, J.A.; McClintock, J.E.; Narayan, R.; Bailyn, C.D.; Hartman, J.D.; Macri, L.; Liu, J.; Pietsch, W.; Remillard, R.A.; Shporer, A.; et al. A 15.65-solar-mass black hole in an eclipsing binary in the nearby spiral galaxy M 33. Nature 2007, 449, 872–875. [Google Scholar] [CrossRef] [PubMed]
- Hyde, E.A.; Russell, D.M.; Ritter, A.; Filipović, M.D.; Kaper, L.; Grieve, K.; O’Brien, A.N. LMC X-1: A New Spectral Analysis of the O-star in the Binary and Surrounding Nebula. Astron. Soc. Pac. 2017, 129, 094201. [Google Scholar] [CrossRef]
- Cooke, R.; Bland-Hawthorn, J.; Sharp, R.; Kuncic, Z. Ionization Cone in the X-ray Binary LMC X-1. Astrophys. J. 2008, 687, L29–L32. [Google Scholar] [CrossRef]
- Smponias, T.; Kosmas, T.S. Modelling the equatorial emission in a microquasar. Mon. Not. R. Astron. Soc. 2011, 412, 1320–1330. [Google Scholar] [CrossRef][Green Version]
- Smponias, T.; Kosmas, T.S. Dynamical and radiative simulations of γ-ray jets in microquasars. Mon. Not. R. Astron. Soc. 2013, 438, 1014–1026. [Google Scholar] [CrossRef][Green Version]
- Böttcher, M.; Dermer, C.D. Photon-Photon Absorption of Very High Energy Gamma Rays from Microquasars: Application to LS 5039. Astrophys. J. 2005, 634, L81–L84. [Google Scholar] [CrossRef]
- Cerutti, B.; Dubus, G.; Malzac, J.; Szostek, A.; Belmont, R.; Zdziarski, A.A.; Henri, G. Absorption of high-energy gamma rays in Cygnus X-3. Astron. Astrophys. 2011, 529, A120. [Google Scholar] [CrossRef][Green Version]
- Vieyro, F.L.; Romero, G.E. Particle transport in magnetized media around black holes and associated radiation. Astron. Astrophys. 2012, 542, A7. [Google Scholar] [CrossRef]
- Marshall, H.L.; Canizares, C.R.; Schulz, N.S. The High-Resolution X-ray Spectrum of SS 433 Using the Chandra HETGS. Astrophys. J. 2002, 564, 941–952. [Google Scholar] [CrossRef]
- Körding, E.G.; Fender, R.P.; Migliari, S. Jet-dominated advective systems: Radio and X-ray luminosity dependence on the accretion rate. Mon. Not. R. Astron. Soc. 2006, 369, 1451–1458. [Google Scholar] [CrossRef]
- Khangulyan, D.; Hnatic, S.; Aharonian, F.; Bogovalov, S. TeV light curve of PSR B1259–63/SS2883. Mon. Not. R. Astron. Soc. 2007, 380, 320–330. [Google Scholar] [CrossRef][Green Version]
- Gallant, Y.A.; Achterberg, A. Ultra-high-energy cosmic ray acceleration by relativistic blast waves. Mon. Not. R. Astron. Soc. 1999, 305, L6–L10. [Google Scholar] [CrossRef]
- Begelman, M.C.; Rudak, B.; Sikora, M. Consequences of Relativistic Proton Injection in Active Galactic Nuclei. Astrophys. J. 1990, 362, 38. [Google Scholar] [CrossRef]
- Romero, G.E.; Torres, D.F.; Kaufman Bernadó, M.M.; Mirabel, I.F. Hadronic gamma-ray emission from windy microquasars. Astron. Astrophys. 2003, 410, L1–L4. [Google Scholar] [CrossRef]
- Romero, G.E.; Okazaki, A.T.; Orellana, M.; Owocki, S.P. Accretion vs. colliding wind models for the gamma-ray binary LS I +61 303: An assessment. Astron. Astrophys. 2007, 474, 15–22. [Google Scholar] [CrossRef]
- Romero, G.E.; Vila, G.S. The proton low-mass microquasar: High-energy emission. Astron. Astrophys. 2008, 485, 623–631. [Google Scholar] [CrossRef]
- Mannheim, K.; Schlickeiser, R. Interactions of cosmic ray nuclei. Astron. Astrophys. 1994, 286, 983–996. [Google Scholar]
- Bosch-Ramon, V.; Romero, G.E.; Paredes, J.M. A broadband leptonic model for gamma-ray emitting microquasars. Astron. Astrophys. 2006, 447, 263–276. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma rays, electrons, and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 034018. [Google Scholar] [CrossRef]
- Gaisser, T.K.; Engel, R.; Resconi, E. Cosmic Rays and Particle Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R. Model for the High-Energy Emission from Blazars. Astrophys. J. 1993, 416, 458. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Gould, R.J. Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases. Rev. Mod. Phys. 1970, 42, 237–271. [Google Scholar] [CrossRef]
- Cherepashchuk, A.M.; Sunyaev, R.A.; Fabrika, S.N.; Postnov, K.A.; Molkov, S.V.; Barsukova, E.A.; Antokhina, E.A.; Irsmambetova, T.R.; Panchenko, I.E.; Seifina, E.V.; et al. INTEGRAL observations of SS433: Results of a coordinated campaign. Astron. Astrophys. 2005, 437, 561–573. [Google Scholar] [CrossRef]
- Orosz, J.A.; McClintock, J.E.; Aufdenberg, J.P.; Remillard, R.A.; Reid, M.J.; Narayan, R.; Gou, L. The mass of the black hole in cygnus X-1. Astrophys. J. 2011, 742, 84. [Google Scholar] [CrossRef]
- Orosz, J.A.; Steeghs, D.; McClintock, J.E.; Torres, M.A.P.; Bochkov, I.; Gou, L.; Narayan, R.; Blaschak, M.; Levine, A.M.; Remillard, R.A.; et al. A new dynamical model for the black hole binary lmc X-1. Astrophys. J. 2009, 697, 573–591. [Google Scholar] [CrossRef]
- Stirling, A.; Spencer, R.; de La Force, C.; Garrett, M.; Fender, R.; Ogley, R. A relativistic jet from Cygnus X-1 in the low/hard X-ray state. Mon. Not. R. Astron. Soc. 2001, 327, 1273–1278. [Google Scholar] [CrossRef]
- Fabrika, S. The jets and supercritical accretion disk in SS433. Astrophys. Space Phys. Rev. 2004, 12, 1–152. [Google Scholar]
- Zhang, J.F.; Li, Z.R.; Xiang, F.Y.; Lu, J.F. Electron transport with re-acceleration and radiation in the jets of X-ray binaries. Mon. Not. R. Astron. Soc. 2017, 473, 3211–3222. [Google Scholar] [CrossRef]
- Kosmas, O.T.; Leyendecker, S. Phase lag analysis of variational integrators using interpolation techniques. PAMM Proc. Appl. Math. Mech. 2012, 12, 677–678. [Google Scholar] [CrossRef]
- Kosmas, O.T.; Leyendecker, S. Family of high order exponential variational integrators for split potential systems. J. Phys. Conf. Ser. 2015, 574, 012002. [Google Scholar] [CrossRef]
- Kosmas, O.T.; Vlachos, D.S. A space-time geodesic approach for phase fitted variational integrators. J. Phys. Conf. Ser. 2016, 738, 012133. [Google Scholar] [CrossRef]
- Papavasileiou, T.V.; Papadopoulos, D.A.; Kosmas, T.S. Astrophysical magnetohydrodynamical outflows in the extragalactic binary system LMC X-1. J. Phys. Conf. Ser. 2020, in press. [Google Scholar]
- Achterberg, A.; Gallant, Y.A.; Kirk, J.G.; Guthmann, A.W. Particle acceleration by ultrarelativistic shocks: Theory and simulations. Mon. Not. R. Astron. Soc. 2001, 328, 393–408. [Google Scholar] [CrossRef]
- Kirk, J.G.; Guthmann, A.W.; Gallant, Y.A.; Achterberg, A. Particle Acceleration at Ultrarelativistic Shocks: An Eigenfunction Method. Astrophys. J. 2000, 542, 235–242. [Google Scholar] [CrossRef]
- Ghisellini, G.; Maraschi, L.; Treves, A. Inhomogeneous synchrotron-self-Compton models and the problem of relativistic beaming of BL Lac objects. Astron. Astrophys. 1985, 146, 204. [Google Scholar]
- Torres, D.F.; Reimer, A. Hadronic beam models for quasars and microquasars. Astron. Astrophys. 2011, 528, L2. [Google Scholar] [CrossRef]
- Lipari, P.; Lusignoli, M.; Meloni, D. Flavor composition and energy spectrum of astrophysical neutrinos. Phys. Rev. D 2007, 75, 123005. [Google Scholar] [CrossRef]
- Berezhko, E.G.; Ellison, D.C. A Simple Model of Nonlinear Diffusive Shock Acceleration. Astrophys. J. 1999, 526, 385–399. [Google Scholar] [CrossRef]
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Babić, A.; Banerjee, B.; Bangale, P.; de Almeida, U.B.; Barrio, J.A.; González, J.B.; et al. Search for very high-energy gamma-ray emission from the microquasar Cygnus X-1 with the MAGIC telescopes. Mon. Not. R. Astron. Soc. 2017, 472, 3474–3485. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Andeen, K.; Anderson, T.; Ansseau, I.; et al. Neutrino astronomy with the next-generation IceCube Neutrino Observatory. arXiv 2019, arXiv:1911.02561. [Google Scholar]
- Albert, A.; André, M.; Anghinolfi, M.; Anton, G.; Ardid, M.; Aubert, J.J.; Avgitas, T.; Baret, B.; Barrios-Martí, J.; Basa, S.; et al. First all-flavor neutrino pointlike source search with the ANTARES neutrino telescope. Phys. Rev. D 2017, 96, 082001. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Andeen, K.; Anderson, T.; et al. All-sky Search for Time-integrated Neutrino Emission from Astrophysical Sources with 7 yr of IceCube Data. Astrophys. J. 2017, 835, 151. [Google Scholar] [CrossRef]
- Aiello, S.; Akrame, S.; Ameli, F.; Anassontzis, E.G.; Andre, M.; Androulakis, G.; Anghinolfi, M.; Anton, G.; Ardid, M.; Aublin, J.; et al. Sensitivity of the KM3NeT/ARCA neutrino telescope to point-like neutrino sources. Astropart. Phys. 2019, 111, 100–110. [Google Scholar] [CrossRef]
- Sacco, B.; Vercellone, S. Present and future of the TeV astronomy with Cherenkov telescopes. arXiv 2010, arXiv:1010.2208. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).