Capture of Massless and Massive Particles by Parameterized Black Holes

Abstract

We study an influence of the leading coefficient of the parameterized line element of the spherically symmetric, static black hole on the capture of massless and massive particles. We have shown that negative (positive) values of $ϵ$ decreases (increases) the radius of characteristic circular orbits and consequently, increases (decreases) the energy and decreases (increases) the angular momentum of the particle moving along these orbits. Moreover, we have calculated and compared the capture cross section of the massive particle in the relativistic and non-relativistic limits. It has been shown that in the case of small deviation from general relativity the capture cross section for the relativistic and nonrelativistic particle has an additional term being linear in the small dimensionless deviation parameter $ϵ$.

1. Introduction

General relativity is considered as the most satisfactory theory of gravitation due to its conceptual and structural elegance, as well as its reasonable agreement with experimental and astronomical observations [1]. The following three observational classical tests are called experimental verification of the Einstein theory in the weak field and slow motion regime: the perihelion precession of the orbit of the planet Mercury, the deflection of the light ray as it passes close to the sun, and the gravitational redshift of light. Consequently, all three tests verify the correctness of general relativity in the weak gravitational field regime. This fact has served as a base for the development of new alternative theories of gravity that perfectly match with general relativity in the weak field regime, but in the strong field regime the main differences could be risen. The best laboratory to test the theory in a strong gravitational field is a black hole (and a neutron star) close environment. Thanks to the development of new modern technologies in recent years, we have obtained several observational breakthrough events such as the detected gravitational waves from the coalescence of two massive black holes or neutron stars in close binaries by the LIGO and Virgo scientific collaborations (for example, see [2,3,4,5,6]) and the discovery of the first image of the supermassive black hole at the center of the elliptic galaxy M87 by the Event Horizon Telescope (EHT) collaboration [7] that gave us an initial possibility to check general relativity in the strong field regime. However, there is still room for alternative theories of gravity [8] as the current sensitivity of technology is not enough to fully exclude them by testing the no-hair theorem and general relativity. With the further development of detectors and the new obtained observational data in the near future, we hopefully will be able to check the validity of all theories one by one in the strong field regime. However, there is a very compact method in which all black hole geometries are written in the generic, model independent form. The generic spacetime geometry could be chosen in such a way that can be used to measure deviations from general relativity via the expansion parameters [9,10] and, depending on the data from observation, one can find the constraints for the appropriate parameters [11,12,13,14,15,16,17,18].

In this paper, we study the capture of massless and massive particles by the black hole whose line element is the parameterized by the Rezzolla–Zhidenko method presented in [10] in terms of the bumpy parameters $ϵ$ and $a_i$ with $i=0,1,2,\cdots$ that defines the deviation from the general relativity. For simplicity, in order to analyze the effect of the parameters to the motion and physical quantities of the particle in non-general relativity, we restrict ourselves to the first two expansion parameters $ϵ$, $a_0$, and $b_0$. However, observational constraints on the PPN parameters impose $a_0=0=b_0$ [10]. Therefore, throughout the paper, we study the effect of parameter $ϵ$ on the motion of the massless and massive particles. The paper is organized as follows: in Section 2, the equations of motion are explored in the spacetime of a spherically symmetric, static black hole described in the parameterized form. In the next Section 3 and Section 4, the motion of the photon and the massive particle including the capture by the black hole have been investigated. The last Section 5 is devoted to the discussion of the main results and future prospects. Throughout the paper, we use the geometrized units in which the Newtonian gravitational constant G, and the speed of light c are $G=c=1$.

2. Equations of Motion

According to [10], the line element of a spherically symmetric, static black hole can be written as

$$d{s}^2=-N^2\left(r\right)d{t}^2+\frac{B^2\left(r\right)}{N^2\left(r\right)}d{r}^2+r^{2}d{\Omega }^2,$$

(1)

where the metric functions N and B depend on the radial coordinate r only and $d{\Omega }^2\equiv d{\theta }^2+{sin}^2\theta d{\varphi }^2$ represents the solid angle element. Through the event horizon $r_0$, one introduces a new dimensionless variable that allows us to compact the radial coordinate as

$$x\equiv 1-\frac{r_0}{r},$$

(2)

where the event horizon is recovered when $x=0$ while spatial infinity corresponds to $x=1$, thus $0\le x\le 1$. Furthermore, we assume that

$$\begin{array}{c}\hfill N^2\left(r\right)=xA\left(x\right).\end{array}$$

(3)

The functions A and B are expanded in terms of the new parameters as

$$\begin{array}{ccc}\hfill A\left(x\right)& =& 1-ϵ(1-x)+(a_0-ϵ){(1-x)}^2+\tilde{A}\left(x\right){(1-x)}^3,\hfill \\ \hfill B\left(x\right)& =& 1+b_0(1-x)+\tilde{B}\left(x\right){(1-x)}^2,\hfill \end{array}$$

where $ϵ$, $a_0$, and $b_0$ are new coefficients and $\tilde{A}$ and $\tilde{B}$ describe the spacetime metric at the horizon and at infinity. It is important to notice that the dimensionless coefficient $ϵ$ is related to the event horizon by

$$ϵ=-\left(1-\frac{2M}{r_0}\right),$$

(4)

where M is the ADM mass. $ϵ$ measures the deviations of the event horizon $r_0$ from $2M$, and it is an important parameter because one can recast all the other coefficients in terms of it. The functions $\tilde{A}\left(x\right)$ and $\tilde{B}\left(x\right)$ are expressed in terms of continued fractions (i.e., Padé series)

$$\begin{array}{ccc}\hfill \tilde{A}\left(x\right)& =& \frac{a_1}{{\displaystyle 1+\frac{{\displaystyle a_{2}x}}{{\displaystyle 1+\frac{{\displaystyle a_{3}x}}{{\displaystyle 1+\dots }}}}}},\hfill \\ \hfill \tilde{B}\left(x\right)& =& \frac{b_1}{{\displaystyle 1+\frac{{\displaystyle b_{2}x}}{{\displaystyle 1+\frac{{\displaystyle b_{3}x}}{{\displaystyle 1+\dots }}}}}},\hfill \end{array}$$

where $a_1,a_2,a_3,\dots$ and $b_1,b_2,b_3,\dots$ are dimensionless constants. In this paper, for simplicity we consider terms up to $O\left(x^3\right)$ order, i.e., $a_i=0$, and $b_i=0$ where $i=1,2,3,\dots$. However, observational constraints, i.e., the Solar System tests of the general relativity at the first PPN parameters, which were done by C. Will in [1] impose that the values of $a_0$ and $b_0$ are as small as $a_0\sim b_0\sim {10}^{-4}$ [10]. Since these values are very small and in the strong field regime (when r is small) where we focus on, their contributions to the spacetime metric are negligible. Therefore, throughout the paper, we adopt the constraint $a_0=0=b_0$. Then, the second metric function takes the form of $B\left(r\right)=1$ and the spacetime line element (1) reduces to the following form:

$$d{s}^2=-N^2\left(r\right)d{t}^2+\frac{d{r}^2}{N^2\left(r\right)}+r^{2}d{\Omega }^2.$$

(5)

Now, one can expand the metric function $N^2\left(r\right)$ in terms of the expansion parameters as

$$N^2\left(r\right)=\left(1-\frac{r_0}{r}\right)\left[1-ϵ\frac{r_0}{r}-ϵ{\left(\frac{r_0}{r}\right)}^2\right].$$

(6)

If $ϵ=0$, one recovers the standard spherically symmetric Schwarzschild spacetime.

At this point, there is all the background necessary to proceed with the calculations. In order to investigate the motion of both massive and massless particles using the same equations of motion, by setting the mass of the particle zero in the latter one, one can easily recover the former case. One can easily notice from the symmetry of the spacetime metric (5) that the momenta corresponding to the time and azimuthal coordinates are conserved due to the stationarity and spherical symmetry, and these conserved momenta are called energy, E, and angular momentum, L, of the particle, respectively, as

$$\begin{array}{ccc}& & N^2\left(r\right)u^t=E,\hfill \\ & & r^2{u}^{\varphi }=L.\hfill \end{array}$$

Hereafter, instead of the energy and angular momentum of the massive particle with mass m, we use the specific energy, $E\to E/m$, and specific angular momentum, $L\to L/m$, notions which define the ones per unit mass. Moreover, for simplicity we consider the motion of the particle as confined at the equatorial plane and by using the normalization condition $u^{\mu }{u}_{\mu }=-1$, one can find the radial velocity of the particle as

$$\begin{array}{c}\hfill {\left(u^r\right)}^2=E^2-V_{\mathrm{eff}},V_{\mathrm{eff}}=N^2\left(r\right)\left(\epsilon +\frac{L^2}{r^2}\right),\end{array}$$

(7)

where $\epsilon =0,1$ for the massless and massive particles, respectively. The effective potential can be separated into two components with one coming from general relativity and the second being of the additional deviation term from $ϵ$ as

$$\begin{array}{c}\hfill V_{\mathrm{eff}}=V_{\mathrm{eff}}^{\mathrm{GR}}+V_{\mathrm{eff}}^{\mathrm{RZ}},\end{array}$$

(8)

where

$$\begin{array}{ccc}& & V_{\mathrm{eff}}^{\mathrm{GR}}=\left(1-\frac{r_0}{r}\right)\left(\epsilon +\frac{L^2}{r^2}\right),\hfill \\ & & V_{\mathrm{eff}}^{\mathrm{RZ}}=-\frac{r_0}{r}\left(1-\frac{r_0^2}{r^2}\right)\left(\epsilon +\frac{L^2}{r^2}\right)ϵ,\hfill \end{array}$$

(9)

Thus, the motion of the particle is fully characterized by the two conserved physical quantities: E and L, in terms of the spacetime parameters: $r_0$ and $ϵ$. In particular, the massive particle moving along the circular orbit has no radial velocity and it is located at the extrema of the effective potential as

$$\begin{array}{c}\hfill u^r=0,V_{\mathrm{eff}}^{\prime }=0.\end{array}$$

(10)

From the above conditions, one can easily find the expressions of the energy and angular momentum of the particle moving along the circular orbit as

$$\begin{array}{ccc}& & E=\frac{\sqrt{2}(r-r_0)\left[r^2-r_0ϵ(r+r_0)\right]}{\sqrt{2r^6-3r^5{r}_0(ϵ+1)+5r^3{r}_0^3ϵ}},\hfill \\ & & L=\frac{r\sqrt{r_0}\sqrt{r^2(ϵ+1)-3r_0^2ϵ}}{\sqrt{2r^3-3r^2{r}_0(ϵ+1)+5r_0^3ϵ}}.\hfill \end{array}$$

(11)

Moreover, if the condition $ϵ<<1$ is applied, the above expressions can be written as the following

$$\begin{array}{ccc}& & E=E^{\mathrm{GR}}+\delta Eϵ+O\left({ϵ}^2\right),\hfill \\ & & L=L^{\mathrm{GR}}+\delta Lϵ+O\left({ϵ}^2\right),\hfill \end{array}$$

(12)

where

$$\begin{array}{ccc}& & E^{\mathrm{GR}}=\frac{\sqrt{2}(r-r_0)}{\sqrt{r}\sqrt{2r-3r_0}},\delta E=-\frac{(r-r_0)\left(r^2{r}_0-2r{r}_0^2-r_0^3\right)}{\sqrt{2}{r}^{5/2}{(2r-3r_0)}^{3/2}},\hfill \\ & & L^{\mathrm{GR}}=\frac{r\sqrt{r_0}}{\sqrt{2r-3r_0}},\delta L=\frac{\sqrt{r_0}\left(r^3-3r{r}_0^2+2r_0^3\right)}{r{(2r-3r_0)}^{3/2}}.\hfill \end{array}$$

(13)

One can find a radius of the innermost stable circular orbit (ISCO) by solving the equation $V_{\mathrm{eff}}^{″}=0$ together with the conditions (10). For small $ϵ$, the radius of ISCO is

$$\begin{array}{c}\hfill r_{\mathrm{ISCO}}=3r_0+\frac{8}{9}{r}_0ϵ+O\left({ϵ}^2\right).\end{array}$$

(14)

The energy and angular momentum of this particle are found to be

$$\begin{array}{ccc}& & E_{\mathrm{ISCO}}=\frac{2\sqrt{2}}{3}-\frac{2\sqrt{2}}{81}ϵ+O\left({ϵ}^2\right),\hfill \\ & & L_{\mathrm{ISCO}}=\sqrt{3}{r}_0+\frac{20}{9\sqrt{3}}{r}_0ϵ+O\left({ϵ}^2\right).\hfill \end{array}$$

(15)

Calculations have shown that for negative (positive) values of $ϵ$, the radius of the ISCO decreases (increases) and consequently, the energy increases (decreases) and the angular momentum of the particle moving along the ISCO decreases (increases).

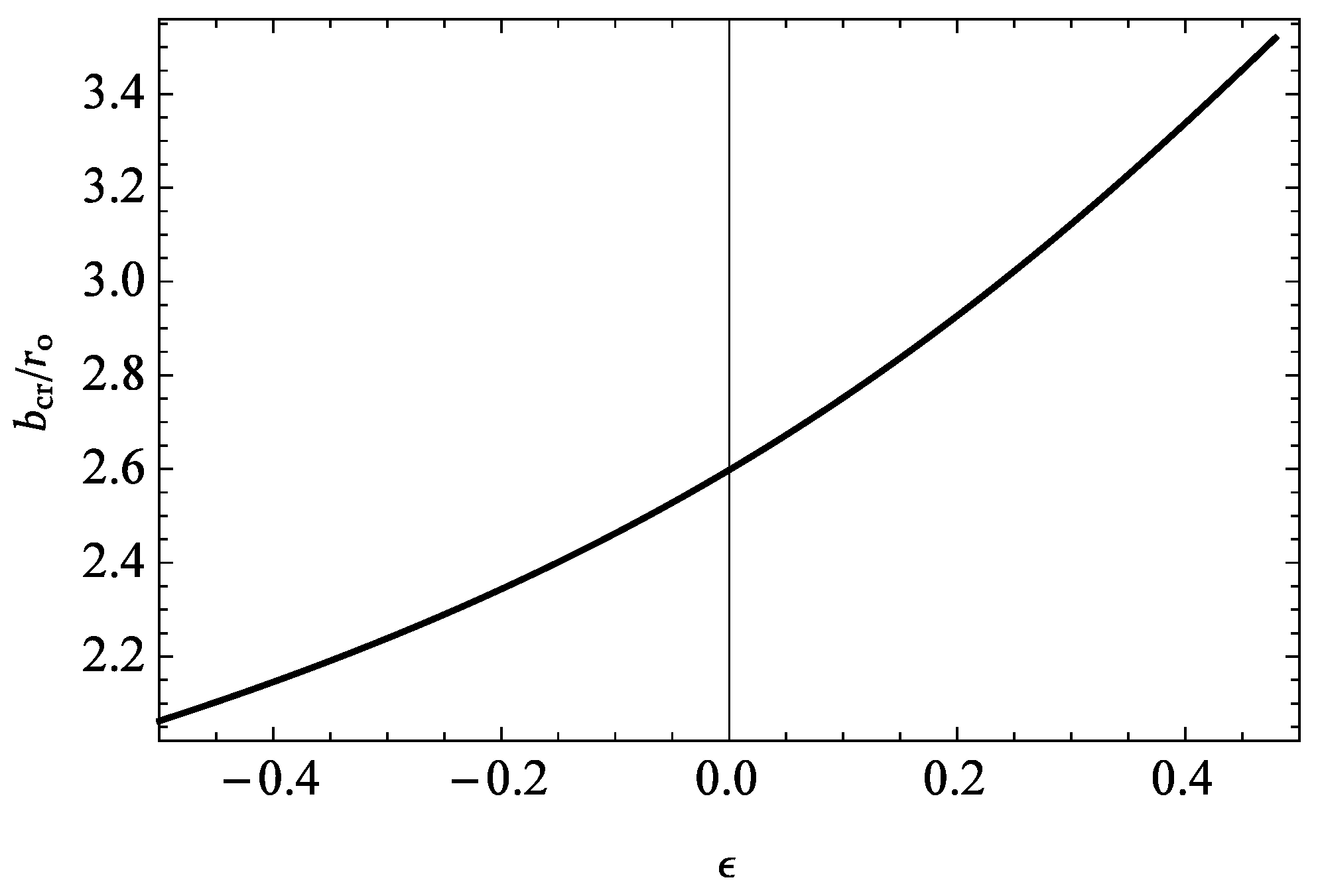
3. Capture of Photons

In this section, we explore the motion of the photon and its capture by a black hole whose line element is given by (5). In both studies, the determination of the impact parameter, b, that defines the closest approach distance of a photon to a black hole that can still pass through is very crucial. It is a well-known fact that the photon passing through the black hole spacetime can approach the black hole until the photonsphere, beyond which it moves along the photonsphere or is captured by the black hole. Therefore, the photonsphere is a boundary between the capture and escape cases. Therefore, our main task in this section is to find the impact parameter, b, of the photon. The impact parameter is defined by $b=L_{\mathrm{cr}}/E$, with $L_{\mathrm{cr}}$ being the critical angular momentum of the photon. For simplicity, one can write the equation of motion (7) for the photon ($\epsilon =0$) by applying the transformation $\lambda \to \lambda L$ for the affine parameter in the following polynomial form:

$$\begin{array}{c}\hfill {\left(u^r\right)}^2=\frac{1}{b^2}-\frac{N^2\left(r\right)}{r^2}.\end{array}$$

(16)

The right hand side of this equation can be written in the monic polynomial form as

$$\begin{array}{ccc}\hfill b^2{r}^5{\left(u^r\right)}^2=& & r^5-b^2{r}^3+b^2{r}_0(ϵ+1)r^2-b^2{r}_0^3ϵ.\hfill \end{array}$$

(17)

It is well-known that the positive zeros ($>r_0$) of the right hand side of (17) define the turning points. One can easily notice from the shape of the effective potential of photon Figure 1 that the possible number of real turning points can be up to two ($r_1$ and $r_2$). Depending on the value of the impact parameter of the photon passing close to the black hole the following scenarios can happen:

(i)

Two turning points $r_0<r_1<r_2$: in this case $b>b_{\mathrm{cr}}$, i.e., either the photon coming from infinity reaches the periastron ($r_2$) and again escapes to infinity, or if the photon is emitted from near the horizon ($r_0<r<r_1$), it reaches an apastron ($r_1$) and falls back to the black hole.

(ii)

Ine turning point $r_0<r_1$: in this case $b=b_{\mathrm{cr}}$, i.e., the photon moves along an unstable circular orbit that corresponds to the peak of the effective potential. Any deviation from the trajectory causes the photon to fall into or escape from the black hole.

(iii)

No turning point: in this case $b<b_{\mathrm{cr}}$, i.e., either the photon coming from infinity falls into the black hole or the photon emitted from near the horizon escapes to infinity.

As it was mentioned in the second point of the above cases, the critical angular momentum corresponds to the maximum of the effective potential where two turning points merge and corresponds to the unstable photonsphere that is located at (or see right panel of Figure 1)

$$\begin{array}{c}\hfill r_{\mathrm{ps}}=\frac{3}{2}{r}_0+\frac{7}{18}{r}_0ϵ+O\left({ϵ}^2\right).\end{array}$$

(18)

Two turning points merge at the photonsphere when the discriminant of the polynomial vanishes. Thus, to find the critical impact parameter, we must solve Equation whose discriminant is equal to zero ($\Delta =0$). To find the discriminant, we set the Sylvester matrix for the resultant of polynomial equal to zero as

$$\begin{array}{c}\hfill \det \left(\begin{array}{ccccccccc}1& 0& -b^2& A& 0& B& 0& 0& 0\\ 0& 1& 0& -b^2& A& 0& B& 0& 0\\ 0& 0& 1& 0& -b^2& A& 0& B& 0\\ 0& 0& 0& 1& 0& -b^2& A& 0& B\\ 5& 0& -3b^2& 2A& 0& 0& 0& 0& 0\\ 0& 5& 0& -3b^2& 2A& 0& 0& 0& 0\\ 0& 0& 5& 0& -3b^2& 2A& 0& 0& 0\\ 0& 0& 0& 5& 0& -3b^2& 2A& 0& 0\\ 0& 0& 0& 0& 5& 0& -3b^2& 2A& 0\end{array}\right)=0,\end{array}$$

(19)

where

$$\begin{array}{c}\hfill A=b^2{r}_0(ϵ+1),B=-b^2{r}_0^3ϵ.\end{array}$$

Equation (19) gives the following equation:

$$\begin{array}{ccc}\hfill & & 4b{}^6{(1-2ϵ)}^2(ϵ+4)-3b{}^4{r}_0^2{(ϵ+1)}^2\{ϵ[36ϵ(ϵ+3)-167]+36\}\hfill \\ & & -3750b{}^2{r}_0^4{ϵ}^2(ϵ+1)+3125r_0^6{ϵ}^3=0.\hfill \end{array}$$

(20)

Due to the cumbersome form of the solution of (20), we do not report its full analytic expression, instead we present the dependence of the critical impact parameter on the spacetime parameter $ϵ$ in Figure 2.

For the small values of $ϵ$, the critical impact parameter of the photon can be written as

$$\begin{array}{c}\hfill b_{\mathrm{cr}}=\frac{3\sqrt{3}}{2}{r}_0+\frac{5\sqrt{3}}{6}{r}_0ϵ+O\left({ϵ}^2\right).\end{array}$$

(21)

If $ϵ=0$ is imposed, one recovers $b_{\mathrm{cr}}=3\sqrt{3}{r}_0/2$ [19,20,21,22,23].

The capture cross section of the photon by the black hole in small deviation from general relativity is found to be

$$\begin{array}{c}\hfill {\sigma }_{\mathrm{capt}}=\frac{27\pi r_0^2}{4}\left(1+\frac{10}{9}ϵ\right)+O\left({ϵ}^2\right).\end{array}$$

(22)

One can notice from the above given results that negative (positive) values of $ϵ$ decrease (increase) the radius of the photonsphere and the critical impact parameter of the photon, and consequently, decrease (increase) the capture cross section of the photon by the black hole.

4. Capture of Massive Particles

In this section, we repeat all calculations presented in the previous section, but now for the massive particle. Again, all the introductory points about the turning points are similar to the case of the photon presented in the previous section. To find the value of the critical angular momentum for the massive particle being enough to escape from the black hole, one needs to investigate again the turning points. To find the turning points, we write the equation of motion (7) with $\epsilon =1$ in the polynomial form as

$$\begin{array}{c}\hfill r^5{\left(u^r\right)}^2=\left(E^2-1\right)r^5+r_0(ϵ+1)r^4-L^2{r}^3+r_0\left[L^2(ϵ+1)-r_0^2ϵ\right]r^2-L^2{r}_0^3ϵ.\end{array}$$

(23)

Since in the case of a massive particle, the effective potential tends to one rather than zero (see Figure 3), the value of the critical impact parameter is defined by $b_{\mathrm{cr}}=L_{\mathrm{cr}}/\sqrt{E^2-1}$, and the possible number of real turning points can be up to three ($r_1$, $r_2$, and $r_3$).

Depending on the value of the impact parameter of the particle passing close to the black hole, the following scenarios can happen:

(i)

Three turning points $r_0<r_1<r_2<r_3$: in this case $b>b_{\mathrm{cr}}$, i.e., either the particle moves along the stable elliptic orbit between periastron ($r_2$) and apastron ($r_3$), or if the particle is emitted from near the horizon ($r_0<r<r_1$), it reaches an apastron ($r_1$) and falls back to the black hole.

(ii)

Two turning points $r_0<r_1<r_2$: this corresponds to $b>b_{\mathrm{cr}}$, i.e., either the particle coming from infinity reaches the periastron ($r_2$) and escapes back to infinity along the hyperbolic orbit, or if it is emitted close to the event horizon, it reaches an apastron ($r_1$) and falls back to the black hole.

(iii)

One turning point $r_0<r_1$: in this case $b=b_{\mathrm{cr}}$, i.e., the particle moves along the unstable circular orbit that corresponds to the peak of the effective potential.

(iv)

No turning point: in this case $b<b_{\mathrm{cr}}$, i.e., either the particle coming from infinity falls into the black hole or the particle emitted from near the horizon escapes to infinity.

As it was pointed out in the third item the critical impact parameter corresponds to the case of one turning point. In the case of the one turning point, two turning points $r_1$ and $r_2$ merge into one and in this case the discriminant vanishes ($\Delta =0$). Again by using the Sylvester matrix we find the equation of the discriminant, however, due to its cumbersome form, we report here only its form for the small $ϵ$ approximation as

$$\begin{array}{ccc}\hfill & & 4L^2\left[4\left(E^2-1\right)E^2-\left(27E^4-36E^2+8\right)L^2{r}_0^2-4r_0^4\right]\hfill \\ & & +ϵ\left[-60\left(E^2-1\right)L^6+\left(285E^4-348E^2+56\right)L^4{r}_0^2\right.\hfill \\ & & \left.-4\left(90E^4-112E^2+17\right)L^2{r}_0^4-64r_0^6\right]=0.\hfill \end{array}$$

(24)

The solution of (24) is quite long even in the small $ϵ$ limit. Therefore, we do not write it here, instead we present the absorption cross section of the relativistic and non-relativistic particles, which is given by $\sigma =\pi b_{\mathrm{cr}}^2$. For the relativistic particle the capture cross section in the case of small deviation from general relativity is determined by

$$\begin{array}{c}\hfill {\sigma }_{\mathrm{capt}}=\frac{27\pi r_0^2}{4}\left[1+\frac{2}{3E^2}+\left(\frac{10}{9}+\frac{76}{81E^2}\right)ϵ\right]+O\left(E^{-4},{ϵ}^2\right),\end{array}$$

(25)

that perfectly matches the one for the Schwarzschild black hole in the general relativity limit [19]. Moreover, in the photon limit, i.e., $E\to \infty$, we recover again the capture cross section of the photon (22).

For the low energy limit or in the non-relativistic limit, i.e., $E=1+{\beta }^2/2$, where $\beta$ is the velocity of the particle relative to the speed of light as $\beta =v/c$, the cross section takes the following form:

$$\begin{array}{c}\hfill {\sigma }_{\mathrm{capt}}=\frac{4\pi r_0^2}{{\beta }^2}\left(1+\frac{3}{2}ϵ\right)+O\left({\beta }^2,{ϵ}^2\right).\end{array}$$

(26)

In the general relativity limit, one recovers the result presented in [19].

5. Conclusions

In this paper, we have studied the capture of massless and massive particles by the spherically symmetric black hole whose line element is described by the Rezzolla–Zhidenko parameterization [10] up to $O\left(x^3\right)$ terms that takes only the coefficient $ϵ$ as nonvanishing, including the PPN constraints. We have shown that negative (positive) values of $ϵ$ decrease (increase) the radii of characteristic circular orbits, such as the photonsphere, marginally bound and innermost stable circular orbits. The results related to the photonsphere can be directly related to the shadow of the black hole whose radius is determined by the critical impact parameter. It stands for that with increasing (decreasing) the value of parameter $ϵ$, the radius of the shadow of the black hole increases (decreases). Due to the phenomenon that the increase in the values of the parameter $ϵ$ increases the radius of characteristic circular orbits, the energy and the angular momentum of the particle moving along these circular orbits increase (decrease).

Moreover, we have calculated and compared the capture cross section of the massive particle in relativistic and non-relativistic limits. It has been shown that in the case of small deviation from general relativity the capture cross Section of the relativistic and nonrelativistic particles have an additional term being linear in the small dimensionless deviation parameter $ϵ$. It has been shown that the massive particles always have bigger capture cross sections than the photon.

We underline that the dependence of spherically symmetric black hole cross sections on the dimensionless deviation parameter $ϵ$ can be proposed as a powerful tool to determine the valid theory of gravity in the strong field regime using observational data on the highly energetic processes in a black hole close environment.