Ion Acoustic Shocks in a Weakly Relativistic Ion-Beam Degenerate Magnetoplasma
Abstract
:1. Introduction
2. Basic Equations
3. Derivation of the KdV–Burgers Equation
3.1. Solution of the KdV–Burgers Equation
3.2. Solution of Oscillatory Shocks
3.3. Bifurcation Analysis
4. Parametric Analysis
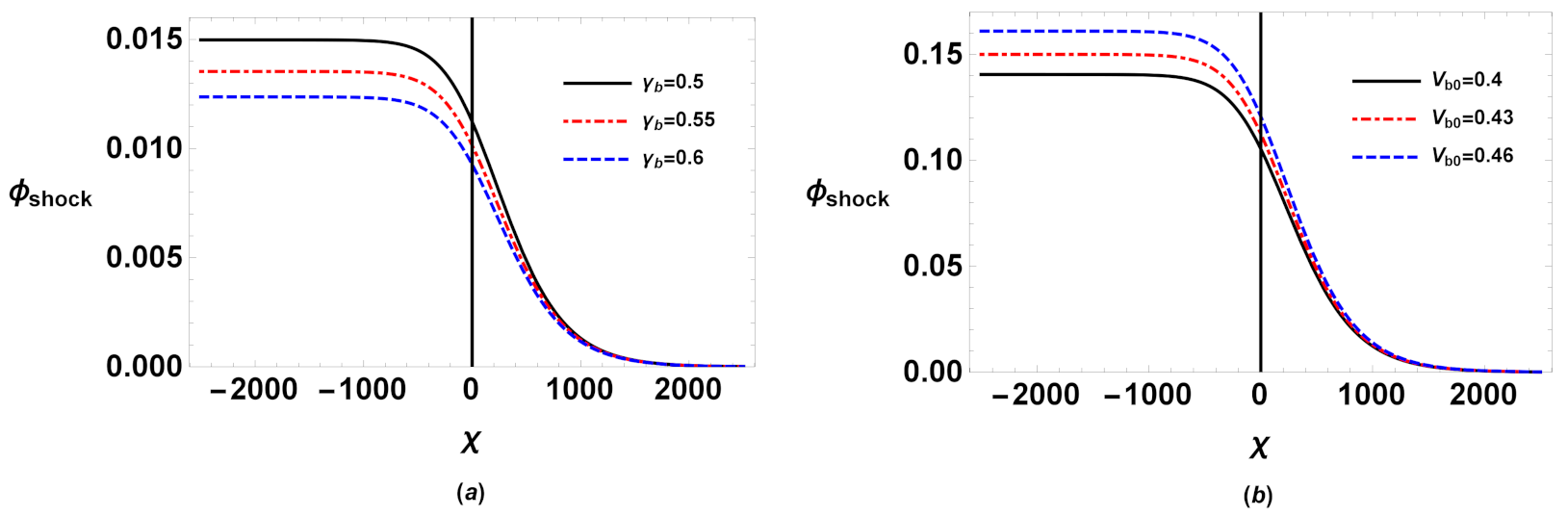
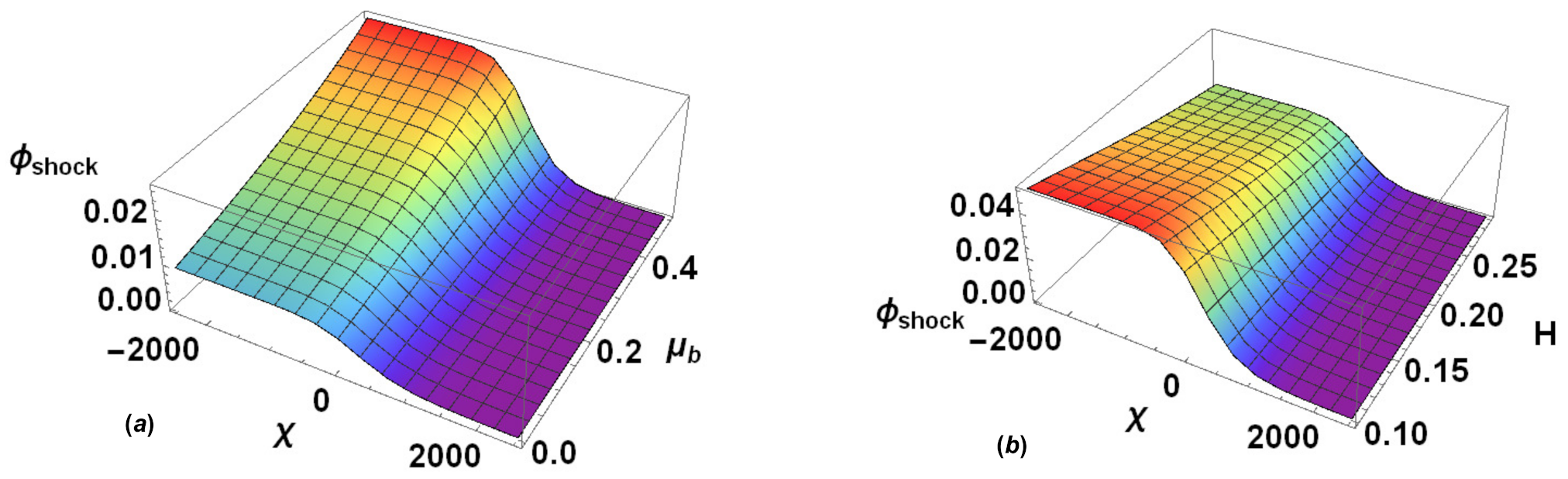
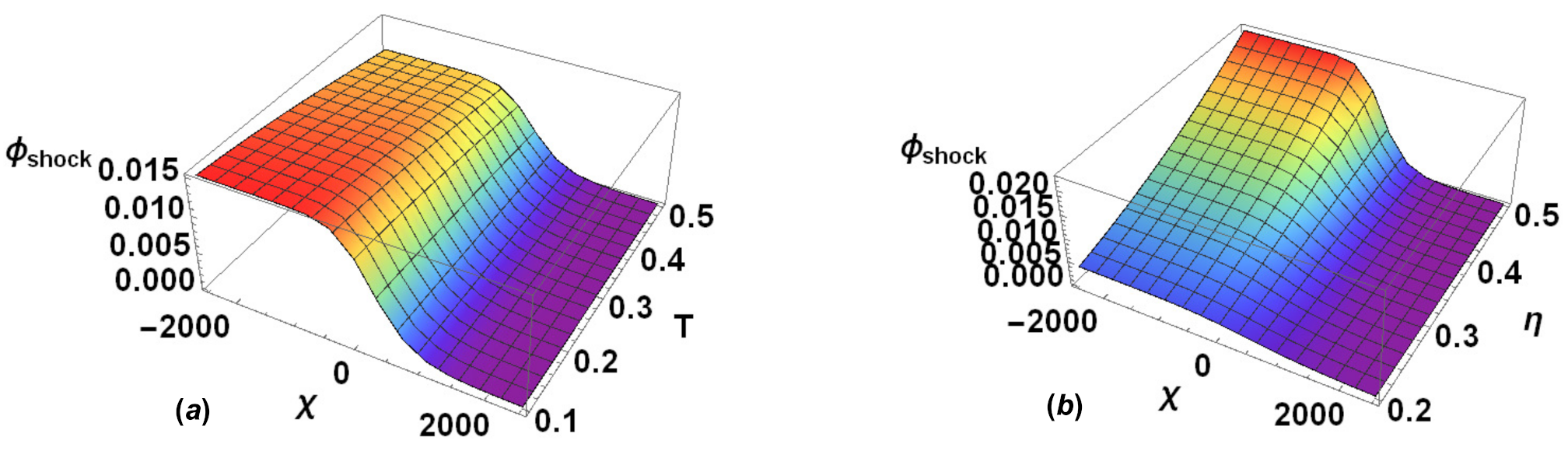
4.1. Variation of Shock Wave Profile
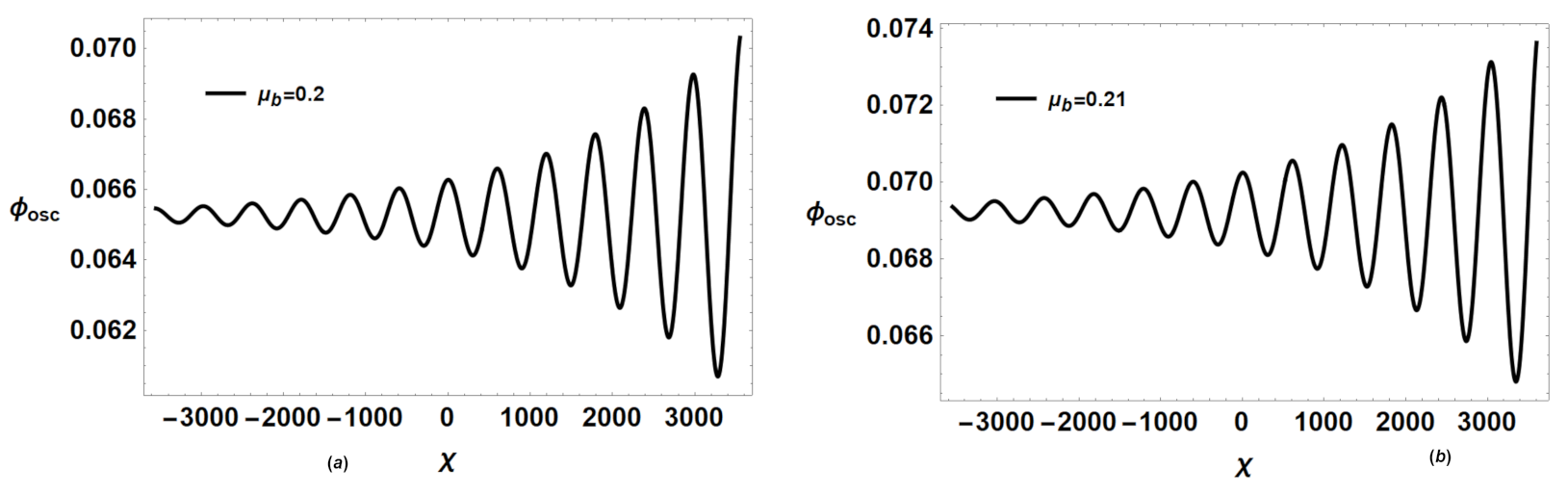
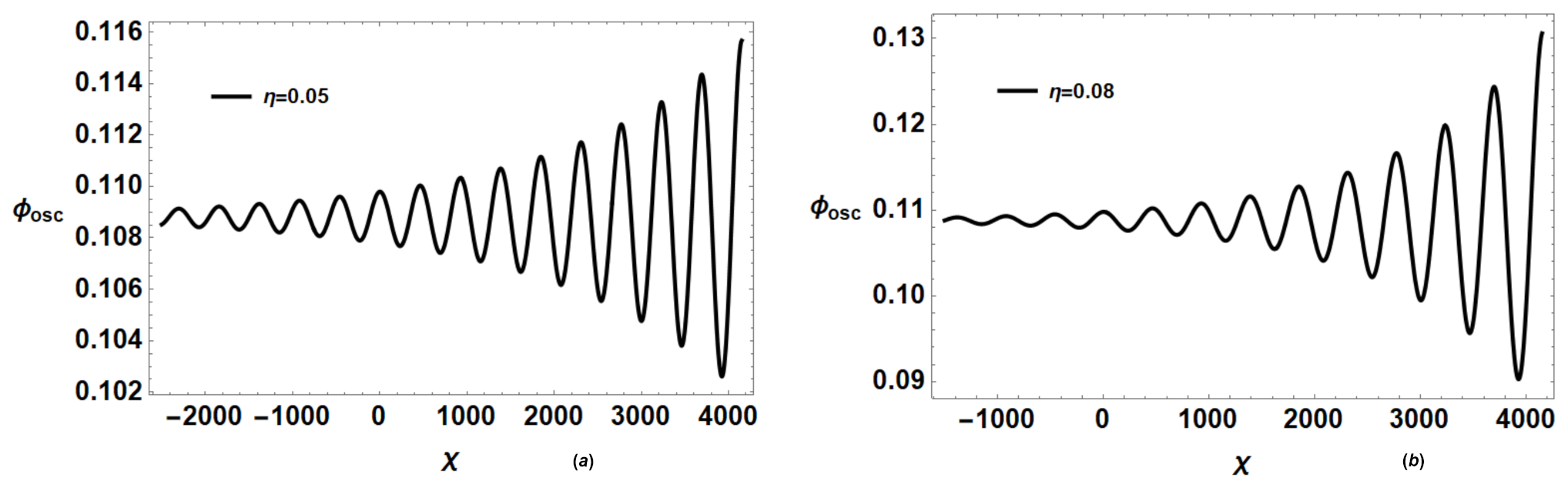
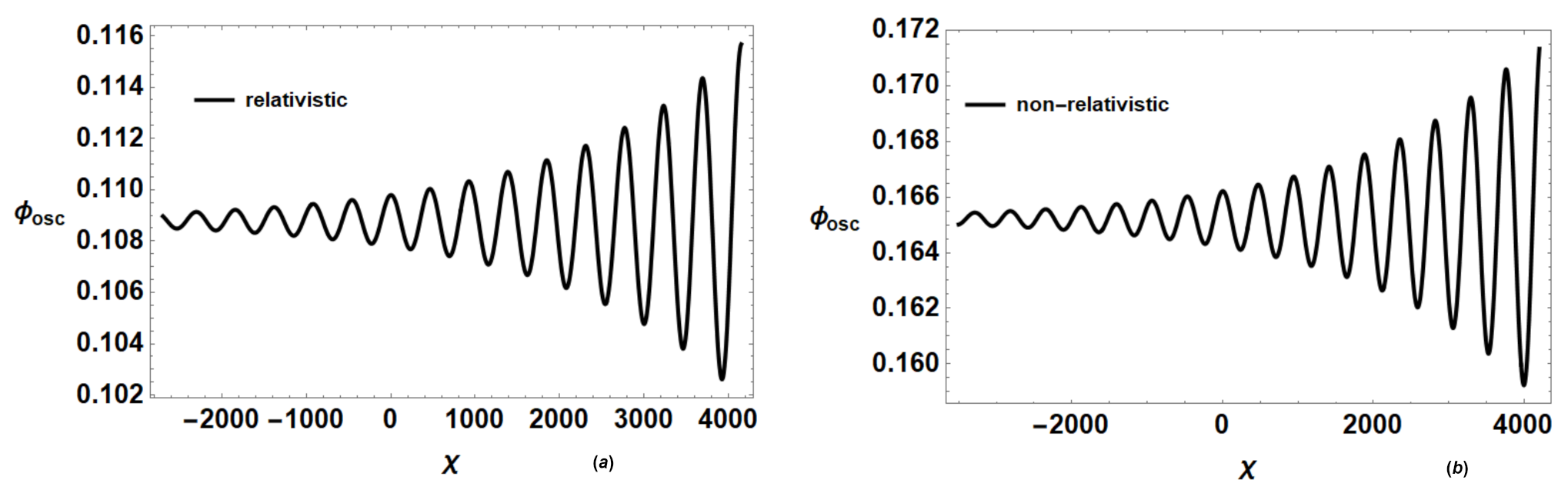
4.2. Variation of Oscillatory Shocks
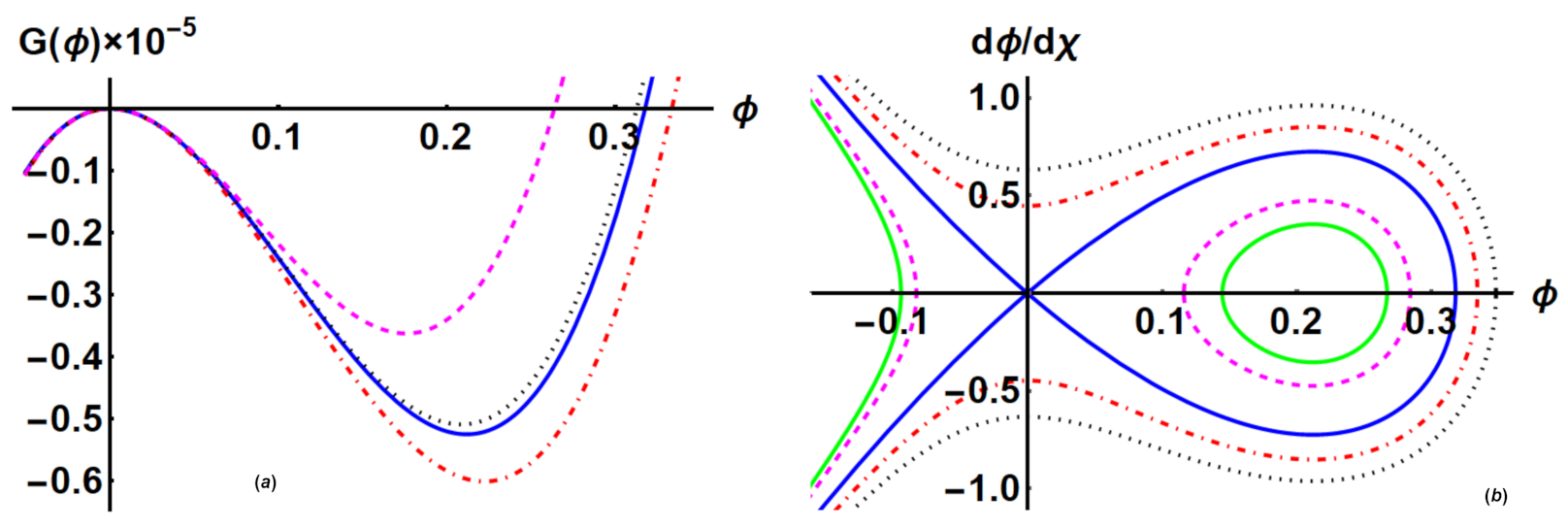
4.3. Variation of Sagdeev Potential and Phase Portraits
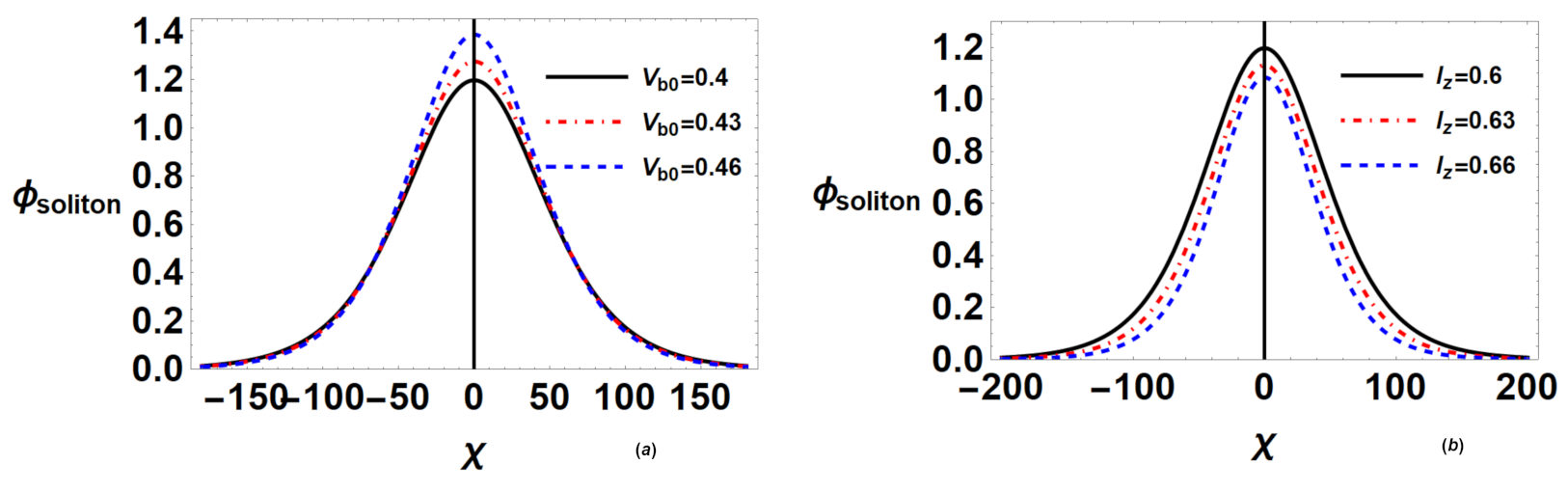
4.4. Variation of Solitary Wave Profile
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Shukla, P.K.; Eliasson, B. Colloquium: Nonlinear collective interactions in quantum plasmas with degenerate electron fluids. Rev. Mod. Phys. 2011, 83, 885. [Google Scholar] [CrossRef] [Green Version]
- Gabdullin, M.T.; Kodanova, S.K.; Ramazanov, T.S.; Issanova, M.K.; Ismagam-betova, T.N. Thermodynamic and dynamical properties of dense ICF plasma. Nukleonika 2016, 61, 125. [Google Scholar] [CrossRef] [Green Version]
- Sharkov, B.Y.; Hoffmann, D.H.H.; Golubev, A.A.; Zhao, Y. High energy density phys-ics with intense ion beams. Matter Radiat. Extremes 2016, 1, 28. [Google Scholar] [CrossRef] [Green Version]
- Adhikary, N.C.; Misra, A.P.; Bailung, H.; Chutia, J. Ion-beam driven dust ion-acoustic solitary waves in dusty plasmas. Phys. Plasmas 2010, 17, 044502. [Google Scholar] [CrossRef] [Green Version]
- Kaur, N.; Singh, M.; Kohli, R.; Saini, N.S. Effect of ion beam on low-frequency cnoidal waves in a non-Maxwellian dusty plasma. IEEE Trans. Plasma Sci. 2017, 46, 768. [Google Scholar] [CrossRef]
- Kaur, N.; Singh, K.; Saini, N.S. Effect of ion beam on the characteristics of ion acoustic Gardner solitons and double layers in a multicomponent superthermal plasma. Phys. Plasmas 2017, 24, 092108. [Google Scholar] [CrossRef]
- Kaur, N.; Singh, K.; Ghai, Y.; Saini, N.S. Nonplanar dust acoustic solitary and rogue waves in an ion beam plasma with superthermal electrons and ions. Plasma Sci. Technol. 2018, 20, 074009. [Google Scholar] [CrossRef]
- Deka, M.K.; Dev, A.N.; Misra, A.P.; Adhikary, N.C. Characteristics of solitary waves in a relativistic degenerate ion beam driven magneto plasma. Phys. Plasmas 2018, 25, 012102. [Google Scholar] [CrossRef] [Green Version]
- Paul, I.; Chatterjee, A.; Paul, S.N. Nonlinear propagation of ion acoustic waves in quan-tum plasma in the presence of an ion beam. Laser Part. Beam 2018, 37, 330–380. [Google Scholar] [CrossRef]
- Kaur, R.; Singh, K.; Saini, N.S. Ion Acoustic Cnoidal Waves in Ion-Beam Dense Plasma in the Presence of Quantizing Magnetic Field. IEEE Trans. Plasma Sci. 2021, 49, 1686. [Google Scholar] [CrossRef]
- Chandrasekhar, S. An Introduction to the Study of Stellar Structures; Dover Publications: New York, NY, USA, 1939; Chapter 10. [Google Scholar]
- Shapiro, L.; Teukolsky, S.A. Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects; John Wiley and Sons: New York, NY, USA, 1973. [Google Scholar]
- Chabrier, C.; Saumon, D.; Potekhin, A.Y. Dense plasmas in astrophysics: From gi-ant planets to neutron stars. J. Phys. A 2006, 39, 4411. [Google Scholar] [CrossRef] [Green Version]
- Marklund, M.; Shukla, P.K. Nonlinear collective effects in photon-photon and photon-plasma interactions. Rev. Mod. Phys. 2006, 78, 591. [Google Scholar] [CrossRef] [Green Version]
- Bingham, R. On the crest of a wake. Nature 2007, 445, 721. [Google Scholar] [CrossRef]
- Mamun, A.A.; Shukla, P.K. Arbitrary amplitude solitary waves and double lay-ers in an ultra-relativistic degenerate dense dusty plasma. Phys. Lett. A 2010, 374, 4238. [Google Scholar] [CrossRef]
- Ghai, Y.; Saini, N.S.; Eliasson, B. Neutrino-driven Instability of Ion Acoustic Waves in an Ultrarelativistic Degenerate Plasma. Astrophys. J. 2019, 884, 27. [Google Scholar] [CrossRef]
- Kaur, N.; Kaur, R.; Saini, N.S. Ion-Acoustic Cnoidal Waves with the Density Effect of Spin-up and Spin-down Degenerate Electrons in a Dense Astrophysical Plasma. Z. Naturforsch. A 2020, 72, 103. [Google Scholar] [CrossRef] [Green Version]
- Soltani, H.; Mohsenpour, T.; Sohbatzadeh, F. Obliquely propagating quantum solitary waves in quantum-magnetized plasma with ultra-relativistic degenerate electrons and positrons. Contri. Plasma Phys. 2019, 59, 1. [Google Scholar] [CrossRef]
- El-Labany, S.K.; El-Taibany, W.F.; Behery, E.E.; Ebd-Elbaki, R. Oblique collision of ion acoustic solitons in a relativistic degenerate plasma. Sci. Rep. 2020, 10, 16152. [Google Scholar] [CrossRef] [PubMed]
- Saini, N.S.; Kaur, R. Ion-acoustic solitary, breathers, and freak waves in a degenerate quantum plasma. Waves Random Complex Media 2021. [Google Scholar] [CrossRef]
- Egedal, J.; Fox, W.; Porkolab, M.; Fasoli, A. Experimental evidence of fast recon-nec-tion via trapped electron motion. Phys. Plasmas 2004, 11, 2844. [Google Scholar] [CrossRef]
- Luque, A.; Schamel, H.; Fedele, R. Quantum corrected electron holes. Phys. Lett. A 2004, 324, 185. [Google Scholar] [CrossRef] [Green Version]
- El-Tantway, S.A.; Shan, S.A.; Akhtar, N.; Elgendy, A.T. Impact of electron trapping in degenerate quantum plasma on the ion-acoustic breathers and super freak waves. Chaos Solitons Fractals 2018, 113, 356. [Google Scholar] [CrossRef]
- Singh, K.; Singh, M.; Kaur, N.; Sethi, P.; Saini, N.S. Ion acoustic shocks in degenerate plasma with trapping in a quantizing magnetic field. AIP Conf. Proc. 2019, 2136, 060002. [Google Scholar]
- Hussain, S.; Ur-Rehman, H.; Mahmood, S. The effect of magnetic field quantization on the propagation of shock waves in quantum plasmas. Phys. Plasmas 2019, 26, 052105. [Google Scholar] [CrossRef]
- Deka, M.K.; Dev, A.N. Landau degeneracy effect on ion beam driven degenerate mag-neto plasma: Evolution of hypersonic soliton. Ann. Phys. 2018, 395, 45. [Google Scholar] [CrossRef]
- Kaur, R.; Singh, K.; Saini, N.S. Heavy-and light-nuclei acoustic dressed shock waves in white dwarfs. Chin. J. Phys. 2021, 72, 286. [Google Scholar] [CrossRef]
- Atteya, A.; Behery, E.E.; El-Taibany, W.F. Ion acoustic shock waves in a degenerate relativistic plasma with nuclei of heavy elements. Eur. Phys. J. Plus 2017, 132, 109. [Google Scholar] [CrossRef]
- Singh, K.; Sethi, P.; Saini, N.S. Nonlinear excitations in a degenerate relativistic mag-neto-rotating quantum plasma. Phys. Plasmas 2019, 26, 092104. [Google Scholar] [CrossRef]
- Singh, K.; Saini, N.S. Effect of Anisotropic Pressure on Electron Acoustic Oscillatory and Monotonic Shocks in Superthermal Magnetoplasma. Radio Sci. 2019, 54, 1192–1203. [Google Scholar] [CrossRef]
- Samanta, U.K.; Saha, A.; Chatterjee, P. Bifurcations of nonlinear ion acoustic travelling waves in the frame of a Zakharov-Kuznetsov equation in magnetized plasma with a kappa distributed elec-tron. Phys. Plasmas 2013, 20, 022111. [Google Scholar] [CrossRef]
- Saha, A.; Chatterjee, P. Dust ion acoustic travelling waves in the framework of a modi-fied Kadomtsev-Petviashvili equation in a magnetized dusty plasma with superthermal electrons. Astro-Phys. Space Sci. 2014, 349, 239. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics Part 1; But-ter-Worth-Heinemann: Oxford, UK, 1980. [Google Scholar]
- Malfliet, W. The tanh method: A tool for solving certain classes of nonlinear evolution and wave equations. J. Comput. Appl. Math. 2004, 164, 529. [Google Scholar] [CrossRef] [Green Version]
- Kourakis, I.; Sultana, S.; Verheest, F. Note on the single-shock solutions of the Korteweg-de Vries-Burgers equation. Astrophys. Space Sci. 2012, 338, 245. [Google Scholar] [CrossRef]
- El-Hanbaly, A.M.; El-Shewy, E.K.; Sallah, M.; Darweesh, H.F. Linear and nonlinear analysis of dust acoustic waves in dissipative space dusty plasmas with trapped ions. J. Theor. Appl. Phys. 2015, 9, 167. [Google Scholar] [CrossRef] [Green Version]
- Koester, D.; Chanmugam, G. Physics of white dwarf stars. Rep. Progr. Phys. 1990, 153, 837. [Google Scholar] [CrossRef]
- Ghosh, S.S.; Lakhina, G.S. Anomalous width variation of rarefactive ion acoustic sol-itary waves in the context of auroral plasmas. Nonlinear Process. Geophys. 2004, 111, 219. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaur, R.; Saini, N.S. Ion Acoustic Shocks in a Weakly Relativistic Ion-Beam Degenerate Magnetoplasma. Galaxies 2021, 9, 64. https://doi.org/10.3390/galaxies9030064
Kaur R, Saini NS. Ion Acoustic Shocks in a Weakly Relativistic Ion-Beam Degenerate Magnetoplasma. Galaxies. 2021; 9(3):64. https://doi.org/10.3390/galaxies9030064
Chicago/Turabian StyleKaur, Rupinder, and Nareshpal Singh Saini. 2021. "Ion Acoustic Shocks in a Weakly Relativistic Ion-Beam Degenerate Magnetoplasma" Galaxies 9, no. 3: 64. https://doi.org/10.3390/galaxies9030064
APA StyleKaur, R., & Saini, N. S. (2021). Ion Acoustic Shocks in a Weakly Relativistic Ion-Beam Degenerate Magnetoplasma. Galaxies, 9(3), 64. https://doi.org/10.3390/galaxies9030064





