Thermodynamic Constraints on the Non-Baryonic Dark Matter Gas Composing Galactic Halos
Abstract
1. Introduction
2. Theory
2.1. Classical Thermodynamics with and without Radiative Transfer
2.2. Kinetic Theories of Gas, Elastic and Inelastic
2.2.1. Gas Temperature Depends on Kinetic Energy
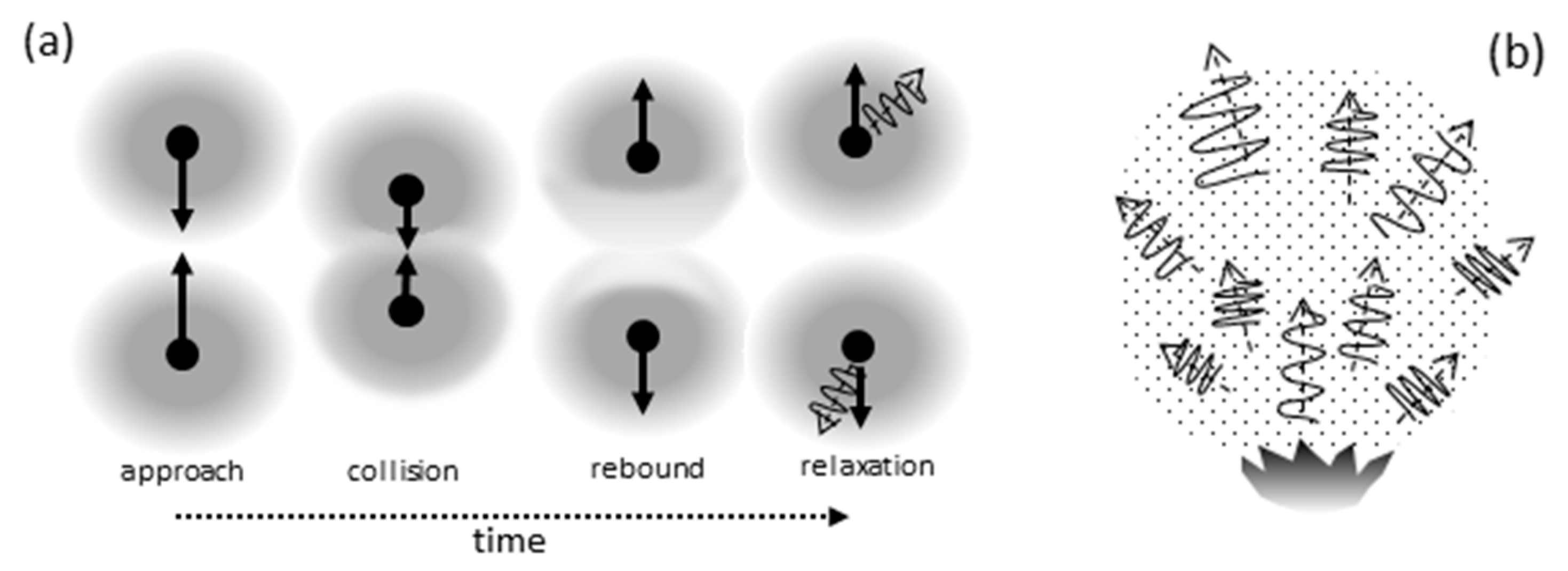
2.2.2. Inelastic Collisions and Blackbody Emissions
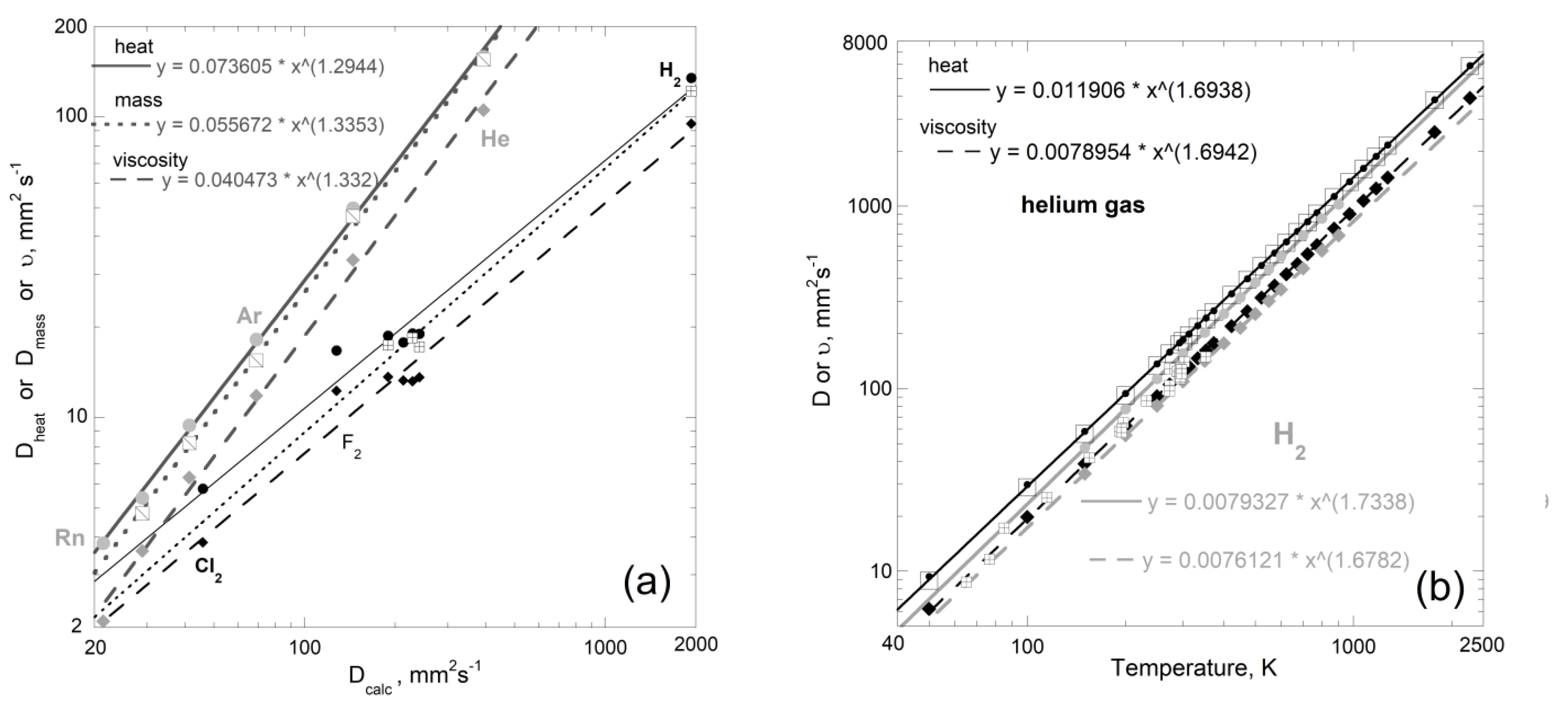
2.2.3. Cross Sections, Interactions during Collisions, and Transport Properties
2.3. Interactions of Matter with Light (Heat)
2.4. Simplifications Associated with Astronomical Scales and Monatomic Baryonic Gases
3. Thermodynamic Behavior of Non-Baryonic Dark Matter Halos
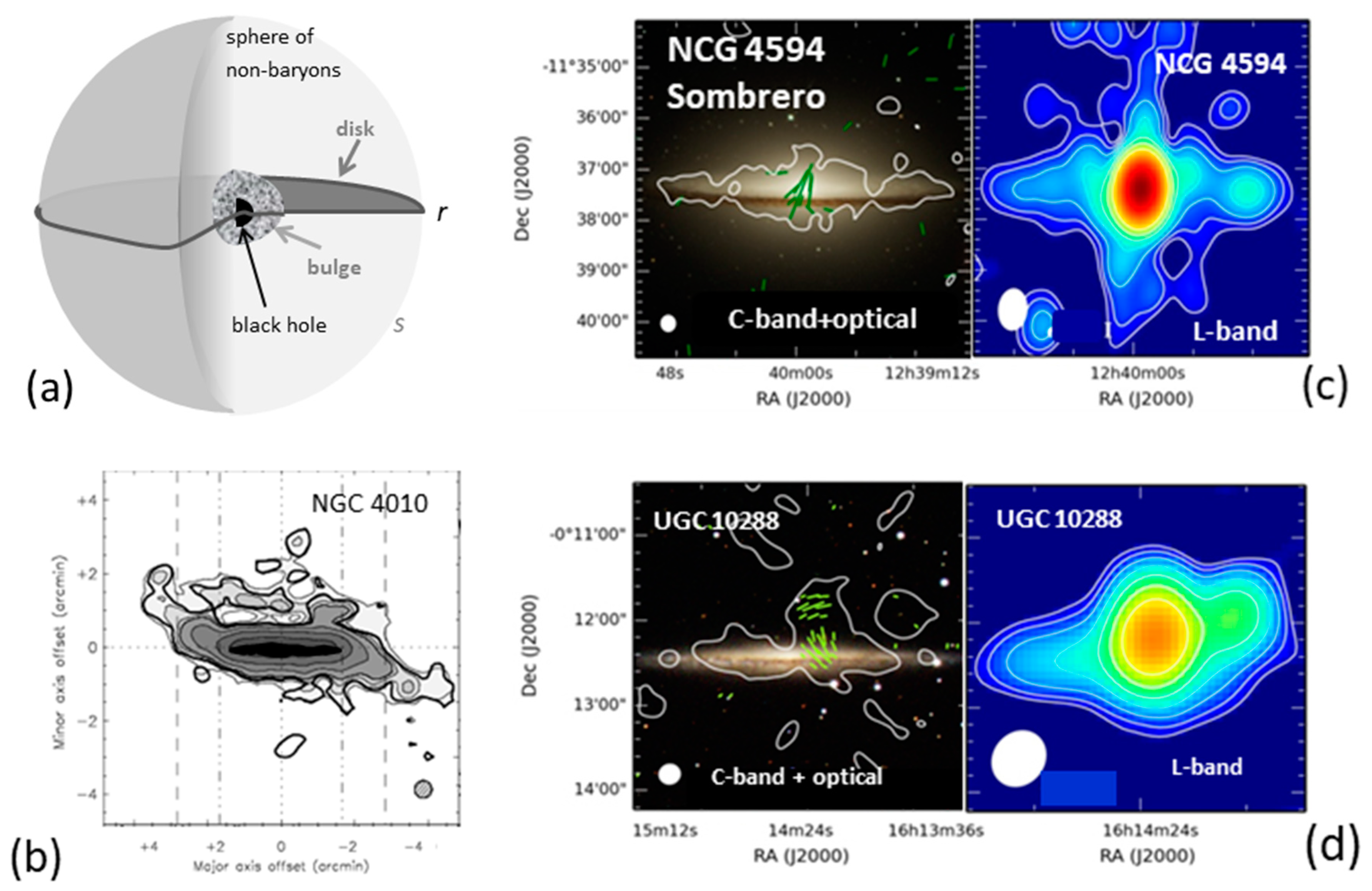
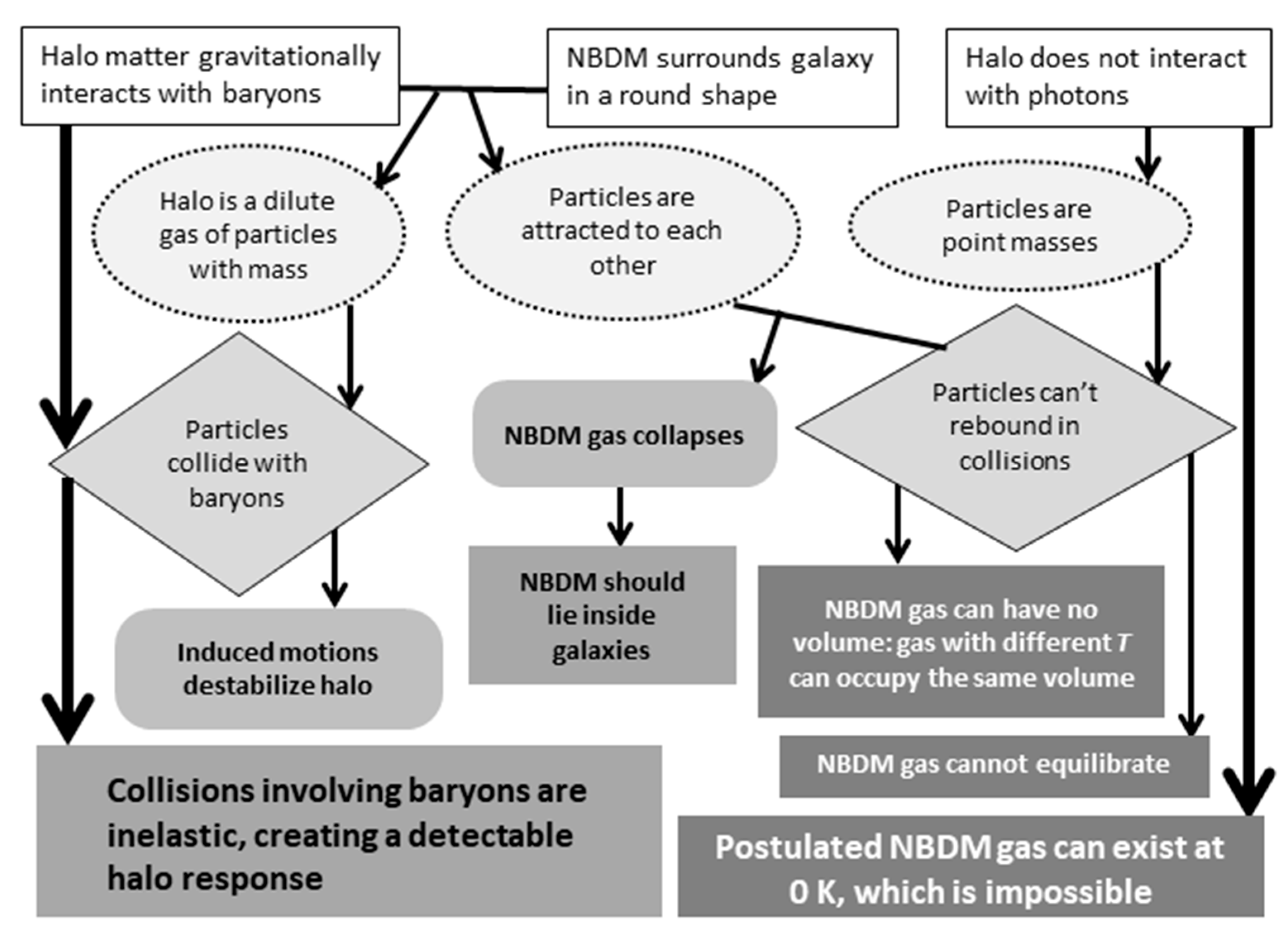
3.1. NBDM Halos Are a Type of Gas
3.1.1. NBDM Gas Contains Particles
3.1.2. Motions and Forces Inside an NBDM Halo
3.2. Gravitation and Collisions
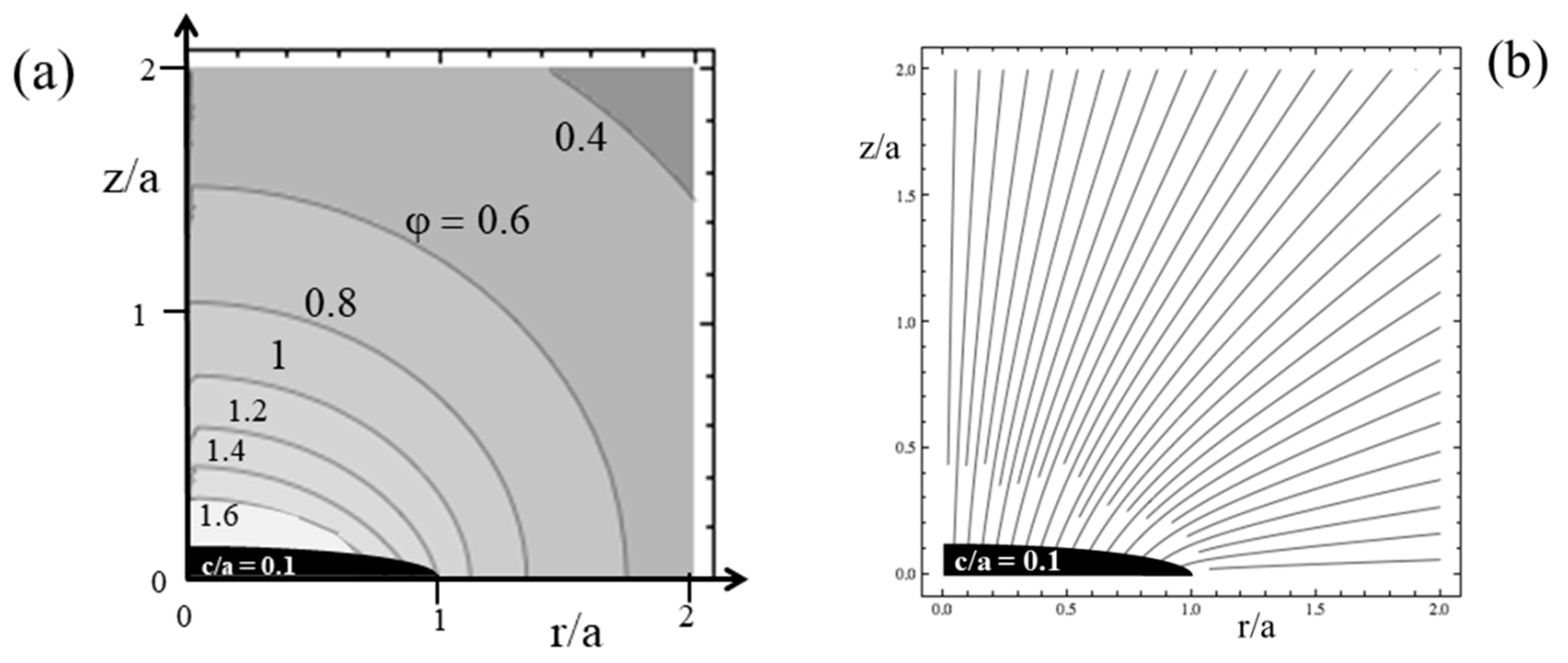
3.2.1. Gravitational Attraction of NBDM to Baryons Requires Collisions
3.2.2. Limitations on the Size of NBDM Particles in View of Their Collisions
3.3. Thermal Consequences of Pure NBDM Halos Not Interacting with Photons
3.3.1. Implications on Halo Gas Volume
3.3.2. Implications on Galaxy Structure
3.3.3. Can the Particles Be Very, Very Tiny Rather Than Being Point Masses?
3.3.4. Summary on the Thermodynamics of a Pure NBDM Gas
3.4. Thermal Consequences of Baryons Colliding with NBDM Particles
4. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Rubin, V.C.; Ford, W.K. Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Faber, S.M.; Gallagher, J.S. Masses and mass-to-light ratios of galaxies. Ann. Rev. Astron. Astrophys. 1979, 17, 135–187. [Google Scholar] [CrossRef]
- Trimble, V. Existence and nature of dark matter in the universe. Ann. Rev. Astron. Astrophys. 1987, 25, 425–472. [Google Scholar] [CrossRef]
- Geist, K. Wimps and machos. In Encyclopedia of Astronomy and Astrophysics; Murdin, P., Ed.; Institute of Physics Publishing: Bristol, UK, 2006. [Google Scholar] [CrossRef]
- Ackermann, M.; Albert, A.; Anderson, B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Bissaldi, E.; et al. Dark matter constraints from observations of 25 Milky Way satellite galaxies with the Fermi Large Area Telescope. Phys. Rev. D 2014, 89, 042001. [Google Scholar] [CrossRef]
- De Vega, H.J.; Salucci, P.; Sanchez, N.G. Observational rotation curves and density profiles versus the Thomas-Fermi galaxy structure theory. Mon. Not. R. Astron. Soc. 2014, 442, 2717–2727. [Google Scholar] [CrossRef]
- Gaitskill, R.J. Direct detection of dark matter. Annu. Rev. Nucl. Part. Sci. 2004, 54, 315–359. [Google Scholar] [CrossRef]
- Dark Matter. Available online: https://en.wikipedia.org/wiki/Dark_matter (accessed on 26 April 2020).
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Feng, J.L. Dark matter candidates from particle physics and methods of detection. Annu. Rev. Astron. Astrophys. 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Giagu, S. WIMP dark matter searches with the ATLAS detector at the LHC. Front. Phys. 2019, 7. [Google Scholar] [CrossRef]
- Nagano, K.; Fujita, T.; Michimura, Y.; Obata, I. Axion dark matter search with interferometric gravitational wave detectors. Phys. Rev. Lett. 2019, 123. [Google Scholar] [CrossRef]
- Garcia-Ruiz, I.; Sancisi, R.; Kuijken, K. Neutral hydrogen and optical observations of edge-on galaxies: Hunting for warps. Astron. Astrophys. 2002, 394, 769–789. [Google Scholar] [CrossRef]
- Wiegert, T.; Irwin, J.; Miskolczi, A.; Schmidt, P.; Carolina Mora, S.; Damas-Segovia, A.; Stein, Y.; English, J.; Rand, R.J.; Santistevan, I. CHANG-ES IV. Radio continuum emission of 35 edge-on galaxies observed with the Karl G. Jansky very large array in D configuration—Data release 1. Astronom. J. 2015, 150, 81. [Google Scholar] [CrossRef]
- CHANG-ES Continuum Halos in Nearby Galaxies- and EVLA Survey. Available online: http://www.queensu.ca/changes (accessed on 26 January 2020).
- Burbidge, G. On the masses and relative velocities of galaxies. Astrophys. J. 1975, 196, L7–L10. [Google Scholar] [CrossRef]
- Bottema, R.; Pestaña, J.L.G. The distribution of dark and luminous matter inferred from extended rotation curves. Mon. Not. R. Astron. Soc. 2015, 448, 2566–2593. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Debated Models for Galactic Rotation Curves: A Review and Mathematical Assessment. Galaxies 2020, 8, 47. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Brownstein, J.R.; Moffat, J.W. Galaxy rotation curves without nonbaryonic dark matter. Astrophys. J. 2006, 636, 721–741. [Google Scholar] [CrossRef]
- Lin, H.-N.; Li, M.-H.; Li, X.; Chang, Z. Galaxy rotation curves in the Grumiller’s modified gravity. Mon. Not. R. Astron. Soc. 2013, 430, 450–458. [Google Scholar] [CrossRef]
- Feng, J.Q.; Gallo, C.F. Mass distribution in rotating thin-disk galaxies according to Newtonian dynamics. Galaxies 2014, 2, 199–222. [Google Scholar] [CrossRef]
- Pavlovich, K.; Pavlovich, A.; Sipols, A. Newtonian explanation of galaxy rotation curves based on distribution of baryonic matter. arXiv 2014, arXiv:1406.2401P. [Google Scholar]
- Marr, J.H. Galaxy rotation curves with lognormal density distribution. Mon. Not. R. Astron. Soc. 2015, 448, 3229. [Google Scholar] [CrossRef]
- McGaugh, S.S. A tale of two paradigms, the mutual incommensurability of LCDM and MOND. Can. J. Phys. 2015, 93, 250–259. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. The physics of galactic spin. Can. J. Phys. 2017, 95, 156–166. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Implications of Geometry and the Theorem of Gauss on Newtonian Gravitational Systems and a Caveat Regarding Poisson’s Equation. Galaxies 2017, 5, 89. [Google Scholar] [CrossRef]
- De Swart, J.G.; Bertone, G.; van Dongen, J. How dark matter came to matter. Nat. Astron. 2017, 1, 0059. [Google Scholar] [CrossRef]
- Suleiman, R. A Model of Dark Matter and Dark Energy Based on Relativizing Newton’s Physics. World J. Condens. Matter Phys. 2018, 8, 130–155. [Google Scholar] [CrossRef][Green Version]
- Zemansky, M.W.; Dittman, R.H. Heat and Thermodynamics, 6th ed.; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Tolman, R.C. Relativity, Thermodynmaics and Cosmology; Oxford University Press: Oxford, UK, 1934. [Google Scholar]
- Reif, F. Fundamentals of Statistical and Thermal Physics; McGraw-Hill Book Company: St. Louis, MO, USA, 1965. [Google Scholar]
- Hofmeister, A.M. Measurements, Mechanisms, and Models of Heat Transport; Elsevier: Amsterdam, The Netherlands, 2019; Chapters 1, 2, 5 and 8. [Google Scholar]
- Fang, T.; Buote, D.A.; Humphrey, P.J.; Canizares, C.R.; Zappacosta, L.; Maiolino, R.; Tagliaferri, G.; Gastaldello, F. Confirmation of X-ray absorption by warm-hot intergalactic medium in the sculptor wall. Astrophys. J. 2010, 714, 1715–1724. [Google Scholar] [CrossRef]
- Sofue, Y.; Rubin, V.C. Rotation curves of spiral galaxies. Ann. Rev. Astron. Astrophys. 2001, 39, 137–174. [Google Scholar] [CrossRef]
- Truesdell, C. The Tragicomical History of Thermodynamics; Springer: New York, NY, USA, 1980. [Google Scholar]
- Fegley, B., Jr. Practical Chemical Thermodynamics for Geoscientists; Academic Press/Elsevier: Waltham, MA, USA, 2015. [Google Scholar]
- Norton, J.D. The impossible process: Thermodynamic reversibility. Stud. Hist. Philos. Mod. Phys. 2016, 55, 43–61. [Google Scholar] [CrossRef]
- Barr, E.S. Historical survey of the early development of the infrared spectral region. Am. J. Phys. 1960, 28, 42–54. [Google Scholar] [CrossRef]
- Purrington, R.D. Physics in the Nineteenth Century; Rutgers University Press: New Brunswick, NJ, USA, 1997. [Google Scholar]
- McGucken, W. Nineteenth-Century Spectroscopy; The Johns Hopkins Press: Baltimore, MD, USA; London, UK, 1969. [Google Scholar]
- Pippard, A.B. The Elements of Classical Thermodynamics; Cambridge University Press: London, UK, 1974. [Google Scholar]
- Williams, B.W. A specific mathematical form for Wien’s displacement law as νmax/T = constant. J. Chem. Educ. 2014, 91, 623. [Google Scholar] [CrossRef]
- Valluri, S.R.; Corless, R.M.; Jeffrey, D.J. Some applications of the Lambert W function to physics. Can. J. Phys. 2000, 78, 823–831. [Google Scholar]
- Marr, J.M.; Wilkin, F.P. A better presentation of Planck’s radiation law. Am. J. Phys. 2012, 80, 339–405. [Google Scholar] [CrossRef]
- Kangro, H. Early History of Planck’s Radiation Law; Taylor and Francis: London, UK, 1976. [Google Scholar]
- Kragh, H. Max Planck: The reluctant revolutionary. Phys. World 2000, 13, 31–35. [Google Scholar] [CrossRef]
- Bergin, E.A.; Tafalla, M. Cold dark clouds: The initial conditions for star formation. Ann. Rev. Astron. Astrophys. 2007, 45, 339–396. [Google Scholar] [CrossRef]
- Trusler, J.P.M. Kinetic Theory of Gases. Available online: http://www.thermopedia.com/content/907/ (accessed on 9 September 2018).
- Brouard, M.; Chadwick, H.; Gordon, S.D.S.; Hornung, B.; Nichols, B.; Aoiz, F.J. Stereodynamics in NO(X)1+Ar inelastic collisions. J. Chem. Phys. 2016, 144, 224301. [Google Scholar] [CrossRef] [PubMed]
- Clausius, R. On a mechanical theorem applicable to heat. Phil. Mag. 1870, 40, 122–127. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Spatial and symmetry constraints as the basis of the virial theorem and astrophysical implications. Can. J. Phys. 2016, 94, 380–388. [Google Scholar] [CrossRef]
- Berberan-Santos, M.N.; Bodunov, E.N.; Polliani, L. The van der Waals equation: Analytical and approximate solutions. J. Math. Chem. 2008, 43, 1437–1457. [Google Scholar] [CrossRef]
- Kestin, J.; Knierrim, K.; Mason, E.A.; Najafi, B.; Ro, S.T.; Waldman, M. Equilibrium and transport properties of the noble gases and their mixtures at low density. J. Phys. Chem. Ref. Data 1984, 13, 229–303. [Google Scholar] [CrossRef]
- Suárez-Iglesias, O.; Medina, I.; Sanz, M.; Pizarro, C.; Bueno, J.L. Self-diffusion in molecular fluids and noble gases: Available data. J. Chem. Eng. Data 2015, 60, 2757–2817. [Google Scholar] [CrossRef]
- Bates, J.B. Infrared emission spectroscopy. Fourier Transform. IR Spect. 1978, 1, 99–142. [Google Scholar]
- Kellogg, O.D. Foundations of Potential Theory; Dover Publications: New York, NY, USA, 1953. [Google Scholar]
- Hofmeister, A.M.; Criss, R.E.; Criss, E.M. Verified solutions for the gravitational attraction to an oblate spheroid: Implications for planet mass and satellite orbits. Planet. Space Sci. 2018, 152, 68–81. [Google Scholar] [CrossRef]
- Brewster, M.Q. Thermal Radiative Transfer and Properties; John Wiley & Sons: New York, NY, USA, 1992. [Google Scholar]
- Siegel, R.; Howell, J.R. Thermal Radiation Heat Transfer; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Wiegert, T.; English, J. Kinematic classification of non-interacting spiral galaxies. New Astron. 2014, 26, 40–61. [Google Scholar] [CrossRef]
- Ferrière, K. The interstellar environment of our galaxy. Rev. Mod. Phys. 2011, 73, 1031. [Google Scholar] [CrossRef]
- NASA/IPAC Extragalactic Database. Available online: https://ned.ipac.caltech.edu/ (accessed on 10 January 2020).
- Müller, I. Entropy: A subtle concept in thermodynamics. In Entropy; Greven, A., Keller, G., Warnecke, G., Eds.; Princeton University Press: Princeton, NJ, USA, 2003; pp. 17–36. [Google Scholar]
- Electromagnetic Spectrum. Available online: https://en.wikipedia.org/wiki/Electromagnetic_spectrum (accessed on 30 April 2020).
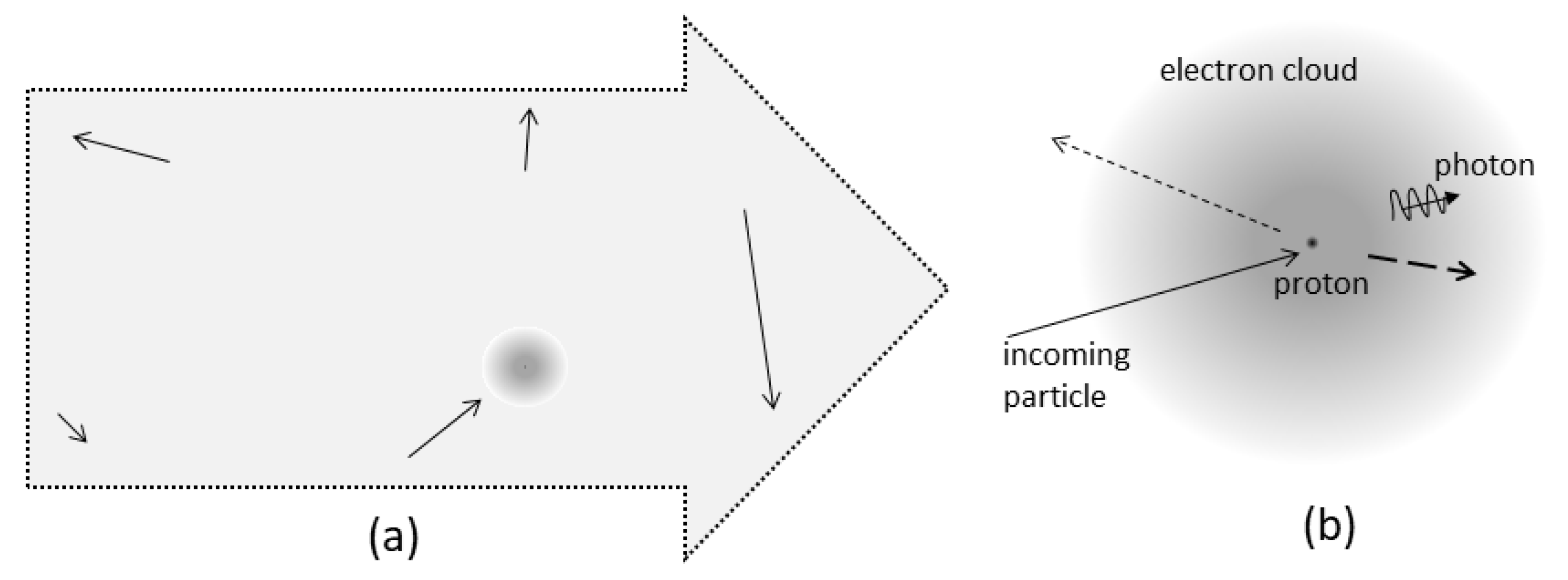
| Postulated Properties of Non-Baryons | Key Consequences 1 |
|---|---|
| Gravitationally interacts with ordinary matter | NBDM has mass; collisions must occur |
| Negligibly interacts with photons | Nearly point masses; elastic collisions |
| Distributed in a large halo around galaxies | A dilute assembly of particles (a gas) |
| Law No. | Classical Statement 1 |
|---|---|
| 0th | Equilibrium between systems is communicable |
| 1st | Energy is conserved if heat is accounted for |
| 2nd | Flow of heat from a colder to a hotter body cannot occur as a sole result |
| 3rd | Absolute zero is unattainable by processes involving finite steps |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmeister, A.M. Thermodynamic Constraints on the Non-Baryonic Dark Matter Gas Composing Galactic Halos. Galaxies 2020, 8, 77. https://doi.org/10.3390/galaxies8040077
Hofmeister AM. Thermodynamic Constraints on the Non-Baryonic Dark Matter Gas Composing Galactic Halos. Galaxies. 2020; 8(4):77. https://doi.org/10.3390/galaxies8040077
Chicago/Turabian StyleHofmeister, Anne M. 2020. "Thermodynamic Constraints on the Non-Baryonic Dark Matter Gas Composing Galactic Halos" Galaxies 8, no. 4: 77. https://doi.org/10.3390/galaxies8040077
APA StyleHofmeister, A. M. (2020). Thermodynamic Constraints on the Non-Baryonic Dark Matter Gas Composing Galactic Halos. Galaxies, 8(4), 77. https://doi.org/10.3390/galaxies8040077




