Gravitational Focusing of Low-Velocity Dark Matter on the Earth’s Surface

Abstract

We show that the Earth acts as a high-efficiency gravitational collector of low-velocity flow of dark matter (DM). The focal point appears on the Earth’s surface, when the DM flow speed is about 17 km/s with respect to the geo-center. We discuss diurnal modulation of the local DM density influenced by the Earth’s gravity. We also touch upon similar effects on galactic and solar system objects.

1. Introduction

The local dark matter (DM) density in the Solar vicinity has been extensively estimated in the last decades using the rotation curve of the Milky Way, and has a converging value of ${\rho }_{\odot }\sim 0.4$ GeV cm${}^{-3}$ [1,2,3]. However, thus measured density gives only an averaged value around the Solar system integrated over the phase space. Information of more specific behaviors of DM as a function of the space (direction) and velocity would be crucial for the direct detection experiments as well as for determining the physical properties of the detected particles from the event count rates [4,5,6]. The DM density distribution as a function of the particle’s velocity, or the spectral DM density (SDD) as well as its time variation (modulation) in the laboratory frame on the Earth’s surface would provide useful information for such experiments.

Annual, monthly, and daily modulations of the flux of SDD due to the motion of the Earth as well as to the gravitational perturbation in the Solar system have been thoroughly investigated [6,7,8,9,10,11]. It has been suggested that the daily modulation of the gravitational focusing by the Earth leads to amplification of the local density to a detectable level [12]. It has been also shown that gravitational focusing of WIMP (weakly interacting massive particles) with zero velocity dispersion in the rest frame enhances the density by ∼${10}^8$ times at a certain focal point in the interplanetary space [13]. Besides the gravity, scattering by the Earth’s nucleons is also suggested to cause modulations [14]. We here, however, consider only the gravitational interaction. If the DM has a directional streaming, the differential SDD at a certain velocity (range) is amplified by the focusing effect due to the gravitational force by a celestial object.

We here consider the gravity of the Earth, which has the largest solid angle among the celestial objects, assuming that the detector is located on the Earth’s surface. We show that DM flux at a particular geo-centric velocity converges on the Earth’s surface with high amplification. Such focusing effect would be useful to be considered not only for the detection purpose but also for interpreting the physics of the measured flux.

2. Focusing by the Earth

We consider a case that the DM streaming is monochromatic, and trace the motion of DM particles by solving the equations of motion

$$\frac{d^2\mathbf{r}}{d{t}^2}=-G\frac{M\left(r\right)}{r^2}\frac{\mathbf{r}}{r},$$

(1)

where $\mathrm{r}=(x,y,z)$ is the geo-centric coordinates. $M\left(r\right)={\int }_0^{r}4\pi p^2\rho \left(s\right)ds$ is the mass of the gravitating body, which is assumed to have spherical density distribution. We neglect the Coriolis force and parallactic aberration due to the spin of the Earth.

2.1. Point Mass

We first examine a case of a point mass, or $M\left(R\right)=const.$ as applied to the gravitational deflection of DM flux by the Sun [7]. A point mass acts as a semi-concave collector, and the DM particles are scattered because of the decreasing deflection angle with increasing impact parameter, resulting in diverging orbits (Figure 1). Hence, focusing occurs only of DM particles with a particular impact parameter, which results in focusing from a small circle (ring on the sky) around the gravitating body.

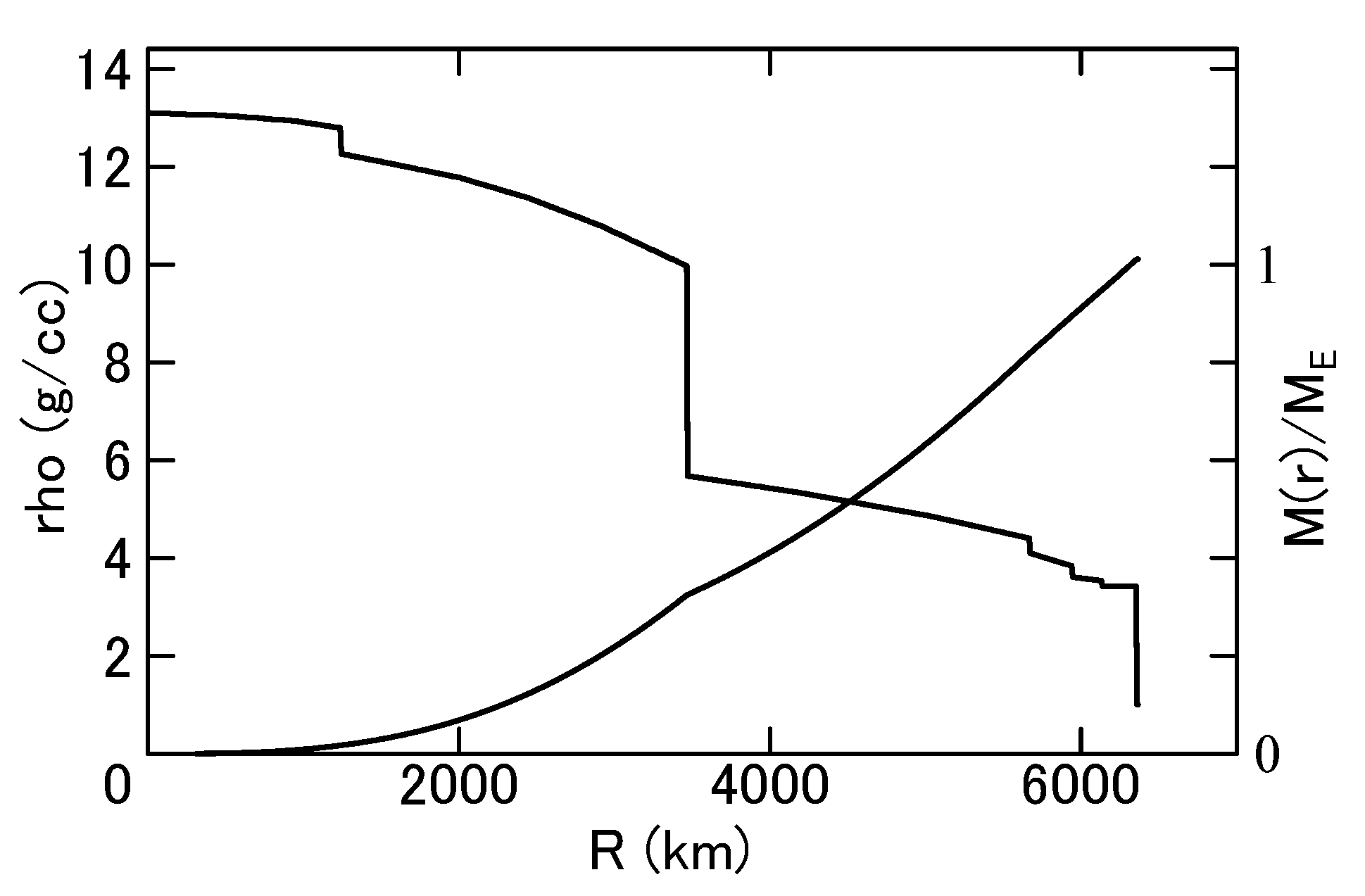
2.2. Uniform Density Sphere

On the other hand, an object like the Earth with sufficiently large solid angle with uniform density acts as a real convex collector having a focal point. The orbits of DM particles are deflected by the Earth’s gravity when the geo-centric velocity is slow enough around $v\sim R_{\mathrm{E}}\sqrt{2\pi G{\rho }_{\mathrm{E}}}\sim 10\mathrm{km}{\mathrm{s}}^{-1}$. Here, $R_{\mathrm{E}}=(R_{\mathrm{eq}.}\times R_{\mathrm{pole}})\simeq {(6378\times 6356)}^{1/2}=6367$ km is the mean radius and ${\rho }_{\mathrm{E}}\sim 5.53$ g cm${}^{-3}$ is the mean density for a total mass of $M_{\mathrm{E}}=5.974\times {10}^{27}$ g.

Figure 1a,b show the orbits of DM particles with initial injection velocity of 6 km s${}^{-1}$ in a spherical gravitational potential in two extreme cases, where the Earth is assumed to be a point mass of $M_{\mathrm{E}}$ and a sphere of uniform density ${\rho }_{\mathrm{E}}$, respectively.

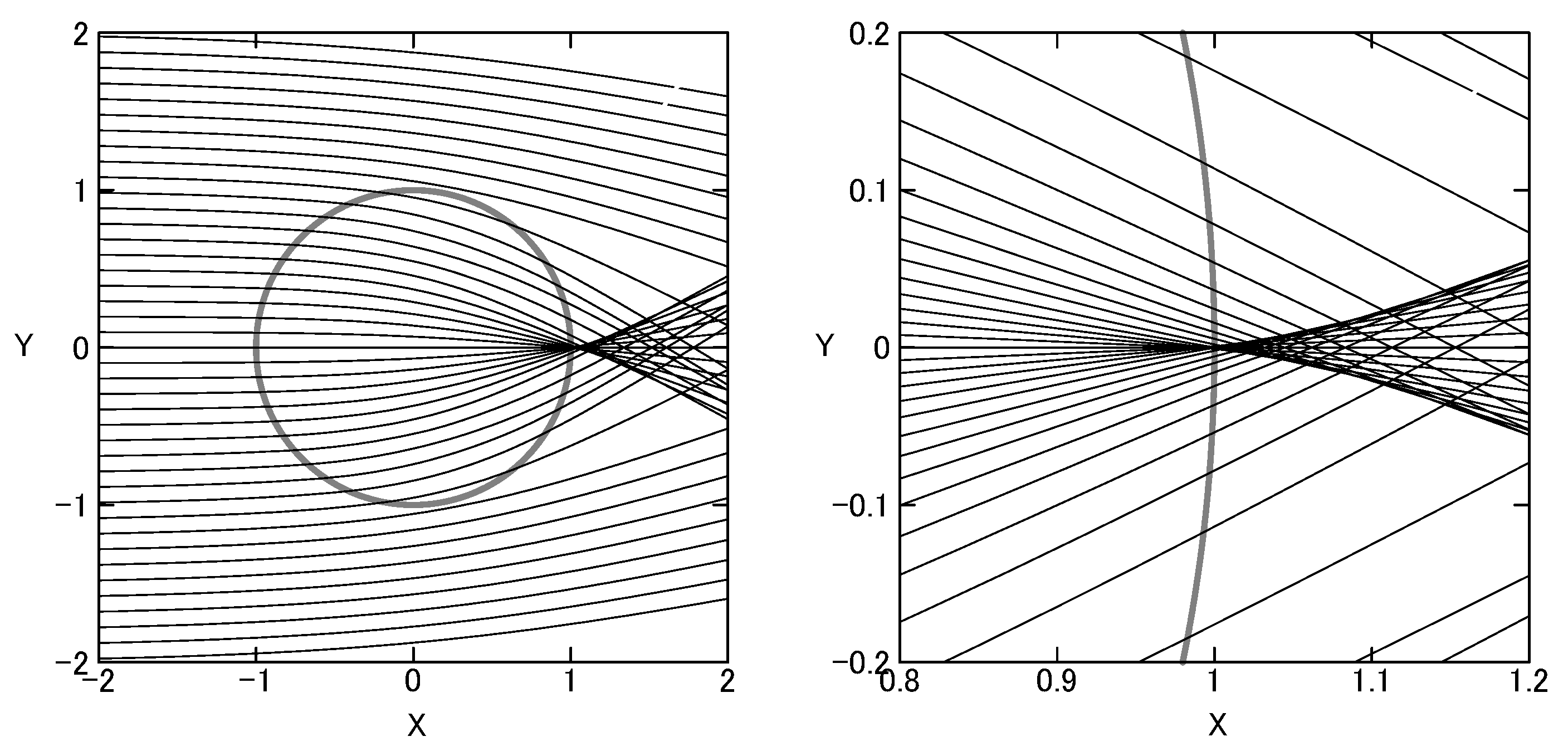
2.3. Gravitational Focusing by the Earth

More realistic orbits of DM particles can be traced by solving the equations of motion in gravitational field of the real Earth. We assume that the Earth is a sphere of radius $R_{\mathrm{E}}$ with density profile as shown in Figure 2 [15]. We take the Cartesian coordinates $(x,y,z)$ with the geo-center being at (0,0,0), x axis is through the detector on the Earth surface toward the zenith, and y and z are perpendicular axes.

We trace the orbits of DM particles put on a plane sufficiently remote from the Earth, or at $x=x_{\mathrm{ini}}=-100R_{\mathrm{E}}$, by integrating the differential equations 1 with initial velocities $v_x=v_{\mathrm{inj}}$, $v_y=0$ and $v_z=0$. Calculations were obtained for various values of $v_{\mathrm{inj}}$. An efficient focusing on the Earth’s surface was found to occur, when the initial velocity is close to $v_{\mathrm{inj}}=17$ km s${}^{-1}$. Figure 3 shows the orbits of DM in such a special case.

The figure shows that DM particles sharply focus on the Earth’s surface, where they cross each other, exhibiting high-efficiency conversion and amplification of the flux. Thus, the Earth plays a role of an ideal collector of DM flow at 17 km s${}^{-1}$. It may be emphasized that the DM flow within $0.2R_{\mathrm{E}}$, or aperture $D\sim 0.4R_{\mathrm{E}}\sim 5000$ km s${}^{-1}$, the collector is almost aberration free, having a sharp focal point (Figure 3). If some aberration is allowed, the aperture diameter is as large $D\sim R_{\mathrm{E}}\sim$ 12,000 km.

3. Spectral Density and Flux Amplification

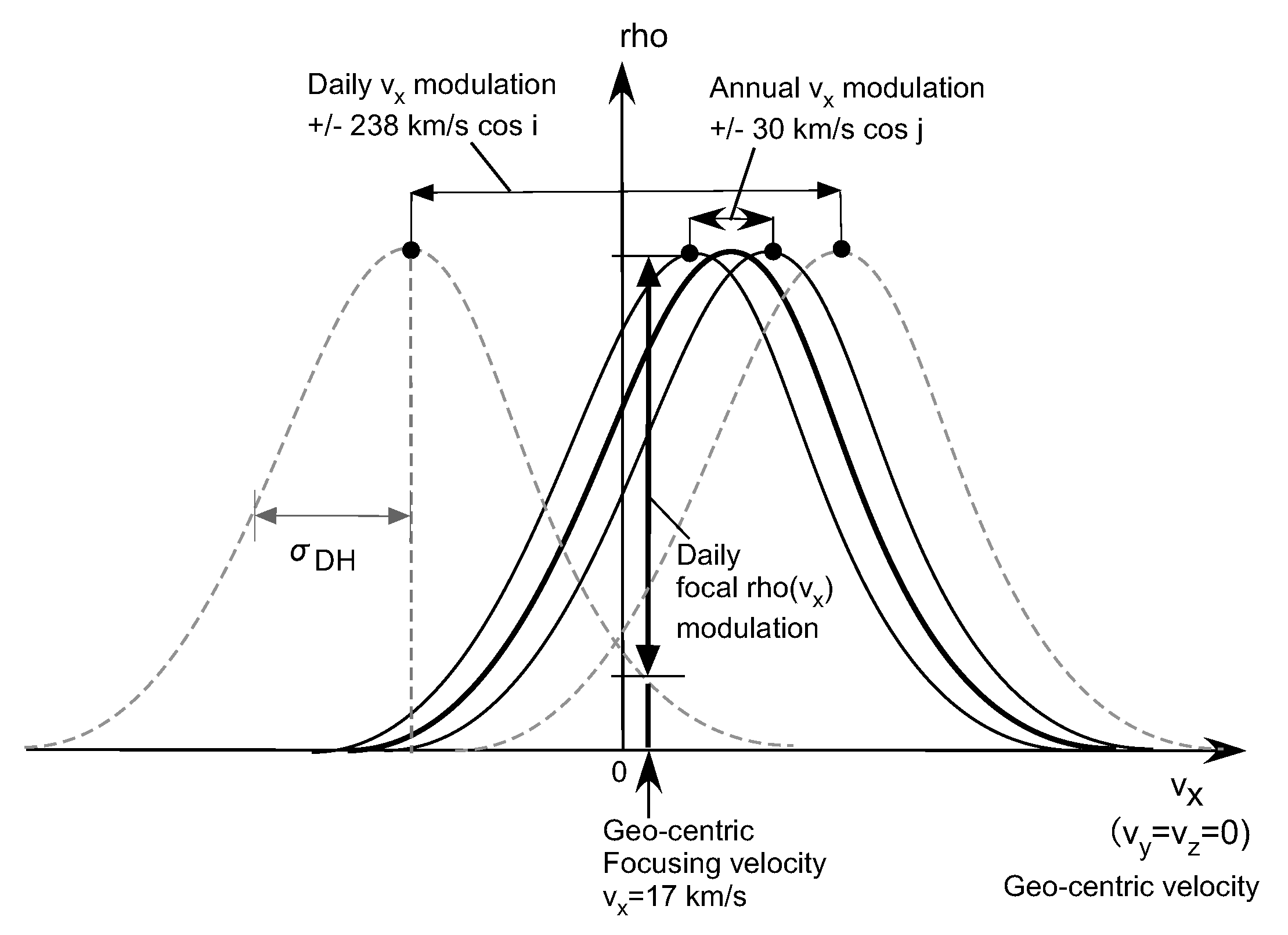
3.1. Spectral DM Density

We assume that the DM particles are distributed uniformly in the space around the Earth, but their velocities are not uniform and anisotropic, obeying the Maxwellian distribution represented by

$$\rho \left(\mathbf{v}\right)=\frac{{\rho }_{\odot }}{{\left(2\pi {\sigma }_{\mathrm{DH}}^2\right)}^{3/2}}exp\left(-\frac{\left[{(v_x+v_{x\mathrm{E}})}^2+{(v_y+v_{y\mathrm{E}})}^2+{(v_z+v_{z\mathrm{E}})}^2\right]}{2{\sigma }_{\mathrm{DH}}^2}\right).$$

(2)

Here, $\mathbf{v}=(v_x,v_y,v_z)$ is the 3D velocity of a DM particle with respect to the geo-center ($v_x\sim 17$ km s${}^{-1}$, $v_y\sim v_z\sim 0$ within $\delta v$), ${\mathbf{v}}_{\mathrm{E}}=(v_{x\mathrm{E}},v_{y\mathrm{E}}{v}_{z\mathrm{E}})$ is the 3D velocity of the Earth with respect to the dark halo in the rest frame fixed to the Milky Way, which include the solar motion, galactic rotation of the local standard of rest (LSR), and Earth’s rotation around the Sun, and ${\sigma }_{\mathrm{DH}}$ is the velocity dispersion of the dark halo.

According to the rotation of the coordinates due to the Earth’s spin, injecting DM flux varies with time and position of the detector. The daily velocity variation (modulation) is large, following the change in the $v_x$ axis direction between the up- and down-stream directions of the Galactic rotation at $V_{\mathrm{rot}}=238$ km s${}^{-1}$ in the DM halo at rest. The amplitude attains maximum, when the $v_x$ axis lies in the plane including the Sun’s motion toward $(l,b)\sim ({90}^{\circ },0^{\circ })$ for a detector located at geographic latitude $\beta \sim \pm {48}^{\circ }$ (Figure 4). The directional aberration of the DM flux due to the spin of the Earth is about ∼$0.46\mathrm{km}{\mathrm{s}}^{-1}/v\cos \beta$ toward the east, where $\beta$ is the geographic latitude, and may be neglected compared with the detector’s angular resolution.

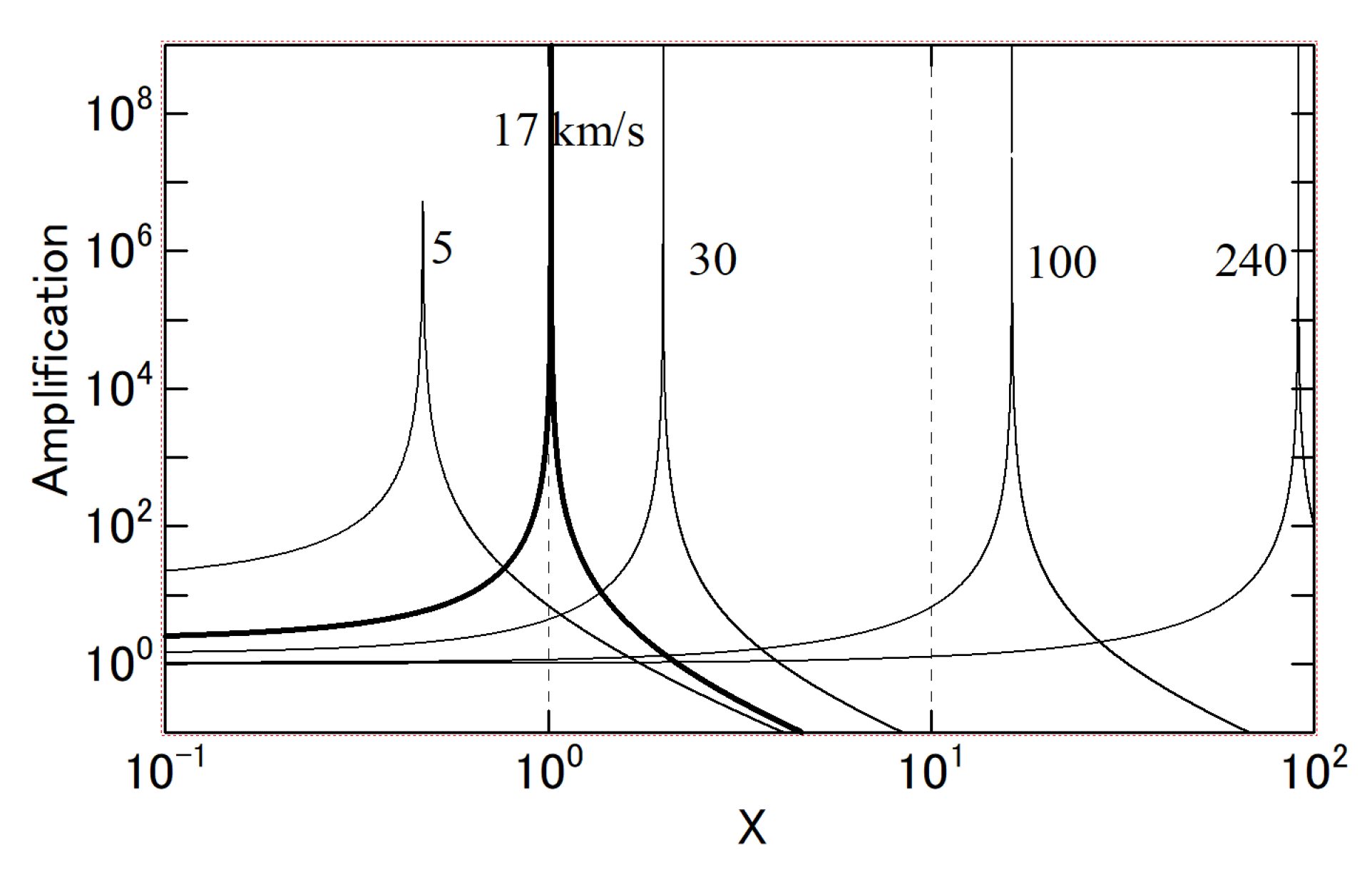
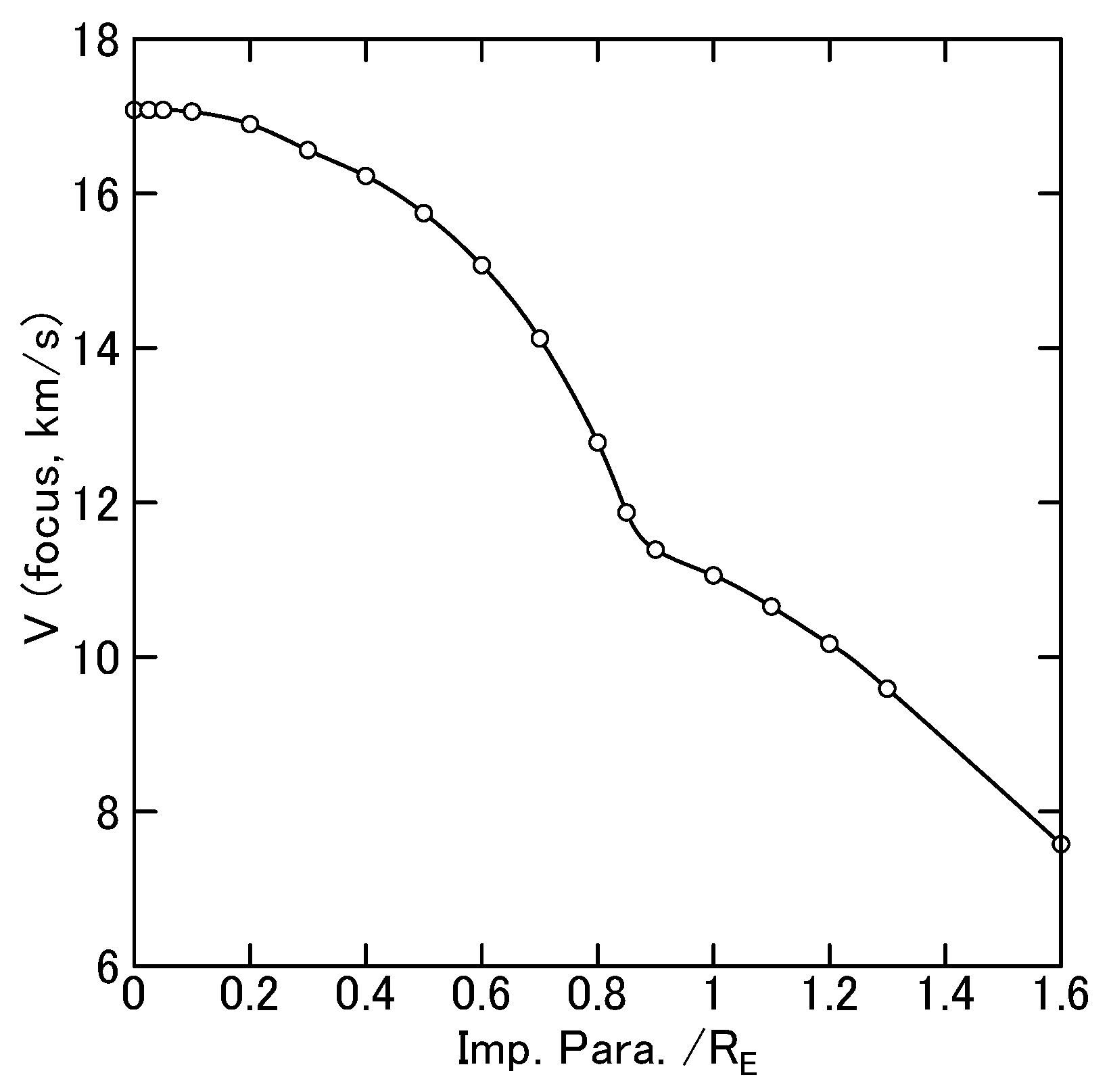
3.2. Amplification

We introduce an amplification factor $\mathcal{A}\left(v\right)$ of DM flux defined by

$$\mathcal{A}\left(v\right)=\frac{S_{\mathrm{aperture}}}{S_{\mathrm{fucus}}}={\left(\frac{r_{\mathrm{aperture}}}{r_{\mathrm{focus}}}\right)}^2,$$

(3)

where $S_{\mathrm{aperture}}=\pi r_{\mathrm{aperture}}^2$ is the collecting area (aperture) of the injection flux enclosed by a circle of the impact parameter $r_{\mathrm{ini}}=r_{\mathrm{aperture}}$, and $S_{\mathrm{focus}}=\pi r_{\mathrm{focus}}^2$ is the focal area, respectively.

In Figure 5 we plot the amplification factor $\mathcal{A}\left(v\right)$ as a function of the distance from the geo-center for DM flows with injection velocity $v=5$, 17, 30, 100 and 240 km s${}^{-1}$ for near axis orbits with initial $y=0.1R_{\mathrm{E}}$. The focal position moves with the injection velocity, and the maximum amplification at the focus on the Earth’s surface is obtained for a particular injection velocity of $v_{\mathrm{inj}}=17$ km s${}^{-1}$. The amplitude reaches as high as $\mathcal{A}\sim {10}^9$ times the initial flux in the present computation. In principle, however, the amplification reaches infinity at the focus according to the geometry of particles’ trajectories crossing the x axis.

By the focusing, DM particles enclosed by an aperture of radius $r_{\mathrm{aperture}}$ in a velocity range $v_x=v-\delta v/2$ and $v+\delta v/2$ are collected, attaining the maximum amplification at the focus to yield DM density as high as

$$\Delta {\rho }_{\mathrm{aperture}}\sim {\left(\frac{r_{\mathrm{aperture}}}{r_{\mathrm{focus}}}\right)}^2\Delta \rho \sim {\left(\frac{r_{\mathrm{aperture}}}{r_{\mathrm{focus}}}\right)}^2{\int }_{v-\delta v/2}^{v+\delta v/2}{\int }_{\delta v/2}^{\delta v/2}{\int }_{\delta v/2}^{\delta v/2}\rho \left(\mathrm{v}\right)d{v}_{x}d{v}_{y}d{v}_z.$$

(4)

The integral part is on the order of $\mathcal{O}\left(1\right){\rho }_{\odot }{(\delta v/{\sigma }_{\mathrm{DH}})}^3$ for small $\delta v_x$ etc., so that the equation may be rewritten for an order-magnitude estimation as

$$\Delta {\rho }_{\mathrm{Earth}}\sim {\rho }_{\odot }{\left(\frac{r_{\mathrm{aperture}}}{r_{\mathrm{focus}}}\right)}^2{\left(\frac{\delta v}{{\sigma }_{\mathrm{DH}}}\right)}^3,$$

(5)

where $\delta \mathbf{v}=\delta v^3=\delta v_x\delta v_y\delta v_z\sim {(0.5\mathrm{km}{\mathrm{s}}^{-1})}^3$ is the 3D velocity bandwidth. For $\mathcal{A}\sim {10}^9$, the amplified DM density ${\rho }_{\mathrm{Earth}}$ attains a value an order of magnitude greater than the non-amplified density ${\rho }_{\odot }$, and the amplified density has diurnal and seasonal modulations. It may be mentioned that everywhere on the Earth’s surface is exposed at any time to such modulating focal flow of DM with $v_{\mathrm{inj}}=17$ km s${}^{-1}$ with the magnitude of amplification depending on the geographic longitude and latitude.

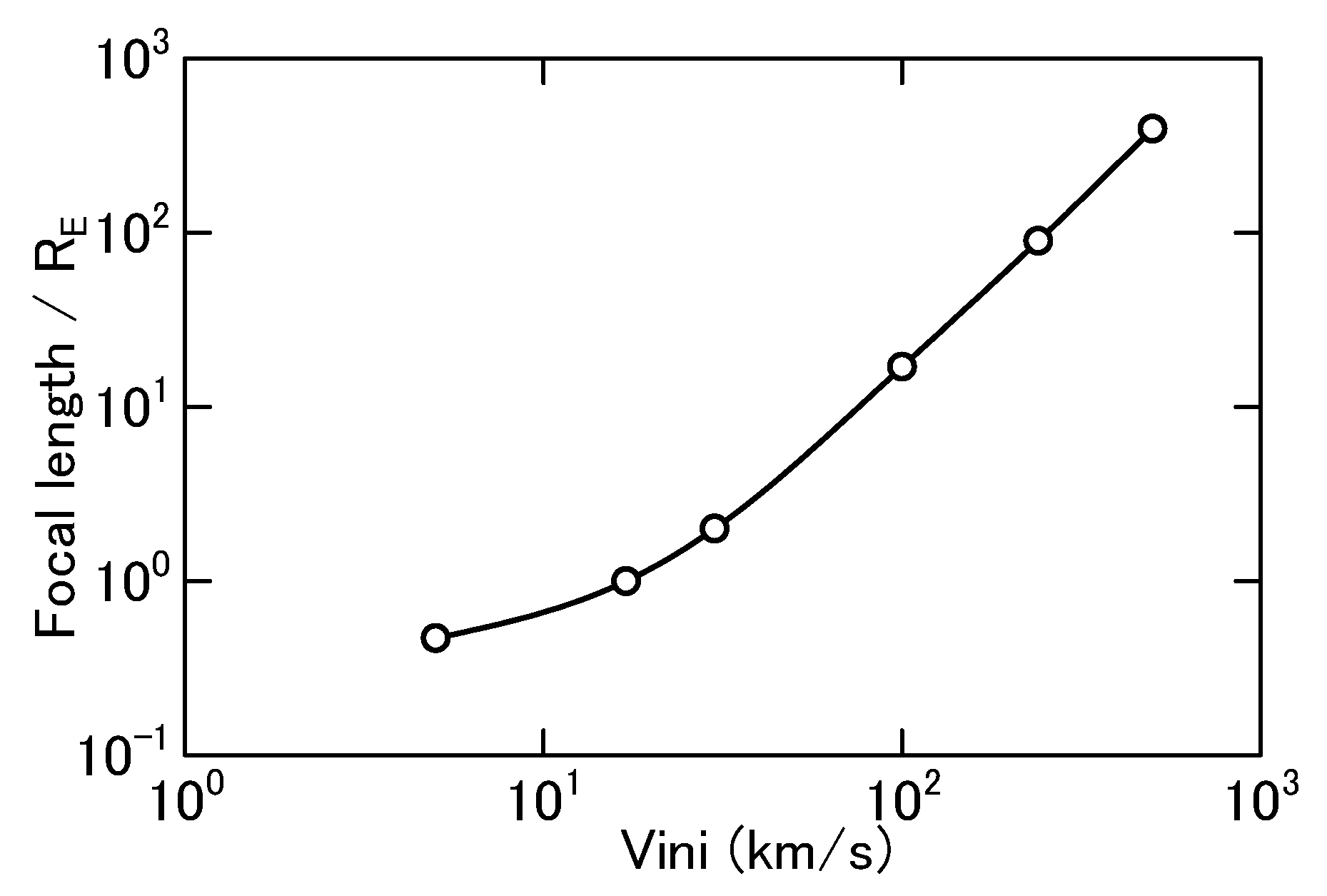
3.3. Focal Length and Focusing Velocity

The focal length of near-axis DM particles varies with the injection velocity, or the higher is the velocity, the more distant is the focus. Figure 6 plots the focal length as a function of the injection velocity. The velocity of large-off axis particles that focus on the Earth’s surface varies with the injection parameter. Figure 7 plots the initial velocity of such DM as a function of the impact parameter.

We also mention that the DM flow is accelerated by the Earth’s gravity, so that particles’ velocity at the focus attains a slightly larger value than the injection velocity as $v_{\mathrm{focus}}=\sqrt{v_{\mathrm{inj}}^2+2G{M}_{\mathrm{E}}/r_{\mathrm{E}}}$. For example, the DM flow at $v_{\mathrm{inj}}=17$ km s${}^{-1}$ focuses on the Earth’s surface (detector) at $v_{\mathrm{focus}}=20$ km s${}^{-1}$.

3.4. Other Focusing Objects

The gravitational focusing applies to the other extended objects like the Moon, planets and the Sun, whose interior density distributions are well known. An extended object of radius $r_{\mathrm{aperture}}$ causes convex-lens like convergence onto a focal point with an amplification proportional to the area of the aperture (Equation (3)). The angular radius, $\theta \sim r_{\mathrm{aperture}}/d$, of the aperture object at a distance d is related to its mass and injection velocity through

$$\theta \sim \eta {\left(\frac{GM}{d}\frac{1}{v_{\mathrm{inj}}^2}\right)}^{1/3},$$

(6)

where $\eta \sim 0.8$ is a factor obtained by numerical calculation of orbits. The Moon acts as a filled-aperture collector of DM flow with injection velocity $\sim 500$ km s${}^{-1}$ onto the Earth. The Sun and Jupiter are too massive, so that the injection velocity is required to be two order of magnitudes higher than ${\sigma }_{\mathrm{DH}}$. Extended galactic objects like molecular clouds are also possible filled-aperture collectors. The Orion molecular cloud ($d\sim 400$ pc, $r_{\mathrm{aperture}}\sim 15$ pc, $M\sim {10}^5{M}_{\odot }$), for example, can collect a DM flow of $\sim 180$ km s${}^{-1}$ with aperture diameter of $2\theta \sim 2^{\circ }$. Such apparent diameters may be compared to that of the Earth on the order of $\sim {30}^{\circ }–{60}^{\circ }$ as shown in the previous subsection.

Alternatively, the objects may be used as concave-lens like collectors, with which a cylindrical DM flow makes an enhanced ring (small circle) around a point mass (e.g., [7]). The apparent radius is also given by Equation (6) by replacing the angular radius by $\theta \sim r_{\mathrm{ring}}/d$. In case of the Sun ($d=1$ AU), a DM flow with injection velocity ∼200 km s${}^{-1}$ and radius (impact parameter) $\sim 60R_{\odot }$ focuses on the Earth, making a DM ring of diameter $2\theta \sim {25}^{\circ }$. The Moon, Jupiter, and the nearest star, $\alpha$ Cen, make rings of $2\theta \sim 0^{\circ }.7$, $\sim 1^{\circ }.6$ and $\sim 0^{\circ }.4$, respectively, for $v_{\mathrm{inj}}\sim 200$ km s${}^{-1}$. The amplified DM density from the ring at the focal point (Earth) is on the order of

$$\Delta {\rho }_{\mathrm{ring}}\sim {\rho }_{\odot }\left(\frac{r_{\mathrm{ring}}}{r_{\mathrm{focus}}}\right){\left(\frac{\delta v}{{\sigma }_{\mathrm{DH}}}\right)}^3.$$

(7)

We finally mention that the parallactic aberration due to the relative orbital velocities between the Earth and the objects is large, which amounts to an order of ∼30 km s${}^{-1}$$/200$ km s${}^{-1}$, causing significant displacement of the ring center toward the ecliptic east by $\sim 9^{\circ }$. For Jupiter, it is on the same order, but the aberration direction changes semi-annually.

4. Summary

We considered possible local modulation of the DM density due to the Earth gravity. We showed that the flow of low-velocity DM at initial geo-centric velocity of $v_{\mathrm{inj}}=17$ km s${}^{-1}$ focuses on the Earth’s surface at the focusing velocity of 20 km s${}^{-1}$ where the flux is significantly amplified. Such amplification may have implication for direct detection experiments of DM and for the interpretation of the physics of detected DM flux.