Rotation Curve of the Milky Way and the Dark Matter Density
Abstract
1. Introduction
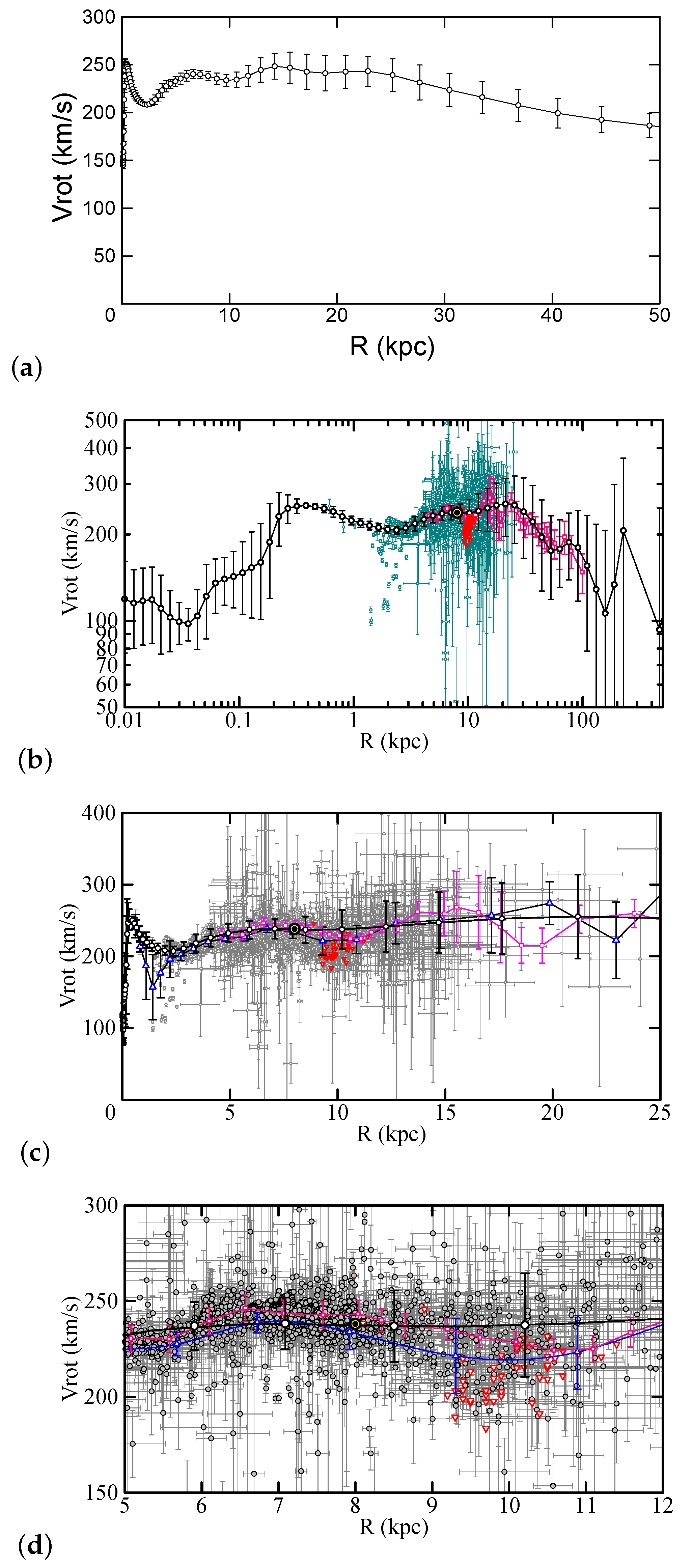
2. Rotation Curve of the Milky Way
2.1. Progress in the Last Decades
2.2. Methods to Determine the Galactic RC
2.2.1. Tangent-Velocity Method
2.2.2. Radial-Velocity + Distance Method
2.2.3. Trigonometric Method
2.2.4. Disk-Thickness Method
2.2.5. Pseudo-RC from Non-Disk Objects
2.3. Unified RC
2.4. Mass Components
2.4.1. Massive Black Hole
2.4.2. De Vaucouleurs Bulge
2.4.3. Exponential Disk
3. Dark Halo
3.1. Dark Halo Models
3.2. Cusp vs Cored Halo
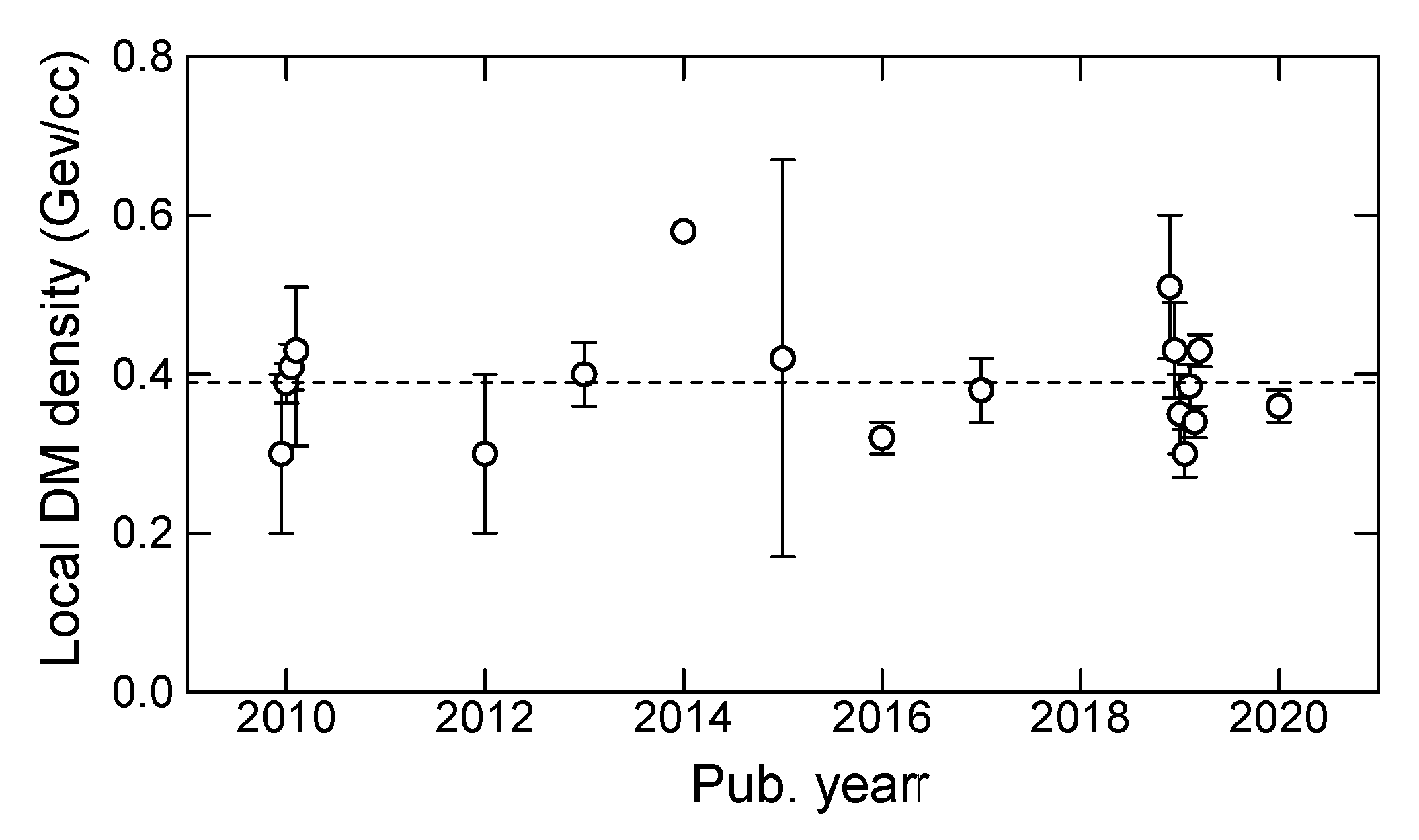
3.3. Central DM Density
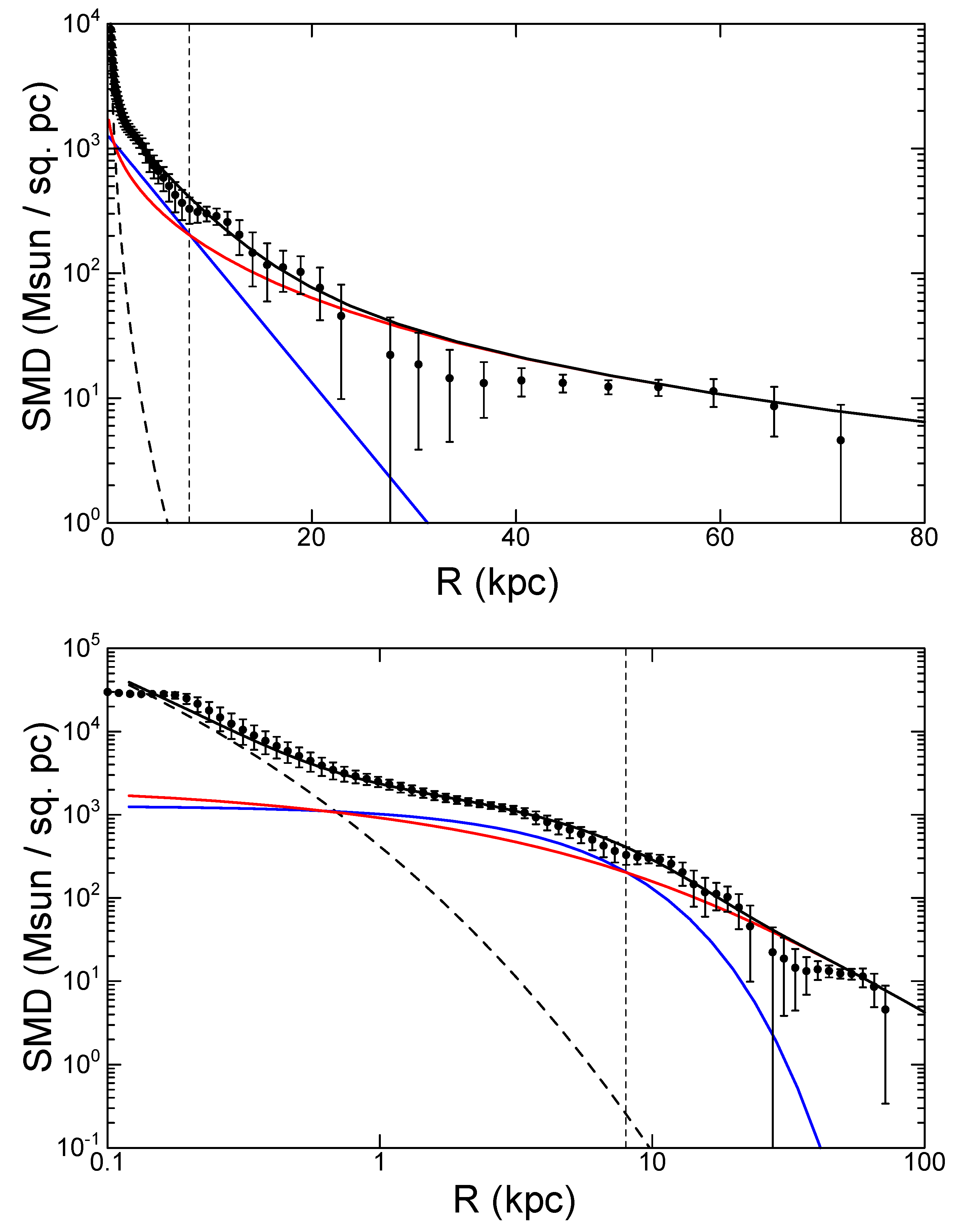
4. DM Density from Direct SMD
4.1. SMD from RC
4.2. Fitting by Bulge, Disk, and Dark Halo
4.3. Local DM Density
4.4. Dependence on the Galactic Constants
5. Summary
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Tables Concerning the RC and SMD of the Milky Way
| Radius | Standard Dev. | |
|---|---|---|
| (kpc) | (km s) | (km s) |
| 0.100 | 144.9 | 3.7 |
| 0.110 | 147.4 | 4.2 |
| 0.121 | 150.4 | 4.8 |
| 0.133 | 153.8 | 6.1 |
| 0.146 | 158.9 | 10.3 |
| 0.161 | 167.4 | 16.1 |
| 0.177 | 180.1 | 22.4 |
| 0.195 | 196.6 | 27.1 |
| 0.214 | 213.6 | 26.9 |
| 0.236 | 227.8 | 22.7 |
| 0.259 | 237.9 | 17.0 |
| 0.285 | 244.4 | 11.8 |
| 0.314 | 248.2 | 7.6 |
| 0.345 | 250.2 | 4.7 |
| 0.380 | 251.0 | 2.9 |
| 0.418 | 250.7 | 2.1 |
| 0.459 | 249.7 | 2.3 |
| 0.505 | 248.0 | 2.9 |
| 0.556 | 245.9 | 3.7 |
| 0.612 | 243.2 | 4.6 |
| 0.673 | 239.8 | 5.7 |
| 0.740 | 235.8 | 6.4 |
| 0.814 | 231.7 | 6.5 |
| 0.895 | 227.8 | 6.0 |
| 0.985 | 224.5 | 5.2 |
| 1.083 | 221.7 | 4.5 |
| 1.192 | 219.1 | 4.0 |
| 1.311 | 216.8 | 3.7 |
| 1.442 | 214.7 | 3.4 |
| 1.586 | 212.7 | 3.1 |
| 1.745 | 210.9 | 2.8 |
| 1.919 | 209.5 | 2.3 |
| 2.111 | 208.5 | 1.8 |
| 2.323 | 208.2 | 1.6 |
| Radius | Standard Dev. | |
|---|---|---|
| (kpc) | (km s) | (km s) |
| 2.555 | 208.9 | 2.2 |
| 2.810 | 210.7 | 3.6 |
| 3.091 | 213.4 | 4.8 |
| 3.400 | 217.2 | 5.9 |
| 3.740 | 222.0 | 6.6 |
| 4.114 | 226.6 | 5.7 |
| 4.526 | 229.5 | 4.4 |
| 4.979 | 231.6 | 4.3 |
| 5.476 | 234.1 | 5.3 |
| 6.024 | 237.2 | 5.7 |
| 6.626 | 239.5 | 5.0 |
| 7.289 | 240.1 | 4.1 |
| 8.018 | 239.0 | 4.4 |
| 8.820 | 236.7 | 5.4 |
| 9.702 | 234.5 | 6.0 |
| 10.672 | 234.2 | 7.1 |
| 11.739 | 237.1 | 9.8 |
| 12.913 | 242.8 | 12.4 |
| 14.204 | 248.5 | 13.3 |
| 15.625 | 249.7 | 14.8 |
| 17.187 | 246.2 | 17.4 |
| 18.906 | 243.3 | 18.3 |
| 20.797 | 243.9 | 17.5 |
| 22.876 | 245.6 | 15.6 |
| 25.164 | 243.7 | 15.2 |
| 27.680 | 237.3 | 16.1 |
| 30.448 | 229.6 | 15.5 |
| 33.493 | 222.5 | 14.1 |
| 36.842 | 215.0 | 14.0 |
| 40.527 | 207.1 | 13.8 |
| 44.579 | 200.3 | 12.7 |
| 49.037 | 194.7 | 11.9 |
| 53.941 | 189.8 | 11.3 |
| 59.335 | 186.2 | 10.4 |
| 65.268 | 184.7 | 9.6 |
| 71.795 | 183.9 | 9.3 |
| 78.975 | 181.4 | 11.0 |
| 86.872 | 175.5 | 14.6 |
| 95.560 | 167.7 | 16.3 |
| Radius | Standard Dev. | |
|---|---|---|
| (kpc) | ||
| 0.100 | 29,933.0 | 861.3 |
| 0.110 | 29,054.0 | 654.8 |
| 0.121 | 28,384.0 | 666.0 |
| 0.133 | 28,160.0 | 570.8 |
| 0.146 | 28,319.0 | 637.2 |
| 0.161 | 28,203.0 | 1406.6 |
| 0.177 | 27,368.0 | 2481.1 |
| 0.195 | 25,014.0 | 3514.2 |
| 0.214 | 21,548.0 | 4357.7 |
| 0.236 | 17,908.0 | 4806.8 |
| 0.259 | 14,804.0 | 4733.1 |
| 0.285 | 12,369.0 | 4231.5 |
| 0.314 | 10,489.0 | 3549.3 |
| 0.345 | 8978.9 | 2929.7 |
| 0.380 | 7736.5 | 2384.1 |
| 0.418 | 6700.8 | 1959.1 |
| 0.459 | 5830.8 | 1636.9 |
| 0.505 | 5090.6 | 1374.2 |
| 0.556 | 4452.0 | 1158.1 |
| 0.612 | 3899.9 | 973.5 |
| 0.673 | 3464.9 | 803.4 |
| 0.740 | 3145.2 | 644.7 |
| 0.814 | 2904.3 | 510.8 |
| 0.895 | 2701.7 | 415.1 |
| 0.985 | 2510.1 | 354.4 |
| 1.083 | 2320.9 | 319.0 |
| 1.192 | 2144.8 | 291.9 |
| 1.311 | 1985.0 | 266.7 |
| 1.442 | 1843.6 | 240.7 |
| 1.586 | 1718.4 | 214.5 |
| 1.745 | 1611.4 | 188.2 |
| 1.919 | 1519.3 | 164.5 |
| 2.111 | 1440.6 | 144.4 |
| 2.323 | 1368.3 | 130.9 |
| Radius | Standard Dev. | |
|---|---|---|
| (kpc) | ||
| 2.555 | 1296.4 | 125.1 |
| 2.810 | 1220.5 | 126.3 |
| 3.091 | 1139.8 | 134.1 |
| 3.400 | 1055.2 | 146.1 |
| 3.740 | 944.3 | 157.4 |
| 4.114 | 824.6 | 161.5 |
| 4.526 | 734.9 | 150.5 |
| 4.979 | 668.3 | 133.7 |
| 5.476 | 600.8 | 123.8 |
| 6.024 | 523.5 | 119.3 |
| 6.626 | 446.8 | 113.6 |
| 7.289 | 383.7 | 101.6 |
| 8.018 | 339.1 | 83.4 |
| 8.820 | 314.1 | 62.2 |
| 9.702 | 303.4 | 43.9 |
| 10.672 | 293.2 | 39.0 |
| 11.739 | 272.0 | 48.2 |
| 12.913 | 229.5 | 58.5 |
| 14.204 | 170.5 | 65.2 |
| 15.625 | 127.5 | 62.4 |
| 17.187 | 114.7 | 46.4 |
| 18.906 | 110.0 | 35.2 |
| 20.797 | 91.8 | 33.5 |
| 22.876 | 61.2 | 34.5 |
| 25.164 | 37.2 | 33.2 |
| 27.680 | 28.0 | 25.4 |
| 30.448 | 24.7 | 17.1 |
| 33.493 | 20.3 | 11.6 |
| 36.842 | 17.3 | 7.8 |
| 40.527 | 17.1 | 4.7 |
| 44.579 | 16.7 | 3.0 |
| 49.037 | 15.2 | 2.3 |
| 53.941 | 14.4 | 2.3 |
| 59.335 | 13.4 | 3.3 |
| 65.268 | 10.6 | 4.3 |
| 71.795 | 6.2 | 4.9 |
References
- Sofue, Y. Rotation and mass in the Milky Way and spiral galaxies. Publ. Astron. Soc. Jpn. 2017, 69, R1. [Google Scholar] [CrossRef]
- Sofue, Y.; Rubin, V. Rotation Curves of Spiral Galaxies. Annu. Rev. Astron. Astrophys. 2001, 39, 137. [Google Scholar] [CrossRef]
- Salucci, P. The distribution of dark matter in galaxies. Astron. Astrophys. Rev. 2019, 27, 2. [Google Scholar] [CrossRef]
- Honma, M.; Nagayama, T.; Ando, K.; Bushimata, T.; Choi, Y.K.; Handa, T.; Hirota, T.; Imai, H.; Jike, T.; Kim, M.K.; et al. Fundamental Parameters of the Milky Way Galaxy Based on VLBI astrometry. Publ. Astron. Soc. Jpn. 2012, 64, 136. [Google Scholar] [CrossRef]
- Honma, M.; Nagayama, T.; Sakai, N. Determining dynamical parameters of the Milky Way Galaxy based on high-accuracy radio astrometry. Publ. Astron. Soc. Jpn. 2015, 67, 70. [Google Scholar] [CrossRef]
- Fich, M.; Tremaine, S. The mass of the Galaxy. Annu. Rev. Astron. Astrophys. 1991, 29, 409. [Google Scholar] [CrossRef]
- Reid, M.J. The distance to the center of the Galaxy. Annu. Rev. Astron. Astrophys. 1993, 31, 345. [Google Scholar] [CrossRef]
- Olling, R.P.; Dehnen, W. The Oort Constants Measured from Proper Motions. Astrophys. J. 2003, 599, 275. [Google Scholar] [CrossRef][Green Version]
- Ghez, A.M.; Salim, S.; Weinberg, N.N.; Lu, J.R.; Do, T.; Dunn, J.K.; Matthews, K.; Morris, M.R.; Yelda, S.; Becklin, E.E.; et al. Measuring Distance and Properties of the Milky Way’s Central Supermassive Black Hole with Stellar Orbits. Astrophys. J. 2008, 689, 1044. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Trippe, S.; Alexander, T.; Genzel, R.; Martins, F.; Ott, T. Monitoring Stellar Orbits Around the Massive Black Hole in the Galactic Center. Astrophys. J. 2009, 692, 1075. [Google Scholar] [CrossRef]
- Reid, M.J.; Menten, K.M.; Zheng, X.W.; Brunthaler, A.; Moscadelli, L.; Xu, Y.; Zhang, B.; Sato, M.; Honma, M.; Hirota, T.; et al. Trigonometric Parallaxes of Massive Star-Forming Regions. VI. Galactic Structure, Fundamental Parameters, and Noncircular Motions. Astrophys. J. 2009, 700, 137. [Google Scholar] [CrossRef]
- Matsunaga, N.; Kawadu, T.; Nishiyama, S.; Nagayama, T.; Hatano, H.; Tamura, M.; Glass, I.S.; Nagata, T. A near-infrared survey of Miras and the distance to the Galactic Centre. Mon. Not. R. Astron. Soc. 2009, 399, 1709. [Google Scholar] [CrossRef]
- Burton, W.B.; Gordon, M.A. Carbon monoxide in the Galaxy. III. The overall nature of its distribution in the equatorial plane. Astron. Astrophys. 1978, 63, 7. [Google Scholar]
- Blitz, L.; Lada, C.J. H2O masers near OB associations. Astrophys. J. 1979, 227, 152–158. [Google Scholar] [CrossRef]
- Clemens, D.P. Massachusetts-Stony Brook Galactic plane CO survey: The galactic disk rotation curve. Astrophys. J. 1985, 295, 422. [Google Scholar] [CrossRef]
- Dehnen, W.; Binney, J. Mass models of the Milky Way. Mon. Not. R. Astron. Soc. 1998, 294, 429. [Google Scholar] [CrossRef]
- Genzel, R.; Eisenhauer, F.; Gillessen, S. The Galactic Center massive black hole and nuclear star cluster. Rev. Mod. Phys. 2010, 82, 3121. [Google Scholar] [CrossRef]
- Battinelli, P.; Demers, S.; Rossi, C.; Gigoyan, K.S. Extension of the C Star Rotation Curve of the Milky Way to 24 kpc. Astrophysics 2013, 56, 68. [Google Scholar] [CrossRef]
- Bhattacharjee, P.; Chaudhury, S.; Kundu, S. Rotation Curve of the Milky Way out to ~200 kpc. Astrophys. J. 2014, 785, 63. [Google Scholar] [CrossRef]
- López-Corredoira, M. Milky Way rotation curve from proper motions of red clump giants. Astron. Astrophys. 2014, 563, A128. [Google Scholar] [CrossRef]
- Bovy, J.; Prieto, C.A.; Beers, T.; Bizyaev, D.; Da Costa, L.N.; Cunha, K.; Ebelke, G.; Eisenstein, D.J.; Frinchaboy, P.M.; Pérez, A.E.G.; et al. The Milky Way’s Circular-velocity Curve between 4 and 14 kpc from APOGEE data. Astrophys. J. 2012, 759, 131. [Google Scholar] [CrossRef]
- Bobylev, V.V.; Bajkova, A.T. Galactic rotation curve and spiral density wave parameters from 73 masers. Astron. Lett. 2013, 39, 809. [Google Scholar] [CrossRef]
- Bobylev, V.V.; Bajkova, A.T. Determination of the galactic rotation curve from OB stars. Astron. Lett. 2015, 41, 473. [Google Scholar] [CrossRef]
- Reid, M.J.; Menten, K.M.; Brunthaler, A.; Zheng, X.W.; Dame, T.M.; Xu, Y.; Wu, Y.; Zhang, B.; Sanna, A.; Sato, M.; et al. Trigonometric Parallaxes of High Mass Star Forming Regions: The Structure and Kinematics of the Milky Way. Astrophys. J. 2014, 783, 130. [Google Scholar] [CrossRef]
- Iocco, F.; Pato, M.; Bertone, G. Evidence for dark matter in the inner Milky Way. Nat. Phys. 2015, 11, 245. [Google Scholar] [CrossRef]
- Iocco, F.; Pato, M. On the dark matter distribution in the Milky Way. J. Phys. Conf. Ser. 2016, 718, 042031. [Google Scholar] [CrossRef]
- Pato, M.; Iocco, F. Galkin: Milky Way Rotation Curve Data Handler; ascl:1711.011; Astrophysics Source Code Library: Houghton, MI, USA, 2017. [Google Scholar]
- Pato, M.; Iocco, F. Galkin: A new compilation of Milky Way rotation curve data. SoftwareX 2017, 6, 54. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, X.; Yuan, H.-B.; Xiang, M.; Zhang, H.-W.; Chen, B.; Ren, J.; Wang, C.; Zhang, Y.; Hou, Y.-H.; et al. The Milky Way’s rotation curve out to 100 kpc and its constraint on the Galactic mass distribution. Mon. Not. R. Astron. Soc. 2016, 463, 2623. [Google Scholar] [CrossRef]
- Krełowski, J.; Galazutdinov, G.; Strobel, A. The Milky Way Rotation Curve Revisited. Publ. Astron. Soc. Pac. 2018, 130, 114302. [Google Scholar] [CrossRef]
- Lin, H.-N.; Li, X. The dark matter profiles in the Milky Way. Mon. Not. R. Astron. Soc. 2019, 487, 5679. [Google Scholar] [CrossRef]
- Eilers, A.-C.; Hogg, D.W.; Rix, H.-W.; Ness, M.K. The Circular Velocity Curve of the Milky Way from 5 to 25 kpc. Astrophys. J. 2019, 871, 120. [Google Scholar] [CrossRef]
- Mróz, P.; Udalski, A.; Skowron, D.M.; Skowron, J.; Soszyński, I.; Pietrukowicz, P.; Szymański, M.K.; Poleski, R.; Kozłowski, S.; Ulaczyk, K. Rotation Curve of the Milky Way from Classical Cepheids. Astrophys. J. 2012, 870, L10. [Google Scholar] [CrossRef]
- Sofue, Y.; Honma, M.; Omodaka, T. Unified Rotation Curve of the Galaxy—Decomposition into de Vaucouleurs Bulge, Disk, Dark Halo, and the 9-kpc Rotation Dip—. Publ. Astron. Soc. Jpn. 2009, 61, 227. [Google Scholar] [CrossRef]
- Sofue, Y. Rotation Curve and Mass Distribution in the Galactic Center - From Black Hole to Entire Galaxy. Publ. Astron. Soc. Jpn. 2013, 65, 118. [Google Scholar] [CrossRef]
- Sofue, Y. Dark halos of M 31 and the Milky Way. Publ. Astron. Soc. Jpn. 2015, 67, 75. [Google Scholar] [CrossRef]
- Fich, M.; Blitz, L.; Stark, A.A. The Rotation Curve of the Milky Way to 2R 0. Astrophys. J. 1989, 342, 272. [Google Scholar] [CrossRef]
- Demers, S.; Battinelli, P. C stars as kinematic probes of the Milky Way disk from 9 to 15 kpc. Astron. Astrophys. 2007, 473, 143. [Google Scholar] [CrossRef]
- Merrifield, M.R. The Rotation Curve of the Milky Way to 2.5 R/o From the Thickness of the HI Layer. Astron. J. 1992, 103, 1552. [Google Scholar] [CrossRef]
- Honma, M.; Sofue, Y. Rotation Curve of the Galaxy. Publ. Astron. Soc. Jpn. 1997, 49, 453. [Google Scholar] [CrossRef]
- Lindqvist, M.; Habing, H.J.; Winnberg, A. OH/IR stars close to the galactic centre. II. Their spatial and kinematics properties and the mass distribution within 5-100 PC from the galactic centre. Astron. Astrophys. 1992, 259, 118. [Google Scholar]
- Honma, M.; Bushimata, T.; Choi, Y.K.; Hirota, T.; Imai, H.; Iwadate, K.; Jike, T.; Kameya, O.; Kamohara, R.; Kan-Ya, Y.; et al. Astrometry of Galactic Star-Forming Region Sharpless 269 with VERA: Parallax Measurements and Constraint on Outer Rotation Curve. Publ. Astron. Soc. Jpn. 2007, 59, 889. [Google Scholar] [CrossRef]
- Sakai, N.; Nakanishi, H.; Matsuo, M.; Koide, N.; Tezuka, D.; Kurayama, T.; Shibata, K.M.; Ueno, Y.; Honma, M. Outer rotation curve of the Galaxy with VERA. III. Astrometry of IRAS 07427-2400 and test of the density-wave theory. Publ. Astron. Soc. Jpn. 2015, 67, 69. [Google Scholar] [CrossRef]
- Nakanishi, H.; Sakai, N.; Kurayama, T.; Matsuo, M.; Imai, H.; Burns, R.A.; Ozawa, T.; Honma, M.; Shibata, K.M.; Kawaguchi, N. Outer rotation curve of the Galaxy with VERA. II. Annual parallax and proper motion of the star-forming region IRAS 21379+5106. Publ. Astron. Soc. Jpn. 2015, 67, 68. [Google Scholar] [CrossRef]
- Callingham, T.M.; Cautun, M.; Deason, A.J.; Frenk, C.S.; Wang, W.; A Gómez, F.; Grand, R.J.J.; Marinacci, F.; Pakmor, R. The mass of the Milky Way from satellite dynamics. Mon. Not. R. Astron. Soc. 2019, 484, 5453. [Google Scholar] [CrossRef]
- Roeser, S.; Demleitner, M.; Schilbach, E. The PPMXL Catalog of Positions and Proper Motions on the ICRS. Combining USNO-B1.0 and the Two Micron All Sky Survey (2MASS). Astron. J. 2010, 139, 2440. [Google Scholar] [CrossRef]
- Pato, M.; Iocco, F.; Bertone, G. Dynamical constraints on the dark matter distribution in the Milky Way. J. Cosmol. Astropart. Phys. 2015, 2015, 001. [Google Scholar] [CrossRef]
- Pato, M.; Iocco, F. The Dark Matter Profile of the Milky Way: A Non-parametric Reconstruction. Astrophys. J. 2015, 803, L3. [Google Scholar] [CrossRef]
- de Vaucouleurs, G. Photoelectric photometry of the Andromeda Nebula in the UBV system. Astrophys. J. 1958, 128, 465. [Google Scholar] [CrossRef]
- Ciotti, L. Stellar systems following the R1/m luminosity law. Astron. Astrophys. 1991, 249, 99. [Google Scholar]
- Trujillo, I.; Asensio Ramos, A.; Rubino-Martín, J.A.; Graham, A.W.; Aguerri, J.A.; Cepa, J.; Gutiérrez, C.M. Triaxial stellar systems following the r1/n luminosity law: An analytical mass-density expression, gravitational torques and the bulge/disc interplay. Mon. Not. R. Astron. Soc. 2002, 333, 510. [Google Scholar] [CrossRef][Green Version]
- Freeman, K.C. On the Disks of Spiral and S0 Galaxies. Astrophys. J. 1970, 160, 811. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Li, Z.-Z.; Jing, Y.P.; Qian, Y.-Z.; Yuan, Z.; Zhao, D.-H. Determination of Dark Matter Halo Mass from Dynamics of Satellite Galaxies. Astrophys. J. 2017, 850, 116. [Google Scholar] [CrossRef]
- Burkert, A. The Structure of Dark Matter Halos in Dwarf Galaxies. Astrophys. J. 1995, 447, L25. [Google Scholar] [CrossRef]
- Salucci, P.; Burkert, A. Dark Matter Scaling Relations. Astrophys. J. 2000, 537, L9. [Google Scholar] [CrossRef]
- Brownstein, J.R.; Moffat, J.W. Galaxy Rotation Curves without Nonbaryonic Dark Matter. Astrophys. J. 2006, 636, 721. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. Simulations of X-ray clusters. Mon. Not. R. Astron. Soc. 1995, 275, 720. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- Moore, B.; Quinn, T.; Governato, F.; Stadel, J.; Lake, G. Cold collapse and the core catastrophe. Mon. Not. R. Astron. Soc. 1999, 310, 1147. [Google Scholar] [CrossRef]
- Fukushige, T.; Kawai, A.; Makino, J. Structure of Dark Matter Halos from Hierarchical Clustering. III. Shallowing of the Inner Cusp. Astrophys. J. 2004, 606, 625. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Silk, J.; Bloemen, H. A Gamma-Ray Constraint on the Nature of Dark Matter. Astrophys. J. 1987, 313, L47. [Google Scholar] [CrossRef]
- Escudero, M.; Hooper, D.; Witte, S.J. Updated collider and direct detection constraints on Dark Matter models for the Galactic Center gamma-ray excess. J. Cosmol. Astropart. Phys. 2017, 2017, 38. [Google Scholar] [CrossRef][Green Version]
- Finkbeiner, D.P. WMAP Microwave Emission Interpreted as Dark Matter Annihilation in the Inner Galaxy. arXiv 2004, arXiv:0409027. [Google Scholar]
- Weber, M.; de Boer, W. Determination of the local dark matter density in our Galaxy. Astron. Astrophys. 2010, 509, A25. [Google Scholar] [CrossRef]
- Catena, R.; Ullio, P. A novel determination of the local dark matter density. J. Cosmol. Astropart. Phys. 2010, 2010, 004. [Google Scholar] [CrossRef]
- Bovy, J.; Tremaine, S. On the Local Dark Matter Density. Astrophys. J. 2012, 756, 89. [Google Scholar] [CrossRef]
- Piffl, T.; Binney, J.; McMillan, P.; Steinmetz, M.; Helmi, A.; Wyse, R.F.G.; Bienaymé, O.; Bland-Hawthorn, J.; Freeman, K.; Gibson, B.K.; et al. Constraining the Galaxy’s dark halo with RAVE stars. Mon. Not. R. Astron. Soc. 2014, 445, 3133. [Google Scholar] [CrossRef]
- McMillan, P.J. The mass distribution and gravitational potential of the Milky Way. Mon. Not. R. Astron. Soc. 2017, 465, 76. [Google Scholar] [CrossRef]
- Salucci, P.; Nesti, F.; Gentile, G.; Frigerio Martins, C. The dark matter density at the Sun’s location. Astron. Astrophys. 2010, 523, A83. [Google Scholar] [CrossRef]
- de Salas, P.F.; Malhan, K.; Freese, K.; Hattori, K.; Valluri, M. On the estimation of the local dark matter density using the rotation curve of the Milky Way. J. Cosmol. Astropart. Phys. 2019, 2019, 37. [Google Scholar] [CrossRef]
- Cautun, M.; Benitez-Llambay, A.; Deason, A.J.; Frenk, C.S.; Fattahi, A.; Gomez, F.A.; Grand, R.J.; Oman, K.A.; Navarro, J.F.; Simpson, C.M. The Milky Way total mass profile as inferred from Gaia DR2. arXiv 2020, arXiv:1911.04557. [Google Scholar] [CrossRef]
- Karukes, E.V.; Benito, M.; Iocco, F.; Trotta, R.; Geringer-Sameth, A. Bayesian reconstruction of the Milky Way dark matter distribution. J. Cosmol. Astropart. Phys. 2019, 2019, 46. [Google Scholar] [CrossRef]

| Authors (Year) | (kpc) | (km s) |
|---|---|---|
| IAU recommended (1982) | 8.2 | 220 |
| Review before 1993 (Reid 1993) [7] | ||
| Olling and Dehnen 2003 [8] | ||
| VLBI Sgr A (Ghez et al., 2008) [9] | ||
| ibid (Gillessen et al., 2009) [10] | ||
| Maser astrometry (Reid et al., 2009) [11] | ||
| Cepheids (Matsunaga et al., 2009) [12] | ||
| VERA (Honma et al., 2012, 2015) [4,5] | ||
| Adopted in this paper | 8.0 | 238 |
| Authors (Year) | Radii (kpc) | Method |
|---|---|---|
| Burton and Gordon (1978) [13] | 0–8 | HI tangent |
| Blitz et al. (1979) [14] | 8–18 | OB-CO assoc. |
| Clemens (1985) [15] | 0–18 | CO/compil. |
| Dehnen and Binney (1998) [16] | 8–20 | compil. + model |
| Genzel et al. (1994–), Ghez et al. (1998–) [9,17] | 0–0.0001 | GC IR spectr. |
| Battinelli, et al. (2013) [18] | 9–24 | C stars |
| Bhattacharjee et al. (2014) [19] | 0–200 | Non-disk objects |
| Lopez-Corredoira (2014) [20] | 5–16 | Red-clump giants, parallax |
| Boby et al. (2012) [21] | 4-14 | NIR spectroscopy |
| Bobylev (2013); — & Bajkova (2015) [22,23] | 5–12 | Masers/OB stars |
| Honma et al. (2012, 2015) [4,5] | 3–20 | Masers, VLBI |
| Reid et al. (2014) [24] | 4-16 | Masers SF regions, VLBI |
| Iocco et al. (2015, 2016); Pato & Iocco (2017a,b) [25,26,27,28] | 1–25 kpc | CO/HI/opt/maser/compil. |
| Huang et al. (2016) [29] | 4.5–100 | HI/opt/red giants |
| Krełowski et al. (2018) [30] | 8–12 | GAIA |
| Lin and Li (2019) [31] | 4–100 | compil. |
| Eilers et al. (2019) [32] | 5–25 | Wise, 2Mass, GAIA |
| Mróz et al. (2019) [33] | 4–20 | Classical cepheids |
| Sofue et al. (2009); Sofue (2013, 2015, this work) [34,35,36] | 0.01–1000 | CO/HI/maser/opt/compil. |
| Component | Parameter | Fitted Value | |
|---|---|---|---|
| Expo. disk | kpc | ||
| NFW dark halo | h | kpc | |
| GeV cm | |||
| GeV cm | 11.9 | ||
| Burkert | ∼ GeV cm | ||
| Brownstein | ∼ GeV cm | ||
| model | ∼ GeV cm |
| Reference | (kpc) | (km s−1) | |
|---|---|---|---|
| Weber and de Boer (2010) [66] | 0.2–0.4 | ||
| Catena and Ulio (2010) [67] | |||
| Bovy and Tremaine (2012) [68] | |||
| Piffl et al. (2014) [69] | 0.58 | ||
| Pato et al. (2015), Pato & Iocco (2015) [47,48] | 230 | ||
| Huang et al. (2016) [29] | 8.34 | 240 | |
| McMillan (2017) [70] | 8.21 | 233.1 | |
| Lin and Li (2019) [31] | 8.1 | 240 | |
| Salucci et al. (2010, 2019) [3,71] | 8.29 | 239 | |
| Eilers et al. (2019) [32] | 8.1 | 229 | |
| de Salas et al. (2019) [72] | 0.3–0.4 | ||
| Cautun et al. (2019) [73] | 8 | 229 | |
| Karukes et al. (2019) [74] | 8.34 | 240 | |
| Sofue (2013) [35] | 8.0 | 238 | |
| —(2020 this paper) | 8.0 | 238 | |
| Average |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sofue, Y. Rotation Curve of the Milky Way and the Dark Matter Density. Galaxies 2020, 8, 37. https://doi.org/10.3390/galaxies8020037
Sofue Y. Rotation Curve of the Milky Way and the Dark Matter Density. Galaxies. 2020; 8(2):37. https://doi.org/10.3390/galaxies8020037
Chicago/Turabian StyleSofue, Yoshiaki. 2020. "Rotation Curve of the Milky Way and the Dark Matter Density" Galaxies 8, no. 2: 37. https://doi.org/10.3390/galaxies8020037
APA StyleSofue, Y. (2020). Rotation Curve of the Milky Way and the Dark Matter Density. Galaxies, 8(2), 37. https://doi.org/10.3390/galaxies8020037




