Debated Models for Galactic Rotation Curves: A Review and Mathematical Assessment
Abstract
1. Introduction and Background
1.1. Evidence Independent of Rotation Cuve Modeling
1.2. Types of Models
1.3. Purpose and Goals
2. Available Data and Approximations Used in its Analysis
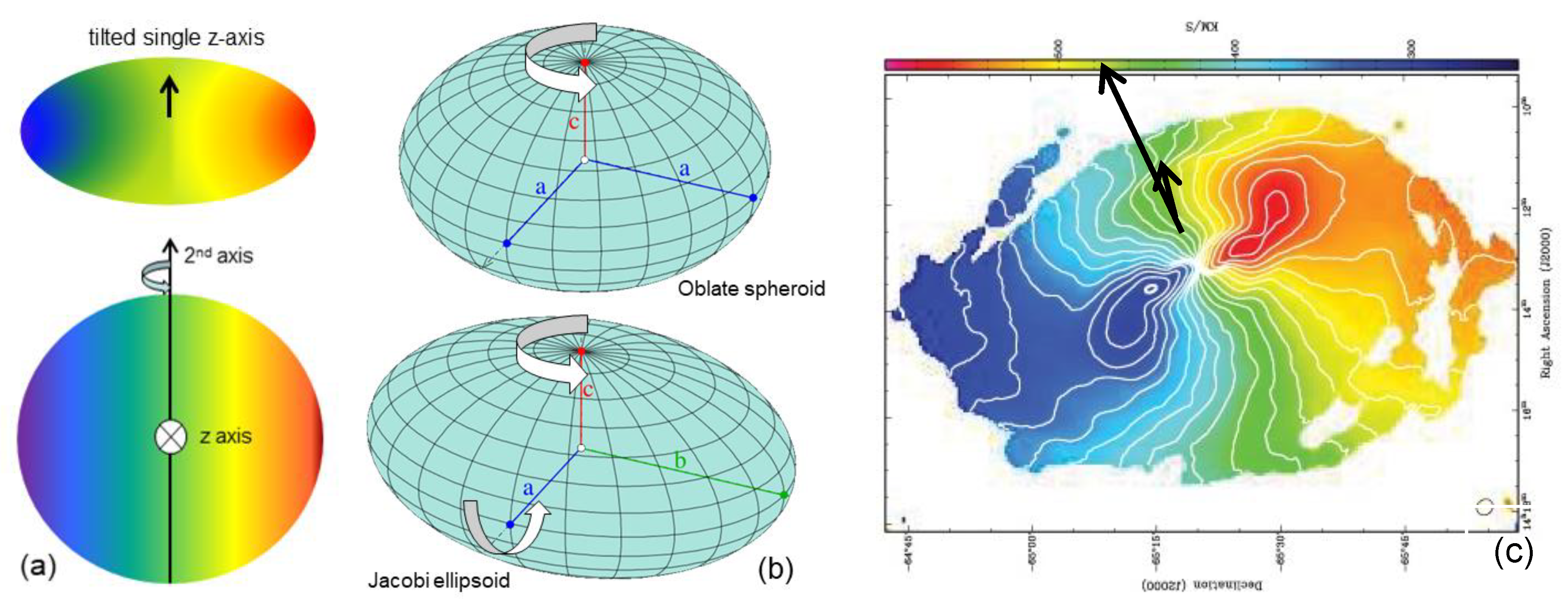
2.1. Shapes from Images
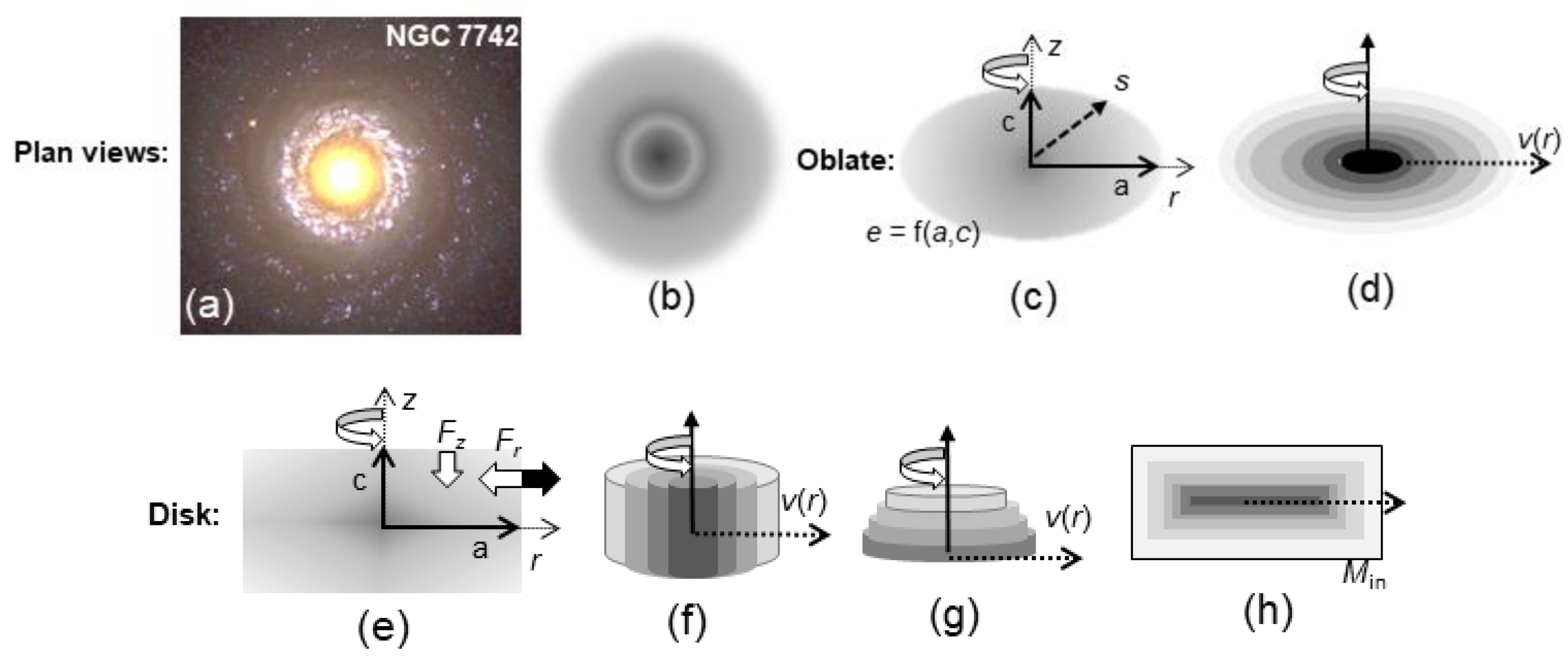
2.1.1. Density Contours of the Oblate Spheroid
2.1.2. Flat Oblate Spheroids are not Thin Disks
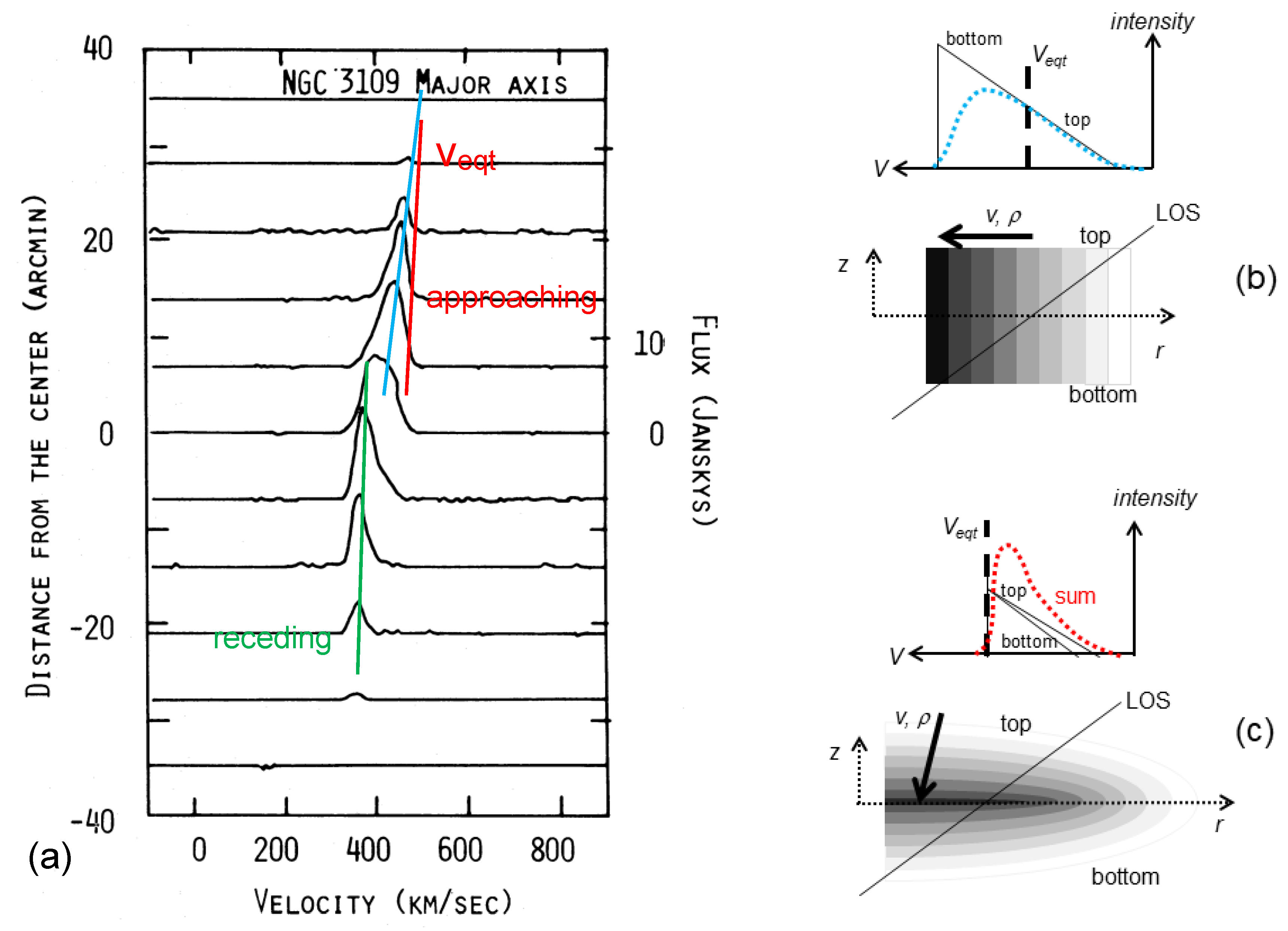
2.2. Rotation Curves from Doppler Shifts
2.2.1. General Approach in Data Analysis
2.2.2. Two Examples
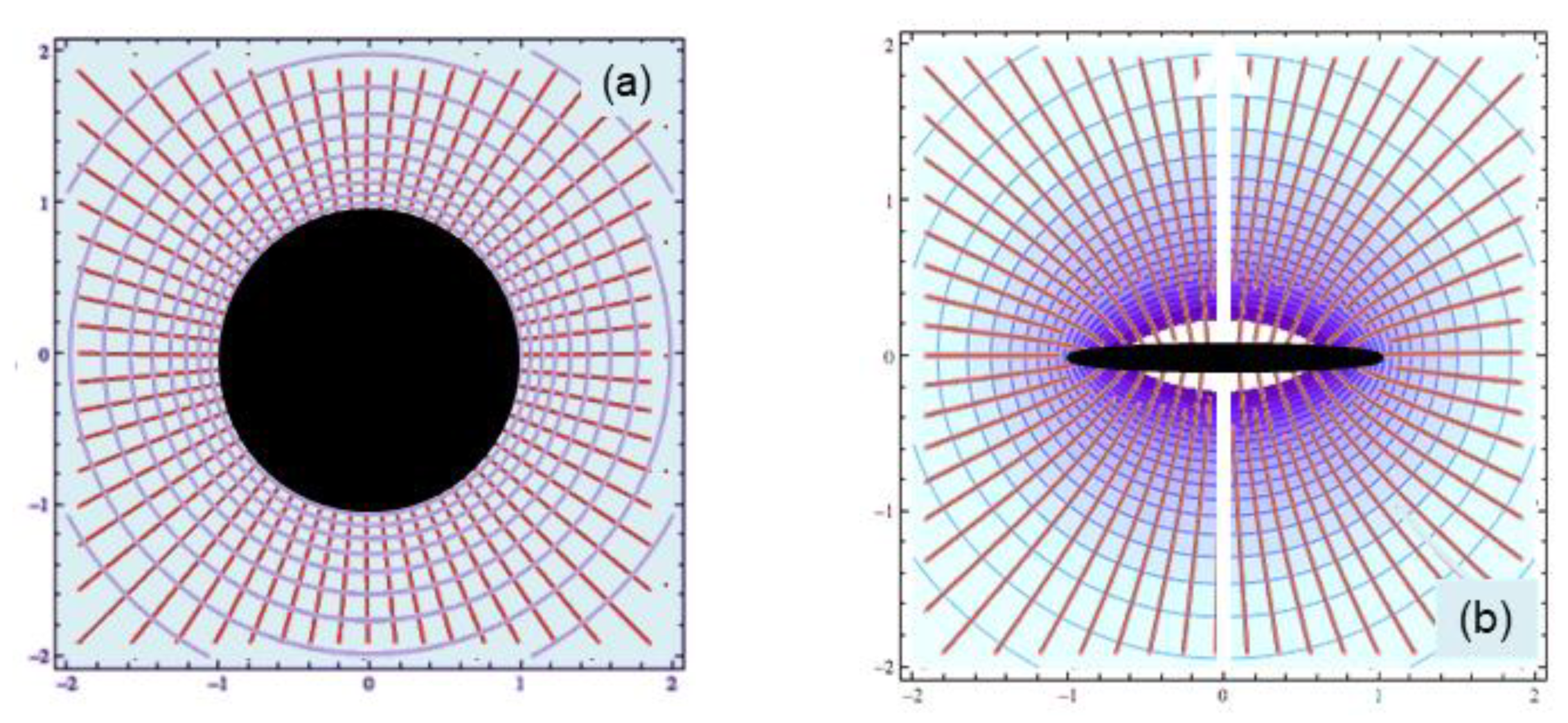
2.2.3. How the Geometrical Control on Density Contours Affects Velocity-Flux Systematics
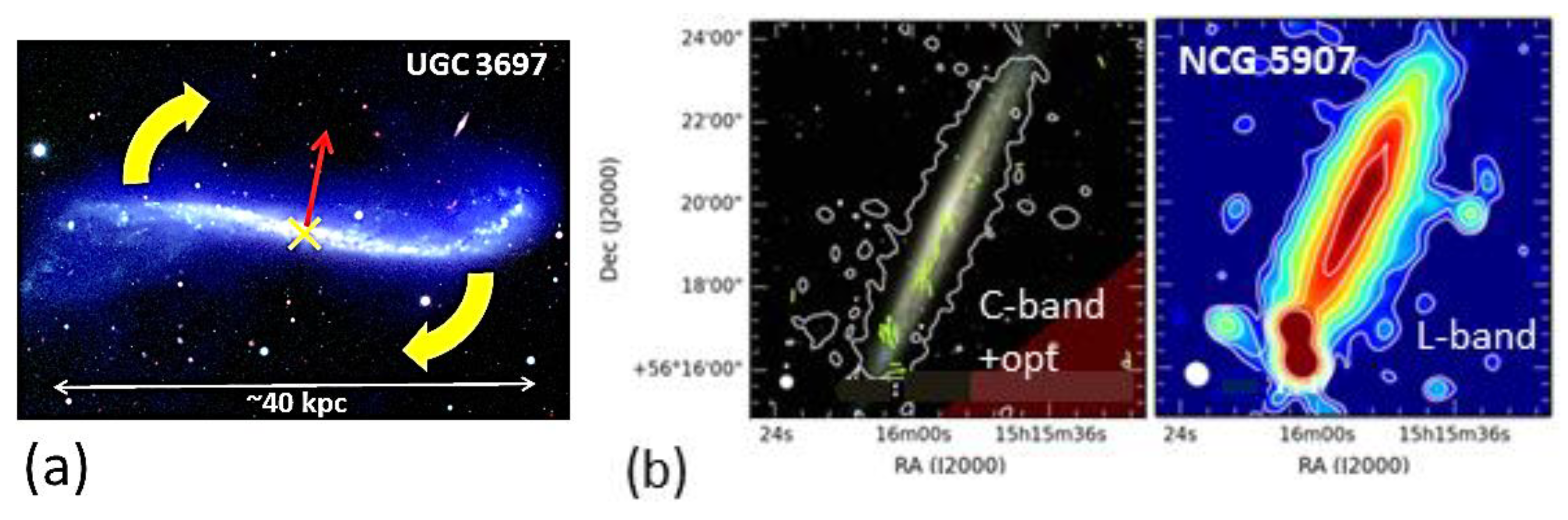
2.2.4. Why Multiple Spin Axes Should Exist
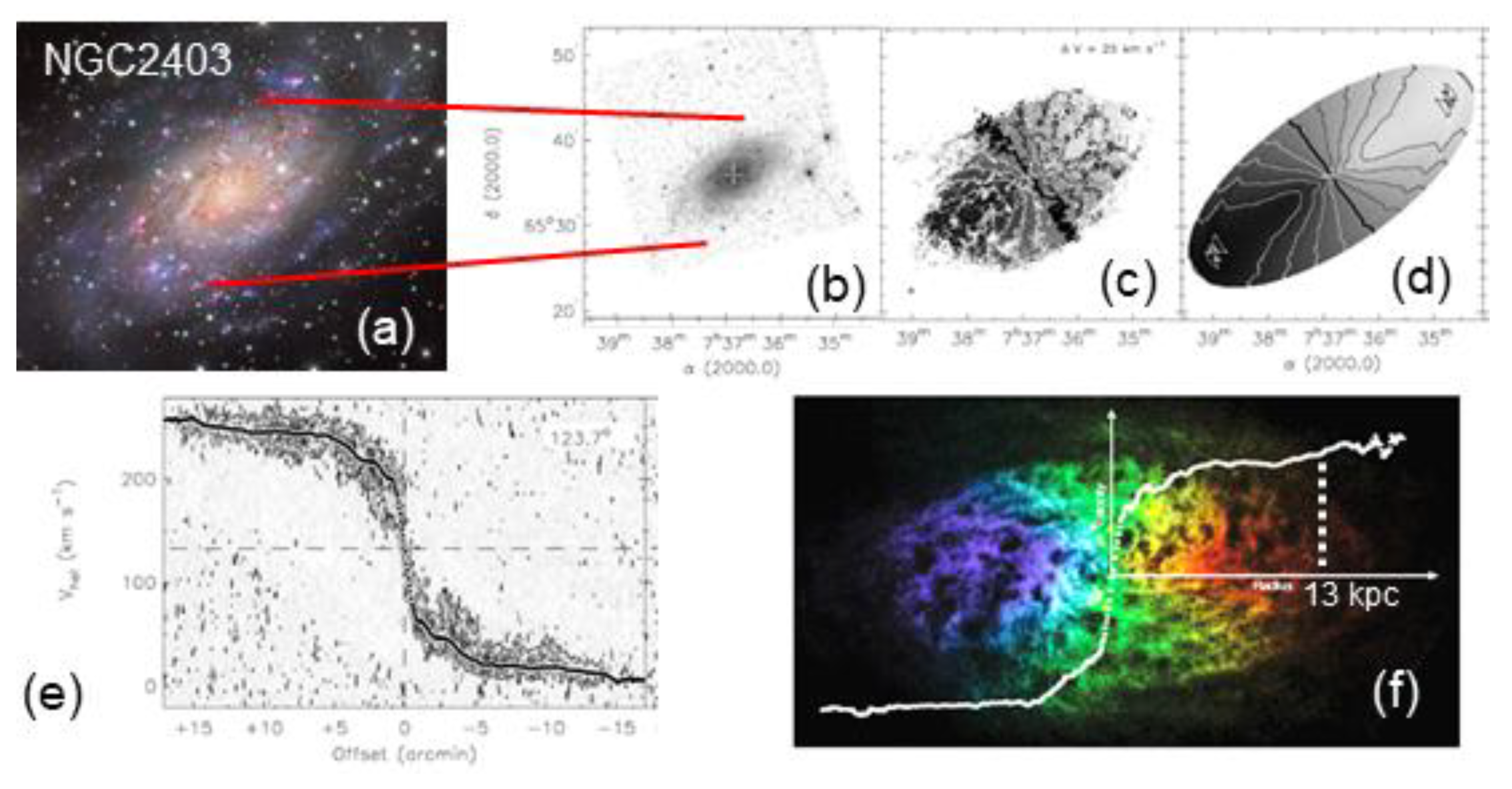
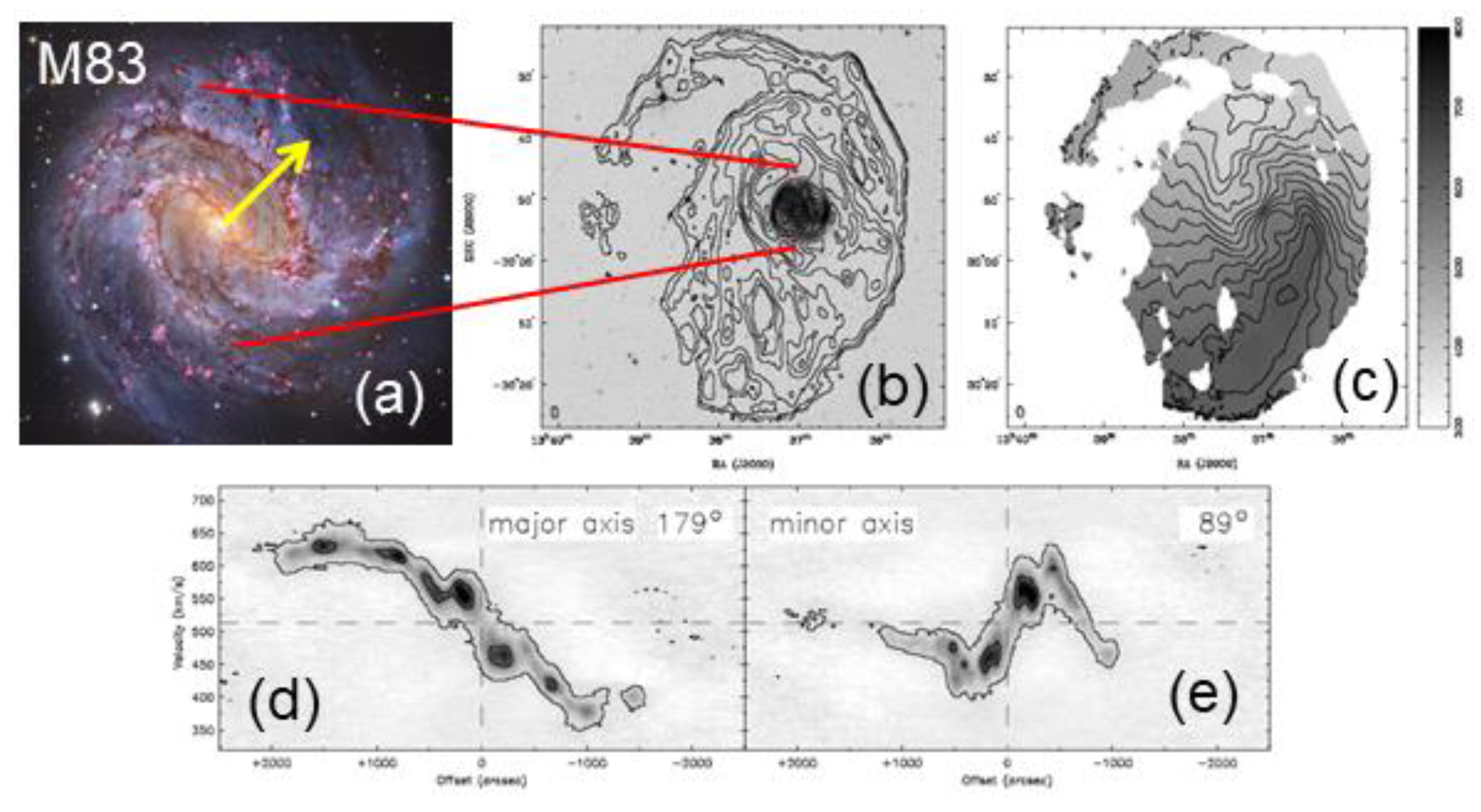
2.2.5. Evidence for Multiple Spin Axes in Doppler Patterns
2.2.6. Evidence for Multiple Spin Axes in Rotation Curves
2.2.7. Summary and Prognosis
3. Forward Models of Galaxies that Presume Nested Orbits
3.1. Synopsis and Evaluation of the Mathematical Underpinnings of Forward Orbital Models
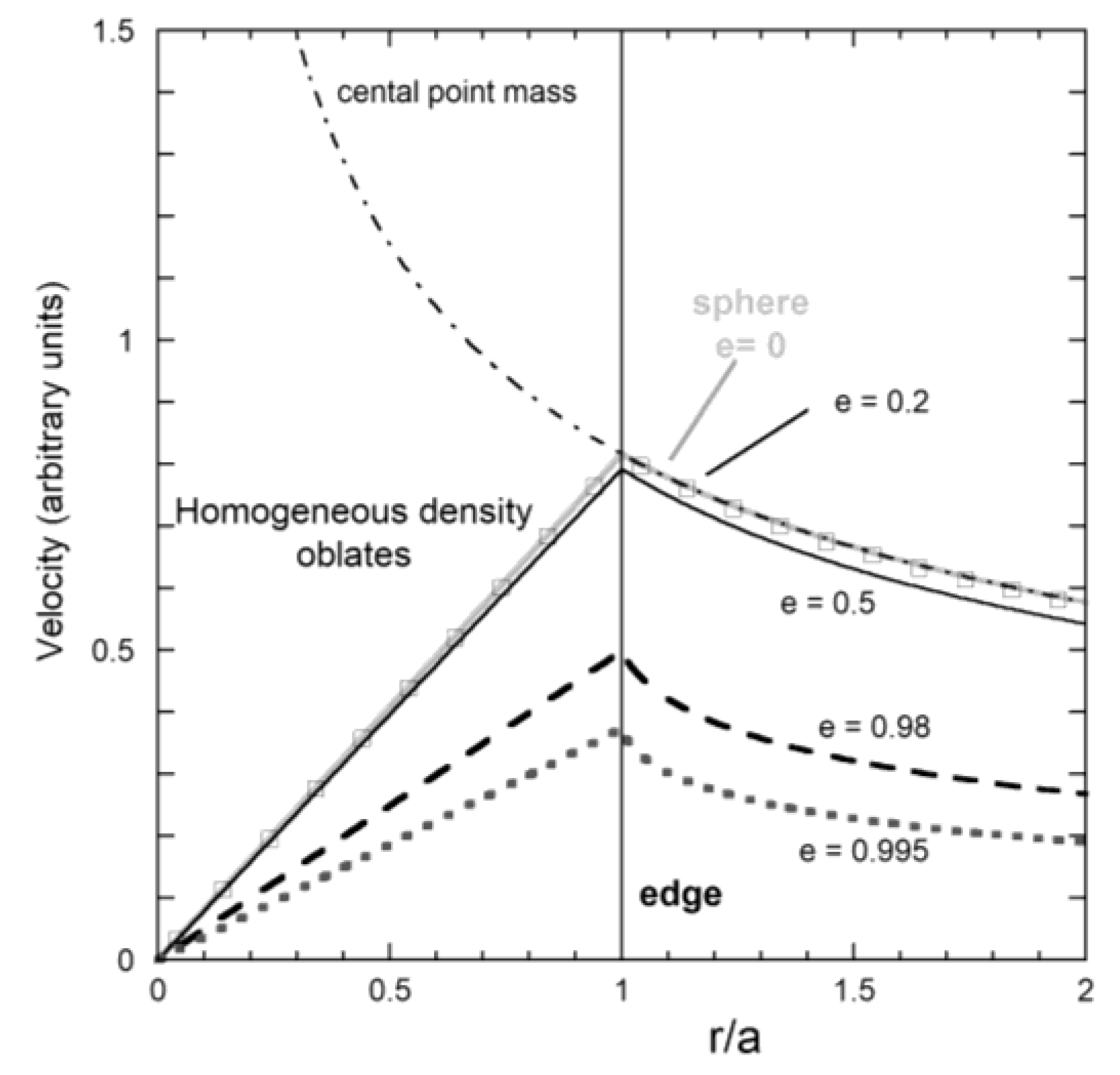
3.1.1. Spheres vs. Point Masses
3.1.2. Oblate Shapes
3.1.3. Approximate Formulae for Rings and Disks
3.1.4. Geometry, Stability, and the Dynamical Mass
3.1.5. Geometry, Coordinate Systems, the Theorem of Gauss, and Logarithmic Potentials
3.1.6. Toomre’s Mathematically Invalid Analysis of the Disk
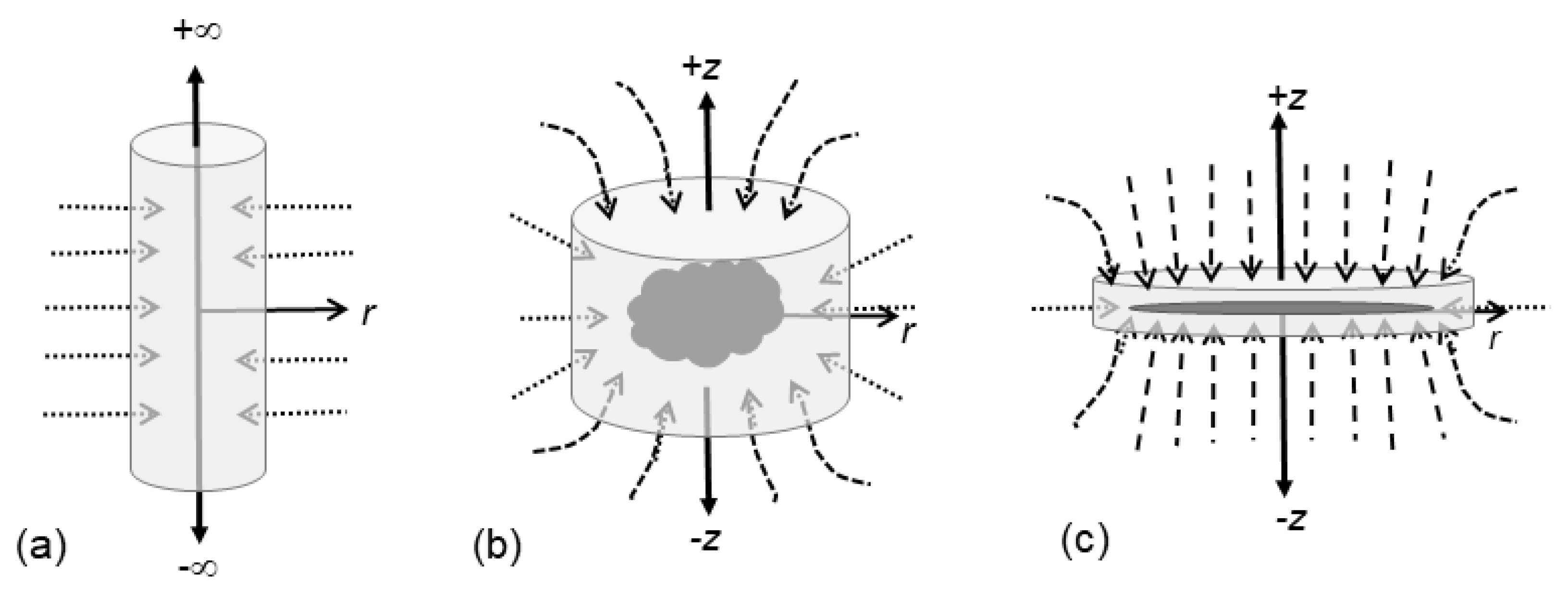
- Flat disks (Figure 2f,g; Figure 11c) require a simple relationship between surface mass density (σ), full thickness (H), and thermodynamic density (ρ):When separation of variables is invoked for a disk of finite thickness, density off the plane at any radius equals the density at z = 0 and that particular r, and thus coaxial cylinders are being considered (Section 3.1.5; also see Section 4). As explicitly stated by Toomre below his 4th equation, no mass can exist off the plane. From (17), no mass off the plane means either H = 0, or the z-dependence of ρ entails a delta function, which amounts to the same thing while requiring separation of variables for ρ (i.e., Perek’s [47] specious declaration, see [14,48]). To provide his 4th equation which contains only surface density, Toomre [46] divided Poisson’s equation by H. Division by 0 invalidates Toomre’s 4th equation, and all equations thereafter, which specify the potential without a z-dependence. It is immaterial whether he set H = 0 before or after division. Additional problems with separation of variables are discussed below.
- Poisson’s equation cannot be applied to a surface, as its use requires volume elements, per the discussion of Garland [66] (see his appendix), who based his work on Kellogg’s [62] 1925 edition. Similarly, MacMillan ([63] p. 124) states that the surface under consideration must be closed, which condition cannot be met by a plane. The above division by H = 0 is a simple explanation for application of (15) to a plane being a faux pas. Proof that an enclosed volume is required for (15) is straightforward per the theorem of Gauss [48].
- Toomre’s 2nd equation proposes a solution to (15) which includes an exponential function of the from exp(−k|z|) where k is a dummy index that is used subsequently in integration. In Toomre’s 4th equation and thereafter he sets z = 0. Obviously, his analysis is limited to the plane, which is invalid, as noted above.
- In his exponential function exp(−k|z|), k must be inversely proportional to some scale length, in accord with dimensional analysis and to provide a dimensionless argument kz. Because the relevant scale length along z is H and H = 0, k must equal some constant divided by H, and so k is infinite. Hence, k does not vary and cannot be used as the variable of integration, which invalidates Toomre’s analysis [63].
- Use of an integral formula for the potential is invalid independent of all other mathematical errors. Because all integrals can be recast as summations, the potential Toomre provided is a summation of simpler component potentials. However, Poisson’s equation is non-homogeneous. From Pinsky [67] (Chapter 1), solutions to non-homogeneous differential equations cannot be summed (i.e., superimposed), as in homogeneous equations such as that of Laplace, where ρ = 0 One can arrive at the finding that Toomre’s 2nd equation cannot solve Poisson’s equation from another perspective: Obviously, the exponential dependence on z in Toomre’s 2nd equation involves separation of the potential into a some function of r multiplied by another function of z. Whereas separation of variables is commonly used to solve homogenous differential equations, it is not possible to solve an inhomogeneous differential equation in this way, e.g., [67].
- Solving (15) using separation of variables is impossible, as revealed by inspection. Separation of variables for the potential requires that density also be a multiplication of two distinct functions, one of z and another of r. For this representation, the RHS of (17) holds at any given radius, and so the density does not depend on z. For this case, the potential cannot depend on z either. Toomre addressed this problem by setting z = 0, which prohibits solving Poisson’s equation.
- From another perspective, in “dropping” the z-dependence of the potential in Toomre’s 2nd equation from his 4th equation and beyond, Toomre assumed that density is independent of z (via Equations (15) and (17)), i.e., he actually assumed that density is constant along the z-axis. Zero is a constant. Coaxial cylinders (Figure 2) is actually the geometry described in [46].
- Due to the properties of the exponential function, Toomre’s component of the potential along z cannot reduce to the exact result for the special axis of a disk, which was known circa 1930 [63]:Equations (11) and (18) respectively reduce to the correct, inverse square dependence of force with distance at great distance, and of potential with inverse distance, if their limits as a/z approach zero are properly evaluated. The exponential function does not reduce to this required functional dependence.
3.1.7. Fundamental Mathematic Problems in Many Post-1998 NOMs Models
- Densities do not sum, as discussed in numerous books on thermodynamics. Importantly, addition of densities in Equation (17) is equivalent to summing solutions of individual differential equations. Use of linear superposition is indeed described in RC literature [58,69]. Again, Poisson’s equation is a non-homogeneous partial differential equation: it is well-known that solutions to such equations cannot be summed (e.g., [67]).
- It is immaterial what component is being summed: velocities, masses, densities (e.g., [30]), or v2, which is generally the case [29,58]. All are equally problematic. All such summations amount to linear superposition, which is allowable only for homogeneous differential equations, i.e., when ρ = 0 everywhere.
3.1.8. Relativistic Orbital Models
3.1.9. Modified Newtonian Orbital Dynamics
3.2. Comparison of Orbital Forward Models
3.2.1. Allowable Number of Free Parameters
3.2.2. Ambiguities in Force Laws
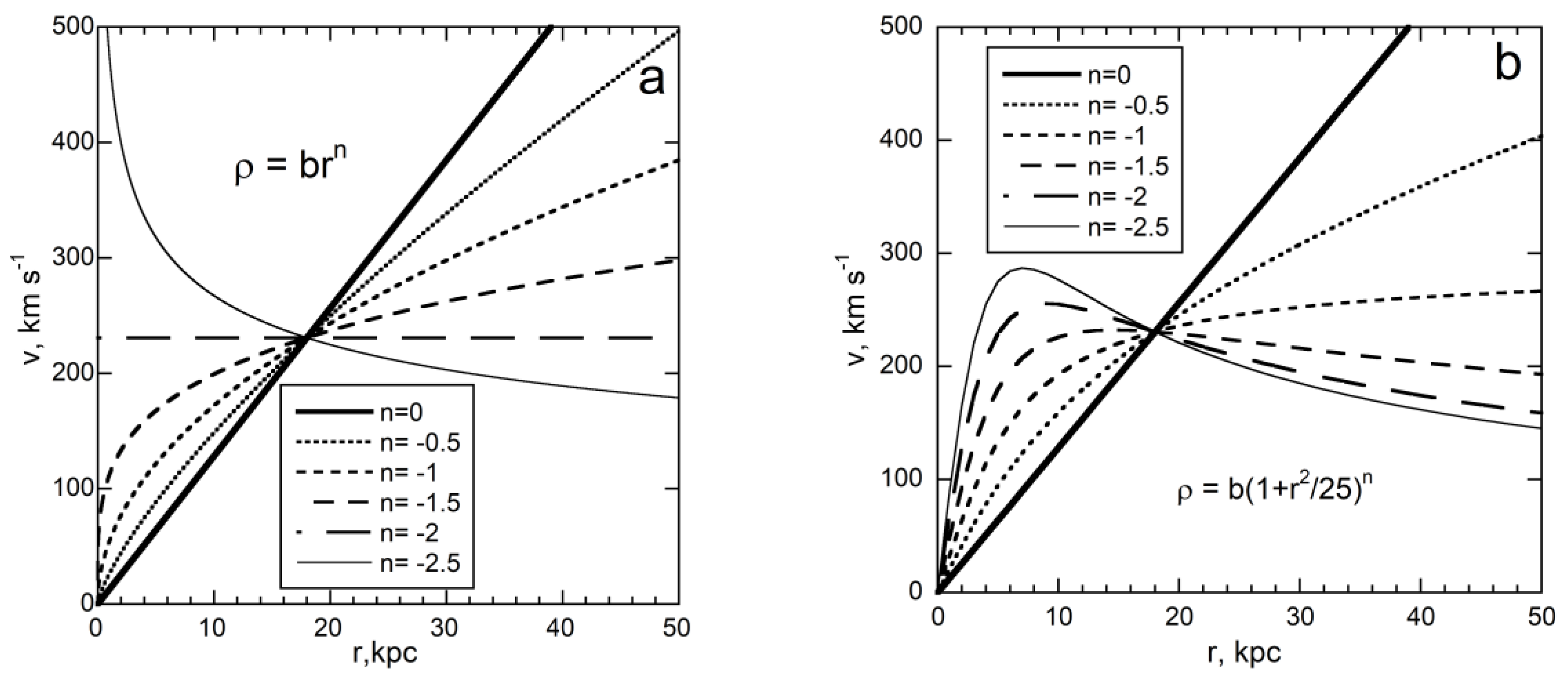
3.2.3. Density Formulations for Disk Models Based on Central Forces
3.2.4. Approximate Analytical Models of the Disk with a Single Density
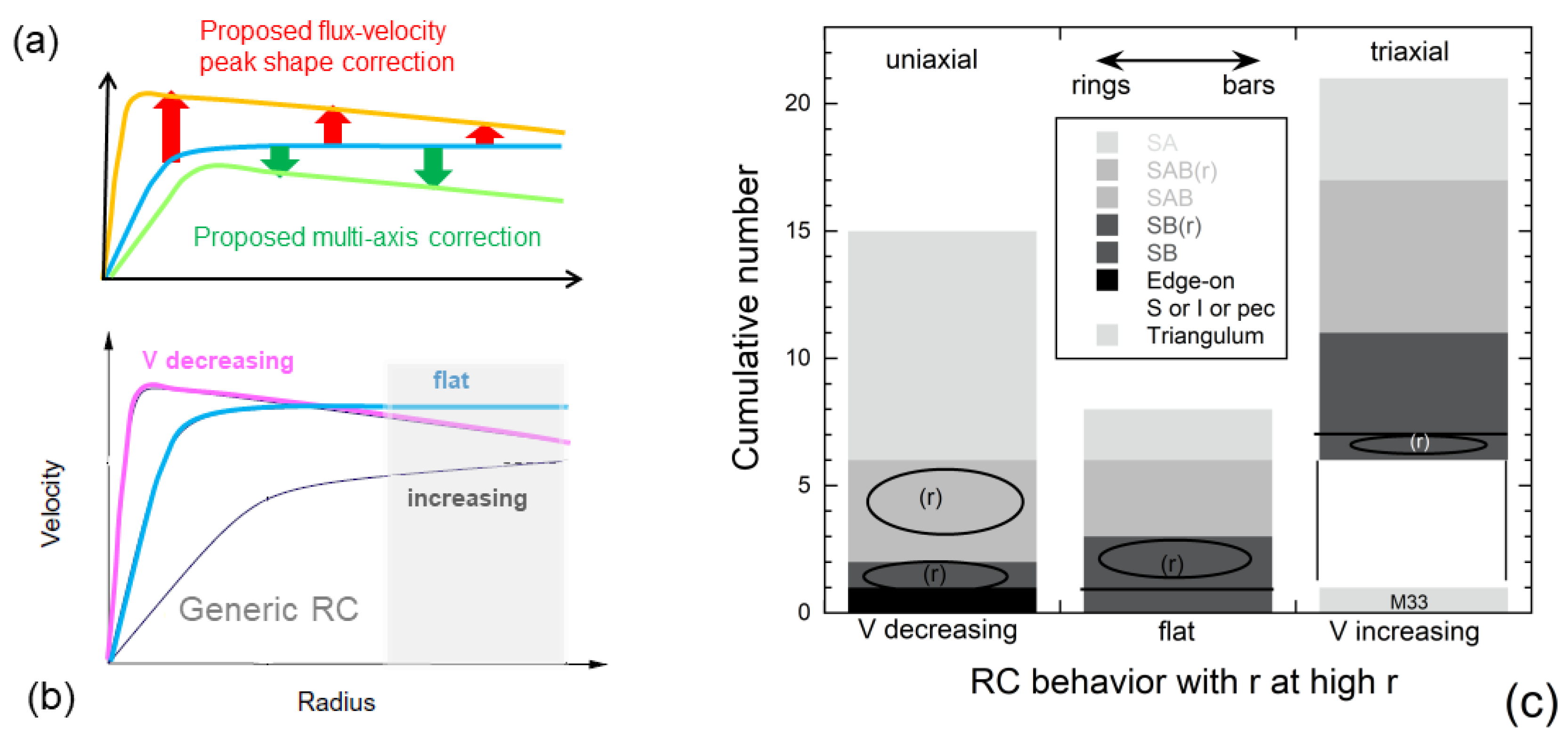
3.2.5. Forward Models of the Spinning, Oblate Shape
3.2.6. Summary
4. Inverse Models of Galactic Rotation
4.1. Numerical Disk-Ring Models
4.1.1. Mathematical Construct
- Values for H are arbitrary, as stated by the authors, who assumed H = 0.01a.
- In this formulation, using σ(r) rather than ρ(r) eliminates the free parameter, H from (26). However, this simplification stems from assuming that density in (24) is independent of z, i.e., ρ(z,r) = ρ(0,r). Hence, the model actually describes rotating coaxial cylinders. As sketched in Figure 1 and Figure 2f, these can be tall, since H is unconstrained.
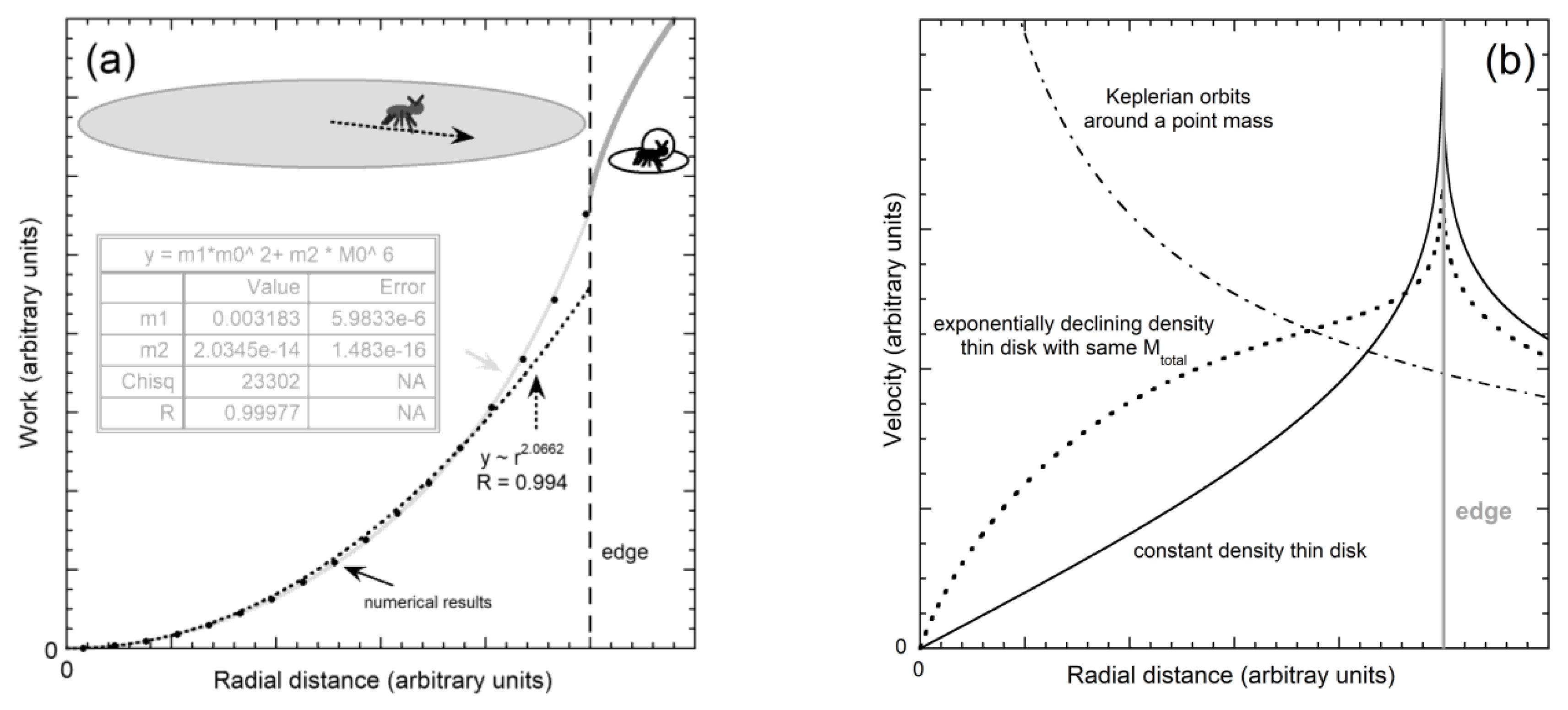
- The limit of q = a was applied in evaluating the integral of (26). This step assumes that material near the edge of the disk affects motions of material near the center. This behavior is unlike Newton’s analysis of self-gravitating spherical and spinning oblate bodies, which shows that only mass internal to the test mass controls its orbit. Evaluation over the entire disk or cylinder is needed because these shapes are not gravitationally stable (Figure 2e).
4.1.2. Results of Ring-Disk Models
4.2. Numerical Mass Summations in the Equatorial Plane
4.2.1. Mathematical Construct
- An equatorial plane of finite radius a is modeled: so no mass exists above or below z = 0.
- Each orbit is affected by all the mass points in this plane: As discussed in Section 4.1.1, no theorem of Newton exists to guide evaluation of an integral (or summation) in a disk geometry.
4.2.2. Results of Mass Summations in the Equatorial Plane
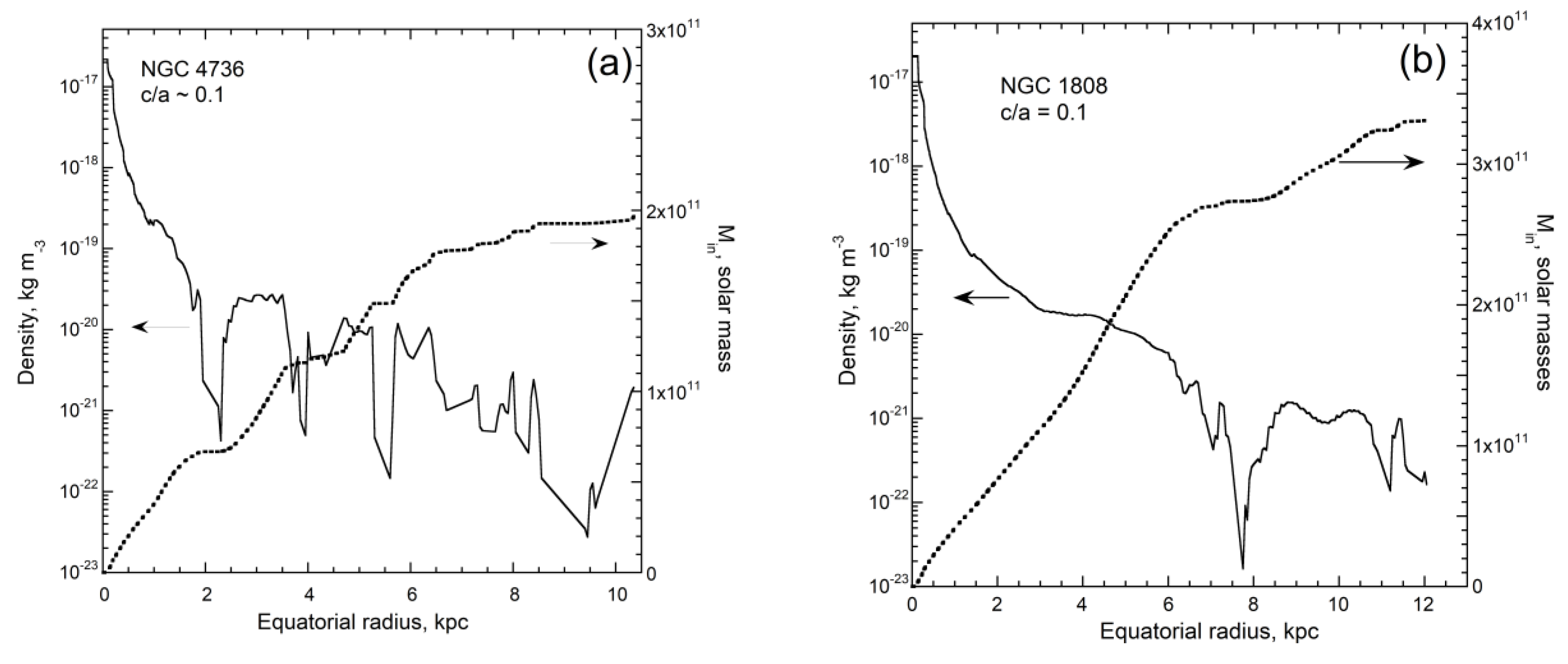
4.3. Analytical Model of the Oblate
4.3.1. Mathematical Construct
4.3.2. Results for Differential Spin
4.4. Comparison of Inverse Models
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- de Swart, J.G.; Bertone, G.; van Dongen, J. How dark matter came to matter. Nat. Astron. 2017, 1, 0059. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K. Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Faber, S.M.; Gallagher, J.S. Masses and mass-to-light ratios of galaxies. Ann. Rev. Astron. Astrophys. 1979, 17, 135–187. [Google Scholar] [CrossRef]
- Burbidge, G. On the masses and relative velocities of galaxies. Astrophys. J. 1975, 196, L7–L10. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- McGaugh, S.S. A tale of two paradigms, the mutual incommensurability of LCDM and MOND. Can. J. Phys. 2015, 93, 250–259. [Google Scholar] [CrossRef]
- Brownstein, J.R.; Moffat, J.W. Galaxy rotation curves without nonbaryonic dark matter. Astrophys. J. 2006, 636, 721–741. [Google Scholar] [CrossRef]
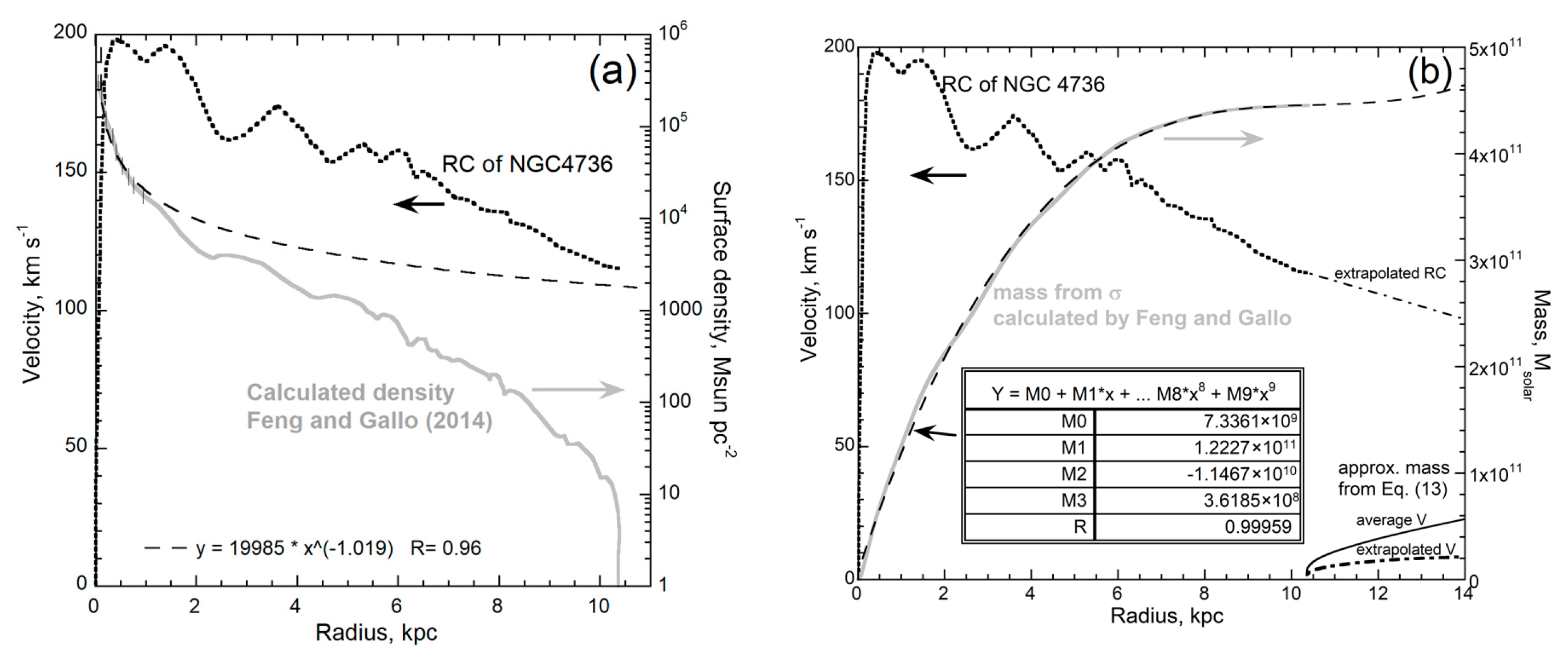
- Feng, J.Q.; Gallo, C.F. Modeling the Newtonian dynamics for rotation curve analysis of thin-diskgalaxies. Res. Astron. Astrophys. 2011, 11, 1429–1448. [Google Scholar] [CrossRef]
- Feng, J.Q. Rotating Disk Galaxies without Dark Matter Based on Scientific Reasoning. Galaxies 2020, 8, 9. [Google Scholar] [CrossRef]
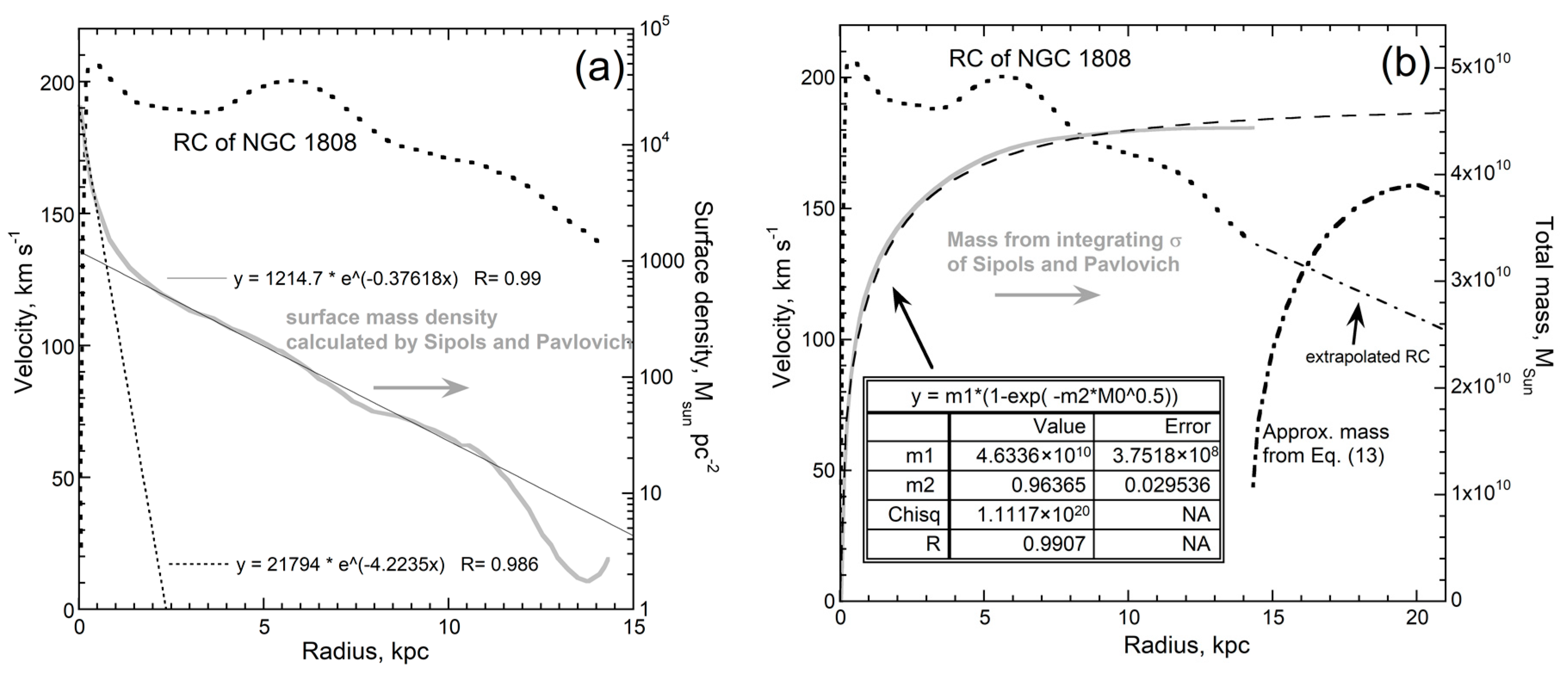
- Pavlovich, K.; Pavlovich, A.; Sipols, A. Newtonian explanation of galaxy rotation curves based on distribution of baryonic matter. arXiv 2014, arXiv:1406.2401P. [Google Scholar]
- Sipols, A.; Pavlovich, A. Dark matter dogma: A study of 214 galaxies. Galaxies 2020, 8, 36. [Google Scholar] [CrossRef]
- Marr, J.H. Galaxy rotation curves with lognormal density distribution. Mon. Not. R. Astron. Soc. 2015, 448, 3229. [Google Scholar] [CrossRef]
- Marr, J.H. Entropy and Mass Distribution in Disc Galaxies. Galaxies 2020, 8, 12. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. The physics of galactic spin. Can. J. Phys. 2017, 95, 156–166. [Google Scholar] [CrossRef]
- Criss, R.E.; Hofmeister, A.M. Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves. Galaxies 2020, 8, 19. [Google Scholar] [CrossRef]
- Forbes, D.A.; Lopez, E.D. On the Origin (and Evolution) of Baryonic Galaxy Halos. Galaxies 2017, 5, 23. Available online: https://www.mdpi.com/journal/galaxies/special_issues/baryonic_galaxy_halos (accessed on 2 April 2020). [CrossRef]
- Tumlinson, J.; Peeples, M.S.; Werk, J.K. The Circumgalactic Medium. Ann. Rev Astron. Astrophys. 2017, 55, 389–432. [Google Scholar] [CrossRef]
- Ackermann, M.; Albert, A.; Anderson, B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Bissaldi, E.; et al. Dark matter constraints from observations of 25 Milky Way satellite galaxies with the Fermi Large Area Telescope. Phys. Rev. D 2014, 89, 042001. [Google Scholar] [CrossRef]
- DeVega, H.J.; Salucci, P.; Sanchez, N.G. Observational rotation curves and density profiles versus the Thomas-Fermi galaxy structure theory. Mon. Not. R. Astron. Soc. 2014, 442, 2717–2727. [Google Scholar] [CrossRef]
- Giagu, S. WIMP dark matter searches with the ATLAS detector at the LHC. Front. Phys. 2019, 7, 75. Available online: https://doi.org/10.3389/fphy.2019.00075 (accessed on 19 February 2020). [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the presence of pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440. [Google Scholar] [CrossRef]
- Nagano, K.; Fujita, T.; Michimura, Y.; Obata, I. Axion dark matter search with interferometric gravitational wave detectors. Phys Rev. Lett. 2019, 123, 111301. [Google Scholar] [CrossRef] [PubMed]
- NRAO. National Radio Astronomy Observatory (see the gallery of images). Available online: https://public.nrao.edu/gallery/warped-disk-of-galaxy-ugc-3697-2/ (accessed on 30 May 2020).
- CHANG-ES. Continuum Halos in Nearby Galaxies- and EVLA Survey. Available online: http://www.queensu.ca/changes (accessed on 26 January 2020).
- Irwin, J.; Irwin, B.; Rainer; Benjamin, R.A.; Dettmar, R.-J.; English, J.; Heald, G.; Henriksen, R.N.; Johnson, M.; Krause, M.; et al. Continuum Halos in Nearby Galaxies: An EVLA Survey (CHANG-ES). I. Introduction to the Survey. Astronom. J. 2012, 144, 43. [Google Scholar] [CrossRef]
- Wiegert, T.; Irwin, J.; Miskolczi, A.; Schmidt, P.; Carolina Mora, S.; Damas-Segovia, A.; Stein, Y.; English, J.; Rand, R.J.; Santistevan, I. CHANG-ES IV: Radio continuum emission of 35 edge-on galaxies observed with the Karl, G. Jansky very large array in D configuration—Data release 1. Astronom. J. 2015, 150, 81. [Google Scholar] [CrossRef]
- Groetsch, C.W. Inverse Problems: Activities for Undergraduates; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ambartsumian, V. On the derivation of the frequency function of space velocities of the stars from the observed radial velocities. Mon. Not. Roy. Astron. Soc. 1936, 96, 172. [Google Scholar] [CrossRef]
- Diaconis, P. Theories of Data Analysis: From Magical Thinking Through Classical Statistics; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Jardel, J.R.; Gebhardt, K.; Shen, J.; Fisher, D.B.; Kormendy, J.; Kinzler, J.; Lauer, T.R.; Richstone, D.; Gültekin, K. Orbit-based dynamical models of the Sombrero galaxy (NGC 4594). Astrophys. J. 2011, 739, 21. [Google Scholar] [CrossRef]
- Kam, Z.S.; Carignan, C.; Chemin, L.; Amram, P.; Epinat, B. Kinematics and mass modelling of M33, Hα observations. Mon. Not. R. Astron. Soc. 2015, 449, 4048–4070. [Google Scholar] [CrossRef]
- McGaugh, S. Predictions and Outcomes for the Dynamics of Rotating Galaxies. Galaxies 2020, 8, 35. [Google Scholar] [CrossRef]
- Lin, H.-N.; Li, M.-H.; Li, X.; Chang, Z. Galaxy rotation curves in the Grumiller’s modified gravity. Mon. Not. R. Astron. Soc. 2013, 430, 450–458. [Google Scholar] [CrossRef]
- Scelza, G.; Stabile, A. Numerical analysis of galactic rotation curves. Astrophys. Space Sci. 2015, 357, 44. [Google Scholar] [CrossRef][Green Version]
- Bottema, R.; Pestaña, J.L.G. The distribution of dark and luminous matter inferred from extended rotation curves. Mon. Not. R. Astron. Soc. 2015, 448, 2566–2593. [Google Scholar] [CrossRef]
- Sofue, Y.; Rubin, V.C. Rotation curves of spiral galaxies. Ann. Rev. Astron. Astrophys. 2001, 39, 137–174. [Google Scholar] [CrossRef]
- Sil’chenko, O.K.; Moiseev, A.V. Nature of nuclear rings in unbarred galaxies: NGC 7742 AND NGC 7217. Astronom. J. 2006, 131, 1336–1346. [Google Scholar]
- Moulton, F.R. An Introduction to Celestial Mechanics; MacMillan: New York, NY, USA, 1914. [Google Scholar]
- Schmidt, M. A model of the distribution of mass in the galactic system. Bul. Astron. Inst. Neth. 1956, 13, 15. [Google Scholar]
- Todhunter, I. A History of the Mathematical Theories of Attraction and Figure of the Earth; MacMillan and Co.: London, UK, 1873. [Google Scholar]
- Criss, R.E. Analytics of planetary rotation: Improved physics with implications for the shape and super-rotation of Earth’s Core. Earth Sci. Rev. 2019, 192, 471–479. [Google Scholar] [CrossRef]
- NASA/IPAC. Extragalactic Database. Available online: https://ned.ipac.caltech.edu/ (accessed on 1 February 2020).
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Criss, R.E.; Hofmeister, A.M. Galactic density and evolution based on the virial theorem, energy minimization, and conservation of angular momentum. Galaxies 2018, 6, 115. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E.; Criss, E.M. Verified solutions for the gravitational attraction to an oblate spheroid: Implications for planet mass and satellite orbits. Planet. Space Sci. 2018, 152, 68–81. [Google Scholar] [CrossRef]
- Toomre, A. On the distribution of matter within highly flattened galaxies. Astrophys. J. 1963, 138, 385–392. [Google Scholar] [CrossRef]
- Perek, L. Heterogeneous spheroids with Gaussian and exponential density laws. Bull. Astron. Inst. Czechoslov. 1958, 9, 208–212. [Google Scholar]
- Hofmeister, A.M.; Criss, R.E. Implications of geometry and the theorem of Gauss on Newtonian gravitational systems and a caveat regarding Poisson’s equation. Galaxies 2017, 5, 89. [Google Scholar] [CrossRef]
- Halliday, D.; Resnick, R. Physics; John Wiley and Sons: New York, NY, USA, 1966. [Google Scholar]
- Begeman, K.G. HI rotation curves of spiral galaxies. I. NGC 3198. Astron. Astrophys. 1989, 223, 47–60. [Google Scholar]
- Sofue, Y. Dark halos of M 31 and the Milky Way. Publ. Astron. Soc. Jpn. 2015, 67, 759. [Google Scholar] [CrossRef]
- Sofue, Y. Rotation curve of Milky Way. Galaxies 2020, 8, 37. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.-H.; Kennicutt, R.C., Jr. High-resolution rotation curves and galaxy mass models from THINGS. Astrophys. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- De Blok, W.J.G. Is there a universal alternative to dark matter? Nat. Astron. 2018, 2, 615–616. [Google Scholar] [CrossRef]
- Transtrum, M.K.; Machta, B.B.; Brown, K.S.; Daniels, B.C.; Myers, C.R.; Sethna, J.P. Perspective: Sloppiness and emergent theories in physics, biology, and beyond. J. Chem. Phys. 2015, 143, 010901. [Google Scholar] [CrossRef]
- Koribalski, B.S.; Wang, J.; Kamphuis, P.; Westmeier, T.; Staveley-Smith, L.; Oh, S.H.; Lopez-Sanchez, A.R.; Wong, O.I.; Ott, J.; de Blok, W.J.G.; et al. The Local Volume HI Survey (LVHIS). Mon. Not. R. Astron. Soc. 2018, 478, 1611–1648. [Google Scholar] [CrossRef]
- Carignan, C. Light and mass distribution of the magellanic-type spiral NGC 3109. Astrophys. J. 1985, 299, 59–73. [Google Scholar] [CrossRef]
- Chemin, L.; Carignan, C.; Foster, T. HI Kinematics and dynamics of Messier 31. Astrophys. J. 2009, 705, 1395–1415. [Google Scholar] [CrossRef]
- Gentile, G.; Salucci, P.; Klein, U.; Vergani, D.; Kalberla, P. Mapping the inner regions of the polar disk galaxy NGC 4650A with MUSE. Mon. Not. R. Astron. Soc. 2004, 351, 903. [Google Scholar] [CrossRef]
- Iodice, E.; Coccato, L.; Combes, F.; de Zeeuw, T.; Arnaboldi, M.; Weilbacher, P.M.; Bacon, R.; Kuntschner, H.; Spavone, M. Mapping the inner regions of the polar disk galaxy NGC 4650A with MUSE. Astron. Astrophys. 2015, 583, A48. [Google Scholar] [CrossRef][Green Version]
- Wiegert, T.; English, J. Kinematic classification of non-interacting spiral galaxies. New Astron. 2014, 26, 40–61. [Google Scholar] [CrossRef]
- Kellogg, O.D. Foundations of Potential Theory; Dover Publications: New York, NY, USA, 1953. [Google Scholar]
- MacMillan, W.D. The Theory of the Potential; McGraw-Hill: New York, NY, USA, 1930. [Google Scholar]
- Feng, J.Q.; Gallo, C.F. Mass distribution in rotating thin-disk galaxies according to Newtonian dynamics. Galaxies 2014, 2, 199–222. [Google Scholar] [CrossRef]
- Evans, N.W.; Bowden, A. Extremely flat halos and the shape of the galaxy. Mon. Not. R. Astron. Soc. 2014, 43, 2–11. [Google Scholar] [CrossRef]
- Garland, G.D. The Earth’s Shape and Gravity; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Pinsky, M.A. Introduction to Partial Differential Equations; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Dehnen, W.; Binney, J. Mass models of the Milky Way. Mon. Not. R. Astron. Soc. 1998, 294, 429. [Google Scholar] [CrossRef]
- Ibata, R.; Lewis, G.F.; Martin, N.F.; Bellazzini, M.; Correnti, M. Does the Sagittarius stream constrain the Milky Way halo to be triaxial? Astrophys. J. Lett. 2013, 765, L155. [Google Scholar] [CrossRef]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian Dynamics as an Alternative to Dark Matter. Ann. Rev. Astron. Astrophys. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Disney, M.J. Modern Cosmology, Science or Folktale? Am. Sci. 2007, 95, 383–385. [Google Scholar] [CrossRef]
- Van Albada, G.D.; Sancisi, R. Dark matter in spiral galaxies. Philos. Trans. R. Soc. Lond. 1986, A320, 447–464. [Google Scholar]
- De Lorenzi, F.O.; Gerhard, L.; Coccato, M.; Arnaboldi, M.; Capaccioli, N.G.; Douglas, K.C.; Freeman, K.; Kuijken, M.R.; Merrifield, N.R.; Napolitano, E.; et al. Debattista, Dearth of dark matter or massive dark halo? Mass-shape-anisotropy degeneracies revealed by NMAGIC dynamical models of the elliptical galaxy NGC 3379. Mon. Not. R. Astron. Soc. 2009, 395, 76. [Google Scholar] [CrossRef]
- Boroson, T. The distribution of luminosity in spiral galaxies. Astrophys. J. Supp. 1981, 46, 177. [Google Scholar] [CrossRef]
- Van Van der Kruit, P.C. The radial distribution of surface brightness in galactic disks. Astron. Astrophys. 1987, 173, 59–80. [Google Scholar]
- Gallo, C.F.; Feng, J.Q. A thin-disk gravitational model for galactic rotation. In Proceedings of the 2nd Crisis Cosmology Conference, Washington, DC, USA, 7–11 September 2009; Volume 413, pp. 289–303. [Google Scholar]
- Emden, R. Gaskuglen—Anwendungen de Mechanischen Wärmetheorie; B.G. Teubner: Leipzig, Germany, 1907. [Google Scholar]
- Maron, S.H.; Prutton, C.F. Fundamental Principles of Physical Chemistry; Macmillan: New York, NY, USA, 1970. [Google Scholar]
- Romanowsky, A.J.; Douglas, N.G.; Arnaboldi, M.; Kuijken, K.; Merrifield, M.R.; Napolitano, N.R.; Capaccioli, M.; Freeman, K. A dearth of dark matter in ordinary elliptical galaxies. Science 2003, 301, 1696–1698. [Google Scholar] [CrossRef]
- Feng, J.Q.; Gallo, C.F. Deficient reasoning for dark matter in galaxies. Phys. Int. 2015, 6, 11–22. [Google Scholar] [CrossRef]
- Sofue, Y.; Tutui, Y.; Honma, M.; Tomita, A.; Takamiya, T.; Koda, J.; Takeda, Y. Central rotation curves of spiral galaxies. Astrophys. J. 1999, 523, 136–146. [Google Scholar] [CrossRef]
- Brandt, J.C. On the distribution of mass in galaxies. I. The large-scale structure of ordinary spirals with applications to M31. Astrophys. J. 1960, 131, 293–303. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Spatial and symmetry constraints as the basis of the Virial Theorem and astrophysical implications. Can. J. Phys. 2016, 94, 380–388. [Google Scholar] [CrossRef]
- Langley, S.P. The history of a doctrine. Am. J. Sci. 1889, 37, 1–23. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order through Fluctuations; J. Wiley and Sons: New York, NY, USA, 1977. [Google Scholar]
- Samuelsen, P.A.; Planck, M.; Kuhn, T.S.; Poincare, H. Science Makes Progress Funeral by Funeral. Available online: https://quoteinvestigator.com/2017/09/25/progress/ (accessed on 24 April 2020).
| Type | Input and Shape | Physical Model | Output | Examples |
|---|---|---|---|---|
| Forward | Surface density; 4 shapes 2 | Orbits under central forces 3 | Simulated RC with NBDM | e.g., [30,31] |
| Forward | Surface density; disk 2 | Orbits under central forces 3 | Simulated RC | [12,13] |
| Forward | Surface density; disk 2 | MOND 4 | Simulated RC | [5,6,32] |
| Forward | Surface density; disk 2 | General relativity 4 | Simulated RC | [7,33,34] |
| Inverse | RC; disk | Elliptical integrals 5 | Surface density vs. radius | [8,9] |
| Inverse | RC; equatorial plane | Point mass attractions 6 | Surface density vs. radius | [10,11] |
| Inverse | RC; spheroid | Virial theorem for spin 7 | Volume density vs. radius | [14,15] |
| Model | Component Geometry 1 | Force Constants | Number of Parameters 4 | Limitations | References or Figures |
|---|---|---|---|---|---|
| NOMs | Disk + NBDM halo + bulge + black hole 2, 3 | G | ≥8 | Densities often summed 2 | [29,30,35,36,51,54,55,56,57,58,59,60,69] 6 |
| Log-Normal | Disk | G | ≥2 | No mass at center | [12,13] |
| MOND | Disk 3 | G + a | ≥3 | Ad hoc force law 5 | [5,6,32,70] |
| Relativity | Disk 3 | G + a | ≥3 | Flexible force law 5 | [7,33,34] |
| Numerical | Ultrathin disk | G | ≥2 | Disks are unstable | Figure 10 |
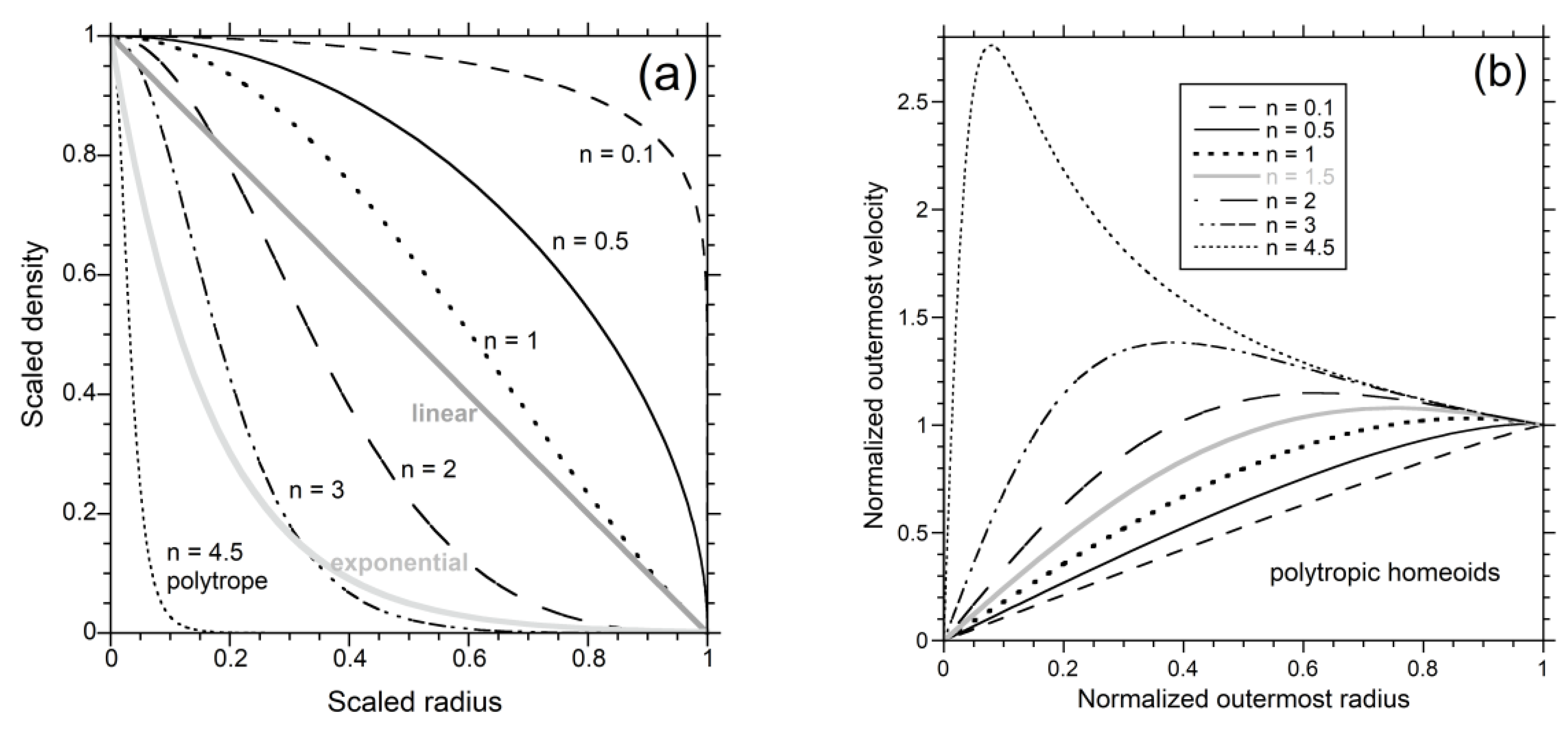
| Spheroid | Homeoid | G | ≥2 | Complex mathematics | Figure 8, Figure 12 and Figure 13 |
| Point mass | point | G | 1 | Unrealistic for galaxies | Figure 10 |
| Model | Geometry | Parameters 1 | Methodology | References |
|---|---|---|---|---|
| Ring integration | Finite thickness disk | Thickness | Numerical | [8,9,64,76,80] |
| Mass summation | Equatorial plane | - | Matrix inversion | [10,11] |
| Spin | Oblate spheroid | Ellipticity | Analytical | [14,15,44,48] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmeister, A.M.; Criss, R.E. Debated Models for Galactic Rotation Curves: A Review and Mathematical Assessment. Galaxies 2020, 8, 47. https://doi.org/10.3390/galaxies8020047
Hofmeister AM, Criss RE. Debated Models for Galactic Rotation Curves: A Review and Mathematical Assessment. Galaxies. 2020; 8(2):47. https://doi.org/10.3390/galaxies8020047
Chicago/Turabian StyleHofmeister, Anne M., and Robert E. Criss. 2020. "Debated Models for Galactic Rotation Curves: A Review and Mathematical Assessment" Galaxies 8, no. 2: 47. https://doi.org/10.3390/galaxies8020047
APA StyleHofmeister, A. M., & Criss, R. E. (2020). Debated Models for Galactic Rotation Curves: A Review and Mathematical Assessment. Galaxies, 8(2), 47. https://doi.org/10.3390/galaxies8020047





