Physics and Phenomenology of Weakly Magnetized, Relativistic Astrophysical Shock Waves
Abstract
1. Introduction
2. The Hydrodynamical View
2.1. Shock Velocity
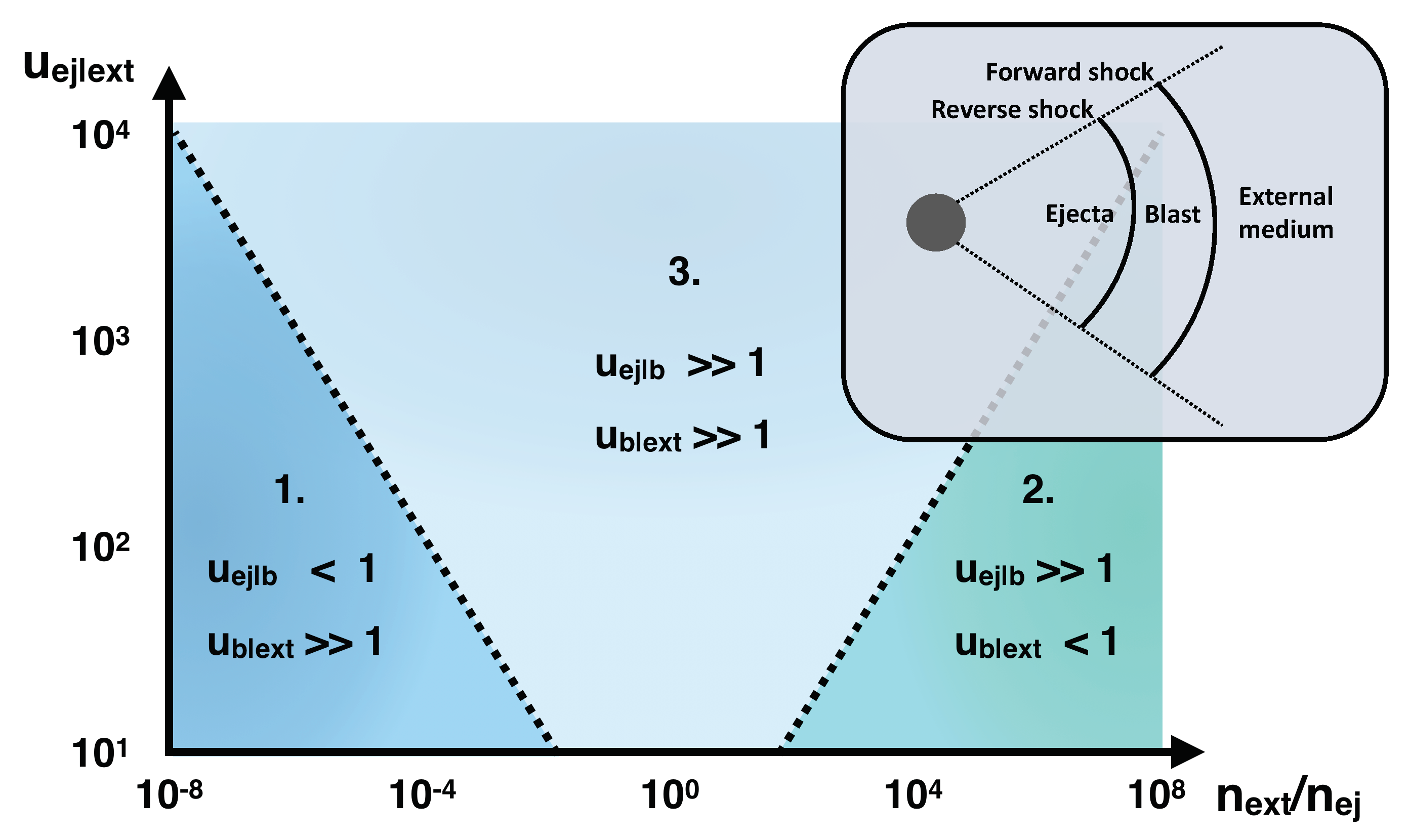
- Assume first that the blast frame is close to the comoving reference frame of the ejecta, which means that the forward shock is ultrarelativistic, while the reverse shock propagating is subrelativistic. This means and . From Equation (1) above, one then infers . This situation occurs when (since ) and .
- Conversely, the blast frame may be close to the external medium frame, in which case the forward shock becomes subrelativistic while the reverse shock is ultrarelativistic. Using arguments similar to those detailed above, one then finds , and . This limit applies when and .
- In between those two extreme limits, both forward and reverse shocks are truly relativistic. Under these conditions, the shock velocities satisfy the following hierarchy: . It then becomes convenient to approximate the relative velocity as . Inserting in Equation (1) then gives . Similarly, one also obtains .
2.2. Shock Jump Conditions
2.3. Relativistic Fermi Acceleration
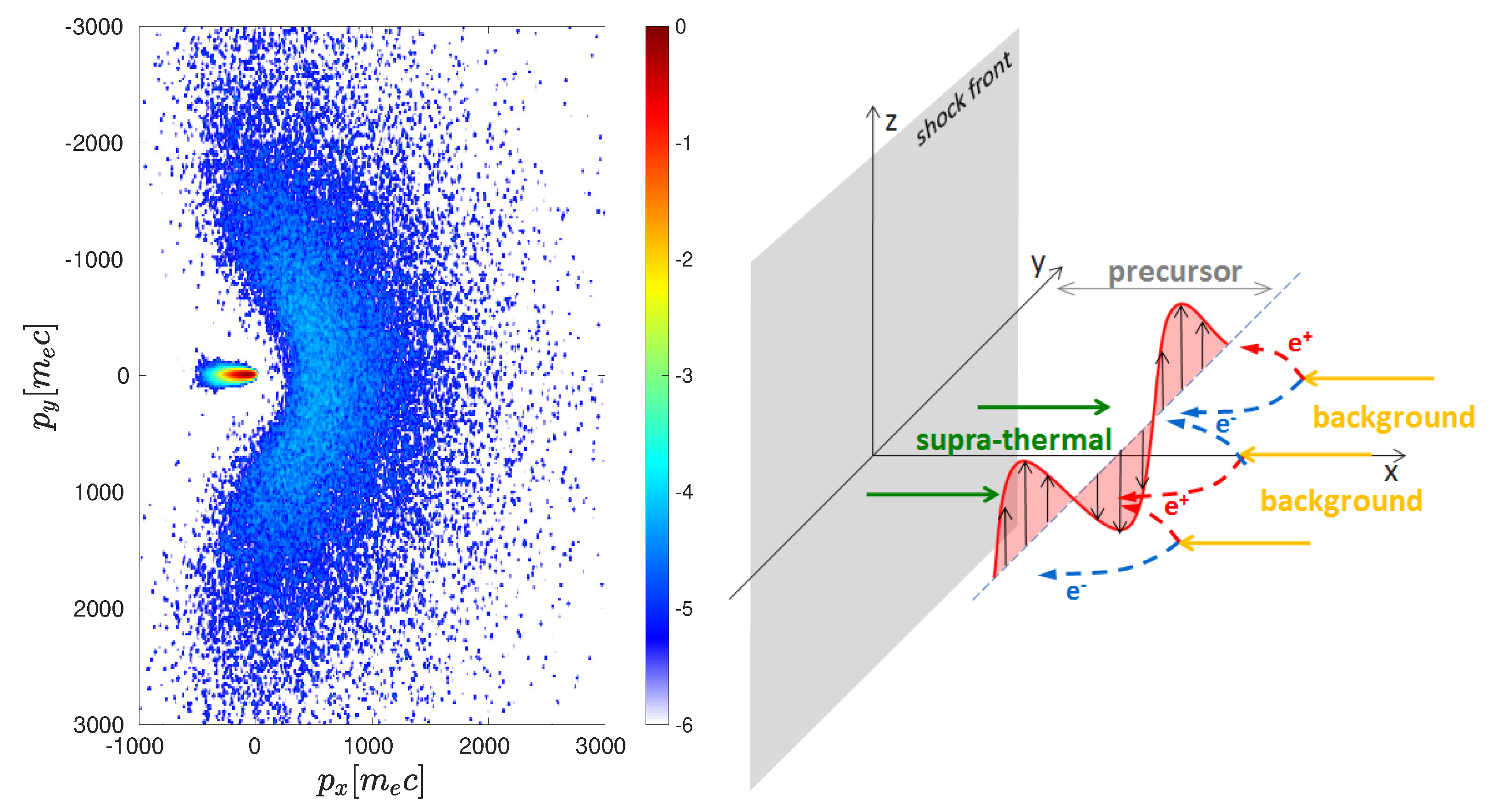
- Given that and , with a particle velocity, accelerated particles do not diffuse spatially in the upstream plasma before returning to the shock front. They rather undergo small-angle diffusion through an electromagnetic microturbulence, or small angle deflection in a large-scale magnetic field, until their parallel velocity along the shock normal (i.e., the direction of propagation of the shock front), becomes smaller than . At that point, the shock catches up with the particle, and the latter is thus sent downstream [35,36].
- As a consequence, if the particle spends a time in the upstream, the distance between the shock front and the particle is of the order of . The corresponding region, located immediately upstream of the shock front, where the accelerated particles mix with the unshocked plasma in the course of their Fermi cycles across the shock surface, is called the shock precursor. It is therefore of very limited extent in the relativistic regime [37]. This has important implications for the development of plasma instabilities, because only those whose growth length scale is short enough, can be excited on the precursor crossing timescale [38,39,40].
- While the spectral index of the momentum spectrum of the accelerated population scales with the shock three-velocity in the sub-relativistic regime, it reaches an asymptotic value in the relativistic regime [35,36,41,42,43,44,45,46,47], see also [48,49,50,51,52,53] for ab initio PIC numerical simulations. The index is here defined by .
- While the notion of a reference frame is of modest significance in the subrelativistic regime, it becomes crucial in the relativistic regime. The notion of an acceleration timescale, in particular, depends strongly on the frame in which it is calculated. The downstream rest frame, which is about equivalent to the shock rest frame, provides a convenient frame for this purpose.
3. The Microphysical View
3.1. Weibel-Mediated Shock Waves at Low Magnetization
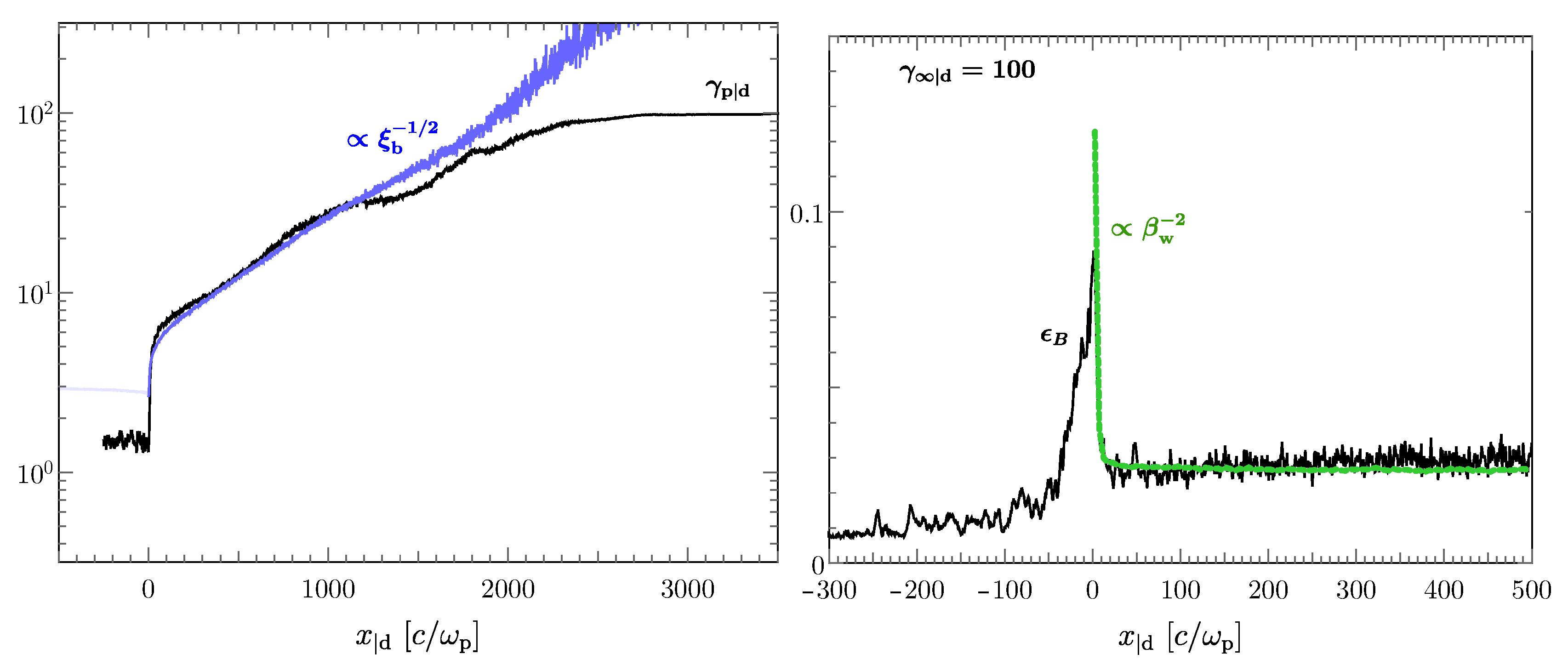
Structure of the Precursor
3.2. Relativistic Shocks of Moderate Magnetization
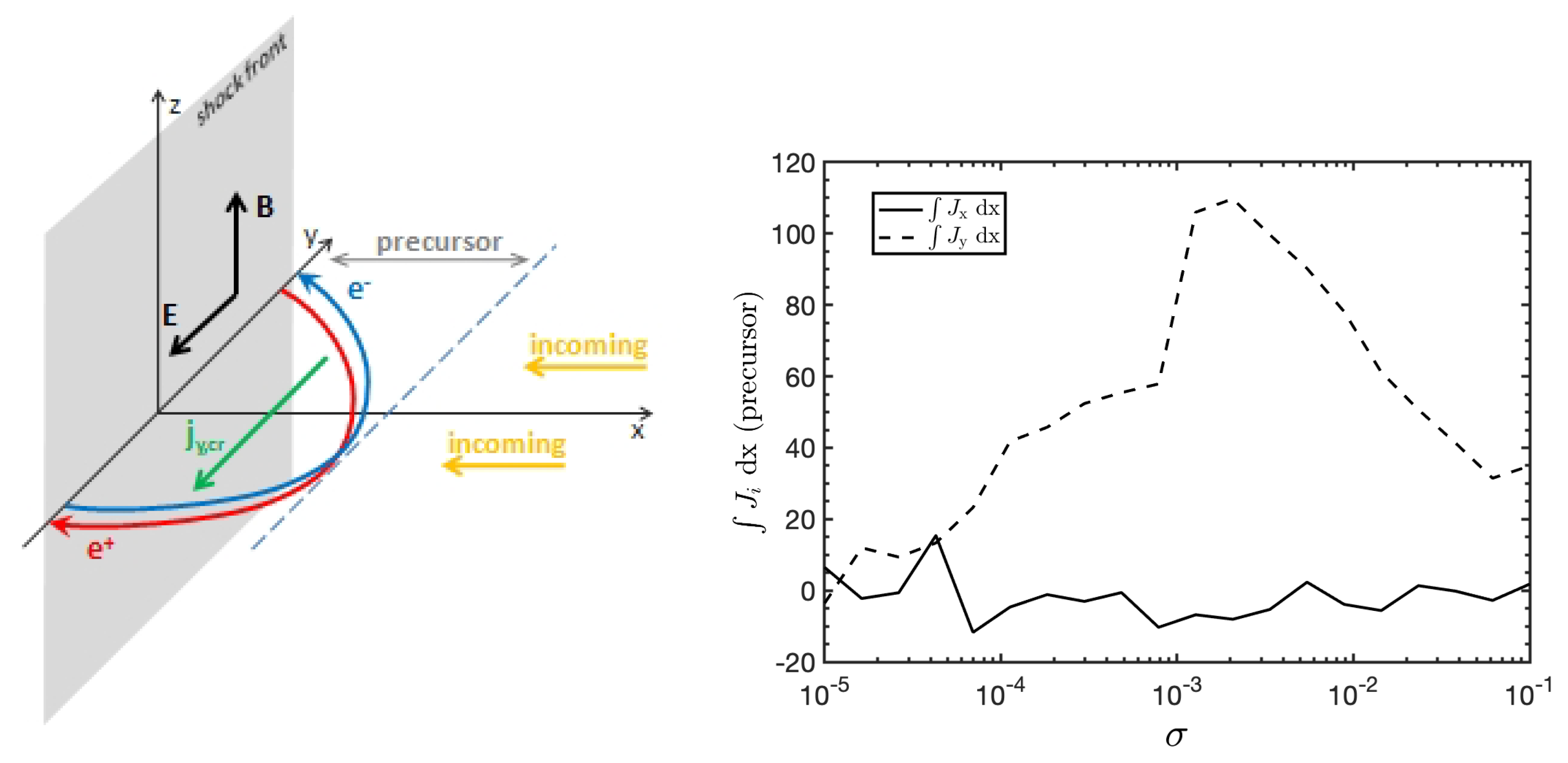
3.2.1. Perpendicular Current Driven Instability
3.2.2. Structure of the Precursor
3.2.3. A View in Terms of Magnetization
4. Phenomenological Consequences
4.1. Acceleration and Spectral Index
4.2. Acceleration Rate and Consequences on the Particle Maximum Energy
4.3. Minimum Electron Lorentz Factor in Electron-Proton Plasmas
4.4. Fate of Downstream Turbulence
5. Open Questions
- Current understanding suggests that particle acceleration should become efficient at low magnetization, , and indeed this matches well what is seen in PIC simulations. However, the phenomenological modeling of pulsar wind nebulae suggests both that the magnetization at the termination shock is significantly higher than the above critical threshold, and that acceleration is near-optimal in those objects, because they are seemingly able to accelerate particles up to the synchrotron burn-off limit (see e.g., [7] and references therein). Observations suggest that particle acceleration takes place close to the termination shock, hence our current theory of relativistic shock acceleration may be currently missing an important item.
- It is important to keep in mind that PIC simulations have so far assumed idealized conditions, meaning a smooth, laminar cold upstream plasma, and that they have been restricted to timescales orders of magnitude below those probed by astrophysical observations. They have also neglected the possible feedback of radiation on the shock structure. The impact of a pre-existing, upstream turbulence, or high amplitude waves, is an important avenue of study for PIC simulations, as this might alter the picture developed earlier. Similarly, any broadband spectrum of radiation generated by the accelerated particles themselves, or by an external source, may have nontrivial and important consequences for the shock physics, through the possible generation of pairs in the shock vicinity (see e.g., [122]).
- More generally speaking, how the precursor evolves on long timescales remains a question of debate. The scaling of the microturbulence amplitude in the shock precursor in the PIC simulations depicted above suggests that some form of saturation has been reached, which, in turn, suggests that such precursors could be extended over arbitrarily long length scales, without altering much of their appearance. At the present stage, one cannot exclude that secondary instabilities, e.g., [92,123,124,125], would grow on top of the primary (CFI, PCI) instability responsible for the shock dynamics in the above models. This could modify the turbulence properties in various ways, by changing its strength and/or its coherence length, with direct consequences for acceleration and phenomenology.
6. Summary, Final Comments
- The electron distribution exhibits a large minimum Lorentz factor close to , if the shock propagates into a plasma with electrons and protons in equal numbers, due to a nontrivial energy transfer between the ions and the electrons of the unshocked plasma, in the shock precursor; by contrast, in a pair shock, the minimum Lorentz factor is of the order of .
- The acceleration rate is significantly slower than Bohm, implying reduced maximal energies for electrons and ions as compared to naive expectations, although large enough, e.g., to produce GeV synchrotron (and TeV inverse Compton) photons, or PeV protons during the early afterglow of gamma-ray bursts.
- The small-scale nature of the turbulence makes it prone to decay through phase mixing, which implies that the effective magnetization may be much smaller in the emission region than in the acceleration region, where it is typically of the order of 0.01.
- The ensuing low value of in the emission region implies that inverse Compton scattering off the synchrotron-produced photons becomes the dominant source of electron cooling, leading to a significant amount of radiation at the highest energies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Romero, G.E.; Boettcher, M.; Markoff, S.; Tavecchio, F. Relativistic Jets in Active Galactic Nuclei and Microquasars. Space Sci. Rev. 2017, 207, 5–61. [Google Scholar] [CrossRef]
- Rieger, F.; Levinson, A. Radio Galaxies at VHE Energies. Galaxies 2018, 6, 116. [Google Scholar] [CrossRef]
- Piran, T. The physics of gamma-ray bursts. Rev. Mod. Phys. 2004, 76, 1143–1210. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts & relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar]
- Nava, L. High-energy emission from gamma-ray bursts. Int. J. Mod. Phys. D 2018, 27, 1842003. [Google Scholar] [CrossRef]
- Bykov, A.M.; Amato, E.; Petrov, A.E.; Krassilchtchikov, A.M.; Levenfish, K.P. Pulsar Wind Nebulae with Bow Shocks: Non-thermal Radiation and Cosmic Ray Leptons. Space Sci. Rev. 2017, 207, 235–290. [Google Scholar] [CrossRef]
- Amato, E. The theory of Pulsar Wind Nebulae: Recent progress. arXiv 2020, arXiv:2001.04442. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Halzen, F. High-energy neutrino astrophysics. Nat. Phys. 2017, 13, 232–238. [Google Scholar] [CrossRef]
- Mészáros, P.; Fox, D.B.; Hanna, C.; Murase, K. Multi-messenger astrophysics. Nat. Rev. Phys. 2019, 1, 585–599. [Google Scholar] [CrossRef]
- Blandford, R.; Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 1987, 154, 1–75. [Google Scholar] [CrossRef]
- Kirk, J.G.; Duffy, P. Particle acceleration and relativistic shocks. J. Phys. G 1999, 25. [Google Scholar] [CrossRef]
- Bykov, A.; Gehrels, N.; Krawczynski, H.; Lemoine, M.; Pelletier, G.; Pohl, M. Particle Acceleration in Relativistic Outflows. Space Sci. Rev. 2012, 173, 309–339. [Google Scholar] [CrossRef]
- Sironi, L.; Keshet, U.; Lemoine, M. Relativistic Shocks: Particle Acceleration and Magnetization. Space Sci. Rev. 2015, 191, 519–544. [Google Scholar] [CrossRef]
- Kirk, J.G.; Lyubarsky, Y.; Petri, J. The Theory of Pulsar Winds and Nebulae. In Neutron Stars and Pulsars; Becker, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 357, p. 421. [Google Scholar]
- Rees, M.J. The M87 jet: Internal shocks in a plasma beam? Mon. Not. Roy. Astron. Soc. 1978, 184, 61P–65P. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. Gamma-ray bursts from internal shocks in a relativistic wind: temporal and spectral properties. Mon. Not. Roy. Astron. Soc. 1998, 296, 275–286. [Google Scholar] [CrossRef]
- Malzac, J. Internal shocks at the origin of the flat spectral energy distribution of compact jets. Mon. Not. Roy. Astron. Soc. 2013, 429, L20–L24. [Google Scholar] [CrossRef]
- Baring, M.G.; Böttcher, M.; Summerlin, E.J. Probing acceleration and turbulence at relativistic shocks in blazar jets. Mon. Not. Roy. Astron. Soc. 2017, 464, 4875–4894. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Hydrodynamic Timescales and Temporal Structure of Gamma-Ray Bursts. Astrophys. J. 1995, 455, L143. [Google Scholar] [CrossRef]
- Taub, A.H. Relativistic Rankine-Hugoniot Equations. Phys. Rev. 1948, 74. [Google Scholar] [CrossRef]
- Akhiezer, I.A.; Polovin, R.V. Theory of Relativistic Magnetohydrodynamic Waves. JETP 1959, 9, 1316. [Google Scholar]
- Lichnerowicz, A. Shock Waves in Relativistic Magnetohydrodynamics. Phys. Scr. 1970, 2, 221–225. [Google Scholar] [CrossRef]
- Blandford, R.D.; McKee, C.F. Fluid dynamics of relativistic blast waves. Phys. Fluids 1976, 19, 1130–1138. [Google Scholar] [CrossRef]
- Pe’er, A.; Long, K.; Casella, P. Dynamical Properties of Internal Shocks Revisited. Astrophys. J. 2017, 846, 54. [Google Scholar] [CrossRef]
- Lemoine, M.; Ramos, O.; Gremillet, L. Corrugation Of Relativistic Magnetized Shock Waves. Astrophys. J. 2016, 827, 44. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Drury, L.O. An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 1983, 46, 973–1027. [Google Scholar] [CrossRef]
- Ellison, D.C.; Jones, F.C.; Reynolds, S.P. First-order Fermi particle acceleration by relativistic shocks. Astroph. J. 1990, 360, 702–714. [Google Scholar] [CrossRef]
- Bednarz, J.; Ostrowski, M. The acceleration time-scale for first-order Fermi acceleration in relativistic shock waves. Mon. Not. Roy. Astron. Soc. 1996, 283. [Google Scholar] [CrossRef]
- Pelletier, G. Fermi Acceleration of Astroparticles; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Lemoine, M.; Pelletier, G.; Revenu, B. On the Efficiency of Fermi Acceleration at Relativistic Shocks. Astrophys. J. Lett. 2006, 645, L129–L132. [Google Scholar] [CrossRef]
- Niemiec, J.; Ostrowski, M.; Pohl, M. Cosmic-Ray Acceleration at Ultrarelativistic Shock Waves: Effects of Downstream Short-Wave Turbulence. Astrophys. J. 2006, 650, 1020–1027. [Google Scholar] [CrossRef][Green Version]
- Marcowith, A.; Ferrand, G.; Grech, M.; Meliani, Z.; Plotnikov, I.; Walder, R. Multi-scale simulations of particle acceleration in astrophysical systems. arXiv 2020, arXiv:2002.09411. [Google Scholar] [CrossRef]
- Gallant, Y.A.; Achterberg, A. Ultra-high-energy cosmic ray acceleration by relativistic blast waves. Month. Not. Roy. Astron. Soc. 1999, 305. [Google Scholar] [CrossRef]
- Achterberg, A.; Gallant, Y.A.; Kirk, J.G.; Guthmann, A.W. Particle acceleration by ultrarelativistic shocks: Theory and simulations. Mon. Not. Roy. Astron. Soc. 2001, 328, 393–408. [Google Scholar] [CrossRef]
- Milosavljević, M.; Nakar, E. The Cosmic-Ray Precursor of Relativistic Collisionless Shocks: A Missing Link in Gamma-Ray Burst Afterglows. Astrophys. J. 2006, 651, 979–984. [Google Scholar] [CrossRef]
- Pelletier, G.; Lemoine, M.; Marcowith, A. Fermi Acceleration at Relativistic Shocks; American Institute of Physics Conference Series; Aharonian, F.A., Hofmann, W., Rieger, F., Eds.; American Institute of Physics: College Park, MD, USA, 2008; Volume 1085, pp. 61–70. [Google Scholar]
- Lemoine, M.; Pelletier, G. On electromagnetic instabilities at ultra-relativistic shock waves. Mon. Not. Roy. Astron. Soc. 2010, 402, 321–334. [Google Scholar] [CrossRef]
- Lemoine, M.; Pelletier, G.; Gremillet, L.; Plotnikov, I. A fast current-driven instability in relativistic collisionless shocks. EPL (Europhysics Lett.) 2014, 106, 55001. [Google Scholar] [CrossRef][Green Version]
- Bednarz, J.; Ostrowski, M. Energy Spectra of Cosmic Rays Accelerated at Ultrarelativistic Shock Waves. Phys. Rev. Lett. 1998, 80, 3911–3914. [Google Scholar] [CrossRef]
- Kirk, J.G.; Guthmann, A.W.; Gallant, Y.A.; Achterberg, A. Particle Acceleration at Ultrarelativistic Shocks: An Eigenfunction Method. Astrophys. J. 2000, 542, 235–242. [Google Scholar] [CrossRef]
- Ellison, D.C.; Double, G.P. Nonlinear particle acceleration in relativistic shocks. Astropart. Phys. 2002, 18, 213–228. [Google Scholar] [CrossRef][Green Version]
- Lemoine, M.; Pelletier, G. Particle Transport in tangled magnetic fields and Fermi acceleration at relativistic Shocks. Astrophys. J. 2003, 589, L73–L76. [Google Scholar] [CrossRef]
- Niemiec, J.; Ostrowski, M. Cosmic-Ray Acceleration at Relativistic Shock Waves with a “Realistic” Magnetic Field Structure. Astrophys. J. 2004, 610, 851–867. [Google Scholar] [CrossRef][Green Version]
- Keshet, U.; Waxman, E. Energy Spectrum of Particles Accelerated in Relativistic Collisionless Shocks. Phys. Rev. Lett. 2005, 94, 111102. [Google Scholar] [CrossRef] [PubMed]
- Warren, D.C.; Ellison, D.C.; Bykov, A.M.; Lee, S.H. Electron and ion acceleration in relativistic shocks with applications to GRB afterglows. Month. Not. Roy. Astron. Soc. 2015, 452, 431–443. [Google Scholar] [CrossRef]
- Spitkovsky, A. Particle Acceleration in Relativistic Collisionless Shocks: Fermi Process at Last? Astrophys. J. Lett. 2008, 682, L5. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Niemiec, J.; Hardee, P.E.; Medvedev, M.; Sol, H.; Mizuno, Y.; Zhang, B.; Pohl, M.; Oka, M.; Hartmann, D.H. Weibel Instability and Associated Strong Fields in a Fully Three-Dimensional Simulation of a Relativistic Shock. Astrophys. J. Lett. 2009, 698, L10. [Google Scholar] [CrossRef]
- Keshet, U.; Katz, B.; Spitkovsky, A.; Waxman, E. Magnetic Field Evolution in Relativistic Unmagnetized Collisionless Shocks. Astrop. J. Lett. 2009, 693, L127–L130. [Google Scholar] [CrossRef]
- Martins, S.F.; Fonseca, R.A.; Silva, L.O.; Mori, W.B. Ion Dynamics and Acceleration in Relativistic Shocks. Astrophy. J. Lett. 2009, 695, L189. [Google Scholar] [CrossRef]
- Haugbølle, T. Three-Dimensional Modeling Of Relativistic Collisionless Ion-Electron Shocks. Astrophys. J. 2011, 739, L42. [Google Scholar] [CrossRef][Green Version]
- Sironi, L.; Spitkovsky, A.; Arons, J. The Maximum Energy of Accelerated Particles in Relativistic Collisionless Shocks. Astrophys. J. 2013, 771, 54. [Google Scholar] [CrossRef]
- Moiseev, S.S.; Sagdeev, R.Z. Collisionless shock waves in a plasma in a weak magnetic field. J. Nucl. Energy Part C Plasma Phys. 1963, 5, 43. [Google Scholar] [CrossRef]
- Lemoine, M.; Li, Z.; Wang, X.Y. On the magnetization of gamma-ray burst blast waves. Mon. Not. Roy. Astron. Soc. 2013, 435, 3009–3016. [Google Scholar] [CrossRef]
- Santana, R.; Barniol Duran, R.; Kumar, P. Magnetic Fields in Relativistic Collisionless Shocks. Astrop. J. 2014, 785, 29. [Google Scholar] [CrossRef]
- Gruzinov, A.; Waxman, E. Gamma-Ray Burst Afterglow: Polarization and Analytic Light Curves. Astrophys. J. 1999, 511, 852–861. [Google Scholar] [CrossRef]
- Medvedev, M.V.; Loeb, A. Generation of Magnetic Fields in the Relativistic Shock of Gamma-Ray Burst Sources. Astrophys. J. 1999, 526, 697–706. [Google Scholar] [CrossRef]
- Li, Z.; Waxman, E. The Upstream Magnetic Field of Collisionless GRB Shocks. Astroph. J. 2006, 651, 328–332. [Google Scholar] [CrossRef]
- Lemoine, M.; Gremillet, L.; Pelletier, G.; Vanthieghem, A. Physics of Weibel-Mediated Relativistic Collisionless Shocks. Phys. Rev. Lett. 2019, 123, 035101. [Google Scholar] [CrossRef]
- Birdsall, C.K.; Langdon, A.B. Plasma Physics via Computer Simulation; Taylor and Francis: New York, NY, USA, 2005. [Google Scholar]
- Godfrey, B.B. Numerical Cherenkov instabilities in electromagnetic particle codes. J. Comput. Phys. 1974, 15, 504–521. [Google Scholar] [CrossRef]
- Godfrey, B.B. Canonical momenta and numerical instabilities in particle codes. J. Comput. Phys. 1975, 19, 58–76. [Google Scholar] [CrossRef]
- Pukhov, A. Three-dimensional electromagnetic relativistic particle-in-cell code VLPL (Virtual Laser Plasma Lab). J. Plasma Phys. 1999, 61, 425–433. [Google Scholar] [CrossRef]
- Vay, J.L.; Geddes, C.G.R.; Cormier-Michel, E.; Grote, D.P. Numerical methods for instability mitigation in the modeling of laser wakefield accelerators in a Lorentz-boosted frame. J. Comput. Phys. 2011, 230, 5908–5929. [Google Scholar] [CrossRef]
- Li, F.; Yu, P.; Xu, X.; Fiuza, F.; Decyk, V.K.; Dalichaouch, T.; Davidson, A.; Tableman, A.; An, W.; Tsung, F.S.; et al. Controlling the numerical Cerenkov instability in PIC simulations using a customized finite difference Maxwell solver and a local FFT based current correction. Comput. Phys. Commun. 2017, 214, 6–17. [Google Scholar] [CrossRef]
- Greenwood, A.D.; Cartwright, K.L.; Luginsland, J.W.; Baca, E.A. On the elimination of numerical Cerenkov radiation in PIC simulations. J. Comput. Phys. 2004, 201, 665–684. [Google Scholar] [CrossRef]
- Godfrey, B.B.; Vay, J.L. Numerical stability of relativistic beam multidimensional PIC simulations employing the Esirkepov algorithm. J. Comp. Phys. 2013, 248, 33–46. [Google Scholar] [CrossRef]
- Godfrey, B.B.; Vay, J.L. Suppressing the Numerical Cherenkov Instability in FDTD PIC Codes. J. Comput. Phys. 2014, 267, 1–6. [Google Scholar] [CrossRef]
- Lemoine, M.; Pelletier, G.; Vanthieghem, A.; Gremillet, L. Physics of relativistic collisionless shocks. III. The suprathermal particles. Phys. Rev. E 2019, 100, 033210. [Google Scholar] [CrossRef] [PubMed]
- Spitkovsky, A. On the Structure of Relativistic Collisionless Shocks in Electron-Ion Plasmas. Astrophys. J. Lett. 2008, 673, L39. [Google Scholar] [CrossRef]
- Ardaneh, K.; Cai, D.; Nishikawa, K.I.; Lembège, B. Collisionless Weibel Shocks and Electron Acceleration in Gamma-Ray Bursts. Astrophys. J. 2015, 811, 57. [Google Scholar] [CrossRef]
- Bret, A.; Gremillet, L.; Bénisti, D.; Lefebvre, E. Exact Relativistic Kinetic Theory of an Electron-Beam Plasma System: Hierarchy of the Competing Modes in the System-Parameter Space. Phys. Rev. Lett. 2008, 100, 205008. [Google Scholar] [CrossRef]
- Bret, A.; Gremillet, L.; Dieckman, M.E. Multidimensional electron beam-plasma instabilities in the relativistic regime. Phys. Plasmas 2010, 17, 120501. [Google Scholar] [CrossRef]
- Bret, A.; Gremillet, L.; Bénisti, D. Exact relativistic kinetic theory of the full unstable spectrum of an electron-beam plasma system with Maxwell-Jüttner distribution functions. Phys. Rev. E 2010, 81, 036402. [Google Scholar] [CrossRef]
- Lemoine, M.; Pelletier, G. Dispersion and thermal effects on electromagnetic instabilities in the precursor of relativistic shocks. Mon. Not. Roy. Astron. Soc. 2011, 417, 1148–1161. [Google Scholar] [CrossRef]
- Rabinak, I.; Katz, B.; Waxman, E. Long-wavelength Unstable Modes in the Far Upstream of Relativistic Collisionless Shocks. Astrophys. J. 2011, 736, 157. [Google Scholar] [CrossRef]
- Shaisultanov, R.; Lyubarsky, Y.; Eichler, D. Stream Instabilities in Relativistically Hot Plasma. Astrophys. J. 2012, 744, 182. [Google Scholar] [CrossRef]
- Weibel, E.S. Spontaneously Growing Transverse Waves in a Plasma Due to an Anisotropic Velocity Distribution. Phys. Rev. Lett. 1959, 2, 83–84. [Google Scholar] [CrossRef]
- Fried, B.D. Mechanism for Instability of Transverse Plasma Waves. Phys. Fluids 1959, 2, 337. [Google Scholar] [CrossRef]
- Chang, P.; Spitkovsky, A.; Arons, J. Long-Term Evolution of Magnetic Turbulence in Relativistic Collisionless Shocks: Electron-Positron Plasmas. Astrophys. J. 2008, 674, 378–387. [Google Scholar] [CrossRef]
- Lemoine, M. Nonlinear collisionless damping of Weibel turbulence in relativistic blast waves. J. Plasma Phys. 2015, 81, 455810101. [Google Scholar] [CrossRef]
- Rossi, E.; Rees, M.J. Gamma-ray burst afterglow emission with a decaying magnetic field. Month. Not. Roy. Astron. Soc. 2003, 339, 881–886. [Google Scholar] [CrossRef]
- Derishev, E.V. Synchrotron emission in the fast cooling regime: Which spectra can be explained? Astrophys. Space Sci. 2007, 309, 157–161. [Google Scholar] [CrossRef]
- Lemoine, M. Synchrotron signature of a relativistic blast wave with decaying microturbulence. Mon. Not. Roy. Astron. Soc. 2013, 428, 845–866. [Google Scholar] [CrossRef][Green Version]
- Lemoine, M. The synchrotron self-Compton spectrum of relativistic blast waves at large Y. Month. Not. Roy. Astron. Soc. 2015, 453, 3772–3784. [Google Scholar] [CrossRef]
- Pelletier, G.; Bykov, A.; Ellison, D.; Lemoine, M. Towards Understanding the Physics of Collisionless Relativistic Shocks. Space Sci. Rev. 2017, 207, 319–360. [Google Scholar] [CrossRef]
- Vanthieghem, A. Theoretical and Numerical Studies of Relativistic Collisionless Shock Waves. Ph.D. Thesis, Sorbonne Université, École doctorale Astronomie et Astrophysique d’Île-de-France, Paris, France, 2019. [Google Scholar]
- Wiersma, J.; Achterberg, A. Magnetic field generation in relativistic shocks. An early end of the exponential Weibel instability in electron-proton plasmas. Astron. Astrophys. 2004, 428, 365–371. [Google Scholar] [CrossRef]
- Achterberg, A.; Wiersma, J. The Weibel instability in relativistic plasmas. I. Linear theory. Astron. Astrophys. 2007, 475, 1–18. [Google Scholar] [CrossRef]
- Achterberg, A.; Wiersma, J.; Norman, C.A. The Weibel instability in relativistic plasmas. II. Nonlinear theory and stabilization mechanism. Astron. Astrophys. 2007, 475, 19–36. [Google Scholar] [CrossRef]
- Vanthieghem, A.; Lemoine, M.; Gremillet, L. Stability analysis of a periodic system of relativistic current filaments. Phys. Plasmas 2018, 25, 072115. [Google Scholar] [CrossRef]
- Kato, T.N. Relativistic Collisionless Shocks in Unmagnetized Electron-Positron Plasmas. Astrophys. J. 2007, 668, 974. [Google Scholar] [CrossRef]
- Pelletier, G.; Gremillet, L.; Vanthieghem, A.; Lemoine, M. Physics of relativistic collisionless shocks: The scattering-center frame. Phys. Rev. E 2019, 100, 013205. [Google Scholar] [CrossRef]
- Lemoine, M.; Vanthieghem, A.; Pelletier, G.; Gremillet, L. Physics of relativistic collisionless shocks. II. Dynamics of the background plasma. Phys. Rev. E 2019, 100, 033209. [Google Scholar] [CrossRef]
- Drury, L.O.; Voelk, J.H. Hydromagnetic shock structure in the presence of cosmic rays. Astrophys. J. 1981, 248, 344–351. [Google Scholar] [CrossRef]
- Ellison, D.C.; Double, G.P. Diffusive shock acceleration in unmodified relativistic, oblique shocks. Astropart. Phys. 2004, 22, 323–338. [Google Scholar] [CrossRef]
- Ellison, D.C.; Warren, D.C.; Bykov, A.M. Monte Carlo Simulations of Nonlinear Particle Acceleration in Parallel Trans-relativistic Shocks. Astrophys. J. 2013, 776, 46. [Google Scholar] [CrossRef]
- Ellison, D.C.; Warren, D.C.; Bykov, A.M. Particle spectra and efficiency in nonlinear relativistic shock acceleration—Survey of scattering models. Mon. Not. Roy. Astron. Soc. 2016, 456, 3090–3099. [Google Scholar] [CrossRef]
- Lemoine, M.; Pelletier, G.; Gremillet, L.; Plotnikov, I. Current-driven filamentation upstream of magnetized relativistic collisionless shocks. Mon. Not. Roy. Astron. Soc. 2014, 440, 1365–1378. [Google Scholar] [CrossRef]
- Alsop, D.; Arons, J. Relativistic magnetosonic solitons with reflected particles in electron-positron plasmas. Phys. Fl. 1988, 31, 839–847. [Google Scholar] [CrossRef]
- Gallant, Y.A.; Hoshino, M.; Langdon, A.B.; Arons, J.; Max, C.E. Relativistic, perpendicular shocks in electron-positron plasmas. Astrophys. J. 1992, 391, 73–101. [Google Scholar] [CrossRef]
- Hoshino, M.; Arons, J.; Gallant, Y.A.; Langdon, A.B. Relativistic magnetosonic shock waves in synchrotron sources—Shock structure and nonthermal acceleration of positrons. Astrophys. J. 1992, 390, 454–479. [Google Scholar] [CrossRef]
- Plotnikov, I.; Sironi, L. The synchrotron maser emission from relativistic shocks in Fast Radio Bursts: 1D PIC simulations of cold pair plasmas. Mon. Not. Roy. Astron. Soc. 2019, 485, 3816–3833. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Pair Shocks: Dependence of Shock Acceleration on Magnetic Obliquity. Astrophys. J. 2009, 698, 1523. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Electron-Ion Shocks. Astrophys. J. 2011, 726, 75. [Google Scholar] [CrossRef]
- Hoshino, M. Wakefield Acceleration by Radiation Pressure in Relativistic Shock Waves. Astrophys. J. 2008, 672, 940–956. [Google Scholar] [CrossRef]
- Iwamoto, M.; Amano, T.; Hoshino, M.; Matsumoto, Y.; Niemiec, J.; Ligorini, A.; Kobzar, O.; Pohl, M. Precursor Wave Amplification by Ion - Electron Coupling through Wakefield in Relativistic Shocks. Astrop. J. Lett. 2019, 883, L35. [Google Scholar] [CrossRef]
- Pelletier, G.; Lemoine, M.; Marcowith, A. On Fermi acceleration and magnetohydrodynamic instabilities at ultra-relativistic magnetized shock waves. Mon. Not. Roy. Astron. Soc. 2009, 393, 587–597. [Google Scholar] [CrossRef][Green Version]
- Bret, A. Weibel, Two-Stream, Filamentation, Oblique, Bell, Buneman...Which One Grows Faster? Astrophys. J. 2009, 699, 990–1003. [Google Scholar] [CrossRef]
- Plotnikov, I.; Grassi, A.; Grech, M. Perpendicular relativistic shocks in magnetized pair plasma. Mon. Not. Roy. Astron. Soc. 2018, 477. [Google Scholar] [CrossRef]
- Lemoine, M.; Revenu, B. Relativistic Fermi acceleration with shock compressed turbulence. Month. Not. Roy. Astron. Soc. 2006, 366, 635–644. [Google Scholar] [CrossRef]
- Keshet, U.; Arad, O.; Lyubarski, Y. Diffusive shock-acceleration: Breakdown of spatial diffusion and isotropy. arXiv 2019, arXiv:1910.08083. [Google Scholar] [CrossRef]
- Lavi, A.; Arad, O.; Nagar, Y.; Keshet, U. Diffusive shock acceleration in N dimensions. arXiv 2020, arXiv:2002.11123. [Google Scholar]
- Plotnikov, I.; Pelletier, G.; Lemoine, M. Particle transport and heating in the microturbulent precursor of relativistic shocks. Mon. Not. Roy. Astron. Soc. 2013, 430, 1280–1293. [Google Scholar] [CrossRef]
- Wang, X.Y.; Liu, R.Y.; Lemoine, M. On the Origin of > 10 GeV Photons in Gamma-Ray Burst Afterglows. Astrop. J. Lett. 2013, 771, L33. [Google Scholar] [CrossRef]
- Van Eerten, H. Gamma-ray burst afterglow blast waves. Int. J. Mod. Phys. D 2018, 27, 1842002. [Google Scholar] [CrossRef]
- Medvedev, M.V. Electron Acceleration in Relativistic Gamma-Ray Burst Shocks. Astrop. J. Lett. 2006, 651, L9–L11. [Google Scholar] [CrossRef][Green Version]
- Kumar, R.; Eichler, D.; Gedalin, M. Electron Heating in a Relativistic, Weibel-unstable Plasma. Astrophys. J. 2015, 806, 165. [Google Scholar] [CrossRef]
- Biteau, J.; Prandini, E.; Costamante, L.; Lemoine, M.; Padovani, P.; Pueschel, E.; Resconi, E.; Tavecchio, F.; Taylor, A.; Zech, A. Progress in unveiling extreme particle acceleration in persistent astrophysical jets. Nat. Astron. 2020, 4, 124–131. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Engels, A.A.; Baack, D.; Babic, A.; Banerjee, B.; de Almeida, U.B.; Barrio, J.A.; Becerra-Gonzalez, J. Observation of inverse Compton emission from a long γ-ray burst. Nature 2019, 575, 459–463. [Google Scholar] [CrossRef]
- Derishev, E.V.; Piran, T. Particle acceleration, magnetization and radiation in relativistic shocks. Mon. Not. Roy. Astron. Soc. 2016, 460, 2036–2049. [Google Scholar] [CrossRef]
- Medvedev, M.V.; Fiore, M.; Fonseca, R.A.; Silva, L.O.; Mori, W.B. Long-Time Evolution of Magnetic Fields in Relativistic Gamma-Ray Burst Shocks. Astrop. J. Lett. 2005, 618, L75–L78. [Google Scholar] [CrossRef]
- Milosavljevic, M.; Nakar, E. Weibel filament decay and thermalization in collisionless shocks and gamma-ray burst afterglows. Astrophys. J. 2006, 641, 978–983. [Google Scholar] [CrossRef]
- Couch, S.M.; Milosavljević, M.; Nakar, E. Shock Vorticity Generation from Accelerated Ion Streaming in the Precursor of Ultrarelativistic Gamma-Ray Burst External Shocks. Astrop. J. 2008, 688, 462–469. [Google Scholar] [CrossRef]
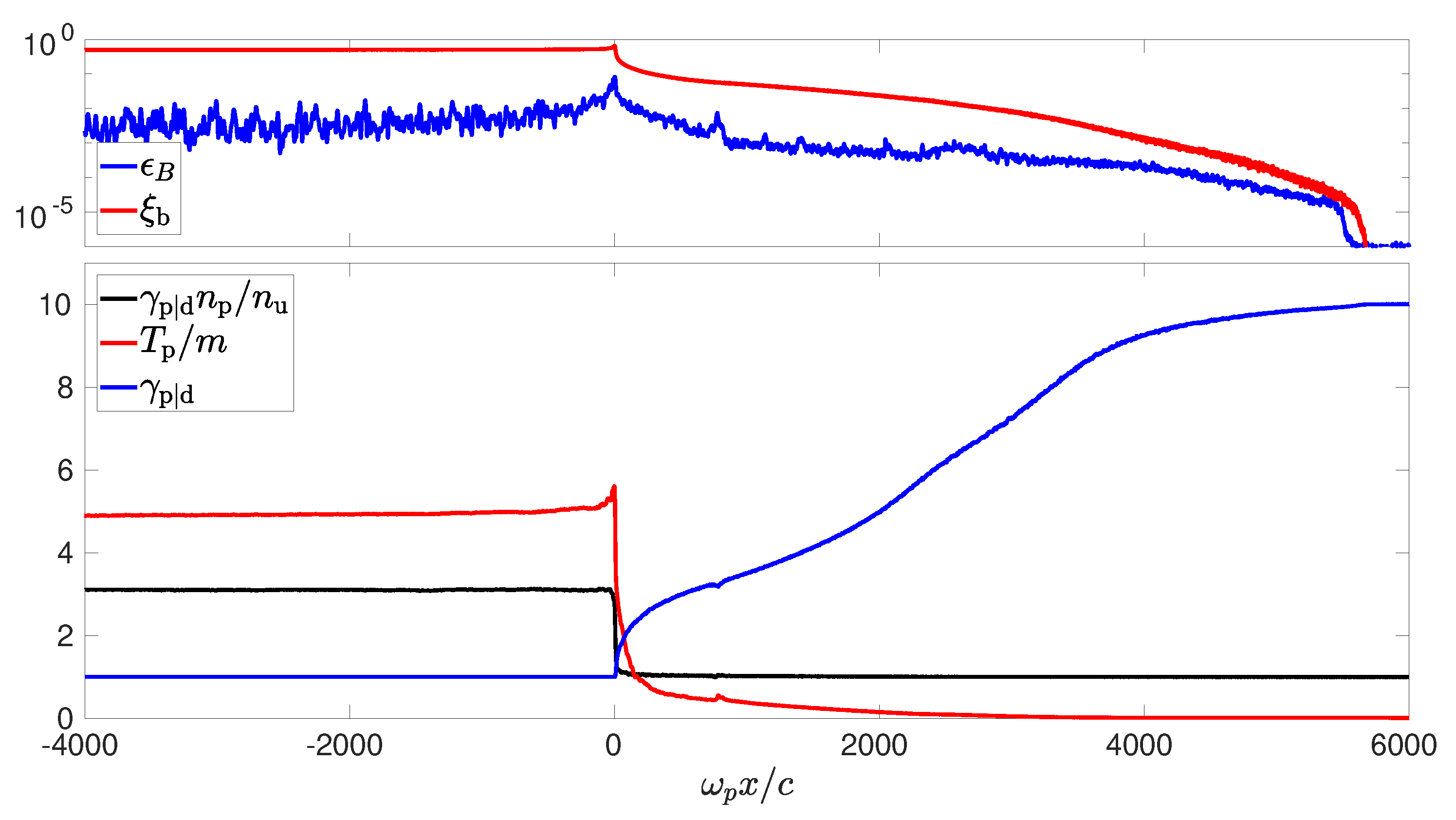
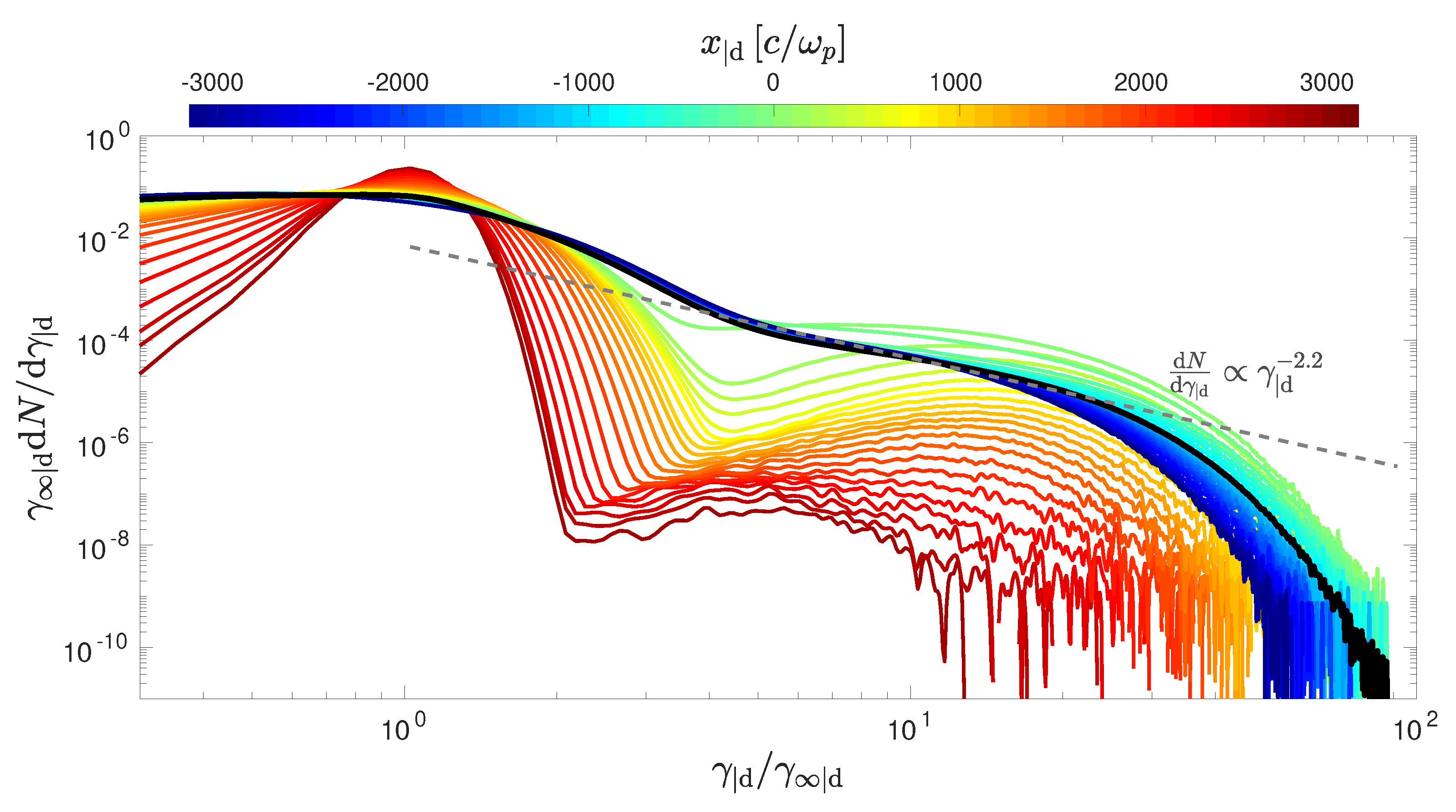
| 1. | Let us note that for a simulation performed in the downstream rest frame, the apparent density of the upstream flow is equal to . This results in an apparent density of the downstream plasma equal to in 3D simulations and to in 2D PIC simulations (see, black line in Figure 4). |
| 2. | We distinguish the effective magnetization in the shock vicinity, from the external magnetization , which pertains to the unshocked ambient plasma. In weakly magnetized shocks, is generically much larger than because electromagnetic instabilities, acting in the shock precursor, strongly amplify any pre-existing magnetic energy density. |
| 3. | More precisely, if represents the position-dependent Lorentz factor of the background plasma with respect to the shock front, with outside the precursor, and inside the precursor, as a result of deceleration, then the correct expression for the scattering length is [70]: , with the turbulence coherence length. The expression in the main text assumes a few, which holds in the near precursor, where deceleration to mildly relativistic values has taken place. |
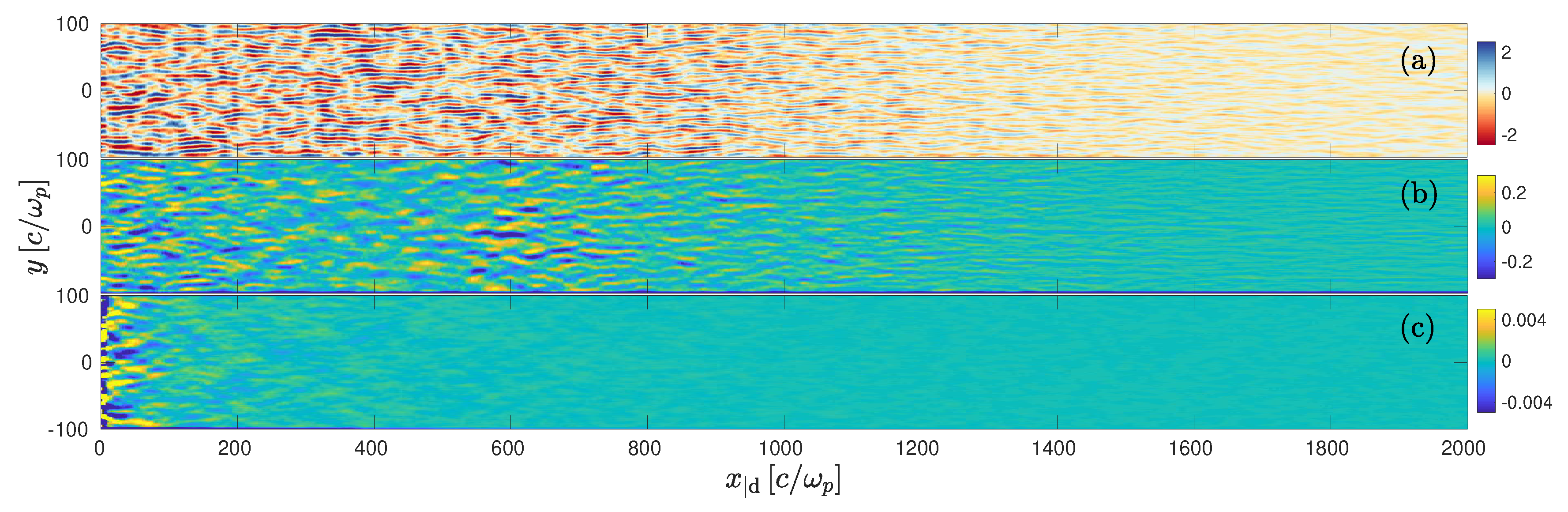
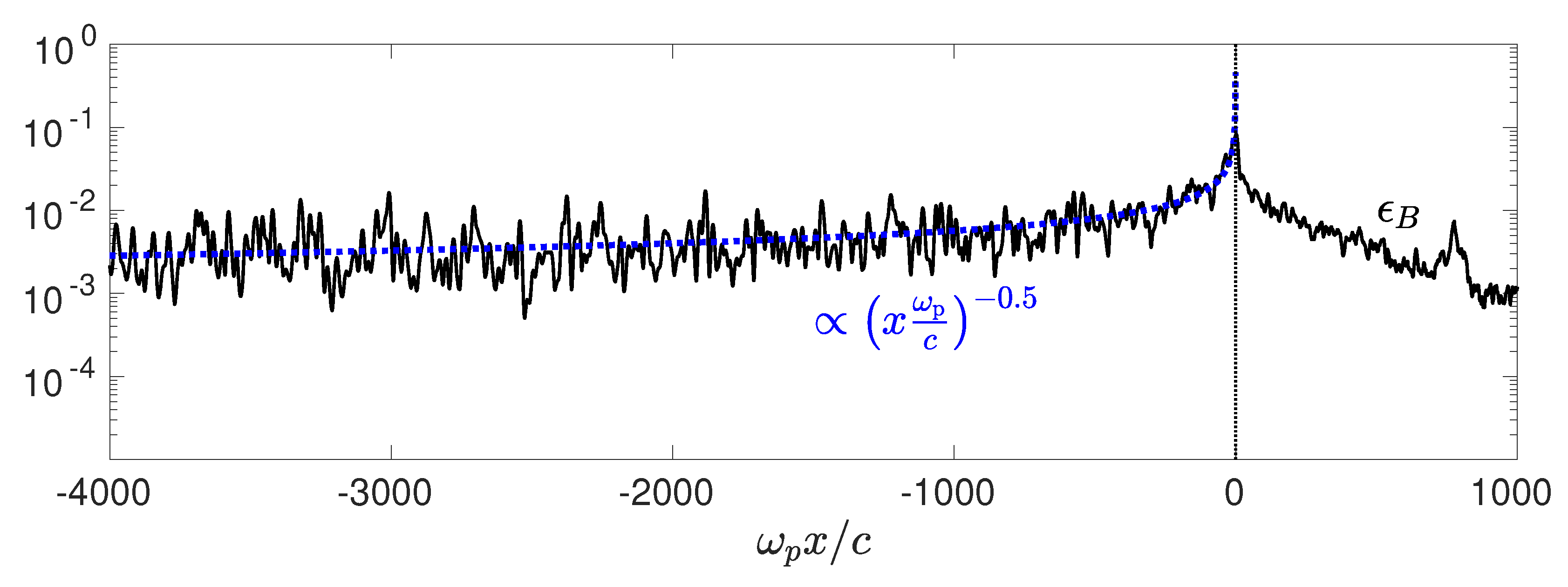
| 4. | In a 2D simulation, the magnetic turbulence spectrum is defined as . |

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanthieghem, A.; Lemoine, M.; Plotnikov, I.; Grassi, A.; Grech, M.; Gremillet, L.; Pelletier, G. Physics and Phenomenology of Weakly Magnetized, Relativistic Astrophysical Shock Waves. Galaxies 2020, 8, 33. https://doi.org/10.3390/galaxies8020033
Vanthieghem A, Lemoine M, Plotnikov I, Grassi A, Grech M, Gremillet L, Pelletier G. Physics and Phenomenology of Weakly Magnetized, Relativistic Astrophysical Shock Waves. Galaxies. 2020; 8(2):33. https://doi.org/10.3390/galaxies8020033
Chicago/Turabian StyleVanthieghem, Arno, Martin Lemoine, Illya Plotnikov, Anna Grassi, Mickael Grech, Laurent Gremillet, and Guy Pelletier. 2020. "Physics and Phenomenology of Weakly Magnetized, Relativistic Astrophysical Shock Waves" Galaxies 8, no. 2: 33. https://doi.org/10.3390/galaxies8020033
APA StyleVanthieghem, A., Lemoine, M., Plotnikov, I., Grassi, A., Grech, M., Gremillet, L., & Pelletier, G. (2020). Physics and Phenomenology of Weakly Magnetized, Relativistic Astrophysical Shock Waves. Galaxies, 8(2), 33. https://doi.org/10.3390/galaxies8020033




