Applications of Stellar Population Synthesis in the Distant Universe
Abstract
1. Introduction
2. Galaxies in the Distant Universe
2.1. The First Stars
2.2. The Lyman Break Technique
2.3. High Redshift Galaxy Spectroscopy
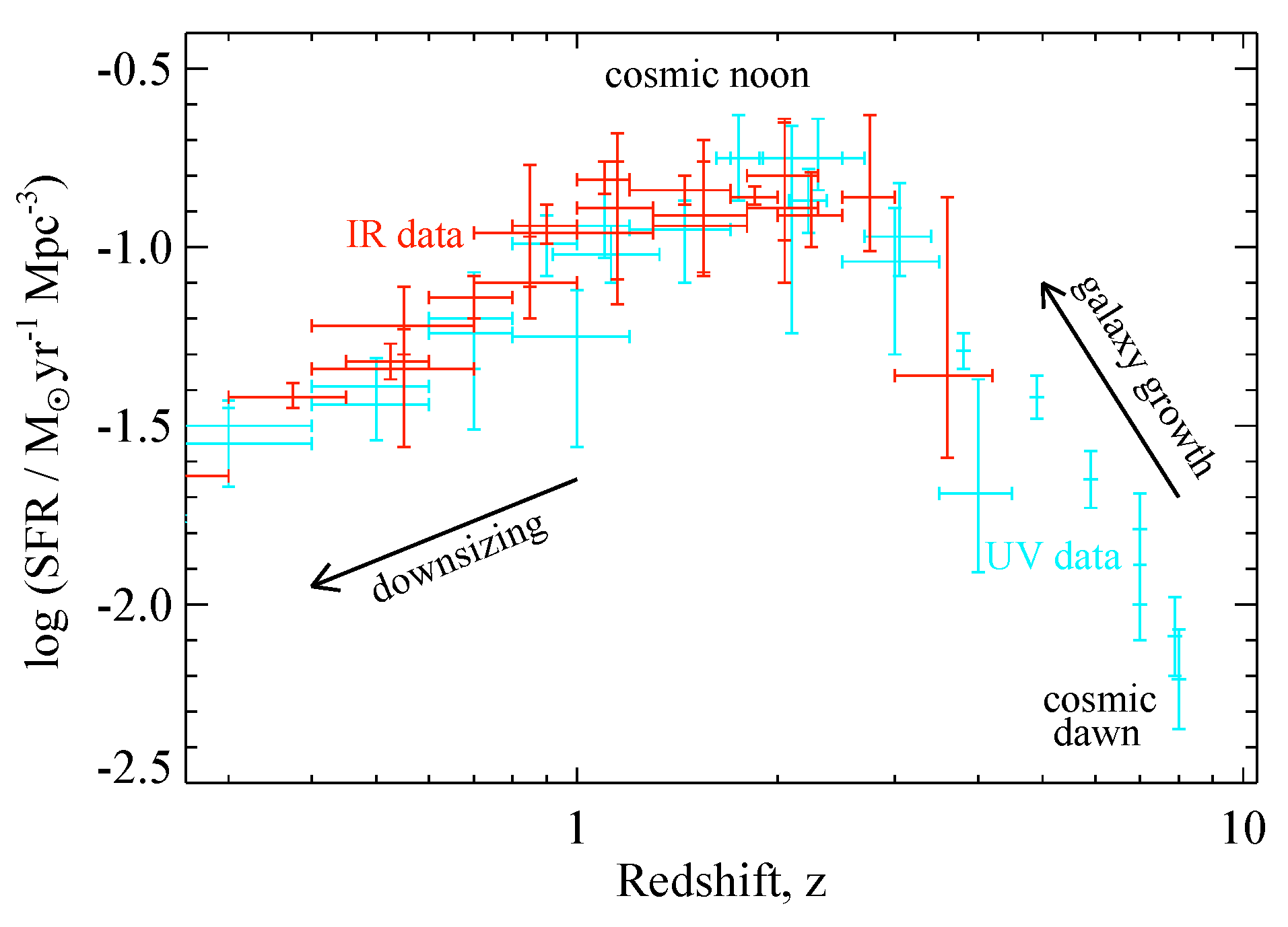
2.4. Distant Galaxies as Probes of Star Formation
2.5. The Critical Importance of Ionising Flux
3. Stellar Population Synthesis and the Binary Challenge
3.1. The Basics of Population Synthesis
3.2. Improving Population Synthesis Models
- Emission in the desired indicator (for example, rest-frame ultraviolet 1500 Å continuum luminosity) is dominated by massive, short lived stars;
- For a given flux from massive stars, the total recently-formed stellar mass (which, in contrast to the light, is typically dominated by lower mass stars) can be estimated from the stellar population model;
- If the star formation rate has been constant for a long enough period (i.e., over ≈100 million years), the rate of massive star death balances that of massive star birth and the relationship between flux and star formation rate is linear.
3.3. The New Generation of Population Synthesis Models
3.3.1. Improved Stellar Models
3.3.2. Improved Atmospheres
3.3.3. Key Examples
3.4. Nebular Gas and Dust Emission Synthesis
4. Model-Critical Science Results
- The epoch of reionisation marks the transition between the neutral intergalactic medium of the Dark Ages to the highly ionised IGM that followed the epoch of Cosmic Dawn. The detection of this transition, through Lyman- line damping and the identification of polarised scattering in the cosmic microwave background radiation, is unambiguous. However, a number of details regarding its sources and interpretation are highly model dependent.
- (a)
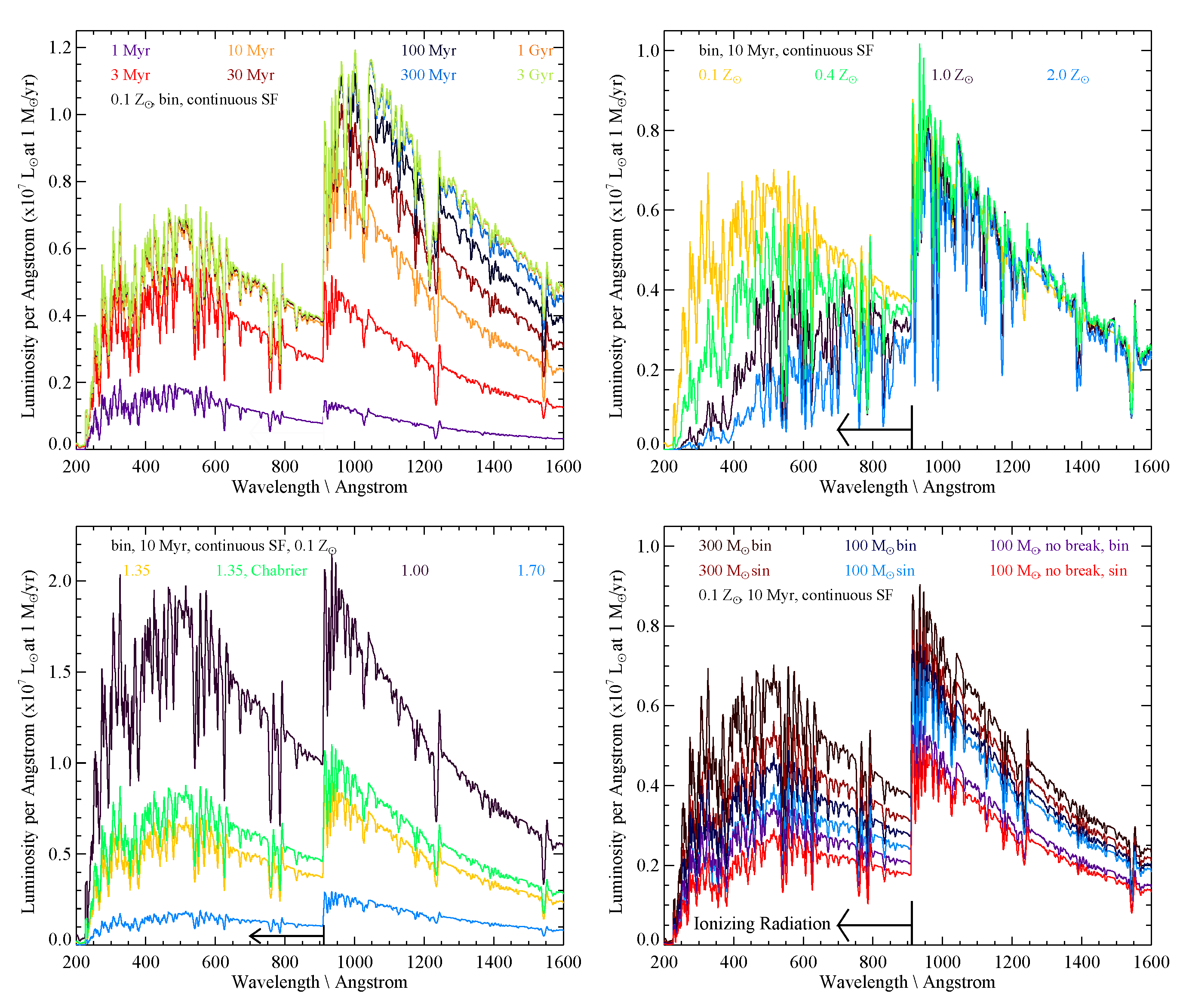
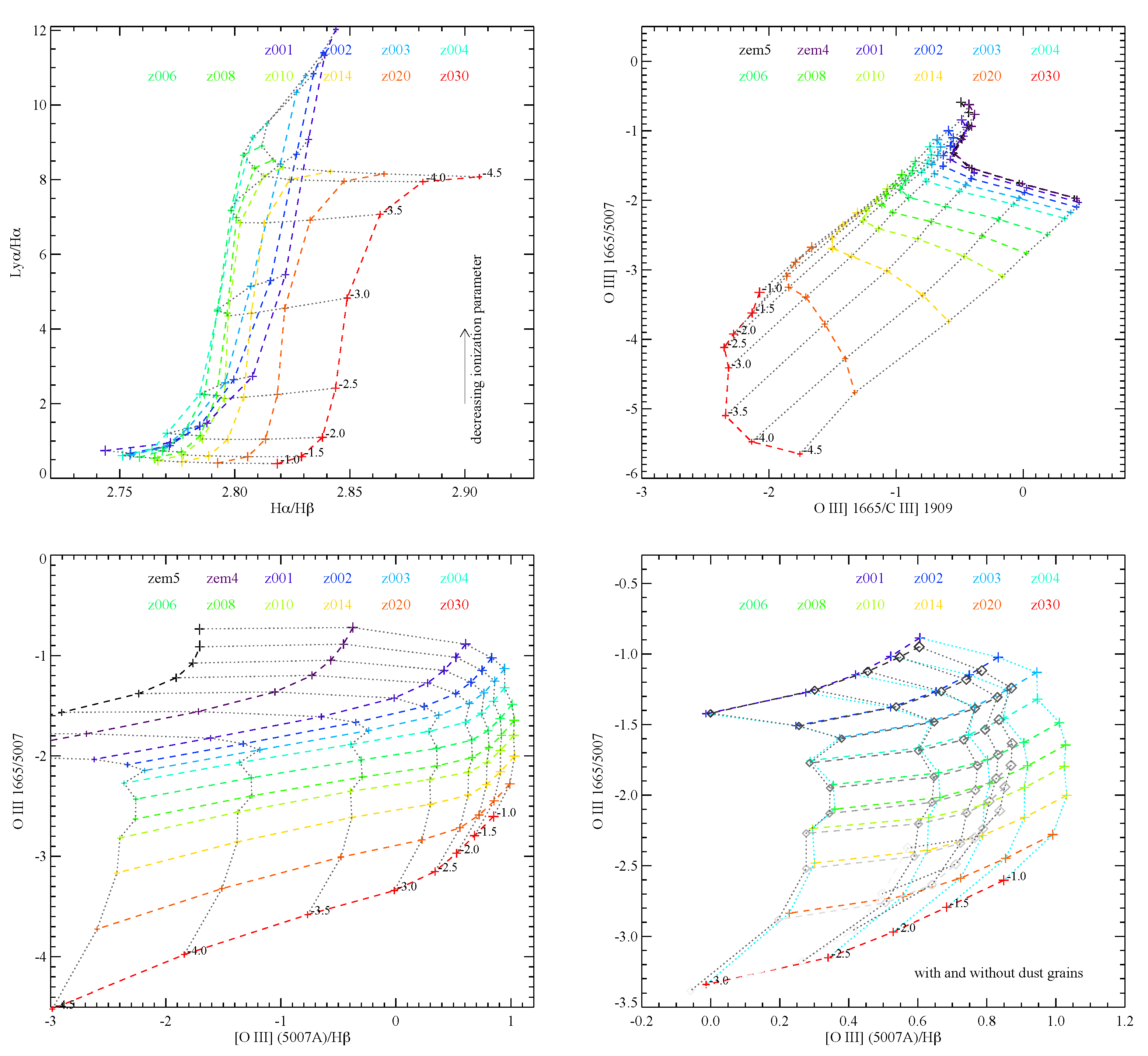
- As has already been discussed, and as is shown by Figure 2, the ionising photon production rate of a given population is highly sensitive to its modelled parameters, amongst them the stellar binary fraction and stellar population age. Figure 2 is presented for the continuous star formation case, which in theory minimises the differences between populations. However, it is still clear that the adoption of different assumptions, including the timescale of the star formation epoch, its metallicity, and IMF can cause large differences in the ionising flux. In particular, small variations in stellar metallicity can dramatically change the ionising photon production without producing large changes to the ultraviolet continuum longwards of the Lyman break (Figure 2, upper right panel). Thus the model assumed can have a large effect on discussions of whether the observed galaxy population produces sufficient photons to drive reionisation, on the role of the faint end slope of the luminosity function and the minimum stellar masses required for high redshift galaxies (see e.g., [67]). As Figure 3 (upper left) indicates, Balmer line strengths and their ratios depend only weakly on the nebular conditions, and an indirect estimator of the ionising photon production efficiency can be derived from the H line flux powered by this radiation. However, a number of authors have taken this analysis a step further, first inferring the H strength from Lyman- emission. Since the resonant Lyman- line is highly dependent on the nebular conditions (see Figure 3), ambiguous interpretation is inevitable.
- (b)
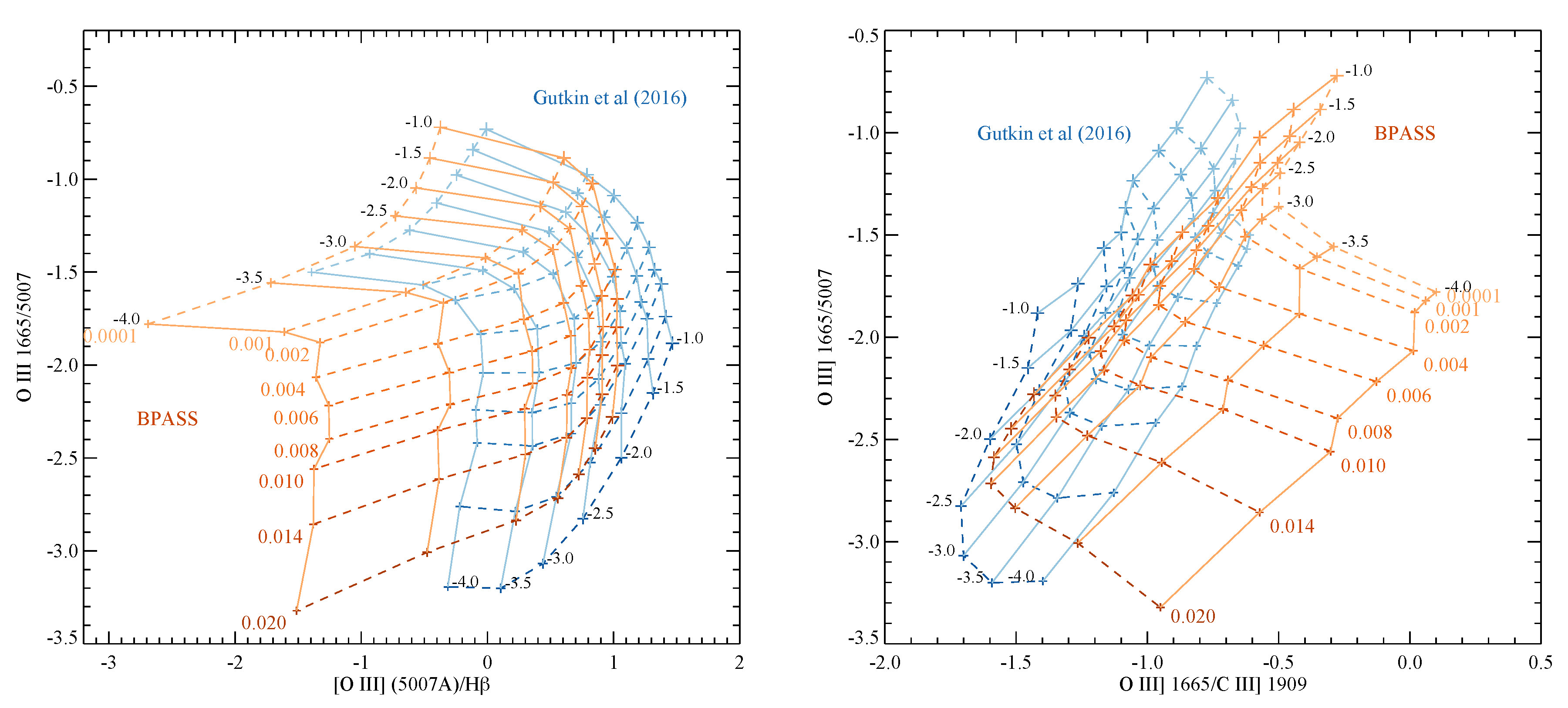
- The escape fraction of ionising photons also plays a crucial role in the above calculations. If photons are produced in stellar photospheres but cannot escape their galaxy haloes, their impact on the IGM will be negligible. There are two major impediments to photon escape: line-of-sight dust extinction and nebular gas absorption. A common assumption in past work has been that the dust extinction of ionising flux shortwards of 912 Å directly tracks that of the observed 1500 Å continuum, such that the photons observed in the latter can be used to infer the former. However, doing so requires the application of a dust extinction law, and there are large uncertainties in the shape of the extinction curve at short wavelengths, which is determined by the dust grain size and composition but which cannot be directly measured [157,158,159]. This introduces large uncertainties in the ionising flux escape due to the dust correction, even before gas extinction is considered.Estimates of the escape fraction in galaxies can be obtained in a number of ways, but perhaps the most important are direct imaging below the Lyman limit or analysis of the nebular emission lines, in both cases using comparisons to the inferred photon flux expected from stellar population models. As already discussed, nebular emission estimates can be heavily affected by assumed nebular gas conditions (Figure 3) and by the shape of the assumed irradiating spectrum, as shown in Figure 4, which compares matched models in the BPASS model grid and those derived by Gutkin et al. [142] from the BC03 2016 release. As Stanway et al. [160] demonstrated, the tension between the high escape fractions required by reionisation modellers and the low typical escape fractions seen in galaxies can be reconciled if models producing a higher photon flux (such as binary models or those at slightly lower metallicity) are used.
- (c)
- A related challenge is determining which physical processes affect the escape fraction and whether it changes over time; i.e., are galaxies with high fractions sparse in gas and dust, or simply patchy, with channels of near unity escape fraction existing in an otherwise opaque medium? In the “picket-fence” scenario, the likely culprits for blowing such channels out are core-collapse supernovae, but for short-lived starbursts, the ionising flux in most models has to have subsided before supernovae begin to occur. By contrast, as Ma et al. [161] and Rosdahl et al. [162] have demonstrated, the longer ionising lifetimes of stars in models including interacting binary star populations make them a prime candidate for the sources of the escaping photons which power reionisation. A similar effect might be obtained from repeated bursts of star formation on short timescales.
- The cosmic volume-averaged star formation density evolution is inferred from the luminosity function of Lyman break galaxies and their conversion into star formation rate functions through model-calibrated factors. As already discussed, these factors are heavily dependent on the assumptions made for stellar populations (see e.g., [57]). Equally important, but perhaps less obvious at first glance, is the dependence of the rest-UV inferred star formation history on corrections for dust extinction. Since these are inferred from fitting the observed colours of a galaxy (or occasionally its emission line ratios or spectrum) with a template and a dust curve, there is inevitable dependence on the stellar population synthesis model used. The bluer spectra predicted by models dominated by steep or top-heavy IMFs, and by binary or rotating stars, may suggest that the dust correction may be larger than those previously estimated using models which exclude those effects.
- Interpretation of the stellar populations responsible for stellar wind driven feedback; outflows; enrichment of the intergalactic medium; and thus, the cosmic chemical evolution, all rely on interpreting the spectra of distant sources, or on making assumptions based on their luminosities, masses and star formation rates in a limited handful of mostly rest-ultraviolet bands. For example modelling chemical enrichment from a stellar population requires assumptions for their star formation rate (model-dependent), core collapse supernovae time delays and rate distributions (model dependent [163]) and white-dwarf or compact merger rates (model dependent [163,164]). In fact, as has been extensively discussed above, and as demonstrated by Figure 3 and Figure 4, all such interpretations rely on the models being used. Indeed, many of the simple models may well fall short of being physical in most scenarios: while observers routinely compare the strengths of oxygen and carbon line features (as in Figure 4, for example) the C/O ratio is itself time-dependant, with different production timescales for the two elements. No simple stellar population synthesis model currently incorporates the details of this evolution in elemental abundance ratios. While this may seem to be less true of evolutionary properties inferred from large scale cosmological simulations (i.e., N-body or hydrodynamic models) of dark matter halo growth, the galaxy evolution models which are built on the haloes are in turn informed and validated against model-dependent interpretations of observational data.
5. The Holistic View
6. Unresolved Challenges
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Tinsley, B.M. Evolution of the Stars and Gas in Galaxies. Astrophys. J. 1968, 151, 547. [Google Scholar] [CrossRef]
- Tinsley, B.M. Synthesis of stellar populations. Mem. Della Soc. Astron. Ital. 1975, 46, 3–68. [Google Scholar]
- Tinsley, B.M.; Gunn, J.E. Evolutionary synthesis of the stellar population in elliptical galaxies. I. Ingredients, broad-band colors, and infrared features. Astrophys. J. 1976, 203, 52–62. [Google Scholar] [CrossRef]
- Leitherer, C.; Ekström, S. Population synthesis at the crossroads. In The Spectral Energy Distribution of Galaxies—SED 2011; Tuffs, R.J., Popescu, C.C., Eds.; Cambridge University Press: Cambridge, UK, 2012; Volume 284. [Google Scholar] [CrossRef]
- Conroy, C. Modeling the Panchromatic Spectral Energy Distributions of Galaxies. Annu. Rev. Astron. Astrophys. 2013, 51, 393–455. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Stanway, E.R.; Xiao, L.; McClelland, L.A.S.; Taylor, G.; Ng, M.; Greis, S.M.L.; Bray, J.C. Binary Population and Spectral Synthesis Version 2.1: Construction, Observational Verification, and New Results. Pub. Astron. Soc. Aust. 2017, 34, e058. [Google Scholar] [CrossRef]
- Dahmer-Hahn, L.G.; Riffel, R.; Rodríguez-Ardila, A.; Martins, L.P.; Kehrig, C.; Heckman, T.M.; Pastoriza, M.G.; Dametto, N.Z. Probing evolutionary population synthesis models in the near infrared with early-type galaxies. Mon. Not. R. Astron. Soc. 2018, 476, 4459–4480. [Google Scholar] [CrossRef]
- Chen, X.Y.; Liang, Y.C.; Hammer, F.; Prugniel, P.; Zhong, G.H.; Rodrigues, M.; Zhao, Y.H.; Flores, H. Comparing six evolutionary population synthesis models by performing spectral synthesis for galaxies. Astronom. Astrophys. 2010, 515, A101. [Google Scholar] [CrossRef]
- Conroy, C.; Gunn, J.E. The Propagation of Uncertainties in Stellar Population Synthesis Modeling. III. Model Calibration, Comparison, and Evaluation. Astrophys. J. 2010, 712, 833–857. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star-Formation History. Annu. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Stanway, E.R. Spectral population synthesis including massive binaries. Mon. Not. R. Astron. Soc. 2009, 400, 1019–1028. [Google Scholar] [CrossRef]
- Pahl, A.J.; Shapley, A.; Faisst, A.L.; Capak, P.L.; Du, X.; Reddy, N.A.; Laursen, P.; Topping, M.W. The Redshift Evolution of Rest-UV Spectroscopic Properties to z ∼ 5. arXiv 2019, arXiv:1910.04179. [Google Scholar]
- Bouwens, R.J.; Illingworth, G.D.; Oesch, P.A.; Trenti, M.; Labbé, I.; Bradley, L.; Carollo, M.; van Dokkum, P.G.; Gonzalez, V.; Holwerda, B.; et al. UV Luminosity Functions at Redshifts z ∼ 4 to z ∼ 10: 10,000 Galaxies from HST Legacy Fields. Astrophys. J. 2015, 803, 34. [Google Scholar] [CrossRef]
- Shapley, A.E. Physical Properties of Galaxies from z = 2–4. Annu. Rev. Astron. Astrophys. 2011, 49, 525–580. [Google Scholar] [CrossRef]
- Stark, D.P. Galaxies in the First Billion Years After the Big Bang. Annu. Rev. Astron. Astrophys. 2016, 54, 761–803. [Google Scholar] [CrossRef]
- Bromm, V.; Larson, R.B. The First Stars. Annu. Rev. Astron. Astrophys. 2004, 42, 79–118. [Google Scholar] [CrossRef]
- Jaacks, J.; Thompson, R.; Finkelstein, S.L.; Bromm, V. Baseline metal enrichment from Population III star formation in cosmological volume simulations. Mon. Not. R. Astron. Soc. 2018, 475, 4396–4410. [Google Scholar] [CrossRef]
- Mebane, R.H.; Mirocha, J.; Furlanetto, S.R. The Persistence of Population III Star Formation. Mon. Not. R. Astron. Soc. 2018, 479, 4544–4559. [Google Scholar] [CrossRef]
- Sobral, D.; Matthee, J.; Darvish, B.; Schaerer, D.; Mobasher, B.; Röttgering, H.J.A.; Santos, S.; Hemmati, S. Evidence for PopIII-like Stellar Populations in the Most Luminous Lyman-α Emitters at the Epoch of Reionization: Spectroscopic Confirmation. Astrophys. J. 2015, 808, 139. [Google Scholar] [CrossRef]
- Bowler, R.A.A.; McLure, R.J.; Dunlop, J.S.; McLeod, D.J.; Stanway, E.R.; Eldridge, J.J.; Jarvis, M.J. No evidence for Population III stars or a Direct Collapse Black Hole in the z = 6.6 Lyman-α emitter ‘CR7’. Mon. Not. R. Astron. Soc. 2017, 469, 448–458. [Google Scholar] [CrossRef]
- Shibuya, T.; Ouchi, M.; Harikane, Y.; Rauch, M.; Ono, Y.; Mukae, S.; Higuchi, R.; Kojima, T.; Yuma, S.; Lee, C.H.; et al. SILVERRUSH. III. Deep optical and near-infrared spectroscopy for Lyα and UV-nebular lines of bright Lyα emitters at z = 6-7. Publ. Astron. Soc. Jpn. 2018, 70, S15. [Google Scholar] [CrossRef]
- Sobral, D.; Matthee, J.; Brammer, G.; Ferrara, A.; Alegre, L.; Röttgering, H.; Schaerer, D.; Mobasher, B.; Darvish, B. On the nature and physical conditions of the luminous Ly α emitter CR7 and its rest-frame UV components. Mon. Not. R. Astron. Soc. 2019, 482, 2422–2441. [Google Scholar] [CrossRef]
- Songaila, A.; Cowie, L.L. Approaching Reionization: The Evolution of the Ly α Forest from z = 4 to z = 6. Astron. J. 2002, 123, 2183–2196. [Google Scholar] [CrossRef]
- Guhathakurta, P.; Tyson, J.A.; Majewski, S.R. A Redshift Limit for the Faint Blue Galaxy Population from Deep U Band Imaging. Astrophys. J. 1990, 357, L9. [Google Scholar] [CrossRef]
- Steidel, C.C.; Pettini, M.; Hamilton, D. Lyman Imaging of High-Redshift Galaxies. III. New Observations of Four QSO Fields. Astron. J. 1995, 110, 2519. [Google Scholar] [CrossRef]
- Steidel, C.C.; Giavalisco, M.; Pettini, M.; Dickinson, M.; Adelberger, K.L. Spectroscopic Confirmation of a Population of Normal Star-forming Galaxies at Redshifts z > 3. Astrophys. J. 1996, 462, L17. [Google Scholar] [CrossRef]
- Steidel, C.C.; Shapley, A.E.; Pettini, M.; Adelberger, K.L.; Erb, D.K.; Reddy, N.A.; Hunt, M.P. A Survey of Star-forming Galaxies in the 1.4 < z < 2.5 Redshift Desert: Overview. Astrophys. J. 2004, 604, 534–550. [Google Scholar] [CrossRef]
- Stanway, E.R.; Bunker, A.J.; McMahon, R.G. Lyman break galaxies and the star formation rate of the Universe at z ∼ 6. Mon. Not. R. Astron. Soc. 2003, 342, 439–445. [Google Scholar] [CrossRef]
- Wilkins, S.M.; Bunker, A.J.; Stanway, E.; Lorenzoni, S.; Caruana, J. The ultraviolet properties of star-forming galaxies—I. HST WFC3 observations of very high redshift galaxies. Mon. Not. R. Astron. Soc. 2011, 417, 717–729. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Illingworth, G.D.; Oesch, P.A.; Labbé, I.; van Dokkum, P.G.; Trenti, M.; Franx, M.; Smit, R.; Gonzalez, V.; Magee, D. UV-continuum Slopes of >4000 z ∼ 4–8 Galaxies from the HUDF/XDF, HUDF09, ERS, CANDELS-South, and CANDELS-North Fields. Astrophys. J. 2014, 793, 115. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Stefanon, M.; Oesch, P.A.; Illingworth, G.D.; Nanayakkara, T.; Roberts-Borsani, G.; Labbé, I.; Smit, R. Newly Discovered Bright z ∼ 9–10 Galaxies and Improved Constraints on Their Prevalence Using the Full CANDELS Area. Astrophys. J. 2019, 880, 25. [Google Scholar] [CrossRef]
- Bouwens, R.; Broadhurst, T.; Illingworth, G. Cloning Dropouts: Implications for Galaxy Evolution at High Redshift. Astrophys. J. 2003, 593, 640–660. [Google Scholar] [CrossRef]
- Stanway, E.R.; Bremer, M.N.; Lehnert, M.D. On contamination and completeness in z > 5 Lyman-break galaxy surveys. Mon. Not. R. Astron. Soc. 2008, 385, 493–510. [Google Scholar] [CrossRef]
- Vulcani, B.; Trenti, M.; Calvi, V.; Bouwens, R.; Oesch, P.; Stiavelli, M.; Franx, M. Characterization and Modeling of Contamination for Lyman Break Galaxy Samples at High Redshift. Astrophys. J. 2017, 836, 239. [Google Scholar] [CrossRef]
- Stanway, E.R.; Bunker, A.J.; McMahon, R.G.; Ellis, R.S.; Treu, T.; McCarthy, P.J. Hubble Space Telescope Imaging and Keck Spectroscopy of z ∼ 6 i-Band Dropout Galaxies in the Advanced Camera for Surveys GOODS Fields. Astrophys. J. 2004, 607, 704–720. [Google Scholar] [CrossRef][Green Version]
- Bunker, A.J.; Stanway, E.R.; Ellis, R.S.; McMahon, R.G. The star formation rate of the Universe at z ∼ 6 from the Hubble Ultra-Deep Field. Mon. Not. R. Astron. Soc. 2004, 355, 374–384. [Google Scholar] [CrossRef]
- Caruana, J.; Bunker, A.J.; Wilkins, S.M.; Stanway, E.R.; Lorenzoni, S.; Jarvis, M.J.; Ebert, H. Spectroscopy of z ∼ 7 candidate galaxies: Using Lyana to constrain the neutral fraction of hydrogen in the high-redshift universe. Mon. Not. R. Astron. Soc. 2014, 443, 2831–2842. [Google Scholar] [CrossRef]
- Hoag, A.; Treu, T.; Pentericci, L.; Amorin, R.; Bolzonella, M.; Bradač, M.; Castellano, M.; Cullen, F.; Fynbo, J.P.U.; Garilli, B.; et al. Constraining Lyman-alpha spatial offsets at 3 < z < 5.5 from VANDELS slit spectroscopy. Mon. Not. R. Astron. Soc. 2019, 488, 706–719. [Google Scholar] [CrossRef]
- Cullen, F.; McLure, R.J.; Dunlop, J.S.; Khochfar, S.; Davé, R.; Amorín, R.; Bolzonella, M.; Carnall, A.C.; Castellano, M.; Cimatti, A.; et al. The VANDELS survey: The stellar metallicities of star-forming galaxies at 2.5 < z < 5.0. Mon. Not. R. Astron. Soc. 2019, 487, 2038–2060. [Google Scholar] [CrossRef]
- Faisst, A.L.; Capak, P.L.; Davidzon, I.; Salvato, M.; Laigle, C.; Ilbert, O.; Onodera, M.; Hasinger, G.; Kakazu, Y.; Masters, D.; et al. Rest-UV Absorption Lines as Metallicity Estimator: The Metal Content of Star-forming Galaxies at z ∼ 5. Astrophys. J. 2016, 822, 29. [Google Scholar] [CrossRef]
- Troncoso, P.; Maiolino, R.; Sommariva, V.; Cresci, G.; Mannucci, F.; Marconi, A.; Meneghetti, M.; Grazian, A.; Cimatti, A.; Fontana, A.; et al. Metallicity evolution, metallicity gradients, and gas fractions at z ∼ 3.4. Astronom. Astrophys. 2014, 563, A58. [Google Scholar] [CrossRef]
- Verhamme, A.; Orlitová, I.; Schaerer, D.; Hayes, M. Using Lyman-α to detect galaxies that leak Lyman continuum. Astronom. Astrophys. 2015, 578, A7. [Google Scholar] [CrossRef]
- Erb, D.K.; Pettini, M.; Shapley, A.E.; Steidel, C.C.; Law, D.R.; Reddy, N.A. Physical Conditions in a Young, Unreddened, Low-metallicity Galaxy at High Redshift. Astrophys. J. 2010, 719, 1168–1190. [Google Scholar] [CrossRef]
- Stark, D.P.; Richard, J.; Charlot, S.; Clément, B.; Ellis, R.; Siana, B.; Robertson, B.; Schenker, M.; Gutkin, J.; Wofford, A. Spectroscopic detections of C III] λ1909 Å at z ∼ 6–7: A new probe of early star-forming galaxies and cosmic reionization. Mon. Not. R. Astron. Soc. 2015, 450, 1846–1855. [Google Scholar] [CrossRef]
- Maseda, M.V.; Brinchmann, J.; Franx, M.; Bacon, R.; Bouwens, R.J.; Schmidt, K.B.; Boogaard, L.A.; Contini, T.; Feltre, A.; Inami, H.; et al. The MUSE Hubble Ultra Deep Field Survey. IV. Global properties of C III] emitters. Astronom. Astrophys. 2017, 608, A4. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Stanway, E.R. The effect of stellar evolution uncertainties on the rest-frame ultraviolet stellar lines of C IV and He II in high-redshift Lyman-break galaxies. Mon. Not. R. Astron. Soc. 2012, 419, 479–489. [Google Scholar] [CrossRef]
- Shapley, A.E.; Steidel, C.C.; Pettini, M.; Adelberger, K.L. Rest-Frame Ultraviolet Spectra of z ∼ 3 Lyman Break Galaxies. Astrophys. J. 2003, 588, 65–89. [Google Scholar] [CrossRef]
- Steidel, C.C.; Strom, A.L.; Pettini, M.; Rudie, G.C.; Reddy, N.A.; Trainor, R.F. Reconciling the Stellar and Nebular Spectra of High-redshift Galaxies. Astrophys. J. 2016, 826, 159. [Google Scholar] [CrossRef]
- Douglas, L.S.; Bremer, M.N.; Lehnert, M.D.; Stanway, E.R.; Milvang-Jensen, B. Spectroscopy of z ∼ 5 Lyman break galaxies in the ESO Remote Galaxy Survey. Mon. Not. R. Astron. Soc. 2010, 409, 1155–1171. [Google Scholar] [CrossRef][Green Version]
- Sanders, R.L.; Shapley, A.E.; Reddy, N.A.; Kriek, M.; Siana, B.; Coil, A.L.; Mobasher, B.; Shivaei, I.; Freeman, W.R.; Azadi, M.; et al. The MOSDEF Survey: Direct-Method Metallicities and ISM Conditions at z ∼ 1.5–3.5. arXiv 2019, arXiv:1907.00013. [Google Scholar] [CrossRef]
- Strom, A.L.; Steidel, C.C.; Rudie, G.C.; Trainor, R.F.; Pettini, M.; Reddy, N.A. Nebular Emission Line Ratios in z ∼ 2–3 Star-forming Galaxies with KBSS-MOSFIRE: Exploring the Impact of Ionization, Excitation, and Nitrogen-to-Oxygen Ratio. Astrophys. J. 2017, 836, 164. [Google Scholar] [CrossRef]
- Shapley, A.E.; Reddy, N.A.; Kriek, M.; Freeman, W.R.; Sanders, R.L.; Siana, B.; Coil, A.L.; Mobasher, B.; Shivaei, I.; Price, S.H.; et al. The MOSDEF Survey: Excitation Properties of z ∼ 2.3 Star-forming Galaxies. Astrophys. J. 2015, 801, 88. [Google Scholar] [CrossRef]
- Steidel, C.C.; Rudie, G.C.; Strom, A.L.; Pettini, M.; Reddy, N.A.; Shapley, A.E.; Trainor, R.F.; Erb, D.K.; Turner, M.L.; Konidaris, N.P.; et al. Strong Nebular Line Ratios in the Spectra of z ∼ 2–3 Star Forming Galaxies: First Results from KBSS-MOSFIRE. Astrophys. J. 2014, 795, 165. [Google Scholar] [CrossRef]
- Cowie, L.L.; Songaila, A.; Hu, E.M.; Cohen, J.G. New Insight on Galaxy Formation and Evolution From Keck Spectroscopy of the Hawaii Deep Fields. Astron. J. 1996, 112, 839. [Google Scholar] [CrossRef]
- Kennicutt, R.C., Jr. Star Formation in Galaxies Along the Hubble Sequence. Annu. Rev. Astron. Astrophys. 1998, 36, 189–232. [Google Scholar] [CrossRef]
- Kennicutt, R.C.; Evans, N.J. Star Formation in the Milky Way and Nearby Galaxies. Annu. Rev. Astron. Astrophys. 2012, 50, 531–608. [Google Scholar] [CrossRef]
- Wilkins, S.M.; Lovell, C.C.; Stanway, E.R. Recalibrating the Cosmic Star Formation History. Mon. Not. R. Astron. Soc. 2019, 490, 5359–5365. [Google Scholar] [CrossRef]
- Greis, S.M.L.; Stanway, E.R.; Levan, A.J.; Davies, L.J.M.; Eldridge, J.J. Radio observations confirm young stellar populations in local analogues to z ∼ 5 Lyman break galaxies. Mon. Not. R. Astron. Soc. 2017, 470, 489–499. [Google Scholar] [CrossRef]
- Stanway, E.R.; Eldridge, J.J. Re-evaluating old stellar populations. Mon. Not. R. Astron. Soc. 2018, 479, 75–93. [Google Scholar] [CrossRef]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Pub. Astronom. Soc. Pac. 2003, 115, 763–795. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Schaerer, D.; Thuan, T.X.; Worseck, G.; Guseva, N.G.; Orlitová, I.; Verhamme, A. Detection of high Lyman continuum leakage from four low-redshift compact star-forming galaxies. Mon. Not. R. Astron. Soc. 2016, 461, 3683–3701. [Google Scholar] [CrossRef]
- Wofford, A.; Leitherer, C.; Salzer, J. Lyα Escape from z ∼ 0.03 Star-forming Galaxies: The Dominant Role of Outflows. Astrophys. J. 2013, 765, 118. [Google Scholar] [CrossRef]
- Vanzella, E.; Fontana, A.; Pentericci, L.; Castellano, M.; Grazian, A.; Giavalisco, M.; Nonino, M.; Cristiani, S.; Zamorani, G.; Vignali, C. A 52 h VLT/FORS2 spectrum of a bright z ∼ 7 HUDF galaxy: No Ly-α emission. Astronom. Astrophys. 2014, 569, A78. [Google Scholar] [CrossRef]
- Puschnig, J.; Hayes, M.; Östlin, G.; Rivera-Thorsen, T.E.; Melinder, J.; Cannon, J.M.; Menacho, V.; Zackrisson, E.; Bergvall, N.; Leitet, E. The Lyman continuum escape and ISM properties in Tololo 1247-232—New insights from HST and VLA. Mon. Not. R. Astron. Soc. 2017, 469, 3252–3269. [Google Scholar] [CrossRef]
- Rutkowski, M.J.; Scarlata, C.; Henry, A.; Hayes, M.; Mehta, V.; Hathi, N.; Cohen, S.; Windhorst, R.; Koekemoer, A.M.; Teplitz, H.I.; et al. The Lyman Continuum Escape Fraction of Emission Line-selected z ∼ 2.5 Galaxies Is Less Than 15%. Astrophys. J. 2017, 841, L27. [Google Scholar] [CrossRef]
- Paardekooper, J.P.; Khochfar, S.; Dalla Vecchia, C. The First Billion Years project: The escape fraction of ionizing photons in the epoch of reionization. Mon. Not. R. Astron. Soc. 2015, 451, 2544–2563. [Google Scholar] [CrossRef]
- Wilkins, S.M.; Feng, Y.; Di-Matteo, T.; Croft, R.; Stanway, E.R.; Bouwens, R.J.; Thomas, P. The Lyman-continuum photon production efficiency in the high-redshift Universe. Mon. Not. R. Astron. Soc. 2016, 458, L6–L9. [Google Scholar] [CrossRef]
- Smit, R.; Bouwens, R.J.; Labbé, I.; Zheng, W.; Bradley, L.; Donahue, M.; Lemze, D.; Moustakas, J.; Umetsu, K.; Zitrin, A.; et al. Evidence for Ubiquitous High-equivalent-width Nebular Emission in z ∼ 7 Galaxies: Toward a Clean Measurement of the Specific Star-formation Rate Using a Sample of Bright, Magnified Galaxies. Astrophys. J. 2014, 784, 58. [Google Scholar] [CrossRef]
- Holden, B.P.; Oesch, P.A.; González, V.G.; Illingworth, G.D.; Labbé, I.; Bouwens, R.; Franx, M.; van Dokkum, P.; Spitler, L. Rest-frame Optical Emission Lines in z ∼ 3.5 Lyman-break-selected Galaxies: The Ubiquity of Unusually High [OIII]/Hβ Ratios at 2 Gyr. Astrophys. J. 2016, 820, 73. [Google Scholar] [CrossRef]
- Stark, D.P.; Ellis, R.S.; Charlot, S.; Chevallard, J.; Tang, M.; Belli, S.; Zitrin, A.; Mainali, R.; Gutkin, J.; Vidal-García, A.; et al. Lyα and C III] emission in z = 7–9 Galaxies: Accelerated reionization around luminous star-forming systems? Mon. Not. R. Astron. Soc. 2017, 464, 469–479. [Google Scholar] [CrossRef]
- De Barros, S.; Oesch, P.A.; Labbé, I.; Stefanon, M.; González, V.; Smit, R.; Bouwens, R.J.; Illingworth, G.D. The GREATS H β + [O III] luminosity function and galaxy properties at z ∼ 8: Walking the way of JWST. Mon. Not. R. Astron. Soc. 2019, 489, 2355–2366. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Tout, C.A. The Structure and Evolution of Stars; World Scientific Publishers: Singapore, 2019. [Google Scholar] [CrossRef]
- Boquien, M.; Burgarella, D.; Roehlly, Y.; Buat, V.; Ciesla, L.; Corre, D.; Inoue, A.K.; Salas, H. CIGALE: A python Code Investigating GALaxy Emission. Astronom. Astrophys. 2019, 622, A103. [Google Scholar] [CrossRef]
- Carnall, A.C.; McLure, R.J.; Dunlop, J.S.; Davé, R. Inferring the star formation histories of massive quiescent galaxies with BAGPIPES: Evidence for multiple quenching mechanisms. Mon. Not. R. Astron. Soc. 2018, 480, 4379–4401. [Google Scholar] [CrossRef]
- Leja, J.; Johnson, B.D.; Conroy, C.; van Dokkum, P.G.; Byler, N. Deriving Physical Properties from Broadband Photometry with Prospector: Description of the Model and a Demonstration of its Accuracy Using 129 Galaxies in the Local Universe. Astrophys. J. 2017, 837, 170. [Google Scholar] [CrossRef]
- Wilkinson, D.M.; Maraston, C.; Goddard, D.; Thomas, D.; Parikh, T. FIREFLY (Fitting IteRativEly For Likelihood analYsis): A full spectral fitting code. Mon. Not. R. Astron. Soc. 2017, 472, 4297–4326. [Google Scholar] [CrossRef]
- Kauffmann, G.; Heckman, T.M.; Tremonti, C.; Brinchmann, J.; Charlot, S.; White, S.D.M.; Ridgway, S.E.; Brinkmann, J.; Fukugita, M.; Hall, P.B.; et al. The host galaxies of active galactic nuclei. Mon. Not. R. Astron. Soc. 2003, 346, 1055–1077. [Google Scholar] [CrossRef]
- Bruzual, G.; Charlot, S. Stellar population synthesis at the resolution of 2003. Mon. Not. R. Astron. Soc. 2003, 344, 1000–1028. [Google Scholar] [CrossRef]
- Tremonti, C.A.; Heckman, T.M.; Kauffmann, G.; Brinchmann, J.; Charlot, S.; White, S.D.M.; Seibert, M.; Peng, E.W.; Schlegel, D.J.; Uomoto, A.; et al. The Origin of the Mass-Metallicity Relation: Insights from 53,000 Star-forming Galaxies in the Sloan Digital Sky Survey. Astrophys. J. 2004, 613, 898–913. [Google Scholar] [CrossRef]
- Brinchmann, J.; Charlot, S.; White, S.D.M.; Tremonti, C.; Kauffmann, G.; Heckman, T.; Brinkmann, J. The physical properties of star-forming galaxies in the low-redshift Universe. Mon. Not. R. Astron. Soc. 2004, 351, 1151–1179. [Google Scholar] [CrossRef]
- Poudel, S.; Kulkarni, V.P.; Cashman, F.H.; Frye, B.; Peroux, C.; Rahmani, H.; Quiret, S. Metal-enriched Galaxies in the First ∼1 Billion Years: Evidence of a Smooth Metallicity Evolution at z ∼ 5. arXiv 2019, arXiv:1910.10023. [Google Scholar] [CrossRef]
- Sanders, R.L.; Shapley, A.E.; Kriek, M.; Freeman, W.R.; Reddy, N.A.; Siana, B.; Coil, A.L.; Mobasher, B.; Davé, R.; Shivaei, I.; et al. The MOSDEF Survey: A Stellar Mass-SFR-Metallicity Relation Exists at z ∼ 2.3. Astrophys. J. 2018, 858, 99. [Google Scholar] [CrossRef]
- Maiolino, R.; Nagao, T.; Grazian, A.; Cocchia, F.; Marconi, A.; Mannucci, F.; Cimatti, A.; Pipino, A.; Ballero, S.; Calura, F.; et al. AMAZE. I. The evolution of the mass-metallicity relation at z > 3. Astronom. Astrophys. 2008, 488, 463–479. [Google Scholar] [CrossRef]
- Curti, M.; Mannucci, F.; Cresci, G.; Maiolino, R. The Mass-Metallicity and the Fundamental Metallicity Relation revisited on a fully Te-based abundance scale for galaxies. arXiv 2019, arXiv:1910.00597. [Google Scholar] [CrossRef]
- Verma, A.; Lehnert, M.D.; Förster Schreiber, N.M.; Bremer, M.N.; Douglas, L. Lyman-break galaxies at z ∼ 5—I. First significant stellar mass assembly in galaxies that are not simply z ∼ 3 LBGs at higher redshift. Mon. Not. R. Astron. Soc. 2007, 377, 1024–1042. [Google Scholar] [CrossRef]
- Heckman, T.M.; Hoopes, C.G.; Seibert, M.; Martin, D.C.; Salim, S.; Rich, R.M.; Kauffmann, G.; Charlot, S.; Barlow, T.A.; Bianchi, L.; et al. The Properties of Ultraviolet-luminous Galaxies at the Current Epoch. Astrophys. J. 2005, 619, L35–L38. [Google Scholar] [CrossRef]
- Stanway, E.R.; Davies, L.J.M. Establishing an analogue population for the most distant galaxies. Mon. Not. R. Astron. Soc. 2014, 439, 2474–2484. [Google Scholar] [CrossRef]
- Heckman, T.M.; Borthakur, S. The Implications of Extreme Outflows from Extreme Starbursts. Astrophys. J. 2016, 822, 9. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Guseva, N.G.; Fricke, K.J.; Henkel, C.; Schaerer, D. The efficiency of ionizing photon production and the radiation energy balance in compact star-forming galaxies. Mon. Not. R. Astron. Soc. 2017, 467, 4118–4130. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Thuan, T.X.; Guseva, N.G. LBT observations of compact star-forming galaxies with extremely high [O III]/[O II] flux ratios: He I emission-line ratios as diagnostics of Lyman continuum leakage. Mon. Not. R. Astron. Soc. 2017, 471, 548–561. [Google Scholar] [CrossRef]
- Yang, H.; Malhotra, S.; Rhoads, J.E.; Wang, J. Blueberry Galaxies: The Lowest Mass Young Starbursts. Astrophys. J. 2017, 847, 38. [Google Scholar] [CrossRef]
- Greis, S.M.L.; Stanway, E.R.; Davies, L.J.M.; Levan, A.J. Physical properties of local star-forming analogues to z ∼ 5 Lyman-break galaxies. Mon. Notices R. Astron. Soc. 2016. [Google Scholar] [CrossRef]
- Ramírez-Agudelo, O.H.; Sana, H.; de Mink, S.E.; Hénault-Brunet, V.; de Koter, A.; Langer, N.; Tramper, F.; Gräfener, G.; Evans, C.J.; Vink, J.S.; et al. The VLT-FLAMES Tarantula Survey. XXI. Stellar spin rates of O-type spectroscopic binaries. Astronom. Astrophys. 2015, 580, A92. [Google Scholar] [CrossRef]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. Mass-loss predictions for O and B stars as a function of metallicity. Astronom. Astrophys. 2001, 369, 574–588. [Google Scholar] [CrossRef]
- Song, H.F.; Meynet, G.; Maeder, A.; Ekström, S.; Eggenberger, P. Massive star evolution in close binaries. Conditions for homogeneous chemical evolution. Astronom. Astrophys. 2016, 585, A120. [Google Scholar] [CrossRef]
- Mandel, I.; de Mink, S.E. Merging binary black holes formed through chemically homogeneous evolution in short-period stellar binaries. Mon. Not. R. Astron. Soc. 2016, 458, 2634–2647. [Google Scholar] [CrossRef]
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Le Bouquin, J.B.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444. [Google Scholar] [CrossRef] [PubMed]
- Sana, H.; de Koter, A.; de Mink, S.E.; Dunstall, P.R.; Evans, C.J.; Hénault-Brunet, V.; Maíz Apellániz, J.; Ramírez-Agudelo, O.H.; Taylor, W.D.; Walborn, N.R.; et al. The VLT-FLAMES Tarantula Survey. VIII. Multiplicity properties of the O-type star population. Astronom. Astrophys. 2013, 550, A107. [Google Scholar] [CrossRef]
- Moe, M.; Kratter, K.M.; Badenes, C. The Close Binary Fraction of Solar-type Stars Is Strongly Anticorrelated with Metallicity. Astrophys. J. 2019, 875, 61. [Google Scholar] [CrossRef]
- de Mink, S.E.; Langer, N.; Izzard, R.G.; Sana, H.; de Koter, A. The Rotation Rates of Massive Stars: The Role of Binary Interaction through Tides, Mass Transfer, and Mergers. Astrophys. J. 2013, 764, 166. [Google Scholar] [CrossRef]
- Stanway, E.R.; Eldridge, J.J.; Greis, S.M.L.; Davies, L.J.M.; Wilkins, S.M.; Bremer, M.N. Interpreting high [O III]/H β ratios with maturing starbursts. Mon. Not. R. Astron. Soc. 2014, 444, 3466–3472. [Google Scholar] [CrossRef]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. 2011, 192, 3. [Google Scholar] [CrossRef]
- Paxton, B.; Smolec, R.; Schwab, J.; Gautschy, A.; Bildsten, L.; Cantiello, M.; Dotter, A.; Farmer, R.; Goldberg, J.A.; Jermyn, A.S.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Pulsating Variable Stars, Rotation, Convective Boundaries, and Energy Conservation. Astrophys. J. Suppl. 2019, 243, 10. [Google Scholar] [CrossRef]
- Hurley, J.R.; Tout, C.A.; Pols, O.R. Evolution of binary stars and the effect of tides on binary populations. Mon. Not. R. Astron. Soc. 2002, 329, 897–928. [Google Scholar] [CrossRef]
- Izzard, R.G.; Glebbeek, E.; Stancliffe, R.J.; Pols, O.R. Population synthesis of binary carbon-enhanced metal-poor stars. Astronom. Astrophys. 2009, 508, 1359–1374. [Google Scholar] [CrossRef]
- Belczynski, K.; Kalogera, V.; Rasio, F.A.; Taam, R.E.; Zezas, A.; Bulik, T.; Maccarone, T.J.; Ivanova, N. Compact Object Modeling with the StarTrack Population Synthesis Code. Astrophys. J. Suppl. 2008, 174, 223–260. [Google Scholar] [CrossRef]
- Klencki, J.; Moe, M.; Gladysz, W.; Chruslinska, M.; Holz, D.E.; Belczynski, K. Impact of inter-correlated initial binary parameters on double black hole and neutron star mergers. Astronom. Astrophys. 2018, 619, A77. [Google Scholar] [CrossRef]
- Figer, D.F. An upper limit to the masses of stars. Nature 2005, 434, 192–194. [Google Scholar] [CrossRef] [PubMed]
- Schneider, F.R.N.; Ramírez-Agudelo, O.H.; Tramper, F.; Bestenlehner, J.M.; Castro, N.; Sana, H.; Evans, C.J.; Sabín-Sanjulián, C.; Simón-Díaz, S.; Langer, N.; et al. The VLT-FLAMES Tarantula Survey. XXIX. Massive star formation in the local 30 Doradus starburst. Astronom. Astrophys. 2018, 618, A73. [Google Scholar] [CrossRef]
- Maeder, A.; Meynet, G. New models of Wolf-Rayet stars and comparison with data in galaxies. Astronom. Astrophys. 1994, 287, 803–816. [Google Scholar]
- Groh, J.H.; Ekström, S.; Georgy, C.; Meynet, G.; Choplin, A.; Eggenberger, P.; Hirschi, R.; Maeder, A.; Murphy, L.J.; Boian, I.; et al. Grids of stellar models with rotation. IV. Models from 1.7 to 120 M⊙ at a metallicity Z = 0.0004. Astronom. Astrophys. 2019, 627, A24. [Google Scholar] [CrossRef]
- Leitherer, C.; Ekström, S.; Meynet, G.; Schaerer, D.; Agienko, K.B.; Levesque, E.M. The Effects of Stellar Rotation. II. A Comprehensive Set of Starburst99 Models. Astrophys. J. Suppl. 2014, 212, 14. [Google Scholar] [CrossRef]
- Conroy, C.; Gunn, J.E.; White, M. The Propagation of Uncertainties in Stellar Population Synthesis Modeling. I. The Relevance of Uncertain Aspects of Stellar Evolution and the Initial Mass Function to the Derived Physical Properties of Galaxies. Astrophys. J. 2009, 699, 486–506. [Google Scholar] [CrossRef]
- Li, Z.; Han, Z. How Binary Interactions Affect Spectral Stellar Population Synthesis. Astrophys. J. 2008, 685, 225–234. [Google Scholar] [CrossRef][Green Version]
- Van Bever, J.; Vanbeveren, D. Hard X-rays emitted by starbursts as predicted by population synthesis models including a realistic fraction of interacting binaries. Astronom. Astrophys. 2000, 358, 462–470. [Google Scholar]
- Zhang, F.; Li, L.; Han, Z. Evolutionary population synthesis for binary stellar population at high spectral resolution: Integrated spectral energy distributions and absorption-feature indices. Mon. Not. R. Astron. Soc. 2005, 364, 503–514. [Google Scholar] [CrossRef]
- Götberg, Y.; de Mink, S.E.; Groh, J.H.; Leitherer, C.; Norman, C. The impact of stars stripped in binaries on the integrated spectra of stellar populations. Astronom. Astrophys. 2019, 629, A134. [Google Scholar] [CrossRef]
- Sheikhi, N.; Hasheminia, M.; Khalaj, P.; Haghi, H.; Zonoozi, A.H.; Baumgardt, H. The binary fraction and mass segregation in Alpha Persei open cluster. Mon. Not. R. Astron. Soc. 2016, 457, 1028–1036. [Google Scholar] [CrossRef]
- Kurucz, R.L. Model atmospheres for G, F, A, B, and O stars. Astrophys. J. Suppl. 1979, 40, 1–340. [Google Scholar] [CrossRef]
- Vazdekis, A.; Sánchez-Blázquez, P.; Falcón-Barroso, J.; Cenarro, A.J.; Beasley, M.A.; Cardiel, N.; Gorgas, J.; Peletier, R.F. Evolutionary stellar population synthesis with MILES—I. The base models and a new line index system. Mon. Not. R. Astron. Soc. 2010, 404, 1639–1671. [Google Scholar] [CrossRef]
- Pickles, A.J. A Stellar Spectral Flux Library: 1150-25000 Å. Pub. Astronom. Soc. Pac. 1998, 110, 863–878. [Google Scholar] [CrossRef]
- Coelho, P.R.T.; Bruzual, G.; Charlot, S. To use or not to use synthetic stellar spectra in population synthesis models? arXiv 2019, arXiv:1910.11902. [Google Scholar] [CrossRef]
- Todt, H.; Sander, A.; Hainich, R.; Hamann, W.R.; Quade, M.; Shenar, T. Potsdam Wolf-Rayet model atmosphere grids for WN stars. Astronom. Astrophys. 2015, 579, A75. [Google Scholar] [CrossRef]
- Hainich, R.; Ramachandran, V.; Shenar, T.; Sand er, A.A.C.; Todt, H.; Gruner, D.; Oskinova, L.M.; Hamann, W.R. PoWR grids of non-LTE model atmospheres for OB-type stars of various metallicities. Astronom. Astrophys. 2019, 621, A85. [Google Scholar] [CrossRef]
- Hamann, W.R.; Gräfener, G.; Liermann, A. The Galactic WN stars. Spectral analyses with line-blanketed model atmospheres versus stellar evolution models with and without rotation. Astronom. Astrophys. 2006, 457, 1015–1031. [Google Scholar] [CrossRef]
- Hamann, W.R.; Gräfener, G. A temperature correction method for expanding atmospheres. Astronom. Astrophys. 2003, 410, 993–1000. [Google Scholar] [CrossRef]
- Gotberg, Y.; de Mink, S.E.; McQuinn, M.; Zapartas, E.; Groh, J.H.; Norman, C. The contribution from stars stripped in binaries to cosmic reionization of hydrogen and helium. arXiv 2019, arXiv:1911.00543. [Google Scholar]
- Götberg, Y.; de Mink, S.E.; Groh, J.H.; Kupfer, T.; Crowther, P.A.; Zapartas, E.; Renzo, M. Spectral models for binary products: Unifying subdwarfs and Wolf-Rayet stars as a sequence of stripped-envelope stars. Astronom. Astrophys. 2018, 615, A78. [Google Scholar] [CrossRef]
- Vink, J.S. Fast and slow winds from supergiants and luminous blue variables. Astronom. Astrophys. 2018, 619, A54. [Google Scholar] [CrossRef]
- Vink, J.S. Very massive stars: A metallicity-dependent upper-mass limit, slow winds, and the self-enrichment of globular clusters. Astronom. Astrophys. 2018, 615, A119. [Google Scholar] [CrossRef]
- Bruzual, G.; Charlot, S.; Gutkin, J.; Vidal García, A. Modeling the ultraviolet emission from young galaxies at high redshift. IAU Gen. Assem. 2015, 29, 2257611. [Google Scholar]
- Plat, A.; Charlot, S.; Bruzual, G.; Feltre, A.; Vidal-García, A.; Morisset, C.; Chevallard, J.; Todt, H. Constraints on the production and escape of ionizing radiation from the emission-line spectra of metal-poor star-forming galaxies. Mon. Not. R. Astron. Soc. 2019, 490, 978–1009. [Google Scholar] [CrossRef]
- Maraston, C. Evolutionary population synthesis: Models, analysis of the ingredients and application to high-z galaxies. Mon. Not. R. Astron. Soc. 2005, 362, 799–825. [Google Scholar] [CrossRef]
- Maraston, C.; Strömbäck, G. Stellar population models at high spectral resolution. Mon. Not. R. Astron. Soc. 2011, 418, 2785–2811. [Google Scholar] [CrossRef]
- Maraston, C.; Pforr, J.; Henriques, B.M.; Thomas, D.; Wake, D.; Brownstein, J.R.; Capozzi, D.; Tinker, J.; Bundy, K.; Skibba, R.A.; et al. Stellar masses of SDSS-III/BOSS galaxies at z ∼ 0.5 and constraints to galaxy formation models. Mon. Not. R. Astron. Soc. 2013, 435, 2764–2792. [Google Scholar] [CrossRef]
- Cassisi, S.; Castellani, M.; Castellani, V. Intermediate-age metal deficient stellar populations: The case of metallicity Z = 0.00001. Astronom. Astrophys. 1997, 317, 108–113. [Google Scholar]
- Choi, J.; Dotter, A.; Conroy, C.; Cantiello, M.; Paxton, B.; Johnson, B.D. Mesa Isochrones and Stellar Tracks (MIST). I. Solar-scaled Models. Astrophys. J. 2016, 823, 102. [Google Scholar] [CrossRef]
- Leja, J.; Johnson, B.D.; Conroy, C.; van Dokkum, P.; Speagle, J.S.; Brammer, G.; Momcheva, I.; Skelton, R.; Whitaker, K.E.; Franx, M.; et al. An Older, More Quiescent Universe from Panchromatic SED Fitting of the 3D-HST Survey. Astrophys. J. 2019, 877, 140. [Google Scholar] [CrossRef]
- Girardi, L.; Bressan, A.; Bertelli, G.; Chiosi, C. Evolutionary tracks and isochrones for low- and intermediate-mass stars: From 0.15 to 7 Msun, and from Z = 0.0004 to 0.03. Astron. Astrophys. 2000, 141, 371–383. [Google Scholar] [CrossRef]
- Sánchez-Blázquez, P.; Peletier, R.F.; Jiménez-Vicente, J.; Cardiel, N.; Cenarro, A.J.; Falcón-Barroso, J.; Gorgas, J.; Selam, S.; Vazdekis, A. Medium-resolution Isaac Newton Telescope library of empirical spectra. Mon. Not. R. Astron. Soc. 2006, 371, 703–718. [Google Scholar] [CrossRef]
- Leitherer, C.; Schaerer, D.; Goldader, J.D.; Delgado, R.M.G.; Robert, C.; Kune, D.F.; de Mello, D.F.; Devost, D.; Heckman, T.M. Starburst99: Synthesis Models for Galaxies with Active Star Formation. Astrophys. J. Suppl. 1999, 123, 3–40. [Google Scholar] [CrossRef]
- Gutkin, J.; Charlot, S.; Bruzual, G. Modelling the nebular emission from primeval to present-day star-forming galaxies. Mon. Not. R. Astron. Soc. 2016, 462, 1757–1774. [Google Scholar] [CrossRef]
- Osterbrock, D.E.; Ferland, G.J. Astrophysics of Gaseous Nebulae and Active Galactic Nuclei; University Science Books: Sausalito, CA, USA, 2006. [Google Scholar]
- Ferland, G.J.; Korista, K.T.; Verner, D.A.; Ferguson, J.W.; Kingdon, J.B.; Verner, E.M. CLOUDY 90: Numerical Simulation of Plasmas and Their Spectra. Pub. Astronom. Soc. Pac. 1998, 110, 761–778. [Google Scholar] [CrossRef]
- Ferland, G.J.; Chatzikos, M.; Guzmán, F.; Lykins, M.L.; van Hoof, P.A.M.; Williams, R.J.R.; Abel, N.P.; Badnell, N.R.; Keenan, F.P.; Porter, R.L.; et al. The 2017 Release Cloudy. Rev. Mex. Astron. 2017, 53, 385–438. [Google Scholar]
- Sutherland, R.S.; Dopita, M.A. Cooling Functions for Low-Density Astrophysical Plasmas. Astrophys. J. Suppl. 1993, 88, 253. [Google Scholar] [CrossRef]
- Kewley, L.J.; Dopita, M.A.; Sutherland, R.S.; Heisler, C.A.; Trevena, J. Theoretical Modeling of Starburst Galaxies. Astrophys. J. 2001, 556, 121–140. [Google Scholar] [CrossRef]
- Xiao, L.; Galbany, L.; Eldridge, J.J.; Stanway, E.R. Core-collapse supernovae ages and metallicities from emission-line diagnostics of nearby stellar populations. Mon. Not. R. Astron. Soc. 2019, 482, 384–401. [Google Scholar] [CrossRef]
- Xiao, L.; Stanway, E.R.; Eldridge, J.J. Emission-line diagnostics of nearby H II regions including interacting binary populations. Mon. Not. R. Astron. Soc. 2018, 477, 904–934. [Google Scholar] [CrossRef]
- Byler, N.; Dalcanton, J.J.; Conroy, C.; Johnson, B.D. Nebular Continuum and Line Emission in Stellar Population Synthesis Models. Astrophys. J. 2017, 840, 44. [Google Scholar] [CrossRef]
- Hirschmann, M.; Charlot, S.; Feltre, A.; Naab, T.; Somerville, R.S.; Choi, E. Synthetic nebular emission from massive galaxies—II. Ultraviolet-line diagnostics of dominant ionizing sources. Mon. Not. R. Astron. Soc. 2019, 487, 333–353. [Google Scholar] [CrossRef]
- Charlot, S.; Fall, S.M. A Simple Model for the Absorption of Starlight by Dust in Galaxies. Astrophys. J. 2000, 539, 718–731. [Google Scholar] [CrossRef]
- Dale, D.A.; Helou, G. The Infrared Spectral Energy Distribution of Normal Star-forming Galaxies: Calibration at Far-Infrared and Submillimeter Wavelengths. Astrophys. J. 2002, 576, 159–168. [Google Scholar] [CrossRef]
- da Cunha, E.; Charlot, S.; Elbaz, D. A simple model to interpret the ultraviolet, optical and infrared emission from galaxies. Mon. Not. R. Astron. Soc. 2008, 388, 1595–1617. [Google Scholar] [CrossRef]
- Da Cunha, E.; Walter, F.; Smail, I.R.; Swinbank, A.M.; Simpson, J.M.; Decarli, R.; Hodge, J.A.; Weiss, A.; Van der Werf, P.P.; Bertoldi, F.; et al. An ALMA Survey of Sub-millimeter Galaxies in the Extended Chandra Deep Field South: Physical Properties Derived from Ultraviolet-to-radio Modeling. Astrophys. J. 2015, 806, 110. [Google Scholar] [CrossRef]
- Buat, V.; Burgarella, D.; Deharveng, J.M.; Kunth, D. Spectral Energy Distributions of starburst galaxies in the 900–1200 Å range. Astronom. Astrophys. 2002, 393, 33–42. [Google Scholar] [CrossRef][Green Version]
- Cullen, F.; McLure, R.J.; Khochfar, S.; Dunlop, J.S.; Dalla Vecchia, C. The First Billion Years project: Constraining the dust attenuation law of star-forming galaxies at z ∼ 5. Mon. Not. R. Astron. Soc. 2017, 470, 3006–3026. [Google Scholar] [CrossRef]
- Reddy, N.A.; Kriek, M.; Shapley, A.E.; Freeman, W.R.; Siana, B.; Coil, A.L.; Mobasher, B.; Price, S.H.; Sanders, R.L.; Shivaei, I. The MOSDEF Survey: Measurements of Balmer Decrements and the Dust Attenuation Curve at Redshifts z ∼ 1.4–2.6. Astrophys. J. 2015, 806, 259. [Google Scholar] [CrossRef]
- Stratta, G.; Gallerani, S.; Maiolino, R. Is GRB 050904 at z = 6.3 absorbed by dust? Astronom. Astrophys. 2011, 532, A45. [Google Scholar] [CrossRef]
- Stanway, E.R.; Eldridge, J.J.; Becker, G.D. Stellar population effects on the inferred photon density at reionization. Mon. Not. R. Astron. Soc. 2016, 456, 485–499. [Google Scholar] [CrossRef]
- Ma, X.; Hopkins, P.F.; Kasen, D.; Quataert, E.; Faucher-Giguëre, C.A.; Kereš, D.; Murray, N.; Strom, A. Binary stars can provide the ‘missing photons’ needed for reionization. Mon. Not. R. Astron. Soc. 2016, 459, 3614–3619. [Google Scholar] [CrossRef]
- Rosdahl, J.; Katz, H.; Blaizot, J.; Kimm, T.; Michel-Dansac, L.; Garel, T.; Haehnelt, M.; Ocvirk, P.; Teyssier, R. The SPHINX cosmological simulations of the first billion years: The impact of binary stars on reionization. Mon. Not. R. Astron. Soc. 2018, 479, 994–1016. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Stanway, E.R.; Tang, P.N. A consistent estimate for gravitational wave and electromagnetic transient rates. Mon. Not. R. Astron. Soc. 2019, 482, 870–880. [Google Scholar] [CrossRef]
- Eldridge, J.J.; Stanway, E.R. BPASS predictions for binary black hole mergers. Mon. Not. R. Astron. Soc. 2016, 462, 3302–3313. [Google Scholar] [CrossRef]
- Stanway, E.R.; Eldridge, J.J. Initial mass function variations cannot explain the ionizing spectrum of low metallicity starbursts. Astronom. Astrophys. 2019, 621, A105. [Google Scholar] [CrossRef]
- Wise, J.H.; Abel, T. Resolving the Formation of Protogalaxies. III. Feedback from the First Stars. Astrophys. J. 2008, 685, 40–56. [Google Scholar] [CrossRef]
- Whalen, D.J.; Johnson, J.L.; Smidt, J.; Meiksin, A.; Heger, A.; Even, W.; Fryer, C.L. The Supernova that Destroyed a Protogalaxy: Prompt Chemical Enrichment and Supermassive Black Hole Growth. Astrophys. J. 2013, 774, 64. [Google Scholar] [CrossRef][Green Version]
- Hartwig, T.; Yoshida, N.; Magg, M.; Frebel, A.; Glover, S.C.O.; Gómez, F.A.; Griffen, B.; Ishigaki, M.N.; Ji, A.P.; Klessen, R.S.; et al. Descendants of the first stars: The distinct chemical signature of second-generation stars. Mon. Not. R. Astron. Soc. 2018, 478, 1795–1810. [Google Scholar] [CrossRef]
- Kewley, L.J.; Nicholls, D.C.; Sutherland, R.S. Understanding Galaxy Evolution Through Emission Lines. Annu. Rev. Astron. Astrophys. 2019, 57, 511–570. [Google Scholar] [CrossRef]
- Moe, M.; Di Stefano, R. Mind Your Ps and Qs: The Interrelation between Period (P) and Mass-ratio (Q) Distributions of Binary Stars. Astrophys. J. Suppl. 2017, 230, 15. [Google Scholar] [CrossRef]
- Hopkins, A.M. The Dawes Review 8: Measuring the Stellar Initial Mass Function. Pub. Astron. Soc. Aust. 2018, 35, 39. [Google Scholar] [CrossRef]
- Walborn, N.R.; Lennon, D.J.; Heap, S.R.; Lindler, D.J.; Smith, L.J.; Evans, C.J.; Parker, J.W. The Ultraviolet and Optical Spectra of Metal-deficient O Stars in the Small Magellanic Cloud. Pub. Astronom. Soc. Pac. 2000, 112, 1243–1261. [Google Scholar] [CrossRef]
- Tramper, F.; Sana, H.; de Koter, A.; Kaper, L.; Ramírez-Agudelo, O.H. The properties of ten O-type stars in the low-metallicity galaxies IC 1613, WLM, and NGC 3109. Astronom. Astrophys. 2014, 572, A36. [Google Scholar] [CrossRef]
- Garcia, M.; Herrero, A.; Najarro, F.; Camacho, I.; Lennon, D.J.; Urbaneja, M.A.; Castro, N. Low-metallicity (sub-SMC) massive stars. In The Lives and Death-Throes of Massive Stars; Eldridge, J.J., Bray, J.C., McClelland, L.A.S., Xiao, L., Eds.; Cambridge University Press: Cambridge, UK, 2017; Volume 329, pp. 313–321. [Google Scholar] [CrossRef]
- Garcia, M.; Evans, C.J.; Bestenlehner, J.M.; Bouret, J.C.; Castro, N.; Cerviño, M.; Fullerton, A.W.; Gieles, M.; Herrero, A.; de Koter, A.; et al. Massive stars in extremely metal-poor galaxies: A window into the past. arXiv 2019, arXiv:1908.04687. [Google Scholar]
- Leitherer, C.; Robert, C.; Heckman, T.M. Atlas of Synthetic Ultraviolet Spectra of Massive Star Populations. Astrophys. J. Suppl. 1995, 99, 173. [Google Scholar] [CrossRef]
- Vink, J.S.; de Koter, A.; Lamers, H.J.G.L.M. New theoretical mass-loss rates of O and B stars. Astronom. Astrophys. 2000, 362, 295–309. [Google Scholar]
- Chrimes, A.A.; Stanway, E.R.; Eldridge, J.J. Binary population synthesis models for core-collapse gamma-ray burst progenitors. Mon. Not. R. Astron. Soc. 2019, 491, 3479–3495. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanway, E.R. Applications of Stellar Population Synthesis in the Distant Universe. Galaxies 2020, 8, 6. https://doi.org/10.3390/galaxies8010006
Stanway ER. Applications of Stellar Population Synthesis in the Distant Universe. Galaxies. 2020; 8(1):6. https://doi.org/10.3390/galaxies8010006
Chicago/Turabian StyleStanway, Elizabeth R. 2020. "Applications of Stellar Population Synthesis in the Distant Universe" Galaxies 8, no. 1: 6. https://doi.org/10.3390/galaxies8010006
APA StyleStanway, E. R. (2020). Applications of Stellar Population Synthesis in the Distant Universe. Galaxies, 8(1), 6. https://doi.org/10.3390/galaxies8010006




