Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves
Abstract
1. Introduction
2. Methodology
2.1. Inverse Models
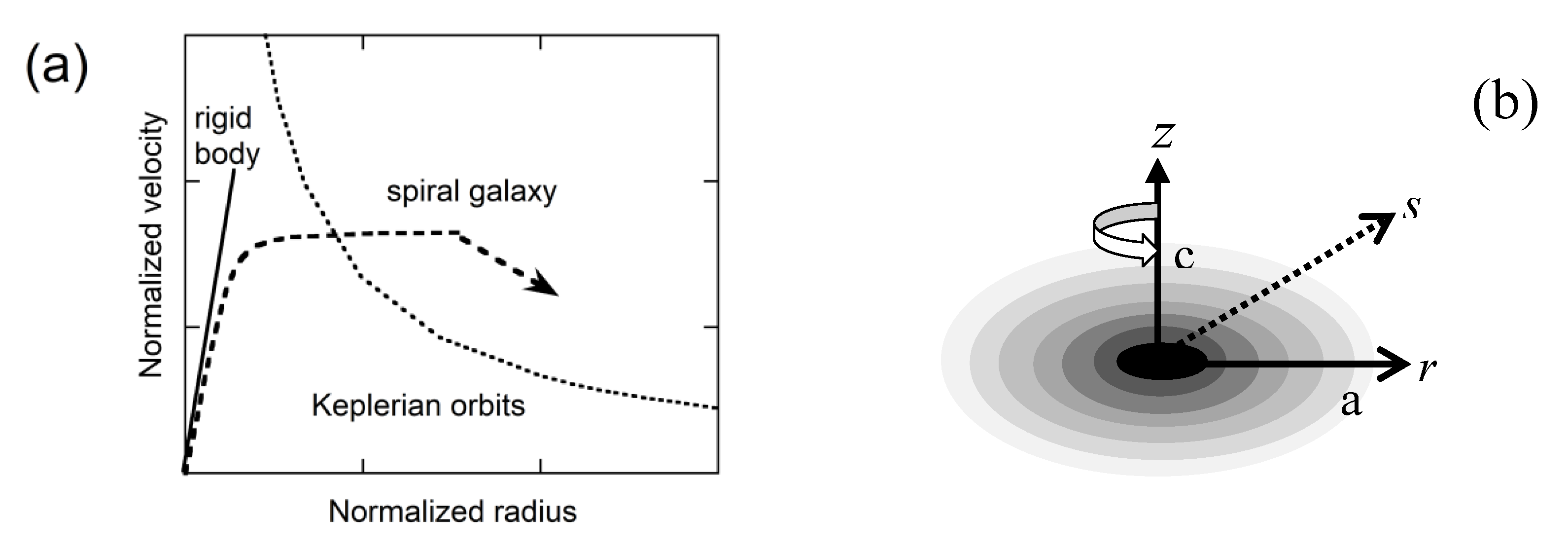
2.2. Homeoid Properties and Their Consistency with Observations
2.3. Tie to Previous Conventions and Equations
2.4. Methodology for Inverse Modelling
2.5. Criteria for Selecting Galaxies and Data Available
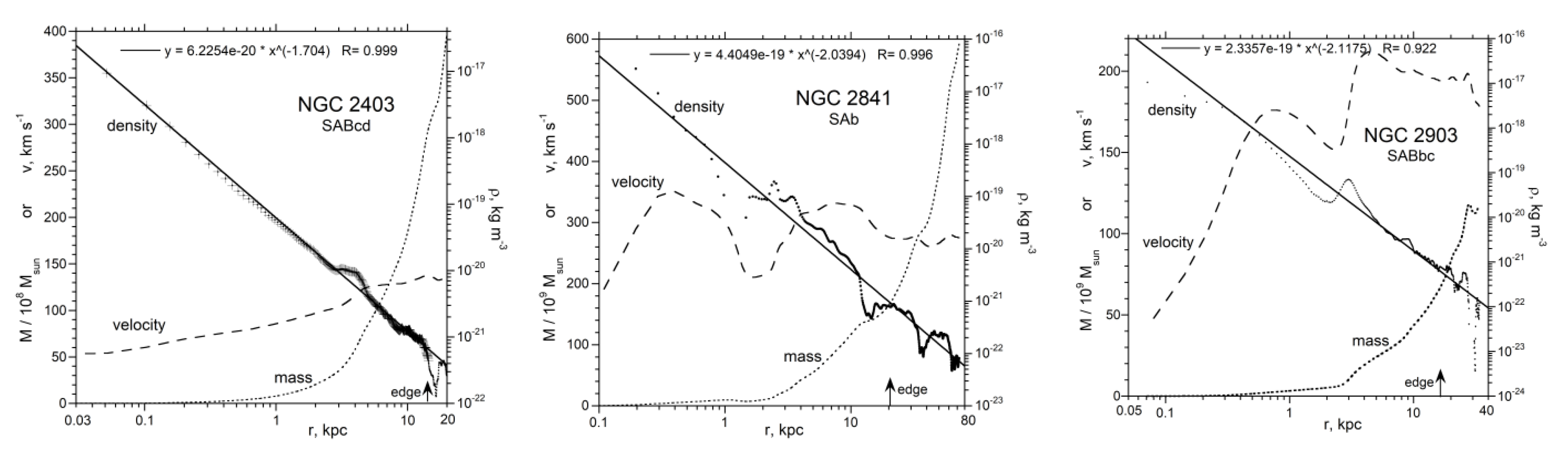
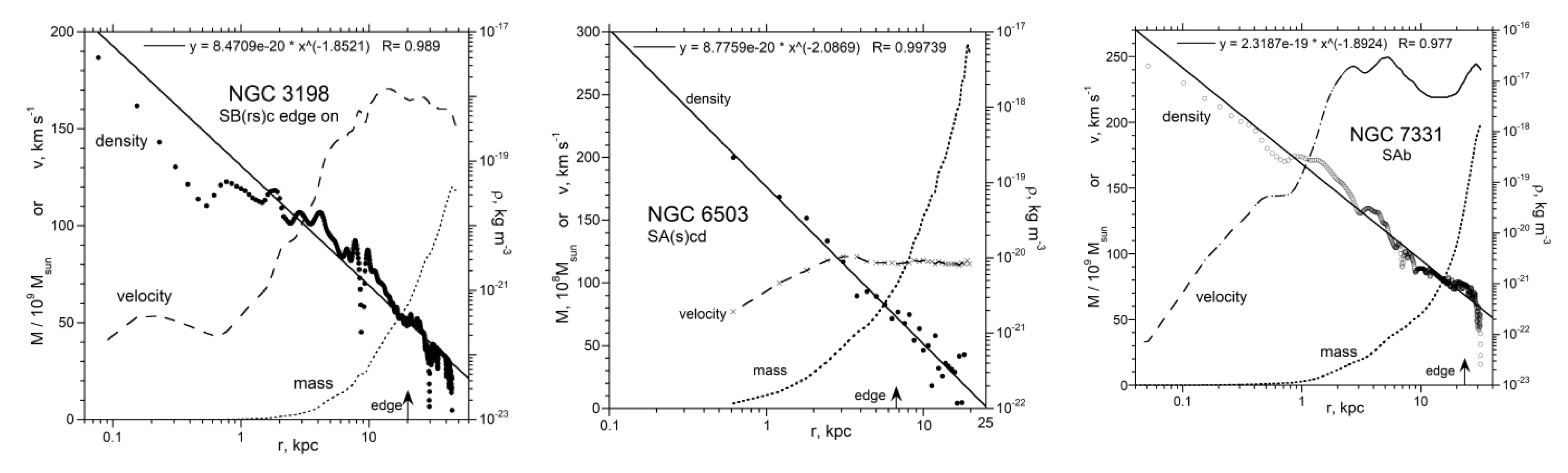
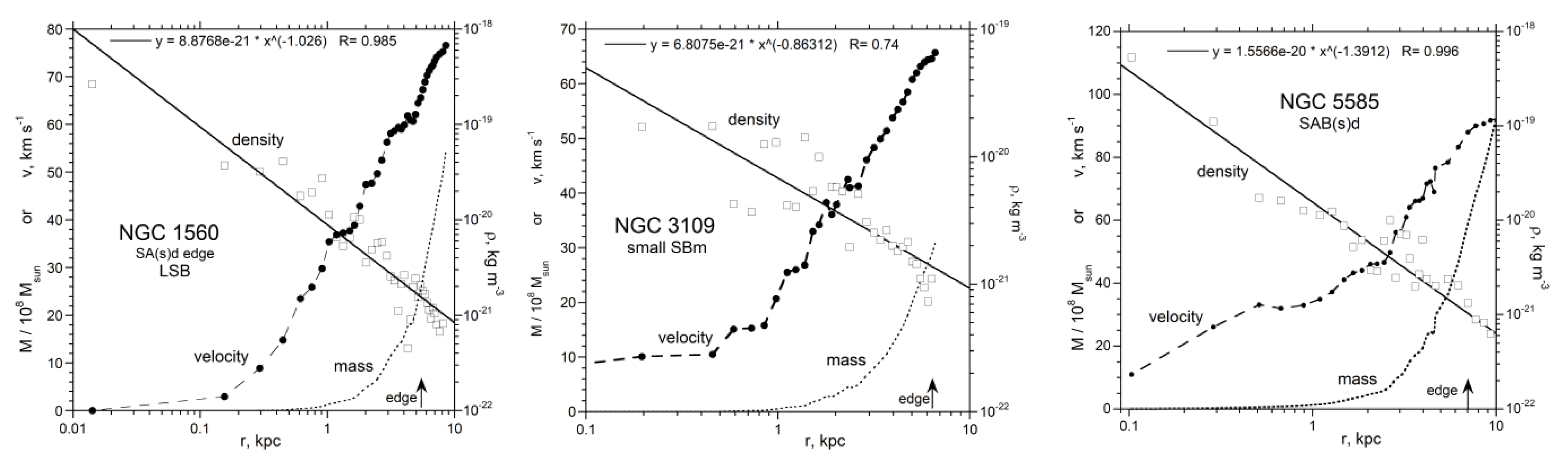
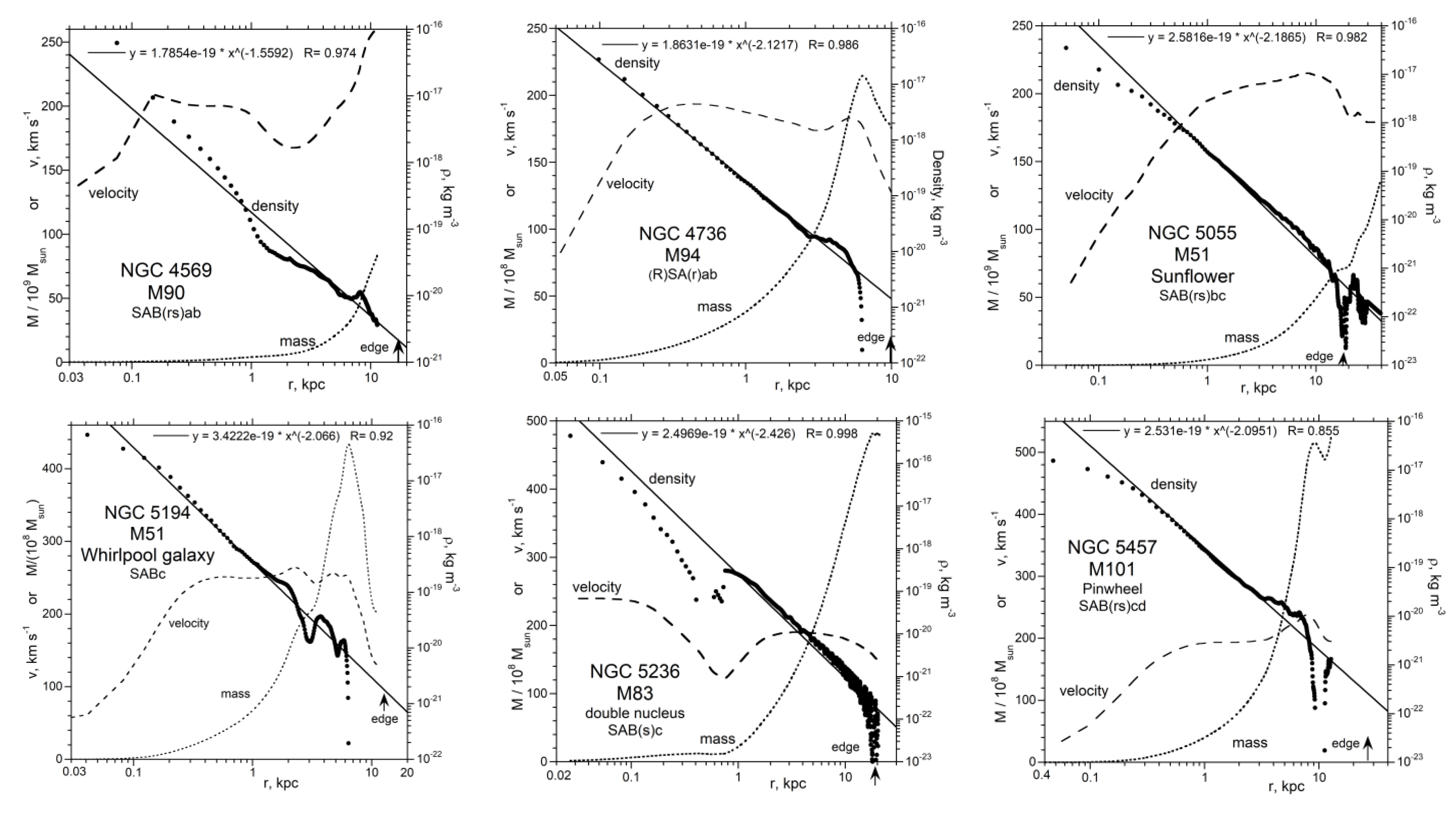
3. Results: Mass and Density from Inverse Models of Rotation Curves
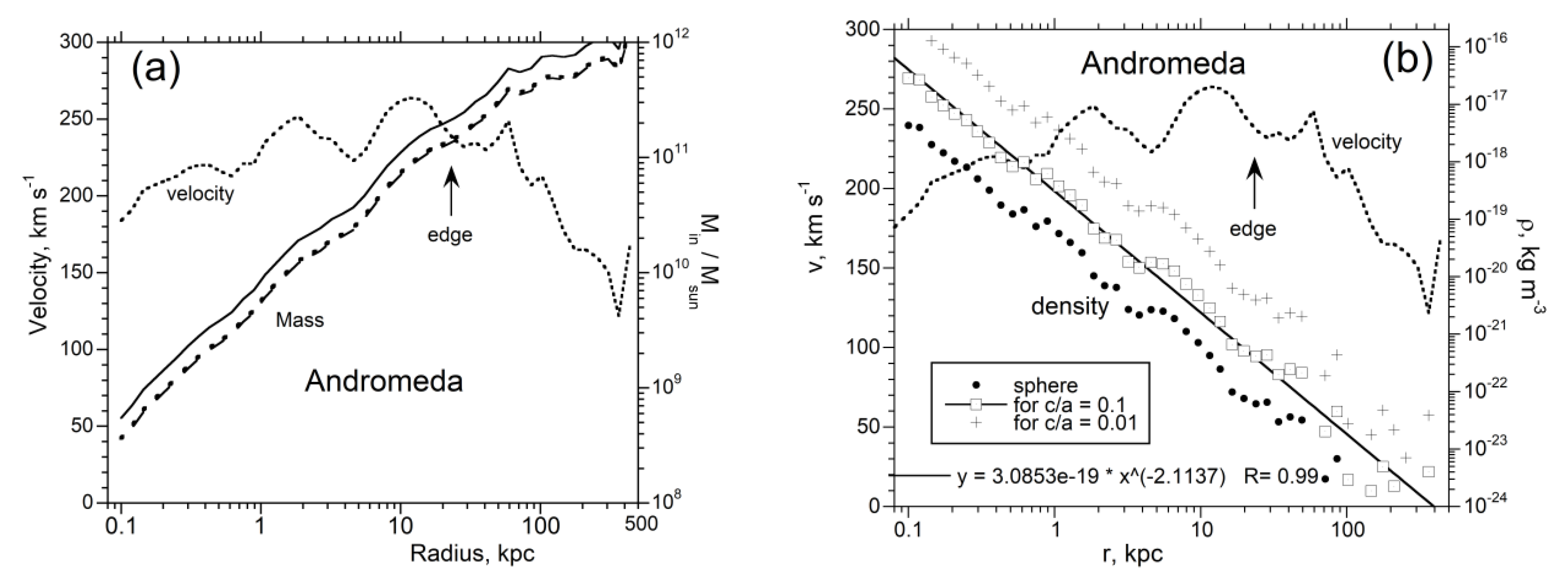
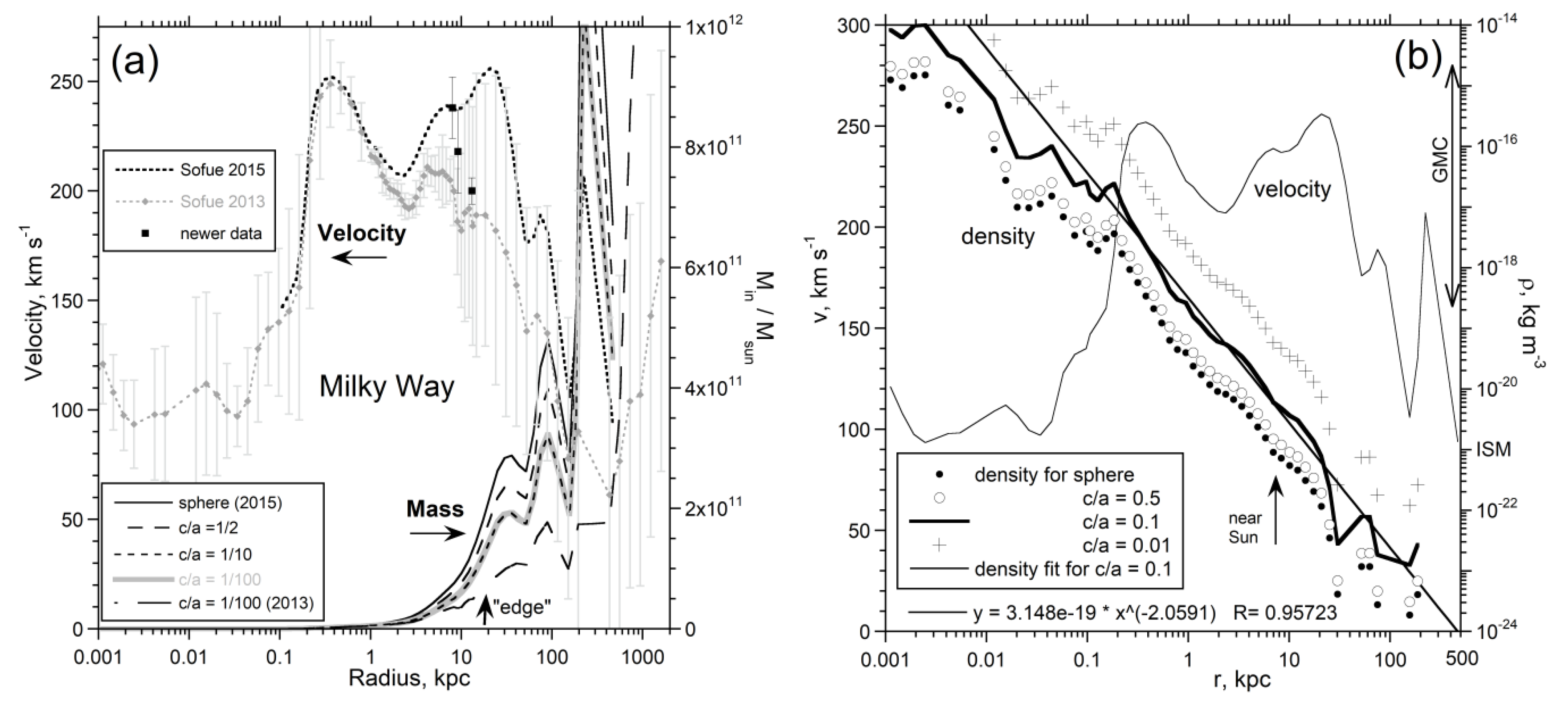
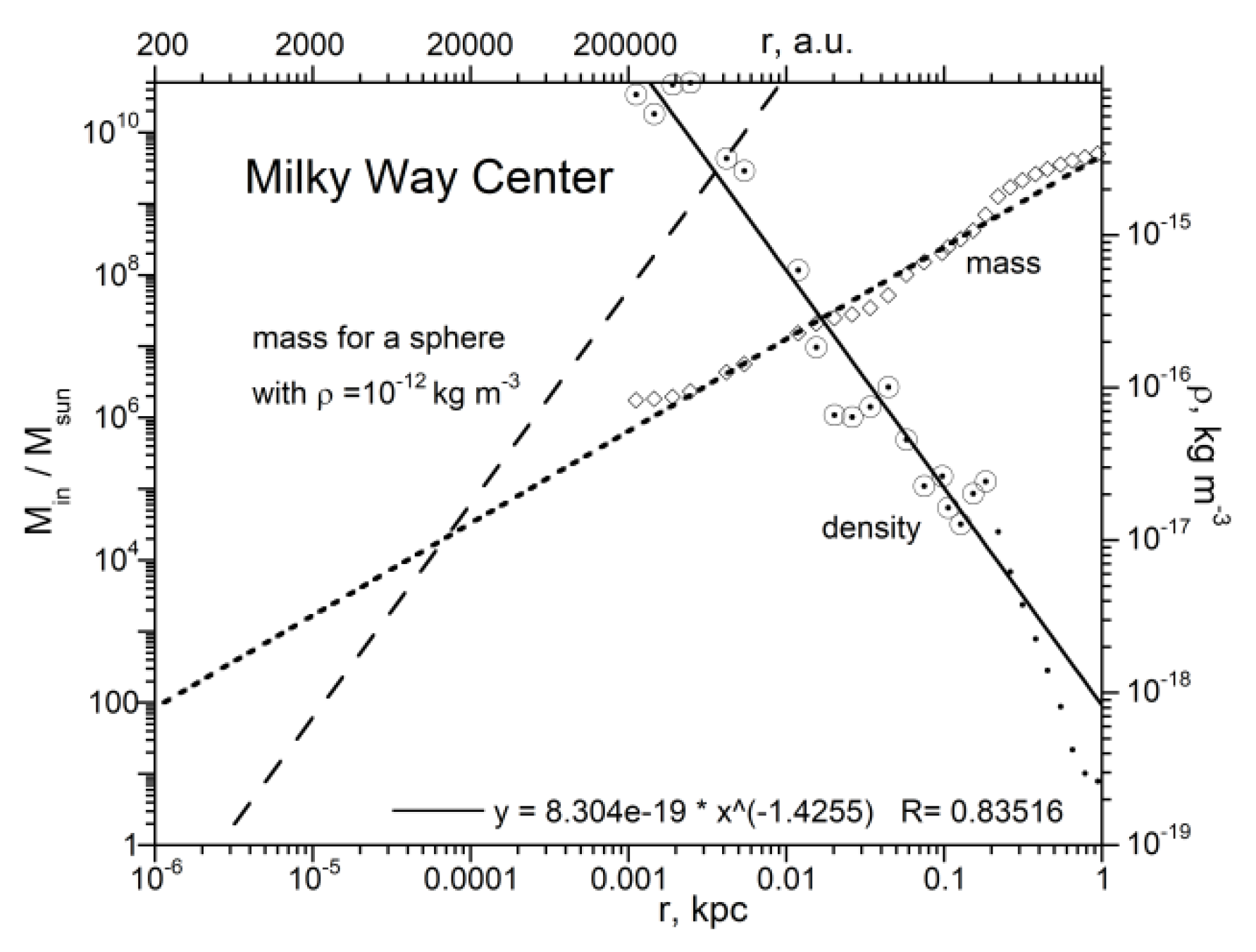
3.1. Detailed Analysis of the Milky Way
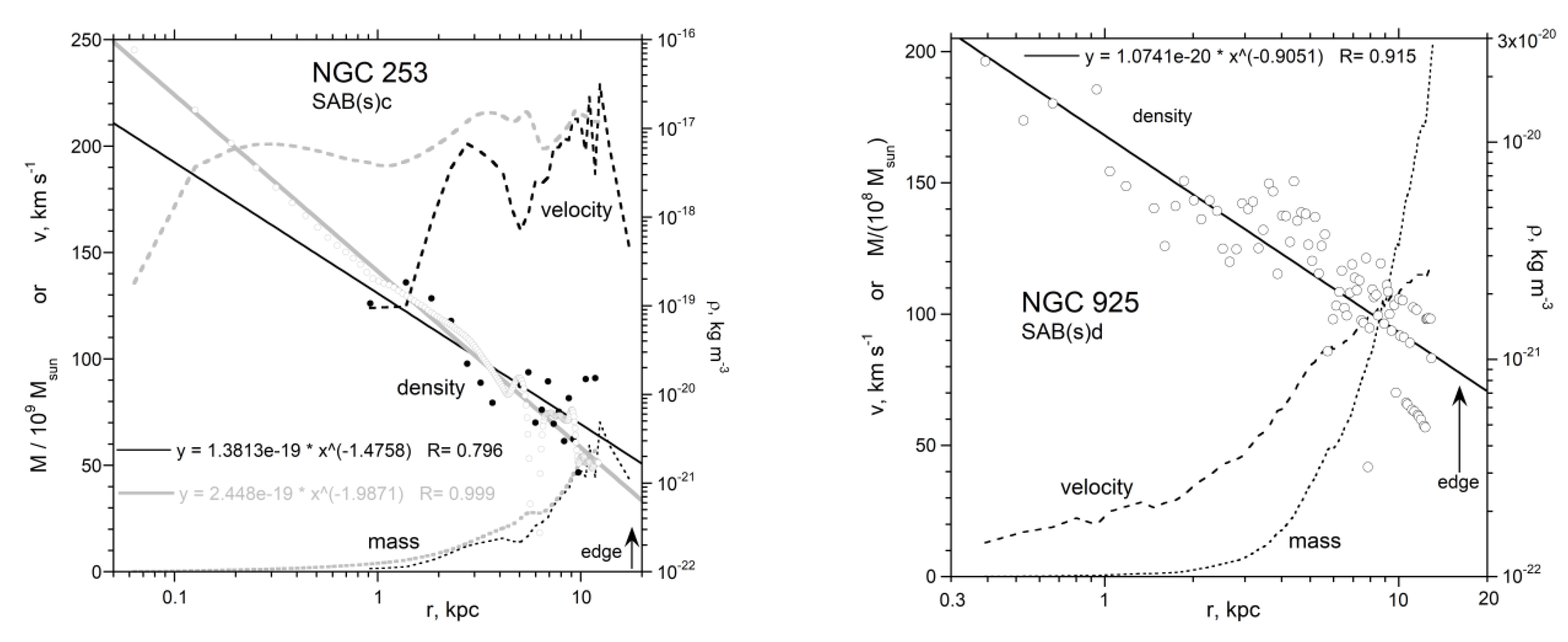
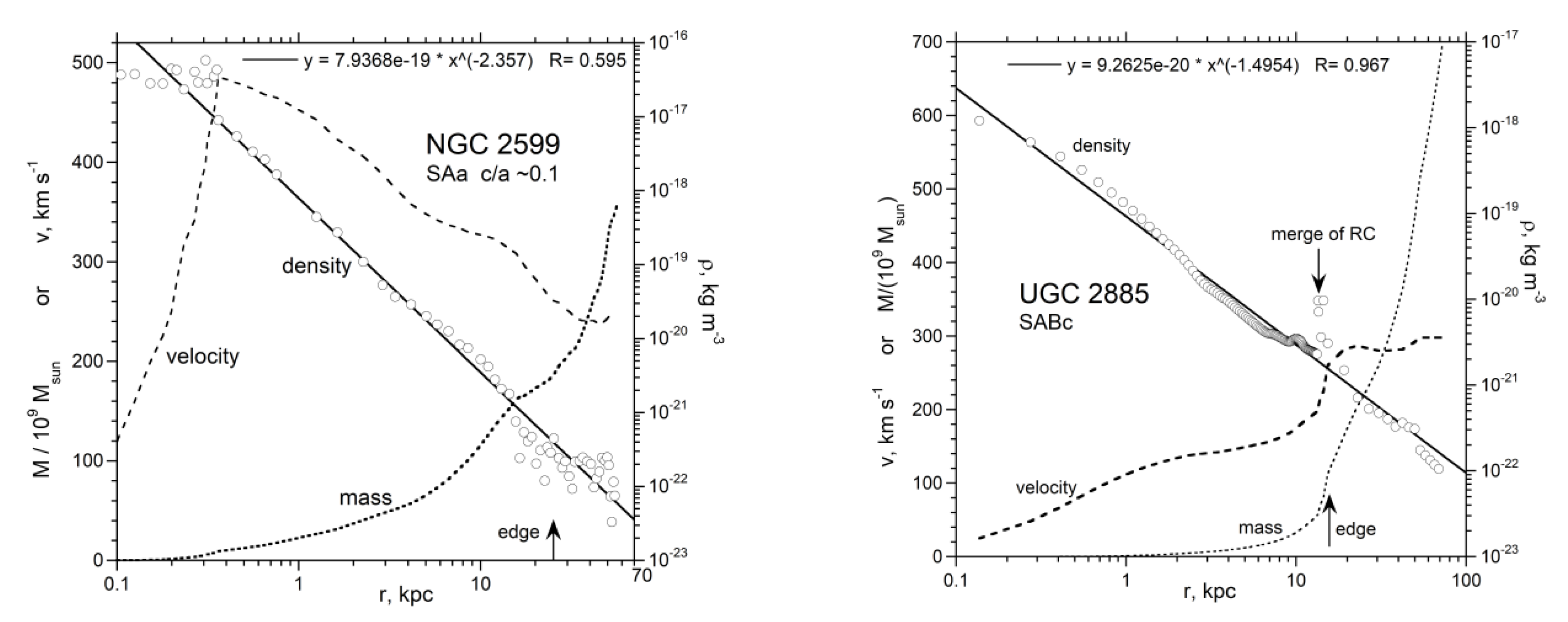
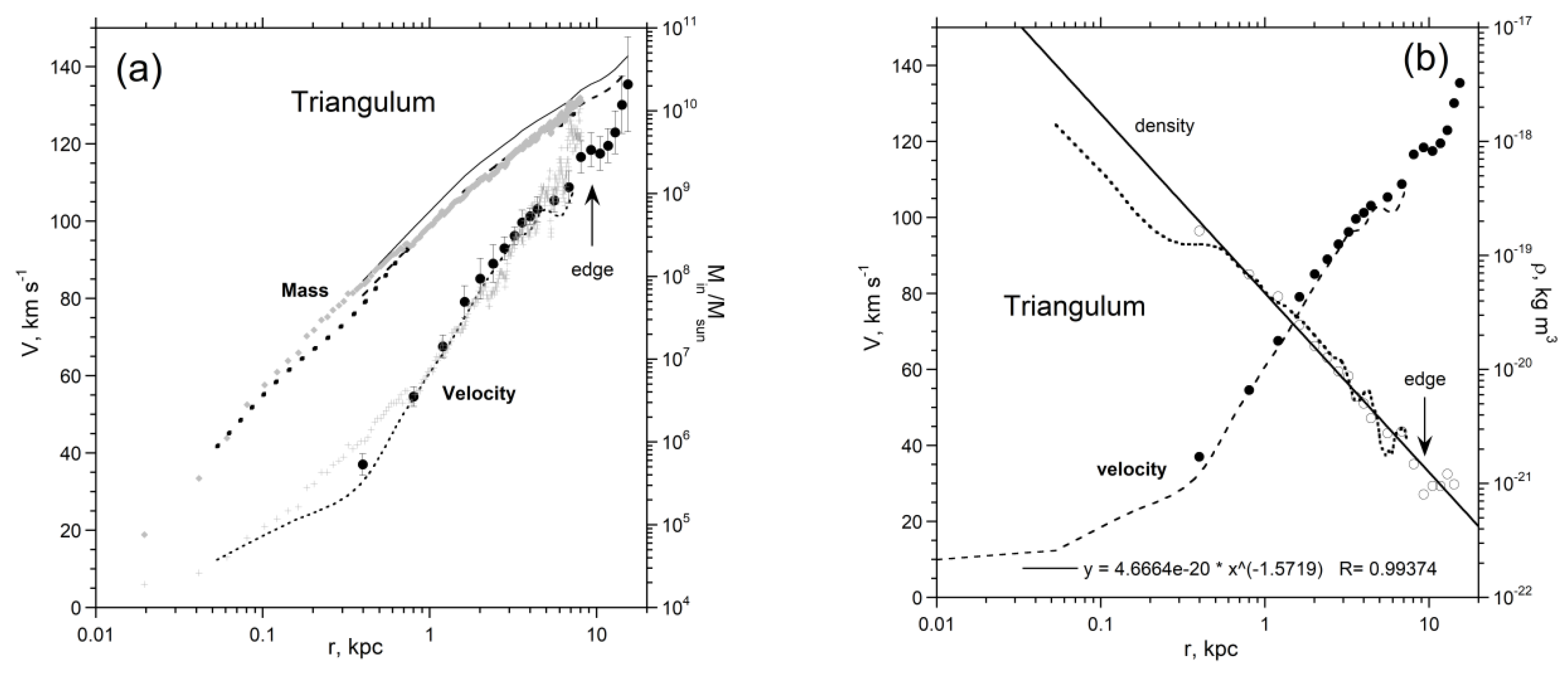
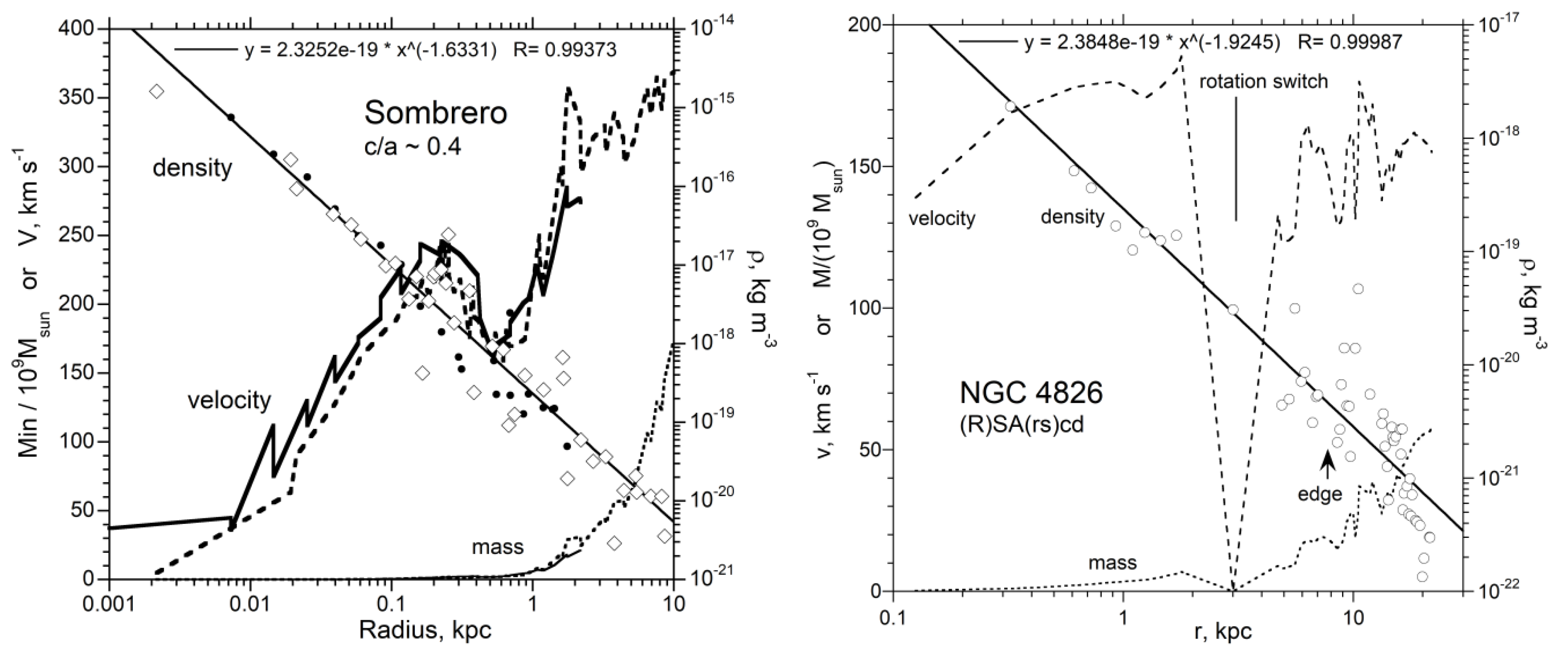
3.2. Well-Studied and/or Illustrative Spiral Galaxies
3.3. “Representative” Galaxies
3.4. Messier Galaxies, including the Virgo Cluster
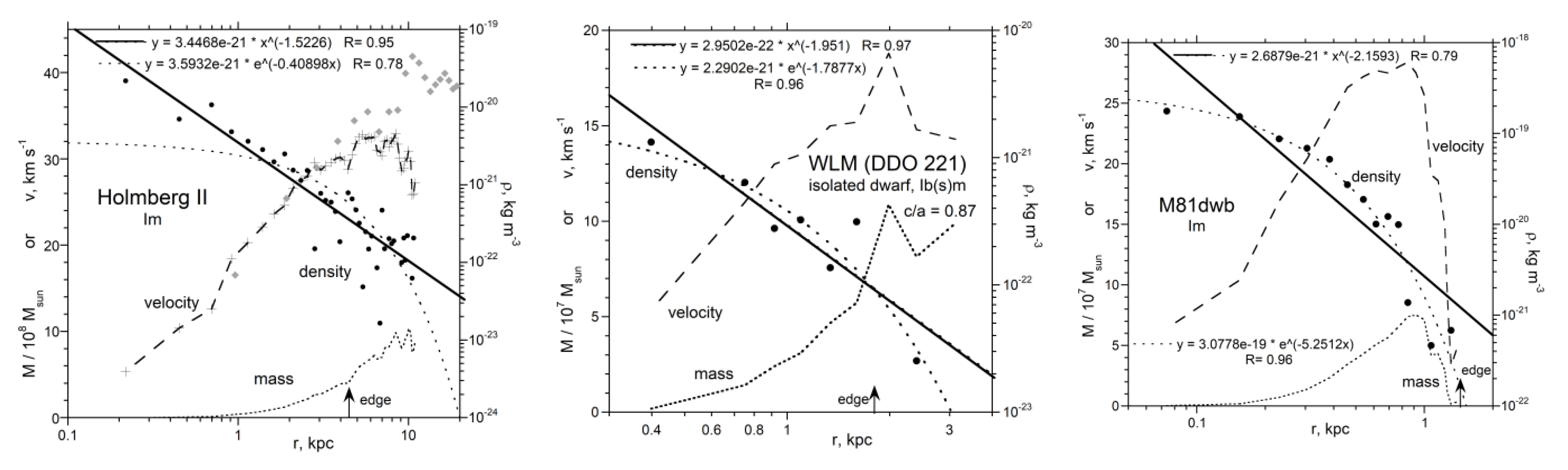
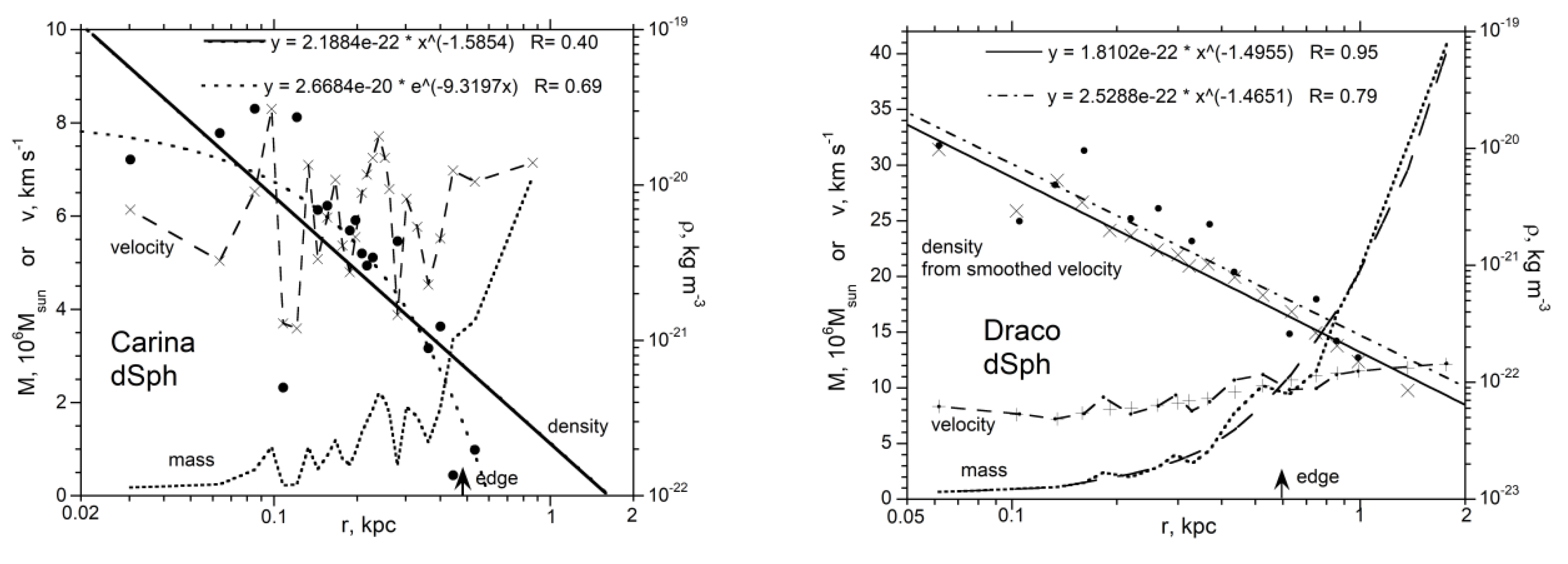
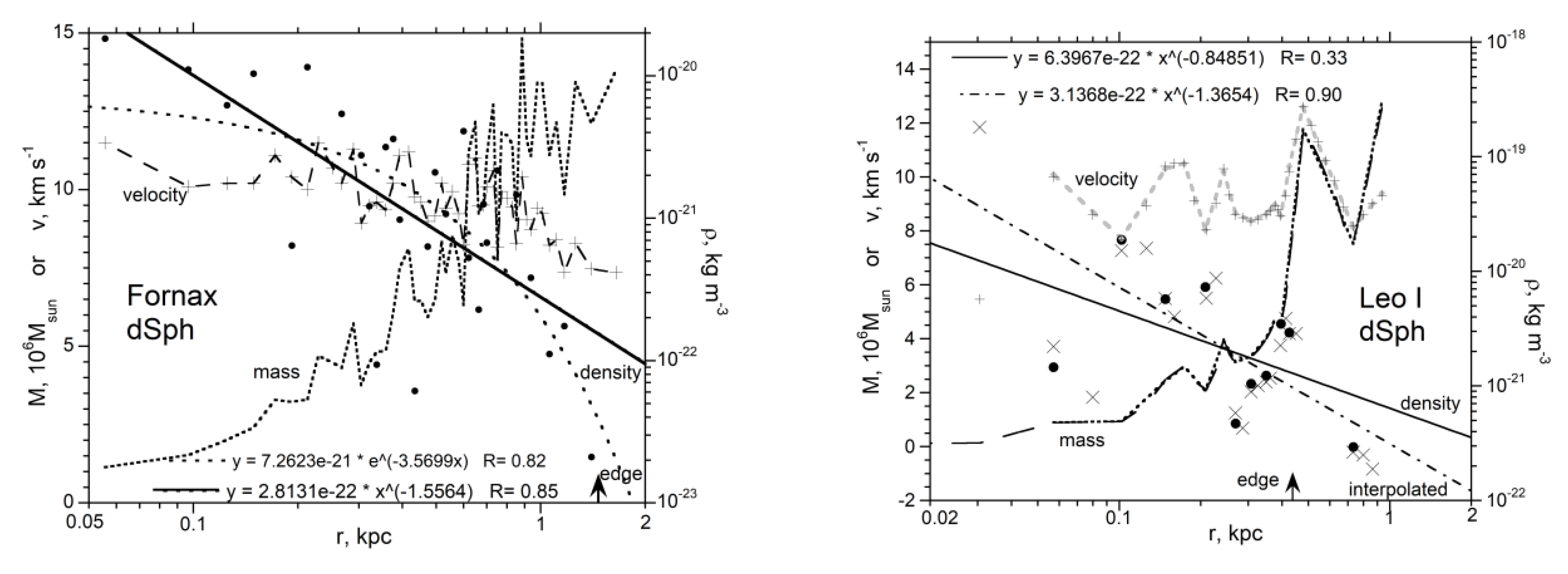
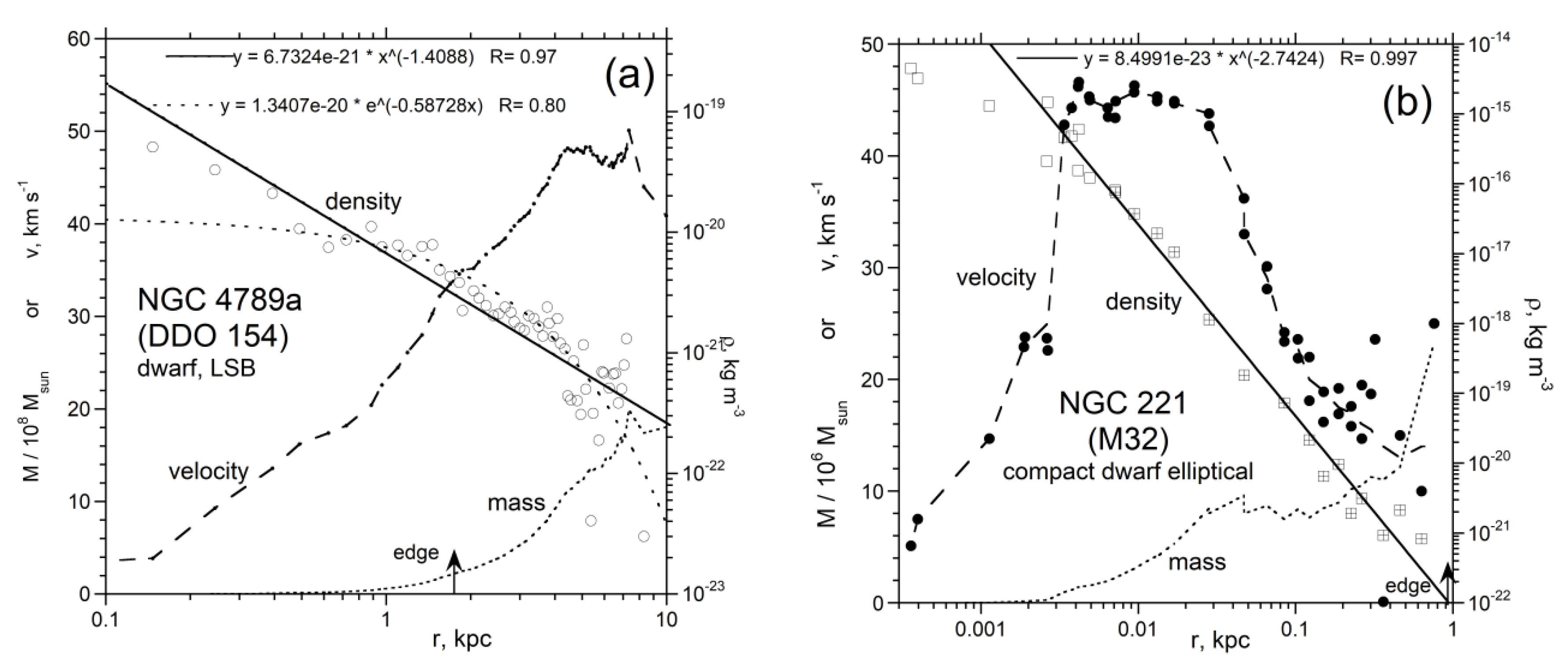
3.5. Dwarf Galaxies
3.6. Lenticular Galaxies
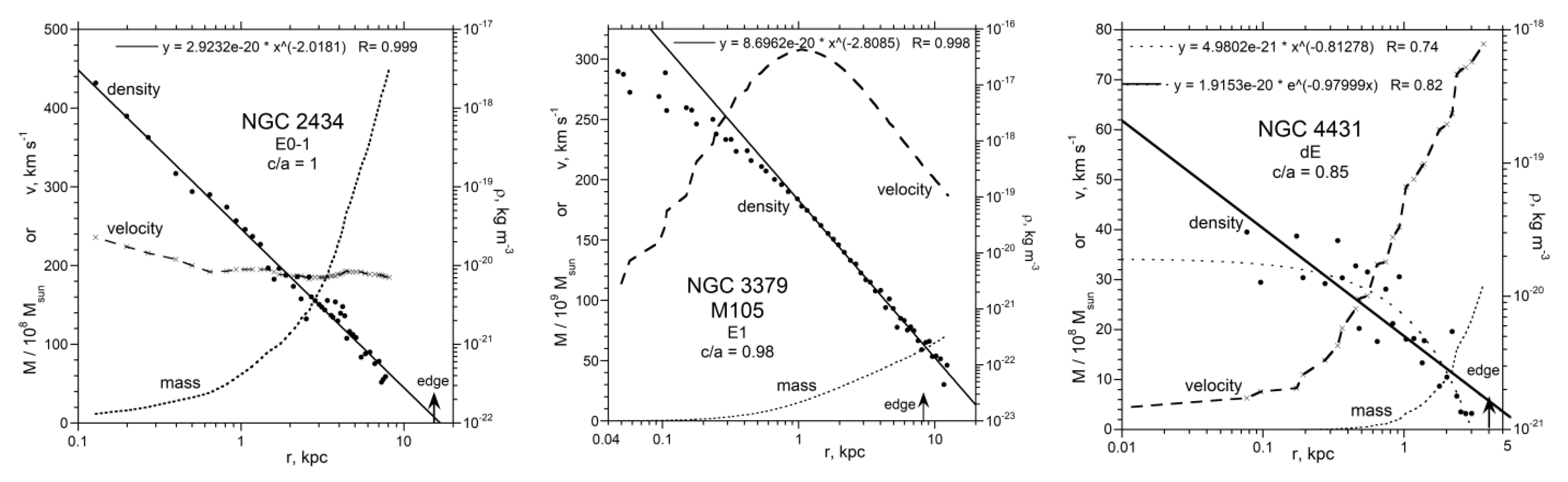
3.7. Elliptical Galaxies
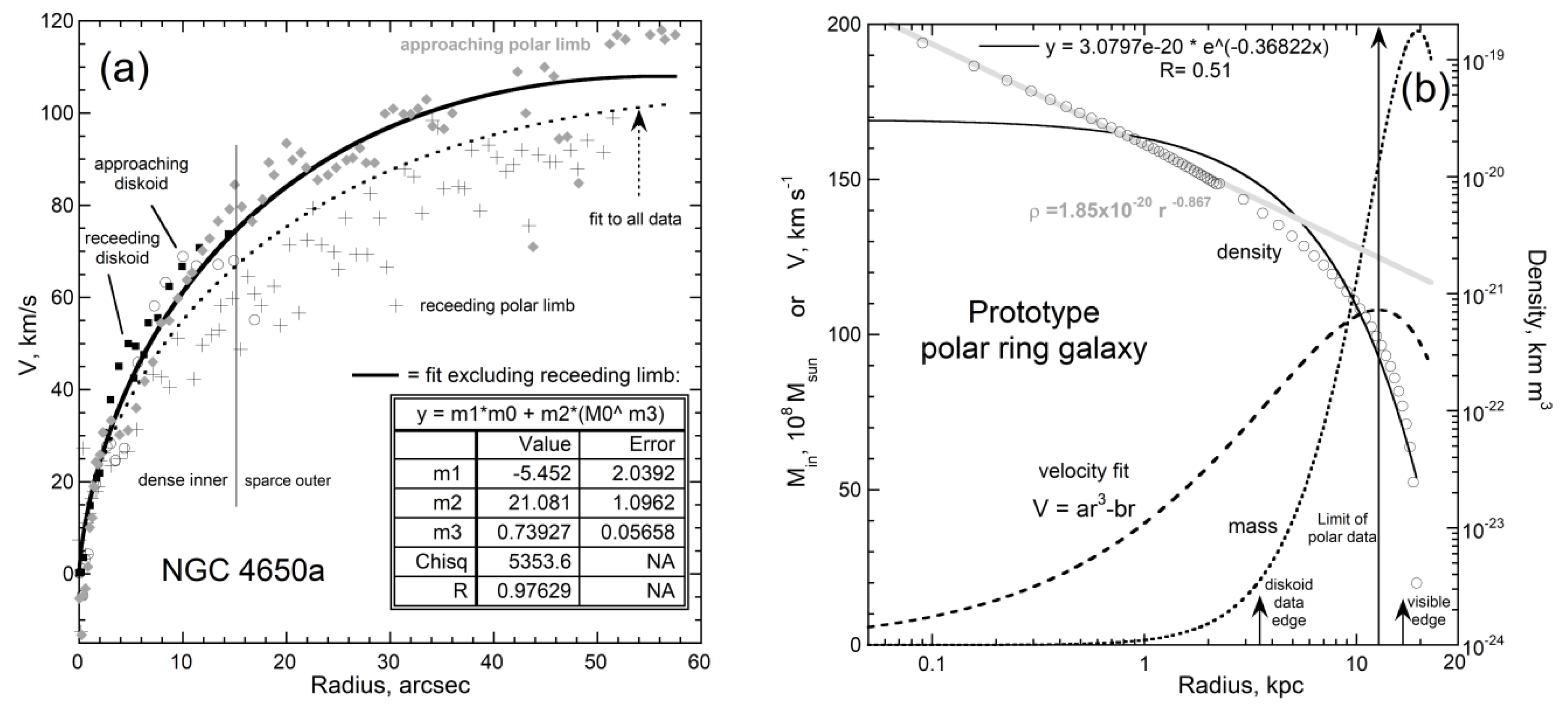
3.8. A Polar Ring Galaxy
4. Discussion
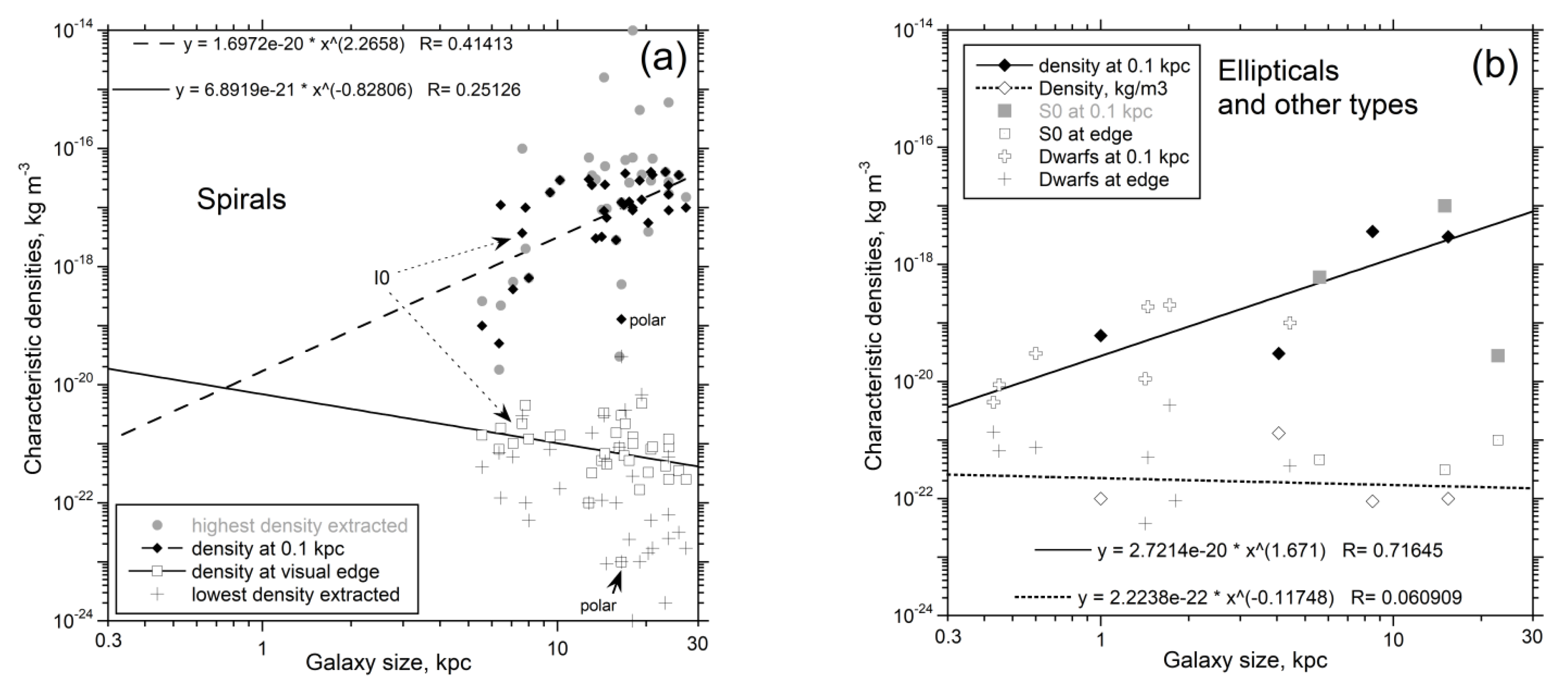
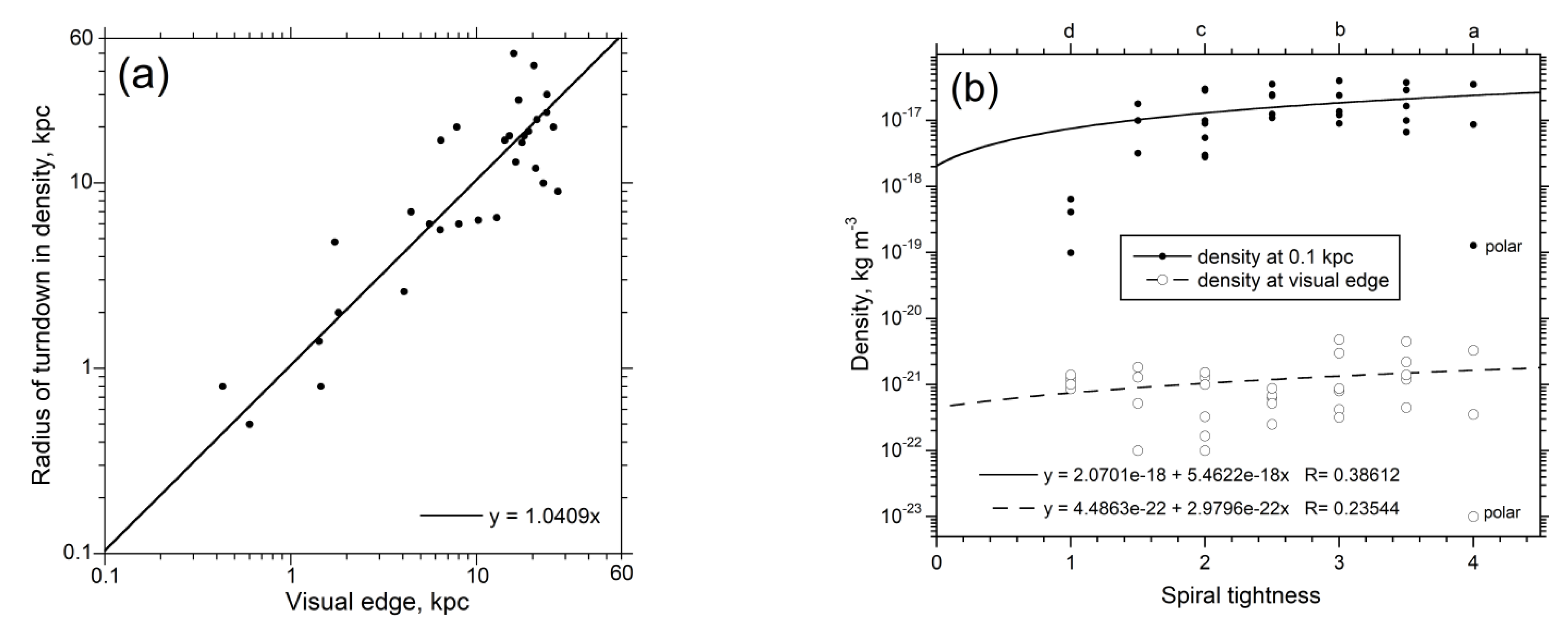
4.1. Trends in Density with Galaxy Size and Morphology
4.2. Comparison of Extracted Density with Independently Known Densities
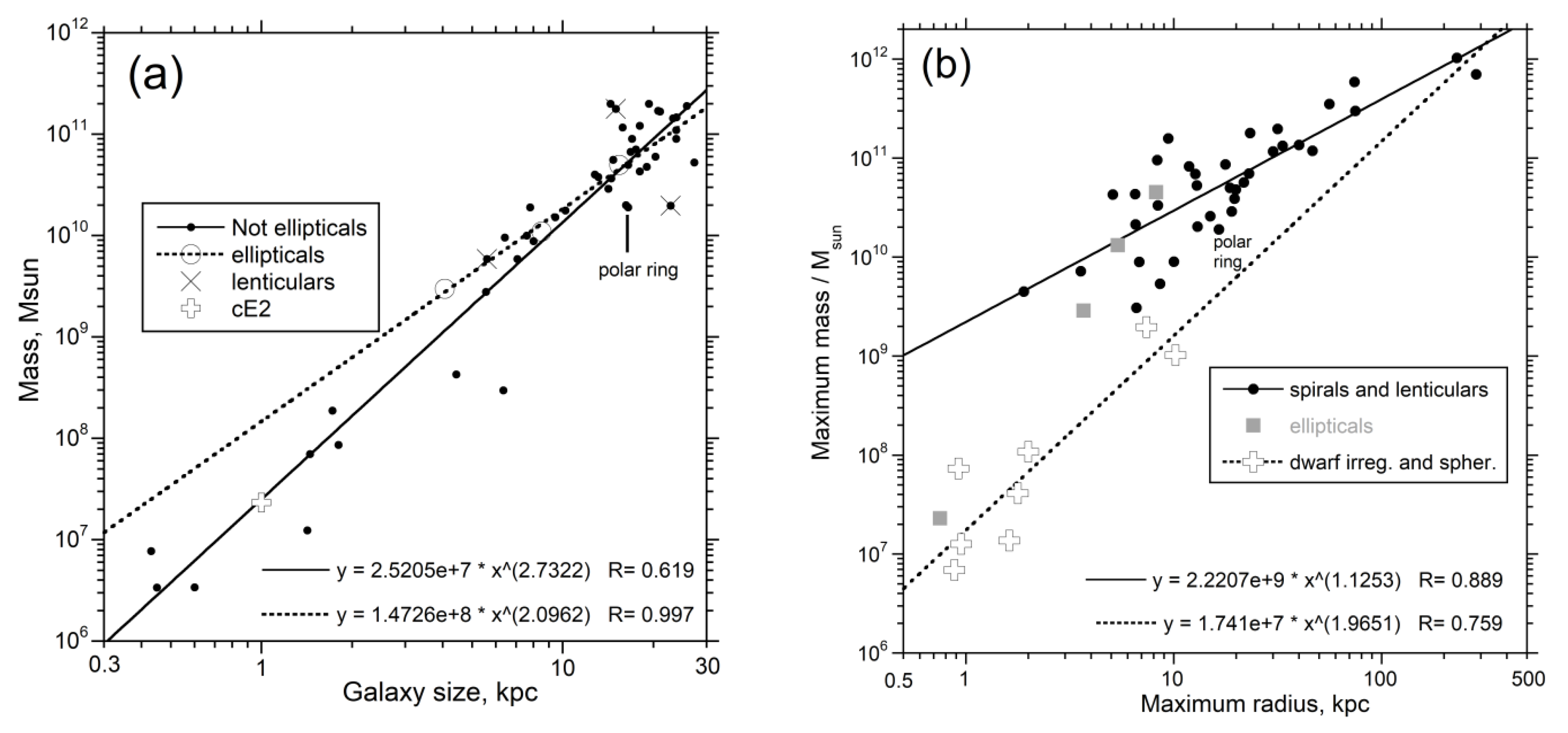
4.3. Dependence of Galactic Mass on Size
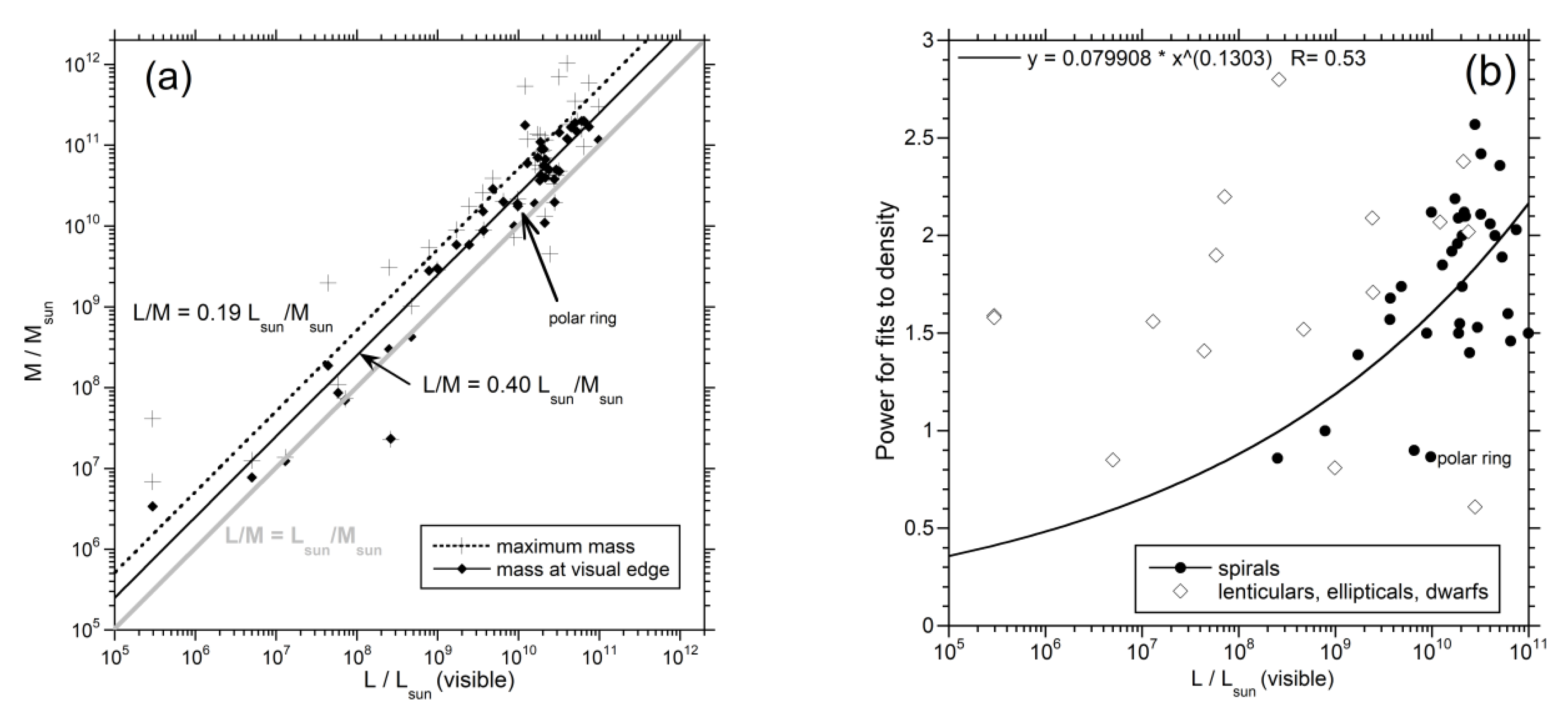
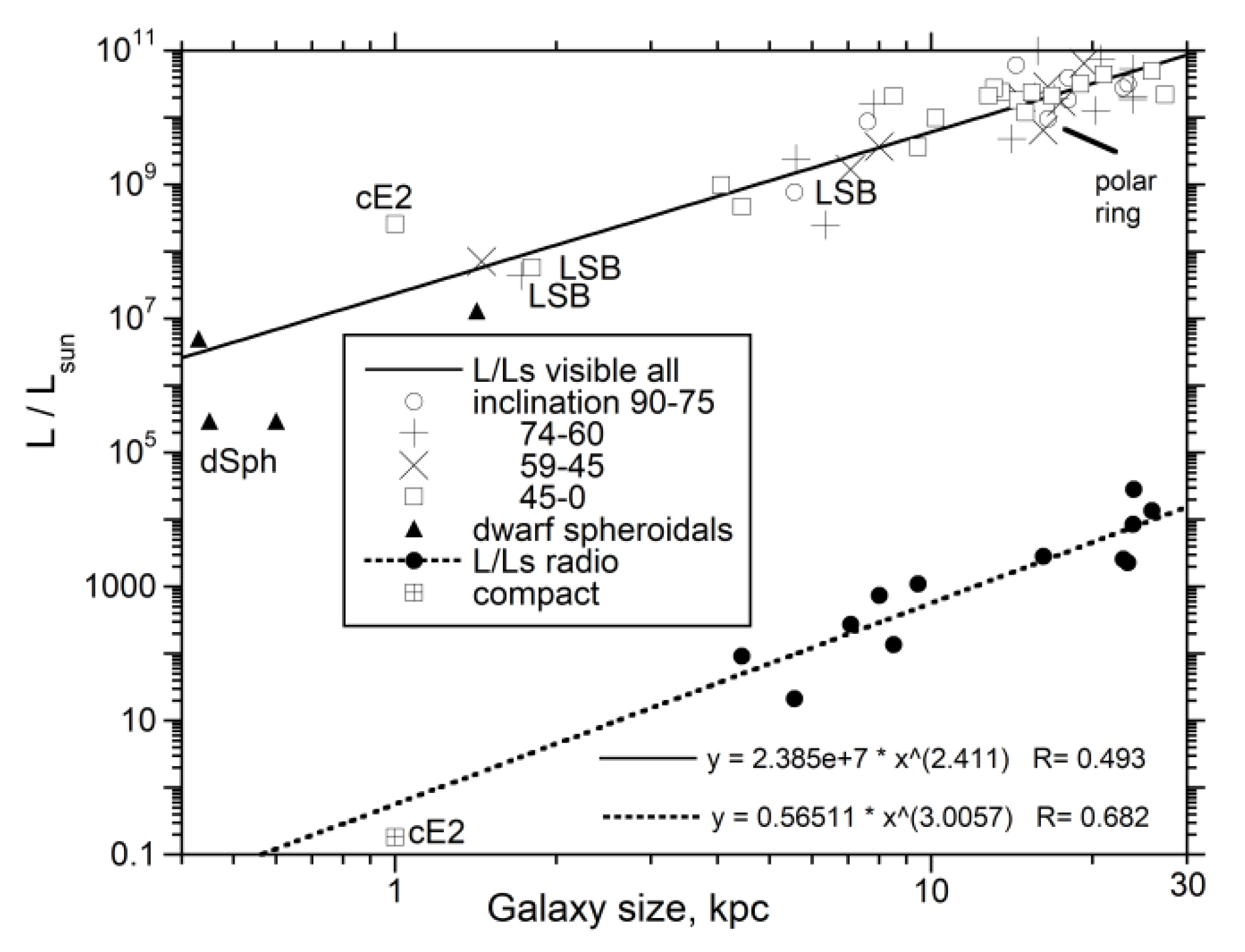
4.4. Relationships of Extracted Parameters with Luminosity
4.5. Non-Baryonic or Non-Luminous Matter?
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A



References
- Kellogg, O.D. Foundations of Potential Theory; Dover Publications: New York, NY, USA, 1953. [Google Scholar]
- Schmidt, M. A model of the distribution of mass in the galactic system. Bul. Astron. Inst. Neth. 1956, 13, 15. [Google Scholar]
- McCarthy, J.E.; Yu Backhaus, E.; Fajans, J. Solving Poisson’s equation with interior conditions. J. Math. Phys. 1998, 239, 6720. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E.; Criss, E.M. Verified solutions for the gravitational attraction to an oblate spheroid: Implications for planet mass and satellite orbits. Planet. Space Sci. 2018, 152, 68–81. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. The physics of galactic spin. Can. J. Phys. 2017, 95, 156–166. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Implications of geometry and the theorem of Gauss on Newtonian gravitational systems and a caveat regarding Poisson’s equation. Galaxies 2017, 5, 89–100. [Google Scholar] [CrossRef]
- Halliday, D.; Resnick, R. Physics; John Wiley and Sons: New York, NY, USA, 1966. [Google Scholar]
- Diaz, R.A.; Herrera, W.J.; Martinez, R. Moments of inertia for solids of revolution and variational methods. Eur. J. Phys. 2006, 27, 183–192. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Spatial and symmetry constraints as the basis of the Virial Theorem and astrophysical implications. Can. J. Phys. 2016, 94, 380–388. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K. Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 1970, 159, 379–403. [Google Scholar] [CrossRef]
- Faber, S.M.; Gallagher, J.S. Masses and mass-to-light ratios of galaxies. Ann. Rev. Astron. Astrophys. 1979, 17, 135–187. [Google Scholar] [CrossRef]
- Dehnen, W.; Binney, J. Mass models of the Milky Way. Mon. Not. R. Astron. Soc. 1998, 294, 429–438. [Google Scholar] [CrossRef]
- Ibata, R.; Lewis, G.F.; Martin, N.F.; Bellazzini, M.; Correnti, M. Does the Sagittarius stream constrain the Milky Way halo to be triaxial? Astrophys. J. Lett. 2013, 765, L155. [Google Scholar] [CrossRef]
- Kam, Z.S.; Carignan, C.; Chemin, L.; Amram, P.; Epinat, B. Kinematics and mass modelling of M33, Hα observations. Mon. Not. R. Astron. Soc. 2015, 449, 4048–4070. [Google Scholar] [CrossRef]
- Fuks, D.B.; Tabachnikov, S. Mathematical Omnibus: Thirty Lectures on Classic Mathematics; American Mathematical Society: Providence, RI, USA, 2007; pp. 417–418. [Google Scholar]
- Doglioni, C.; Panza, G. Polarized plate tectonics. Adv. Geophys. 2015, 56, 1–167. [Google Scholar]
- Zhang, J.; Song, X.; Li, Y.; Richards, P.; Sun, X.; Waldhauser, F. Inner core differential motion confirmed by earthquake waveform doublets. Science 2005, 309, 1357–1359. [Google Scholar] [CrossRef] [PubMed]
- Criss, R.E. Analytics of planetary rotation: Improved physics with implications for the shape and super-rotation of Earth’s Core. Earth Sci. Rev. 2019, 192, 471–479. [Google Scholar] [CrossRef]
- Dufton, P.L.; Dunstall, P.R.; Evans, C.J.; Brott, I.; Cantiello, M.; de Koter, A.; de Mink, S.E.; Fraser, M.; Hénault-Brunet, V.; Howarth, I.D.; et al. The VLT-FLAMES tarantula survey: The fastest rotating O-type star and shortest period LMC pulsar—Remnants of a supernova disrupted binary? Astrophys. J. 2011, 743, L22:1–L22:6. [Google Scholar] [CrossRef][Green Version]
- Todhunter, I. A History of the Mathematical Theories of Attraction and Figure of the Earth; MacMillan and Co.: London, UK, 1873; reprinted in Dover Publications: New York, NY, USA, 1962. [Google Scholar]
- Wiegert, T.; Irwin, J.; Miskolczi, A.; Schmidt, P.; Carolina Mora, S.; Damas-Segovia, A.; Stein, Y.; English, J.; Rand, R.J.; Santistevan, I. CHANG-ES. IV. Radio continuum emission of 35 edge-on galaxies observed with the Karl G. Jansky very large array in D configuration—Data release 1. Astronom. J. 2015, 150, 81. [Google Scholar] [CrossRef]
- CHANG-ES Continuum Halos in Nearby Galaxies- and EVLA Survey. Available online: http://www.queensu.ca/changes (accessed on 26 January 2020).
- NASA/IPAC Extragalactic Database. Available online: https://ned.ipac.caltech.edu/ (accessed on 1 December 2015).
- Carignan, C. Light and mass distribution of the magellanic-type spiral NGC 3109. Astrophys. J. 1985, 299, 59–73. [Google Scholar] [CrossRef]
- Jarrett, T.H.; Chester, T.; Cutri, R.; Schneider, S.E.; Huchra, J.P. The 2MASS Large Galaxy Atlas. Astron. J. 2003, 125, 525–554. [Google Scholar] [CrossRef]
- Gadotti, D.A.; Sánchez-Janssen, R. Surprises in image decomposition of edge-on galaxies: Does Sombrero have a (classical) bulge? Mon. Not. R. Ast. Soc. 2012, 423, 877. [Google Scholar] [CrossRef]
- Criss, R.E.; Hofmeister, A.M. Galactic density and evolution based on the virial theorem, energy minimization, and conservation of angular momentum. Galaxies 2018, 6, 115–135. [Google Scholar] [CrossRef]
- Moulton, F.R. An Introduction to Celestial Mechanics; MacMillan: New York, NY, USA, 1914. [Google Scholar]
- Burbidge, E.M.; Burbidge, G.R.; Prendergast, K.H. The rotation and mass of NGC 2146. Astrophys. J. 1959, 130, 739–748. [Google Scholar] [CrossRef]
- Emden, R. Gaskuglen—Anwendungen de Mechanischen Wärmetheorie; Teubner, B.G.: Leipzig, Germany, 1907. [Google Scholar]
- Romanowsky, A.J.; Douglas, N.G.; Arnaboldi, M.; Kuijken, K.; Merrifield, M.R.; Napolitano, N.R.; Capaccioli, M.; Freeman, K. A dearth of dark matter in ordinary elliptical galaxies. Science 2003, 301, 1696–1698. [Google Scholar] [CrossRef]
- LeDrew, G. The real starry sky. J. R. Astron. Soc. Can. 2011, 95, 322–324. [Google Scholar]
- Luyten, W.J. A new determination of the luminosity function. Mon. Not. R. Astron. Soc. 1968, 139, 221–224. [Google Scholar] [CrossRef][Green Version]
- Ferrière, K. The interstellar environment of our galaxy. Rev. Mod. Phys. 2011, 73, 1031. [Google Scholar] [CrossRef]
- Fang, T.; Buote, D.A.; Humphrey, P.J.; Canizares, C.R.; Zappacosta, L.; Maiolino, R.; Tagliaferri, G.; Gastaldello, F. Confirmation of X-ray absorption by warm-hot intergalactic medium in the Sculptor wall. Astrophys. J. 2010, 714, 1715–1724. [Google Scholar] [CrossRef]
- Outer Space. Available online: https://en.wikipedia.org/wiki/Outer_space (accessed on 1 January 2016).
- Craig, I.J.D.; Brown, J.C. Inverse Problems in Astronomy; Adam Hilger Ltd.: Bristol, UK, 1986. [Google Scholar]
- Groetsch, C.W. Inverse Problems: Activities for Undergraduates; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ambartsumian, V. On the derivation of the frequency function of space velocities of the stars from the observed radial velocities. Mon. Not. Roy. Astron. Soc. 1936, 96, 172. [Google Scholar] [CrossRef]
- Sofue, Y.; Reuter, H.-P.; Krause, M.; Wielebinski, R.; Nakai, N. Peculiar rotations of molecular gas in M82—Keplerian disk and slowly rotating halo. Astrophys. J. 1992, 395, 126. [Google Scholar] [CrossRef]
- Swaters, R.A.; Sancisi, R.; van der Hulst, J.M. The H I Halo of NGC 891. Astrophys. J. 1997, 491, 140. [Google Scholar] [CrossRef]
- Forbes, D.A.; Cortesi, A.; Pota, V.; Foster, C.; Romanowsky, A.J.; Merrifield, M.R.; Brodie, J.P.; Strader, J.; Coccato, L.; Napolitano, N. Radially extended kinematics in the S0 galaxy NGC 2768 from planetary nebulae, globular clusters and starlight. Mon. Not. R. Astron. Soc. 2012, 426, 975. [Google Scholar] [CrossRef]
- Finkelman, I.; Funes, J.G.; Brosch, N. Polar ring galaxies in the Galaxy Zoo. Mon. Not. Royal Ast. Soc. 2012, 422, 2386–2398. [Google Scholar] [CrossRef][Green Version]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Velázquez, J.J.L. Singularity formation for the Stephan problem. In Partial Differential Equations: Theory and Numerical Solution; Necas, J., Jager, W., Stara, J., John, O., Najzar, K., Eds.; Chapman and Hall: Boca Raton, FL, USA, 2000; pp. 312–335. [Google Scholar]
- Arnold, V.I.; Kozlov, V.V.; Neishtadt, A.I. Mathematical Aspects of Classical and Celestial Mechanics; Springer: Berlin, Germany, 2006. [Google Scholar]
- Sofue, Y.; Rubin, V.C. Rotation curves of spiral galaxies. Ann. Rev. Astron. Astrophys. 2001, 39, 137–174. [Google Scholar] [CrossRef]
- Wiegert, T.; English, J. Kinematic classification of non-interacting spiral galaxies. New Astron. 2014, 26, 40–61. [Google Scholar] [CrossRef]
- Sersic, J.L. Extragalactic Astronomy. In Geophysics and Astrophysics Monographs, v. 20; D. Reidel Publishing Co.: Dordrecht, The Netherlands, 1982; p. 61. [Google Scholar]
- Marr, J.H. Galaxy rotation curves with lognormal density distribution. Mon. Not. R. Astron. Soc. 2015, 448, 3229–3241. [Google Scholar] [CrossRef]
- Brandt, J.C. On the distribution of mass in galaxies. I. The large-scale structure of ordinary spirals with applications to M31. Astrophys. J. 1960, 131, 293–303. [Google Scholar] [CrossRef]
- Lambas, D.G.; Maddox, S.J.; Loveday, J. On the true shapes of galaxies. Mon. Not. Roy. Astron. Soc. 1992, 258, 404. [Google Scholar] [CrossRef]
- Sofue, Y.; Koda, J.; Nakanishi, H.; Onodera, S. The Virgo high-resolution CO survey, II. Rotation curves and dynamical mass distributions. Publ. Astron. Soc. Jpn. 2003, 55, 59–74. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.-H.; Kennicutt, R.C., Jr. High-resolution rotation curves and galaxy mass models from THINGS. Astrophys. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- Howley, K.M.; Guhathakurta, P.; van der Marel, R.; Geha, M.; Kalirai, J.; Yniguez, B.; Kirby, E.; Cuillandre, J.-C.; Gilbert, K. Internal stellar kinematics of M32 from the SPLASH survey, dark halo constraints. Astrophys. J. 2013, 765, 65. [Google Scholar] [CrossRef]
- Redshift Independent Distances (NED-D). Available online: https://ned.ipac.caltech.edu/Library/Distances/ (accessed on 31 January 2020).
- Sofue, Y. Mass distribution and rotation curve in the galaxy. In Planets, Stars and Stellar Systems; Gilmore, G., Ed.; Springer: New York, NY, USA, 2013; p. 985. [Google Scholar]
- Sofue, Y. Rotation curve and mass distribution in the galactic center—From black hole to entire galaxy. Pub. Astron. Soc. Japan 2013, 65, 118. [Google Scholar] [CrossRef]
- Sofue, Y. Dark halos of M 31 and the Milky Way. Publ. Astron. Soc. Jpn. 2015, 67, 759. [Google Scholar] [CrossRef]
- Watkins, L.L.; Van Der Marel, R.P.; Sangmo, S.T.; Evans, N.W. Evidence for an intermediate-mass Milky Way from Gaia DR2 halo globular cluster motions. Astrophys. J. 2019, 873, 118. [Google Scholar] [CrossRef]
- Noordermeer, E.; van der Hulst, J.M.; Sancisi, R.; Swaters, R.S.; van Albada, T.S. The mass distribution in early-type disc galaxies, declining rotation curves and correlations with optical properties. Mon. Not. R. Astron. Soc. 2007, 376, 513–546. [Google Scholar] [CrossRef]
- Roelfsema, P.R.; Allen, R.J. Radio observations of H I in UGC 2885, the largest identified SC galaxy. Astron. Astrophys. 1985, 146, 213–222. [Google Scholar]
- Greco, J.P.; Martini, P.; Thompson, T.A. Measurement of the mass and stellar population distribution in M82 with the LBT. Astrophys. J. 2012, 757, 24. [Google Scholar] [CrossRef]
- Bottema, R.; Pestaña, J.L.G. The distribution of dark and luminous matter inferred from extended rotation curves. Mon. Not. R. Astron. Soc. 2015, 448, 2566–2593. [Google Scholar] [CrossRef]
- Sofue, Y. Galaxy, ISM, and Radio Astronomy. Available online: http//www.ioa.s.u-tokyo.ac.jp/~sofue/ (accessed on 15 June 2015).
- Sofue, Y.; Tutui, Y.; Honma, M.; Tomita, A.; Takamiya, T.; Koda, J.; Takeda, Y. Central rotation curves of spiral galaxies. Astrophys. J. 1999, 523, 136–146. [Google Scholar] [CrossRef]
- Pavlovich, K.; Pavlovich, A.; Sipols, A. Newtonian explanation of galaxy rotation curves based on distribution of baryonic matter. arXiv 2014, arXiv:1406.2401P. [Google Scholar]
- Rix, H.-W.; de Zeeuw, P.T.; Cretton, N.; van der Marel, R.P.; Carollo, C.M. Dynamical modeling of velocity profiles, the dark halo around the elliptical galaxy NGC 2434. Astrophys. J. 1997, 488, 702. [Google Scholar] [CrossRef][Green Version]
- Hlavacek-Larrondo, J.; Carignan, C.; Daigle, O.; de Denus-Baillargeon, M.-M.; Marcelin, M.; Epinat, B.; Hernandez, O. Deep H alpha observations of NGC 253, a very extended and possibly declining rotation curve? Mon. Not. R. Ast. Soc. 2011, 411, 71–84. [Google Scholar] [CrossRef]
- Corbelli, E.; Salucci, P. The extended rotation curve and the dark matter halo of M33. Mon. Not. R. Ast. Soc. 2000, 311, 441–447. [Google Scholar] [CrossRef]
- Jardel, J.R.; Gebhardt, K.; Shen, J.; Fisher, D.B.; Kormendy, J.; Kinzler, J.; Lauer, T.R.; Richstone, D.; Gültekin, K. Orbit-based dynamical models of the Sombrero galaxy (NGC 4594). Astrophys. J. 2011, 739, 21. [Google Scholar] [CrossRef]
- Kormendy, J.; Westphal, D.J. Noncircular gas velocities and the radial dependence of mass-to-light ratio in NGC 4594 (the Sombrero Galaxy). Astrophys. J. 1989, 338, 752–760. [Google Scholar] [CrossRef]
- Leaman, R.; Venn, K.A.; Brooks, A.M.; Battaglia, G.; Cole, A.A.; Ibata, R.A.; Irwin, M.J.; McConnachie, A.W.; Mendel, J.T.; Tolstoy, E. The resolved structure and dynamics of an isolated dwarf galaxy, A VLT and Keck spectroscopic survey of WLM. Astrophys. J. 2012, 750, 33. [Google Scholar] [CrossRef]
- Oh, S.-H.; de Blok, W.J.G.; Walter, F.; Brinks, E.; Kennicutt, R.C., Jr. High-resolution dark matter density profiles of THINGS dwarf galaxies, correcting for noncircular motions. Astron. J. 2008, 136, 2761–2781. [Google Scholar] [CrossRef]
- Salucci, P.; Wilkinson, M.I.; Walker, M.G.; Gilmore, G.F.; Grebel, E.K.; Koch, A.; Frigerio Martins, C.; Wyse, R.F.G. Dwarf spheroidal galaxy kinematics and spiral galaxy scaling laws. Mon. Not. R. Ast. Soc. 2012, 420, 2034. [Google Scholar] [CrossRef]
- Walker, M.G.; Mateo, M.; Olszewski, E.W.; Gnedin, O.Y.; Wang, X.; Sen, B.; Woodroofe, M. Velocity dispersion profiles of seven dwarf spheroidal galaxies. Astrophys. J. 2007, 667, L53. [Google Scholar] [CrossRef]
- Walker, M.G.; Mateo, M.; Olszewski, E.W. Stellar velocities in the Carina, Fornax, Sculptor, and Sextans dSph galaxies, data from the Magellan/MMFS survey. Astronom. J. 2009, 137, 3100. [Google Scholar] [CrossRef]
- Mateo, M.; Olszewski, E.W.; Walker, M.G. The velocity dispersion profile of the remote dwarf spheroidal galaxy Leo I, A tidal hit and run? Astrophys. J. 2008, 675, 20. [Google Scholar] [CrossRef]
- Toloba, E.; Guhathakurta, P.; Peletier, R.F.; Boselli, A.; Lisker, T.; Falcón-Barroso, J.; Simon, J.D.; van de Ven, G.; Paudel, S.; Emsellem, E.; et al. Stellar kinematics and structural properties of Virgo cluster dwarf early-type galaxies from the SMAKCED Project. II. The survey and a systematic analysis of kinematic anomalies and asymmetries. Astrophys. J. Suppl. 2014, 215, 17. [Google Scholar] [CrossRef]
- Iodice, E.; Coccato, L.; Combes, F.; de Zeeuw, T.; Arnaboldi, M.; Weilbacher, P.M.; Bacon, R.; Kuntschner, H.; Spavone, M. Mapping the inner regions of the polar disk galaxy NGC 4650A with MUSE. Astron. Astrophys. 2015, 583, A48. [Google Scholar] [CrossRef][Green Version]
- Honma, M.; Nagayama, T.; Ando, K.; Bushimata, T.; Choi, Y.K.; Handa, T.; Hirota, T.; Imai, H.; Jike, T.; Kim, M.K.; et al. Fundamental parameters of the Milky Way Galaxy based on VLBI astrometry. Pub. Astr. Soc. Japan 2012, 64, 136. [Google Scholar] [CrossRef]
- Nakanishi, H.; Sakai, N.; Kurayama, T.; Matsuo, M.; Imai, H.; Burns, R.A.; Ozawa, T.; Honma, M.; Shibata, K.; Kawaguchi, N. Outer rotation curve of the Galaxy with VERA. II. Annual parallax and proper motion of the star-forming region IRAS 21379+5106. Pub. Astr. Soc. Jpn. 2015, 67, 6813. [Google Scholar] [CrossRef]
- Mateo, M.L. Dwarf galaxies of the Local Group. Ann. Rev. Astron. Astrophys. 1998, 36, 435–506. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Pflamm-Altenburg, J.; Kroupa, P. The VPOS: A vast polar structure of satellite galaxies, globular clusters and streams around the Milky Way. Mon. Not. R. Ast. Soc. 2012, 423, 1109–1126. [Google Scholar] [CrossRef]
- Bureau, M.; Carignan, C. Environment, RAM pressure, and shell formation in Holmberg II. Astron. J. 2002, 123, 1316. [Google Scholar] [CrossRef]
- Khoperskov, S.A.; Moiseev, A.V.; Khoperskov, A.V.; Saburova, A.S. To be or not to be oblate: The shape of the dark matter halo in polar ring galaxies. Mon. Not. R. Ast. Soc. 2014, 441, 2650–2662. [Google Scholar] [CrossRef]
- Lehner, N.; Howk, J.C.; Wakker, B.P. Evidence for a massive, extended circumgalactic medium around the Andromeda galaxy. Astrophys. J. 2015, 804, 79. [Google Scholar] [CrossRef]
- Boroson, T. The distribution of luminosity in spiral galaxies. Astrophys. J. Supp. 1981, 46, 177. [Google Scholar] [CrossRef]
- Sparke, L.S.; Gallagher, J.S. Galaxies in the Universe; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Zombeck, M.V. Handbook of Space Astronomy and Astrophysics; Cambridge Univ. Press: Cambridge, UK, 2007. [Google Scholar]
- Disney, M.J.; Romano, J.D.; Garcia-Appadoo, D.A.; West, A.A.; Dalcanton, J.J.; Cortese, L. Galaxies appear simpler than expected. Nature 2008, 455, 1082–1084. [Google Scholar] [CrossRef] [PubMed]
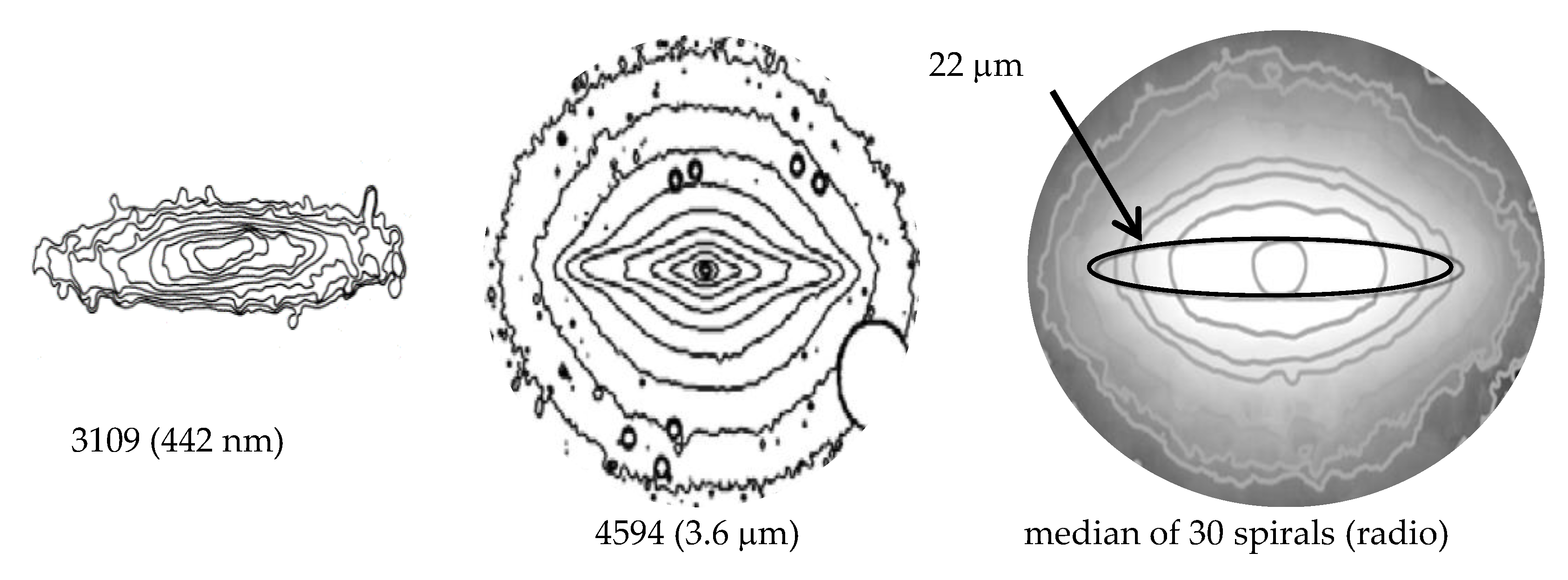

| Density | |||
|---|---|---|---|
| Object or Region | kg m−3 | Msun pc−3 | H Atoms cm−3 |
| Dispersed Solar System 1 | 5.2×10−9 | 8×1010 | 1012 |
| Molecular Cloud Core | 2×10−15 | 30,000 | >106 |
| Globular Cluster Core | 7×10−18–10−16 | ~100–1500 | 0.4–6×104 |
| Best Laboratory Vacuum | 10−17 | 150 | 6×103 |
| Globular Cluster | ~7×10−18 | ~0.5 | ~4200 |
| Giant Molecular Cloud | ~10−18 | ~15 | ~600 |
| Solar Neighborhood 2 | ~3×10−21 | ~0.04 | ~2 |
| Interstellar Medium 3 | ~10−21 | ~0.02 | ~0.6 |
| Intergalactic Medium 4 | ~5×10−26 | ~7×10−7 | ~3×10−5 |
| Baryons in Universe 5 | ~10−26 | ~10−7 | ~6×10−6 |
| Type | Input | Physical Model | Output |
|---|---|---|---|
| Forward | density and shape 2 | Newtonian orbits | RC fits |
| Forward | density in a disk-like shape | MOND 3 | RC fits |
| Inverse | RC and c/a data | Virial theorem 4 | density vs. radius |
| Shape or Type 1 | Object | c/a1 | Ellipticity | Arcsin(e)/e |
|---|---|---|---|---|
| Sphere | NGC 2434, 4494 | 1 | 0 | 1.0000 |
| E1 | NGC 3379 | 0.98 | 0.2 | 1.0068 |
| cE2, spheroidal | M32; WLM 2 | 0.87 | 0.49 | 1.0451 |
| S0 | UGC 3993 | 0.75 | 0.66 | 1.0921 |
| E6 | NGC 2768, 4431 | 0.52 | 0.85 | 1.1953 |
| Sombrero | NGC 4594 | 0.4 | 0.917 | 1.2655 |
| Irregular | NGC 3034 | 0.38 | 0.925 | 1.2768 |
| S0/a | NGC 7286 | 0.36 | 0.93 | 1.2843 |
| Flat oblate | All other spirals 3 | 0.1 | 0.995 | 1.4781 |
| Infinite oblate | Limiting value | ~0 | 1 | 1.5708 |
| NGC | Other Name | Type | Notes | Refs. | Distance (Mpc) | Lvis (LSun,vis) | L211 (LSun,21) | Edge 2 (kpc) |
|---|---|---|---|---|---|---|---|---|
| Well-Studied Spirals | ||||||||
| - | Milky Way | SBc | inside view | [57,58] | 4×1010 | 18 | ||
| 224 | Andromeda | SA(s)b | nearby, bulge | [59] | 0.78 | 3.19×1010 | 2300 | 23.3 |
| 253 | SAB(s)c | starburst | [69] | 3.16 | 1.88×1010 | 18 | ||
| 598 | Triangulum | SA(s)cd | no bulge | [14,70] | 0.84 | 3.65×109 | 1110 | 9.45 |
| 925 | SAB(s)d | large H cloud | [54] | 8.6 | 6.50×109 | 2830 | 16.2 | |
| 2599 | UGC 4458 | SAa | high velocity | [61] | 64.2 | 5.01×1010 | 13,800 | 25.8 |
| 3034 | M82 | I0, edge-on3 | starburst | [63] | 4.01 | 8.81×109 | 7.6 | |
| 4594 | Sombrero | SA(s)a | huge bulge | [71,72] | 10.0 | 6.10×1010 | 14.4 | |
| 4826 | M64-Evil Eye | (R)SA(rs)ab | counter rotating | [54] | 5.16 | 1.60×1010 | 7.8 | |
| 7793 | SA(s)d | jets, bulge | [54] | 3.93 | 3.70×109 | 739 | 8.0 | |
| - | UGC 2855 | SABc | distant | [62,67] | 79 | 9.90×1010 | 15.8 | |
| Spirals with Desirable Characteristics | ||||||||
| 1560 | SA(s)d | LSB, edge on | [64] | 3.28 | 7.80×108 | 21.5 | 5.56 | |
| 2403 | SAB(s)cd | bright in HII | [66] | 3.48 | 4.81×109 | 14.15 | ||
| 2841 | SA(r)b | LINER, bulge | [66] | 17.6 | 7.43×1010 | 20.73 | ||
| 2903 | SAB(rs)bc | starburst | [66] | 8.70 | 2.15×1010 | 16.8 | ||
| 3109 | SB(s)m | small, edge on | [64] | 1.33 | 2.51×108 | 6.35 | ||
| 3198 | SB(rs)c | psuedobulge | [65] | 14.0 | 1.28×1010 | 20.3 | ||
| 4789a | DDO 154 | IB(s)m | LSB, dwarf | [64] | 3.84 | 4.40×107 | 1.72 | |
| 5585 | SAB(s)d | psuedobulge | [64] | 8.0 | 1.71×109 | 277 | 7.07 | |
| 6503 | SA(s)cd | LINER | [64] | 5.52 | 2.42×109 | 6.42 | ||
| 7331 | SA(s)b | bulge | [66] | 14.3 | 5.32×1010 | 28,300 | 23.84 | |
| Messier Spirals | ||||||||
| 1068 | M77 | (R)SA(rs)b | Seyfert | [66] | 12.65 | 2.94×1010 | 16.5 | |
| 3031 | M81 | SA(s)ab | grand design | [66] | 3.71 | 2.04×1010 | 14.7 | |
| 4192 | M98 | SAB(s)ab | active nucleus | [53] | 15.61 | 2.05×1010 | 8620 | 23.8 |
| 4254 | M99 | SA(s)c | star forming | [53] | 15.43 | 2.44×1010 | 13.5 | |
| 4258 | M106 | SAB(rs)bc | LINER | [66] | 7.46 | 1.87×1010 | 23.8 | |
| 4303 | M61 | SAB(rs)bc | supernovae | [66] | 12.0 | 1.83×1010 | 14.5 | |
| 4321 | M100 | SAB(s)bc | grand design | [66] | 16.56 | 4.46×1010 | 21.0 | |
| 4501 | M88 | SA(rs)b | Seyfert | [53] | 18.79 | 6.50×1010 | 19.3 | |
| 4548 | M91 | SB(rs)b | LINER | [53] | 16.36 | 2.78×1010 | 13.1 | |
| 4569 | M90 | SAB(rs)ab | LINER | [66] | 12.29 | 1.93×1010 | 17.0 | |
| 4736 | M94 | (R)SA(r)ab | LINER, ring | [66] | 5.02 | 9.85×109 | 10.2 | |
| 5055 | M63 Sunflower | SA(rs)bc | flocculent | [66] | 8.0 | 1.73×1010 | 17.5 | |
| 5194 | M51 Whirlpool | SABc | has companion | [66] | 7.85 | 2.14×1010 | 12.8 | |
| 5236 | M83 | SAB(s)c | two nuclei | [66] | 4.8 | 3.20×1010 | 19.0 | |
| 5457 | M101 Pinwheel | SAB(rs)cd | star forming | [66] | 6.81 | 2.22×1010 | 27.3 | |
| Dwarf Irregular and Spheroidal Galaxies | ||||||||
| - | WLM | Ib(s)m | isolated LSB | [73] | 0.985 | 5.83×107 | 1.8 | |
| - | M81dWb | Im | star forming | [74] | 7.66 | 7.13×107 | 1.45 | |
| - | Holmberg II | Im | star forming | [74] | 3.30 | 4.70×108 | 92.4 | 4.43 |
| - | Carina | dSph, dE3 | classical dSph | [75,76,77,78] | 0.103 | 2.95×105 | 0.45 | |
| - | Draco | dSph, Epec | classical dSph | [75,76,77,78] | 0.082 | 2.95×105 | 0.60 | |
| - | Fornax | dSph, dE4 | classical dSph | [75,76,77,78] | 0.139 | 1.30×107 | 1.42 | |
| - | Leo I | dSph, dE3 | classical dSph | [75,76,77,78] | 0.246 | 4.99×106 | 0.43 | |
| Lenticular and Elliptical Galaxies | ||||||||
| - | UGC3993 | S0? | bulge | [61] | 62 | 1.21×1010 | 15 | |
| 7286 | UGC12043 | S0/a | no bulge | [61] | 20.5 | 2.45×109 | 5.6 | |
| 2768 | S0-E6 edge | Seyfert, jets | [42] | 19.3 | 2.80×1010 | 2570 | 22.8 | |
| 3379 | M105 | E1 | elliptical | [31] | 11.0 | 2.11×1010 | 138 | 8.5 |
| 2434 | E0-1 | elliptical | [68] | 26.9 | 2.38×1010 | 15.4 | ||
| 221 | M32 | cE2 | compact dwarf | [55] | 0.775 | 2.61×108 | 0.183 | 1.0 |
| 4431 | VCC1010 | dE, SA0(r) | dwarf elliptical | [79] | 16 | 9.87×108 | 4.06 | |
| Polar Ring or Disk Galaxies | ||||||||
| 4560A | The prototype | S0/a pec? | 2 ⊥ disks | [80] | 46.4 | 9.67×109 | 16.5 | |
| Visible Edge Properties | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name | Min (MSun) | Lvis/Min (LSun/MSun) | Density (kg m−3) | rturndown (kpc) | Lowest ρ (kg m−3) | ρ at 0.1 kpc (kg m−3) | Highest ρ (kg m−3) | Power 1 | rmax (kpc) | Mmax (MSun) |
| Large Well-Studied Spirals | ||||||||||
| Milky Way | 1.21×1011 | 0.330 | 1.30×10−21 | 18–30 | 1.0×10−24 | 1.00×10−17 | 1.00×10−14 | −2.06 | 230 | 1.03×1012 |
| 224 | 1.44×1011 | 0.222 | 4.20×10−22 | ? | 2.0×10−24 | 4.00×10−17 | 4.00×10−17 | −2.11 | 285 | 7.03×1011 |
| 253 | 4.30×1010 | 0.437 | 1.00×10−21 | ? | 2.8×10−22 | 9.00×10−18 | 7.00×10−17 | −1.5, −2.0 | 12.68 | 6.90×1010 |
| 598 | 1.52×1010 | 0.240 | 1.30×10−21 | ? | 8.0×10−22 | 1.80×10−17 | 1.80×10−17 | −1.57 | 15 | 2.60×1010 |
| 925 | 2.00×1010 | 0.325 | 8.60×10−22 | 13 | 8.6×10−22 | 3.00×10−20 | −0.9 | 13 | 2.03×1010 | |
| 2599 | 1.90×1011 | 0.264 | 3.51×10−22 | 20? | 3.1×10−23 | 3.54×10−17 | 3.54×10−17 | −2.36 | 56 | 3.52×1011 |
| 3034 | 1.00×1010 | 0.881 | 2.20×10−21 | ? | 3.0×10−21 | 3.70×10−18 | 1.00×10−16 | −1.5, −1.9 | 3.57 | 7.20×109 |
| 4594 | 2.00×1011 | 0.305 | 3.30×10−21 | ? | 3.0×10−21 | 8.70×10−18 | 1.60×10−15 | −1.6 | 9.4 | 1.58×1011 |
| 4826 | 1.90×1010 | 0.842 | 4.50×10−21 | 20 | 1.0×10−22 | 1.00×10−17 | 2.00×10−18 | −1.92 | 21.7 | 5.69×1010 |
| 7793 | 8.80×109 | 0.421 | 1.20×10−21 | 6–7 | 5.0×10−23 | 6.40×10−19 | 6.40×10−19 | −1.68 | 6.82 | 8.96×109 |
| UGC 2885 | 1.17×1011 | 0.846 | 1.53×10−21 | 50 | 1.0×10−22 | 2.80×10−18 | 2.80×10−18 | −1.5 | 74.7 | 3.00×1011 |
| Spirals with Desirable Characteristics | ||||||||||
| 1560 | 2.80×109 | 0.279 | 1.40×10−21 | 6 | 4.0×10−22 | 9.90×10−20 | 2.60×10−19 | −1.0 | 8.6 | 5.40×109 |
| 2403 | 2.90×1010 | 0.166 | 5.20×10−22 | 17 | 1.1×10−22 | 3.20×10−18 | 9.20×10−18 | −1.74 | 19.6 | 3.90×1010 |
| 2841 | 1.70×1011 | 0.437 | 8.02×10−22 | 12 | 5.0×10−23 | 4.00×10−17 | 2.85×10−17 | −2.03 | 74 | 5.90×1011 |
| 2903 | 6.70×1010 | 0.321 | 6.30×10−22 | 28 | 5.0×10−25 | 1.10×10−17 | 1.10×10−17 | −2.12 | 30 | 1.17×1011 |
| 3109 | 2.99×108 | 0.839 | 8.00×10−22 | 5.6 | 7.0×10−22 | 5.00×10−20 | 1.80×10−20 | −0.86 | 6.62 | 3.08×109 |
| 3198 | 6.00×1010 | 0.213 | 3.26×10−22 | 43 | 1.4×10−23 | 5.50×10−18 | 3.90×10−18 | −1.85 | 46.4 | 1.19×1011 |
| 4789a | 1.88×108 | 0.234 | 3.90×10−21 | 4.8 | 3.0×10−23 | 2.00×10−19 | 5.00×10−20 | −1.41 2 | 7.40 | 1.97×109 |
| 5585 | 5.90×109 | 0.290 | 1.01×10−21 | - | 6.0×10−22 | 4.12×10−19 | 5.50×10−19 | −1.39 | 10 | 9.00×109 |
| 6503 | 9.58×109 | 0.253 | 1.84×10−21 | 17 | 1.2×10−22 | 1.10×10−17 | 2.20×10−19 | −2.09 | 19 | 2.9×1010 |
| 7331 | 1.47×1011 | 0.362 | 8.70×10−22 | 30 | 2.5×10−23 | 9.00×10−18 | 1.70×10−17 | −1.89 | 31.6 | 1.98×1011 |
| Messier Spirals | ||||||||||
| 1068 | 5.00×1010 | 0.588 | 3.00×10−21 | - | 3.0×10−20 | 1.22×10−17 | 1.22×10−17 | −1.53 | 5.09 | 4.29×1010 |
| 3031 | 5.60×1010 | 0.364 | 4.50×10−22 | - | 9.3×10−24 | 6.70×10−18 | 9.60×10−18 | −2.0 | 23 | 7.00×1010 |
| 4192 | 9.00×1010 | 0.228 | 1.20×10−21 | ? | 6.0×10−22 | 1.66×10−17 | 2.70×10−17 | −1.74 | 17.7 | 8.65×1010 |
| 4254 | >2x1010 | <1 | ~5x10−21 | - | ~2x10−21 | 3.00×10−18 | 3.00×10−17 | −1.4 | 1.9 | 4.50×109 |
| 4258 | 1.10×1011 | 0.170 | 2.50×10−22 | 24 | 6.3×10−23 | 2.38×10−17 | 6.00×10−16 | −2.09 | 33.4 | 1.33×1011 |
| 4303 | 3.68×1010 | 0.497 | 6.81×10−22 | - | 5.0×10−22 | 2.44×10−17 | 5.00×10−17 | −1.96 | 18.6 | 5.00×1010 |
| 4321 | 1.68×1011 | 0.265 | 8.80×10−22 | 22 | 1.7×10−23 | 3.57×10−17 | 6.70×10−17 | −2.00 | 23.3 | 1.80×1011 |
| 4501 | 2.00×1011 | 0.325 | 4.80×10−21 | - | 6.8×10−21 | 1.36×10−17 | 3.60×10−17 | −1.46 | 8.32 | 9.54×1010 |
| 4548 | 3.80×1010 | 0.732 | 3.20×10−22 | - | 1.5×10−21 | 2.40×10−17 | 3.50×10−17 | −2.57 | 8.39 | 3.33×1010 |
| 4569 | 9.00×1010 | 0.214 | 2.20×10−21 | - | 3.7×10−21 | 3.78×10−17 | 6.39×10−17 | −1.55 | 11.8 | 8.27×1010 |
| 4736 | 1.77×1010 | 0.556 | 1.40×10−21 | 6.3 | 1.7×10−22 | 2.90×10−17 | 2.90×10−17 | −2.12 | 6.55 | 2.14×1010 |
| 5055 | 7.07×1010 | 0.245 | 5.21×10−22 | 16.5 | 2.4×10−23 | 1.25×10−17 | 2.63×10−17 | −2.19 | 40 | 1.36×1011 |
| 5194 | 4.00×1010 | 0.535 | 1.00×10−22 | 6.5 | 1.0×10−22 | 3.00×10−17 | 7.00×10−17 | −2.1 | 6.51 | 4.32×1010 |
| 5236 | 4.79×1010 | 0.668 | 1.66×10−22 | 19 | 1.0×10−23 | 2.85×10−17 | 4.48×10−16 | −2.42 | 19.90 | 4.83×1010 |
| 5457 | 5.26×1010 | 0.422 | 2.50×10−22 | 9 | 1.7×10−23 | 1.00×10−17 | 1.50×10−17 | −2.10 | 12.90 | 5.29×1010 |
| Dwarf Irregular and Spheroidal Galaxies | ||||||||||
| WLM | 8.63×107 | 0.676 | 9.20×10−23 | 2 | 2.3×10−23 | - | 6.60×10−22 | −1.9 2 | 2.0 | 1.08×108 |
| M81dWb | 7.00×107 | 1.02 | 5.00×10−22 | 0.8 | 4.5×10−22 | 1.87×10−19 | 1.90×10−19 | −2.2 2 | 0.92 | 7.31×107 |
| Holmberg II | 4.28×108 | 1.10 | 3.64×10−22 | 7 | 1.6×10−23 | 1.00×10−19 | 2.20×10−20 | −1.52 | 10.2 | 1.02×109 |
| Carina | 3.38×106 | 0.087 | 6.50×10−22 | - | 1.4×10−22 | 8.70×10−21 | 3.00×10−20 | −1.59 2 | 0.88 | 6.88×106 |
| Draco | 3.40×106 | 0.087 | 7.40×10−22 | 0.5 | 1.3×10−22 | 3.00×10−20 | 3.10×10−20 | −1.58 | 1.78 | 4.10×107 |
| Fornax | 1.24×107 | 1.047 | 3.73×10−23 | 1.4 | 2.0×10−23 | 1.10×10−20 | 2.00×10−20 | −1.56 2 | 1.62 | 1.37×107 |
| Leo I | 7.74×106 | 0.647 | 1.36×10−21 | 0.8 | 1.8×10−22 | 4.40×10−21 | 2.00×10−20 | −0.85 | 0.95 | 1.26×107 |
| Lenticular and Elliptical Galaxies | ||||||||||
| UGC 3993 | 1.78×1011 | 0.068 | 3.10×10−22 | 18? | 4.0×10−23 | 1.00×10−17 | 8.00×10−19 | −2.07 | 54.6 | 5.40×1011 |
| 7286 | 5.90×109 | 0.415 | 4.60×10−22 | ? | 6.0×10−23 | 6.00×10−19 | 7.00×10−20 | −1.71 | 15.7 | 1.77×1010 |
| 2768 | 1.98×1010 | 1.41 | 1.00×10−21 | 10 | 4.0×10−22 | 2.75×10−20 | 2.75×10−20 | −0.61 | 21.8 | 1.96×1010 |
| 3379 | 1.10×1010 | 1.92 | 9.00×10−23 | - | 9.0×10−23 | 3.64×10−18 | 1.10×10−17 | −2.38 | 5.38 | 1.32×1010 |
| 2434 | 5.00×1010 | 0.476 | 1.00×10−22 | - | 5.0×10−22 | 2.95×10−18 | 2.95×10−18 | −2.02 | 8.22 | 4.54×1010 |
| 221 | 2.33×107 | 11.20 | 1.00×10−22 | - | 8.0×10−22 | 6.10×10−20 | 4.20×10−15 | −2.8 | 0.75 | 2.30×107 |
| 4431 | 3.00×109 | 0.33 | 1.30×10−21 | 2.6 | 1.3×10−21 | 3.00×10−20 | 3.00×10−20 | −0.8 2 | 3.68 | 2.88×109 |
| Polar Ring or Disk Galaxies | ||||||||||
| 4650A | 1.90×1010 | 0.51 | 1.0×10−23 | 18 | 1.0×10−22 | 1.28×10−19 | 5.00×10−19 | −0.87 | 13.0 | 1.60×1010 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Criss, R.E.; Hofmeister, A.M. Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves. Galaxies 2020, 8, 19. https://doi.org/10.3390/galaxies8010019
Criss RE, Hofmeister AM. Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves. Galaxies. 2020; 8(1):19. https://doi.org/10.3390/galaxies8010019
Chicago/Turabian StyleCriss, Robert E., and Anne M. Hofmeister. 2020. "Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves" Galaxies 8, no. 1: 19. https://doi.org/10.3390/galaxies8010019
APA StyleCriss, R. E., & Hofmeister, A. M. (2020). Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves. Galaxies, 8(1), 19. https://doi.org/10.3390/galaxies8010019