Abstract
A review is given of a priori predictions made for the dynamics of rotating galaxies. One theory—MOND—has had many predictions corroborated by subsequent observations. While it is sometimes possible to offer post hoc explanations for these observations in terms of dark matter, it is seldom possible to use dark matter to predict the same phenomena.
1. Introduction
The dark matter problem remains unsolved after decades of intensive research. The observational evidence for mass discrepancies in extragalactic systems is overwhelming, but a laboratory detection of dark matter particles is still lacking. While the need for “dark matter” is clear, its existence remains hypothetical.
I place “dark matter” in quotes because the widespread use of this term presupposes the answer. All that is really known is that the application of conventional dynamics to the visible mass distributions of extragalactic systems fails to explain the observed motions. Though this discrepancy is clear and the evidence is abundant [1,2,3], much of this evidence is ambiguous as to whether the cause is unseen mass—literal dark matter—or a failure of the equations that lead to its inference [4,5,6].
At present, the mainstream paradigm (the “normal component”, as Feyerabend called it [7]) is lambda cold dark matter (CDM). This paradigm works if and only if the cold dark matter (CDM) it presupposes is a real, physical substance, and not merely an abstraction that is convenient to cosmic calculations. This has motivated extensive laboratory searches for plausible dark matter candidates [8,9,10]. These remarkable experiments [11,12] have excluded essentially all of the parameter space in which the hypothesized dark matter particles were expected [13] to reside. This provides one motivation for considering ideas outside the normal component, including new dark matter candidates and modified dynamics.
Another motivation arises if a theory makes successful predictions. Novel predictions that provide unique tests of hypotheses are the keystone of the scientific method. The gold standard for scientific predictions are those made in advance of the observation [14]. Here I highlight important a priori predictions made by the modified Newtonian dynamics (MOND) [15,16,17] that meet this gold standard. I also discuss the contemporaneous expectation for dark matter.
I make no attempt to cover all aspects of MOND and the mass discrepancy problem here, as the subject is now vast. More extensive reviews of MOND are provided elsewhere [18,19,20,21,22,23,24], as are reviews of the relevant data [5,6,25,26,27,28]. Here I focus on tests of a priori predictions utilizing the most accurate data that relate to the subject [28,29].
2. Predictions and Tests
General relativity has been tested with extraordinary precision in the solar system [30], and high acceleration systems, such as binary neutron stars [31] and merging black holes [32]. In contrast, it manifestly fails in systems that exhibit mass discrepancies; hence the need for dark matter. Attempts to modify dynamics often start by noting that problem systems—galaxies, clusters of galaxies, and the universe as a whole—are much bigger than the systems where established theory works so well. Consequently, it is tempting to imagine that the force law changes on some length scale so that its effects are imperceptible in the solar system but pronounced in galaxies. This approach immediately runs afoul of the observation that some large galaxies appear to require little dark matter, while some small galaxies evince large discrepancies. Modifications based on a length scale can be generically excluded [4].
Size is not the only scale that sets problematic systems apart from solar system tests of gravity. The typical accelerations of stars in galaxies are of order 1 Å s or less; this is eleven orders of magnitude less than we experience on the surface of the Earth, and many orders of magnitude removed from sensitive solar system probes. MOND [15] hypothesizes a change to the effective force law at low accelerations, . The acceleration scale is empirically determined to be [33]. The value of has been remarkably stable, having not changed meaningfully in decades [34].
As noted in the original publication [15], MOND is not a complete theory that replaces general relativity. Indeed, MOND may be either a modification of gravity (Newton’s universal gravitation) or a modification of the law of inertia (: the inertial mass may differ from the gravitational charge at low accelerations) [15,23]. Perhaps it is only an effective theory that arises for reasons we have yet to imagine. Irrespective of why it happens, strong predictions follow once a force is hypothesized.
MOND contains Newton in the limit of high acceleration: for , the effective acceleration , where is the usual Newtonian gravitational force per unit mass. Everything is “normal” until we reach the regime of low acceleration (); an immediate corollary is that the need for dark matter should never appear at high accelerations. Unique predictions of MOND emerge in the deep MOND regime: for , the effective acceleration becomes . Intriguingly, dynamics become scale invariant in this deep MOND regime [35]. The Newtonian and deep MOND regimes are connected by a theoretically arbitrary but empirically well-constrained interpolation function whose details are only relevant within a factor of a few of . The essence of the idea is captured by the asymptotic limits at high and low accelerations, which is where the important predictions arise.
In the following, I review observational tests of the specific predictions elaborated in Section 8 of [16] that have been subsequently tested.
2.1. Tully–Fisher and the Mass–Asymptotic Speed Relation
“The relation should hold exactly”. —M. Milgrom [16]
One consequence of MOND is a relation between the mass of a galaxy and its rotation speed. One immediately recognizes this mass–asymptotic speed relation (MASR) [23] as the basis of the empirical Tully–Fisher relation [36],
provided that luminosity is a proxy for mass () and line-width is a proxy for rotation speed (). The Tully–Fisher relation provides several tests of MOND.
Testing the MASR requires careful measurement of both the mass and the asymptotic speed.
Many rotation curves are observed to be flat, but it sometimes happens that the observational sensitivity tapers off before the asymptotic rotation speed is obtained. One must therefore take care to test the theory and not just the limits of data quality [28]: the result will differ from the prediction if either of the proxies for mass or are imperfect [37].
The flat rotation velocity measured from resolved rotation curves provides a better proxy for than line-widths. It is still only a proxy, as rotation curves in MOND may approach a constant rotation speed quickly, but may also decline slowly or rise gradually depending on the details of the mass distribution [16]. This morphology is clearly seen in the data [28,38]. Nevertheless, it is often possible1 to measure to within 5% [37,42].
Another important effect is geometric: flattened mass distributions like spiral galaxies rotate faster than the spherically equivalent distribution [43]. The MASR predicts a Tully–Fisher-like relation of the form
where is a factor of order unity that accounts for the flattened geometries of disk galaxies. This can be computed analytically for a razor thin exponential disk (see Equation (16) of [5]), with the result that at four disk scale lengths. For disks of realistic finite thickness, [44]. As a practical matter, this quantity likely has some intrinsic scatter [45], and may vary systematically with mass or morphological type. Systematic variation would affect the slope of the BTFR.
Empirically, the data evince a baryonic Tully–Fisher relation (BTFR) [46]
Here M includes all relevant forms of baryonic mass: stars, their remnants, all phases of interstellar gas, and dust. In practice, the dominant forms of baryonic mass in late type galaxies are stars (including the corresponding remnants) and atomic gas. We estimate the baryonic mass using stellar population models [47,48] to estimate mass-to-light ratios and near-IR luminosities [29,49] in the band of the Spitzer Space Telescope so that . The gas mass is estimated from the atomic gas mass corrected for the hydrogen fraction (see [50]) so that the total baryonic mass is .
The BTFR is equivalent to the MASR if is an adequate proxy for , the slope , and the normalization A is consistent with for realistic galaxy masses. Another important implication of the MASR that follows from MOND is that it is only the baryonic mass of a galaxy that sets its asymptotic rotation speed, not as in Newtonian dynamics. We discuss these distinct aspects of the MOND prediction for the BTFR in turn.
Property 1.
MASR Normalization.
The normalization of the MASR predicted by MOND is determined by fundamental constants: .
Do the data corroborate the prediction of MOND?
Yes. For finite thickness disk galaxies with , the prediction of the MASR corresponds to a BTFR with . This is consistent with the available data for rotationally supported galaxies [37,41,42,44,51,52,53,54,55].
Was the prediction made a priori?
No. This is a good test of MOND, but one has to appeal to data to set the value of in the first place. Consequently, this test of MOND is successful, but does not meet the gold standard of an a priori prediction.
What does dark matter predict?
The expectation for the normalization of the Tully–Fisher relation in CDM was discussed at length in [55]. Nominally, one expects a higher normalization than observed [56,57,58], in the sense that the are more baryons available in dark matter halos to form stars than apparently do so [59]. One of the primary reasons for invoking highly efficient feedback in more recent numerical simulations is to prevent the otherwise inevitable cooling and subsequent formation into stars of these excess baryons.
Property 2.
MASR Slope.
Do the data corroborate the prediction of MOND?
Yes. The data are consistent with the predicted slope . Figure 1 shows the data reviewed by [28] along with the MOND prediction. The line representing MOND has not been fit. It has a slope and a normalization , as discussed above [44]. Clearly, these data are consistent with the prediction of MOND.
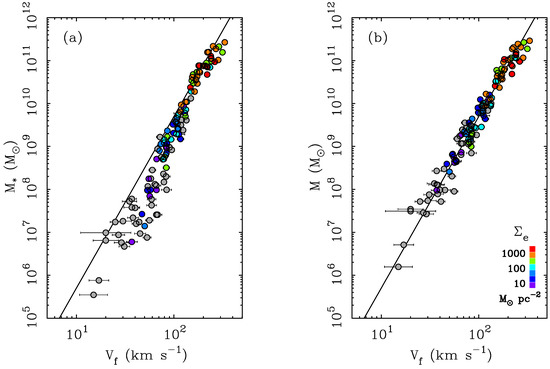
Figure 1.
Tully–Fisher relations: the flat rotation speed as a function of (a) stellar mass, and (b) baryonic mass (). Gas masses follow from observed 21cm fluxes [60]. Stellar masses are estimated from observed luminosities and a population synthesis prescription for the stellar mass-to-light ratio: [48]. Here, and throughout the paper unless otherwise noted, we adopt for star forming disks and for bulge components in the band (often called [3.6]) of the Spitzer Space Telescope [47,61,62]. Rotation speeds are obtained from resolved rotation curves that are extended enough to measure [37,42,55]. Points are color coded by the effective stellar surface density when known from Spitzer data [29,49], ranging from low (blue) to high (red) surface brightness (scale inset). The gray points are gas dominated low surface brightness (LSB) galaxies that meet the quality criteria discussed by [55] but do not have Spitzer data. The line is the prediction of MOND [16] for the value of found by [33] before these data existed.
An important consideration in constraining the slope of the BTFR is the dynamic range in the data. Observational selection effects severely bias galaxy samples in favor of high luminosity, high surface brightness (HSB) galaxies and against low luminosity and low surface brightness (LSB) galaxies [28,63]. Consequently, most realizations of the Tully–Fisher relation are dominated by high mass galaxies, and sample only a narrow range in mass: the bulk of most data sets are confined to spiral galaxies with , typically with only a few galaxies down to ∼. This results in a systematic underestimate of the fitted slope [64]. As the dynamic range over which data are available has expanded () [52,53,65,66], the slope steepens and [66].
Was the prediction made a priori?
Yes and no. The Tully–Fisher relation was known prior to the development of MOND [36,67], such that it was not an a priori prediction. The slope was highly uncertain when MOND was developed: Milgrom quotes the range [16]. A slope of 4 is within that range, but there was no guarantee that the data would settle on that value.
An important consequence of the slope 4 MASR of MOND is the location of low mass galaxies in the BTFR plane [54,68]. Rotation speeds of the low mass galaxies represented by grey points in Figure 1 were not known at the time MOND was hypothesized. Yet it was possible to use MOND to successfully predict the rotation speeds of these objects. This prediction follows directly from the statement of the MASR. Its specific application in this context was discussed by [44] and subsequently applied by [54]. This does constitute a successful a priori prediction.
What does dark matter predict?
CDM does not make a specific prediction for the BTFR. It does predict a mass–rotation speed relation for dark matter halos: [56,69]. To connect this to the BTFR, we must introduce proportionality factors and that relate the observed baryonic mass to the total mass and the observed rotation speed to that predicted at the virial radius [55]. These necessary proportionality factors are not cleanly predicted by galaxy formation models. The obvious assumption is that they be constants [69]; this predicts a slope that is inconsistent with the observations. Various effects during galaxy formation may steepen the slope [70,71], but typically only to . It often happens that CDM models [72] induce curvature (variable x) in the BTFR that is not observed (Figure 1). Indeed, it has become difficult to avoid such curvature given the shape of the abundance matching relation [73]. One can tune models to impose a slope of 4 [74], but then one has a fine-tuned model which is not satisfactory. This approach has a propensity to violate other constraints. For example, one can vary in the models of [69] to obtain the desired BTFR slope. The required variation () then ruins the otherwise good agreement with the disk size–mass relation that is obtained with constant [69]. One cannot have it both ways; one property can be fit, but not both. More elaborate models can be constructed with more parameters, but these violate Occam’s rule of parsimony, and inevitably lack predictive power: they chase the data rather than predict it [75].
Property 3.
Baryonic Mass and Flat Velocity.
A fundamental prediction of MOND is that the physical basis of the Tully–Fisher relation is a relation between flat rotation speed and baryonic mass. All the normal mass matters. It does not matter whether the mass is in the form of a star or gas.
Do the data corroborate the prediction of MOND?
Yes. The BTFR (Figure 1) is a direct consequence of the MASR in MOND.
Was the prediction made a priori?
Yes. The absolute nature of the MASR was emphasized in the original papers [16]. The importance of gas and stars in this context was not widely appreciated until much later.
What does dark matter predict?
I am not aware of any dark matter models that addressed this aspect of the Tully–Fisher relation prior to the empirical identification of the BTFR [46]. This is unsurprising, since the BTFR is something of a non-sequitur in CDM: dark matter plays no direct role in its construction. It is often assumed that is set by the dark matter halo, but this presupposition is inadequate, as the baryons make a non-negligible contribution to in HSB galaxies (see below).
Property 4.
Surface Brightness Independence.
“Disk galaxies with low surface brightness provide particularly strong tests”.—M. Milgrom [16]
An important consequence of the absolute nature of the MASR is that there should be no residuals from the BTFR. The only variables that appear are the total baryonic mass and the flat rotation speed. Neither size nor surface brightness appear in the equation, so there should be no dependence on these quantities.
Do the data corroborate the prediction of MOND?
Yes. The absence of surface brightness residuals was recognized in the mid-90s by several independent groups [76,77,78] and has been confirmed many times since. Galaxies of different surface brightness all fall on the same BTFR (Figure 1).
Was the prediction made a priori?
Yes. This was explicitly predicted [16]: “We predict, for example, that the proportionality factor in the relation for (LSB) galaxies is the same as for the high surface density galaxies”.
What does dark matter predict?
Conventionally, it had been expected that LSB galaxies should shift off of the Tully–Fisher relation defined by HSB galaxies [16,67], since the rotation speed depends on size as well as mass: . By squaring this, we obtain . It was argued [67] that a Tully–Fisher relation of the form follows if the surface brightness is the same for all galaxies, as was then believed [79]. This fails when confronted with data for LSB galaxies [76], which have different by definition.
The absence of the anticipated residuals poses a fine-tuning problem for conventional dynamics [4,80]. The observed flat rotation speed is the sum of a declining luminous contribution and increasing dark contribution: . Galaxies span a wide range of surface brightness at a given mass, but are indistinguishable to Tully–Fisher [4,5,28,81,82]. As surface brightness declines at fixed mass, declines with it, so must increase to precisely compensate and keep unchanged. The only way to avoid this fine-tuning is if all galaxies are dark matter dominated [80] so that at all relevant radii [80,83]. This limit requires implausibly low stellar masses [84], and is directly contradicted by the observed dependence of rotation curve shape on surface brightness [28,45,81,82,85,86,87,88].
2.2. Predictions for Rotation Curves
“Rotation curves calculated on the basis of the observed mass distribution and the modified dynamics should agree with the observed velocity curves”.—M. Milgrom [16]
This simple statement has a variety of testable consequences.
Property 5.
Flat Rotation Curves.
The striking flatness of the rotation curves of spiral galaxies [89,90] was an animating motivation for both dark matter and MOND. That they are observed to be so is thus not an a priori prediction. It is nevertheless a test: one should not observe galaxies that show a Keplerian decline. So far, rotation curves remain flat indefinitely far out [91,92].
Do the data corroborate the prediction of MOND?
Yes.
Was the prediction made a priori?
No: flat rotation curves were the motivation for MOND, not a prediction thereof. The theory takes flat rotation curves to be axiomatic, an expectation that could be falsified but has not been [91].
What does dark matter predict?
Flat rotation curves were a primary motivation for dark matter, not a prediction thereof. It is generally possible to fit a variety of dark matter halos to the data, once given [93,94]. It is another matter to predict rotation curves a priori. It is easy to build plausible-seeming models with rotation curves that are not as flat as those observed—indeed, it is hard to avoid [4]. Models with realistic rotation curve shapes are restricted to an unnaturally narrow range of the available parameter space [95,96,97].
Property 6.
The Acceleration Discrepancy.
A straightforward property to compute for a galaxy is the enclosed dynamical mass-to-light ratio. Assuming a spherical mass distribution, the dynamical mass enclosed within radius r is simply . This may be compared to the luminosity or baryonic mass enclosed by the same radius, giving some idea of the amount of dark matter required. This can be quantified by the mass discrepancy [25,98,99], which is the ratio of the observed centripetal acceleration to that predicted by the observed baryons: . The equation with the ratio of dynamical to baryonic mass is not exact because spiral galaxies are not spherical. Consequently, a more accurate name would be the acceleration discrepancy [100].
In MOND, the amplitude of the discrepancy depends on the distribution of luminous mass. If we interpret this in terms of conventional dynamics, we should find that the enclosed dynamical mass-to-light ratio varies predictably [16]. Specifically, there should be no discrepancy when accelerations are above the critical value . That is, the dynamical mass-to-light ratio should be comparable to that expected for the stellar population mass-to-light ratio (typically of order unity in solar units, depending on pass-band [48]). A transition should occur at , after which the discrepancy should increase with increasing radius as the acceleration declines (for a flat rotation curve, ). The transition radius should vary systematically from galaxy to galaxy: it is that is constant. Consequently, the discrepancy should be larger and set in at smaller radii in galaxies of lower surface brightness, which are predicted to have lower accelerations.
Indeed, the point of MOND is that the mass discrepancy is an acceleration-dependent phenomenon. Hence the amplitude of the discrepancy D should correlate with acceleration. This is apparent in Figure 2b, a purely empirical correlation that has been known for a long time [25,98,99] and which has become especially clear with the availability of near-IR data from Spitzer [34].
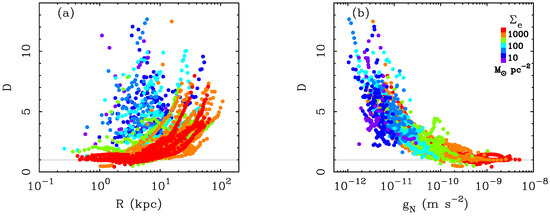
Figure 2.
The amplitude of the acceleration discrepancy of galaxies in the SPARC database [29] as a function of (a) radius and (b) the expected acceleration. Each point is an accurate (), resolved measurement, with multiple measurements per galaxy. The centripetal acceleration is measured from rotation curves while that predicted for the observed baryons is computed by solving the Poisson equation for the observed distribution of stars and gas. Points are color coded by the effective stellar surface densities of their galaxies (legend), as in Figure 1. The need for dark matter () appears gradually at large radii in high surface brightness (HSB) galaxies but is greater and sets in at smaller radii in galaxies of progressively lower surface brightness (a). This behavior was anticipated by MOND [16], along with the correlation of the amplitude of the discrepancy with acceleration (b).
Do the data corroborate the prediction of MOND?
Yes. All aspects of the prediction are apparent in Figure 2 (see also Figure 3 of [5]). In the highest surface brightness spiral galaxies, the accelerations are close to at small radii, and there is little indication of a dynamical discrepancy. The discrepancy appears gradually as one goes out in radius, as seen in a steadily increasing dynamical mass-to-baryonic mass ratio. As we consider galaxies of progressively lower surface brightness, the discrepancy appears sooner, at smaller radii, and is also larger in amplitude. An important empirical point is that it is surface brightness, not luminosity [4,101], that determins and drives the correlation with D [25,34,98,99].
Was the prediction made a priori?
Yes. This prediction was first explicitly tested [5] some 15 years after it was published [16]. It has become increasingly clear as the data have improved [34].
What does dark matter predict?
I am not aware of an explicit prediction having been made for this observation in the context of dark matter. It is now widely known that LSB galaxies tend to be dark matter dominated, but that is a recognition driven entirely by the data [81,102]. There was no reason to expect this to be the case a priori. MOND was the only theory to correctly predict this behavior in advance of its observation.
Property 7.
Rotation Curves Shapes.
“The rotation curve of a galaxy can remain flat down to very small radii, as observed, only if the galaxy’s average surface density falls in some narrow range of values which agrees with the Fish and Freeman laws. For smaller , the velocity rises more slowly to the asymptotic value”.—M. Milgrom [16]
Do the data corroborate the prediction of MOND?
Yes. In MOND, the shapes of rotation curves follow from their baryonic mass distributions. Bright, high surface brightness spirals are predicted to have steeply rising rotation curves that flatten quickly, or even decline before flattening. Low surface brightness galaxies should have slowly rising rotation curves that only gradually approach the flat velocity. Precisely this morphology is observed [5,22,28,38].
Was the prediction made a priori?
Yes. Flat rotation curves were known at the time that MOND was developed. However, the overall shapes of rotation curves were only beginning to be explored. Milgrom’s quote above nicely summarizes the state of knowledge at that time. Rotation curves that remain flat to small radii can only occur in MOND for HSB galaxies—hence his explicit comment about a galaxy’s average surface density. The rotation curves of LSB galaxies were essentially unknown. Indeed, at the time, it was widely believed that rotationally supported galaxies all had essentially the same surface brightness (Freeman’s Law [79]), and LSB galaxies did not exist. Hence it is remarkable that an explicit prediction was made for LSB galaxies, let alone that this prediction was realized by subsequent observations [5,103].
What does dark matter predict?
There are many schools of thought as to what should happen with LSB galaxies, once they were recognized to exist. These fall into two broad categories [4]. In one, it was imagined that LSB galaxies were stretched out versions of HSB galaxies, residing in late-forming dark matter halos that were themselves of lower average density. This hypothesis is rejected by the absence of surface brightness residuals in the BTFR (Figure 1), as LSB galaxies should have lower overall rotation speeds simply because , and by construction, they have larger radii at a given mass.
A more persistent school of thought is that galaxies of the same stellar mass reside in halos of the same total mass. Size follows from the initial angular momentum of the parent dark matter halo [104], and the lack of BTFR residuals with surface brightness can be explained if and only if the stellar disk is sufficiently sub-maximal that it does not impact . However, if this is the case, then the rotation curve is dominated by dark matter halos, which are expected to be very self-similar at a given mass [105]. This predicts that galaxies of the same mass have not only the same , but that the entire shape of the rotation curve should be very nearly the same. This expectation is not realized; there is a greater diversity of observed rotation curve shapes [28,45,81,82,85,86,87] than is predicted by such models [88]. This diversity is obvious in Figure 3: LSB galaxies have slowly rising rotation curves, and HSB galaxies have rapidly rising rotation curves, just as predicted by MOND: the distribution of baryons matters as does their total mass. The hypothesis that should be essentially the same for galaxies of the same mass—still present in some modern galaxy formation simulations [88]—is rejected by the data.
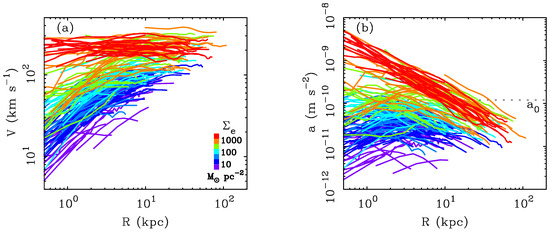
Figure 3.
The (a) rotation curves of galaxies in the SPARC database [29] and (b) the corresponding centripetal acceleration curves . Each line is one galaxy; the MOND acceleration scale is noted in (b). Galaxies are color coded by the effective stellar surface densities, as in Figure 1 and Figure 2. High surface brightness spirals have rotation curves that rise sharply and flatten quickly. These are Freeman disks like those known at the time that MOND was developed. In contrast, LSB galaxies were essentially unknown at that time. They were subsequently observed [5] to have slowly rising rotation curves that only gradually turn over and approach the flat velocity, as predicted by MOND [16]. The direct connection between stellar surface density and dynamical acceleration predicted by MOND is illustrated by the rainbow variation in (b): low surface brightness galaxies have low accelerations (often well below ), while high surface brightness galaxies have high accelerations.
Property 8.
Surface Density Follows from Surface Brightness.
In MOND, the dynamical surface density should follow from the surface density of baryonic mass. This surface density of stars is well traced by the surface brightness in the near-infrared (e.g., the K-band at or the band of the Spitzer Space Telescope). The mass surface density is traced by the dynamics: . Consequently, we expect a correlation between surface brightness and measured acceleration.
Do the data corroborate the prediction of MOND?
Yes. This is apparent directly from the observed dynamical accelerations (Figure 4). These vary in direct correspondence to the observed surface brightness. Low surface brightness systems have low accelerations; high surface brightness galaxies display high accelerations. There is a clear continuum from one end of the galaxy spectrum to the other. This happens despite the enormous scatter in the size–surface brightness plane.
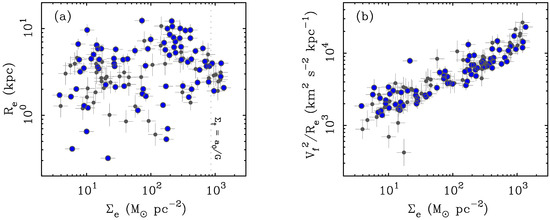
Figure 4.
The effective stellar mass surface density of galaxies [29] as functions of their (a) effective radii and (b) characteristic accelerations. A galaxy must have a rotation curve that is extended enough to measure [42] to appear in this diagram. Larger points are galaxies with distances that are accurate to better than 20%; smaller points have less accurate distances. Effective surface brightness is converted to a surface mass density assuming a [3.6] . Galaxies exist over a wide range in size and surface brightness, with no particular correlation, up to a practical maximum in each (a). In contrast, there is a strong correlation between the characteristic acceleration and surface brightness (b), as anticipated by MOND. The scale is noted as a dotted line in (a).
Was the prediction made a priori?
Yes. Figure 4 is purely empirical. It simply plots the data [29]; there is no fitting of any sort. The correlation apparent in Figure 4 directly indicates the connection between surface brightness and acceleration, which traces the dynamical surface density. That this should happen was predicted a priori by MOND at its inception.
What does dark matter predict?
In order to predict how surface density correlates with surface brightness, one needs to know both. Dark matter-only simulations provide excellent predictions for what the density profiles of dark matter halos should be [105], but are mute about the surface brightnesses of the galaxies they contain. Hydrodynamical simulations obtain a variety of results for the distribution of baryons, and there is no clear consensus about what this should be [106]. Consequently, CDM makes no clear prediction for this observable.
Property 9.
Predicting Rotation Curves
In MOND, the dynamics should follow from the observed mass distribution. To perform this test, we need to calculate the Newtonian gravitational potential associated with the observed mass, calculate the corresponding force in MOND, and observe a tracer of that force. Rotation curves provide a test in which this ideal is nearly achieved.
It is possible to predict rotation curves from the baryonic mass distribution of galaxies: the atomic gas is traced by 21cm observations while the stellar mass is well-traced by the near-IR light. With the adopted mass-to-light ratio, we convert the surface brightness profiles of galaxies observed by Spitzer [49] into mass models [29] that represent the gravitational potential of the stars. The same has been done for the gas in the course of obtaining 21cm rotation curves (see the many references in [29]). These mass models are representations of the Newtonian gravitational potential of stars and gas (e.g., Figure 5). These potentials add linearly and predict radial accelerations that must match the centripetal acceleration to sustain circular motion.
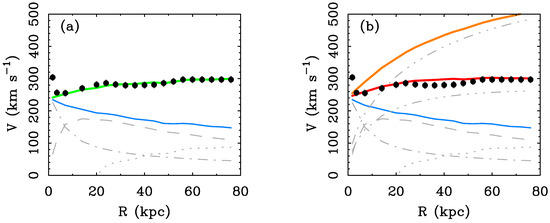
Figure 5.
Rotation curve and mass models for the giant spiral galaxy UGC 2885 () in (a) MOND and (b) CDM. Mass models of the individual components are shown as gray lines: dotted for the gas, dashed for the stellar disk (for at [3.6]), dash-dotted for the bulge (), and dash-triple dotted for the dark matter halos in (b). A thin blue solid line shows the sum of baryonic components: this is the expected rotation without dark matter or MOND. A thick solid line shows the corresponding rotation that is predicted in MOND (green line in a) and CDM (red and orange lines in (b)). In the latter case, two approaches are taken to predict the mass of the dark matter halo (see text). Assuming [69] results in the red line that performs almost as well as MOND. Using abundance matching [73] results in the orange line that overshoots the data.
The observed stars and gas () fall short of explaining the centripetal acceleration indicated by rotation curves ()—hence the need for dark matter or MOND. In the former case, we simply attribute any excess to dark matter. In MOND, there is a mathematical relation between what we see and what we get [107]:
where is an interpolation function that smoothly joins the high and low acceleration regimes [15,108,109]. This is not specified theoretically, but is constrained empirically to be something very close to the so-called “simple” function [110,111]. Here we adopt [109]
which describes the data well [34]. Once we specify this function, we can use Equation (4) to predict rotation curves from the baryonic mass distribution.
Figure 5 shows an example rotation curve prediction. First, the Newtonian acceleration is estimated using the nominal mass-to-light ratios for the stellar components. We then use Equation (4) to obtain the MOND-predicted acceleration. This is shown as the green line () in Figure 5a. This provides a remarkably good match to the data for a hands-free prediction. Only the first point is missed; this is because our nominal bulge mass-to-light ratio in a bit small for this galaxy—in a fit, it grows to [112]. This is within the range of expected variation. Moreover, this must be the case in either theory. It occurs in the high acceleration limit, so MOND gives no boost. Nor can we invoke a dark matter halo, as the rotation curve declines steeply after the first point, just as the shape of the bulge light distribution predicts, while the rotation curve of the dark matter halo must rise monotonically if it is to fit the data further out. In either case, we need a higher mass-to-light ratio for the bulge.
The successful MOND prediction of the rotation curve of UGC 2885 seen in Figure 5 is not a fluke; it is the general rule. Figure 6 shows the residuals of MOND-predicted rotation curves for 175 galaxies for which all necessary, credible data (a Spitzer map of the stellar mass, an HI map of the atomic gas mass, and a rotation curve) are available. No fitting has been performed in Figure 6a, which simply plots the ratio of the observed velocity to that predicted by MOND for the nominal mass-to-light ratio. The same has been assumed for all galaxies: what you see is what you get. That it was possible to effectively predicted rotation curves with near-IR surface photometry was also noted by [113]. The same holds in galaxies where atomic gas is the dominant form of baryonic mass [114], as the stellar mass-to-light ratio matters little for such galaxies.
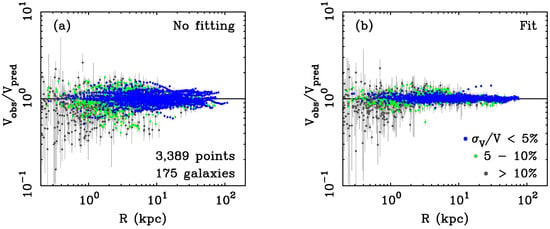
Figure 6.
Ratio of the observed velocity to that predicted by MOND, without (a) and with (b) fitting. All available data for galaxies from the SPARC database [29] are shown. Each point represents one resolved datum along the rotation curves of these galaxies. Points are color coded by measurement accuracy, as noted in the inset. No fitting has been performed in (a): the same nominal mass-to-light ratio ([3.6] for the disk and for the bulge) has been adopted for all galaxies to predict the velocity—i.e., the equivalent of the green line in Figure 5a for all SPARC galaxies. This procedure returns the correct velocity to within 0.15 dex for 90% of the data. The small scatter in (a) is further reduced (b) by fitting [112] for the optimal mass-to-light ratio of each galaxy (Figure 7).
The result of fitting the data [112] is shown in Figure 6b. The scatter declines as expected, albeit by a modest factor: the raw prediction with a constant mass-to-light ratio for all galaxies in Figure 6a is already pretty good. The reduction in scatter here manifests in an increased scatter in the stellar mass-to-light ratio (see below). This must happen; a constant makes for a nice, hands-free assumption, but there must be some intrinsic scatter in this quantity. It turns out that the scatter so induced is about that expected from variations in the star formation histories of galaxies [61]. There is the expected amount of variation in the mass-to-light ratio, leaving little room for intrinsic scatter in the underlying relation.
A subtle point worth noting is that the deviations seen at small radii in Figure 6 velocity skew preferentially to . This is the effect that is expected from the combination of observational resolution (“beam smearing”) and asymmetric drift (non-circular motion). It is hard to measure the velocity accurately as small radii where the gradient of the rotation curve is large so that different velocities contribute within the first beam; the result is often an underestimate of the true rotation speed. It is also the case that non-circular motions sometimes make up a large fraction of the kinetic energy at small radii so that the measured velocity sometimes falls short of the desired circular velocity of the gravitational potential. These effects both result in a systematic skew in the sense observed, particularly in the lowest quality data (the grey points in Figure 6).
Do the data corroborate the prediction of MOND?
Yes. The predictive ability of MOND is as good as can be expected given the fundamental limitation of converting the observed starlight into the corresponding stellar mass. One can reduce the scatter in Figure 6a by treating as an adjustable parameter. The efficacy of this procedure is apparent in Figure 6b and has been demonstrated many times before [6,22,26,33,103,115,116]. There are, of course, exceptions: galaxies that do not fit in detail. For example, NGC 2841 was long considered problematic [117], but a good fit falls out of a Bayesian analysis [112]. Still, problematic cases persist (e.g., NGC 2915). There are always cases like this in astronomy; it would be suspicious if all the data could be fit without some outliers. The failure rate increases as data quality declines, as expected. We should not lose sight of the forest for the occasional outlying tree.
Was the prediction made a priori?
That it should be possible to predict rotation curves from the observed mass distribution of galaxies was predicted a priori. The extent to which this is possible for any individual galaxy is limited by astrophysical uncertainties in how well we can measure the mass distribution; in particular, the unavoidable uncertainty in . That it is possible to come as close as illustrated by Figure 6 is a remarkable accomplishment.
What does dark matter predict?
CDM makes clear predictions for the rotation curves of dark matter halos [105]. Predictions for the observable properties of galaxies are model-dependent. Many different models are possible; Figure 5 illustrates two possibilities.
In order to predict the rotation curve of a specific galaxy, we need a mechanism to specify the dark matter halo within which it resides. Perhaps the most obvious mechanism at present is offered by the stellar mass–halo mass relation obtained from abundance matching [73]. A massive galaxy like UGC 2885 with should reside in a halo of mass (see Figure 6 of [73]). Together with the halo mass–concentration relation [118], this predicts the expected rotation attributable to the dark matter halo. Adding this in quadrature with the baryonic component results in the orange line depicted in Figure 5b. This grossly over-predicts the observed rotation.
If one did this exercise twenty years ago (I did), then the stellar mass–halo mass relation from abundance matching was not yet available. The common approach then was to assume a constant disk to halo ratio around [69]. Adopting this, we predict . This comes much closer to matching the observed rotation, performing almost as well as MOND in predicting the rotation curve.
The good performance of assuming a disk fraction is certainly a fluke. We could just as easily have assumed or 0.025 (both values considered by [69]), and we would again mispredict the rotation curve. There is no reason to expect, a prior, that this particular galaxy should have this particular disk fraction. We can fit the data to infer , but we cannot predict the rotation curve. If we use one galaxy to fix , we then get incorrect results for other galaxies: must vary with mass [59].
The stellar mass–halo mass relation of abundance matching is now an essential element of the CDM paradigm [119], so the discrepancy of the optimal disk fraction from this relation cannot be ignored. It is tempting to conclude that this particular galaxy happens to be an outlier in the scatter about the mean – relation, by chance having a small total mass for its observed stellar mass. This is equivalent to suggesting that it has an abnormally low velocity (the green line in Figure 5 rather than the expected orange line). This in turn predicts that it should sit far off of the Tully–Fisher relation defined by other galaxies of the same stellar mass. It does not. Indeed, in general, there is too little scatter in the BTFR to accommodate that expected in the stellar mass–halo mass relation.
There exist many other possibilities in the context of CDM that are not considered here. Indeed, we have ignored processes that must be relevant, like adiabatic compression of the halo [95], and any form of stellar feedback (though this is usually said not to be important in galaxies of this high mass). It seems common to imagine that the solution lies in getting the combination of these effects right, but really this makes the problem worse, not better: there is no unique way to predict rotation curves with CDM. A huge number of models are possible; many are plausible. Nature appears to have declined to implement any reasonable CDM model. The best we can hope to do is very precisely mimic the behavior of MOND, reproducing after the fact the phenomenology it correctly predicted in advance.
Property 10.
Stellar Population Mass-to-Light Ratios.
The stellar mass-to-light ratio is the only physical parameter available to MOND fits. A considerable amount is known about stellar populations, so these provide an independent check. If MOND is simply a strange fitting function, there is no need for its fitting parameter to return plausible mass-to-light ratios. If instead there is something to it, then the fitted values of should make sense in terms of stellar populations.
Figure 7a shows the stellar mass-to-light ratios for SPARC galaxies as assumed throughout this work ([3.6] for stellar disks and for bulges). The luminosity-weighted mass-to-light ratio is shown, so the slight variation seen for a few points is from differences in the bulge fraction. Most galaxies appear as beads on a string. This morphology is anathema to stellar populations, which must inevitably suffer scatter from variations in the star formation history, the metallicity distribution of the stars, and differences in the IMF (Initial Mass Function: the distribution of masses with which stars form). In short, the absence of scatter in Figure 7a is unphysical. This suffices only as a first estimate, but there must be some intrinsic scatter in .
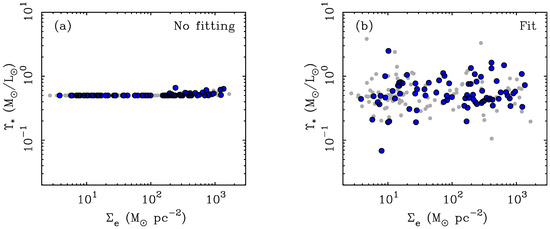
Figure 7.
The effective surface densities of SPARC galaxies and their stellar mass-to-light ratios as obtained (a) from assuming constant at [3.6] for stellar disks and for bulges, and (b) by fitting rotation curves [112]. Large blue points are galaxies with distances known to better than 20%; smaller grey points are galaxies with less accurate distances. The absence of scatter in (a) is anathema to stellar populations; there must be some intrinsic scatter in this quantity from variations in the star formation history from galaxy to galaxy. The scatter seen in (b) is consistent with that expected from intrinsic scatter in [47,61,62] and observational uncertainties [34,38,112].
In Figure 6 we predicted rotation curves using the shown in Figure 7a. Figure 7b shows the stellar mass-to-light ratios obtained from rotation curve fits [112]. This is what is required to eliminate nearly all the scatter in Figure 6, transferring it from deviations in the predicted velocity to the scatter that appears here. The amount of scatter required to make rotation curve fits could have been arbitrarily large. Instead, it is rather modest. Indeed, the scatter in seen in Figure 7b is consistent with that expected from the combination of observational errors and intrinsic scatter in stellar population (∼ dex at [3.6] [61]) stemming simply from variations in the star formation history. There is little room for other plausible sources of variation, like galaxy-to-galaxy differences in the average IMF. Given that some intrinsic scatter in is inevitable, it is hard to imagine a more favorable outcome.
Do the data corroborate the prediction of MOND?
Yes. The stellar mass-to-light ratios of MOND fits (Figure 7 [6,22,112]) are in excellent accord with the expectations of stellar population models [47,48,61,62,120,121]. The amplitude of is consistent with what is expected for a Kroupa or Chabrier IMF, which are practically indistinguishable. Heavier or lighter IMFs are disfavored. The scatter increases from red to blue bandpasses, as expected, and the expected color- relations are also recovered [22,66].
Was the prediction made a priori?
No, and it cannot be. The test here is whether the mass-to-light ratios required in MOND fits are consistent with the astrophysical expectations of stellar population models. To a remarkable extent, they are.
What does dark matter predict?
I am not aware of any mechanism by which a similar test could be made in CDM as the stellar mass-to-light ratio does not play an equivalent role in determining the dynamics that specify the rotation curve. In MOND, is uniquely specified, within the uncertainties, while in dark matter models there is an unavoidable degeneracy between dark and luminous mass [93], precluding a unique test.
Property 11.
The Correspondence of Features.
An important aspect of galaxy dynamics is the observed correspondence between features observed in the baryonic mass distribution and those seen in rotation curves. The “bumps and wiggles” in one are reflected in the other. This is known among experts as “Renzo’s Rule” [122].
It was recognized early on [123] that the observed correspondence of bumps and wiggles implied that stars were the dominant mass component at small radii. The correspondence exists because the stellar mass dominates the gravitational potential, so features in the stellar distribution are necessarily reflected in the rotation curve. This situation is generally known as maximum disk: the stellar mass is close to the maximum allowed by the rotation curve [124,125,126].
In HSB galaxies, the maximum disk mass is generally comparable to or slightly higher than what is expected for stellar populations (0.7 vs. at [3.6] for disks and 0.8 vs. 0.7 for bulges, with substantial individual variation [84]). In these situations, the correspondence between photometric and kinematic features is natural: the stars dominate the gravitational potential at small radii. The bulge of UGC 2885 in Figure 5 is one example. There are many others [28,84,124,125].
The situation is different in LSB galaxies. Since the stellar mass is spread over a greater radius, the contribution of the stars to the total velocity is reduced simply because . For the masses expected for stellar populations, LSB galaxies are far removed from being maximal. One might choose to favor the maximum disk mass-to-light ratio over the stellar population expectation, but this would violate the constraints discussed above: LSB galaxies cannot be maximal and also fall on the BTFR. Imposing maximum disk mass-to-light ratios would induce surface-brightness correlated scatter in Figure 1 that is not present in the raw data.
Thin, dynamically cold stellar disks can support features like spiral arms while quasi-spherical, dynamically hot dark matter halos cannot [43]. One therefore expects the correspondence between features to dissipate as surface brightness decreases and the dark matter halo comes to dominate. Nevertheless, the correspondence of features persists (Figure 8 [85,86,87,122,127]).
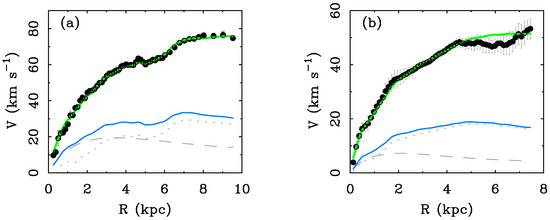
Figure 8.
Rotation curves and mass models for the dwarf galaxies (a) NGC 1560 [22,33,128] and (b) DDO 154 [91,112,116]. The MOND fits (green lines) necessarily follow the detailed shape of the features seen in the baryonic mass distributions (light blue lines). Gas (dotted lines) dominates the mass budget in these low surface density galaxies; the stars (dashed lines) and their mass-to-light ratio have little leverage on the fit.
Figure 8 shows two examples that illustrate the correspondence of photometric and kinematic features in low surface density galaxies. NGC 1560 has a prominent dip from 5–6 kpc in both the baryonic and total rotation curve [33,128]. DDO 154 has a more subtle correspondence between the two, with kinks around 0.5, 2, and 5 kpc [91]. These are not happenstance; this is the general rule [112,122]: details like this are subsumed in the residuals for all the galaxies in Figure 6.
The majority of the baryonic mass in the galaxies in Figure 8 is in the form of gas, not stars. Consequently, there is no leverage to fit the data by adjusting the stellar mass-to-light ratio: the shape of the rotation curve follows directly from the observed distribution of gas. As emphasized by [114], galaxies like these provide very nearly a direct prediction without any fitting. However, there are nuisance parameters that need to be considered [112]. The distance and inclination is measured independently for each galaxy, but of course these are not known perfectly well. These influence the baryonic mass () and rotation speed [through ]. The case of DDO 154 provides a good illustration of both effects. Distance estimates to DDO 154 range2 from 3 to 6 Mpc. The formally most accurate measurement is Mpc [129,130]. If we hold the distance fixed at 4.04 Mpc, then the shape of the rotation curve is the same but the amplitude slightly overshoots the data (see Figure S5 of [131]). Distances are never known perfectly; treating it as a nuisance parameter in a Bayesian fit with a prior that matches the measurement uncertainty leads to Mpc [112]. This small reduction in the distance is the difference between overshooting the data and the excellent fit seen in Figure 8. Similarly, the inclination is not perfectly well known. In the case of DDO 154, it becomes particularly uncertain at large radii (see Figure 81 of [91]) where the shape of the rotation curve becomes dodgy. The slight mismatch in the shape of the MOND fit in the outer fringes of DDO 154 is a good thing: it cannot be fooled into tracing unphysical variations [103].
A good theory should not only fit the data, it should also fail to fit data that are incorrect. To test this, an outright mistake in the baryon distribution was intentionally introduced by [103]. An acceptable MOND fit to these incorrect data could not be found: confronted with a situation in which it should fail, it did so. In contrast, there is substantially more freedom in fits with dark matter halos: one could happily fit the data without noticing that the baryonic distribution was wrong, much less notice a detail like a slight issue with the distance.
The experiment of using an incorrect baryon distribution has been unintentionally replicated by [131] in the case of D631-7 (the first example in their Figure S5). D631-7 is a gas rich galaxy similar to those in Figure 8. However, only a total gas mass is available; the detailed gas distribution is not. For inclusion in the SPARC database [29], a scaling relation between gas mass and radius was applied to make a crude estimate of the gas distribution [29,38]. This estimate is certainly wrong in detail, and indeed, the MOND fit that [131] obtain using it is a poor match to the data—as it should be in such a circumstance. In contrast, the fit [131] make with dark matter shows no indication of a problem. There is sufficient freedom in fits with dark matter halos to absorb even gross errors in the input data; they are incapable of failing when they should [103].
Do the data corroborate the prediction of MOND?
Yes. In MOND, the detailed shape of the rotation curve must follow from the observed distribution of mass. This is what is observed.
Was the prediction made a priori?
Yes and no. That this should be generally be the case was anticipated in the original papers [16]. For specific galaxies, this prediction must be made on a case by case basis. Figure 6 illustrates how well rotation curves can be predicted.
What does dark matter predict?
The conventional expectation is that dark matter halos should not support the same features that are seen in the luminous disk. Dynamically hot dark matter halos that dominate the mass budget should not be affected by the small minority of mass in the disks of LSB galaxies, and are not able to sustain similar features on their own [43]. Any one case might be dismissed as a happenstance of some non-equilibrium event, but the specific cases illustrated in Figure 8 are not the exception; they are examples of the general rule (Figure 6). The widespread correspondence between features in the baryonic mass profiles and the kinematics of LSB galaxies is contradictory to any flavor of dark matter that does not interact with baryons by some mechanism more direct than gravity.
2.3. Disk Stability
There are many indications of mass discrepancies in extragalactic astronomy and cosmology [1,4,6,22,24]. One of the early indications was disk stability. Left to themselves, spiral disks that are not embedded in dark matter halos are subject to a violent bar instability [132]. Maintaining thin, stable, dynamically cold spiral disks for the better part of a Hubble time seems to require some assistance [133,134,135]. A simple way to think of this is a competition between disk self-gravity, which drives instabilities like bars and spiral arms, and the gravity of a dynamically hot dark matter halo, which tends to suppress these instabilities. Explaining the observed morphologies of spiral disks requires some of both.
Property 12.
The Freeman Limit.
The highest surface brightness galaxies have the most disk self-gravity, so are most subject to self-destructive instabilities. These HSB galaxies are at the Freeman limit, which is a generalization of Freeman’s Law [79]. LSB galaxies exist in great numbers [63,136,137,138]; what was called Freeman’s Law is not a constancy of surface brightness for all galaxies, but an upper limit on surface brightness that disk galaxies do not exceed [63,137].
A first investigation of disk stability in MOND was discussed in [139], and numerical simulations have been conducted by [140,141,142,143,144,145]. The basic result is that MOND stabilizes galaxy disks without a dark matter halo. There are two essential predictions that appear already in the first work [139] and persist in the numerical simulations: disk galaxies can only exist in the MOND regime, and the amount of stability predicted for LSB galaxies differs from that expected with dark matter halos.
Do the data corroborate the prediction of MOND?
Yes. Bare Newtonian disks should suffer the usual instability in the absence of dark matter, so are predicted not to exist. This sets an upper limit to the surface brightness, as stabilizing accelerations are only obtained for . The observed value of the Freeman limit corresponds well to (Figure 4 [22]).
Note that the scale appears in disk stability in a way that is different from its appearance in galaxy kinematics. In kinematic relations like the BTR, it appears with Netwon’s constant as the product . In disk stability, it appears through the ratio with Newton’s constant: . Hence the scale appears in galaxy data in distinct ways that are unique to MOND.
Was the prediction made a priori?
No and yes. The Freeman surface brightness was known before MOND was invented, and before the first investigation of disk stability therein. However, it was correctly anticipated [139] that the Freeman surface brightness was a limit rather than a universal value at a time when most of the community interpreted it to be the latter.
What does dark matter predict?
Disk stability in CDM depends, crudely speaking, on the disk-to-halo ratio. If this is too large, the disk becomes unstable. The dense, cuspy halos that emerge from numerical simulations are capable of stabilizing disks of considerably higher surface density than the Freeman limit [146]; the scale had to be inserted into models by hand [4,147]. There is no reason that the threshold for stability should be that predicted by MOND, as observed.
Property 13.
Vertical Velocity Dispersions.
“An analog of the Oort discrepancy should exist in all galaxies and become more severe with increasing [radius] in a predictable way”.—M. Milgrom [16].
The vertical velocity dispersions of disk galaxies are related to their stability. Disks are dynamically cold, in the sense that [148,149]. Cold disks are especially subject to instabilities [148,149], which was an important consideration driving early work [132] and remains an important consideration today. A related property is the Oort discrepancy; i.e., the excess vertical velocity dispersion over that which can be explained by the Newtonian restoring force to the stellar disk.
Conventionally, the Oort discrepancy should be modest. Near the disk, the stars dominate the mass budget and provide the lion’s share of the restoring force. It is only as one looks to high vertical distances from the center of the plane that one begins to notice the contribution of the quasi-spherical dark matter halo.
In MOND, the amplitude of the discrepancy depends on the acceleration. In high acceleration regimes, there should be no discrepancy. The discrepancy should appear around , and grow larger as accelerations decrease. In HSB galaxies, the severity of the Oort discrepancy should increase with radius because acceleration decreases with radius (Figure 3b). Interpreted conventionally, one would infer a dark matter halo that is very squashed near the disk plane, or even a disk of dark matter, transitioning to a more spherical potential farther out. The quantitative details of how this occurs may be theory-specific: not all theories [107,150,151,152] that follow the basic tenets of MOND [153] need necessarily be identical in this regard.
Do the data corroborate the prediction of MOND?
For this test, the results are mixed. In general, the shape of the predicted velocity dispersion profile is often correct, but the amplitude is frequently over-predicted. This makes no sense in either MOND or dark matter. MOND should get both right. In dark matter, the shape of should follow the prediction of Newton [154], not MOND. A similar conundrum arises for clusters of galaxies [24,155,156,157,158].
In the Milky Way, the rotation curve is well described by MOND, which successfully predicted its outer slope [159]. However, the vertical velocities are over-predicted [160] by ∼[161]. This is about a discrepancy, so dark matter is favored by the vertical velocity data, provided that we spot it MOND-like behavior in the radial direction. It is not obvious that this make sense in principle, and it leads to a puzzle in practice. The local dark matter density inferred from the rotation curve is ∼ [162] while that from vertical motions implies twice as much: ∼ [163]. This implies a squashed halo [163], but this is contrary to the findings of [161] for which a spherical halo is a reasonable fit.
In external galaxies, we encounter a similar problem. This challenging observation has been undertaken by the DiskMass project [164], with the result that disks are not merely cold dynamically, but downright frigid. Using conventional dynamics, the observed vertical velocity dispersions imply stellar mass-to-light ratios that are a factor of ∼2 [149] or more [165] lower than expected for stellar populations [48]. This is equivalent to removing all stars of mass < from a Kroupa IMF. This is not a viable solution, as it implies that the sun and lower mass stars that are numerically common locally do not exist in other galaxies. The problem gets worse in MOND, which predicts larger velocity dispersions [166]. However, the shape of the radial variation is well-predicted [167]; the problem is a small offset between the observed and predicted dispersion that remains roughly constant as varies by a large factor. Since the result makes little sense in the conventional context [168,169], it is not surprising that it does not work for MOND either. As in the Milky Way, we are confronted with a situation that is problematic for both paradigms.
There are some qualitative suggestions of MOND-like behavior in this context. The velocity dispersions of the gas in the outer regions of galaxies are consistently higher than can be sustained by the restoring force of the Newtonian disk [170]. This leads to the inference of highly flattened dark matter halos [171] or dark disk components [154] distinct from quasi-spherical halos, or some non-gravitational effect. That the velocity dispersion in these low density regions are higher than expected conventionally is the qualitative signature of MOND. By the same token, there exist ultrathin disk galaxies [172,173,174] that are difficult to sustain conventionally with the weak restoring of their low surface density stellar disks: they should be much thicker than observed. That these galaxies are thin follows naturally from the enhanced restoring force provided by MOND (see Figure 9 of [5]).
There is no clear conclusion that can be drawn from the vertical velocity dispersion data at this time. There are a number of qualitative indications of MOND-like behavior, especially in low surface density systems where its effects should be pronounced. However, its quantitative predictions persistently over-predict vertical velocities in the best observed systems, albeit by a small amount.
Was the prediction made a priori?
Yes. It remains the irrevocable prediction that the vertical velocity dispersion should follow from the observed distribution of baryonic mass. However, the details of the quantitative prediction may depend on whether MOND is a modification of gravity [107,150] or inertia [151,152].
What does dark matter predict?
The prediction of conventional dynamics with dark matter depends on the detailed distribution of both dark and luminous mass. The former is not observed, so we are free to assign to each dark matter halo whatever degree of flattening is required to fit the data. This is not as satisfactory as an a priori prediction, but it should be possible to predict the distribution of halo shapes [118,175,176] to make a statistical test. I am not aware of a conclusive observational test of this type.
Property 14.
Spiral Structure in LSB Galaxies.
“In LSB disks, it is conceivable that the minimum disk mass required to generate spiral arms might exceed the maximum disk mass allowed by the rotation curve”.—S. McGaugh [5]
For disk galaxies near the Freeman limit, the stability provided by a dark matter halo is about the same as that provided by MOND. However, the two theories diverge to lower accelerations. In order to explain the amplitude of the rotation curve, the disk-to-halo ratio must steadily decline as the surface brightness declines: LSB galaxies are dark matter dominated. Consequently, they should be very stable [177]. In contrast, the stability provided by MOND does not continue to increase indefinitely in the regime of very low accelerations, instead saturating after a mild increase [139,140].
The difference in the predicted stability properties of LSB disk galaxies leads to a difference in the expected morphology. Dark matter halos over-stabilize low surface density disks, suppressing the development of bars and spiral arms [145,177]. In contrast, MOND predicts a more similar development of such features in high and low surface brightness disks, with numerical simulations showing remarkably realistic morphologies [141].
Though dark matter halos were originally invoked to stabilize disks [132], it was also recognized early that the disk-to-halo ratio should not be too low, or it would over-stabilize disks and suppress the observed spiral modes. This marginal stability condition places a lower limit on the masses of the stellar disks [178]. This minimum disk is not far removed from maximum disk for HSB galaxies. In contrast, LSB galaxies are well below maximum disk: for the stellar masses expected from population synthesis, stars contribute little to the gravitational potential, even at small radii [44,84].
As a consequence, LSB galaxies should not exhibit bars or spiral structure if embedded in dominant dark matter halos [177]. Though there are certainly differences in morphology between HSB and LSB galaxies, these are modest and there is no lack of examples of LSB galaxies with bars [179] and spiral arms (Figure 9 [180,181,182]). This observation is natural in MOND, as there is ample disk self-gravity to drive the observed spiral structure, and little dynamical friction to slow bars, which are observed to have higher pattern speeds [183] than expected when dark matter dominates [184,185].
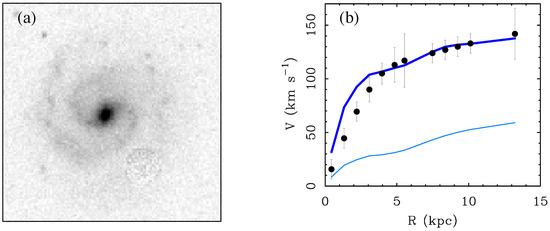
Figure 9.
The low surface brightness galaxy F568-1, as seen (a) in the V-band [180], together with (b) its rotation curve and mass model [29]. The lower blue line is the mass model for the nominal stellar disk with , which has a [3.6] and corresponding V-band . The disk-to-halo ratio is small, so spiral structure should be suppressed [177,178]. The upper blue line shows the disk rotation curve with the mass required to explain the observed spiral structure in (a) in the context of dark matter [187]. The stellar disk must be very heavy: , with in [3.6] and in the V-band. This is well in excess of the mass expected for a stellar population. Indeed, the stellar disk is so heavy that it leaves no room for dark matter and exceeds the observed rotation for kpc. Taken at face value, this poses a contradiction for any flavor of dark matter, as predicted by [5].
Figure 9 shows the example of the LSB galaxy F568-1. This galaxy is dim but large, with a disk scale length kpc [29], somewhat larger than that of the Milky Way [186]. Its diffuse stellar disk exhibits a clear two-armed, grand design spiral pattern. This should be strongly suppressed by the dominant dark matter halo: the disk-to-halo ratio is tiny, so there is insufficient disk self-gravity to drive the instabilities that feed spiral structure. And yet, there it is.
If MOND is the cause of spiral structure in LSB galaxies, then it is straightforward to predict [5] how this would be interpreted in conventional terms. Specifically, if one were to apply the marginal stability condition [178] to LSB galaxies, one would infer unnaturally large disk masses [5]. F568-1 (Figure 9) has a [3.6] luminosity of [29], so population synthesis leads us to expect . In order to explain the observed spiral structure of F568-1, the conventional analysis requires [187]. This is an order of magnitude more than expected for a normal stellar population, and comparable to the much brighter Milky Way [188]. Scaled to this mass, the rotation curve of the disk accounts for essentially all the mass in this LSB galaxy (Figure 9b). There is no room left for the dark matter halo, and formally the disk exceeds the observed rotation at small radii. Taken at face value, more mass is required to drive spiral structure than is allowed by the rotation curve. This is the contradiction to conventional dynamics anticipated in the quote above [5].
More generally, the expectation is that the conventional analysis of spiral structure in LSB galaxies will indicate a stellar mass in excess of that which is reasonable for stellar populations. This more general prediction is realized in the LSB galaxies for which a careful analysis has been performed [187,189,190]. Quoting from these works: “these estimates seem to indicate that the disks of low surface brightness galaxies might be much more massive than currently thought. This puzzling result contradicts stellar population synthesis models” [187]; “When I apply this method to the disks of low surface brightness galaxies, I find unexpectedly high mass-to light ratios” [189]; and “For four low-surface-brightness galaxies, we find the disk masses corresponding to the marginal stability condition to be significantly higher than one may expect from their brightness” [190]. These statements are exactly what was predicted to happen if disk stability is provided by MOND rather than a dark matter halo.
It may be tempting to take these high masses literally rather than accept that they might be due to MOND. Note, however, that all the correlations discussed above follow from stellar masses that are very much in accord with our expectations for stellar populations. If instead we adopt these higher masses, it will vastly increase the scatter in the BTFR (Figure 1), building in a correlation of residuals with surface density where there are none with surface brightness, and make nonsense of the correlations seen in Figure 3 and Figure 4. We cannot fix this without breaking those.
Do the data corroborate the prediction of MOND?
Yes. Application of modal analysis resulted in precisely the predicted effect.
Was the prediction made a priori?
Yes. This was the obvious effect that could be anticipated for a conventional analysis [5].
What does dark matter predict?
Nominally, one expects LSB galaxies with stellar disk masses that are reasonable from the perspective of stellar populations to be more stable than observed due to their tiny disk-to-halo ratios [177]. There are any number of effects that could be invoked which might or might not circumvent this baseline expectation. These do nothing to explain why the observed phenomenon follows from the predictions of MOND.
3. Discussion
“In science, all new and startling facts must encounter in sequence the responses
- It is not true!
- It is contrary to orthodoxy.
- We knew it all along”.
—L. Agassiz (paraphrased)
We have now completed each step in this progression. The results of the earliest rotation curve data for LSB galaxies [191] were disputed3 (it is not true!); attempts to pose the results in an empirical framework [99] independent of MOND were met with antipathy4 (it is against orthodoxy!), and more recently, improved data [34] corroborating the results in [99] are now frequently described5 as “natural” (we knew it all along).
Unfortunately, we did not know it all along. We have been surprised at every turn: these were startling facts, when new. Only one theory succeeded in predicting these phenomena in advance: MOND. It has met the gold standard of scientific prediction repeatedly for a wide variety of phenomena, including many beyond the scope of this review [22,24,206,207,208,209]. I do not see how this can be a fluke.
A common reaction at this juncture is “MOND may get X right, but it gets6 Y wrong. Therefore dark matter must be correct”. The second sentence does not follow from the first, as it presupposes that dark matter automatically explains everything that MOND predicted in advance. This fails to address why MOND has predictive power that dark matter lacks: just saying “dark matter does it” is not a satisfactory scientific explanation. We need to understand X irrespective of Y, not use Y as an excuse to ignore X.
The set X of properties discussed here is listed in Table 1. These include many successful a priori predictions of MOND. In contrast, many of these observations are problematic for the dark matter paradigm. There is no good reason for properties (3), (6), (9), and (12) to arise in the context of dark matter: they were not predicted, and require fine-tuning to explain [4,5,24,44,54,55,83,98,99]. Properties (4), (11), and (14) appear to be outright contradictions to the dark matter interpretation of galaxy dynamics. Whether they amount to a falsification depends on where we set that bar: what would constitute a falsification of the dark matter? At the very least, it is disturbing that a completely different theory correctly predicted a wide range of phenomena that the dark matter paradigm did not.

Table 1.
MOND Predictions and Tests.
In most cases, the MOND-predicted properties in Table 1 are obvious in the data with no fitting whatsoever. For example, of the four properties of the MASR, only its normalization must be fit. Once the value of is specified, the slope is fixed, and is consistent with subsequently obtained data. That the MASR would be independent of surface brightness was also a genuine, and conventionally unexpected, a priori prediction. That the relation was fundamentally one between baryonic mass and was first anticipated by MOND.
In a similar manner, many of the predicted properties of rotation curves follow directly without recourse to fitting. This includes the amplitude of the acceleration discrepancy (Figure 2), the shapes of rotation curves (Figure 3), and the dependence of acceleration on surface brightness (Figure 4). The predictions of MOND can be seen directly in the data.
In order to make detailed rotation curve fits, we must treat the stellar mass-to-light ratio as a fit parameter. This one degree of freedom is unavoidable in any theory. MOND fits work well with a single, universal value of [26,112,113]. The value of is not allowed to vary from galaxy to galaxy, and there is no indication7 in the data of a need to do so [112]. An independent test of the best-fit values of is provided by stellar population synthesis models. The agreement with these the two could hardly be better (Figure 7).
When the cold dark matter paradigm became widely accepted, the only properties in Table 1 that had seriously informed its development was that rotation curves are flat and the Oort discrepancy exists. These were taken to mean that there had to be dark matter, and little more. The Tully–Fisher relation was known at the time, but was widely viewed as a method to determine distances, not inform theory. The remaining elements of Table 1 were essentially unknown, or, in the case of Freeman’s Law, widely misinterpreted. It is not obvious that we would develop the same paradigm had we known then what we know now.
4. Conclusions
Many predictions of MOND have been corroborated over the years. It has repeatedly met the gold standard of the scientific method in which predictions are made in advance of their observation. The dark matter paradigm does not share a comparable record of predictive success in galaxy dynamics.
There are three broad categories of interpretation admitted by the data discussed here.
- The data corroborate the predictions of MOND because there is something to it.
- The physics of galaxy formation somehow mimic MOND, at least for rotating galaxies.
- There is something new and different going on that we have yet to imagine.
These are essentially identical to the possibilities discussed over 20 years ago [5], with the addition of (3), which is sufficiently vague to always be a logical possibility. There has been some progress in this direction, with hypotheses for dark fluids [211], or bipolar [212] or superfluid [213] dark matter with built-in MOND-like behavior while retaining the putative successes of CDM on large scales. There remains a great deal to be explored in this direction.
Nevertheless, the obvious interpretation of the data discussed here is (1): MOND gets all these predictions correct, in advance of their observation, because there is something to it. This motivates the search for a satisfactory theory that encompasses both general relativity and MOND. Some progress has been made along these lines [22,23,214,215,216,217,218], but overall, shockingly little effort has been made to investigate in this possibility.
In contrast, an enormous amount of effort has been invested in (2), a thorough discussion of which is well beyond the scope of this review. However, the basic problem is simple: MOND has made many successful, a priori predictions that dark matter did not. We are obliged to adjust our dark matter models to accommodate the successful predictions of a contrary theory.
There remains a considerable amount that we do not understand about the universe, including whether the invisible particles hypothesized to dominate its mass budget actually exist.
“The normal component (i.e., the accepted paradigm and its adherents) is large and well entrenched. Hence, a change of the normal component is very noticeable. So is the resistance of the normal component to change. This resistance becomes especially strong and noticeable in periods where a change seems to be imminent”.—P. Feyerabend [7]
Funding
This research has been supported in part by NSF grant PHY-1911909 and NASA grant 80NSSC19K0570.
Acknowledgments
The author is grateful to many colleagues for critical conversations over the years; in particular, Greg Bothun, Jim Schombert, Doug Richstone, Joel Bregman, Jim Peebles, Houjun Mo, Simon White, Donald Lynden-Bell, Chris Mihos, Thijs van der Hulst, Renzo Sancisi, Erwin de Blok, Bob Sanders, Vera Rubin, Moti Milgrom, Jerry Sellwood, David Merritt, Arthur Kosowsky, James Binney, Frank van den Bosch, Roelof de Jong, Eric Bell, Rachel Kuzio de Naray, Benoit Famaey, Pavel Kroupa, Marcel Pawlowski, Federico Lelli, Hongsheng Zhao, and Xavier Hernandez.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BTFR | Baryonic Tully–Fisher relation |
| CDM | Cold dark matter |
| HSB | High surface brightness |
| IMF | Initial mass function |
| CDM | Lambda cold dark matter |
| LSB | Low surface brightness |
| MASR | Mass–asymptotic speed relationn |
| MOND | Modified Newtonian dynamics |
References
- Faber, S.M.; Gallagher, J.S. Masses and mass-to-light ratios of galaxies. Ann. Rev. Astron. Astrophys. 1979, 17, 135–187. [Google Scholar] [CrossRef]
- Trimble, V. Existence and nature of dark matter in the universe. Ann. Rev. Astron. Astrophys. 1987, 25, 425–472. [Google Scholar] [CrossRef]
- Ostriker, J.P. Astronomical tests of the cold dark matter scenario. Ann. Rev. Astron. Astrophys. 1993, 31, 689–716. [Google Scholar] [CrossRef]
- McGaugh, S.S.; de Blok, W.J.G. Testing the Dark Matter Hypothesis with Low Surface Brightness Galaxies and Other Evidence. Astrophys. J. 1998, 499, 41. [Google Scholar] [CrossRef]
- McGaugh, S.S.; de Blok, W.J.G. Testing the Hypothesis of Modified Dynamics with Low Surface Brightness Galaxies and Other Evidence. Astrophys. J. 1998, 499, 66. [Google Scholar] [CrossRef]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian Dynamics as an Alternative to Dark Matter. Ann. Rev. Astron. Astrophys. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Feyerabend, P. Problems of Empiricism; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Peebles, P.J.E. Dark matter and the origin of galaxies and globular star clusters. Astrophys. J. 1984, 277, 470–477. [Google Scholar] [CrossRef]
- Steigman, G.; Turner, M.S. Cosmological constraints on the properties of weakly interacting massive particles. Nucl. Phys. B 1985, 253, 375–386. [Google Scholar] [CrossRef]
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Ann. Rev. Astron. Astrophys. 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Porter, T.A.; Johnson, R.P.; Graham, P.W. Dark Matter Searches with Astroparticle Data. Ann. Rev. Astron. Astrophys. 2011, 49, 155–194. [Google Scholar] [CrossRef]
- Baudis, L.; Brown, A.; Capelli, C.; Galloway, M.; Kazama, S.; Kish, A.; Reichard, S.; Wulf, J.; XENON Collaboration. Dark Matter Search Results from a One Ton-Year Exposure of XENON1T. Phys. Rev. Lett. 2018, 121, 111302. [Google Scholar] [CrossRef]
- Trotta, R.; Feroz, F.; Hobson, M.; Roszkowski, L.; Ruiz de Austri, R. The impact of priors and observables on parameter inferences in the constrained MSSM. J. High Energy Phys. 2008, 2008, 024. [Google Scholar] [CrossRef]
- Merritt, D. Cosmology and convention. Stud. Hist. Philos. Mod. Phys. 2017, 57, 41–52. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics—Implications for galaxies. Astrophys. J. 1983, 270, 371–389. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the newtonian dynamics: Implications for galaxy systems. Astrophys. J. 1983, 270, 384–389. [Google Scholar] [CrossRef]
- Milgrom, M. The modified dynamics—A status review. In Dark Matter in Astrophysics and Particle Physics; Klapdor-Kleingrothaus, H.V., Baudis, L., Eds.; Springer: Berlin, Germany, 1999; p. 443. [Google Scholar]
- Milgrom, M. MOND—A Pedagogical Review. Acta Phys. Pol. B 2001, 32, 3613. [Google Scholar]
- Bekenstein, J. The modified Newtonian dynamics - MOND and its implications for new physics. Contemp. Phys. 2006, 47, 387–403. [Google Scholar] [CrossRef]
- Milgrom, M. The MOND paradigm. arXiv 2008, arXiv:0801.3133. [Google Scholar]
- Famaey, B.; McGaugh, S.S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Relativ. 2012, 15, 10. [Google Scholar] [CrossRef]
- Milgrom, M. The MOND paradigm of modified dynamics. Scholarpedia 2014, 9, 31410. [Google Scholar] [CrossRef]
- McGaugh, S.S. A tale of two paradigms: The mutual incommensurability of ΛCDM and MOND. Can. J. Phys. 2015, 93, 250–259. [Google Scholar] [CrossRef]
- Sanders, R.H. Mass discrepancies in galaxies: Dark matter and alternatives. A&Ar 1990, 2, 1–28. [Google Scholar] [CrossRef]
- Sanders, R.H. The Published Extended Rotation Curves of Spiral Galaxies: Confrontation with Modified Dynamics. Astrophys. J. 1996, 473, 117. [Google Scholar] [CrossRef]
- McGaugh, S.S. Observational Constraints on the Acceleration Discrepancy Problem. arXiv 2006, arXiv:astro-ph/0606351. [Google Scholar]
- McGaugh, S.S.; Lelli, F.; Li, P.; Schombert, J. Dynamical Regularities in Galaxies. arXiv 2019, arXiv:1909.02011. [Google Scholar]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry and Accurate Rotation Curves. Astron. J. 2016, 152, 157. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Begeman, K.G.; Broeils, A.H.; Sanders, R.H. Extended rotation curves of spiral galaxies - Dark haloes and modified dynamics. Mon. Not. R. Astron. Soc. 1991, 249, 523–537. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Lelli, F.; Schombert, J.M. Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 201101. [Google Scholar] [CrossRef] [PubMed]
- Milgrom, M. The Mond Limit from Spacetime Scale Invariance. Astrophys. J. 2009, 698, 1630–1638. [Google Scholar] [CrossRef]
- Tully, R.B.; Fisher, J.R. A new method of determining distances to galaxies. Astron. Astrophys. 1977, 54, 661–673. [Google Scholar]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Desmond, H.; Katz, H. The baryonic Tully-Fisher relation for different velocity definitions and implications for galaxy angular momentum. Mon. Not. R. Astron. Soc. 2019, 484, 3267–3278. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Pawlowski, M.S. One Law to Rule Them All: The Radial Acceleration Relation of Galaxies. Astrophys. J. 2017, 836, 152. [Google Scholar] [CrossRef]
- Ogle, P.M.; Jarrett, T.; Lanz, L.; Cluver, M.; Alatalo, K.; Appleton, P.N.; Mazzarella, J.M. A Break in Spiral Galaxy Scaling Relations at the Upper Limit of Galaxy Mass. Astrophys. J. 2019, 884, L11. [Google Scholar] [CrossRef]
- Noordermeer, E.; van der Hulst, J.M.; Sancisi, R.; Swaters, R.S.; van Albada, T.S. The mass distribution in early-type disc galaxies: Declining rotation curves and correlations with optical properties. Mon. Not. R. Astron. Soc. 2007, 376, 1513–1546. [Google Scholar] [CrossRef]
- Noordermeer, E.; Verheijen, M.A.W. The high-mass end of the Tully-Fisher relation. Mon. Not. R. Astron. Soc. 2007, 381, 1463–1472. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. The Small Scatter of the Baryonic Tully-Fisher Relation. Astrophys. J. 2016, 816, L14. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Galaxies with Extended Rotation Curves and the Stellar Mass of Rotating Galaxies. Astrophys. J. 2005, 632, 859–871. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Pawlowski, M.S. The Relation between Stellar and Dynamical Surface Densities in the Central Regions of Disk Galaxies. Astrophys. J. 2016, 827, L19. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. Astrophys. J. 2000, 533, L99–L102. [Google Scholar] [CrossRef] [PubMed]
- Schombert, J.; McGaugh, S. Stellar Populations and the Star Formation Histories of LSB Galaxies: III. Stellar Population Models. Publ. Astron. Soc. Aust. 2014, 31, e036. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M. Color-Mass-to-light-ratio Relations for Disk Galaxies. Astron. J. 2014, 148, 77. [Google Scholar] [CrossRef]
- Schombert, J.M.; McGaugh, S. Stellar Populations and the Star Formation Histories of LSB Galaxies: IV Spitzer Surface Photometry of LSB Galaxies. Publ. Astron. Soc. Aust. 2014, 31, e011. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Lelli, F.; Schombert, J.M. Scaling Relations for Molecular Gas and Metallicity: Impact on the Baryonic Tully-Fisher Relation. Res. Notes Am. Astron. Soc. 2020, 4, 45. [Google Scholar] [CrossRef]
- Verheijen, M.A.W. The Ursa Major Cluster of Galaxies. V. H I Rotation Curve Shapes and the Tully-Fisher Relations. Astrophys. J. 2001, 563, 694–715. [Google Scholar] [CrossRef]
- Stark, D.V.; McGaugh, S.S.; Swaters, R.A. A First Attempt to Calibrate the Baryonic Tully-Fisher Relation with Gas-Dominated Galaxies. Astron. J. 2009, 138, 392–401. [Google Scholar] [CrossRef]
- Trachternach, C.; de Blok, W.J.G.; McGaugh, S.S.; van der Hulst, J.M.; Dettmar, R. The baryonic Tully-Fisher relation and its implication for dark matter halos. Astron. Astrophys. 2009, 505, 577–587. [Google Scholar] [CrossRef]
- McGaugh, S.S. Novel Test of Modified Newtonian Dynamics with Gas Rich Galaxies. Phys. Rev. Lett. 2011, 106, 121303. [Google Scholar] [CrossRef] [PubMed]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Gas-rich Galaxies as a Test of ΛCDM and MOND. Astron. J. 2012, 143, 40. [Google Scholar] [CrossRef]
- Steinmetz, M.; Navarro, J.F. The Cosmological Origin of the Tully-Fisher Relation. Astrophys. J. 1999, 513, 555–560. [Google Scholar] [CrossRef][Green Version]
- Navarro, J.F.; Steinmetz, M. The Core Density of Dark Matter Halos: A Critical Challenge to the ΛCDM Paradigm? Astrophys. J. 2000, 528, 607–611. [Google Scholar] [CrossRef]
- Mayer, L.; Moore, B. The baryonic mass-velocity relation: Clues to feedback processes during structure formation and the cosmic baryon inventory. Mon. Not. R. Astron. Soc. 2004, 354, 477–484. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; de Blok, W.J.G.; Zagursky, M.J. The Baryon Content of Cosmic Structures. Astrophys. J. 2010, 708, L14–L17. [Google Scholar] [CrossRef]
- Draine, B.T. Physics of the Interstellar and Intergalactic Medium; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Meidt, S.E.; Schinnerer, E.; van de Ven, G.; Zaritsky, D.; Peletier, R.; Knapen, J.H.; Sheth, K.; Regan, M.; Querejeta, M.; Muñoz-Mateos, J.C.; et al. Reconstructing the Stellar Mass Distributions of Galaxies Using S4G IRAC 3.6 and 4.5 μm Images. II. The Conversion from Light to Mass. Astrophys. J. 2014, 788, 144. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. The mass-to-light ratios and the star formation histories of disc galaxies. Mon. Not. R. Astron. Soc. 2019, 483, 1496–1512. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Bothun, G.D.; Schombert, J.M. Galaxy Selection and the Surface Brightness Distribution. Astron. J. 1995, 110, 573. [Google Scholar] [CrossRef]
- Akritas, M.G.; Bershady, M.A. Linear Regression for Astronomical Data with Measurement Errors and Intrinsic Scatter. Astrophys. J. 1996, 470, 706. [Google Scholar] [CrossRef]
- Begum, A.; Chengalur, J.N.; Karachentsev, I.D.; Sharina, M.E. Baryonic Tully-Fisher relation for extremely low mass Galaxies. Mon. Not. R. Astron. Soc. 2008, 386, 138–144. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M. Weighing Galaxy Disks with the Baryonic Tully-Fisher Relation. Astrophys. J. 2015, 802, 18. [Google Scholar] [CrossRef]
- Aaronson, M.; Huchra, J.; Mould, J. The infrared luminosity/H I velocity-width relation and its application to the distance scale. Astrophys. J. 1979, 229, 1–13. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Wolf, J. Local Group Dwarf Spheroidals: Correlated Deviations from the Baryonic Tully-Fisher Relation. Astrophys. J. 2010, 722, 248–261. [Google Scholar] [CrossRef]
- Mo, H.J.; Mao, S.; White, S.D.M. The formation of galactic discs. Mon. Not. R. Astron. Soc. 1998, 295, 319–336. [Google Scholar] [CrossRef]
- Bullock, J.S.; Kolatt, T.S.; Sigad, Y.; Somerville, R.S.; Kravtsov, A.V.; Klypin, A.A.; Primack, J.R.; Dekel, A. Profiles of dark haloes: Evolution, scatter and environment. Mon. Not. R. Astron. Soc. 2001, 321, 559–575. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Weinberg, D.H.; Pizagno, J.; Prada, F.; Rix, H. Dark Matter Halos of Disk Galaxies: Constraints from the Tully-Fisher Relation. Astrophys. J. 2007, 671, 1115–1134. [Google Scholar] [CrossRef]
- Trujillo-Gomez, S.; Klypin, A.; Primack, J.; Romanowsky, A.J. Galaxies in ΛCDM with Halo Abundance Matching: Luminosity-Velocity Relation, Baryonic Mass-Velocity Relation, Velocity Function, and Clustering. Astrophys. J. 2011, 742, 16. [Google Scholar] [CrossRef]
- Bullock, J.S.; Boylan-Kolchin, M. Small-Scale Challenges to the ΛCDM Paradigm. Ann. Rev. Astron. Astrophys. 2017, 55, 343–387. [Google Scholar] [CrossRef]
- van den Bosch, F.C. Semianalytical Models for the Formation of Disk Galaxies. I. Constraints from the Tully-Fisher Relation. Astrophys. J. 2000, 530, 177–192. [Google Scholar] [CrossRef][Green Version]
- Sanders, R.H. Dark matter—Modified dynamics: Reaction vs. Prediction. arXiv 2019, arXiv:1912.00716. [Google Scholar]
- Zwaan, M.A.; van der Hulst, J.M.; de Blok, W.J.G.; McGaugh, S.S. The Tully-Fisher relation for low surface brightness galaxies: implications for galaxy evolution. Mon. Not. R. Astron. Soc. 1995, 273, L35–L38. [Google Scholar] [CrossRef]
- Sprayberry, D.; Bernstein, G.M.; Impey, C.D.; Bothun, G.D. The mass-to-light ratios of low surface brightness spiral galaxies: Clues from the Tully-Fisher relation. Astrophys. J. 1995, 438, 72–82. [Google Scholar] [CrossRef]
- Hoffman, G.L.; Salpeter, E.E.; Farhat, B.; Roos, T.; Williams, H.; Helou, G. Arecibo H i Mapping of a Large Sample of Dwarf Irregular Galaxies. Astrophys. J. Suppl. 1996, 105, 269. [Google Scholar] [CrossRef]
- Freeman, K.C. On the Disks of Spiral and S0 Galaxies. Astrophys. J. 1970, 160, 811. [Google Scholar] [CrossRef]
- Courteau, S.; Rix, H. Maximal Disks and the Tully-Fisher Relation. Astrophys. J. 1999, 513, 561–571. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S. Does Low Surface Brightness Mean Low Density? Astrophys. J. 1996, 469, L89. [Google Scholar] [CrossRef]
- Tully, R.B.; Verheijen, M.A.W. The Ursa Major Cluster of Galaxies. II. Bimodality of the Distribution of Central Surface Brightnesses. Astrophys. J. 1997, 484, 145. [Google Scholar] [CrossRef]
- McGaugh, S.S. Balance of Dark and Luminous Mass in Rotating Galaxies. Phys. Rev. Lett. 2005, 95, 171302. [Google Scholar] [CrossRef]
- Starkman, N.; Lelli, F.; McGaugh, S.; Schombert, J. A new algorithm to quantify maximum discs in galaxies. Mon. Not. R. Astron. Soc. 2018, 480, 2292–2301. [Google Scholar] [CrossRef]
- Swaters, R.A.; Sancisi, R.; van Albada, T.S.; van der Hulst, J.M. The rotation curves shapes of late-type dwarf galaxies. Astron. Astrophys. 2009, 493, 871–892. [Google Scholar] [CrossRef]
- Swaters, R.A.; Sancisi, R.; van der Hulst, J.M.; van Albada, T.S. The link between the baryonic mass distribution and the rotation curve shape. Mon. Not. R. Astron. Soc. 2012, 425, 2299–2308. [Google Scholar] [CrossRef]
- Lelli, F.; Fraternali, F.; Verheijen, M. A scaling relation for disc galaxies: Circular-velocity gradient versus central surface brightness. Mon. Not. R. Astron. Soc. 2013, 433, L30–L34. [Google Scholar] [CrossRef]
- Oman, K.A.; Navarro, J.F.; Fattahi, A.; Frenk, C.S.; Sawala, T.; White, S.D.M.; Bower, R.; Crain, R.A.; Furlong, M.; Schaller, M.; et al. The unexpected diversity of dwarf galaxy rotation curves. Mon. Not. R. Astron. Soc. 2015, 452, 3650–3665. [Google Scholar] [CrossRef]
- Rubin, V.C.; Thonnard, N.; Ford, W.K., Jr. Extended rotation curves of high-luminosity spiral galaxies. IV—Systematic dynamical properties, SA through SC. Astrophys. J. 1978, 225, L107–L111. [Google Scholar] [CrossRef]
- Bosma, A. 21-cm line studies of spiral galaxies. II—The distribution and kinematics of neutral hydrogen in spiral galaxies of various morphological types. Astron. J. 1981, 86, 1825–1846. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648–2719. [Google Scholar] [CrossRef]
- Brouwer, M.M.; Visser, M.R.; Dvornik, A.; Hoekstra, H.; Kuijken, K.; Valentijn, E.A.; Bilicki, M.; Blake, C.; Brough, S.; Buddelmeijer, H.; et al. First test of Verlinde’s theory of emergent gravity using weak gravitational lensing measurements. Mon. Not. R. Astron. Soc. 2017, 466, 2547–2559. [Google Scholar] [CrossRef]
- Kent, S.M. Dark Matter in Spiral Galaxies. II. Galaxies with H I Rotation Curves. Astron. J. 1987, 93, 816. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. A comprehensive catalog of dark matter halo models for SPARC galaxies. arXiv 2020, arXiv:2001.10538. [Google Scholar] [CrossRef]
- Sellwood, J.A.; McGaugh, S.S. The Compression of Dark Matter Halos by Baryonic Infall. Astrophys. J. 2005, 634, 70–76. [Google Scholar] [CrossRef]
- Disney, M.J.; Romano, J.D.; Garcia-Appadoo, D.A.; West, A.A.; Dalcanton, J.J.; Cortese, L. Galaxies appear simpler than expected. Nature 2008, 455, 1082–1084. [Google Scholar] [CrossRef] [PubMed]
- Dubinski, J.; Mihos, J.C.; Hernquist, L. Constraining Dark Halo Potentials with Tidal Tails. Astrophys. J. 1999, 526, 607–622. [Google Scholar] [CrossRef]
- McGaugh, S.S. How Galaxies Don’t Form: The Effective Force Law in Disk Galaxies. In Galaxy Dynamics—A Rutgers Symposium; Merritt, D.R., Valluri, M., Sellwood, J.A., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 1999; Volume 182, p. 528. [Google Scholar]
- McGaugh, S.S. The Mass Discrepancy-Acceleration Relation: Disk Mass and the Dark Matter Distribution. Astrophys. J. 2004, 609, 652–666. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Non-Newtonian gravitation and causality. In Developments in General Relativity, Astrophysics and Quantum Theory; Institute of Physics Publishing: Bristol, UK, 1990; pp. 155–174. [Google Scholar]
- McGaugh, S. The Third Law of Galactic Rotation. Galaxies 2014, 2, 601–622. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S. The dark and visible matter content of low surface brightness disc galaxies. Mon. Not. R. Astron. Soc. 1997, 290, 533–552. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S. Testing Modified Newtonian Dynamics with Low Surface Brightness Galaxies: Rotation Curve FITS. Astrophys. J. 1998, 508, 132–140. [Google Scholar] [CrossRef]
- Fall, S.M.; Efstathiou, G. Formation and rotation of disc galaxies with haloes. Mon. Not. R. Astron. Soc. 1980, 193, 189–206. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Scannapieco, C.; Wadepuhl, M.; Parry, O.H.; Navarro, J.F.; Jenkins, A.; Springel, V.; Teyssier, R.; Carlson, E.; Couchman, H.M.P.; Crain, R.A.; et al. The Aquila comparison project: The effects of feedback and numerical methods on simulations of galaxy formation. Mon. Not. R. Astron. Soc. 2012, 423, 1726–1749. [Google Scholar] [CrossRef]
- Milgrom, M. Quasi-linear formulation of MOND. Mon. Not. R. Astron. Soc. 2010, 403, 886–895. [Google Scholar] [CrossRef]
- Milgrom, M.; Sanders, R.H. Rings and Shells of “Dark Matter” as MOND Artifacts. Astrophys. J. 2008, 678, 131–143. [Google Scholar] [CrossRef]
- McGaugh, S.S. Milky Way Mass Models and MOND. Astrophys. J. 2008, 683, 137–148. [Google Scholar] [CrossRef]
- Famaey, B.; Binney, J. Modified Newtonian dynamics in the Milky Way. Mon. Not. R. Astron. Soc. 2005, 363, 603–608. [Google Scholar] [CrossRef]
- Hees, A.; Famaey, B.; Angus, G.W.; Gentile, G. Combined Solar system and rotation curve constraints on MOND. Mon. Not. R. Astron. Soc. 2016, 455, 449–461. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. Fitting the radial acceleration relation to individual SPARC galaxies. Astron. Astrophys. 2018, 615, A3. [Google Scholar] [CrossRef]
- Sanders, R.H.; Verheijen, M.A.W. Rotation Curves of Ursa Major Galaxies in the Context of Modified Newtonian Dynamics. Astrophys. J. 1998, 503, 97–108. [Google Scholar] [CrossRef]
- Sanders, R.H. The prediction of rotation curves in gas-dominated dwarf galaxies with modified dynamics. Mon. Not. R. Astron. Soc. 2019, 485, 513–521. [Google Scholar] [CrossRef]
- Swaters, R.A.; Sanders, R.H.; McGaugh, S.S. Testing Modified Newtonian Dynamics with Rotation Curves of Dwarf and Low Surface Brightness Galaxies. Astrophys. J. 2010, 718, 380–391. [Google Scholar] [CrossRef]
- Gentile, G.; Famaey, B.; de Blok, W.J.G. THINGS about MOND. Astron. Astrophys. 2011, 527, A76. [Google Scholar] [CrossRef]
- Bottema, R.; Pestaña, J.L.G.; Rothberg, B.; Sand ers, R.H. MOND rotation curves for spiral galaxies with Cepheid-based distances. Astron. Astrophys. 2002, 393, 453–460. [Google Scholar] [CrossRef]
- Dutton, A.A.; Macciò, A.V. Cold dark matter haloes in the Planck era: Evolution of structural parameters for Einasto and NFW profiles. Mon. Not. R. Astron. Soc. 2014, 441, 3359–3374. [Google Scholar] [CrossRef]
- Wechsler, R.H.; Tinker, J.L. The Connection Between Galaxies and Their Dark Matter Halos. Ann. Rev. Astron. Astrophys. 2018, 56, 435–487. [Google Scholar] [CrossRef]
- Bell, E.F.; de Jong, R.S. Stellar Mass-to-Light Ratios and the Tully-Fisher Relation. Astrophys. J. 2001, 550, 212–229. [Google Scholar] [CrossRef]
- Portinari, L.; Sommer-Larsen, J.; Tantalo, R. On the mass-to-light ratio and the initial mass function in disc galaxies. Mon. Not. R. Astron. Soc. 2004, 347, 691–719. [Google Scholar] [CrossRef]
- Sancisi, R. The visible matter—Dark matter coupling. In Dark Matter in Galaxies; Ryder, S., Pisano, D., Walker, M., Freeman, K., Eds.; IAU Symposium; Cambridge University Press: Cambridge, UK, 2004; Volume 220, p. 233. [Google Scholar]
- van Albada, T.S.; Sancisi, R. Dark Matter in Spiral Galaxies. Philos. Trans. R. Soc. Lond. Ser. A 1986, 320, 447–464. [Google Scholar] [CrossRef]
- Sellwood, J.A. Dynamical Constraints on Disk Masses. In Galaxy Dynamics—A Rutgers Symposium; Merritt, D.R., Valluri, M., Sellwood, J.A., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 1999; Volume 182. [Google Scholar]
- Palunas, P.; Williams, T.B. Maximum Disk Mass Models for Spiral Galaxies. Astron. J. 2000, 120, 2884–2903. [Google Scholar] [CrossRef]
- Freeman, K.C. Dark Matter from the Observational Perspective. In American Institute of Physics Conference Series; Debattista, V.P., Popescu, C.C., Eds.; AIP Publishing: Melville, NY, USA, 2010; Volume 1240, pp. 309–318. [Google Scholar] [CrossRef]
- Verheijen, M.; de Blok, E. The HSB/LSB Galaxies NGC 2403 and UGC 128. Ap&SS 1999, 269, 673–674. [Google Scholar] [CrossRef]
- Gentile, G.; Baes, M.; Famaey, B.; van Acoleyen, K. Mass models from high-resolution HI data of the dwarf galaxy NGC 1560. Mon. Not. R. Astron. Soc. 2010, 406, 2493–2503. [Google Scholar] [CrossRef]
- Tully, R.B.; Rizzi, L.; Shaya, E.J.; Courtois, H.M.; Makarov, D.I.; Jacobs, B.A. The Extragalactic Distance Database. Astron. J. 2009, 138, 323–331. [Google Scholar] [CrossRef]
- Jacobs, B.A.; Rizzi, L.; Tully, R.B.; Shaya, E.J.; Makarov, D.I.; Makarova, L. The Extragalactic Distance Database: Color-Magnitude Diagrams. Astron. J. 2009, 138, 332–337. [Google Scholar] [CrossRef]
- Ren, T.; Kwa, A.; Kaplinghat, M.; Yu, H.B. Reconciling the Diversity and Uniformity of Galactic Rotation Curves with Self-Interacting Dark Matter. PRX 2019, 9, 031020. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Peebles, P.J.E. A Numerical Study of the Stability of Flattened Galaxies: Or, can Cold Galaxies Survive? Astrophys. J. 1973, 186, 467–480. [Google Scholar] [CrossRef]
- Sellwood, J.A. Secular evolution in disk galaxies. Rev. Mod. Phys. 2014, 86, 1–46. [Google Scholar] [CrossRef]
- Sellwood, J.A. Bar Instability in Disk-Halo Systems. Astrophys. J. 2016, 819, 92. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Shen, J.; Li, Z. The global stability of M33: Still a puzzle. Mon. Not. R. Astron. Soc. 2019, 486, 4710–4723. [Google Scholar] [CrossRef]
- Disney, M.J. Visibility of galaxies. Nature 1976, 263, 573–575. [Google Scholar] [CrossRef]
- Allen, R.J.; Shu, F.H. The extrapolated central surface brightness of galaxies. Astrophys. J. 1979, 227, 67–72. [Google Scholar] [CrossRef]
- Cross, N.; Driver, S.P. The bivariate brightness function of galaxies and a demonstration of the impact of surface brightness selection effects on luminosity function estimations. Mon. Not. R. Astron. Soc. 2002, 329, 579–587. [Google Scholar] [CrossRef]
- Milgrom, M. On Stability of Galactic Disks in the Modified Dynamics and the Distribution of Their Mean Surface-Brightness. Astrophys. J. 1989, 338, 121. [Google Scholar] [CrossRef]
- Brada, R.; Milgrom, M. Stability of Disk Galaxies in the Modified Dynamics. Astrophys. J. 1999, 519, 590–598. [Google Scholar] [CrossRef]
- Tiret, O.; Combes, F. Evolution of spiral galaxies in modified gravity. II. Gas dynamics. Astron. Astrophys. 2008, 483, 719–726. [Google Scholar] [CrossRef]
- Jiménez, M.A.; Hernandez, X. Disk stability under MONDian gravity. arXiv 2014, arXiv:1406.0537. [Google Scholar]
- Thies, I.; Kroupa, P.; Famaey, B. Simulating disk galaxies and interactions in Milgromian dynamics. arXiv 2016, arXiv:1606.04942. [Google Scholar]
- Sánchez-Salcedo, F.J.; Martínez-Gómez, E.; Aguirre-Torres, V.M.; Hernández-Toledo, H.M. Low-mass disc galaxies and the issue of stability: MOND versus dark matter. Mon. Not. R. Astron. Soc. 2016, 462, 3918–3936. [Google Scholar] [CrossRef]
- Banik, I.; Milgrom, M.; Zhao, H. Toomre stability of disk galaxies in quasi-linear MOND. arXiv 2018, arXiv:1808.10545. [Google Scholar]
- Sellwood, J.A.; Evans, N.W. The Stability of Disks in Cusped Potentials. Astrophys. J. 2001, 546, 176–188. [Google Scholar] [CrossRef]
- Dalcanton, J.J.; Spergel, D.N.; Summers, F.J. The Formation of Disk Galaxies. Astrophys. J. 1997, 482, 659–676. [Google Scholar] [CrossRef]
- Oh, S.; de Blok, W.J.G.; Walter, F.; Brinks, E.; Kennicutt, R.C. High-Resolution Dark Matter Density Profiles of THINGS Dwarf Galaxies: Correcting for Noncircular Motions. Astron. J. 2008, 136, 2761–2781. [Google Scholar] [CrossRef]
- Martinsson, T.P.K.; Verheijen, M.A.W.; Westfall, K.B.; Bershady, M.A.; Andersen, D.R.; Swaters, R.A. The DiskMass Survey. VII. The distribution of luminous and dark matter in spiral galaxies. Astron. Astrophys. 2013, 557, A131. [Google Scholar] [CrossRef]
- Bekenstein, J.; Milgrom, M. Does the missing mass problem signal the breakdown of Newtonian gravity? Astrophys. J. 1984, 286, 7–14. [Google Scholar] [CrossRef]
- Milgrom, M. Dynamics with a Nonstandard Inertia-Acceleration Relation: An Alternative to Dark Matter in Galactic Systems. Ann. Phys. 1994, 229, 384–415. [Google Scholar] [CrossRef]
- Milgrom, M. The modified dynamics as a vacuum effect. Phys. Lett. A 1999, 253, 273–279. [Google Scholar] [CrossRef]
- Milgrom, M. MOND laws of galactic dynamics. Mon. Not. R. Astron. Soc. 2014, 437, 2531–2541. [Google Scholar] [CrossRef]
- Das, M.; McGaugh, S.S.; Ianjamasimanana, R.; Schombert, J.; Dwarakanath, K.S. Tracing the Dynamical Mass in Galaxy Disks Using H i Velocity Dispersion and Its Implications for the Dark Matter Distribution in Galaxies. Astrophys. J. 2020, 889, 10. [Google Scholar] [CrossRef]
- Sanders, R.H. Clusters of galaxies with modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 2003, 342, 901–908. [Google Scholar] [CrossRef]
- Sanders, R.H. Neutrinos as cluster dark matter. Mon. Not. R. Astron. Soc. 2007, 380, 331–338. [Google Scholar] [CrossRef]
- Angus, G.W.; Famaey, B.; Buote, D.A. X-ray group and cluster mass profiles in MOND: Unexplained mass on the group scale. Mon. Not. R. Astron. Soc. 2008, 387, 1470–1480. [Google Scholar] [CrossRef]
- Tian, Y.; Umetsu, K.; Ko, C.M.; Donahue, M.; Chiu, I.N. The Radial Acceleration Relation in CLASH Galaxy Clusters. arXiv 2020, arXiv:2001.08340. [Google Scholar]
- McGaugh, S.S. The Imprint of Spiral Arms on the Galactic Rotation Curve. Astrophys. J. 2019, 885, 87. [Google Scholar] [CrossRef]
- McGaugh, S.S. The Surface Density Profile of the Galactic Disk from the Terminal Velocity Curve. Astrophys. J. 2016, 816, 42. [Google Scholar] [CrossRef]
- Lisanti, M.; Moschella, M.; Outmezguine, N.J.; Slone, O. Testing Dark Matter and Modifications to Gravity using Local Milky Way Observables. arXiv 2018, arXiv:1812.08169. [Google Scholar] [CrossRef]
- McGaugh, S.S. A Precise Milky Way Rotation Curve Model for an Accurate Galactocentric Distance. Res. Notes Am. Astron. Soc. 2018, 2, 156. [Google Scholar] [CrossRef]
- Bienaymé, O.; Famaey, B.; Siebert, A.; Freeman, K.C.; Gibson, B.K.; Gilmore, G.; Grebel, E.K.; Bland-Hawthorn, J.; Kordopatis, G.; Munari, U.; et al. Weighing the local dark matter with RAVE red clump stars. Astron. Astrophys. 2014, 571, A92. [Google Scholar] [CrossRef]
- Bershady, M.A.; Verheijen, M.A.W.; Swaters, R.A.; Andersen, D.R.; Westfall, K.B.; Martinsson, T. The DiskMass Survey. I. Overview. Astrophys. J. 2010, 716, 198–233. [Google Scholar] [CrossRef]
- Swaters, R.A.; Bershady, M.A.; Martinsson, T.P.K.; Westfall, K.B.; Andersen, D.R.; Verheijen, M.A.W. The Link between Light and Mass in Late-type Spiral Galaxy Disks. Astrophys. J. 2014, 797, L28. [Google Scholar] [CrossRef]
- Angus, G.W.; Gentile, G.; Swaters, R.; Famaey, B.; Diaferio, A.; McGaugh, S.S.; Heyden, K.J.v.d. Mass models of disc galaxies from the DiskMass Survey in modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 2015, 451, 3551–3580. [Google Scholar] [CrossRef][Green Version]
- Milgrom, M. Critical take on “Mass models of disk galaxies from the DiskMass Survey in MOND”. arXiv 2015, arXiv:1511.08087. [Google Scholar]
- Angus, G.W.; Gentile, G.; Famaey, B. Dynamical measurement of the stellar surface density of face-on galaxies. Astron. Astrophys. 2016, 585, A17. [Google Scholar] [CrossRef]
- Aniyan, S.; Freeman, K.C.; Gerhard, O.E.; Arnaboldi, M.; Flynn, C. The influence of a kinematically cold young component on disc-halo decompositions in spiral galaxies: Insights from solar neighbourhood K-giants. Mon. Not. R. Astron. Soc. 2016, 456, 1484–1494. [Google Scholar] [CrossRef][Green Version]
- Meurer, G.R.; Staveley-Smith, L.; Killeen, N.E.B. HI and dark matter in the windy starburst dwarf galaxy NGC 1705. Mon. Not. R. Astron. Soc. 1998, 300, 705–717. [Google Scholar] [CrossRef][Green Version]
- Olling, R.P. The Highly Flattened Dark Matter Halo of NGC 4244. Astron. J. 1996, 112, 481. [Google Scholar] [CrossRef]
- Matthews, L.D.; Gallagher, J.S.I.; van Driel, W. The Extraordinary “Superthin” Spiral Galaxy UGC 7321. I. Disk Color Gradients and Global Properties from Multiwavelength Observations. Astron. J. 1999, 118, 2751–2766. [Google Scholar] [CrossRef]
- Matthews, L.D. The Extraordinary “Superthin” Spiral Galaxy UGC 7321. II. The Vertical Disk Structure. Astron. J. 2000, 120, 1764–1778. [Google Scholar] [CrossRef][Green Version]
- Matthews, L.D.; Uson, J.M. H I Imaging Observations of Superthin Galaxies. II. IC 2233 and the Blue Compact Dwarf NGC 2537. Astron. J. 2008, 135, 291–318. [Google Scholar] [CrossRef][Green Version]
- Springel, V.; White, S.D.M.; Hernquist, L. The shapes of simulated dark matter halos. In Dark Matter in Galaxies; Ryder, S., Pisano, D., Walker, M., Freeman, K., Eds.; IAU Symposium; Cambridge University Press: Cambridge, UK, 2004; Volume 220, p. 421. [Google Scholar]
- Chua, K.T.E.; Pillepich, A.; Vogelsberger, M.; Hernquist, L. Shape of dark matter haloes in the Illustris simulation: Effects of baryons. Mon. Not. R. Astron. Soc. 2019, 484, 476–493. [Google Scholar] [CrossRef]
- Mihos, J.C.; McGaugh, S.S.; de Blok, W.J.G. Dynamical Stability and Environmental Influences in Low Surface Brightness Disk Galaxies. Astrophys. J. 1997, 477, L79–L83. [Google Scholar] [CrossRef]
- Athanassoula, E.; Bosma, A.; Papaioannou, S. Halo parameters of spiral galaxies. Astron. Astrophys. 1987, 179, 23–40. [Google Scholar]
- Peters, W.; Kuzio de Naray, R. Characterizing bars in low surface brightness disc galaxies. Mon. Not. R. Astron. Soc. 2018, 476, 2938–2961. [Google Scholar] [CrossRef]
- Schombert, J.; Maciel, T.; McGaugh, S.S. Stellar Populations and the Star Formation Histories of LSB Galaxies—Part I: Optical and Hα Imaging. Adv. Astron. 2011, 2011, 143698. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D. The Morphology of Low Surface Brightness Disk Galaxies. Astron. J. 1995, 109, 2019. [Google Scholar] [CrossRef]
- Schombert, J.M. On the Structural Differences between Disk and Dwarf Galaxies. Astron. J. 2006, 131, 296–303. [Google Scholar] [CrossRef][Green Version]
- Peters, W.; Kuzio de Naray, R. Bar properties and photometry of barred low surface brightness disc galaxies. Mon. Not. R. Astron. Soc. 2019, 484, 850–868. [Google Scholar] [CrossRef]
- Debattista, V.P.; Sellwood, J.A. Constraints from Dynamical Friction on the Dark Matter Content of Barred Galaxies. Astrophys. J. 2000, 543, 704–721. [Google Scholar] [CrossRef]
- Weiner, B.J.; Williams, T.B.; van Gorkom, J.H.; Sellwood, J.A. The Disk and Dark Halo Mass of the Barred Galaxy NGC 4123. I. Observations. Astrophys. J. 2001, 546, 916–930. [Google Scholar] [CrossRef]
- Bovy, J.; Rix, H.W. A Direct Dynamical Measurement of the Milky Way’s Disk Surface Density Profile, Disk Scale Length, and Dark Matter Profile at 4 kpc <~ R <~ 9 kpc. Astrophys. J. 2013, 779, 115. [Google Scholar] [CrossRef]
- Fuchs, B. Massive disks in low surface brightness galaxies. Astrophys. Space Sci. 2003, 284, 719–722. [Google Scholar] [CrossRef]
- Bland-Hawthorn, J.; Gerhard, O. The Galaxy in Context: Structural, Kinematic, and Integrated Properties. Ann. Rev. Astron. Astrophys. 2016, 54, 529–596. [Google Scholar] [CrossRef]
- Fuchs, B. Dynamics of the disks of nearby galaxies. Astron. Nachrichten 2008, 329, 916. [Google Scholar] [CrossRef]
- Saburova, A.S.; Zasov, A.V. Gravitational stability and mass estimation of stellar disks. Astron. Nachrichten 2013, 334, 785. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; McGaugh, S.S.; van der Hulst, J.M. HI observations of low surface brightness galaxies: Probing low-density galaxies. Mon. Not. R. Astron. Soc. 1996, 283, 18–54. [Google Scholar] [CrossRef]
- van den Bosch, F.C.; Robertson, B.E.; Dalcanton, J.J.; de Blok, W.J.G. Constraints on the Structure of Dark Matter Halos from the Rotation Curves of Low Surface Brightness Galaxies. Astron. J. 2000, 119, 1579–1591. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Rubin, V.C.; de Blok, W.J.G. High-Resolution Rotation Curves of Low Surface Brightness Galaxies. I. Data. Astron. J. 2001, 122, 2381–2395. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Bosma, A. High-resolution rotation curves of low surface brightness galaxies. Astron. Astrophys. 2002, 385, 816–846. [Google Scholar] [CrossRef]
- Swaters, R.A.; Madore, B.F.; van den Bosch, F.C.; Balcells, M. The Central Mass Distribution in Dwarf and Low Surface Brightness Galaxies. Astrophys. J. 2003, 583, 732–751. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Bosma, A.; McGaugh, S. Simulating observations of dark matter dominated galaxies: Towards the optimal halo profile. Mon. Not. R. Astron. Soc. 2003, 340, 657–678. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; McGaugh, S.S.; de Blok, W.J.G.; Bosma, A. High-Resolution Optical Velocity Fields of 11 Low Surface Brightness Galaxies. Astrophys. J. 2006, 165, 461–479. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; McGaugh, S.S.; de Blok, W.J.G. Mass Models for Low Surface Brightness Galaxies with High-Resolution Optical Velocity Fields. Astrophys. J. 2008, 676, 920–943. [Google Scholar] [CrossRef]
- Hayashi, E.; Navarro, J.F.; Springel, V. The shape of the gravitational potential in cold dark matter haloes. Mon. Not. R. Astron. Soc. 2007, 377, 50–62. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; McGaugh, S.S.; Mihos, J.C. Constraining the NFW Potential with Observations and Modeling of Low Surface Brightness Galaxy Velocity Fields. Astrophys. J. 2009, 692, 1321–1332. [Google Scholar] [CrossRef]
- Kuzio de Naray, R.; Kaufmann, T. Recovering cores and cusps in dark matter haloes using mock velocity field observations. Mon. Not. R. Astron. Soc. 2011, 414, 3617–3626. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Benítez-Llambay, A.; Schaller, M.; Theuns, T.; Frenk, C.S.; Bower, R.; Schaye, J.; Crain, R.A.; Navarro, J.F.; Fattahi, A. Mass-Discrepancy Acceleration Relation: A Natural Outcome of Galaxy Formation in Cold Dark Matter Halos. Phys. Rev. Lett. 2017, 118, 161103. [Google Scholar] [CrossRef] [PubMed]
- Navarro, J.F.; Benítez-Llambay, A.; Fattahi, A.; Frenk, C.S.; Ludlow, A.D.; Oman, K.A.; Schaller, M.; Theuns, T. The origin of the mass discrepancy-acceleration relation in ΛCDM. Mon. Not. R. Astron. Soc. 2017, 471, 1841–1848. [Google Scholar] [CrossRef]
- Dutton, A.A.; Macciò, A.V.; Obreja, A.; Buck, T. NIHAO-XVIII. Origin of the MOND phenomenology of galactic rotation curves in a ΛCDM universe. Mon. Not. R. Astron. Soc. 2019, 485, 1886–1899. [Google Scholar] [CrossRef]
- Wheeler, C.; Hopkins, P.F.; Doré, O. The Radial Acceleration Relation Is a Natural Consequence of the Baryonic Tully-Fisher Relation. Astrophys. J. 2019, 882, 46. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Milgrom, M. Andromeda Dwarfs in Light of Modified Newtonian Dynamics. Astrophys. J. 2013, 766, 22. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Milgrom, M. Andromeda Dwarfs in Light of MOND. II. Testing Prior Predictions. Astrophys. J. 2013, 775, 139. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; McGaugh, S.S. Perseus I and the NGC 3109 association in the context of the Local Group dwarf galaxy structures. Mon. Not. R. Astron. Soc. 2014, 440, 908–919. [Google Scholar] [CrossRef]
- McGaugh, S.S. MOND Prediction for the Velocity Dispersion of the “Feeble Giant” Crater II. Astrophys. J. 2016, 832, L8. [Google Scholar] [CrossRef]
- Rodrigues, D.C.; Marra, V.; del Popolo, A.; Davari, Z. Absence of a fundamental acceleration scale in galaxies. Nat. Astron. 2018, 2, 668–672. [Google Scholar] [CrossRef]
- Zhao, H.; Li, B. Dark Fluid: A Unified Framework for Modified Newtonian Dynamics, Dark Matter, and Dark Energy. Astrophys. J. 2010, 712, 130–141. [Google Scholar] [CrossRef]
- Blanchet, L. Gravitational polarization and the phenomenology of MOND. Class. Quantum Gravity 2007, 24, 3529–3539. [Google Scholar] [CrossRef]
- Berezhiani, L.; Khoury, J. Theory of dark matter superfluidity. Phys. Rev. D 2015, 92, 103510. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Relativistic gravitation theory for the modified Newtonian dynamics paradigm. Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Milgrom, M. Bimetric MOND gravity. Phys. Rev. D 2009, 80, 123536. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Skordis, C.; Złośnik, T. Gravitational alternatives to dark matter with tensor mode speed equaling the speed of light. Phys. Rev. D 2019, 100, 104013. [Google Scholar] [CrossRef]
- Hernandez, X.; Sussman, R.A.; Nasser, L. Approaching the Dark Sector through a bounding curvature criterion. Mon. Not. R. Astron. Soc. 2019, 483, 147–151. [Google Scholar] [CrossRef]
| 1. | It is also possible to mistakenly conclude that MOND is incorrect [39] by utilizing an inadequate proxy for [40,41]. |
| 2. | The NASA/IPAC Extragalactic Database (NED) is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. |
| 3. | Systematic errors were repeatedly invoked. First it was beam smearing [192]. This was a legitimate concern in a minority of cases; it was addressed by improving the spatial resolution of the data with long slit observations [193,194]. Then concerns were raised that these observations suffered from slit alignment errors [195]. This was never a serious concern [193,196], as confirmed by subsequent improvements to the data [197,198]. A variety of physical effects were then invoked; e.g., grossly non-circular motions [199], which could also be excluded [200,201]. This is what it looks like when the normal component makes excuses to disregard the obvious implications of inconvenient data. |
| 4. | At the 2006 conference Galaxies in the Cosmic Web, I showed [99] that the systematic dependence of the mass discrepancy on acceleration seen in Figure 2b was true empirically irrespective of MOND. In response, a prominent galaxy formation theorist shouted, “We don’t have to explain MOND!” |
| 5. | Recent papers describing the observed MONDian phenomenology as natural in CDM include [131,202,203,204,205]. If it were natural, it would have fallen out of CDM models long ago [4,69]. |
| 6. | Most commonly, Y = clusters of galaxies or large scale structure. These are discussed in [24] and references therein. |
| 7. | The literature contains contradictory statements on this point [210], but these usually stem from holding MOND to a higher standard than dark matter. Galaxies that have bad fits in MOND also have bad dark matter fits (in terms of [94]). This is a sign that the uncertainties have been underestimated, not that must vary or that all conceivable models are wrong. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).