Dark Matter Haloes and Subhaloes
Abstract
| Contents | |
| 1 Introduction | 2 |
| 2 Formation of Dark Matter Haloes | 3 |
| 2.1 Initial Conditions: The Primordial Power Spectrum in the Linear Regime | 3 |
| 2.2 The Non-Linear Regime: N-Body Simulation Methods | 5 |
| 2.3 The Non-Linear Regime: Initial Conditions and The Emergence of the CosmicWeb | 7 |
| 2.4 The Structural Properties of Dark Matter Haloes | 11 |
| 3 Halo Mergers and the Emergence of Subhaloes | 18 |
| 3.1 Halo Mass Assembly: Smooth Accretion vs Mergers | 18 |
| 3.2 Evolution of Subhaloes: Initial Conditions | 19 |
| 3.3 Dynamics of Subhaloes | 21 |
| 3.4 The Abundance, Spatial Distribution and Internal Structure of Dark Matter Subhaloes | 28 |
| 3.5 The Impact of the Nature of the Dark Matter | 32 |
| 4 Outlook | 33 |
| 4.1 The Impact of Baryonic Physics on Dark Matter Structure | 34 |
| 4.2 Astrophysical Tests of the Nature of the Dark Matter | 36 |
| References | 39 |
1. Introduction
2. Formation of Dark Matter Haloes
2.1. Initial Conditions: The Primordial Power Spectrum in the Linear Regime
2.2. The Non-Linear Regime: N-Body Simulation Methods
2.3. The Non-Linear Regime: Initial Conditions and The Emergence of the Cosmic Web
- (i)
- create a realization of an unperturbed cube of side L by distributing N particles homogeneously in a lattice or in a glass-like configuration15 to avoid imprinting a grid-like pattern in the simulation.
- (ii)
- perturbations of wavelength down to the Nyquist frequency of the particle distribution are represented by plane waves of spatial frequency in Fourier space, , whose amplitudes and phases are drawn at random from a Gaussian distribution with variance proportional to the desired linear power spectrum. The density field and its gravitational potential in real space are then obtained by an inverse Fourier transform. Using the Zel’dovich approximation [70], or the more accurate second-order Lagrangian perturbation theory (e.g., [71]), these fields are used to compute the displacements needed to transform the uniform N-particle distribution in part (i) into a distribution that has the desired power spectrum.
2.4. The Structural Properties of Dark Matter Haloes
3. Halo Mergers and the Emergence of Subhaloes
3.1. Halo Mass Assembly: Smooth Accretion vs Mergers
3.2. Evolution of Subhaloes: Initial Conditions
3.3. Dynamics of Subhaloes
3.4. The Abundance, Spatial Distribution and Internal Structure of Dark Matter Subhaloes
3.5. The Impact of the Nature of the Dark Matter
4. Outlook
4.1. The Impact of Baryonic Physics on Dark Matter Structure
4.2. Astrophysical Tests of the Nature of the Dark Matter
Funding
Acknowledgments
Conflicts of Interest
References
- Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Walker, M.G.; Mateo, M.; Olszewski, E.W.; Peñarrubia, J.; Evans, N.W.; Gilmore, G. A Universal Mass Profile for Dwarf Spheroidal Galaxies? Astrophys. J. 2009, 704, 1274–1287. [Google Scholar] [CrossRef]
- Łokas, E.L.; Mamon, G.A. Dark matter distribution in the Coma cluster from galaxy kinematics: Breaking the mass-anisotropy degeneracy. Mon. Not. R. Astron. Soc. 2003, 343, 401–412. [Google Scholar]
- Springel, V.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef] [PubMed]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Kahlhoefer, F. Review of LHC dark matter searches. Int. J. Mod. Phys. A 2017, 32, 1730006. [Google Scholar] [CrossRef]
- Xenon Collaboration. Dark Matter Search Results from a One Ton-Year Exposure of XENON1T. Phys. Rev. Lett. 2018, 121, 111302. [Google Scholar] [CrossRef]
- ADMX Collaboration. Search for Invisible Axion Dark Matter with the Axion Dark Matter Experiment. Phys. Rev. Lett. 2018, 120, 151301. [Google Scholar] [CrossRef]
- Fermi-LAT Collaboration; DES Collaboration. Searching for Dark Matter Annihilation in Recently Discovered Milky Way Satellites with Fermi-Lat. Astrophys. J. 2017, 834, 110. [Google Scholar] [CrossRef]
- Horiuchi, S.; Humphrey, P.J.; Oñorbe, J.; Abazajian, K.N.; Kaplinghat, M.; Garrison-Kimmel, S. Sterile neutrino dark matter bounds from galaxies of the Local Group. Phys. Rev. D 2014, 89, 025017. [Google Scholar] [CrossRef]
- Gondolo, P.; Gelmini, G. Cosmic abundances of stable particles: Improved analysis. Nucl. Phys. B 1991, 360, 145–179. [Google Scholar] [CrossRef]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric dark matter. Phys. Rep. 1996, 267, 195–373. [Google Scholar] [CrossRef]
- Davis, M.; Efstathiou, G.; Frenk, C.S.; White, S.D.M. The evolution of large-scale structure in a universe dominated by cold dark matter. Astrophys. J. 1985, 292, 371–394. [Google Scholar] [CrossRef]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of the invisible axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar] [CrossRef]
- Boyarsky, A.; Drewes, M.; Lasserre, T.; Mertens, S.; Ruchayskiy, O. Sterile Neutrino Dark Matter. arXiv 2018, arXiv:1807.07938. [Google Scholar] [CrossRef]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef]
- Tulin, S.; Yu, H.B. Dark matter self-interactions and small scale structure. Phys. Rep. 2018, 730, 1–57. [Google Scholar] [CrossRef]
- Zurek, K.M. Asymmetric Dark Matter: Theories, signatures, and constraints. Phys. Rep. 2014, 537, 91–121. [Google Scholar] [CrossRef]
- Buckley, M.R.; Zavala, J.; Cyr-Racine, F.Y.; Sigurdson, K.; Vogelsberger, M. Scattering, damping, and acoustic oscillations: Simulating the structure of dark matter halos with relativistic force carriers. Phys. Rev. D 2014, 90, 043524. [Google Scholar] [CrossRef]
- Cyr-Racine, F.Y.; Sigurdson, K.; Zavala, J.; Bringmann, T.; Vogelsberger, M.; Pfrommer, C. ETHOS: An effective theory of structure formation: From dark particle physics to the matter distribution of the Universe. Phys. Rev. D 2016, 93, 123527. [Google Scholar] [CrossRef]
- Meszaros, P. The behaviour of point masses in an expanding cosmological substratum. Astron. Astrophys. 1974, 37, 225–228. [Google Scholar]
- Green, A.M.; Hofmann, S.; Schwarz, D.J. The first WIMPy halos. J. Cosm. Part. Phys. 2005, 8, 3. [Google Scholar] [CrossRef]
- Bringmann, T. Particle models and the small-scale structure of dark matter. New J. Phys. 2009, 11, 105027. [Google Scholar] [CrossRef]
- Bœhm, C.; Riazuelo, A.; Hansen, S.H.; Schaeffer, R. Interacting dark matter disguised as warm dark matter. Phys. Rev. D 2002, 66, 083505. [Google Scholar] [CrossRef]
- Bœhm, C.; Schewtschenko, J.A.; Wilkinson, R.J.; Baugh, C.M.; Pascoli, S. Using the Milky Way satellites to study interactions between cold dark matter and radiation. Mon. Not. R. Astron. Soc. 2014, 445, L31–L35. [Google Scholar] [CrossRef]
- Loeb, A.; Zaldarriaga, M. Small-scale power spectrum of cold dark matter. Phys. Rev. D 2005, 71, 103520. [Google Scholar] [CrossRef]
- Viel, M.; Becker, G.D.; Bolton, J.S.; Haehnelt, M.G. Warm dark matter as a solution to the small scale crisis: New constraints from high redshift Lyman-α forest data. Phys. Rev. D 2013, 88, 043502. [Google Scholar] [CrossRef]
- Schive, H.Y.; Chiueh, T.; Broadhurst, T.; Huang, K.W. Contrasting Galaxy Formation from Quantum Wave Dark Matter, ψDM, with ΛCDM, using Planck and Hubble Data. Astrophys. J. 2016, 818, 89. [Google Scholar] [CrossRef]
- Cole, S.; Percival, W.J.; Peacock, J.A.; Norberg, P.; Baugh, C.M.; Frenk, C.S.; Baldry, I.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; et al. The 2dF Galaxy Redshift Survey: Power-spectrum analysis of the final data set and cosmological implications. Mon. Not. R. Astron. Soc. 2005, 362, 505–534. [Google Scholar] [CrossRef]
- Percival, W.J.; Nichol, R.C.; Eisenstein, D.J.; Frieman, J.A.; Fukugita, M.; Loveday, J.; Pope, A.C.; Schneider, D.P.; Szalay, A.S.; Tegmark, M.; et al. The Shape of the Sloan Digital Sky Survey Data Release 5 Galaxy Power Spectrum. Astrophys. J. 2007, 657, 645–663. [Google Scholar] [CrossRef]
- Zavala, J.; Lovell, M.R.; Vogelsberger, M.; Burger, J.D. The diverse dark matter density at sub-kiloparsec scales in Milky Way satellites:implications for the nature of dark matter. arXiv 2019, arXiv:1904.09998. [Google Scholar]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The cosmological constant. Annu. Rev. Astron. Astrophys. 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Baumann, D.; Nicolis, A.; Senatore, L.; Zaldarriaga, M. Cosmological non-linearities as an effective fluid. J. Cosmol. Astropart. Phys. 2012, 7, 51. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Hertzberg, M.P.; Senatore, L. The effective field theory of cosmological large scale structures. J. High Energy Phys. 2012, 9, 82. [Google Scholar] [CrossRef]
- Gunn, J.E.; Gott, J.R., III. On the Infall of Matter Into Clusters of Galaxies and Some Effects on Their Evolution. Astrophys. J. 1972, 176, 1. [Google Scholar] [CrossRef]
- Sheth, R.K.; Mo, H.J.; Tormen, G. Ellipsoidal collapse and an improved model for the number and spatial distribution of dark matter haloes. Mon. Not. R. Astron. Soc. 2001, 323, 1–12. [Google Scholar] [CrossRef]
- Cooray, A.; Sheth, R. Halo models of large scale structure. Phys. Rep. 2002, 372, 1–129. [Google Scholar] [CrossRef]
- Davis, M.; Peebles, P.J.E. On the integration of the BBGKY equations for the development of strongly nonlinear clustering in an expanding universe. Astrophys. J. Suppl. 1977, 34, 425–450. [Google Scholar] [CrossRef]
- Smith, R.E.; Peacock, J.A.; Jenkins, A.; White, S.D.M.; Frenk, C.S.; Pearce, F.R.; Thomas, P.A.; Efstathiou, G.; Couchman, H.M.P. Stable clustering, the halo model and non-linear cosmological power spectra. Mon. Not. R. Astron. Soc. 2003, 341, 1311–1332. [Google Scholar] [CrossRef]
- Afshordi, N.; Mohayaee, R.; Bertschinger, E. Hierarchy in the phase space and dark matter astronomy. Phys. Rev. D 2010, 81, 101301. [Google Scholar] [CrossRef]
- Zavala, J.; Afshordi, N. Clustering in the phase space of dark matter haloes—II. Stable clustering and dark matter annihilation. Mon. Not. R. Astron. Soc. 2014, 441, 1329–1339. [Google Scholar] [CrossRef]
- Zavala, J.; Afshordi, N. Universal clustering of dark matter in phase space. Mon. Not. R. Astron. Soc. 2016, 457, 986–992. [Google Scholar] [CrossRef]
- Hahn, O.; Abel, T.; Kaehler, R. A new approach to simulating collisionless dark matter fluids. Mon. Not. R. Astron. Soc. 2013, 434, 1171–1191. [Google Scholar] [CrossRef]
- Angulo, R.E.; Hahn, O.; Abel, T. The warm dark matter halo mass function below the cut-off scale. Mon. Not. R. Astron. Soc. 2013, 434, 3337–3347. [Google Scholar] [CrossRef]
- Dehnen, W.; Read, J.I. N-body simulations of gravitational dynamics. Eur. Phys. J. Plus 2011, 126, 55. [Google Scholar] [CrossRef]
- Dehnen, W. Towards optimal softening in three-dimensional N-body codes—I. Minimizing the force error. Mon. Not. R. Astron. Soc. 2001, 324, 273–291. [Google Scholar] [CrossRef]
- Klypin, A.A.; Shandarin, S.F. Three-dimensional numerical model of the formation of large-scale structure in the Universe. Mon. Not. R. Astron. Soc. 1983, 204, 891–907. [Google Scholar] [CrossRef]
- Melott, A.L. Massive neutrinos in large-scale gravitational clustering. Astrophys. J. 1983, 264, 59–78. [Google Scholar] [CrossRef]
- Frenk, C.S.; White, S.D.M.; Davis, M. Nonlinear evolution of large-scale structure in the universe. Astrophys. J. 1983, 271, 417–430. [Google Scholar] [CrossRef]
- Hockney, R.W.; Eastwood, J.W. Computer Simulation Using Particles; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Efstathiou, G.; Eastwood, J.W. On the clustering of particles in an expanding universe. Mon. Not. R. Astron. Soc. 1981, 194, 503–525. [Google Scholar] [CrossRef]
- Barnes, J.; Hut, P. A hierarchical O(N log N) force-calculation algorithm. Nature 1986, 324, 446–449. [Google Scholar] [CrossRef]
- Springel, V. The cosmological simulation code GADGET-2. Mon. Not. R. Astron. Soc. 2005, 364, 1105–1134. [Google Scholar] [CrossRef]
- Kochanek, C.S.; White, M. A Quantitative Study of Interacting Dark Matter in Halos. Astrophys. J. 2000, 543, 514–520. [Google Scholar] [CrossRef]
- Davé, R.; Spergel, D.N.; Steinhardt, P.J.; Wandelt, B.D. Halo Properties in Cosmological Simulations of Self-interacting Cold Dark Matter. Astrophys. J. 2001, 547, 574–589. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Loeb, A. Subhaloes in self-interacting galactic dark matter haloes. Mon. Not. R. Astron. Soc. 2012, 423, 3740–3752. [Google Scholar] [CrossRef]
- Rocha, M.; Peter, A.H.G.; Bullock, J.S.; Kaplinghat, M.; Garrison-Kimmel, S.; Oñorbe, J.; Moustakas, L.A. Cosmological simulations with self-interacting dark matter—I. Constant-density cores and substructure. Mon. Not. R. Astron. Soc. 2013, 430, 81–104. [Google Scholar] [CrossRef]
- Robertson, A.; Massey, R.; Eke, V. Cosmic particle colliders: Simulations of self-interacting dark matter with anisotropic scattering. Mon. Not. R. Astron. Soc. 2017, 467, 4719–4730. [Google Scholar] [CrossRef]
- Lynden-Bell, D.; Eggleton, P.P. On the consequences of the gravothermal catastrophe. Mon. Not. R. Astron. Soc. 1980, 191, 483–498. [Google Scholar] [CrossRef]
- Koda, J.; Shapiro, P.R. Gravothermal collapse of isolated self-interacting dark matter haloes: N-body simulation versus the fluid model. Mon. Not. R. Astron. Soc. 2011, 415, 1125–1137. [Google Scholar] [CrossRef]
- Schive, H.Y.; Chiueh, T.; Broadhurst, T. Cosmic structure as the quantum interference of a coherent dark wave. Nat. Phys. 2014, 10, 496–499. [Google Scholar] [CrossRef]
- Mocz, P.; Vogelsberger, M.; Robles, V.H.; Zavala, J.; Boylan-Kolchin, M.; Fialkov, A.; Hernquist, L. Galaxy formation with BECDM—I. Turbulence and relaxation of idealized haloes. Mon. Not. R. Astron. Soc. 2017, 471, 4559–4570. [Google Scholar] [CrossRef] [PubMed]
- Efstathiou, G.; Davis, M.; White, S.D.M.; Frenk, C.S. Numerical techniques for large cosmological N-body simulations. Astrophys. J. Suppl. 1985, 57, 241–260. [Google Scholar] [CrossRef]
- Hahn, O.; Abel, T. Multi-scale initial conditions for cosmological simulations. Mon. Not. R. Astron. Soc. 2011, 415, 2101–2121. [Google Scholar] [CrossRef]
- Jenkins, A. A new way of setting the phases for cosmological multiscale Gaussian initial conditions. Mon. Not. R. Astron. Soc. 2013, 434, 2094–2120. [Google Scholar] [CrossRef]
- Sirko, E. Initial Conditions to Cosmological N-Body Simulations, or, How to Run an Ensemble of Simulations. Astrophys. J. 2005, 634, 728–743. [Google Scholar] [CrossRef]
- Mo, H.; van den Bosch, F.C.; White, S. Galaxy Formation and Evolution; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- White, S.D.M. Formation and Evolution of Galaxies. In Cosmology and Large Scale Structure; Schaeffer, R., Silk, J., Spiro, M., Zinn-Justin, J., Eds.; Cambridge University Press: Cambridge, UK, 1996; p. 349. [Google Scholar]
- Zel’dovich, Y.B. Gravitational instability: An approximate theory for large density perturbations. Astron. Astrophys. 1970, 5, 84–89. [Google Scholar]
- Jenkins, A. Second-order Lagrangian perturbation theory initial conditions for resimulations. Mon. Not. R. Astron. Soc. 2010, 403, 1859–1872. [Google Scholar] [CrossRef]
- Pontzen, A.; Roškar, R.; Stinson, G.S.; Woods, R.; Reed, D.M.; Coles, J.; Quinn, T.R. Pynbody: Astrophysics Simulation Analysis for Python. Astrophysics Source Code Library. ascl:1305.002. 2013. Available online: https://pynbody.github.io/pynbody/#acknowledging-pynbody-in-scientific-publications (accessed on 24 September 2019).
- Smith, R.E.; Markovic, K. Testing the warm dark matter paradigm with large-scale structures. Phys. Rev. D 2011, 84, 063507. [Google Scholar] [CrossRef]
- Wang, J.; White, S.D.M. Discreteness effects in simulations of hot/warm dark matter. Mon. Not. R. Astron. Soc. 2007, 380, 93–103. [Google Scholar] [CrossRef]
- Lovell, M.R.; Frenk, C.S.; Eke, V.R.; Jenkins, A.; Gao, L.; Theuns, T. The properties of warm dark matter haloes. Mon. Not. R. Astron. Soc. 2014, 439, 300–317. [Google Scholar] [CrossRef]
- Hobbs, A.; Read, J.I.; Agertz, O.; Iannuzzi, F.; Power, C. NOVel Adaptive softening for collisionless N-body simulations: Eliminating spurious haloes. Mon. Not. R. Astron. Soc. 2016, 458, 468–479. [Google Scholar] [CrossRef][Green Version]
- Boylan-Kolchin, M.; Springel, V.; White, S.D.M.; Jenkins, A.; Lemson, G. Resolving cosmic structure formation with the Millennium-II Simulation. Mon. Not. R. Astron. Soc. 2009, 398, 1150–1164. [Google Scholar] [CrossRef]
- Frenk, C.S.; White, S.D.M.; Davis, M.; Efstathiou, G. The formation of dark halos in a universe dominated by cold dark matter. Astrophys. J. 1988, 327, 507–525. [Google Scholar] [CrossRef]
- Kuhlen, M.; Vogelsberger, M.; Angulo, R. Numerical simulations of the dark universe: State of the art and the next decade. Phys. Dark Univ. 2012, 1, 50–93. [Google Scholar] [CrossRef]
- Potter, D.; Stadel, J.; Teyssier, R. PKDGRAV3: beyond trillion particle cosmological simulations for the next era of galaxy surveys. Comput. Astrophys. Cosmol. 2017, 4, 2. [Google Scholar] [CrossRef]
- Geller, M.J.; Huchra, J.P. Mapping the universe. Science 1989, 246, 897–903. [Google Scholar] [CrossRef]
- Gott, J.R., III; Jurić, M.; Schlegel, D.; Hoyle, F.; Vogeley, M.; Tegmark, M.; Bahcall, N.; Brinkmann, J. A Map of the Universe. Astrophys. J. 2005, 624, 463–484. [Google Scholar] [CrossRef]
- Colless, M.; Dalton, G.; Maddox, S.; Sutherland, W.; Norberg, P.; Cole, S.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Collins, C.; et al. The 2dF Galaxy Redshift Survey: Spectra and redshifts. Mon. Not. R. Astron. Soc. 2001, 328, 1039–1063. [Google Scholar] [CrossRef]
- Croton, D.J.; Springel, V.; White, S.D.M.; De Lucia, G.; Frenk, C.S.; Gao, L.; Jenkins, A.; Kauffmann, G.; Navarro, J.F.; Yoshida, N. The many lives of active galactic nuclei: Cooling flows, black holes and the luminosities and colours of galaxies. Mon. Not. R. Astron. Soc. 2006, 365, 11–28. [Google Scholar] [CrossRef]
- Springel, V.; Frenk, C.S.; White, S.D.M. The large-scale structure of the Universe. Nature 2006, 440, 1137–1144. [Google Scholar] [CrossRef] [PubMed]
- Bardeen, J.M.; Bond, J.R.; Kaiser, N.; Szalay, A.S. The statistics of peaks of Gaussian random fields. Astrophys. J. 1986, 304, 15–61. [Google Scholar] [CrossRef]
- White, S.D.M.; Frenk, C.S. Galaxy formation through hierarchical clustering. Astrophys. J. 1991, 379, 52–79. [Google Scholar] [CrossRef]
- Kauffmann, G.; Nusser, A.; Steinmetz, M. Galaxy formation and large-scale bias. Mon. Not. R. Astron. Soc. 1997, 286, 795–811. [Google Scholar] [CrossRef]
- Kauffmann, G.; Colberg, J.M.; Diaferio, A.; White, S.D.M. Clustering of galaxies in a hierarchical universe—I. Methods and results at z = 0. Mon. Not. R. Astron. Soc. 1999, 303, 188–206. [Google Scholar] [CrossRef]
- Benson, A.J.; Cole, S.; Frenk, C.S.; Baugh, C.M.; Lacey, C.G. The nature of galaxy bias and clustering. Mon. Not. R. Astron. Soc. 2000, 311, 793–808. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Tormen, G.; Kauffmann, G. Populating a cluster of galaxies—I. Results at [formmu2]z = 0. Mon. Not. R. Astron. Soc. 2001, 328, 726–750. [Google Scholar] [CrossRef]
- Lacey, C.G.; Baugh, C.M.; Frenk, C.S.; Benson, A.J.; Bower, R.G.; Cole, S.; Gonzalez-Perez, V.; Helly, J.C.; Lagos, C.D.P.; Mitchell, P.D. A unified multiwavelength model of galaxy formation. Mon. Not. R. Astron. Soc. 2016, 462, 3854–3911. [Google Scholar] [CrossRef]
- White, S.D.M.; Frenk, C.S.; Davis, M. Clustering in a neutrino-dominated universe. Astrophys. J. Lett. 1983, 274, L1–L5. [Google Scholar] [CrossRef]
- Angulo, R.E.; White, S.D.M. The birth and growth of neutralino haloes. Mon. Not. R. Astron. Soc. 2010, 401, 1796–1803. [Google Scholar] [CrossRef]
- Stücker, J.; Busch, P.; White, S.D.M. The median density of the Universe. Mon. Not. R. Astron. Soc. 2018, 477, 3230–3246. [Google Scholar] [CrossRef]
- White, M. The mass of a halo. Astron. Astrophys. 2001, 367, 27–32. [Google Scholar] [CrossRef]
- Cuesta, A.J.; Prada, F.; Klypin, A.; Moles, M. The virialized mass of dark matter haloes. Mon. Not. R. Astron. Soc. 2008, 389, 385–397. [Google Scholar] [CrossRef]
- Cole, S.; Lacey, C. The structure of dark matter haloes in hierarchical clustering models. Mon. Not. R. Astron. Soc. 1996, 281, 716. [Google Scholar] [CrossRef]
- Eke, V.R.; Cole, S.; Frenk, C.S. Cluster evolution as a diagnostic for Omega. Mon. Not. R. Astron. Soc. 1996, 282, 263–280. [Google Scholar] [CrossRef]
- Bryan, G.L.; Norman, M.L. Statistical Properties of X-Ray Clusters: Analytic and Numerical Comparisons. Astrophys. J. 1998, 495, 80–99. [Google Scholar] [CrossRef]
- Jenkins, A.; Frenk, C.S.; White, S.D.M.; Colberg, J.M.; Cole, S.; Evrard, A.E.; Couchman, H.M.P.; Yoshida, N. The mass function of dark matter haloes. Mon. Not. R. Astron. Soc. 2001, 321, 372–384. [Google Scholar] [CrossRef]
- Warren, M.S.; Abazajian, K.; Holz, D.E.; Teodoro, L. Precision Determination of the Mass Function of Dark Matter Halos. Astrophys. J. 2006, 646, 881–885. [Google Scholar] [CrossRef]
- Lukić, Z.; Heitmann, K.; Habib, S.; Bashinsky, S.; Ricker, P.M. The Halo Mass Function: High-Redshift Evolution and Universality. Astrophys. J. 2007, 671, 1160–1181. [Google Scholar] [CrossRef]
- Tinker, J.; Kravtsov, A.V.; Klypin, A.; Abazajian, K.; Warren, M.; Yepes, G.; Gottlöber, S.; Holz, D.E. Toward a Halo Mass Function for Precision Cosmology: The Limits of Universality. Astrophys. J. 2008, 688, 709–728. [Google Scholar] [CrossRef]
- Trujillo-Gomez, S.; Klypin, A.; Primack, J.; Romanowsky, A.J. Galaxies in ΛCDM with Halo Abundance Matching: Luminosity-Velocity Relation, Baryonic Mass-Velocity Relation, Velocity Function, and Clustering. Astrophys. J. 2011, 742, 16. [Google Scholar] [CrossRef]
- Hellwing, W.A.; Frenk, C.S.; Cautun, M.; Bose, S.; Helly, J.; Jenkins, A.; Sawala, T.; Cytowski, M. The Copernicus Complexio: a high-resolution view of the small-scale Universe. Mon. Not. R. Astron. Soc. 2016, 457, 3492–3509. [Google Scholar] [CrossRef]
- Crain, R.A.; Theuns, T.; Dalla Vecchia, C.; Eke, V.R.; Frenk, C.S.; Jenkins, A.; Kay, S.T.; Peacock, J.A.; Pearce, F.R.; Schaye, J.; et al. Galaxies-intergalactic medium interaction calculation—I. Galaxy formation as a function of large-scale environment. Mon. Not. R. Astron. Soc. 2009, 399, 1773–1794. [Google Scholar] [CrossRef]
- Press, W.H.; Schechter, P. Formation of Galaxies and Clusters of Galaxies by Self-Similar Gravitational Condensation. Astrophys. J. 1974, 187, 425–438. [Google Scholar] [CrossRef]
- Bond, J.R.; Cole, S.; Efstathiou, G.; Kaiser, N. Excursion set mass functions for hierarchical Gaussian fluctuations. Astrophys. J. 1991, 379, 440–460. [Google Scholar] [CrossRef]
- Bower, R.G. The evolution of groups of galaxies in the Press-Schechter formalism. Mon. Not. R. Astron. Soc. 1991, 248, 332–352. [Google Scholar] [CrossRef]
- Schneider, A.; Smith, R.E.; Reed, D. Halo mass function and the free streaming scale. Mon. Not. R. Astron. Soc. 2013, 433, 1573–1587. [Google Scholar] [CrossRef]
- Bose, S.; Hellwing, W.A.; Frenk, C.S.; Jenkins, A.; Lovell, M.R.; Helly, J.C.; Li, B. The Copernicus Complexio: Statistical properties of warm dark matter haloes. Mon. Not. R. Astron. Soc. 2016, 455, 318–333. [Google Scholar] [CrossRef]
- Schewtschenko, J.A.; Wilkinson, R.J.; Baugh, C.M.; Bœhm, C.; Pascoli, S. Dark matter-radiation interactions: The impact on dark matter haloes. Mon. Not. R. Astron. Soc. 2015, 449, 3587–3596. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Cyr-Racine, F.Y.; Pfrommer, C.; Bringmann, T.; Sigurdson, K. ETHOS—An effective theory of structure formation: Dark matter physics as a possible explanation of the small-scale CDM problems. Mon. Not. R. Astron. Soc. 2016, 460, 1399–1416. [Google Scholar] [CrossRef]
- Benson, A.J.; Farahi, A.; Cole, S.; Moustakas, L.A.; Jenkins, A.; Lovell, M.; Kennedy, R.; Helly, J.; Frenk, C. Dark matter halo merger histories beyond cold dark matter—I. Methods and application to warm dark matter. Mon. Not. R. Astron. Soc. 2013, 428, 1774–1789. [Google Scholar] [CrossRef]
- Leo, M.; Baugh, C.M.; Li, B.; Pascoli, S. A new smooth-k space filter approach to calculate halo abundances. J. Cosmol. Astropart. Phys. 2018, 4, 010. [Google Scholar] [CrossRef]
- Sameie, O.; Benson, A.J.; Sales, L.V.; Yu, H.B.; Moustakas, L.A.; Creasey, P. The effect of dark matter-dark radiation interactions on halo abundance—A Press-Schechter approach. arXiv 2018, arXiv:1810.11040. [Google Scholar] [CrossRef]
- Cyr-Racine, F.Y.; Sigurdson, K. Cosmology of atomic dark matter. Phys. Rev. D 2013, 87, 103515. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Navarro, J.F.; Ludlow, A.; Springel, V.; Wang, J.; Vogelsberger, M.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Helmi, A. The diversity and similarity of simulated cold dark matter haloes. Mon. Not. R. Astron. Soc. 2010, 402, 21–34. [Google Scholar] [CrossRef]
- Anderhalden, D.; Diemand, J. Density profiles of CDM microhalos and their implications for annihilation boost factors. J. Cosmol. Astropart. Phys. 2013, 4, 009. [Google Scholar] [CrossRef]
- Ishiyama, T. Hierarchical Formation of Dark Matter Halos and the Free Streaming Scale. Astrophys. J. 2014, 788, 27. [Google Scholar] [CrossRef]
- Angulo, R.E.; Hahn, O.; Ludlow, A.D.; Bonoli, S. Earth-mass haloes and the emergence of NFW density profiles. Mon. Not. R. Astron. Soc. 2017, 471, 4687–4701. [Google Scholar] [CrossRef]
- Delos, M.S.; Erickcek, A.L.; Bailey, A.P.; Alvarez, M.A. Density profiles of ultracompact minihalos: Implications for constraining the primordial power spectrum. Phys. Rev. D 2018, 98, 063527. [Google Scholar] [CrossRef]
- Bullock, J.S.; Kolatt, T.S.; Sigad, Y.; Somerville, R.S.; Kravtsov, A.V.; Klypin, A.A.; Primack, J.R.; Dekel, A. Profiles of dark haloes: Evolution, scatter and environment. Mon. Not. R. Astron. Soc. 2001, 321, 559–575. [Google Scholar] [CrossRef]
- Eke, V.R.; Navarro, J.F.; Steinmetz, M. The Power Spectrum Dependence of Dark Matter Halo Concentrations. Astrophys. J. 2001, 554, 114–125. [Google Scholar] [CrossRef]
- Wechsler, R.H.; Bullock, J.S.; Primack, J.R.; Kravtsov, A.V.; Dekel, A. Concentrations of Dark Halos from Their Assembly Histories. Astrophys. J. 2002, 568, 52–70. [Google Scholar] [CrossRef]
- Neto, A.F.; Gao, L.; Bett, P.; Cole, S.; Navarro, J.F.; Frenk, C.S.; White, S.D.M.; Springel, V.; Jenkins, A. The statistics of Λ CDM halo concentrations. Mon. Not. R. Astron. Soc. 2007, 381, 1450–1462. [Google Scholar] [CrossRef]
- Zhao, D.H.; Jing, Y.P.; Mo, H.J.; Börner, G. Accurate Universal Models for the Mass Accretion Histories and Concentrations of Dark Matter Halos. Astrophys. J. 2009, 707, 354–369. [Google Scholar] [CrossRef]
- Prada, F.; Klypin, A.A.; Cuesta, A.J.; Betancort-Rijo, J.E.; Primack, J. Halo concentrations in the standard Λ cold dark matter cosmology. Mon. Not. R. Astron. Soc. 2012, 423, 3018–3030. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Navarro, J.F.; Angulo, R.E.; Boylan-Kolchin, M.; Springel, V.; Frenk, C.; White, S.D.M. The mass-concentration-redshift relation of cold dark matter haloes. Mon. Not. R. Astron. Soc. 2014, 441, 378–388. [Google Scholar] [CrossRef]
- Sánchez-Conde, M.A.; Prada, F. The flattening of the concentration-mass relation towards low halo masses and its implications for the annihilation signal boost. Mon. Not. R. Astron. Soc. 2014, 442, 2271–2277. [Google Scholar] [CrossRef]
- Diemer, B.; Kravtsov, A.V. A Universal Model for Halo Concentrations. Astrophys. J. 2015, 799, 108. [Google Scholar] [CrossRef]
- Klypin, A.; Yepes, G.; Gottlöber, S.; Prada, F.; Heß, S. MultiDark simulations: The story of dark matter halo concentrations and density profiles. Mon. Not. R. Astron. Soc. 2016, 457, 4340–4359. [Google Scholar] [CrossRef]
- Pilipenko, S.V.; Sánchez-Conde, M.A.; Prada, F.; Yepes, G. Pushing down the low-mass halo concentration frontier with the Lomonosov cosmological simulations. Mon. Not. R. Astron. Soc. 2017, 472, 4918–4927. [Google Scholar] [CrossRef]
- Wang, J.; Navarro, J.F.; Frenk, C.S.; White, S.D.M.; Springel, V.; Jenkins, A.; Helmi, A.; Ludlow, A.; Vogelsberger, M. Assembly history and structure of galactic cold dark matter haloes. Mon. Not. R. Astron. Soc. 2011, 413, 1373–1382. [Google Scholar] [CrossRef]
- Springel, V.; Wang, J.; Vogelsberger, M.; Ludlow, A.; Jenkins, A.; Helmi, A.; Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Aquarius Project: The subhaloes of galactic haloes. Mon. Not. R. Astron. Soc. 2008, 391, 1685–1711. [Google Scholar] [CrossRef]
- Vera-Ciro, C.A.; Sales, L.V.; Helmi, A.; Frenk, C.S.; Navarro, J.F.; Springel, V.; Vogelsberger, M.; White, S.D.M. The shape of dark matter haloes in the Aquarius simulations: Evolution and memory. Mon. Not. R. Astron. Soc. 2011, 416, 1377–1391. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Helmi, A.; Springel, V.; White, S.D.M.; Wang, J.; Frenk, C.S.; Jenkins, A.; Ludlow, A.; Navarro, J.F. Phase-space structure in the local dark matter distribution and its signature in direct detection experiments. Mon. Not. R. Astron. Soc. 2009, 395, 797–811. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics: Second Edition; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Ludlow, A.D.; Navarro, J.F.; White, S.D.M.; Boylan-Kolchin, M.; Springel, V.; Jenkins, A.; Frenk, C.S. The density and pseudo-phase-space density profiles of cold dark matter haloes. Mon. Not. R. Astron. Soc. 2011, 415, 3895–3902. [Google Scholar] [CrossRef]
- Hansen, S.H.; Moore, B. A universal density slope Velocity anisotropy relation for relaxed structures. New Astron. 2006, 11, 333–338. [Google Scholar] [CrossRef]
- Taylor, J.E.; Navarro, J.F. The Phase-Space Density Profiles of Cold Dark Matter Halos. Astrophys. J. 2001, 563, 483–488. [Google Scholar] [CrossRef]
- Bertschinger, E. Self-similar secondary infall and accretion in an Einstein-de Sitter universe. Astrophys. J. Suppl. 1985, 58, 39–65. [Google Scholar] [CrossRef]
- Eddington, A.S. The distribution of stars in globular clusters. Mon. Not. R. Astron. Soc. 1916, 76, 572–585. [Google Scholar] [CrossRef]
- Jing, Y.P.; Suto, Y. Triaxial Modeling of Halo Density Profiles with High-Resolution N-Body Simulations. Astrophys. J. 2002, 574, 538–553. [Google Scholar] [CrossRef]
- Hayashi, E.; Navarro, J.F.; Springel, V. The shape of the gravitational potential in cold dark matter haloes. Mon. Not. R. Astron. Soc. 2007, 377, 50–62. [Google Scholar] [CrossRef]
- Ganeshaiah Veena, P.; Cautun, M.; van de Weygaert, R.; Tempel, E.; Jones, B.J.T.; Rieder, S.; Frenk, C.S. The Cosmic Ballet: Spin and shape alignments of haloes in the cosmic web. Mon. Not. R. Astron. Soc. 2018, 481, 414–438. [Google Scholar] [CrossRef]
- Bonamigo, M.; Despali, G.; Limousin, M.; Angulo, R.; Giocoli, C.; Soucail, G. Universality of dark matter haloes shape over six decades in mass: Insights from the Millennium XXL and SBARBINE simulations. Mon. Not. R. Astron. Soc. 2015, 449, 3171–3182. [Google Scholar] [CrossRef]
- Vega-Ferrero, J.; Yepes, G.; Gottlöber, S. On the shape of dark matter haloes from MultiDark Planck simulations. Mon. Not. R. Astron. Soc. 2017, 467, 3226–3238. [Google Scholar] [CrossRef]
- Despali, G.; Giocoli, C.; Tormen, G. Some like it triaxial: The universality of dark matter halo shapes and their evolution along the cosmic time. Mon. Not. R. Astron. Soc. 2014, 443, 3208–3217. [Google Scholar] [CrossRef]
- Lovell, M.R.; Eke, V.; Frenk, C.S.; Gao, L.; Jenkins, A.; Theuns, T.; Wang, J.; White, S.D.M.; Boyarsky, A.; Ruchayskiy, O. The haloes of bright satellite galaxies in a warm dark matter universe. Mon. Not. R. Astron. Soc. 2012, 420, 2318–2324. [Google Scholar] [CrossRef]
- Colín, P.; Avila-Reese, V.; Valenzuela, O. Substructure and Halo Density Profiles in a Warm Dark Matter Cosmology. Astrophys. J. 2000, 542, 622–630. [Google Scholar] [CrossRef]
- Avila-Reese, V.; Colín, P.; Valenzuela, O.; D’Onghia, E.; Firmani, C. Formation and Structure of Halos in a Warm Dark Matter Cosmology. Astrophys. J. 2001, 559, 516–530. [Google Scholar] [CrossRef]
- Colín, P.; Valenzuela, O.; Avila-Reese, V. On the Structure of Dark Matter Halos at the Damping Scale of the Power Spectrum with and without Relict Velocities. Astrophys. J. 2008, 673, 203–214. [Google Scholar] [CrossRef]
- Schneider, A.; Smith, R.E.; Macciò, A.V.; Moore, B. Non-linear evolution of cosmological structures in warm dark matter models. Mon. Not. R. Astron. Soc. 2012, 424, 684–698. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Bose, S.; Angulo, R.E.; Wang, L.; Hellwing, W.A.; Navarro, J.F.; Cole, S.; Frenk, C.S. The mass-concentration-redshift relation of cold and warm dark matter haloes. Mon. Not. R. Astron. Soc. 2016, 460, 1214–1232. [Google Scholar] [CrossRef]
- Dalcanton, J.J.; Hogan, C.J. Halo Cores and Phase-Space Densities: Observational Constraints on Dark Matter Physics and Structure Formation. Astrophys. J. 2001, 561, 35–45. [Google Scholar] [CrossRef]
- Macciò, A.V.; Paduroiu, S.; Anderhalden, D.; Schneider, A.; Moore, B. Cores in warm dark matter haloes: A Catch 22 problem. Mon. Not. R. Astron. Soc. 2012, 424, 1105–1112. [Google Scholar] [CrossRef]
- Shao, S.; Gao, L.; Theuns, T.; Frenk, C.S. The phase-space density of fermionic dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 430, 2346–2357. [Google Scholar] [CrossRef]
- Colín, P.; Avila-Reese, V.; Valenzuela, O.; Firmani, C. Structure and Subhalo Population of Halos in a Self-interacting Dark Matter Cosmology. Astrophys. J. 2002, 581, 777–793. [Google Scholar] [CrossRef]
- Balberg, S.; Shapiro, S.L.; Inagaki, S. Self-Interacting Dark Matter Halos and the Gravothermal Catastrophe. Astrophys. J. 2002, 568, 475–487. [Google Scholar] [CrossRef]
- Lynden-Bell, D.; Wood, R. The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. Mon. Not. R. Astron. Soc. 1968, 138, 495. [Google Scholar] [CrossRef]
- Pollack, J.; Spergel, D.N.; Steinhardt, P.J. Supermassive Black Holes from Ultra-strongly Self-interacting Dark Matter. Astrophys. J. 2015, 804, 131. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Schutz, K.; Slatyer, T.R. Evaporating the Milky Way halo and its satellites with inelastic self-interacting dark matter. Mon. Not. R. Astron. Soc. 2019, 484, 5437–5452. [Google Scholar] [CrossRef]
- Yoshida, N.; Springel, V.; White, S.D.M.; Tormen, G. Weakly Self-interacting Dark Matter and the Structure of Dark Halos. Astrophys. J. Lett. 2000, 544, L87–L90. [Google Scholar] [CrossRef]
- Zavala, J.; Vogelsberger, M.; Walker, M.G. Constraining self-interacting dark matter with the Milky Way’s dwarf spheroidals. Mon. Not. R. Astron. Soc. 2013, 431, L20–L24. [Google Scholar] [CrossRef]
- Brinckmann, T.; Zavala, J.; Rapetti, D.; Hansen, S.H.; Vogelsberger, M. The structure and assembly history of cluster-sized haloes in self-interacting dark matter. Mon. Not. R. Astron. Soc. 2018, 474, 746–759. [Google Scholar] [CrossRef]
- Peter, A.H.G.; Rocha, M.; Bullock, J.S.; Kaplinghat, M. Cosmological simulations with self-interacting dark matter—II. Halo shapes versus observations. Mon. Not. R. Astron. Soc. 2013, 430, 105–120. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J. Direct detection of self-interacting dark matter. Mon. Not. R. Astron. Soc. 2013, 430, 1722–1735. [Google Scholar] [CrossRef]
- Genel, S.; Bouché, N.; Naab, T.; Sternberg, A.; Genzel, R. The Growth of Dark Matter Halos: Evidence for Significant Smooth Accretion. Astrophys. J. 2010, 719, 229–239. [Google Scholar] [CrossRef]
- Gill, S.P.D.; Knebe, A.; Gibson, B.K. The evolution of substructure—III. The outskirts of clusters. Mon. Not. R. Astron. Soc. 2005, 356, 1327–1332. [Google Scholar] [CrossRef]
- Sales, L.V.; Navarro, J.F.; Abadi, M.G.; Steinmetz, M. Cosmic ménage à trois: The origin of satellite galaxies on extreme orbits. Mon. Not. R. Astron. Soc. 2007, 379, 1475–1483. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Navarro, J.F.; Springel, V.; Jenkins, A.; Frenk, C.S.; Helmi, A. The Unorthodox Orbits of Substructure Halos. Astrophys. J. 2009, 692, 931–941. [Google Scholar] [CrossRef]
- Giocoli, C.; Tormen, G.; Sheth, R.K.; van den Bosch, F.C. The substructure hierarchy in dark matter haloes. Mon. Not. R. Astron. Soc. 2010, 404, 502–517. [Google Scholar] [CrossRef]
- Srisawat, C.; Knebe, A.; Pearce, F.R.; Schneider, A.; Thomas, P.A.; Behroozi, P.; Dolag, K.; Elahi, P.J.; Han, J.; Helly, J.; et al. Sussing Merger Trees: The Merger Trees Comparison Project. Mon. Not. R. Astron. Soc. 2013, 436, 150–162. [Google Scholar] [CrossRef]
- Fakhouri, O.; Ma, C.P. The nearly universal merger rate of dark matter haloes in ΛCDM cosmology. Mon. Not. R. Astron. Soc. 2008, 386, 577–592. [Google Scholar] [CrossRef]
- Fakhouri, O.; Ma, C.P.; Boylan-Kolchin, M. The merger rates and mass assembly histories of dark matter haloes in the two Millennium simulations. Mon. Not. R. Astron. Soc. 2010, 406, 2267–2278. [Google Scholar] [CrossRef]
- Poole, G.B.; Mutch, S.J.; Croton, D.J.; Wyithe, S. Convergence properties of halo merger trees; halo and substructure merger rates across cosmic history. Mon. Not. R. Astron. Soc. 2017, 472, 3659–3682. [Google Scholar] [CrossRef]
- Lacey, C.; Cole, S. Merger rates in hierarchical models of galaxy formation. Mon. Not. R. Astron. Soc. 1993, 262, 627–649. [Google Scholar] [CrossRef]
- Parkinson, H.; Cole, S.; Helly, J. Generating dark matter halo merger trees. Mon. Not. R. Astron. Soc. 2008, 383, 557–564. [Google Scholar] [CrossRef]
- Cole, S.; Lacey, C.G.; Baugh, C.M.; Frenk, C.S. Hierarchical galaxy formation. Mon. Not. R. Astron. Soc. 2000, 319, 168–204. [Google Scholar] [CrossRef]
- Benson, A.J. Orbital parameters of infalling dark matter substructures. Mon. Not. R. Astron. Soc. 2005, 358, 551–562. [Google Scholar] [CrossRef]
- Tormen, G. The rise and fall of satellites in galaxy clusters. Mon. Not. R. Astron. Soc. 1997, 290, 411–421. [Google Scholar] [CrossRef]
- Jiang, L.; Cole, S.; Sawala, T.; Frenk, C.S. Orbital parameters of infalling satellite haloes in the hierarchical ΛCDM model. Mon. Not. R. Astron. Soc. 2015, 448, 1674–1686. [Google Scholar] [CrossRef]
- Wetzel, A.R. On the orbits of infalling satellite haloes. Mon. Not. R. Astron. Soc. 2011, 412, 49–58. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P.; Zemp, M.; Moore, B.; Potter, D.; Stadel, J. Clumps and streams in the local dark matter distribution. Nature 2008, 454, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Rocha, M.; Peter, A.H.G.; Bullock, J. Infall times for Milky Way satellites from their present-day kinematics. Mon. Not. R. Astron. Soc. 2012, 425, 231–244. [Google Scholar] [CrossRef]
- Vogelsberger, M.; White, S.D.M. Streams and caustics: The fine-grained structure of Λ cold dark matter haloes. Mon. Not. R. Astron. Soc. 2011, 413, 1419–1438. [Google Scholar] [CrossRef]
- Natarajan, A.; Sikivie, P. Inner caustics of cold dark matter halos. Phys. Rev. D 2006, 73, 023510. [Google Scholar] [CrossRef]
- Vogelsberger, M.; White, S.D.M.; Mohayaee, R.; Springel, V. Caustics in growing cold dark matter haloes. Mon. Not. R. Astron. Soc. 2009, 400, 2174–2184. [Google Scholar] [CrossRef]
- Onions, J.; Knebe, A.; Pearce, F.R.; Muldrew, S.I.; Lux, H.; Knollmann, S.R.; Ascasibar, Y.; Behroozi, P.; Elahi, P.; Han, J.; et al. Subhaloes going Notts: The subhalo-finder comparison project. Mon. Not. R. Astron. Soc. 2012, 423, 1200–1214. [Google Scholar] [CrossRef]
- Klypin, A.; Gottlöber, S.; Kravtsov, A.V.; Khokhlov, A.M. Galaxies in N-Body Simulations: Overcoming the Overmerging Problem. Astrophys. J. 1999, 516, 530–551. [Google Scholar] [CrossRef]
- Neyrinck, M.C.; Gnedin, N.Y.; Hamilton, A.J.S. VOBOZ: An almost-parameter-free halo-finding algorithm. Mon. Not. R. Astron. Soc. 2005, 356, 1222–1232. [Google Scholar] [CrossRef]
- Knollmann, S.R.; Knebe, A. AHF: Amiga’s Halo Finder. Astrophys. J. Suppl. 2009, 182, 608–624. [Google Scholar] [CrossRef]
- Han, J.; Jing, Y.P.; Wang, H.; Wang, W. Resolving subhaloes’ lives with the Hierarchical Bound-Tracing algorithm. Mon. Not. R. Astron. Soc. 2012, 427, 2437–2449. [Google Scholar] [CrossRef]
- Han, J.; Cole, S.; Frenk, C.S.; Benitez-Llambay, A.; Helly, J. HBT+: An improved code for finding subhaloes and building merger trees in cosmological simulations. Mon. Not. R. Astron. Soc. 2018, 474, 604–617. [Google Scholar] [CrossRef]
- Tormen, G.; Moscardini, L.; Yoshida, N. Properties of cluster satellites in hydrodynamical simulations. Mon. Not. R. Astron. Soc. 2004, 350, 1397–1408. [Google Scholar] [CrossRef]
- Maciejewski, M.; Colombi, S.; Springel, V.; Alard, C.; Bouchet, F.R. Phase-space structures—II. Hierarchical Structure Finder. Mon. Not. R. Astron. Soc. 2009, 396, 1329–1348. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Wechsler, R.H.; Wu, H.Y. The ROCKSTAR Phase-space Temporal Halo Finder and the Velocity Offsets of Cluster Cores. Astrophys. J. 2013, 762, 109. [Google Scholar] [CrossRef]
- Tormen, G.; Diaferio, A.; Syer, D. Survival of substructure within dark matter haloes. Mon. Not. R. Astron. Soc. 1998, 299, 728–742. [Google Scholar] [CrossRef]
- Tollet, É.; Cattaneo, A.; Mamon, G.A.; Moutard, T.; van den Bosch, F.C. On stellar mass loss from galaxies in groups and clusters. Mon. Not. R. Astron. Soc. 2017, 471, 4170–4193. [Google Scholar] [CrossRef]
- Taylor, J.E.; Babul, A. The Dynamics of Sinking Satellites around Disk Galaxies: A Poor Man’s Alternative to High-Resolution Numerical Simulations. Astrophys. J. 2001, 559, 716–735. [Google Scholar] [CrossRef]
- Zentner, A.R.; Bullock, J.S. Halo Substructure and the Power Spectrum. Astrophys. J. 2003, 598, 49–72. [Google Scholar] [CrossRef]
- Zentner, A.R.; Berlind, A.A.; Bullock, J.S.; Kravtsov, A.V.; Wechsler, R.H. The Physics of Galaxy Clustering. I. A Model for Subhalo Populations. Astrophys. J. 2005, 624, 505–525. [Google Scholar] [CrossRef]
- Johnston, K.V. A Prescription for Building the Milky Way’s Halo from Disrupted Satellites. Astrophys. J. 1998, 495, 297–308. [Google Scholar] [CrossRef]
- Van den Bosch, F.C.; Ogiya, G. Dark matter substructure in numerical simulations: A tale of discreteness noise, runaway instabilities, and artificial disruption. Mon. Not. R. Astron. Soc. 2018, 475, 4066–4087. [Google Scholar] [CrossRef]
- Van den Bosch, F.C.; Ogiya, G.; Hahn, O.; Burkert, A. Disruption of dark matter substructure: Fact or fiction? Mon. Not. R. Astron. Soc. 2018, 474, 3043–3066. [Google Scholar] [CrossRef]
- Hayashi, E.; Navarro, J.F.; Taylor, J.E.; Stadel, J.; Quinn, T. The Structural Evolution of Substructure. Astrophys. J. 2003, 584, 541–558. [Google Scholar] [CrossRef]
- Spitzer, L., Jr. Disruption of Galactic Clusters. Astrophys. J. 1958, 127, 17. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Hernquist, L.; Ostriker, J.P. Tidal Shocking by Extended Mass Distributions. Astrophys. J. 1999, 514, 109–118. [Google Scholar] [CrossRef]
- Aguilar, L.A.; White, S.D.M. Tidal interactions between spherical galaxies. Astrophys. J. 1985, 295, 374. [Google Scholar] [CrossRef]
- Aguilar, L.A.; White, S.D.M. The Density Profiles of Tidally Stripped Galaxies. Astrophys. J. 1986, 307, 97. [Google Scholar] [CrossRef]
- Kazantzidis, S.; Mayer, L.; Mastropietro, C.; Diemand, J.; Stadel, J.; Moore, B. Density Profiles of Cold Dark Matter Substructure: Implications for the Missing-Satellites Problem. Astrophys. J. 2004, 608, 663–679. [Google Scholar] [CrossRef]
- Moore, B.; Katz, N.; Lake, G.; Dressler, A.; Oemler, A. Galaxy harassment and the evolution of clusters of galaxies. Nature 1996, 379, 613–616. [Google Scholar] [CrossRef]
- Ogiya, G.; Burkert, A. Dynamical friction and scratches of orbiting satellite galaxies on host systems. Mon. Not. R. Astron. Soc. 2016, 457, 2164–2172. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Ma, C.P.; Quataert, E. Dynamical friction and galaxy merging time-scales. Mon. Not. R. Astron. Soc. 2008, 383, 93–101. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Dynamical Friction. I. General Considerations: The Coefficient of Dynamical Friction. Astrophys. J. 1943, 97, 255. [Google Scholar] [CrossRef]
- Van den Bosch, F.C.; Lewis, G.F.; Lake, G.; Stadel, J. Substructure in Dark Halos: Orbital Eccentricities and Dynamical Friction. Astrophys. J. 1999, 515, 50–68. [Google Scholar] [CrossRef]
- Hernquist, L. An analytical model for spherical galaxies and bulges. Astrophys. J. 1990, 356, 359–364. [Google Scholar] [CrossRef]
- Han, J.; Cole, S.; Frenk, C.S.; Jing, Y. A unified model for the spatial and mass distribution of subhaloes. Mon. Not. R. Astron. Soc. 2016, 457, 1208–1223. [Google Scholar] [CrossRef]
- Klypin, A.A.; Trujillo-Gomez, S.; Primack, J. Dark Matter Halos in the Standard Cosmological Model: Results from the Bolshoi Simulation. Astrophys. J. 2011, 740, 102. [Google Scholar] [CrossRef]
- Jiang, F.; van den Bosch, F.C. Statistics of dark matter substructure—III. Halo-to-halo variance. Mon. Not. R. Astron. Soc. 2017, 472, 657–674. [Google Scholar] [CrossRef]
- Gao, L.; White, S.D.M.; Jenkins, A.; Stoehr, F.; Springel, V. The subhalo populations of ΛCDM dark haloes. Mon. Not. R. Astron. Soc. 2004, 355, 819–834. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P. Formation and Evolution of Galaxy Dark Matter Halos and Their Substructure. Astrophys. J. 2007, 667, 859–877. [Google Scholar] [CrossRef]
- Gao, L.; Navarro, J.F.; Frenk, C.S.; Jenkins, A.; Springel, V.; White, S.D.M. The Phoenix Project: The dark side of rich Galaxy clusters. Mon. Not. R. Astron. Soc. 2012, 425, 2169–2186. [Google Scholar] [CrossRef]
- Garrison-Kimmel, S.; Boylan-Kolchin, M.; Bullock, J.S.; Lee, K. ELVIS: Exploring the Local Volume in Simulations. Mon. Not. R. Astron. Soc. 2014, 438, 2578–2596. [Google Scholar] [CrossRef]
- Griffen, B.F.; Ji, A.P.; Dooley, G.A.; Gómez, F.A.; Vogelsberger, M.; O’Shea, B.W.; Frebel, A. The Caterpillar Project: A Large Suite of Milky Way Sized Halos. Astrophys. J. 2016, 818, 10. [Google Scholar] [CrossRef]
- Gao, L.; Frenk, C.S.; Boylan-Kolchin, M.; Jenkins, A.; Springel, V.; White, S.D.M. The statistics of the subhalo abundance of dark matter haloes. Mon. Not. R. Astron. Soc. 2011, 410, 2309–2314. [Google Scholar] [CrossRef]
- Angulo, R.E.; Lacey, C.G.; Baugh, C.M.; Frenk, C.S. The fate of substructures in cold dark matter haloes. Mon. Not. R. Astron. Soc. 2009, 399, 983–995. [Google Scholar] [CrossRef][Green Version]
- Boylan-Kolchin, M.; Springel, V.; White, S.D.M.; Jenkins, A. There’s no place like home? Statistics of Milky Way-mass dark matter haloes. Mon. Not. R. Astron. Soc. 2010, 406, 896–912. [Google Scholar] [CrossRef]
- Rodríguez-Puebla, A.; Behroozi, P.; Primack, J.; Klypin, A.; Lee, C.; Hellinger, D. Halo and subhalo demographics with Planck cosmological parameters: Bolshoi-Planck and MultiDark-Planck simulations. Mon. Not. R. Astron. Soc. 2016, 462, 893–916. [Google Scholar] [CrossRef]
- Ghigna, S.; Moore, B.; Governato, F.; Lake, G.; Quinn, T.; Stadel, J. Density Profiles and Substructure of Dark Matter Halos: Converging Results at Ultra-High Numerical Resolution. Astrophys. J. 2000, 544, 616–628. [Google Scholar] [CrossRef]
- Diemand, J.; Moore, B.; Stadel, J. Velocity and spatial biases in cold dark matter subhalo distributions. Mon. Not. R. Astron. Soc. 2004, 352, 535–546. [Google Scholar] [CrossRef]
- Nagai, D.; Kravtsov, A.V. The Radial Distribution of Galaxies in Λ Cold Dark Matter Clusters. Astrophys. J. 2005, 618, 557–568. [Google Scholar] [CrossRef]
- Diemand, J.; Kuhlen, M.; Madau, P. Dark Matter Substructure and Gamma-Ray Annihilation in the Milky Way Halo. Astrophys. J. 2007, 657, 262–270. [Google Scholar] [CrossRef]
- Gao, L.; De Lucia, G.; White, S.D.M.; Jenkins, A. Galaxies and subhaloes in ΛCDM galaxy clusters. Mon. Not. R. Astron. Soc. 2004, 352, L1–L5. [Google Scholar] [CrossRef]
- Navarro, J.F.; Hayashi, E.; Power, C.; Jenkins, A.R.; Frenk, C.S.; White, S.D.M.; Springel, V.; Stadel, J.; Quinn, T.R. The inner structure of ΛCDM haloes—III. Universality and asymptotic slopes. Mon. Not. R. Astron. Soc. 2004, 349, 1039–1051. [Google Scholar] [CrossRef]
- Gao, L.; Navarro, J.F.; Cole, S.; Frenk, C.S.; White, S.D.M.; Springel, V.; Jenkins, A.; Neto, A.F. The redshift dependence of the structure of massive Λ cold dark matter haloes. Mon. Not. R. Astron. Soc. 2008, 387, 536–544. [Google Scholar] [CrossRef]
- Vera-Ciro, C.A.; Helmi, A.; Starkenburg, E.; Breddels, M.A. Not too big, not too small: The dark haloes of the dwarf spheroidals in the Milky Way. Mon. Not. R. Astron. Soc. 2013, 428, 1696–1703. [Google Scholar] [CrossRef][Green Version]
- Dutton, A.A.; Macciò, A.V. Cold dark matter haloes in the Planck era: Evolution of structural parameters for Einasto and NFW profiles. Mon. Not. R. Astron. Soc. 2014, 441, 3359–3374. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Navarro, J.F.; McConnachie, A.W. The Tidal Evolution of Local Group Dwarf Spheroidals. Astrophys. J. 2008, 673, 226–240. [Google Scholar] [CrossRef]
- Moliné, Á.; Sánchez-Conde, M.A.; Palomares-Ruiz, S.; Prada, F. Characterization of subhalo structural properties and implications for dark matter annihilation signals. Mon. Not. R. Astron. Soc. 2017, 466, 4974–4990. [Google Scholar] [CrossRef]
- Barber, C.; Starkenburg, E.; Navarro, J.F.; McConnachie, A.W. Galactic tides and the shape and orientation of dwarf galaxy satellites. Mon. Not. R. Astron. Soc. 2015, 447, 1112–1125. [Google Scholar] [CrossRef]
- Vera-Ciro, C.A.; Sales, L.V.; Helmi, A.; Navarro, J.F. The shape of dark matter subhaloes in the Aquarius simulations. Mon. Not. R. Astron. Soc. 2014, 439, 2863–2872. [Google Scholar] [CrossRef]
- Bose, S.; Hellwing, W.A.; Frenk, C.S.; Jenkins, A.; Lovell, M.R.; Helly, J.C.; Li, B.; Gonzalez-Perez, V.; Gao, L. Substructure and galaxy formation in the Copernicus Complexio warm dark matter simulations. Mon. Not. R. Astron. Soc. 2017, 464, 4520–4533. [Google Scholar] [CrossRef]
- Dooley, G.A.; Peter, A.H.G.; Vogelsberger, M.; Zavala, J.; Frebel, A. Enhanced tidal stripping of satellites in the galactic halo from dark matter self-interactions. Mon. Not. R. Astron. Soc. 2016, 461, 710–727. [Google Scholar] [CrossRef]
- Nishikawa, H.; Boddy, K.K.; Kaplinghat, M. Accelerated core collapse in tidally stripped self-interacting dark matter halos. arXiv 2019, arXiv:1901.00499. [Google Scholar]
- Sawala, T.; Frenk, C.S.; Fattahi, A.; Navarro, J.F.; Theuns, T.; Bower, R.G.; Crain, R.A.; Furlong, M.; Jenkins, A.; Schaller, M.; et al. The chosen few: The low-mass haloes that host faint galaxies. Mon. Not. R. Astron. Soc. 2016, 456, 85–97. [Google Scholar] [CrossRef]
- Sameie, O.; Yu, H.B.; Sales, L.V.; Vogelsberger, M.; Zavala, J. Self-Interacting Dark Matter Subhalos in the Milky Way’s Tides. arXiv 2019, arXiv:1904.07872. [Google Scholar]
- Kahlhoefer, F.; Kaplinghat, M.; Slatyer, T.R.; Wu, C.L. Diversity in density profiles of self-interacting dark matter satellite halos. arXiv 2019, arXiv:1904.10539. [Google Scholar]
- Arkani-Hamed, N.; Finkbeiner, D.P.; Slatyer, T.R.; Weiner, N. A theory of dark matter. Phys. Rev. D 2009, 79, 015014. [Google Scholar] [CrossRef]
- Todoroki, K.; Medvedev, M.V. Dark matter haloes in the multicomponent model—I. Substructure. Mon. Not. R. Astron. Soc. 2019, 483, 3983–4003. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Hu, W. Baryonic Features in the Matter Transfer Function. Astrophys. J. 1998, 496, 605–614. [Google Scholar] [CrossRef]
- White, S.D.M.; Rees, M.J. Core condensation in heavy halos — A two-stage theory for galaxy formation and clustering. Mon. Not. R. Astron. Soc. 1978, 183, 341–358. [Google Scholar] [CrossRef]
- Tseliakhovich, D.; Hirata, C. Relative velocity of dark matter and baryonic fluids and the formation of the first structures. Phys. Rev. D 2010, 82, 083520. [Google Scholar] [CrossRef]
- Bower, R.G.; Benson, A.J.; Malbon, R.; Helly, J.C.; Frenk, C.S.; Baugh, C.M.; Cole, S.; Lacey, C.G. Breaking the hierarchy of galaxy formation. Mon. Not. R. Astron. Soc. 2006, 370, 645–655. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Faber, S.M.; Flores, R.; Primack, J.R. Contraction of dark matter galactic halos due to baryonic infall. Astrophys. J. 1986, 301, 27–34. [Google Scholar] [CrossRef]
- Mo, H.J.; Mao, S.; White, S.D.M. The formation of galactic discs. Mon. Not. R. Astron. Soc. 1998, 295, 319–336. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Kravtsov, A.V.; Klypin, A.A.; Nagai, D. Response of Dark Matter Halos to Condensation of Baryons: Cosmological Simulations and Improved Adiabatic Contraction Model. Astrophys. J. 2004, 616, 16–26. [Google Scholar] [CrossRef]
- Schaller, M.; Frenk, C.S.; Bower, R.G.; Theuns, T.; Jenkins, A.; Schaye, J.; Crain, R.A.; Furlong, M.; Dalla Vecchia, C.; McCarthy, I.G. Baryon effects on the internal structure of ΛCDM haloes in the EAGLE simulations. Mon. Not. R. Astron. Soc. 2015, 451, 1247–1267. [Google Scholar] [CrossRef]
- Lovell, M.R.; Pillepich, A.; Genel, S.; Nelson, D.; Springel, V.; Pakmor, R.; Marinacci, F.; Weinberger, R.; Torrey, P.; Vogelsberger, M.; et al. The fraction of dark matter within galaxies from the IllustrisTNG simulations. Mon. Not. R. Astron. Soc. 2018, 481, 1950–1975. [Google Scholar] [CrossRef]
- Efstathiou, G. Suppressing the formation of dwarf galaxies via photoionization. Mon. Not. R. Astron. Soc. 1992, 256, 43P–47P. [Google Scholar] [CrossRef]
- Babul, A.; Rees, M.J. On dwarf elliptical galaxies and the faint blue counts. Mon. Not. R. Astron. Soc. 1992, 255, 346–350. [Google Scholar] [CrossRef]
- Okamoto, T.; Gao, L.; Theuns, T. Mass loss of galaxies due to an ultraviolet background. Mon. Not. R. Astron. Soc. 2008, 390, 920–928. [Google Scholar] [CrossRef]
- Thoul, A.A.; Weinberg, D.H. Hydrodynamic Simulations of Galaxy Formation. II. Photoionization and the Formation of Low-Mass Galaxies. Astrophys. J. 1996, 465, 608. [Google Scholar] [CrossRef]
- Barkana, R.; Loeb, A. The Photoevaporation of Dwarf Galaxies during Reionization. Astrophys. J. 1999, 523, 54–65. [Google Scholar] [CrossRef]
- Bullock, J.S.; Kravtsov, A.V.; Weinberg, D.H. Reionization and the Abundance of Galactic Satellites. Astrophys. J. 2000, 539, 517–521. [Google Scholar] [CrossRef]
- Gnedin, N.Y. Effect of Reionization on Structure Formation in the Universe. Astrophys. J. 2000, 542, 535–541. [Google Scholar] [CrossRef]
- Benson, A.J.; Lacey, C.G.; Baugh, C.M.; Cole, S.; Frenk, C.S. The effects of photoionization on galaxy formation—I. Model and results at z = 0. Mon. Not. R. Astron. Soc. 2002, 333, 156–176. [Google Scholar] [CrossRef]
- Somerville, R.S. Can Photoionization Squelching Resolve the Substructure Crisis? Astrophys. J. Lett. 2002, 572, L23–L26. [Google Scholar] [CrossRef]
- Hoeft, M.; Yepes, G.; Gottlöber, S.; Springel, V. Dwarf galaxies in voids: Suppressing star formation with photoheating. Mon. Not. R. Astron. Soc. 2006, 371, 401–414. [Google Scholar] [CrossRef]
- Ocvirk, P.; Gillet, N.; Shapiro, P.R.; Aubert, D.; Iliev, I.T.; Teyssier, R.; Yepes, G.; Choi, J.H.; Sullivan, D.; Knebe, A.; et al. Cosmic Dawn (CoDa): The First Radiation-Hydrodynamics Simulation of Reionization and Galaxy Formation in the Local Universe. Mon. Not. R. Astron. Soc. 2016, 463, 1462–1485. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.S.; Crain, R.A.; Jenkins, A.; Schaye, J.; Theuns, T.; Zavala, J. The abundance of (not just) dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 431, 1366–1382. [Google Scholar] [CrossRef]
- Larson, R.B. Effects of supernovae on the early evolution of galaxies. Mon. Not. R. Astron. Soc. 1974, 169, 229–246. [Google Scholar] [CrossRef]
- Dekel, A.; Silk, J. The origin of dwarf galaxies, cold dark matter, and biased galaxy formation. Astrophys. J. 1986, 303, 39–55. [Google Scholar] [CrossRef]
- Navarro, J.F.; Eke, V.R.; Frenk, C.S. The cores of dwarf galaxy haloes. Mon. Not. R. Astron. Soc. 1996, 283, L72–L78. [Google Scholar] [CrossRef]
- Read, J.I.; Gilmore, G. Mass loss from dwarf spheroidal galaxies: The origins of shallow dark matter cores and exponential surface brightness profiles. Mon. Not. R. Astron. Soc. 2005, 356, 107–124. [Google Scholar] [CrossRef]
- Gnedin, O.Y.; Zhao, H. Maximum feedback and dark matter profiles of dwarf galaxies. Mon. Not. R. Astron. Soc. 2002, 333, 299–306. [Google Scholar] [CrossRef]
- Governato, F.; Brook, C.; Mayer, L.; Brooks, A.; Rhee, G.; Wadsley, J.; Jonsson, P.; Willman, B.; Stinson, G.; Quinn, T.; et al. Bulgeless dwarf galaxies and dark matter cores from supernova-driven outflows. Nature 2010, 463, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Pontzen, A.; Governato, F. How supernova feedback turns dark matter cusps into cores. Mon. Not. R. Astron. Soc. 2012, 421, 3464–3471. [Google Scholar] [CrossRef]
- Di Cintio, A.; Brook, C.B.; Macciò, A.V.; Stinson, G.S.; Knebe, A.; Dutton, A.A.; Wadsley, J. The dependence of dark matter profiles on the stellar-to-halo mass ratio: A prediction for cusps versus cores. Mon. Not. R. Astron. Soc. 2014, 437, 415–423. [Google Scholar] [CrossRef]
- Chan, T.K.; Kereš, D.; Oñorbe, J.; Hopkins, P.F.; Muratov, A.L.; Faucher-Giguère, C.A.; Quataert, E. The impact of baryonic physics on the structure of dark matter haloes: The view from the FIRE cosmological simulations. Mon. Not. R. Astron. Soc. 2015, 454, 2981–3001. [Google Scholar] [CrossRef]
- Tollet, E.; Macciò, A.V.; Dutton, A.A.; Stinson, G.S.; Wang, L.; Penzo, C.; Gutcke, T.A.; Buck, T.; Kang, X.; Brook, C.; et al. NIHAO - IV: Core creation and destruction in dark matter density profiles across cosmic time. Mon. Not. R. Astron. Soc. 2016, 456, 3542–3552. [Google Scholar] [CrossRef]
- Read, J.I.; Agertz, O.; Collins, M.L.M. Dark matter cores all the way down. Mon. Not. R. Astron. Soc. 2016, 459, 2573–2590. [Google Scholar] [CrossRef]
- Moore, B. Evidence against dissipation-less dark matter from observations of galaxy haloes. Nature 1994, 370, 629–631. [Google Scholar] [CrossRef]
- Oman, K.A.; Navarro, J.F.; Fattahi, A.; Frenk, C.S.; Sawala, T.; White, S.D.M.; Bower, R.; Crain, R.A.; Furlong, M.; Schaller, M.; et al. The unexpected diversity of dwarf galaxy rotation curves. Mon. Not. R. Astron. Soc. 2015, 452, 3650–3665. [Google Scholar] [CrossRef]
- Oman, K.A.; Marasco, A.; Navarro, J.F.; Frenk, C.S.; Schaye, J.; Benítez-Llambay, A. Non-circular motions and the diversity of dwarf galaxy rotation curves. Mon. Not. R. Astron. Soc. 2019, 482, 821–847. [Google Scholar] [CrossRef]
- Benitez-Llambay, A.; Frenk, C.S.; Ludlow, A.D.; Navarro, J.F. Baryon-induced dark matter cores in the EAGLE simulations. arXiv 2018, arXiv:1810.04186. [Google Scholar] [CrossRef]
- Bose, S.; Frenk, C.S.; Jenkins, A.; Fattahi, A.; Gómez, F.A.; Grand, R.J.J.; Marinacci, F.; Navarro, J.F.; Oman, K.A.; Pakmor, R.; et al. No cores in dark matter-dominated dwarf galaxies with bursty star formation histories. Mon. Not. R. Astron. Soc. 2019, 486, 4790–4804. [Google Scholar] [CrossRef]
- Peirani, S.; Kay, S.; Silk, J. Active galactic nuclei and massive galaxy cores. Astron. Astrophys. 2008, 479, 123–129. [Google Scholar] [CrossRef]
- Duffy, A.R.; Schaye, J.; Kay, S.T.; Dalla Vecchia, C.; Battye, R.A.; Booth, C.M. Impact of baryon physics on dark matter structures: A detailed simulation study of halo density profiles. Mon. Not. R. Astron. Soc. 2010, 405, 2161–2178. [Google Scholar] [CrossRef]
- Teyssier, R.; Moore, B.; Martizzi, D.; Dubois, Y.; Mayer, L. Mass distribution in galaxy clusters: The role of Active Galactic Nuclei feedback. Mon. Not. R. Astron. Soc. 2011, 414, 195–208. [Google Scholar] [CrossRef]
- Martizzi, D.; Teyssier, R.; Moore, B. Cusp-core transformations induced by AGN feedback in the progenitors of cluster galaxies. Mon. Not. R. Astron. Soc. 2013, 432, 1947–1954. [Google Scholar] [CrossRef]
- Peirani, S.; Dubois, Y.; Volonteri, M.; Devriendt, J.; Bundy, K.; Silk, J.; Pichon, C.; Kaviraj, S.; Gavazzi, R.; Habouzit, M. Density profile of dark matter haloes and galaxies in the HORIZON-AGN simulation: The impact of AGN feedback. Mon. Not. R. Astron. Soc. 2017, 472, 2153–2169. [Google Scholar] [CrossRef]
- D’Onghia, E.; Springel, V.; Hernquist, L.; Keres, D. Substructure Depletion in the Milky Way Halo by the Disk. Astrophys. J. 2010, 709, 1138–1147. [Google Scholar] [CrossRef]
- Kazantzidis, S.; Łokas, E.L.; Callegari, S.; Mayer, L.; Moustakas, L.A. On the Efficiency of the Tidal Stirring Mechanism for the Origin of Dwarf Spheroidals: Dependence on the Orbital and Structural Parameters of the Progenitor Disky Dwarfs. Astrophys. J. 2011, 726, 98. [Google Scholar] [CrossRef]
- Zolotov, A.; Brooks, A.M.; Willman, B.; Governato, F.; Pontzen, A.; Christensen, C.; Dekel, A.; Quinn, T.; Shen, S.; Wadsley, J. Baryons Matter: Why Luminous Satellite Galaxies have Reduced Central Masses. Astrophys. J. 2012, 761, 71. [Google Scholar] [CrossRef]
- Sawala, T.; Pihajoki, P.; Johansson, P.H.; Frenk, C.S.; Navarro, J.F.; Oman, K.A.; White, S.D.M. Shaken and stirred: The Milky Way’s dark substructures. Mon. Not. R. Astron. Soc. 2017, 467, 4383–4400. [Google Scholar] [CrossRef]
- Garrison-Kimmel, S.; Hopkins, P.F.; Wetzel, A.; Bullock, J.S.; Boylan-Kolchin, M.; Keres, D.; Faucher-Giguere, C.A.; El-Badry, K.; Lamberts, A.; Quataert, E.; et al. The Local Group on FIRE: Dwarf galaxy populations across a suite of hydrodynamic simulations. arXiv 2018, arXiv:1806.04143. [Google Scholar] [CrossRef]
- Dubois, Y.; Pichon, C.; Welker, C.; Le Borgne, D.; Devriendt, J.; Laigle, C.; Codis, S.; Pogosyan, D.; Arnouts, S.; Benabed, K.; et al. Dancing in the dark: Galactic properties trace spin swings along the cosmic web. Mon. Not. R. Astron. Soc. 2014, 444, 1453–1468. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Genel, S.; Springel, V.; Torrey, P.; Sijacki, D.; Xu, D.; Snyder, G.; Nelson, D.; Hernquist, L. Introducing the Illustris Project: Simulating the coevolution of dark and visible matter in the Universe. Mon. Not. R. Astron. Soc. 2014, 444, 1518–1547. [Google Scholar] [CrossRef]
- Schaye, J.; Crain, R.A.; Bower, R.G.; Furlong, M.; Schaller, M.; Theuns, T.; Dalla Vecchia, C.; Frenk, C.S.; McCarthy, I.G.; Helly, J.C.; et al. The EAGLE project: Simulating the evolution and assembly of galaxies and their environments. Mon. Not. R. Astron. Soc. 2015, 446, 521–554. [Google Scholar] [CrossRef]
- Khandai, N.; Di Matteo, T.; Croft, R.; Wilkins, S.; Feng, Y.; Tucker, E.; DeGraf, C.; Liu, M.S. The MassiveBlack-II simulation: The evolution of haloes and galaxies to z 0. Mon. Not. R. Astron. Soc. 2015, 450, 1349–1374. [Google Scholar] [CrossRef]
- Pillepich, A.; Springel, V.; Nelson, D.; Genel, S.; Naiman, J.; Pakmor, R.; Hernquist, L.; Torrey, P.; Vogelsberger, M.; Weinberger, R.; et al. Simulating galaxy formation with the IllustrisTNG model. Mon. Not. R. Astron. Soc. 2018, 473, 4077–4106. [Google Scholar] [CrossRef]
- Goodenough, L.; Hooper, D. Possible Evidence For Dark Matter Annihilation In The Inner Milky Way From The Fermi Gamma Ray Space Telescope. arXiv 2009, arXiv:0910.2998. [Google Scholar]
- Bulbul, E.; Markevitch, M.; Foster, A.; Smith, R.K.; Loewenstein, M.; Randall, S.W. Detection of an Unidentified Emission Line in the Stacked X-Ray Spectrum of Galaxy Clusters. Astrophys. J. 2014, 789, 13. [Google Scholar] [CrossRef]
- Boyarsky, A.; Ruchayskiy, O.; Iakubovskyi, D.; Franse, J. Unidentified Line in X-Ray Spectra of the Andromeda Galaxy and Perseus Galaxy Cluster. Phys. Rev. Lett. 2014, 113, 251301. [Google Scholar] [CrossRef] [PubMed]
- Ruchayskiy, O.; Boyarsky, A.; Iakubovskyi, D.; Bulbul, E.; Eckert, D.; Franse, J.; Malyshev, D.; Markevitch, M.; Neronov, A. Searching for decaying dark matter in deep XMM-Newton observation of the Draco dwarf spheroidal. Mon. Not. R. Astron. Soc. 2016, 460, 1390–1398. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Akamatsu, H.; Akimoto, F.; Allen, S.W.; Angelini, L.; Arnaud, K.A.; Audard, M.; Awaki, H.; Axelsson, M.; Bamba, A.; et al. Hitomi Constraints on the 3.5 keV Line in the Perseus Galaxy Cluster. Astrophys. J. Lett. 2017, 837, L15. [Google Scholar] [CrossRef]
- Klypin, A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where Are the Missing Galactic Satellites? Astrophys. J. 1999, 522, 82–92. [Google Scholar] [CrossRef]
- Moore, B.; Ghigna, S.; Governato, F.; Lake, G.; Quinn, T.; Stadel, J.; Tozzi, P. Dark Matter Substructure within Galactic Halos. Astrophys. J. 1999, 524, L19–L22. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. Too big to fail? The puzzling darkness of massive Milky Way subhaloes. Mon. Not. R. Astron. Soc. 2011, 415, L40–L44. [Google Scholar] [CrossRef]
- Walker, M.G.; Peñarrubia, J. A Method for Measuring (Slopes of) the Mass Profiles of Dwarf Spheroidal Galaxies. Astrophys. J. 2011, 742, 20. [Google Scholar] [CrossRef]
- Kroupa, P.; Theis, C.; Boily, C.M. The great disk of Milky-Way satellites and cosmological sub-structures. Astron. Astrophys. 2005, 431, 517–521. [Google Scholar] [CrossRef]
- Ibata, R.A.; Ibata, N.G.; Lewis, G.F.; Martin, N.F.; Conn, A.; Elahi, P.; Arias, V.; Fernando, N. A Thousand Shadows of Andromeda: Rotating Planes of Satellites in the Millennium-II Cosmological Simulation. Astrophys. J. Lett. 2014, 784, L6. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Famaey, B.; Jerjen, H.; Merritt, D.; Kroupa, P.; Dabringhausen, J.; Lüghausen, F.; Forbes, D.A.; Hensler, G.; Hammer, F.; et al. Co-orbiting satellite galaxy structures are still in conflict with the distribution of primordial dwarf galaxies. Mon. Not. R. Astron. Soc. 2014, 442, 2362–2380. [Google Scholar] [CrossRef]
- Wadepuhl, M.; Springel, V. Satellite galaxies in hydrodynamical simulations of Milky Way sized galaxies. Mon. Not. R. Astron. Soc. 2011, 410, 1975–1992. [Google Scholar] [CrossRef]
- Simpson, C.M.; Grand, R.J.J.; Gómez, F.A.; Marinacci, F.; Pakmor, R.; Springel, V.; Campbell, D.J.R.; Frenk, C.S. Quenching and ram pressure stripping of simulated Milky Way satellite galaxies. Mon. Not. R. Astron. Soc. 2018, 478, 548–567. [Google Scholar] [CrossRef]
- Mashchenko, S.; Couchman, H.M.P.; Wadsley, J. The removal of cusps from galaxy centres by stellar feedback in the early Universe. Nature 2006, 442, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, M.D.; Katz, N. Bar-driven Dark Halo Evolution: A Resolution of the Cusp-Core Controversy. Astrophys. J. 2002, 580, 627–633. [Google Scholar] [CrossRef]
- Müller, O.; Jerjen, H.; Pawlowski, M.S.; Binggeli, B. Testing the two planes of satellites in the Centaurus group. Astron. Astrophys. 2016, 595, A119. [Google Scholar] [CrossRef]
- Cautun, M.; Bose, S.; Frenk, C.S.; Guo, Q.; Han, J.; Hellwing, W.A.; Sawala, T.; Wang, W. Planes of satellite galaxies: When exceptions are the rule. Mon. Not. R. Astron. Soc. 2015, 452, 3838–3852. [Google Scholar] [CrossRef]
- Müller, O.; Pawlowski, M.S.; Jerjen, H.; Lelli, F. A whirling plane of satellite galaxies around Centaurus A challenges cold dark matter cosmology. Science 2018, 359, 534–537. [Google Scholar] [CrossRef]
- Libeskind, N.I.; Frenk, C.S.; Cole, S.; Helly, J.C.; Jenkins, A.; Navarro, J.F.; Power, C. The distribution of satellite galaxies: The great pancake. Mon. Not. R. Astron. Soc. 2005, 363, 146–152. [Google Scholar] [CrossRef][Green Version]
- Shao, S.; Cautun, M.; Frenk, C.S. Evolution of galactic planes of satellites in the EAGLE simulation. arXiv 2019, arXiv:1904.02719. [Google Scholar] [CrossRef]
- Wang, J.; Frenk, C.S.; Navarro, J.F.; Gao, L.; Sawala, T. The missing massive satellites of the Milky Way. Mon. Not. R. Astron. Soc. 2012, 424, 2715–2721. [Google Scholar] [CrossRef]
- Kennedy, R.; Frenk, C.; Cole, S.; Benson, A. Constraining the warm dark matter particle mass with Milky Way satellites. Mon. Not. R. Astron. Soc. 2014, 442, 2487–2495. [Google Scholar] [CrossRef]
- Lovell, M.R.; Bose, S.; Boyarsky, A.; Cole, S.; Frenk, C.S.; Gonzalez-Perez, V.; Kennedy, R.; Ruchayskiy, O.; Smith, A. Satellite galaxies in semi-analytic models of galaxy formation with sterile neutrino dark matter. Mon. Not. R. Astron. Soc. 2016, 461, 60–72. [Google Scholar] [CrossRef]
- Callingham, T.M.; Cautun, M.; Deason, A.J.; Frenk, C.S.; Wang, W.; Gómez, F.A.; Grand, R.J.J.; Marinacci, F.; Pakmor, R. The mass of the Milky Way from satellite dynamics. Mon. Not. R. Astron. Soc. 2019, 484, 5453–5467. [Google Scholar] [CrossRef]
- Lovell, M.R.; Gonzalez-Perez, V.; Bose, S.; Boyarsky, A.; Cole, S.; Frenk, C.S.; Ruchayskiy, O. Addressing the too big to fail problem with baryon physics and sterile neutrino dark matter. Mon. Not. R. Astron. Soc. 2017, 468, 2836–2849. [Google Scholar] [CrossRef]
- Burger, J.D.; Zavala, J. The nature of core formation in dark matter haloes: Adiabatic or impulsive? Mon. Not. R. Astron. Soc. 2019, 485, 1008–1028. [Google Scholar] [CrossRef]
- Rees, M.J. Lyman absorption lines in quasar spectra—Evidence for gravitationally-confined gas in dark minihaloes. Mon. Not. R. Astron. Soc. 1986, 218, 25P–30P. [Google Scholar] [CrossRef]
- Benítez-Llambay, A.; Navarro, J.F.; Frenk, C.S.; Sawala, T.; Oman, K.; Fattahi, A.; Schaller, M.; Schaye, J.; Crain, R.A.; Theuns, T. The properties of ‘dark’ ΛCDM haloes in the Local Group. Mon. Not. R. Astron. Soc. 2017, 465, 3913–3926. [Google Scholar] [CrossRef]
- Carlberg, R.G. Dark Matter Sub-halo Counts via Star Stream Crossings. Astrophys. J. 2012, 748, 20. [Google Scholar] [CrossRef]
- Erkal, D.; Belokurov, V.; Bovy, J.; Sand ers, J.L. The number and size of subhalo-induced gaps in stellar streams. Mon. Not. R. Astron. Soc. 2016, 463, 102–119. [Google Scholar] [CrossRef]
- Amorisco, N.C.; Gómez, F.A.; Vegetti, S.; White, S.D.M. Gaps in globular cluster streams: Giant molecular clouds can cause them too. Mon. Not. R. Astron. Soc. 2016, 463, L17–L21. [Google Scholar] [CrossRef]
- Erkal, D.; Koposov, S.E.; Belokurov, V. A sharper view of Pal 5’s tails: Discovery of stream perturbations with a novel non-parametric technique. Mon. Not. R. Astron. Soc. 2017, 470, 60–84. [Google Scholar] [CrossRef]
- Bovy, J.; Erkal, D.; Sanders, J.L. Linear perturbation theory for tidal streams and the small-scale CDM power spectrum. Mon. Not. R. Astron. Soc. 2017, 466, 628–668. [Google Scholar] [CrossRef]
- Mao, S.; Schneider, P. Evidence for substructure in lens galaxies? Mon. Not. R. Astron. Soc. 1998, 295, 587. [Google Scholar] [CrossRef]
- Schneider, P.; Weiss, A. The gravitational lens equation near cusps. Astron. Astrophys. 1992, 260, 1–13. [Google Scholar]
- Metcalf, R.B.; Madau, P. Compound Gravitational Lensing as a Probe of Dark Matter Substructure within Galaxy Halos. Astrophys. J. 2001, 563, 9–20. [Google Scholar] [CrossRef]
- Dalal, N.; Kochanek, C.S. Direct Detection of Cold Dark Matter Substructure. Astrophys. J. 2002, 572, 25–33. [Google Scholar] [CrossRef]
- Xu, D.; Sluse, D.; Gao, L.; Wang, J.; Frenk, C.; Mao, S.; Schneider, P.; Springel, V. How well can cold dark matter substructures account for the observed radio flux-ratio anomalies. Mon. Not. R. Astron. Soc. 2015, 447, 3189–3206. [Google Scholar] [CrossRef]
- Hsueh, J.W.; Enzi, W.; Vegetti, S.; Auger, M.; Fassnacht, C.D.; Despali, G.; Koopmans, L.V.E.; McKean, J.P. SHARP – VII. New constraints on warm dark matter free-streaming properties and substructure abundance from flux-ratio anomalous lensed quasars. arXiv 2019, arXiv:1905.04182. [Google Scholar]
- Iršič, V.; Viel, M.; Haehnelt, M.G.; Bolton, J.S.; Cristiani, S.; Becker, G.D.; D’Odorico, V.; Cupani, G.; Kim, T.S.; Berg, T.A.M.; et al. New constraints on the free-streaming of warm dark matter from intermediate and small scale Lyman-α forest data. Phys. Rev. D 2017, 96, 023522. [Google Scholar] [CrossRef]
- Vegetti, S.; Koopmans, L.V.E. Bayesian strong gravitational-lens modelling on adaptive grids: Objective detection of mass substructure in Galaxies. Mon. Not. R. Astron. Soc. 2009, 392, 945–963. [Google Scholar] [CrossRef]
- Vegetti, S.; Lagattuta, D.J.; McKean, J.P.; Auger, M.W.; Fassnacht, C.D.; Koopmans, L.V.E. Gravitational detection of a low-mass dark satellite galaxy at cosmological distance. Nature 2012, 481, 341–343. [Google Scholar] [CrossRef] [PubMed]
- Keeton, C.R. A Catalog of Mass Models for Gravitational Lensing. arXiv 2001, arXiv:astro-ph/0102341. [Google Scholar]
- Vegetti, S.; Koopmans, L.V.E.; Bolton, A.; Treu, T.; Gavazzi, R. Detection of a dark substructure through gravitational imaging. Mon. Not. R. Astron. Soc. 2010, 408, 1969–1981. [Google Scholar] [CrossRef]
- Vegetti, S.; Despali, G.; Lovell, M.R.; Enzi, W. Constraining sterile neutrino cosmologies with strong gravitational lensing observations at redshift z = 0.2. Mon. Not. R. Astron. Soc. 2018, 481, 3661–3669. [Google Scholar] [CrossRef]
- Vegetti, S.; Koopmans, L.V.E.; Auger, M.W.; Treu, T.; Bolton, A.S. Inference of the cold dark matter substructure mass function at z = 0.2 using strong gravitational lenses. Mon. Not. R. Astron. Soc. 2014, 442, 2017–2035. [Google Scholar] [CrossRef]
- Hezaveh, Y.D.; Dalal, N.; Marrone, D.P.; Mao, Y.Y.; Morningstar, W.; Wen, D.; Blandford, R.D.; Carlstrom, J.E.; Fassnacht, C.D.; Holder, G.P.; et al. Detection of Lensing Substructure Using ALMA Observations of the Dusty Galaxy SDP.81. Astrophys. J. 2016, 823, 37. [Google Scholar] [CrossRef]
- Nightingale, J.; Dye, S.; Massey, R. AutoLens: Automated Modeling of a Strong Lens’s Light, Mass and Source. arXiv 2017. [Google Scholar] [CrossRef]
- Brewer, B.J.; Huijser, D.; Lewis, G.F. Trans-dimensional Bayesian inference for gravitational lens substructures. Mon. Not. R. Astron. Soc. 2016, 455, 1819–1829. [Google Scholar] [CrossRef]
- Diaz Rivero, A.; Cyr-Racine, F.Y.; Dvorkin, C. On the Power Spectrum of Dark Matter Substructure in Strong Gravitational Lenses. arXiv 2017, arXiv:1707.04590. [Google Scholar] [CrossRef]
- Li, R.; Frenk, C.S.; Cole, S.; Wang, Q.; Gao, L. Projection effects in the strong lensing study of subhaloes. Mon. Not. R. Astron. Soc. 2017, 468, 1426–1432. [Google Scholar] [CrossRef]
- Despali, G.; Vegetti, S.; White, S.D.M.; Giocoli, C.; van den Bosch, F.C. Modelling the line-of-sight contribution in substructure lensing. Mon. Not. R. Astron. Soc. 2018, 475, 5424–5442. [Google Scholar] [CrossRef]
- Li, R.; Frenk, C.S.; Cole, S.; Gao, L.; Bose, S.; Hellwing, W.A. Constraints on the identity of the dark matter from strong gravitational lenses. Mon. Not. R. Astron. Soc. 2016, 460, 363–372. [Google Scholar] [CrossRef]
| 1 | Equal amounts of dark matter and anti-dark matter. |
| 2 | By strong, we mean that the cross-section for self-interaction is of the order of the nuclear cross-section for visible matter (set by the strong force). |
| 3 | Some SIDM models are motivated by the baryon asymmetry; in these models, dark matter, unlike traditional WIMPs, shares this asymmetry (for a review of asymmetric dark matter see [19]). |
| 4 | In contrast to WDM, the damping of small structures is not due to free-streaming, but to a collisional, Silk-like, damping. |
| 5 | The (co-moving) free-streaming scale is given by: , where is the age of the universe at the time when the dark matter particles become non-relativistic (at a temperature ); is the scale factor at ( in the radiation-dominated era); and is the scale factor at the time of matter-radiation equality. |
| 6 | For cold particles, we have assumed CDM WIMPs, which requires taking into account the kinetic decoupling temperature and epoch; specifically, we took Equation (43) of [23]. |
| 7 | Please note that acoustic oscillations are also present in WIMP-CDM models (e.g., [27]), but they occur at much smaller scales than in relevant hidden dark sector models where they can be of galactic scale. |
| 8 | We use , where is the mean dark matter density today. |
| 9 | For a review see e.g., Section 3 of [46]. |
| 10 | By this we mean an average of the fine-grained distribution function in the collisionless Boltzmann equation over the scales resolved in the simulation, typically several times the interparticle separation. |
| 11 | In principle, each particle can have an individual softening, see e.g., Section 4 of [47]. |
| 12 | The introduction of a softening scale in the density (or potential) suppresses gravitational two-body large-angle scatterings which are artificial for an approximately continuous dark matter density distribution. |
| 13 | In Fourier space, Equation (6) is simply a multiplication . |
| 14 | For a review of the force computation methods see Section 3.5 of [46]. |
| 15 | The particles are initially placed at random in the simulation cube and then left to evolve under a repulsive force by reversing the sign of the gravitational force until they reach an equilibrium configuration that has no discernible grid pattern [69]. |
| 16 | A sufficiently large volume is needed to sample large-scale modes that remain approximately linear during the simulation where power is transferred from large to small scales; without appropriate large-scale sampling, the clustering is no longer accurate once perturbations on the scale of the cube become non-linear. |
| 17 | In practice, power below the Nyquist frequency is generated non-linearly so the resolution of the simulation is not limited by the Nyquist frequency but rather by the gravitational softening scale, . |
| 18 | Reproduced from Michael Boylan-Kolchin et al. Resolving cosmic structure formation with the Millennium-II Simulation. MNRAS (2009) 398 (3): 1150-1164, doi: 10.1111/j.1365-2966.2009.15191.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following u. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 19 | For a review of the state of cosmological simulations circa 2012 see [79]. |
| 20 | This is only true if, on the scales of interest, the primordial power spectrum grows monotonically towards large k. |
| 21 | Reproduced from Volker Springel et al. The Aquarius Project: the subhaloes of galactic haloes. MNRAS (2008) 391 (4): 1685–1711, doi: 10.1111/j.1365-2966.2008.14066.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/391/4/1685/1747035. |
| 22 | Reproduced from Julio Navarro et al. The diversity and similarity of simulated cold dark matter haloes. MNRAS (2010) 402 (1): 21–34, doi: 10.1111/j.1365-2966.2009.15878.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/402/1/21/1028856. |
| 23 | Reproduced from Carlos Vera-Ciro et al. The shape of dark matter haloes in the Aquarius simulations: evolution and memory. MNRAS (2011) 416 (2): 1377–1391, doi: 10.1111/j.1365-2966.2011.19134.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/416/2/1377/1061105. |
| 24 | Reproduced from Mark Vogelsberger et al. Phase-space structure in the local dark matter distribution and its signature in direct detection experiments. MNRAS (2009) 395 (2): 797–811, doi: 10.1111/j.1365-2966.2009.14630.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/395/2/797/1747020. The figures mentioned in footnotes 21–24 are not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 25 | Given the limited resolution of simulations, local in this sense refers to regions of at least (10 kpc) as in [140]. |
| 26 | Reproduced from Mark Vogelsberger et al. Subhaloes in self-interacting galactic dark matter haloes. MNRAS (2012) 423 (4): 3740–3752, doi: 10.1111/j.1365-2966.2012.21182.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/423/4/3740/1749150. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 27 | Reproduced from Mark Lovell et al. The haloes of bright satellite galaxies in a warm dark matter universe. MNRAS (2012) 420 (3): 2318–2324, doi: 10.1111/j.1365-2966.2011.20200.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/420/3/2318/979379. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 28 | This functional form has been corroborated by [112], but the parameters in the two studies are different. The formula is nevertheless a good approximation to the general behavior. |
| 29 | The gravothermal collapse [164] is a familiar process in globular clusters, where the inner regions have negative specific heat that is smaller than the positive specific heat in the outer regions. In the case of globular clusters, the collapse can be prevented by the formation of binary stars at the center. In the case of a SIDM halo, since the interactions are purely elastic, the process is expected to continue until a black hole forms. The black hole efficiently accretes the inner core of the SIDM halo (e.g., [165]). This discussion refers strictly to elastic self-scattering. If collisions are inelastic, then the energy released needs to be taken into account and, in fact, it could prevent the gravothermal collapse; see [166]. |
| 30 | Reproduced from Carlo Giocoli et al. The substructure hierarchy in dark matter haloes . MNRAS (2010) 404 (1): 502–517, doi: 10.1111/j.1365-2966.2010.16311.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/404/1/502/3101607. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 31 | Reproduced from Volker Springel et al. The Aquarius Project: the subhaloes of galactic haloes. MNRAS (2008) 391 (4): 1685–1711, doi: 10.1111/j.1365-2966.2008.14066.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/391/4/1685/1747035. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 32 | Another set of parameters that can be used to define the orbit are the apocentre and pericenter. Different parametrizations can be transformed into one another since they are all related to the potential, . |
| 33 | Reproduced from Lilian Jian et al. Orbital parameters of infalling satellite haloes in the hierarchical CDM model. MNRAS (2015) 448 (2): 1674–1686, doi: 10.1093/mnras/stv053. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/448/2/1674/1053529. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 34 | This estimate is based on an extrapolation over many orders of magnitude of the subhalo mass function determined in simulations down to the free-streaming mass of WIMP-CDM particles. We discuss this in more detail below. |
| 35 | Reproduced from Miguel Rocha et al. Infall times for Milky Way satellites from their present-day kinematics. MNRAS (2012) 425 (1): 231–244, doi: 10.1111/j.1365-2966.2012.21432.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/425/1/231/998181. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 36 | Reproduced from Mark Vogelsberger and Simon D. M. White. Streams and caustics: the fine-grained structure of cold dark matter haloes. MNRAS (2011) 413 (2): 1419–1438, doi: 10.1111/j.1365-2966.2011.18224.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/413/2/1419/1070092. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 37 | Caustics represent folds in the fine-grained phase-space distribution function, which in CDM evolves according to the collisionless Boltzmann equation (Equation (1)). Before the formation of non-linear structures, CDM particles are distributed nearly uniformly in space with small density and velocity perturbations and very small thermal velocities. CDM particles thus occupy a thin, approximately three -dimensional, sheet in 6D phase-space volume. Since CDM particles are collisionless and evolve according to Equation (1), the fine-grained phase-space density is conserved during gravitational evolution (this was discussed earlier in the context of the maximum phase-space density in WDM models in Section 2.4), which implies that the original thin sheet can be stretched and folded but it cannot be broken. Caustics appear where folds occur, and have very large spatial densities, limited only by primordial thermal motions (e.g., [190,191,192]). |
| 38 | |
| 39 | |
| 40 | Reproduced from Frank C van den Bosch and Go Ogiya. Dark matter substructure in numerical simulations: a tale of discreteness noise, runaway instabilities, and artificial disruption. MNRAS (2018) 475 (3): 4066–4087, doi: 10.1093/mnras/sty084. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/475/3/4066/4797185. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 41 | Reproduced from Frank C van den Bosch et al. Disruption of dark matter substructure: fact or fiction? MNRAS (2018) 474 (3): 3043–3066, doi: 10.1093/mnras/stx2956. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/474/3/3043/4638541. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 42 | ©AAS. Reproduced with permission. For the original article, please visit the following https://iopscience.iop.org/article/10.1086/420840. |
| 43 | Reproduced from Go Ogiya and Andreas Burkert. Dynamical friction and scratches of orbiting satellite galaxies on host systems. MNRAS (2016) 457 (2): 2164–2172, doi: 10.1093/mnras/stw091. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/457/2/2164/970692. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 44 | Reproduced from Michael Boylan-Kolchin et al. Dynamical friction and galaxy merging timescales . MNRAS (2008) 383 (1): 93–101, doi: 10.1111/j.1365-2966.2007.12530.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/383/1/93/1067887. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 45 | The Hernquist halo profile [221] has the same asymptotic behavior at the center as the NFW halo and has the advantage that the velocity distribution function in the isotropic case has an analytic form (see Equation (11)), which makes it particularly simple to set up initial conditions for simulating haloes in dynamical equilibrium. |
| 46 | The values for these parameters reported in [218] are: , , , and , but we point out that in this study both the halo and the subhalo were modeled as Hernquist profiles. |
| 47 | Equation (18) was only explored for values of the circularity in the range and for ; the lower limits were imposed to avoid radial orbits that would take the subhalo so close to the center of the halo in the first orbit that the tidal effects of the galaxy cannot be ignored. So far we have not discussed baryonic effects, but it is worth mentioning them here since Equation (18) was not investigated outside this range and might not be valid there even in the absence of a central galaxy. |
| 48 | ©AAS. Reproduced with permission. For the original article, please visit the following https://iopscience.iop.org/article/10.1088/0004-637X/740/2/102. |
| 49 | |
| 50 | Although the introduction of a third parameter will obviously improve the quality of the fit, the Einasto profile is, in fact, a slightly better fit to simulations than the 2-parameter NFW profile even after one of the parameters () is fixed to an appropriate value. For instance, fixing gives a better fit than NFW to haloes across a range of halo masses [240]. |
| 51 | Reproduced from Volker Springel et al. The Aquarius Project: the subhaloes of galactic haloes. MNRAS (2008) 391 (4): 1685–1711, doi: 10.1111/j.1365-2966.2008.14066.x. By permission of Oxford University Press on behalf of the Royal Astronomical Society. For the original article, please visit the following https://academic.oup.com/mnras/article/391/4/1685/1747035. This figure is not included under the CC-BY license of this publication. For permissions, please email: journals.permissions@oup.com. |
| 52 | We note that there is a typo in the caption of Figure 28 in [138], which gives the fitting function for and ( M M). |
| 53 | |
| 54 | For a clear illustration of the evolutionary track of subhaloes in the plane due to tidal stripping, see Figure 8 of [243]. |
| 55 | |
| 56 | This is true only for elastic SIDM, and for cross sections that do not exceed the gravothermal collapse threshold, cmg, for dwarf-size haloes (see the last paragraphs of Section 2.4). Although the regime of gravothermal collapse has been known for a couple of decades [162,163], a comprehensive analysis of this regime has yet to be carried out (see [32,249,251,252] for recent developments in this interesting regime). |
| 57 | There is a class of inelastic SIDM models in which the dark matter can have ground and excited states (e.g., [253]), and in which scattering between the excited and ground states can result in energy injection at the center of dark matter haloes thus altering their structure. Only until very recently have these models began to be explored with simulations [166,254]. |
| 58 | Large relative velocities between gas and dark matter inherited from the photon-baryon coupling before recombination can impede the growth of gravitational perturbations and stop gas from accreting into the first haloes [257]. This process, however, is only thought to be relevant for the formation of the first stars. |
| 59 | This mass threshold is smaller at higher redshifts, see e.g., Figure 3 of [266]. |
| 60 | |
| 61 | |
| 62 | See [325] for an opposed view. |
| 63 | This halo mass was estimated assuming a truncated pseudo-Jaffe profile (see e.g., Equation (42) in [350]). The inferred mass is likely to be larger if an NFW profile is assumed instead. For instance, a similar dark matter substructure detected with lensing was reported by [351] with a mass of ∼ M assuming a truncated pseudo-Jaffe profile, while assuming an NFW profile this substructure is estimated to have a mass of ∼ M [352]. |
| 64 | This has been demonstrated explicitly for the case of Einstein ring distortions but it may hold true for other tests as well. |
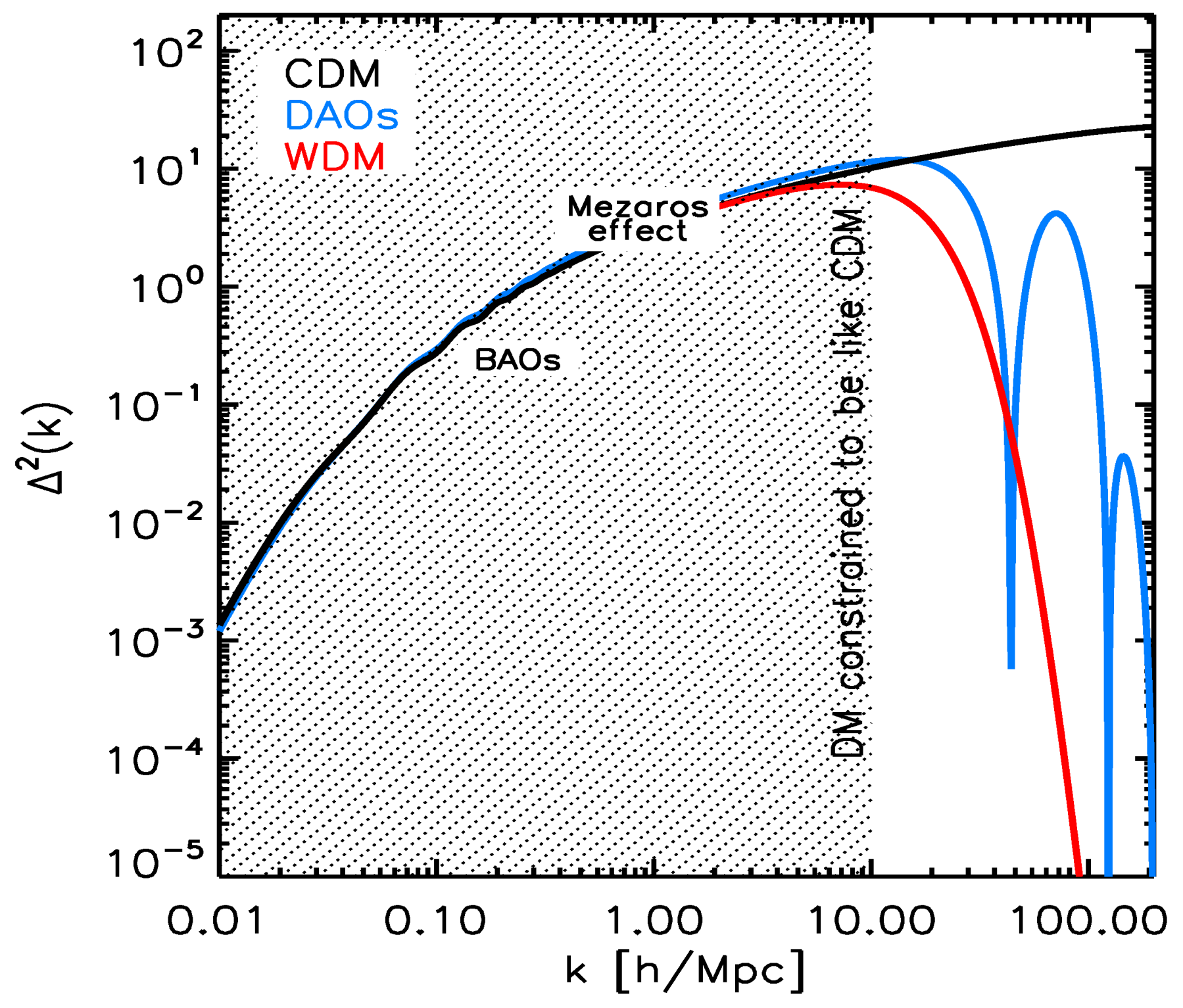
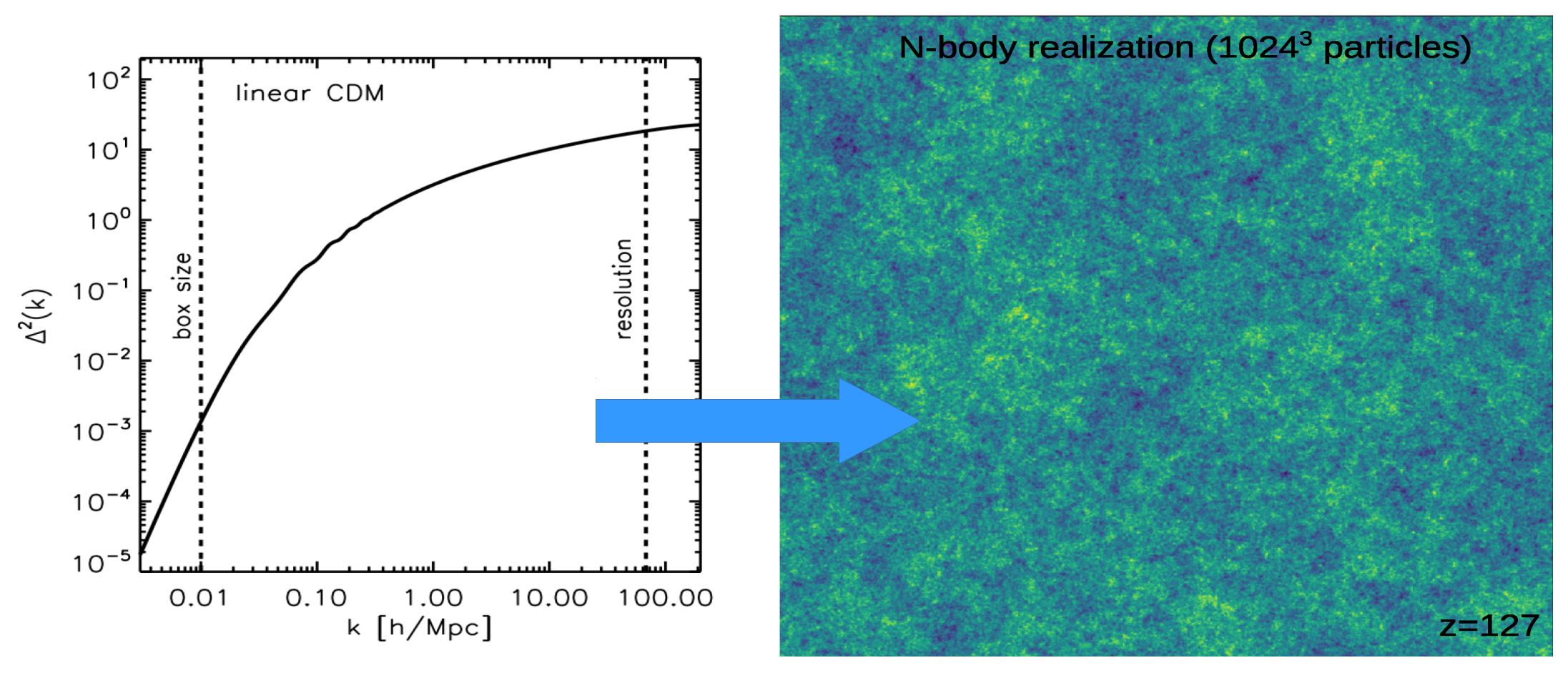
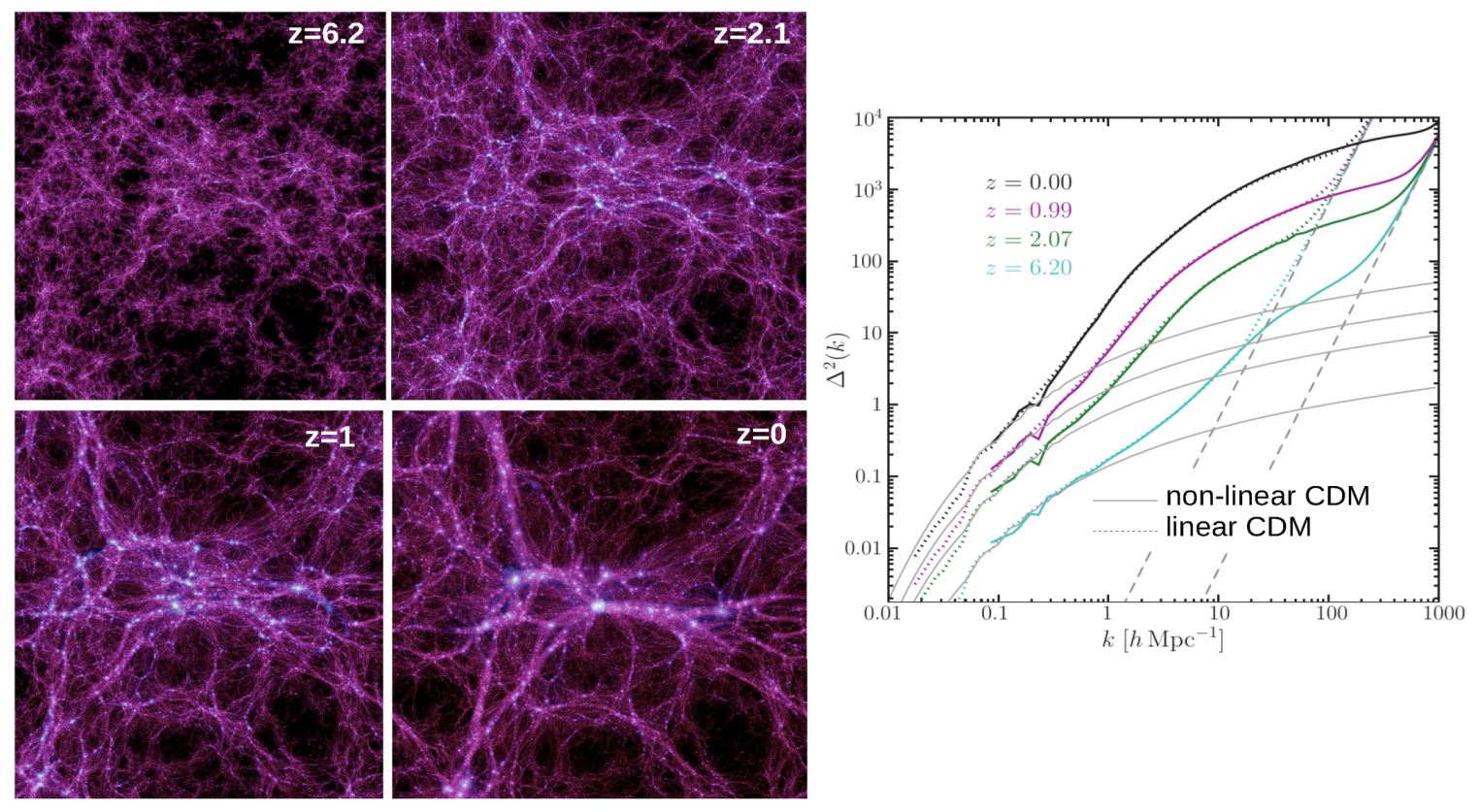
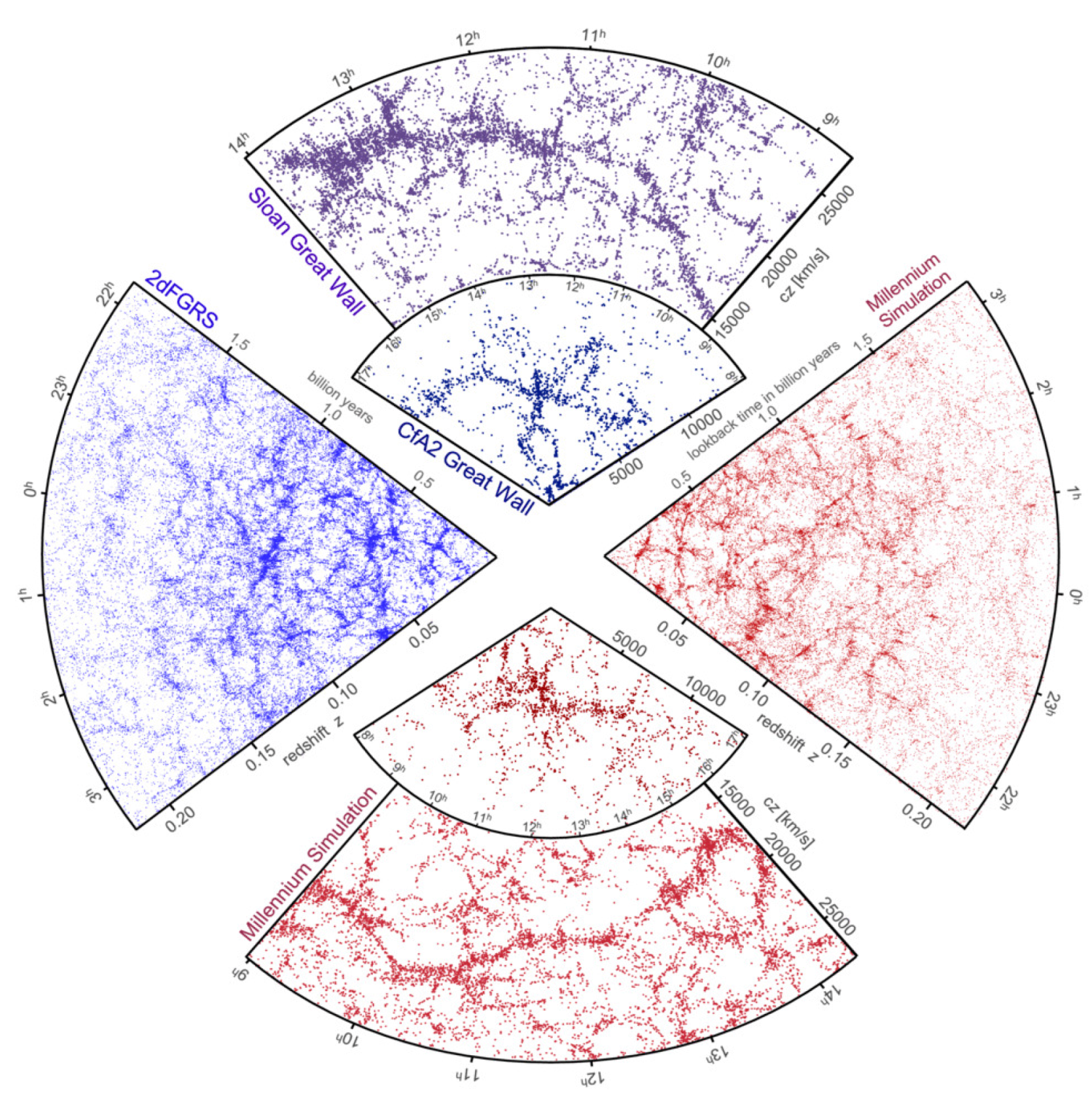
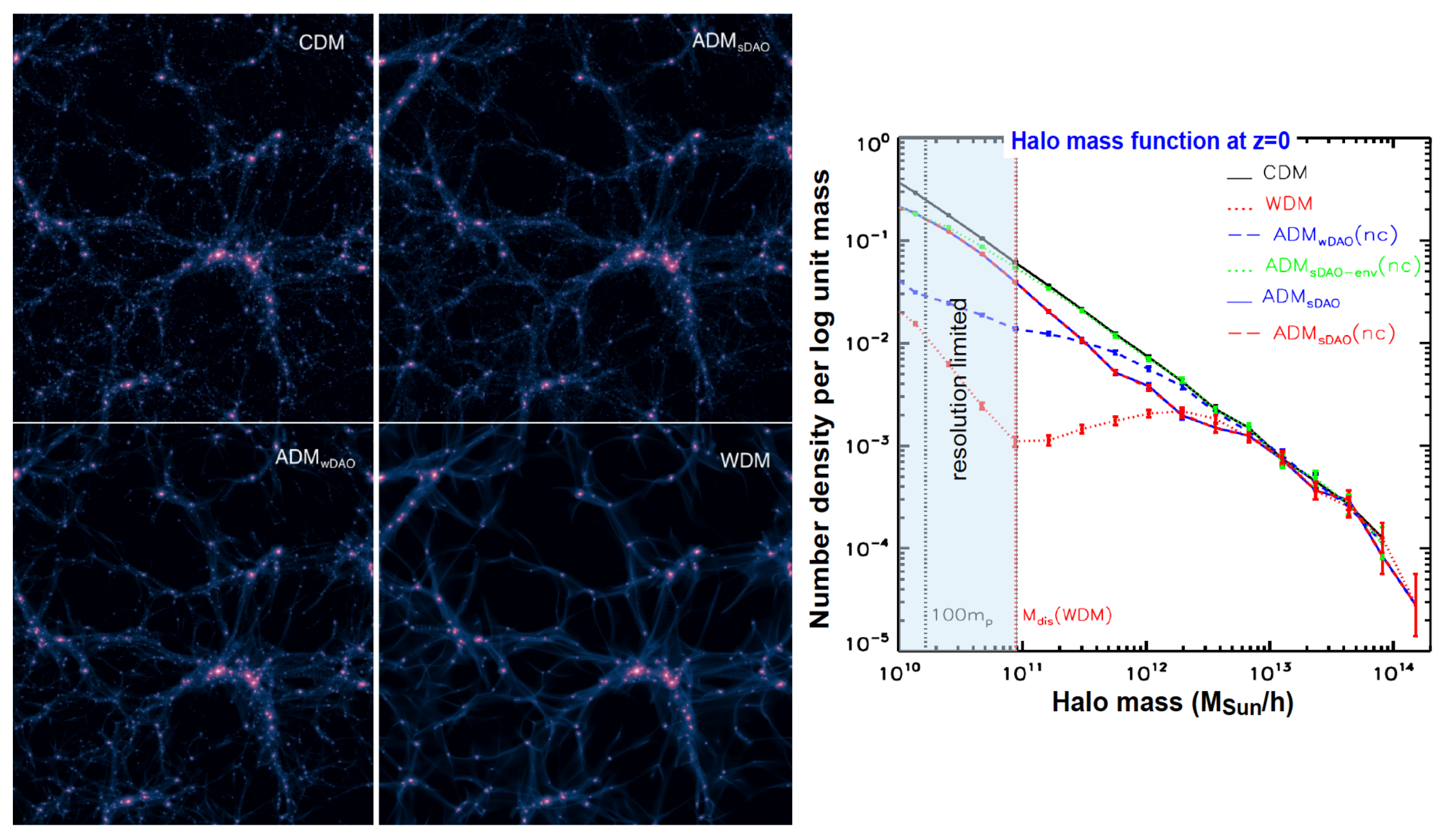
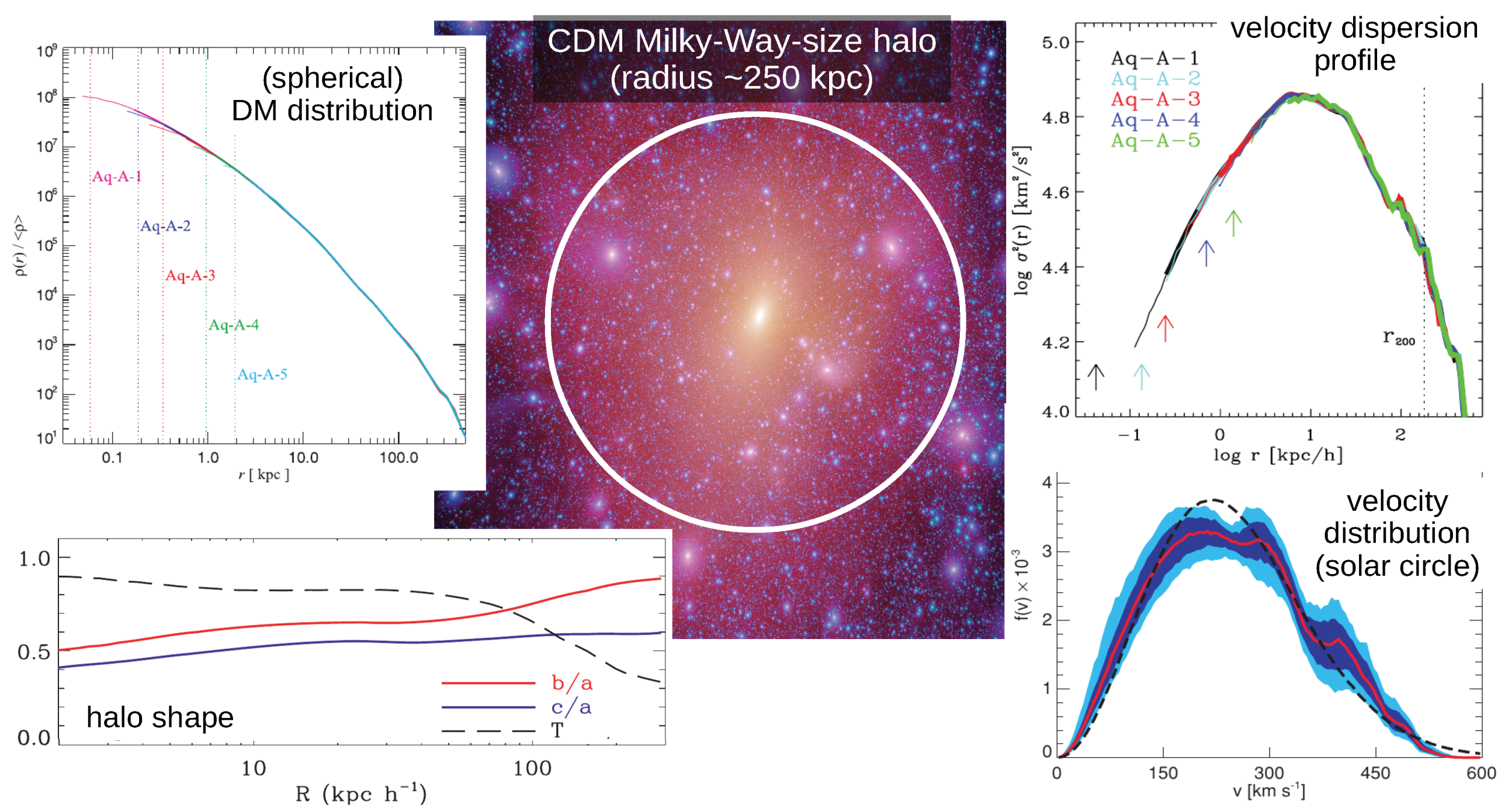
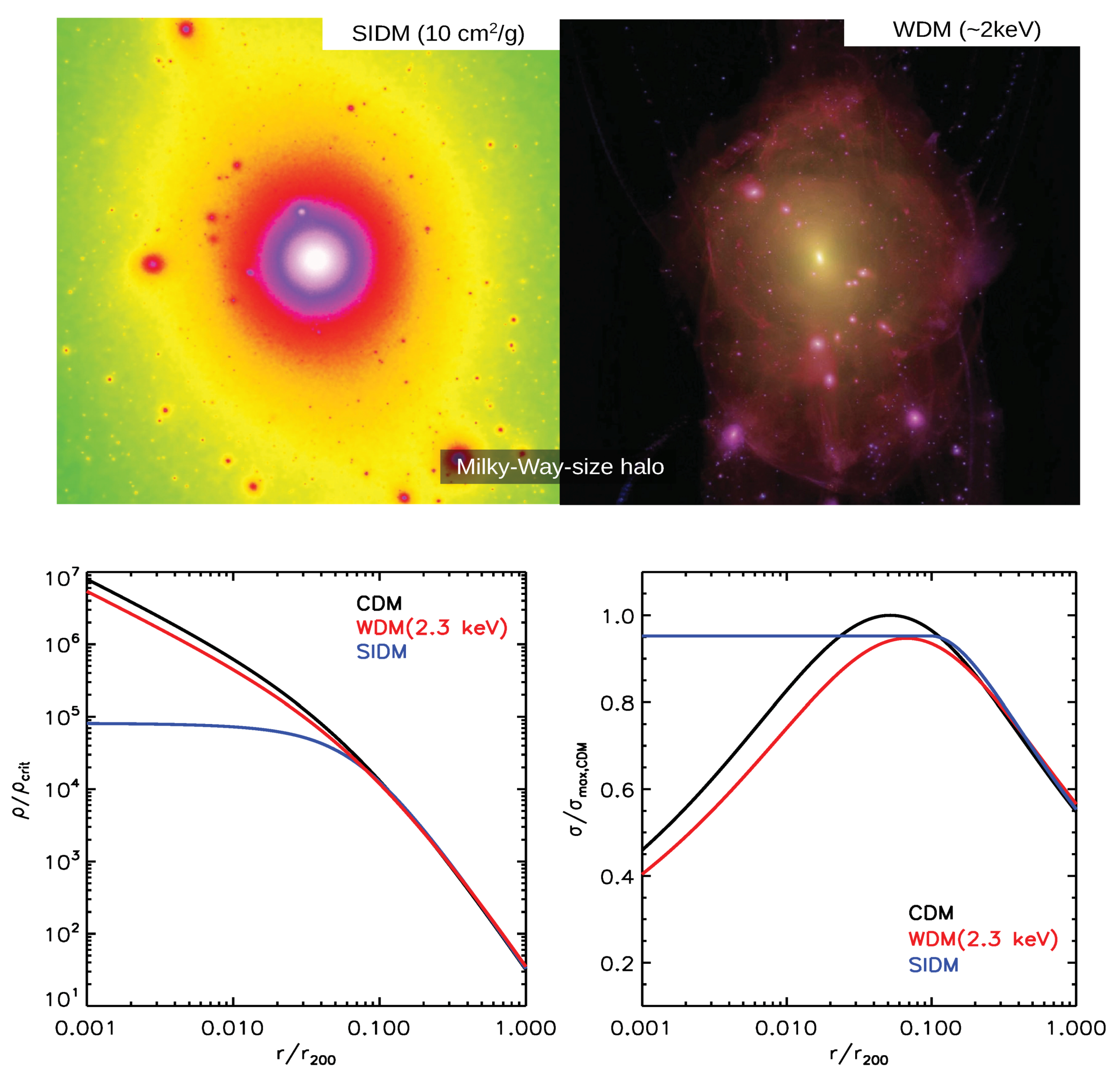
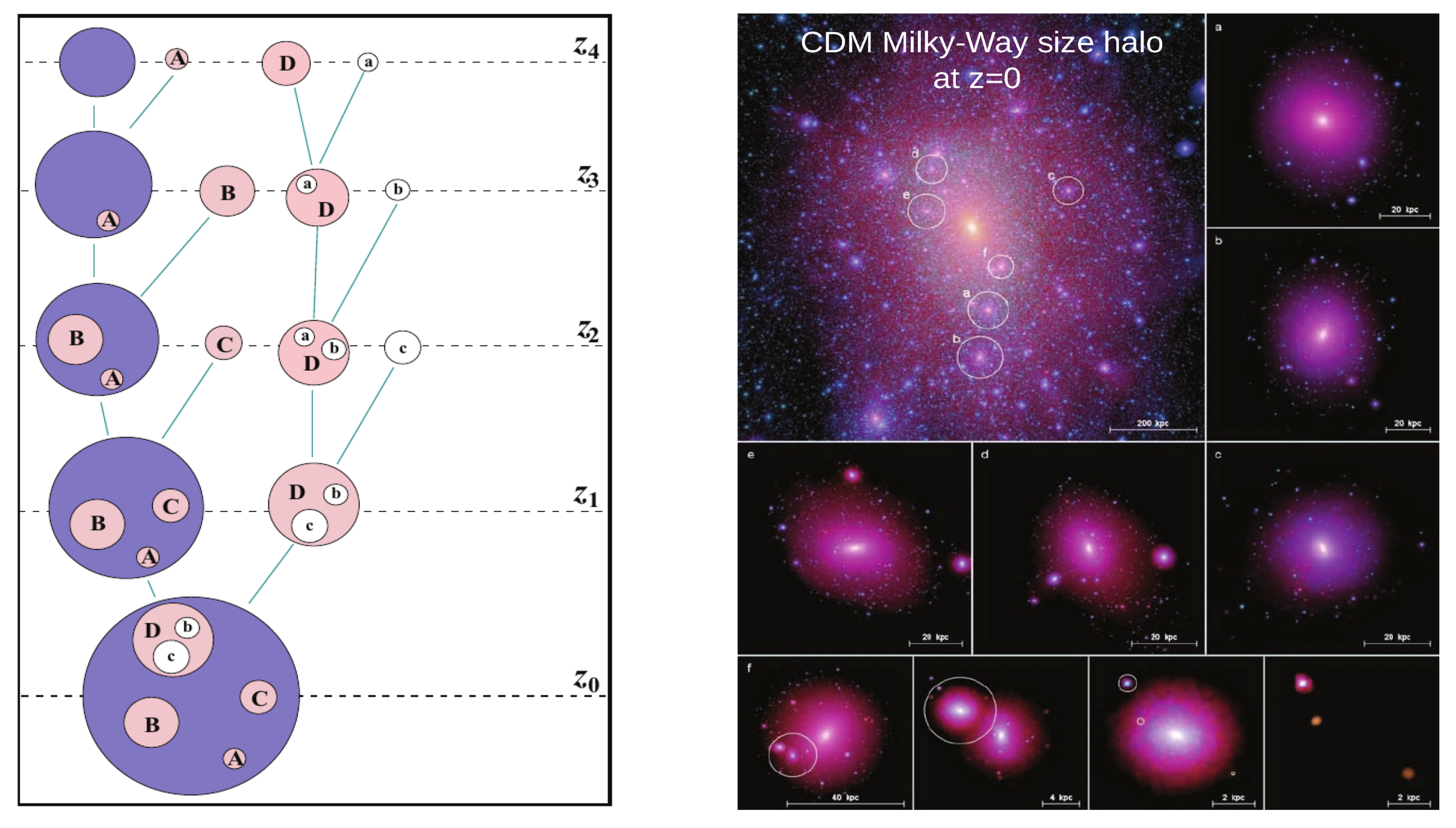
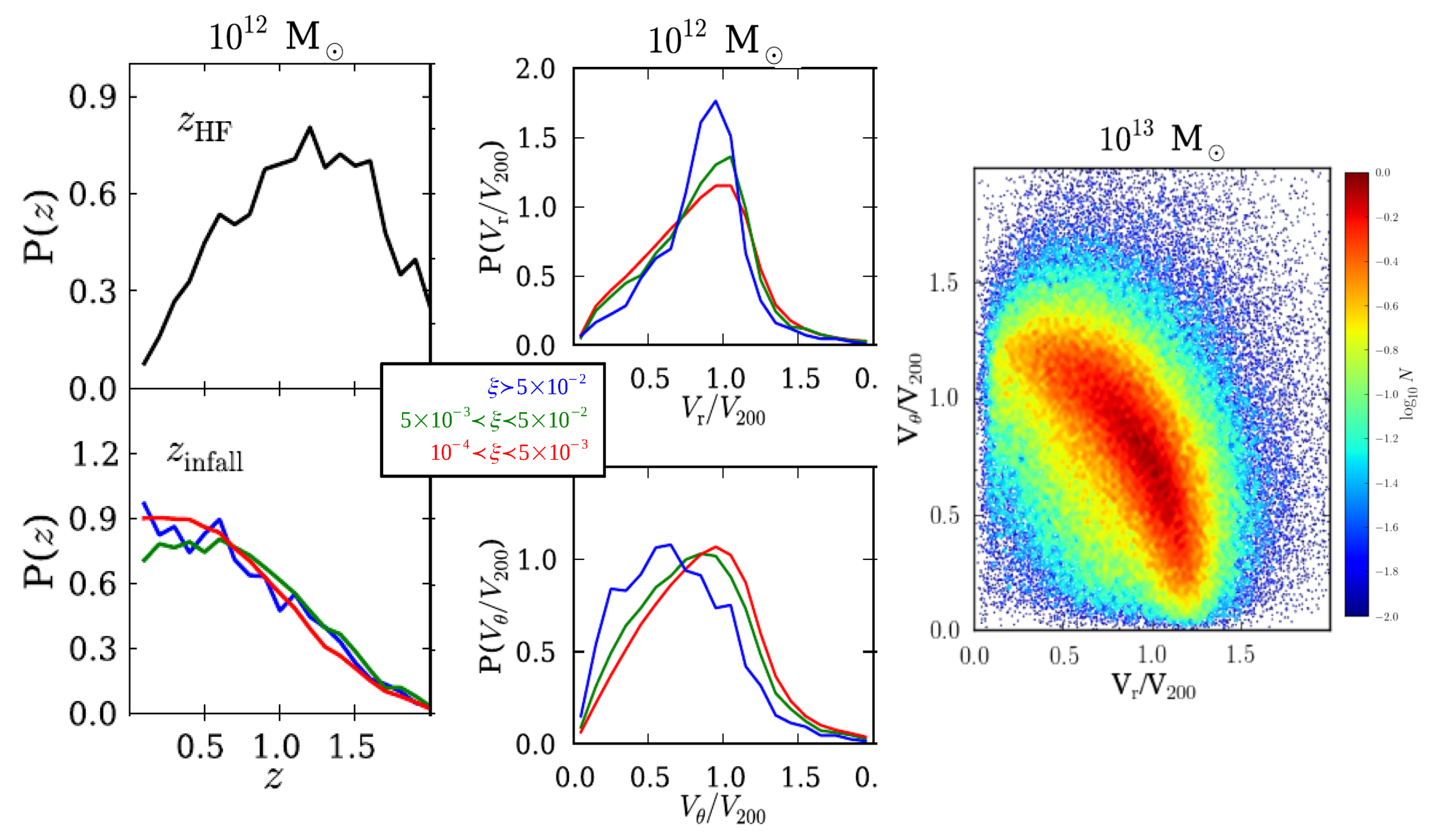
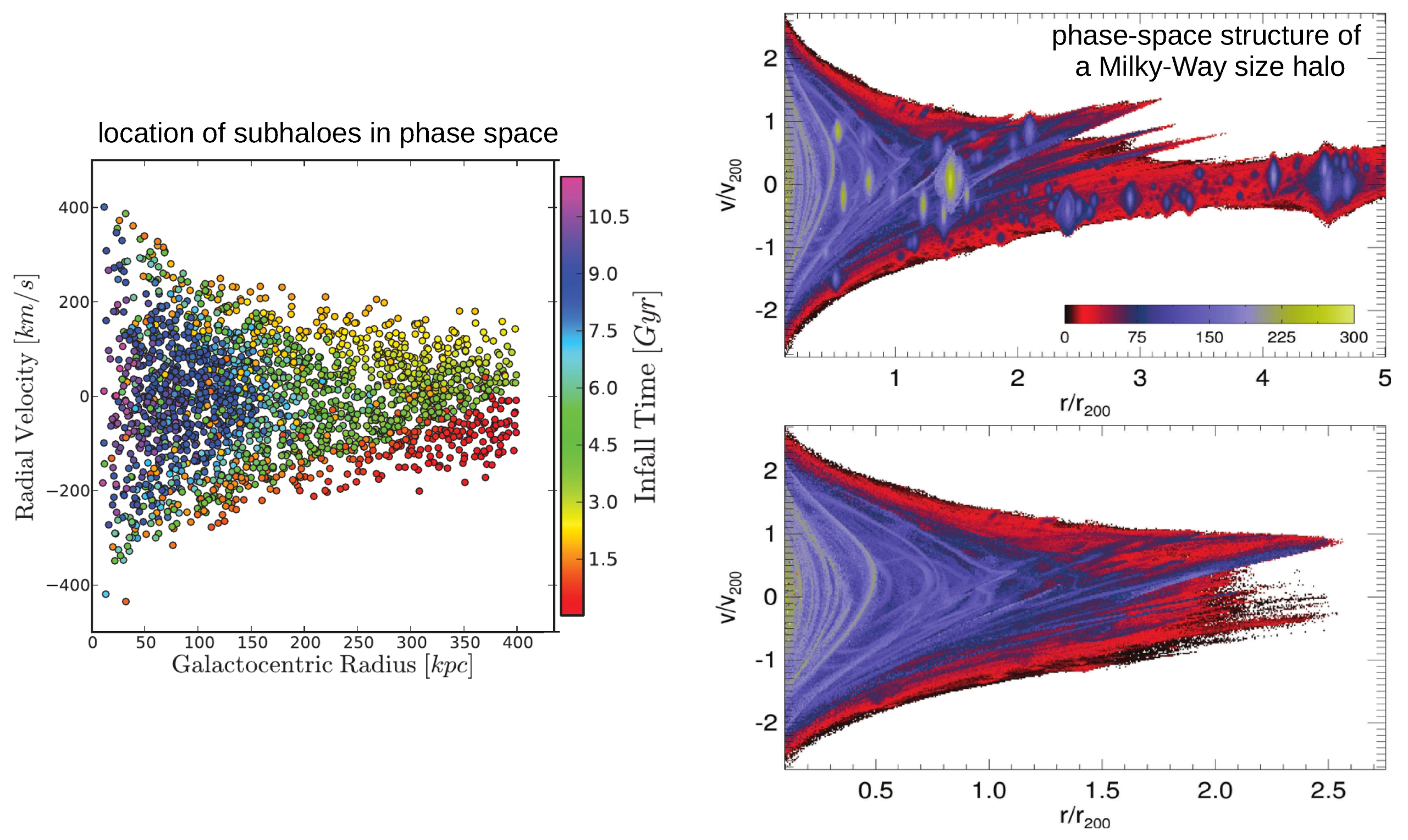
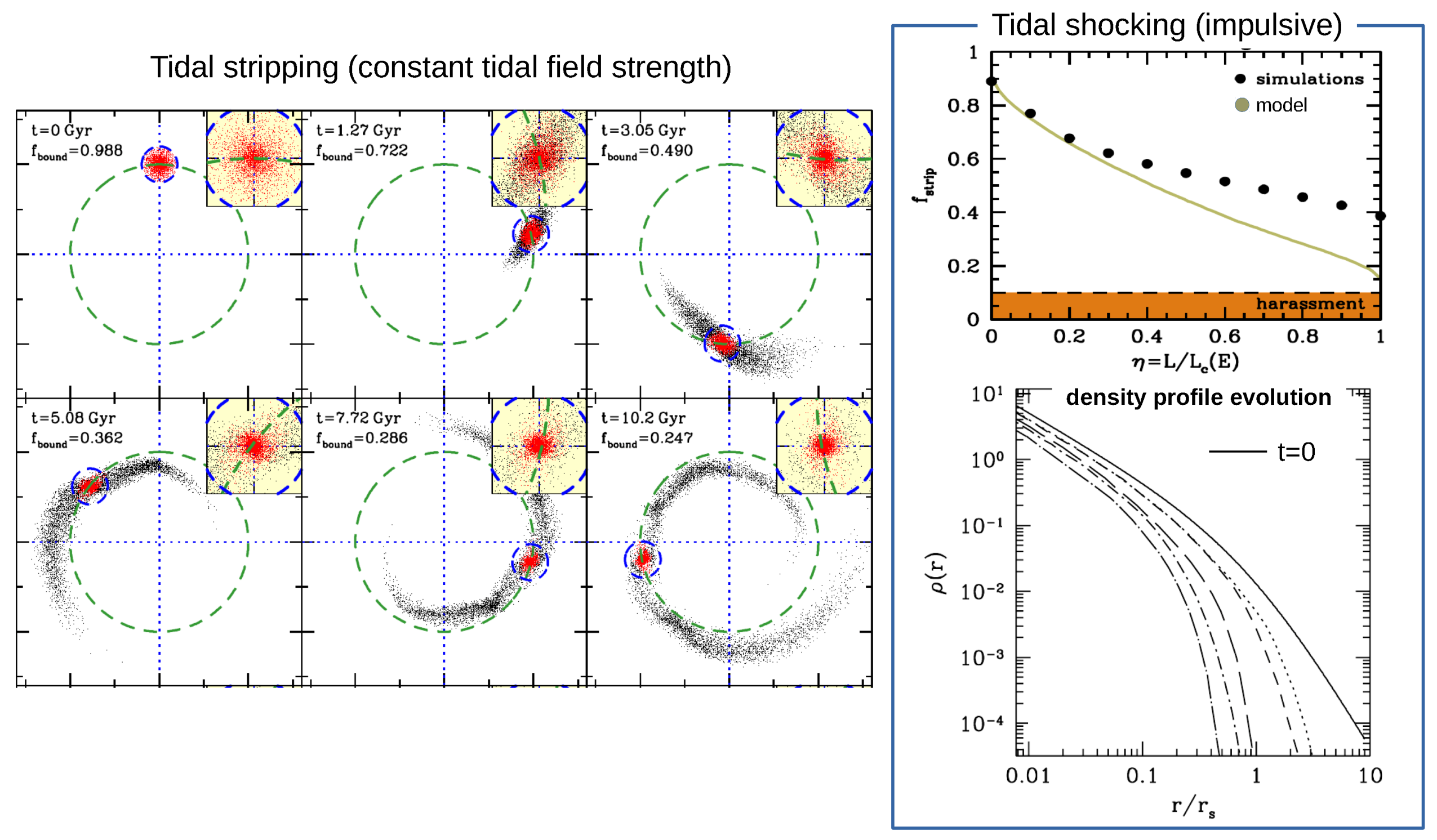
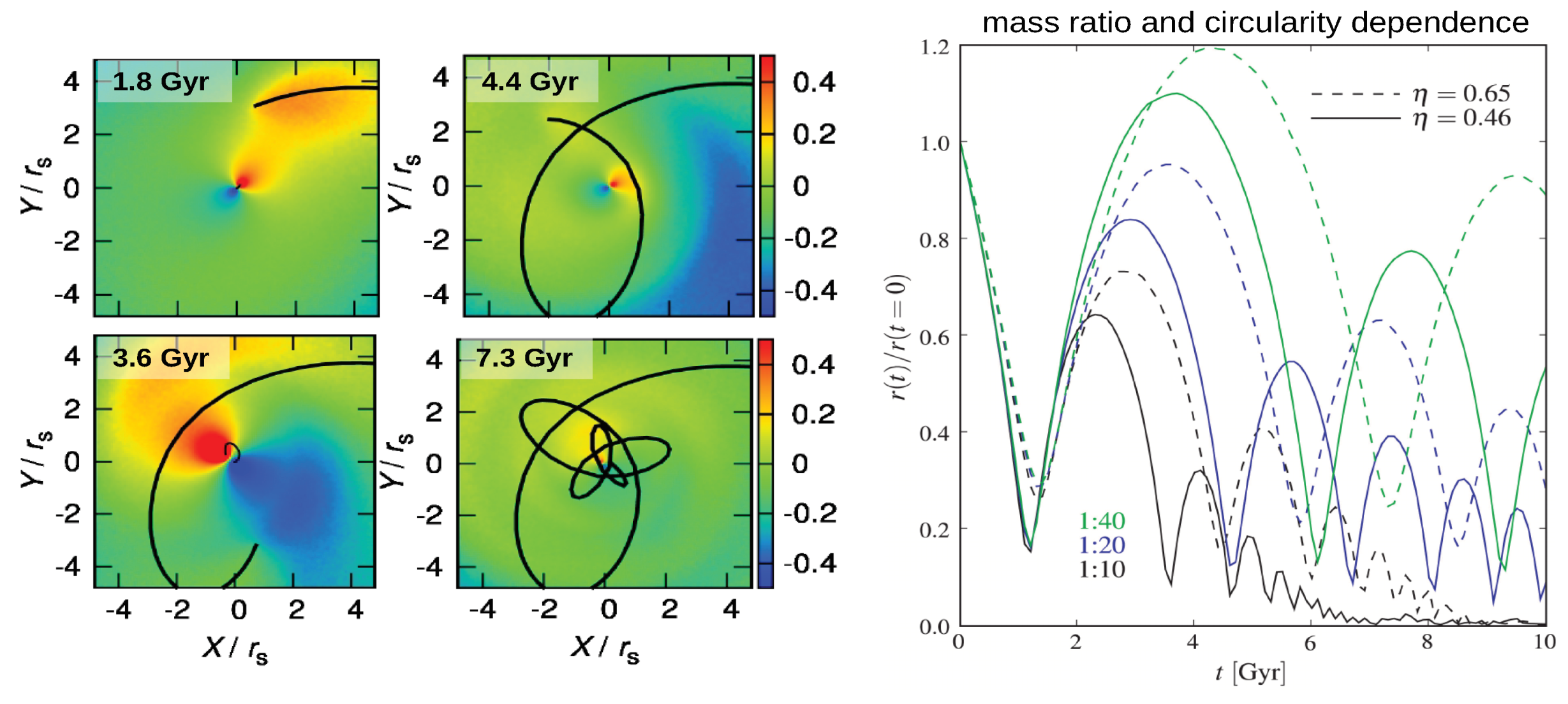
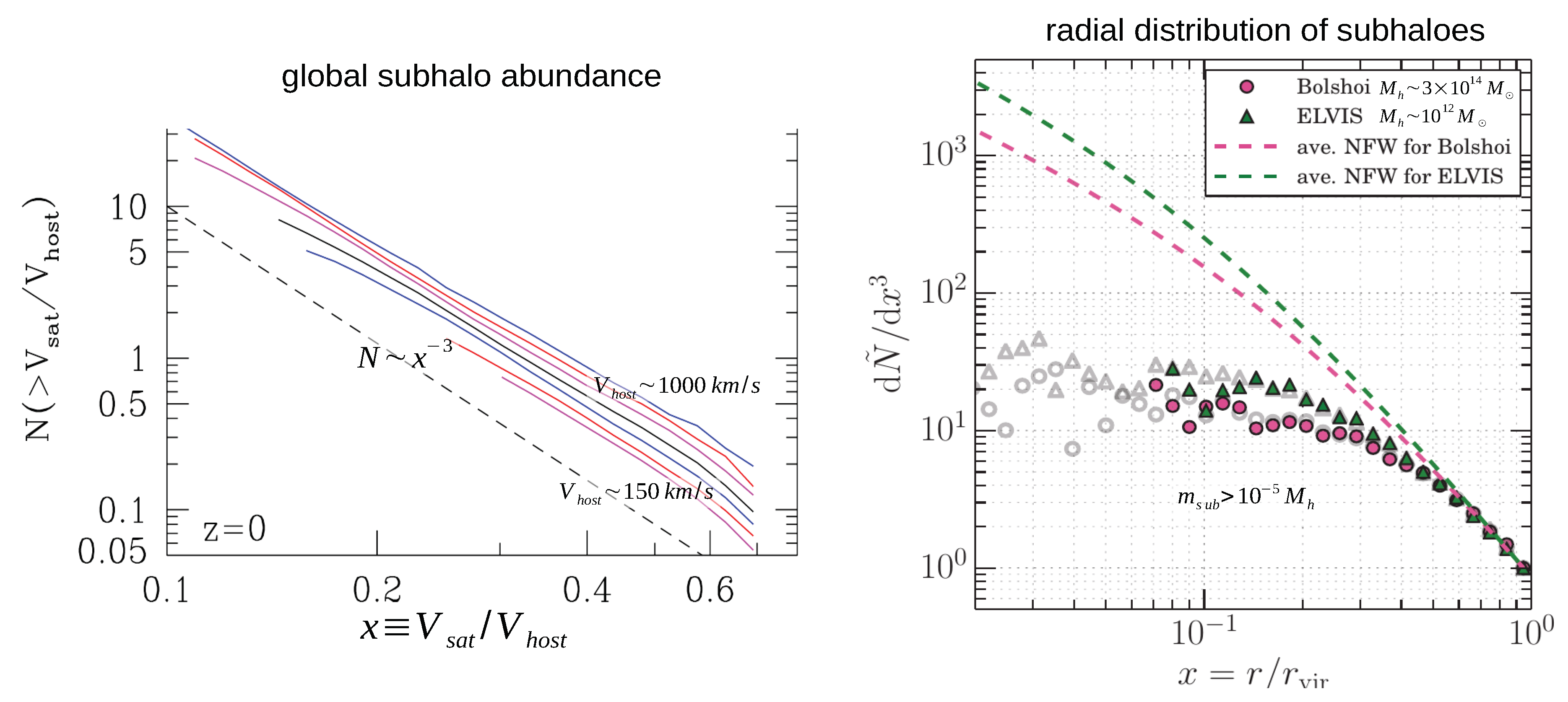
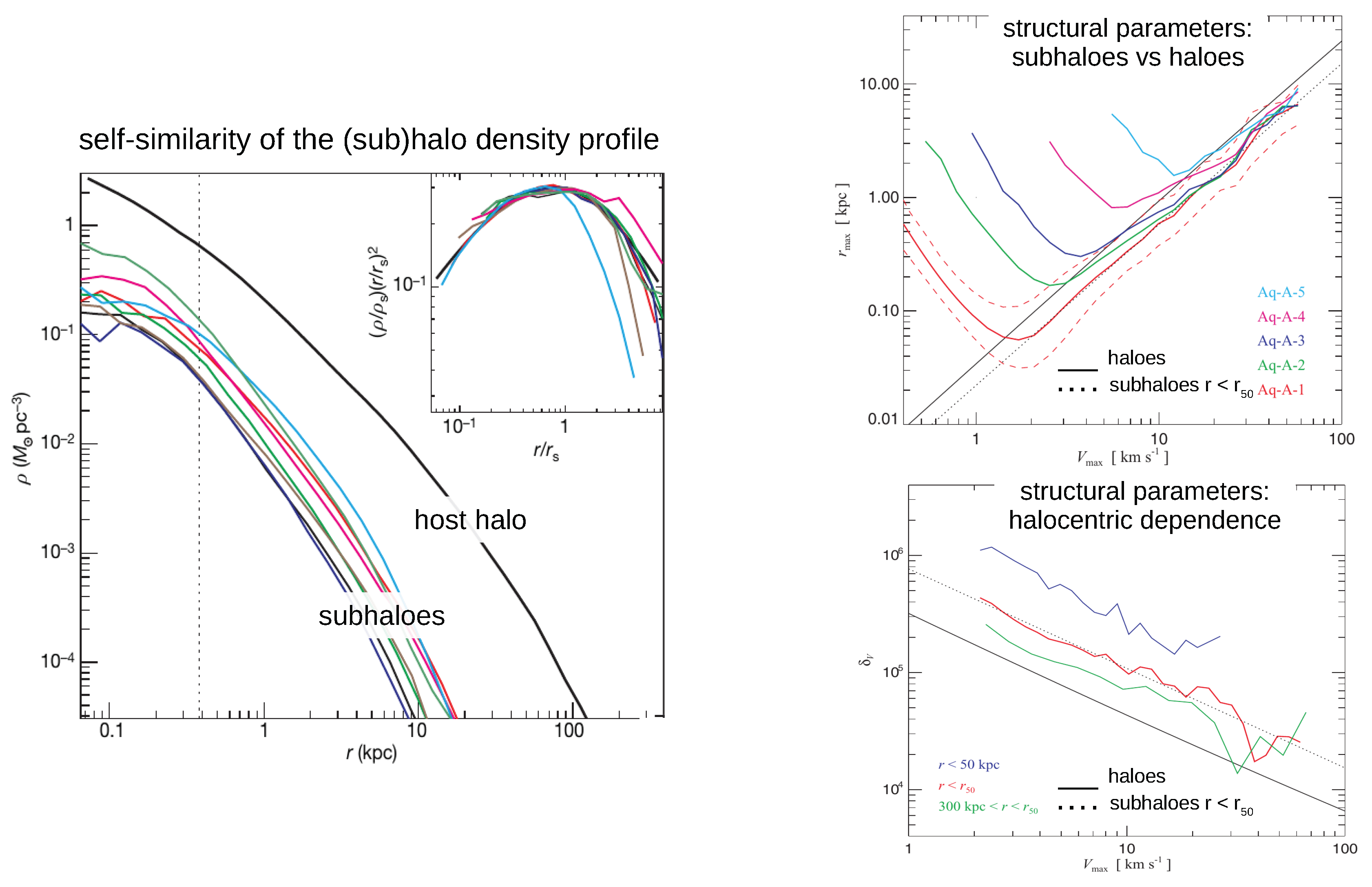
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavala, J.; Frenk, C.S. Dark Matter Haloes and Subhaloes. Galaxies 2019, 7, 81. https://doi.org/10.3390/galaxies7040081
Zavala J, Frenk CS. Dark Matter Haloes and Subhaloes. Galaxies. 2019; 7(4):81. https://doi.org/10.3390/galaxies7040081
Chicago/Turabian StyleZavala, Jesús, and Carlos S. Frenk. 2019. "Dark Matter Haloes and Subhaloes" Galaxies 7, no. 4: 81. https://doi.org/10.3390/galaxies7040081
APA StyleZavala, J., & Frenk, C. S. (2019). Dark Matter Haloes and Subhaloes. Galaxies, 7(4), 81. https://doi.org/10.3390/galaxies7040081




