Determining Evolution of Cosmological Constant, Gravitational Constant and Speed of Light Using Nonadiabatic Cosmological Model and LLR Findings
Abstract
1. Introduction
2. Theory
2.1. Nonadiabatic Phenomenology
2.2. Cosmological Models
2.3. Evolutionary Equation of State
2.4. Evolutionary Gravitational Constant and Speed of Light
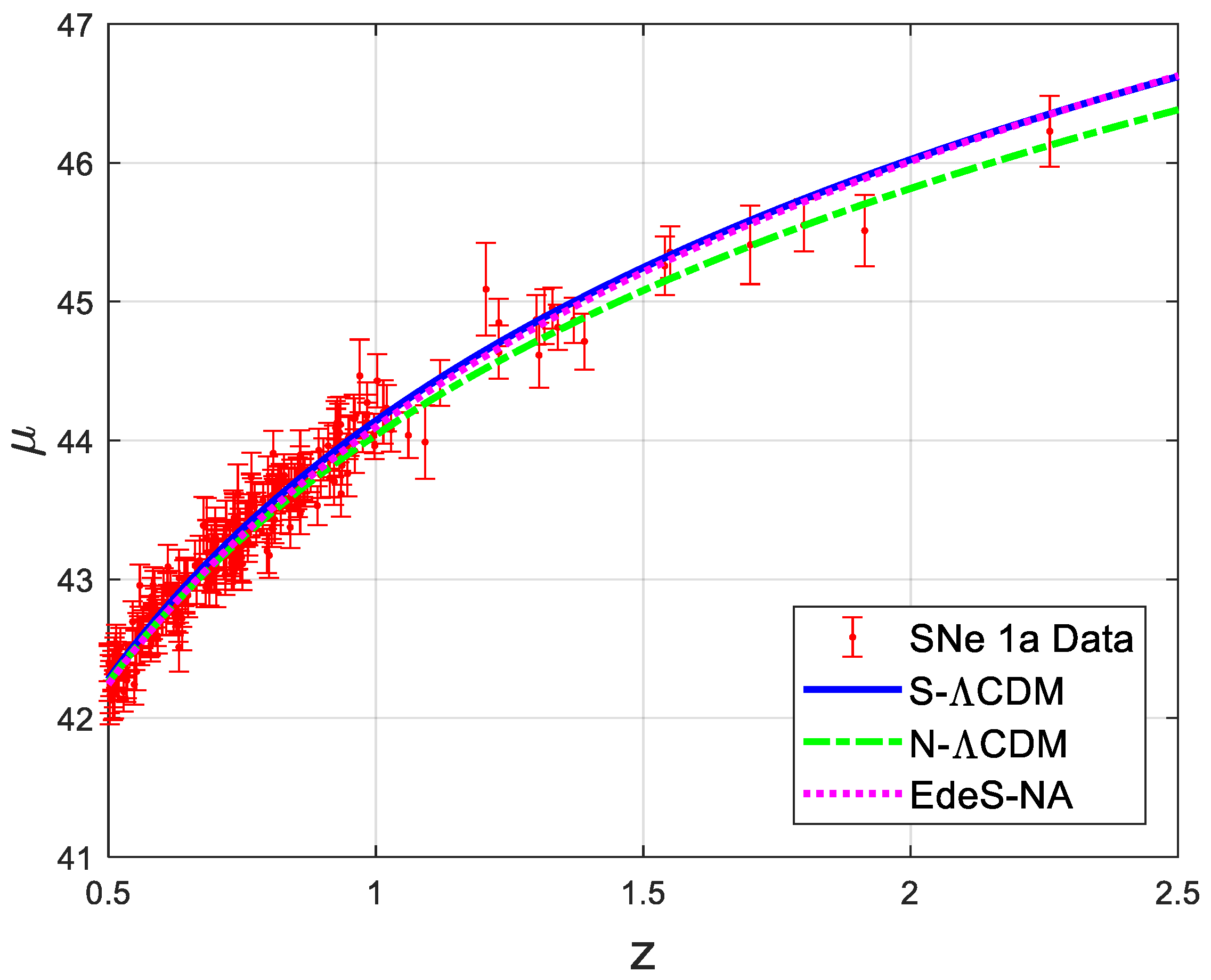
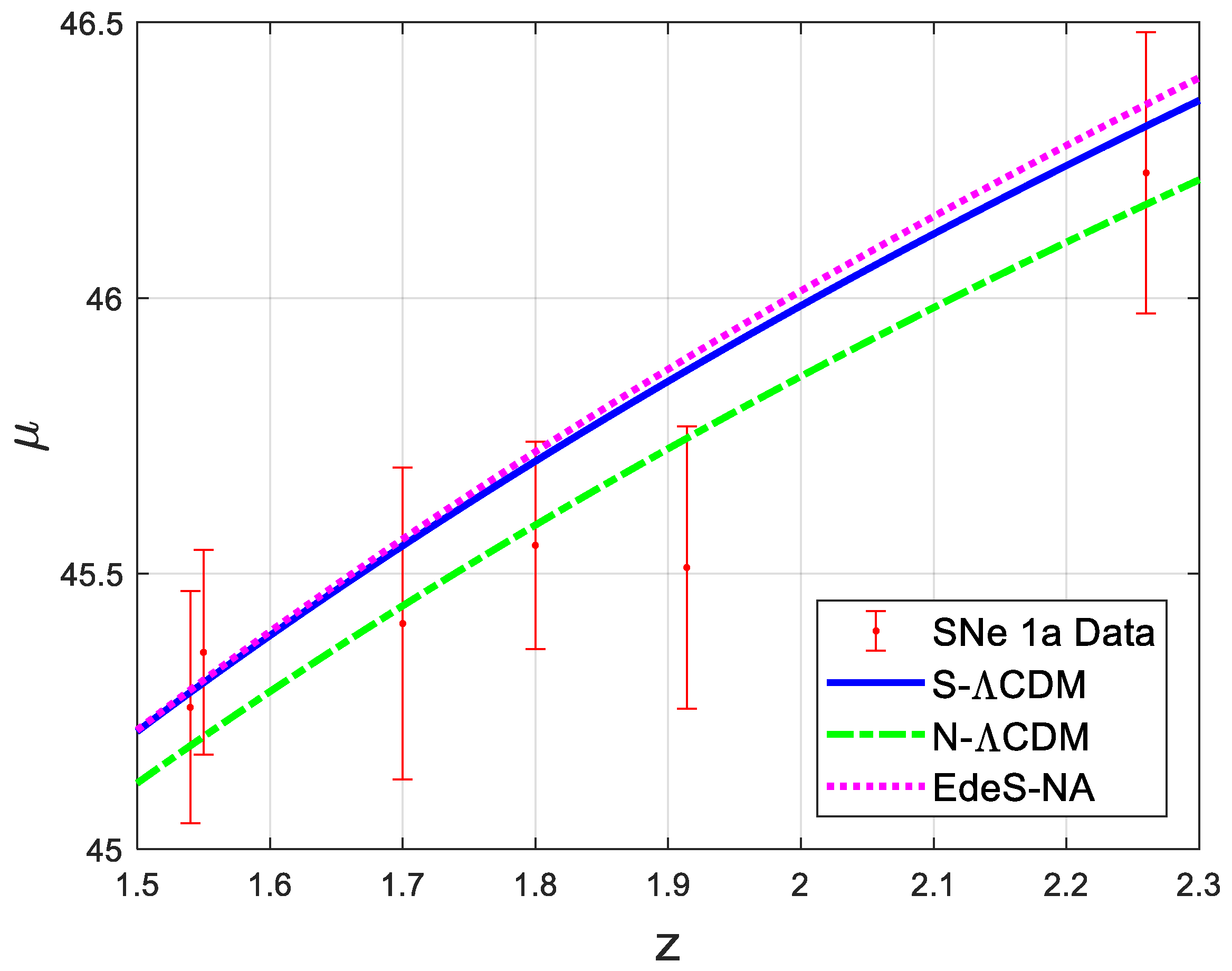
3. Results
- (a)
- Assume that the error bars represented by the variance are incorrect in the same proportion for all data points in a dataset, and thus the error in estimating using Equation (30) is affected in the same proportion for all models.
- (b)
- Assume further that the standard CDM model gives , and calculate the corresponding for the degree of freedom for the dataset being analysed.
- (c)
- Compare the above value with that actually determined. Find the ratio of the two values and use it as a multiplier to normalize values of of all the models for the dataset in the category.
- (d)
- Use the normalized values of to determine the probability for each model. Consider models giving higher value than 50% better than the CDM model for the data set used, and vice versa.
4. Discussion
- (a)
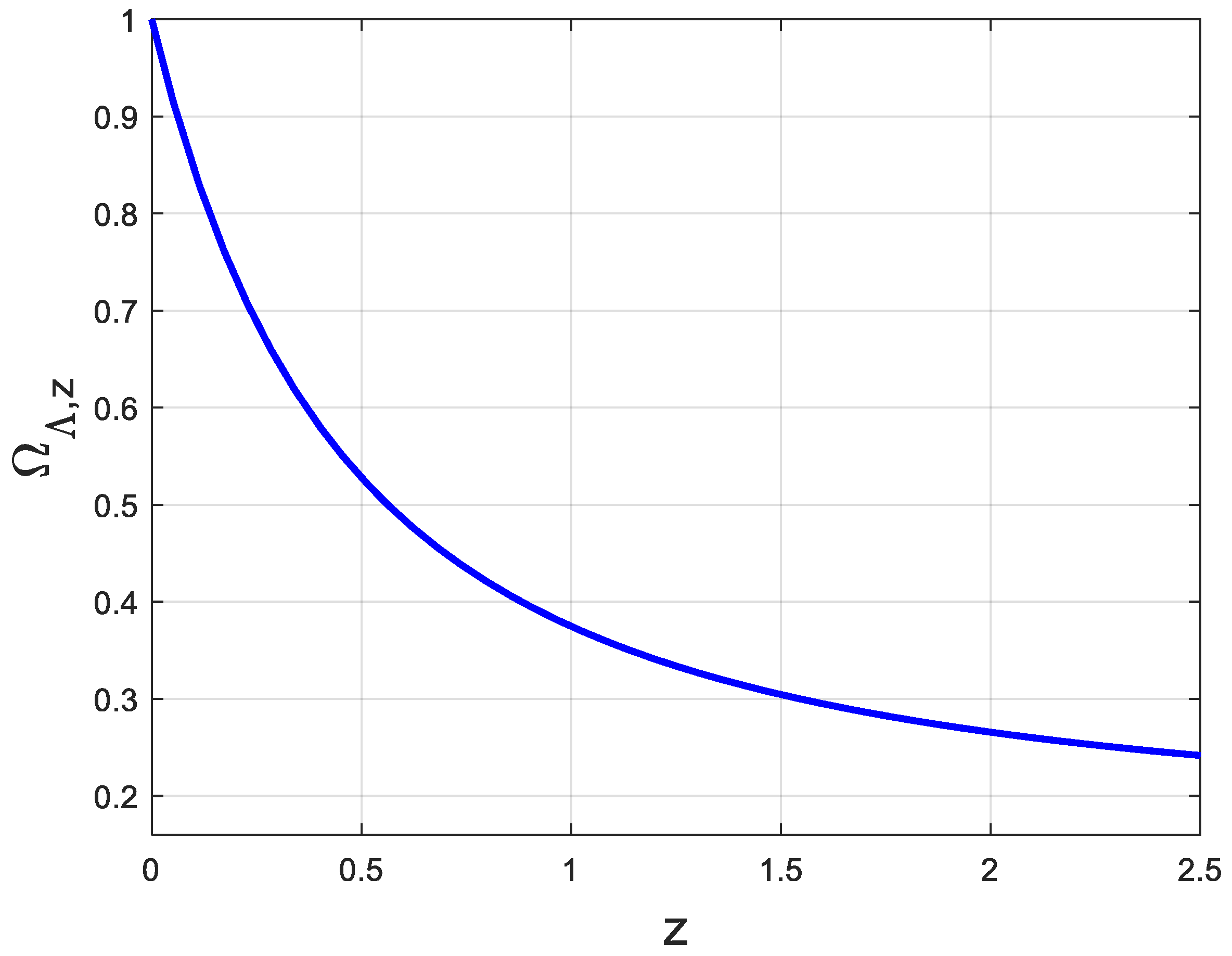
- The nonadiabaticity of the universe when considered as dark energy density has redshift dependence proportional to , Equation (18).
- (b)
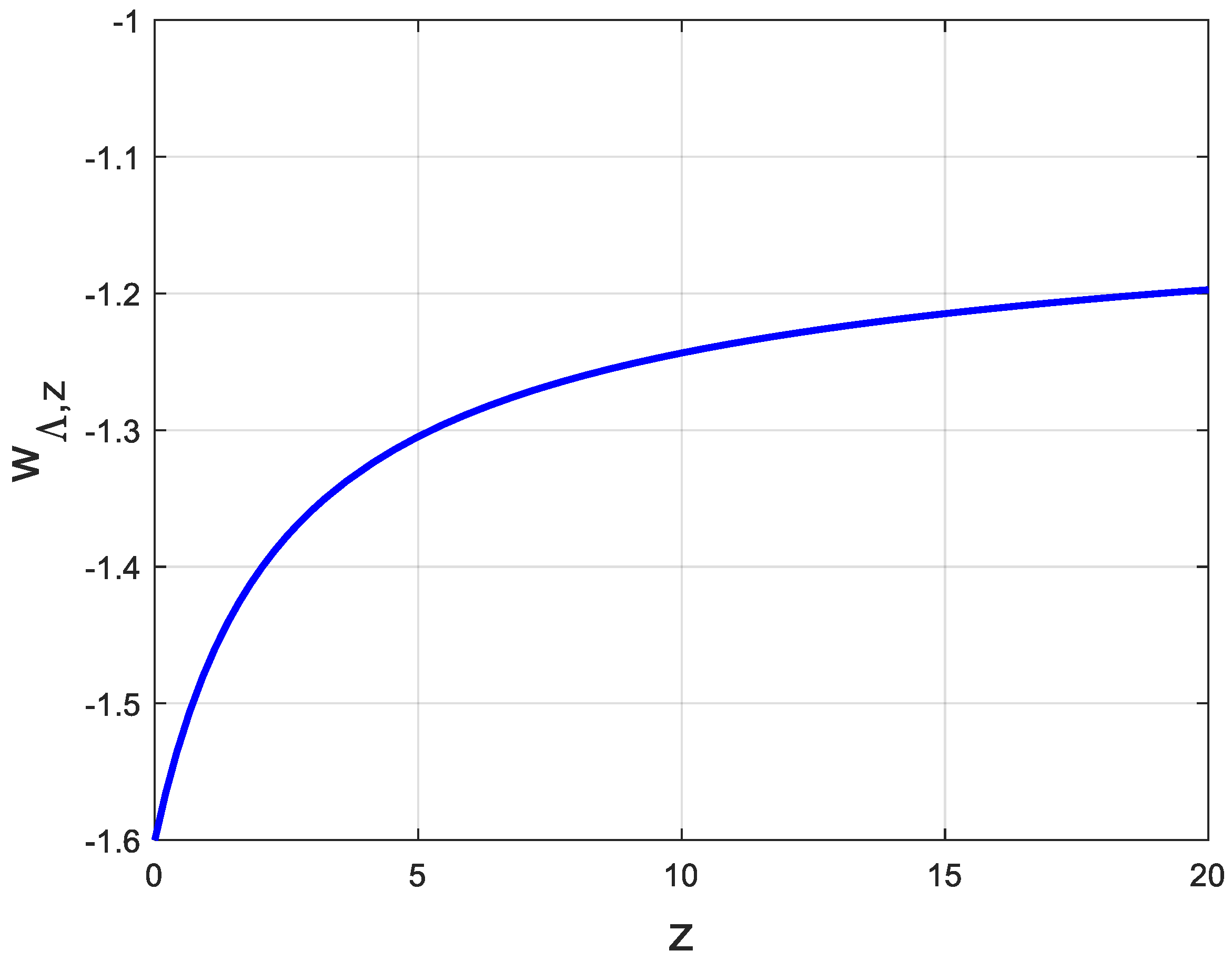
- Similarly, the equation state parameter for matter can be considered to evolve as Equation (23). Alternatively, the equation of state parameter for dark energy may be taken to be , Equation (24).
- (c)
- All or a portion of the nonadiabadicity of the universe may be due to the variation of the gravitational constant and the speed of light through the relation , Equation (26). This, when combined with the LLR data analysis Equation (29), yields and when we assume all the nonadiabadicity is vested in and .
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- COSINE-100 Collaboration. An experiment to search for dark-matter interactions using sodium iodide detectors. Nature 2018, 564, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Bernabei, R.; Belli, P.; Bussolotti, A.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Dai, C.J.; d’Angelo, A.; Di Marco, A.; He, H.L.; et al. First model independent results from DAMA/LIBRA-phase2. arXiv 2018, arXiv:1805.10486. Available online: https://arxiv.org/abs/1805.10486 (accessed on 25 June 2019).
- Farnes, J.S. A unifying theory of dark energy and dark matter: Negative masses and matter creation within a modified ΛCDM framework. Astron. Astrophys. 2018, 620, A92. [Google Scholar] [CrossRef]
- Weyl, H. Eine neue Erweiterung der Relativistätstheorie. Annalen der Physik 1919, 59, 129. [Google Scholar]
- Eddington, A.S. New Pathways in Science; Cambridge University Press: Cambridge, UK, 1934. [Google Scholar]
- Dirac, P.A.M. The cosmological constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Einstein, A. Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. Jahrbuch fur Radioaktivitat und Elektronik 1907, 4, 411–462. [Google Scholar]
- Dicke, R.H. Gravitation without a principle of equivalence. Rev. Mod. Phys. 1957, 29, 363. [Google Scholar] [CrossRef]
- Petit, J.P. An interpretation of cosmological model with variable light velocity. Mod. Phys. Lett. 1988, A3, 1527–1532. [Google Scholar] [CrossRef]
- Moffat, J.W. Superluminary universe: A possible solution to the initial value problem in cosmology. Int. J. Mod. Phys. 1993, D2, 351. [Google Scholar] [CrossRef]
- Salzano, V.; Dabrowski, M.P. Statistical hierarchy of varying speed of light theories. Astrophys. J. 2017, 851, 97. [Google Scholar] [CrossRef]
- Duff, M. Comment on time-variation of fundamental constants. arXiv 2016, arXiv:Hep-th/0208093 v4. Available online: https://arxiv.org/abs/hep-th/0208093 (accessed on 25 June 2019).
- Ellis, G.F.R.; Uzan, J.P. ‘c’ is the speed of light, isn’t it? Am. J. Phys. 2005, 73, 240–253. [Google Scholar] [CrossRef]
- Uzan, J.-P. The fundamental constants and their variation: Observational status and theoretical motivation. Rev. Mod. Phys. 2003, 75, 403. [Google Scholar] [CrossRef]
- Uzan, J.P. Varying constants, gravitation and cosmology. Living Rev. Relativ. 2011, 14, 2. [Google Scholar] [CrossRef] [PubMed]
- Duff, M.J. How fundamental are fundamental constants? arXiv 2014, arXiv:1412.2040. Available online: https://arxiv.org/abs/1412.2040 (accessed on 25 June 2019).
- Chiba, T. Constancy of the constants of nature: Updates. Prog. Phys. 2011, 126, 993–1019. [Google Scholar] [CrossRef]
- Martins, C.J.A.P. The status of varying constants: A review of physics, searches and implications. Rep. Prog. Phys. 2017, 80, 126902. [Google Scholar] [CrossRef] [PubMed]
- Magueijo, J. New varying speed of light theories. Rep. Prog. Phys. 2003, 66, 2025. [Google Scholar] [CrossRef]
- Gupta, R.P. Varying physical constants, astrometric anomalies, redshift and Hubble units. Galaxies 2019, 7, 55. [Google Scholar] [CrossRef]
- Gupta, R.P. SNe Ia redshift in a nonadiabatic universe. Universe 2018, 4, 104. [Google Scholar] [CrossRef]
- Chevallier, M.; Polarski, D. Accelerating universe with scaling dark matter. Int. J. Mod. Phys. 2001, D10, 213–223. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef] [PubMed]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The complete light curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined pantheon samzple. Astrophys. J. 2018, 859, 101, data file taken from: Catalogs of Cosmologically Useful Type Ia Supernovae from Pan-STARRS (“PS1COSMO”). Available online: https://archive.stsci.edu/hlsps/ps1cosmo/scolnic/hlsp_ps1cosmo_panstarrs_gpc1_all_model_v1_lcparam-full.txt (accessed on 11 December 2018).
- Ryden, B. Introduction to Cosmology; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints of the equation of state of the universe in various parametrization. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Luongo, O.; Ruggeri, A.C. Cosmographic constraints and cosmic fluids. Galaxies 2013, 1, 216–260. [Google Scholar] [CrossRef]
- Gruber, C.; Luongo, D. Cosmographic analysis of the equation of state of the universe through Padé approximations. Phys. Rev. D 2014, 89, 103506. [Google Scholar] [CrossRef]
- Dunsby, P.K.S.; Luongo, O. On the theory and application of modern cosmography. Int. J. Geom. Meth. Mod. Phys. 2016, 13, 1630002. [Google Scholar] [CrossRef]
- Capoziello, S.; D’Agostino, R.; Luongo, O. Cosmographic Analysis with Chebyshev polynomials. Mon. Not. Roy. Astron. Soc. 2018, 476, 3924–3938. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Precision cosmology with Padé rational approximations: Theoretical predictions versus observational limits. Phys. Rev. D 2014, 90, 043531. [Google Scholar] [CrossRef]
- Gupta, R.P. Static and dynamic components of the redshift. Int. J. Astron. Astrophys. 2018, 8, 219–229. [Google Scholar] [CrossRef]
- Hofmann, F.; Müller, J. Relativistic tests with lunar laser ranging. Class. Quant. Grav. 2018, 35, 035015. [Google Scholar] [CrossRef]
- Merkowitz, S.M. Test of gravity using lunar laser ranging. Living. Rev. Rel. 2010, 13, 7. [Google Scholar] [CrossRef]
- Gupta, R.P. Weighing Cosmological Models with SNe Ia and Gamma Ray Burst Redshift Data. Universe 2019, 5, 102. [Google Scholar] [CrossRef]
- Walker, J. Chi-Square Calculator. 2019. Available online: https://www.fourmilab.ch/rpkp/experiments/analysis/chiCalc.html (accessed on 25 June 2019).
- Vishwakarma, R.G.; Narlikar, J.V. Is it no longer necessary to test cosmologies with type 1a supernovae? Universe 2018, 4, 73. [Google Scholar] [CrossRef]

| Action/Item | S-ΛCDM | N-ΛCDM | EdeS-NA | S-ΛCDM | N-ΛCDM | EdeS-NA | S-ΛCDM | N-ΛCDM | EdeS-NA |
|---|---|---|---|---|---|---|---|---|---|
| Parameterized | Model dataset z < 0.5; 832 points | Model dataset z < 1.0; 1025 points | Model dataset z < 1.5; 1042 points | ||||||
| R0 | 4259 ± 34 | 4228 ± 35 | 4327 ± 18 | 4269 ± 27 | 4207 ± 29 | 4333 ± 16 | 4271 ± 26 | 4205 ± 28 | 4333 ± 16 |
| Ωm,0 | 0.2601 ± 0.0457 | 0.4345 ± .035 | 1 (Fixed) | 0.2793 ± 0.0261 | 0.4069 ± 0.0219 | 1 (Fixed) | 0.2818 ± 0.0249 | 0.4042 ± 0.0210 | 1 (Fixed) |
| H0 | 70.39 ± 0.56 | 70.90 ± 0.58 | 69.29 ± 0.29 | 70.23 ± 0.44 | 71.26 ± 0.49 | 69.19 ± 0.25 | 70.19 ± 0.42 | 71.30 ± 0.47 | 69.19 ± 0.25 |
| χ2 | 863.5 | 861.9 | 881.2 | 1018 | 1022 | 1038 | 1033 | 1036 | 1052 |
| DOF | 830 | 831 | 1023 | 1024 | 1040 | 1041 | |||
| P% | 20.39 | 21.49 | 11.05 | 53.82 | 50.29 | 37.34 | 55.53 | 52.91 | 39.95 |
| R2 | 0.9961 | 0.9961 | 0.9961 | 0.9969 | 0.9969 | 0.9969 | 0.9970 | 0.9970 | 0.9969 |
| RMSE | 1.020 | 1.019 | 1.030 | 0.9977 | 0.9993 | 1.007 | 0.9965 | 0.9982 | 1.005 |
| Model Fit | Dataset z > 0.5; 216 points | Dataset z > 0.5; 216 points | Dataset z > 0.5; 216 points | ||||||
| χ2 | 176.9 | 185.7 | 175.1 | NOT APPLICABLE SINCE THIS DATASET INCLUDES THE DATASET USED TO PARAMETERIZE THE MODEL | NOT APPLICABLE SINCE THIS DATASET INCLUDES THE DATASET USED TO PARAMETERIZE THE MODEL | ||||
| DOF | 216 | ||||||||
| P% | 97.59 | 93.31 | 98.10 | ||||||
| R2 | 0.9605 | 0.9585 | 0.9609 | ||||||
| RMSE | 0.905 | 0.9271 | 0.9003 | ||||||
| Model Fit | Dataset z > 1.0; 23 points | Dataset z > 1.0; 23 points | |||||||
| χ2 | 19.54 | 18.81 | 17.83 | 17.59 | 16.55 | 17.95 | NOT APPLICABLE SINCE THIS DATASET INCLUDES THE DATASET USED TO PARAMETERIZE THE MODEL | ||
| DOF | 23 | ||||||||
| P% | 66.94 | 71.21 | 76.66 | 77.93 | 83.07 | 76.01 | |||
| R2 | 0.8741 | 0.8788 | 0.8851 | 0.8867 | 0.8934 | 0.8844 | |||
| RMSE | 0.9216 | 0.9044 | 0.8805 | 0.8746 | 0.8483 | 0.8834 | |||
| Model Fit | Dataset z > 1.5; 6 points | ||||||||
| χ2 | 4.090 | 2.066 | 3.569 | 3.167 | 1.745 | 3.649 | 3.076 | 1.731 | 3.649 |
| DOF | 6 | ||||||||
| P% | 66.44 | 91.35 | 73.49 | 78.76 | 94.15 | 72.40 | 79.92 | 94.27 | 72.40 |
| R2 | 0.5993 | 0.7975 | 0.6504 | 0.6897 | 0.8291 | 0.6424 | 0.6986 | 0.8304 | 0.6424 |
| RMSE | 0.8256 | 0.5869 | 0.7712 | 0.7265 | 0.5392 | 0.7799 | 0.716 | 0.5371 | 0.7799 |
| Action/Item | S-ΛCDM | N-ΛCDM | EdeS-NA | S-ΛCDM | N-ΛCDM | EdeS-NA | S-ΛCDM | N-ΛCDM | EdeS-NA |
|---|---|---|---|---|---|---|---|---|---|
| Parameterized | Model dataset z < 0.5; 832 points | Model dataset z < 1.0; 1025 points | Model dataset z < 1.5; 1042 points | ||||||
| Normalized χ2 | 829.3 | 827.8 | 846.3 | 1018 | 1022 | 1038 | 1033 | 1036 | 1052 |
| DOF | 830 | 831 | 1023 | 1024 | 1040 | 1041 | |||
| Normalized P% | 50.00 | 51.50 | 34.85 | 50.00 | 46.77 | 34.08 | 50.00 | 47.66 | 35.00 |
| Model Fit | Dataset z > 0.5; 216 points | Dataset z > 0.5; 216 points | Dataset z > 0.5; 216 points | ||||||
| Normalized χ2 | 215.3 | 226 | 213.1 | NOT APPLICABLE SINCE THIS DATASET INCLUDES THE DATASET USED TO PARAMETERIZE THE MODEL | NOT APPLICABLE SINCE THIS DATASET INCLUDES THE DATASET USED TO PARAMETERIZE THE MODEL | ||||
| DOF | 216 | ||||||||
| Normalized P% | 50.00 | 30.64 | 54.30 | ||||||
| Model Fit | Dataset z > 1.0; 23 points | Dataset z > 1.0; 23 points | |||||||
| Normalized χ2 | 22.34 | 21.50 | 20.38 | 22.34 | 21.02 | 22.79 | NOT APPLICABLE SINCE THIS DATASET INCLUDES THE DATASET USED TO PARAMETERIZE THE MODEL | ||
| DOF | 23 | ||||||||
| Normalized P% | 50.00 | 55.05 | 61.88 | 50.00 | 57.98 | 47.30 | |||
| Model Fit | Dataset z > 1.5; 6 points | ||||||||
| Normalized χ2 | 5.348 | 2.702 | 4.667 | 5.348 | 2.947 | 6.162 | 5.348 | 3.019 | 6.344 |
| DOF | 6 | ||||||||
| Normalized P% | 50.00 | 84.52 | 58.71 | 50.00 | 81.54 | 40.52 | 50.00 | 80.64 | 38.57 |
| Average P% | 50.00 | 55.43 | 52.44 | 50.00 | 62.10 | 40.63 | 50.00 | 64.15 | 36.79 |
| Av. Pred. P% | 50.00 | 56.74 | 58.30 | 50.00 | 69.76 | 43.91 | 50.00 | 80.64 | 38.57 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, R.P. Determining Evolution of Cosmological Constant, Gravitational Constant and Speed of Light Using Nonadiabatic Cosmological Model and LLR Findings. Galaxies 2019, 7, 67. https://doi.org/10.3390/galaxies7030067
Gupta RP. Determining Evolution of Cosmological Constant, Gravitational Constant and Speed of Light Using Nonadiabatic Cosmological Model and LLR Findings. Galaxies. 2019; 7(3):67. https://doi.org/10.3390/galaxies7030067
Chicago/Turabian StyleGupta, Rajendra P. 2019. "Determining Evolution of Cosmological Constant, Gravitational Constant and Speed of Light Using Nonadiabatic Cosmological Model and LLR Findings" Galaxies 7, no. 3: 67. https://doi.org/10.3390/galaxies7030067
APA StyleGupta, R. P. (2019). Determining Evolution of Cosmological Constant, Gravitational Constant and Speed of Light Using Nonadiabatic Cosmological Model and LLR Findings. Galaxies, 7(3), 67. https://doi.org/10.3390/galaxies7030067





