Lighting Up Dark Matter Haloes

Abstract

Previous chapters of this issue have focused on the formation and evolution of cosmic structures under the influence of gravity alone. In order to make a close link between theoretical models of structure formation and observational data, it is necessary to consider the gas-dynamical and radiative processes that drive the evolution of the baryonic components of dark matter halos. These processes cover many orders of magnitude in physical sizes and time-scales and are entangled in a complex network of actions, back-reactions, and self-regulations. In addition, our understanding of them is far from being complete, even when viewed in isolation. This chapter provides a brief review of the techniques that are commonly used to link the physical properties of galaxies with the dark matter halos in which they reside. I discuss the main features of these methods, as well as their aims, limits, and complementarities.

1. Introduction

In the last few decades, a number of different observational tests of the standard cosmological paradigm have ushered in a new era of precision cosmology. Our current standard model for structure formation, the $\Lambda$CDM paradigm, is able to reproduce simultaneously several observational constraints, including the temperature fluctuations in the cosmic microwave background, the power spectrum of low redshift galaxies, and the acceleration of the cosmic expansion inferred from supernovae explosions. While this cosmological paradigm appears to be firmly established, a theory of galaxy formation continues to be elusive, and our understanding of the physical processes that determine the observed variety of galaxies is at best rudimentary. Although much progress has been made, both on the theoretical and observational side, understanding how galaxies form and evolve remains one of the most outstanding questions of modern astrophysics. In addition to being an interesting question in its own right, galaxy formation also has important implications for cosmological studies. In fact, a number of cosmological probes rely on galaxies as tracers of the large-scale structure (e.g., those based on measurements of galaxy clustering and weak lensing). A better understanding of the galaxy formation process is therefore crucial in order to improve our knowledge of the cosmic mass-energy budget.

Different techniques have been used in the past decades to link the observed properties of galaxies to those of the dark matter halos in which they reside. Most of the models currently available exhibit a remarkable agreement with a large number of observations for the galaxy population in the local Universe (e.g., the observed relations between stellar mass, gas mass, and metallicity; the observed luminosity, color, and morphology distributions; the observed two-point correlation functions). When analyzed in detail, however, at least some of these comparisons highlight significant and often systematic (i.e., common to most of the models discussed in the recent literature) disagreements, which are the subject of active research.

In this chapter, I provide a brief review of the primary techniques that have been used to “light up dark matter halos”, i.e., to populate dark matter halos with galaxies whose physical properties resemble those we estimate at different cosmic epochs and in different environments. Specifically, I will introduce and review methods based on a statistical description of the link between dark matter halos and galaxies in Section 2 and methods based on direct hydro-dynamical simulations of the galaxy formation process in Section 4. Section 3 focuses on semi-analytic models; these methods include an explicit modeling of the galaxy formation process based on observationally- and/or theoretically-motivated prescriptions and are embedded in a full cosmological context. I will focus on the basic ingredients of the methods considered, highlighting their aims, limits, and complementarities. A complete review of the past work taking advantage of these techniques is beyond the aims of this chapter. I will, however, try to summarize the state-of-the-art as of today, providing references to relevant studies.

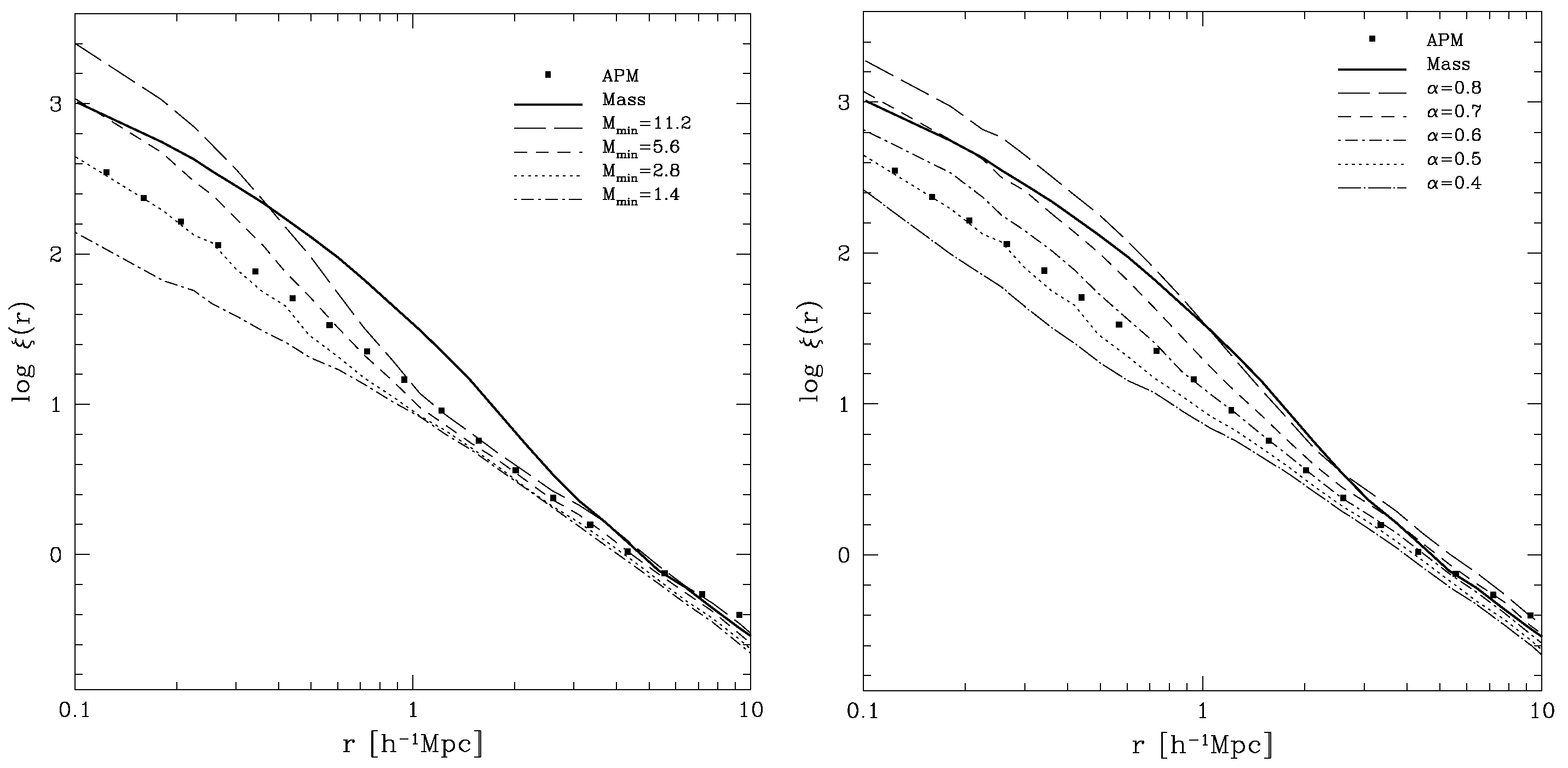
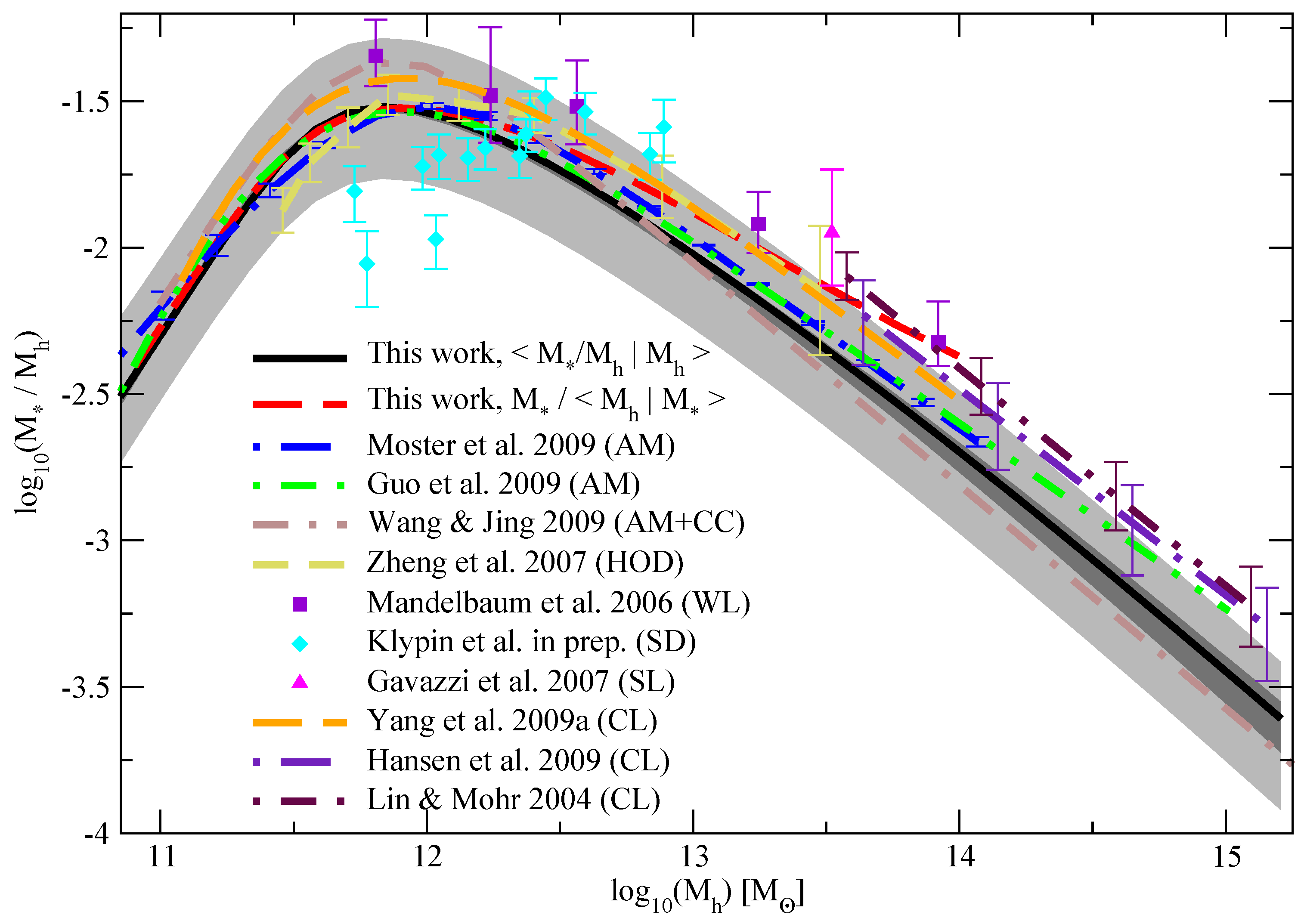
2. Statistical/Empirical Methods to Populate Dark Matter Halos

These methods essentially bypass any explicit modeling of the physical processes driving galaxy formation and evolution and specify the link between dark matter halos and galaxies in a purely statistical fashion. A first description of the “halo occupation framework” can be found in early work by Neyman and Scott [1]; the technique has become very popular in more recent years and provides a powerful formalism to understand galaxy clustering (e.g., [2,3,4,5] and the references therein). A classical halo occupation distribution (HOD) model is constructed by (i) specifying the probability that a halo of a given mass (M) contains a certain number (N) of galaxies of a particular class (this defines the “halo occupation distribution” $P\left(N\right|M)$); and (ii) assuming a spatial distribution of galaxies inside dark matter halos; the typical assumption is that galaxies follow the distribution of dark matter. Model parameters can then be efficiently constrained by using galaxy clustering data.

For example, a simple model can be constructed assuming that galaxies follow a Navarro, Frenk, and White [6] distribution, and that the mean number of galaxies per halo, above a certain luminosity threshold, is given by:

$$N_{\mathrm{avg}}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}M<M_{\min }\hfill \\ {(M/M_1)}^{\alpha }\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(1)

In the above equation, $M_{\min }$ is a cutoff halo mass below which halos cannot contain galaxies; and $M_1$ corresponds to the mass of halos that contain, on average, one galaxy. Figure 1 shows the influence of the parameters $M_{\min }$ (left panel) and $\alpha$ (right panel) on the predicted two-point galaxy correlation function and demonstrates that these observational measurements can be efficiently used to constrain the HOD parameters.

The simple approach just outlined can be extended to constrain halo occupation as a function of other galaxy physical properties (e.g., luminosity, color, etc.). For example, it is possible to define a “conditional luminosity function” $\Phi \left(L\right|M)dL$ that specifies the average number of galaxies that reside in a halo of given mass M and that have luminosities in the range $L\pm dL/2$. This quantity provides a direct link between the observed galaxy luminosity function and the halo mass function:

$$\Phi \left(L\right)={\int }_0^{\infty }\Phi \left(L\right|M)n\left(M\right)dM$$

One can also express the total luminosity of a halo of a given mass as a function of the conditional luminosity function:

$$<L\left(M\right)>={\int }_0^{\infty }\Phi \left(L\right|M)LdL$$

Since the halo mass function depends on the cosmology adopted, this formalism can be employed to constrain both galaxy formation (i.e., derive information on the luminosities of galaxies populating halos of given mass) and cosmology. For example, van den Bosch, Mo, and Yang [8] used this approach to break the degeneracy between the bias and the linear amplitude of mass fluctuations (${\sigma }_8$). Their work suggested, well before the result was confirmed by the WMAPthird-year results [9], that both the matter density (${\Omega }_{\mathrm{m}}$) and the mass variance ${\sigma }_8$ were lower than the concordance values than assumed.

The method described above is conceptually simple and relatively easy to implement. As outlined, it can be constrained using the increasing amount of available information on the clustering properties of galaxies at different cosmic epochs, and it provides important statistical constraints for galaxy formation models. It remains difficult, however, to move from this purely statistical characterization of the link between dark matter halos and galaxies to a more physical understanding of the galaxy formation process itself. In addition, the method described above implicitly assumes that the number of galaxies (of a given type) populating a dark matter halo depends only on the halo mass. This assumption was supported by early numerical work that found no residual dependence of halo clustering on concentration or formation time1 (see, e.g., [10,11]). A re-analysis of the same data, however, showed that close pairs of halos form at slightly higher redshift than more widely-separated halo pairs, suggesting that halos in dense regions form at slightly earlier times than halos of the same mass in less dense regions [12]. These results were later confirmed by numerical work that analyzed the properties of dark matter halos in large volumes with high resolution and found a clear dependence of the clustering amplitude on the halo formation time (e.g., [13,14]). The effect becomes more important with decreasing halo mass (which explains why it was not clearly identified in earlier work, based on lower resolution simulations): the “oldest” 10 percent of the halos with mass M$\sim {10}^{11}{\mathrm{M}}_{\odot }$ is more than five-times more strongly correlated than the “youngest” 10 percent. If galaxy properties correlate strongly with the halo formation history, this “assembly bias” might reflect in the galaxy spatial distribution and/or in the distribution of galaxy properties. This, in turn, can have an important impact on the possibility to use galaxy clustering measurements for precision cosmology experiments (e.g., [15,16]). Some methods to correct the standard HOD formalism for assembly bias have been proposed. For example, Hearin et al. [17] introduced the so-called “decorated HOD”, which describes the halo occupation statistics in terms of two halo properties (e.g., mass and concentration or formation time) rather than only mass. Given the relevance of galaxy clustering measurements in cosmological studies, that of assembly bias remains a subject of active current research ([18,19,20,21]) and the references therein.

A variant of the classical HOD approach is provided by the subhalo abundance matching (SHAM) technique. The method consists of assigning observable galaxy properties (stellar mass or luminosity) to the subhalo population identified in an N-body simulation, assuming a monotonic relation between these properties and some property of the substructure (typically the mass or the maximum circular velocity of dark matter halos at the time of “accretion”, i.e., when the halo was first accreted onto a larger structure, becoming a subhalo) [22,23]. At variance with the classical HOD approach described above, this approach accounts for the dependence of halo history on the environment implicitly (i.e., it includes assembly bias). As for the classical HOD, however, the method does not require an explicit treatment of the physics of galaxy formation (this is, actually, a non-parametric method), and therefore, it cannot be used to constrain the physical processes driving galaxy formation and evolution.

Figure 2 shows different determinations of the stellar-to-halo mass relation obtained using abundance matching techniques [24,25,26], compared with estimates based on alternative approaches, as well as with direct measurements. The good agreement with independent observations suggests that the basic assumption of a monotonic relation between the stellar mass and the maximum mass (or circular velocity) attained by the subhalo during its history is not fundamentally wrong. There are two important aspects of the approach that need to be considered with caution: (1) the intrinsic scatter between galaxy stellar mass and halo mass; and (2) numerical resolution effects. In addition, of course, one should consider all statistical and systematic uncertainties affecting the estimates of galaxy stellar masses, the galaxy mass function, and the halo mass function (for a detailed discussion of these sources of error, see [24]).

As for the scatter in stellar mass at fixed halo mass, this is typically assumed to be well described by a log-normal distribution, and it is assumed to be constant across all halo masses. While this convenient assumption appears to be in agreement with current measurements, HOD methods require an increase of the scatter with stellar mass to reproduce clustering measurements [5]. In addition, if a significant assembly bias exists in the real Universe, this has a strong impact on the detail of how galaxies populate the scatter in the stellar mass-halo mass relation. This, in turn, plays an important role in determining the correlation function of galaxies [34]. Therefore, caution should be used when applying abundance matching (and/or HOD) methods that adopt random scatter in the relation between stellar and halo mass.

The issue of numerical resolution is also a delicate one: a critical aspect of the abundance matching technique is the need to identify all dark matter subhalos associated with galaxies orbiting within dark matter halos. Dark matter subhalos are fragile systems that are rapidly and efficiently destroyed below the resolution limit of the simulation [35,36]. Depending on the mass resolution of the simulation used (and to some extent also on the subhalo identification algorithm employed), subhalos can “disappear” well before the galaxies they host should be lost by disruption or merging. This can affect the properties of galaxies on scales where the abundance of subhalos has numerically converged (i.e., does not depend on the simulation resolution and size). For example, Guo and White [37] have compared subhalo catalogs extracted from the Millennium Simulation [38] and Millennium II Simulation [39] and demonstrated that subhalo abundances agree to better than 10 percent only for subhalos with infall mass corresponding to at least 1000 particles in the Millennium Simulation. This has a significant effect on the small-scale clustering of subhalos at separations up to 1 Mpc (see also the discussion in [23]). The issue of dependence on numerical resolution can be addressed by tracing the “orphan” galaxies (those that have prematurely lost their parent dark matter substructure), as is done in the semi-analytic framework (see below). This comes, however, at the expenses of losing the simplicity of the approach, as one needs to make assumptions about the lifetimes and the orbits of satellite galaxies.

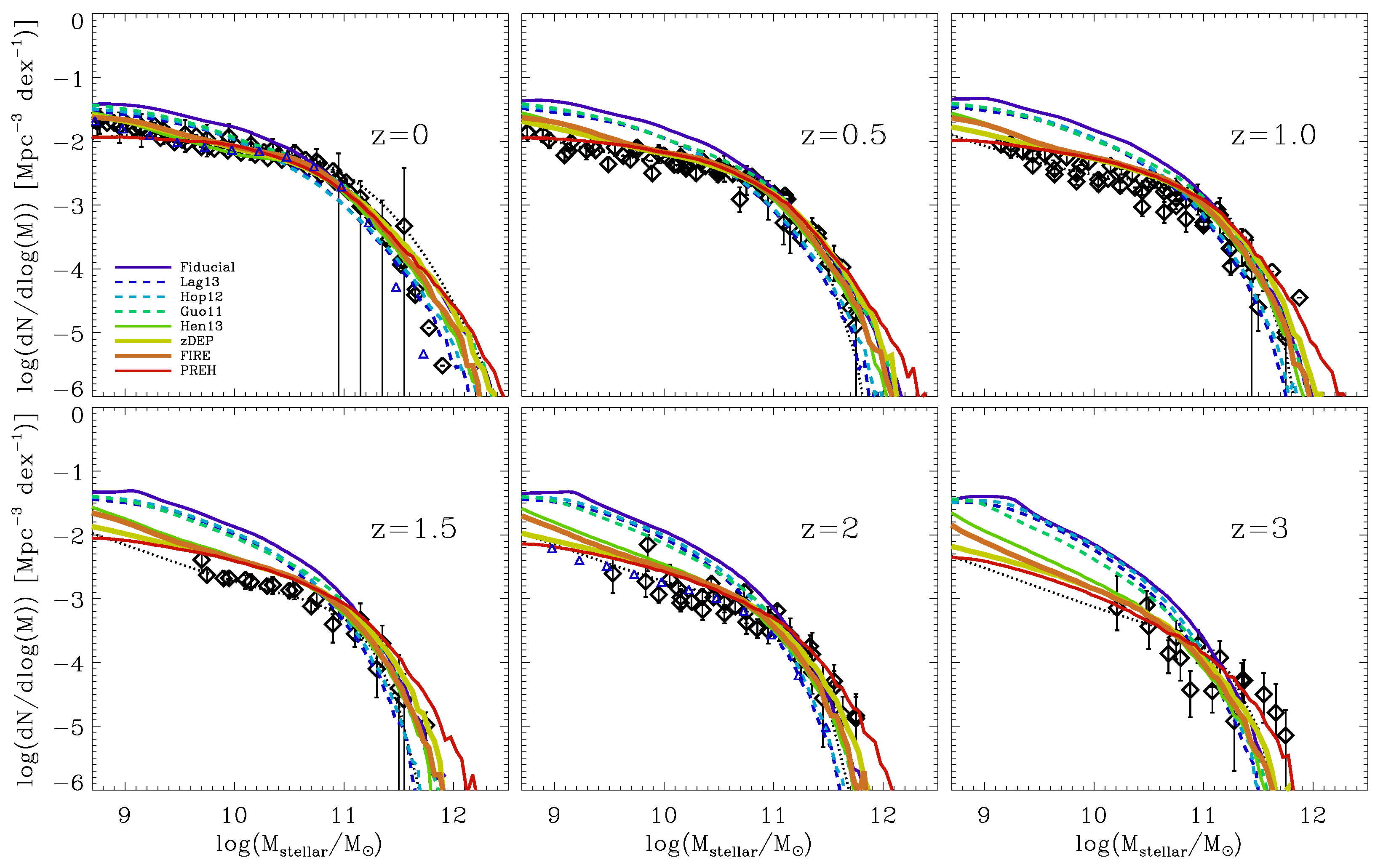
3. Semi-Analytic Models of Galaxy Formation

In semi-analytic models of galaxy formation, the evolution of the baryonic components of dark matter halos is modeled invoking simple, yet physically- and/or observationally-motivated prescriptions. The backbone of a semi-analytic model is a statistical representation of the growth of dark matter halos, i.e., what in jargon is called a “merger tree”. This can be either constructed analytically (e.g., using the extended Press and Schechter formalism, e.g., [40,41]) or extracted from numerical simulations (e.g., [42,43]). Once the backbone of the model is constructed, galaxy formation and evolution can be coupled to the merger trees using a set of analytic/numerical prescriptions to describe complex physical processes like star formation, supernovae, and AGN feedback processes, etc. Adopting this formalism, it is possible to express the full galaxy formation process through a set of differential equations that describe the variation in mass of the different galactic components (e.g., gas, stars, metals). Given our limited understanding of the physical processes at play, the equations/parametrizations used contain “free parameters”, whose values are typically chosen to provide a reasonable agreement with a given set of observational data in the local Universe.

The techniques find their seeds in the pioneering work by White and Rees [44], which have been laid out in a more detailed form in the early 1990s [45,46] and have been substantially extended and refined in the last years by a number of different groups. In their first renditions, semi-analytic models relied on Monte Carlo realizations of merging histories of individual objects, generated using the extended Press–Schechter theory (e.g., [47]). An important improvement came from the coupling of semi-analytic techniques with large resolution N-body simulations, which can be used to specify the location and evolution of dark matter halos: the birthplaces of luminous galaxies [2,48]. On a next level of complexity, some more recent implementations of these techniques have explicitly taken into account dark matter substructures, i.e., the halos within which galaxies form are still followed when they are accreted onto a more massive system [49,50]. One important caveat to bear in mind regarding these methods is that, as mentioned above, dark matter substructures are fragile systems that are rapidly and efficiently destroyed. Depending on the resolution of the simulations used, substructures can “disappear” well before the actual merger/accretion between galaxies can take place. In most of the published semi-analytic models, it is assumed that galaxies residing in substructures that are stripped below the resolution limit of the simulation can survive, as “orphan galaxies”, for a residual merging time that is given by some variants of the classical dynamical friction formula (e.g., [51]).

One great advantage of models based on numerical merger trees, with respect to techniques based on the extended Press–Schechter formalism, is that they provide full dynamical and spatial information about model galaxies. Using realistic mock catalogs generated with these “hybrid” methods, accurate and straightforward comparisons with observational data can be carried out. Since N-body simulations can handle large numbers of particles, the approach can access a very large dynamic range in mass and spatial resolution, at small computational cost. In addition, since the computational times are limited, these methods also allow a fast exploration of the parameter space and an efficient investigation of the influence of specific physical assumptions. Figure 3 shows, on the left, the spatial distribution of galaxies obtained applying a semi-analytic model to a constrained realization of the local Universe. Model galaxies are shown as colored symbols and are super-imposed on the dark matter distribution. The right panel shows light-cones constructed coupling a semi-analytic model to a large cosmological high-resolution simulation, compared to observations from the 2 dF Galaxy Redshift Survey and a portion of the Sloan Digital Sky Survey (observational data are shown in blue/violet, while mock data in red).

Thanks to their flexibility, limited computational costs, and easy access to a large dynamic range in mass and spatial resolution, semi-analytic models represent an ideal tool to make detailed predictions of galaxy populations at different cosmic epochs and in cosmological volumes. In recent years, these models have successfully overcome important problems related to the evolution of low mass galaxies ([53] and the references therein). These problems manifested in particular as (i) a dramatic over-prediction of the number densities of low to intermediate-mass galaxies; and (ii) stellar populations significantly older than observational measurements, in the same galaxy mass range. Early attempts to address these problems focused on the simplified treatment adopted for satellite galaxies: when a galaxy is accreted onto a larger structure (i.e., when it becomes a satellite), its reservoir of hot gas is stripped and is not able to replenish the galaxy with new fuel for star formation. Until approximately one decade ago, the typical assumption was that of an instantaneous stripping of the hot gas reservoir associated with infalling galaxies. This induced a rapid decline of the star formation history of satellite galaxies, creating a significant excess of passive galaxies with respect to observational estimates [54,55]. Later work [56,57,58] adopted a more gradual stripping of the hot gas reservoir finding a better, albeit not yet satisfactory, agreement with observational data. Somewhat surprisingly, recent work has shown that these problems can be significantly reduced2 by modifying the stellar feedback scheme, while still assuming an instantaneous stripping of the hot gas reservoir of infalling satellites. Figure 4 shows the redshift evolution of the galaxy stellar mass function for different implementations of stellar feedback (lines of different colors and style) within the GAEAsemi-analytic model [59]. For details on the individual models adopted, I refer to the original paper. Here, I would like to stress the difference between the stellar feedback scheme adopted in previous renditions of the model (the fiducial model, shown in violet) and the new scheme adopted in the reference GAEA model (the FIREmodel, shown in orange). The latter adopts parametrizations based on the FIRE hydrodynamical simulations [60] that, in the framework of the GAEA model, allow us to reproduce nicely the observed evolution of the galaxy stellar mass function over the entire redshift range considered. The same model also reproduces quite well a number of other important observational constraints, including the observed correlation between galaxy stellar mass and gaseous/stellar metallicity (without using the chemical yield as a free parameter) and the estimated fraction of passive galaxies as a function of galaxy mass and halo mass. The model is, of course, not without problems: in particular, massive galaxies appear to be too active with respect to observational estimates in the local Universe, while the overall level of (specific) star formation appears to be biased low with respect to observational measurements at $z\gtrsim 2$ (see also [61]). The latter problem appears to be shared by most recently-published semi-analytic models, as well as by hydro-dynamical simulations (see below).

Many sophisticated semi-analytic models have been published in recent years. They exhibit a different, but impressive level of agreement with observational measurements at different cosmic epochs and have been further implemented to include a detailed treatment of chemical enrichment accounting for non-instantaneous recycling of gas, metals, and energy (e.g., [62,63,64]), an explicit modeling of the partition of the cold gas component in atomic and molecular gas [61,65,66,67], and in a few cases also the formation and destruction of dust [68].

The ever-increasing amount of information we are gathering of galaxy populations at different cosmic epochs provides continuous new challenges to these models. A significant boost in the use of these theoretical methods to interpret observational data has come through the public release of different model catalogs applied to large cosmological simulations. At the time of writing, different databases can be queried to download results from different semi-analytic models (e.g., [69]) (more recently, public databases have been constructed also for hydrodynamical simulations). A large number of papers has been published taking advantage of these tools, which demonstrates great interest from the astronomical community. In turn, this has led to a rapid verification and refinement of the theoretical models.

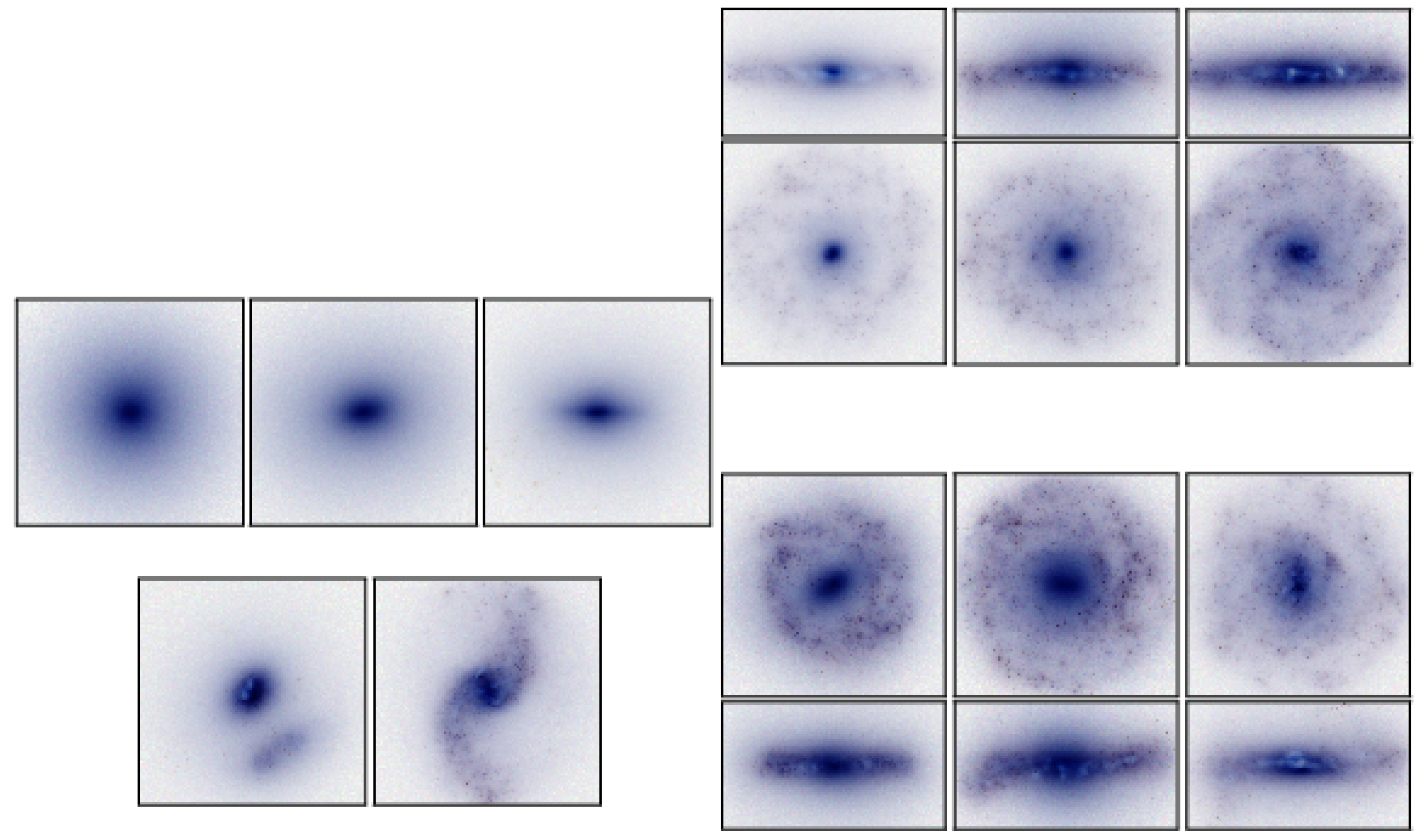
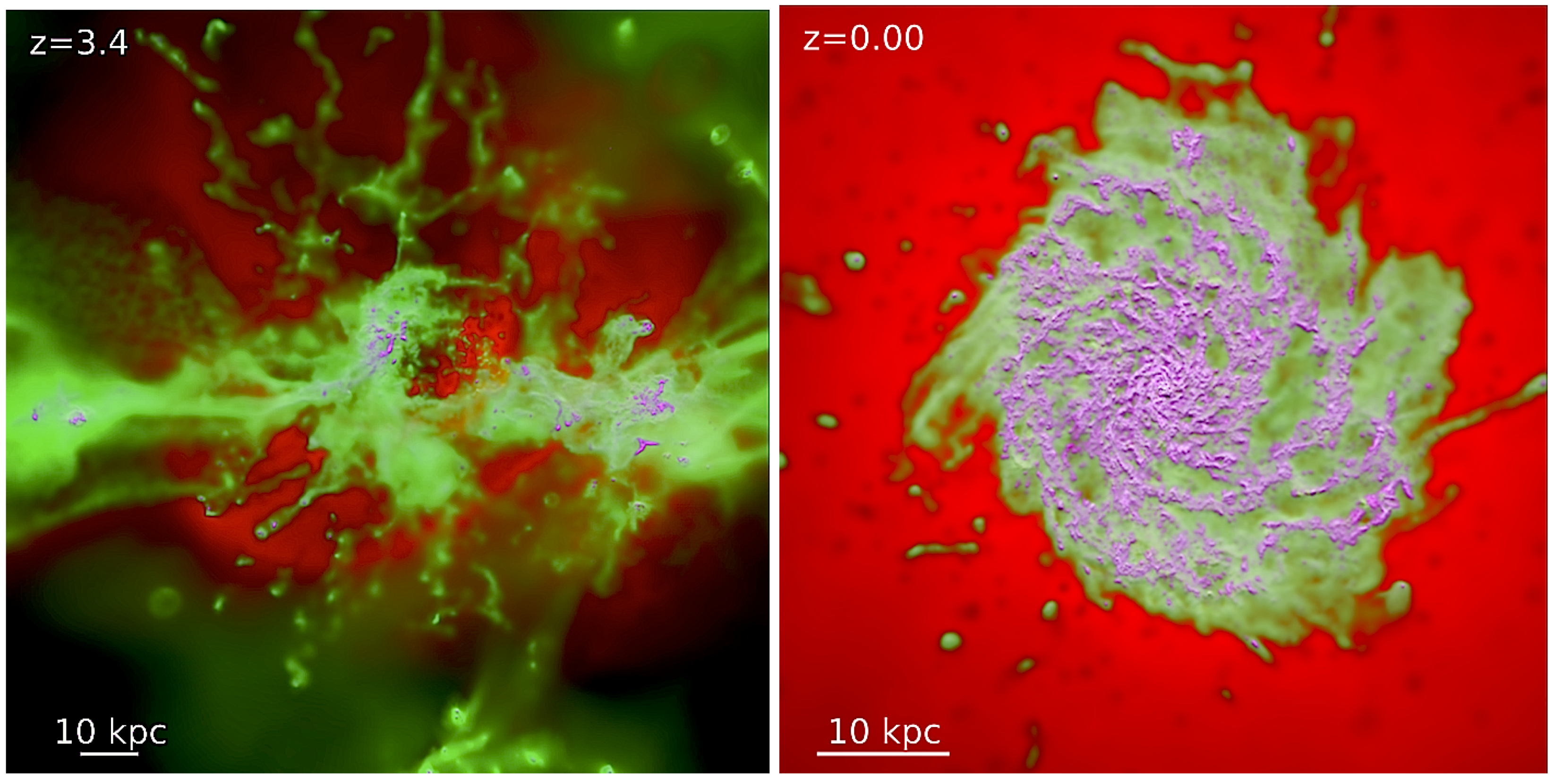
4. Hydrodynamical Simulations

The most direct way to model the evolution of the visible components of dark matter halos is through hydrodynamical simulations. Different approaches can be used to include gas physics in N-body simulations. The most straightforward technique is adopted in smoothed particle hydrodynamics (SPH) codes. These are based on a Lagrangian method, which works by dividing the fluid into a set of discrete elements (particles). These have a spatial distance (“smoothing length”), over which their properties are smoothed by a kernel function. Any physical quantity of a particle (for example, density, temperature, and chemical composition) can then be obtained by summing the relevant properties of all the particles that lie within the range of the kernel. The contributions of individual particle to a certain physical property are weighted according to their distance from the particle of interest and to their density. The Lagrangian nature of the method means that regions of high density are automatically better resolved than regions of low density, so that it is possible to study many orders of magnitude in the fluid properties. Because of the smoothing over the density, however, SPH codes have problems in resolving and treating dynamical instabilities developing at sharp interfaces in a multi-phase fluid (e.g., shocks, [70]). It is possible to alleviate these problems by introducing artificial mixing terms or by modifying the treatment of artificial viscosity (e.g., [71,72]), but it is unclear if these methods provide a universal solution without introducing other limitations under different conditions. More recent studies have published new implementations of SPH with significantly improved accuracy for simulations of galaxy formation and the large-scale structure. These include a pressure-entropy formulation with a modified kernel, a higher order estimate of velocity gradients, and modified schemes for artificial viscosity and conduction [73,74].

An alternative scheme is adopted in Eulerian codes in which the fluid equations are solved on a grid that is fixed in time and that can be “refined” several times to increase the resolution in regions of interest (adaptive mesh refinement (AMR)). This method is thus well adapted for capturing shocks and discontinuities, but typically translates into a larger computational cost with respect to SPH-based codes. In addition, also AMR codes suffer from fundamental problems that make the calculation inaccurate in certain regimes (for a detailed discussion of the weaknesses of SPH and AMR methods, I refer to Springel [75]). The most serious concern, for simulations of galaxy formation with AMR codes, is perhaps the lack of Galilean invariance, which makes the results sensitive to the presence of bulk velocities [76]. In recent years, more sophisticated codes have been published, which retain the advantages of the SPH and AMR techniques while avoiding most of the problems, but increase the computational costs (e.g., the AREPOcode [75] that uses an unstructured moving mesh, and the GIZMOcode [77] based on a novel meshless scheme.)

With respect to empirical/statistical methods and semi-analytic models, direct hydrodynamical simulations offer the advantage of an explicit description of the gas dynamics. This comes, however, at the expenses of computational costs and flexibility, particularly if one is interested in simulations of galaxy formation in large cosmological volumes. Additionally, and perhaps more importantly, complex physical processes such as star formation, feedback, black hole formation, etc., still have to be included as “sub-grid physics”. This is necessary either because the resolution of the simulation is inadequate to treat the specific process considered or simply because we do not have a complete theory to make first principles calculations of the physical problem under consideration (unfortunately, this is almost always the case in galaxy formation).

Current state-of-the-art full hydrodynamic cosmological simulations include the HORIZON-AGN simulation [78], the Magneticum Pathfinder simulation [79,80], the Illustris project [81], the Evolution and Assembly of GaLaxies and their Environments (EAGLE) project [82], the MUFASAsimulations [83], and the BAHAMASproject [84]. Among these, EAGLE and Illustris are those that combine the largest volume and highest resolution. Both consist of suites of cosmological simulations of a standard $\Lambda$ cold dark matter Universe and include sub-grid models for radiative cooling, star formation, stellar mass-loss, and metal enrichment, feedback from massive stars, gas accretion onto super massive black holes, and AGN feedback. The EAGLE suite includes volumes ranging from 25–100 comoving Mpc, run using a tree-PMsmoothed particle hydrodynamics code. In the largest simulated volume, galaxies are resolved down to stellar masses of the order of a few times ${10}^8{\mathrm{M}}_{\odot }$. The Illustris simulation has been run with the new code AREPO, and the highest resolution run corresponds to a volume and resolution comparable to that of the largest EAGLE volume. Figure 5 shows examples of galaxies from the EAGLE simulation3, illustrating the variety of morphological properties for galaxies at z = 0. Each image is 60 kpc on a side; both face-on and edge-on projections are shown for disk galaxies. This “synthetic” image was created using radiative transfer calculations with the code skirt [85] at the wavelengths corresponding to the SDSS bands u, g, and r. The calculation assumes that 30 percent of the metals are locked up in dust grains.

Both the EAGLE and Illustris simulations have been tuned primarily to reproduce the galaxy stellar mass function observed in the local Universe (in EAGLE, galaxy sizes are also used as an additional constraint), and albeit giving predictions that differ in the detail, they both show a remarkable level of agreement with different measurements of the baryonic components of dark matter halos as a function of cosmic time. Both are, of course, not without problems: e.g., the galaxy formation model used in the EAGLE project leads to a fraction of passive satellites that decreases with increasing stellar mass, which is opposite to what is observed [86]. In addition, the fraction of passive satellites predicted by these simulations is still significantly larger than observed at intermediate to low galaxy masses (as mentioned above, this has been, and to some level still is, a long-standing problem for theoretical models of galaxy formation, e.g., [87]). Predictions from the EAGLE simulations also appear to be offset low with respect to observational measurements of the cosmic star formation rate density and of the star-forming main sequence [88]. Various tensions were identified between predictions from the Illustris simulation and observational measurements, which led to a revision of the physical model and in particular of the modeling adopted for galactic winds and AGN feedback (the IllustrisTNGproject [89]). An extensive analysis of these new simulations is ongoing. A detailed review of the outcome of these simulations, as well as of the many others available (some of which are mentioned above) is beyond the scope of this review. Here, I would like to stress that large hydrodynamical cosmological simulations represent an important investment of resources. Yet, the resolution achieved is such that most of the physical processes at play need to be included using sub-grid prescriptions. An increase of the resolution would not improve the situation, as it generally moves the need to formulate “effective models” on smaller scales, which often requires the inclusion of additional physical processes. In addition, even when the increase in resolution is not as drastic, the parameters of the subgrid models typically need to be re-calibrated, something that has been named “weak convergence” [82].

Much higher resolution than typically achieved within cosmological boxes can be obtained in cosmological re-simulations of individual halos. These take advantage of the “zoom” technique: first, a (lower resolution) cosmological dark matter-only simulation of a large region is used to select a suitable target halo, or a region of interest. The particles in and around the selected halo (usually all the particles within two- to five-times the virial radius) are then traced back to their initial Lagrangian region and are replaced by a larger number of lower mass particles, including gas particles. The same fluctuation distribution as in the parent simulation, but now extended to smaller scales to account for the increase in resolution, is used to perturb the particle distribution. This resampling of the initial conditions allows a localized increase in mass and force resolution. Outside the high-resolution region, particles of variable mass (increasing with distance from the high-resolution region) are used, so that the computational effort is concentrated on the region of interest, while still maintaining a faithful representation of the large-scale density and velocity field of the parent simulation.

At galaxy scales, simulations have traditionally had problems reproducing disc-dominated galaxies resembling our own Milky Way. One major problem has been known as the “angular momentum catastrophe”: baryons condense early in clumps that then fall into larger halos and merge via dynamical friction. This produces a net and significant transfer of angular momentum from the baryons to the dark matter. As a result, simulated discs were generally too small and had up to ten-times less angular momentum than real disc galaxies. Recent numerical work has shown that this problem is in part due to limited resolution and related numerical effects, which cause artificial angular momentum loss and spurious bulge formation (for a detailed discussion, see e.g., Mayer, Governato, and Kaufmann [90]). These studies have, however, also shown that one of the most crucial ingredients for simulations of realistic disk-like galaxies is an accurate modeling of star formation and stellar feedback (see, e.g., Murante et al. [91] and the references and historical introduction therein). Figure 6 shows the gas density distribution in a zoom-in simulation of a Milky-Way like halo from the FIRE simulations [60], mentioned in the previous section. The resolution of the simulation is very high (among the highest carried out in the recent literature): the dark matter particle mass in the high-resolution region is $1.38\times {10}^5{\mathrm{M}}_{\odot }{\mathrm{h}}^{-1}$, and the initial baryonic particle mass in the same region is $2.7\times {10}^4{\mathrm{M}}_{\odot }{\mathrm{h}}^{-1}$. The particular galaxy shown in this figure undergoes a violent starburst at $z\sim 3$, leading to a strong outflow of hot and warm gas. At present day, a relaxed and well-ordered disk has formed, with cold gas tracing a well-defined spiral structure.

The degree of sophistication reached by current hydrodynamical simulations is impressive and the level of agreement with observational data encouraging. Recent work has also focused on the inclusion of “non-standard” galaxy formation physics like magnetic fields and cosmic rays (see, e.g., [92,93]). However, different (plausible and often equally successful) physical models for stellar feedback have been proposed (see the discussion in [94]), and it remains difficult to discriminate between them (we will come back to this issue below). Understanding how exactly stellar feedback operates is a complex task, because the mechanisms at play occur on the scales of the multiphase structure of the inter-stellar medium (ISM). The UV photons emitted by young stars efficiently ionize the surrounding medium, dissociating molecular hydrogen (H${}_2$). Photons also carry momentum, which acts as a pressure force. Numerical work has shown that this radiative feedback represents a slow and inefficient way to couple radiation to the surrounding gas [95], unless radiation pressure can be significantly boosted by photon trapping (UV radiation is absorbed by dust and re-emitted in the far-IR, which can enhance significantly the momentum output). Therefore, tracing the dense ISM regions where star formation takes place requires radiative transfer calculations of H${}_2$ dissociation, as well as a treatment for dust and H${}_2$ self-shielding. The energy output from supernovae can lead to even more profound transformations of the ISM surrounding star-forming regions and likely provides the engine driving large-scale galactic outflows. Recently, different groups have carried out high-resolution simulations of supernovae remnants in inhomogeneous media and analyzed the role of vertical disk stratification [96,97,98]. These detailed calculations have shown that mechanisms like stellar winds and ionizing radiations play an important role in reducing the gas density at which supernovae explode, thereby allowing an efficient propagation of the blast-wave. Since, however, these simulations neglect the galactic environment and assume a simplified geometry, it is difficult to use them to predict realistic mass/energy loss rates.

5. Complementarities of the Different Approaches

Clearly, each of the methods described above has its own advantages and weaknesses. Summarizing, very schematically, what has been discussed in the previous sections:

• Empirical/statistical methods are characterized by a very intuitive framework and a very limited computational demand. They are able to provide useful statistical constraints on galaxy formation, but it remains difficult to translate this information into a deeper physical understanding of the galaxy formation process;
• Semi-analytic models are very flexible, have limited computational costs, and allow access to a large dynamical range in spatial and mass resolution. They neglect, however, an explicit treatment of the gas dynamics, and only a limited amount of information is accessible as for the spatial distribution of the baryonic components.
• Hydro-dynamical simulations include an explicit and accurate treatment of the gas dynamics, as well as full spatial information about the baryons. As a tool to study galaxy formation on cosmological scales, however, they are still limited by relatively high computational costs. In addition, and perhaps more importantly, the complex physical processes driving galaxy formation and evolution still need to be included resorting to sub-resolution/effective models.

Given the weaknesses and advantages summarized above, different scientific questions/problems point to a different ideal tools. For example, in the case one needs to develop or optimize an algorithm for data analysis, empirical methods provide a very efficient way to test the algorithm in realistic cases, at least over the redshift range where observational data are available to construct the model. As discussed above, however, it is difficult to translate the information obtained employing this approach into constraints on physical processes driving baryonic evolution, unless the methods are made more complex (effectively moving in the direction of semi-analytic techniques). Interpreting observational data in terms of physical processes can only be achieved by using an approach that explicitly accounts for them, i.e., semi-analytic models or hydrodynamical simulations. As evident from the previous discussion, there is a high level of complementarity and synergy between these two techniques: the limited computational cost of semi-analytic methods allows a very efficient exploration of the parameter space and investigation of the influence of different parametrizations. Hydrodynamical simulations (in controlled experiments) are used, on the other hand, to characterize processes like galaxy mergers and cold gas ram-pressure stripping, thereby building prescriptions that can be used within semi-analytic models. Hydrodynamical simulations are also necessary when one wants to make detailed studies of the spatially-resolved properties of individual systems.

Our understanding of the physical processes at play is such that these are included, both in semi-analytic models and in hydrodynamical simulations, using effective parametrizations, with the free parameters typically being tuned to reproduce specific sets of observables. One criticism that is often raised is that these models have “too many” free parameters. However, the number of these parameters is not larger than the number of published (or possible) comparisons with different and independent sets of observational data. In addition, it is important to realize that these parameters are not “statistical” but “physical”: a change of any of them has consequences on different predictable quantities. As a consequence, there is actually little parameter degeneracy for a given set of prescriptions, if a wide range of model predictions is considered. In fact, it is also crucial to bear in mind that what matters is not the value of a given parameter, but the actual parametrization adopted. Therefore, caution is needed when using statistical techniques for parameter estimation (e.g., [99,100]). Given the large number of parameters typically involved, these tools are certainly useful to efficiently explore the parameter space and to determine to what extent a given physical model is able to reproduce a given set of observational constraints. However, the approach is not ideal to understand the relative importance of different processes and/or of the parametrizations adopted.

Another criticism that is often heard is related to the limited predictive power of our theoretical models. The concern here is often related to our inability to model physical processes from first principles and to the consequent need to resort to sub-resolution/effective schemes. The fact that, e.g., different stellar feedback schemes can lead to a reasonable agreement with observational data is often deemed to limit our ability to improve our understanding of how gas and metals are ejected into the inter-stellar medium significantly. In most cases, however, agreement is shown for a specific subset of observational data, and additional comparisons can be carried out with theoretical predictions (i.e., expectations for quantities that have not been considered when constructing/tuning the model). These additional comparisons often highlight disagreements with observations or it is possible to construct specialized observational tests to falsify specific predictions. No model/simulation is without problems, and it is exactly from the failures of the models that we improve our physical understanding of baryon evolution.

6. Concluding Remarks

As discussed in Section 1, galaxy formation is a very difficult physical problem because it involves a variety of phenomena that act on different physical scales and at different times and that interact in many possible ways. In addition, both theoretically and observationally, we have a very limited understanding of most of the physical processes that should be taken into account. Given the complexity of the problem, it is clear that we are not yet (and perhaps we will never be) in the position of being able to model galaxy formation “from first principles”. A number of different techniques have been used in the literature to populate dark matter halos with baryons. In the previous sections, I have focused on the basics, aims, and limits of three main approaches: statistical/empirical methods, hydrodynamical simulations, and semi-analytic models.

As discussed above, these tools are highly complementary, and their optimal use ultimately depends on the questions/goals to be addressed. None of these methods, unsurprisingly, provides “the model” that reproduces the observable Universe. In fact, it is perhaps naive (certainly very ambitious) to expect to be able to model the beauty and complexity of our Universe in a computer, albeit with very sophisticated and numerically-expensive methods. This does not mean, however, that these tools are not useful and that we cannot advance in our knowledge of galaxy formation. In fact, we have made incredible progress in the past decades, by continuously falsifying predictions/expectations from our theoretical models with the ever-increasing amount of observational information we are gathering.

These are very exciting times for studying galaxy formation and evolution: in the last few years, we have witnessed the accumulation of a huge amount of information through wide, deep, and multi-wavelength surveys of the local and distant Universe. A new flood of data is just behind the corner as new facilities rapidly move into operation (e.g., JWST, LSST, Euclid, ALMA, SKA). Theoretical models that try to reproduce the ever-more detailed observational picture of the Universe will also require ever-more complex modeling. Only by keeping the close link between theoretical predictions and observational data will it be possible to shed further light on the physical processes governing galaxy formation and evolution.