Plasmas in Gamma-Ray Bursts: Particle Acceleration, Magnetic Fields, Radiative Processes and Environments
Abstract
1. Introduction
2. Acceleration of Particles in Shock Waves
3. Magnetic Fields in GRBs
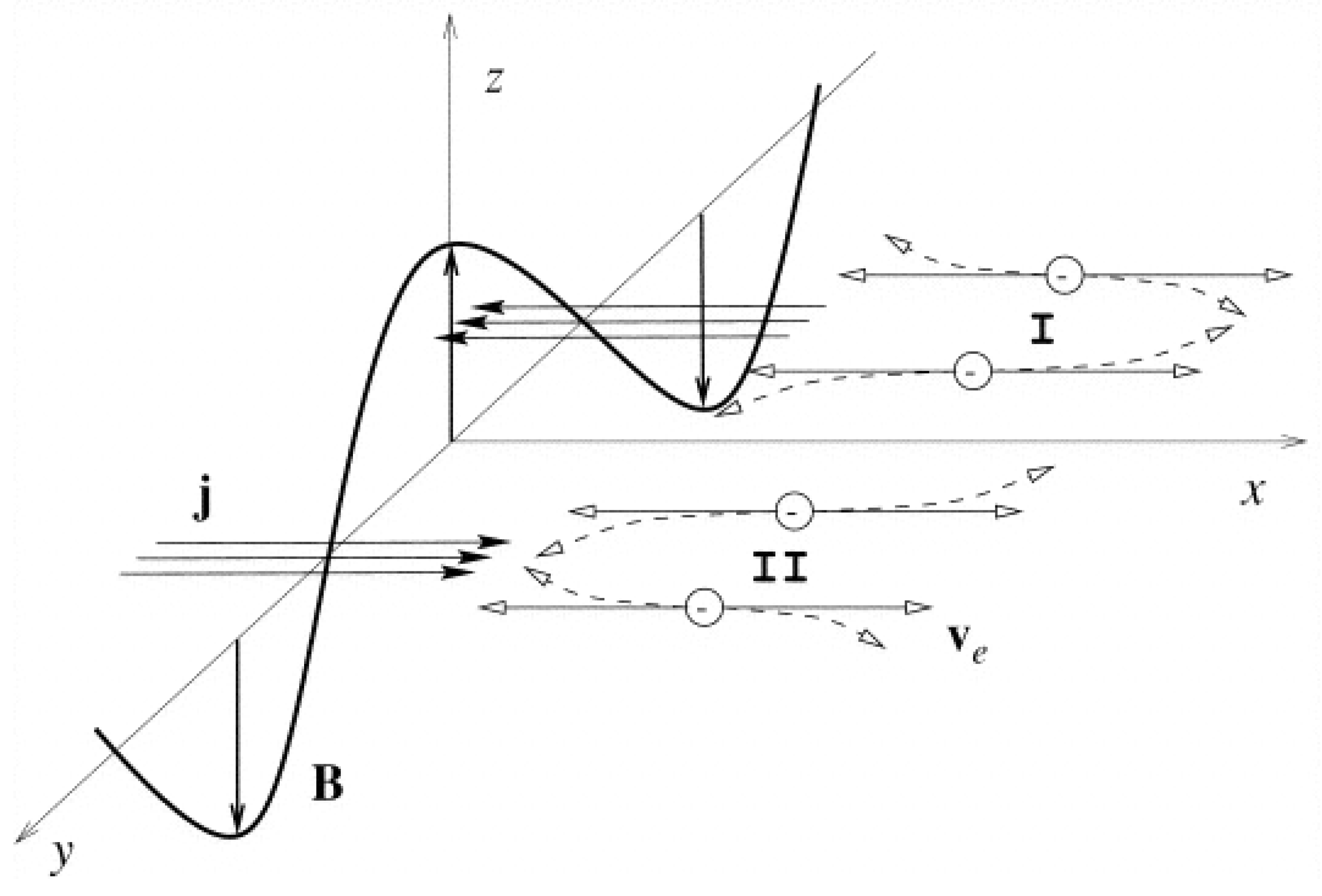
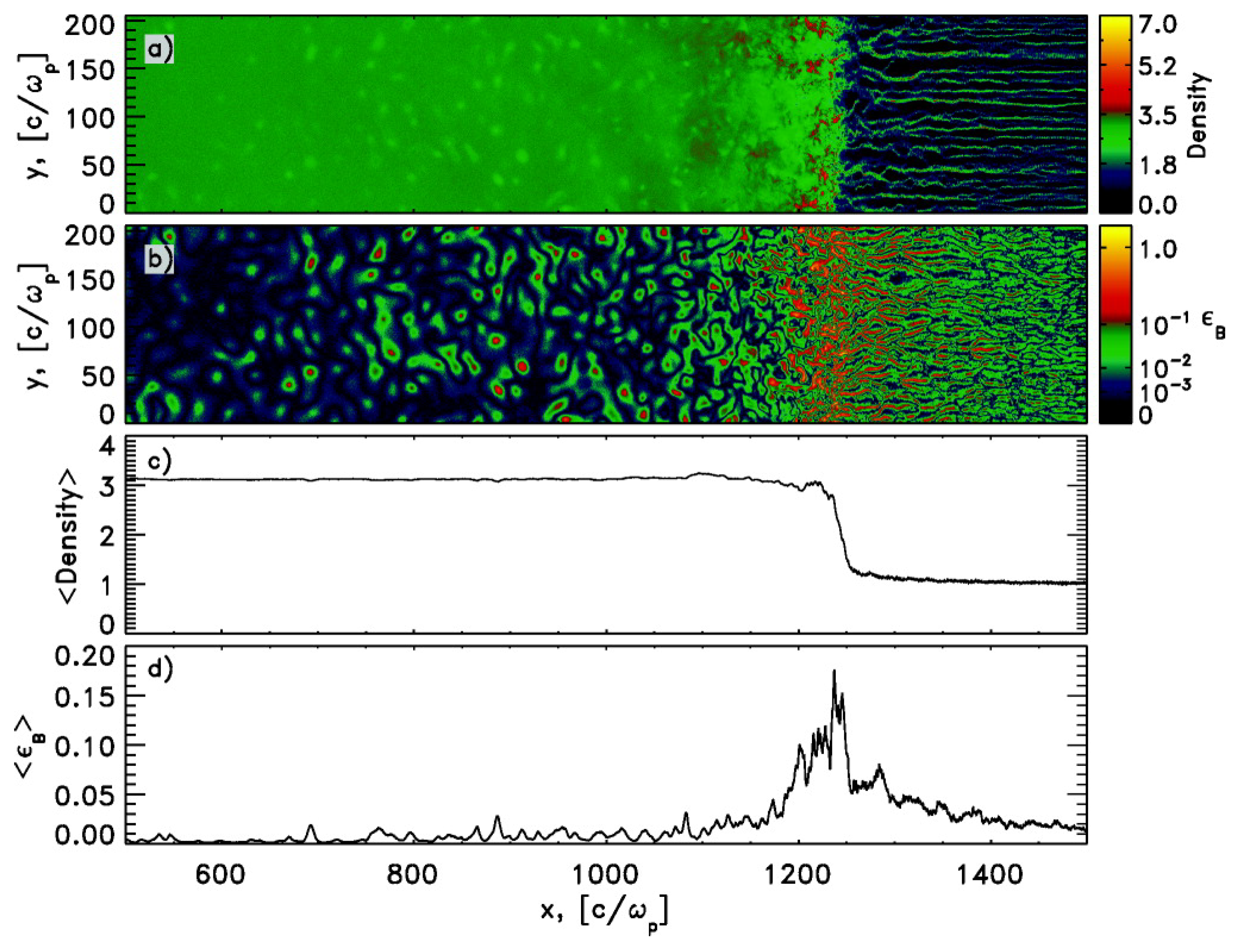
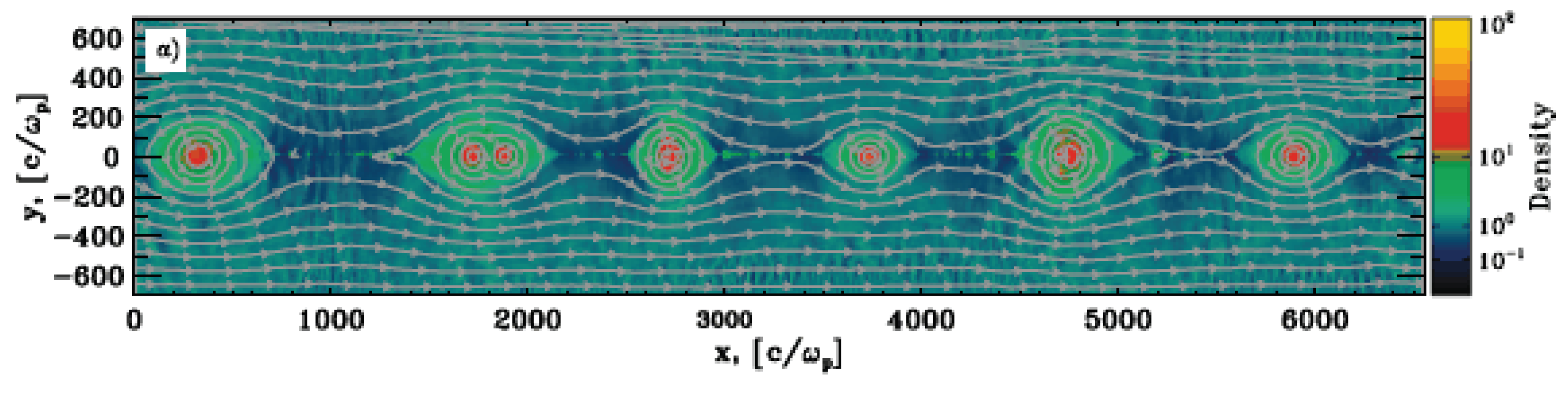
3.1. Magnetic Field Generation in Shock Waves
3.2. Highly Magnetized Plasma during GRB Prompt Emission?
3.2.1. Motivation
3.2.2. Detailed Models
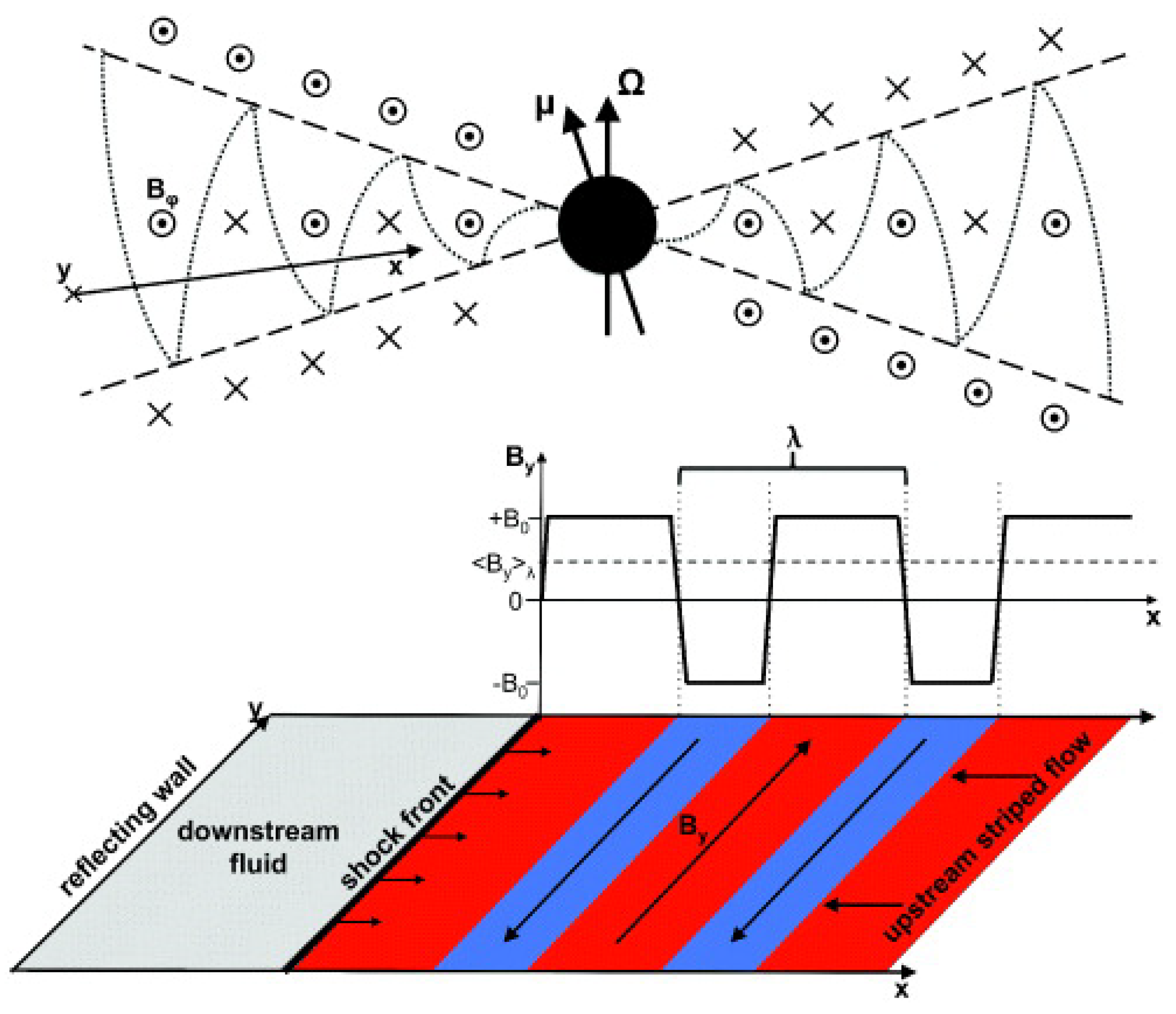
3.3. Acceleration of Particles in Highly Magnetized Plasma: Magnetic Reconnection Process
4. Photon Field in GRB Plasmas
4.1. Radiative Processes: The Classical Ideas
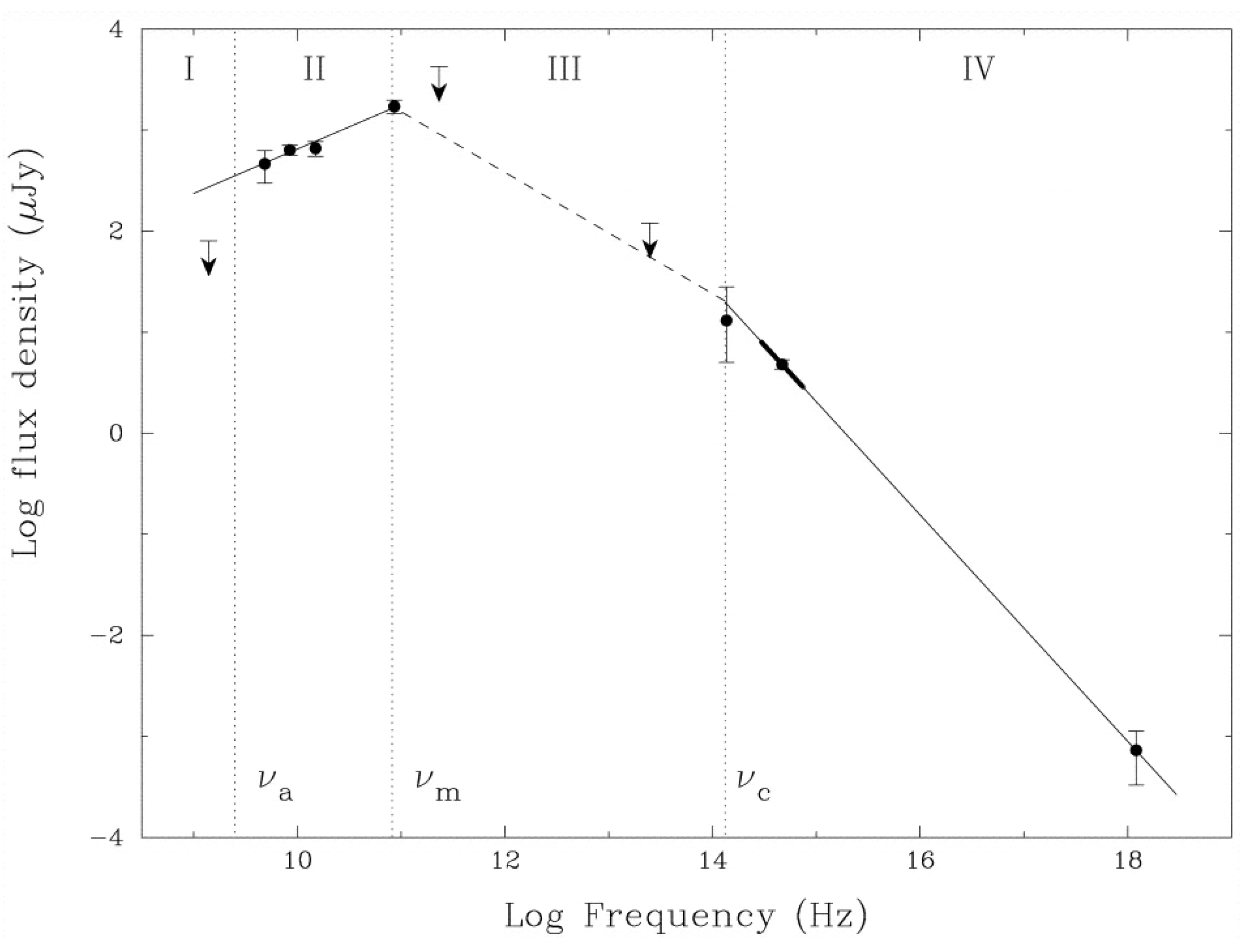
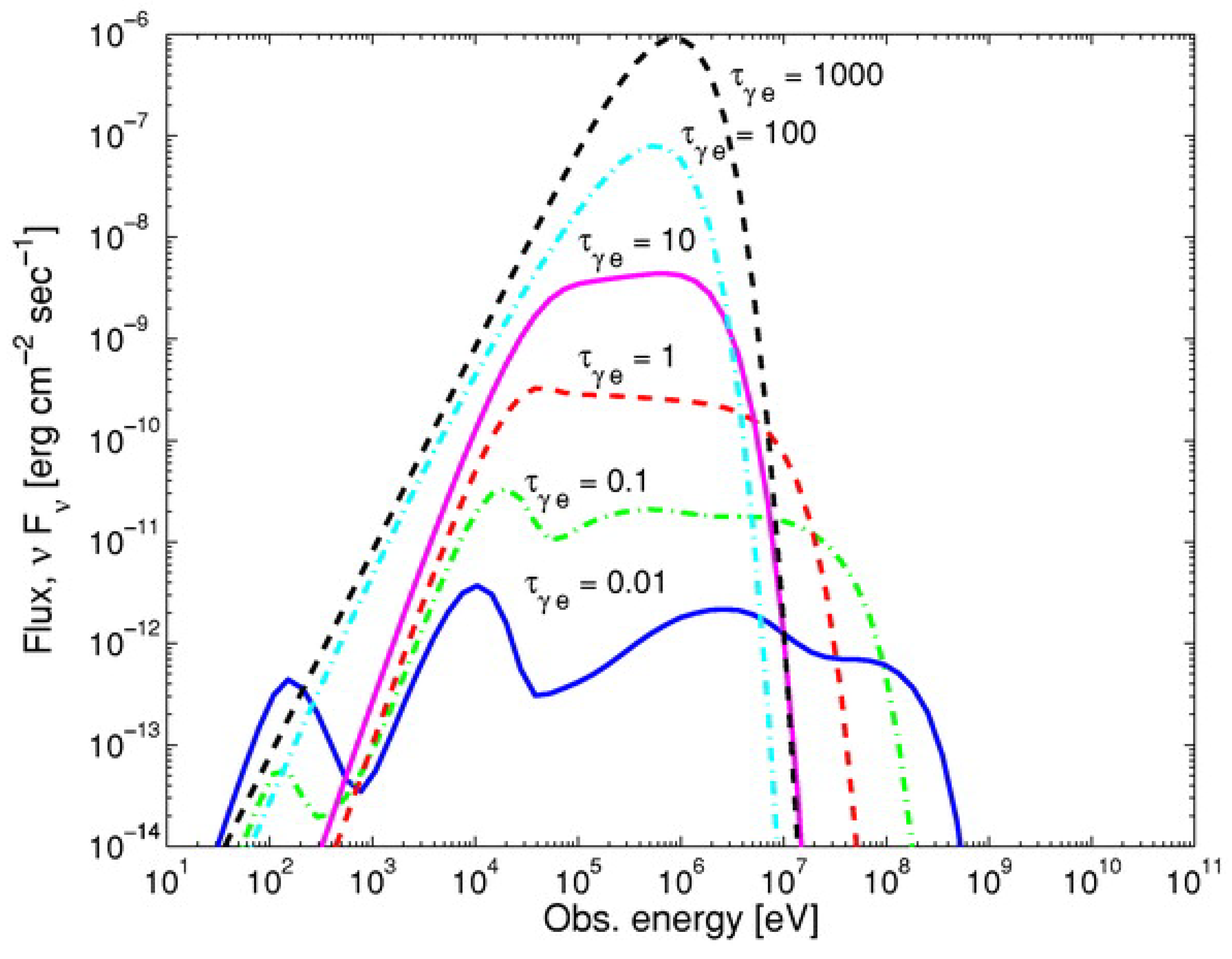
4.2. Photospheric Emission and GRB Dynamics
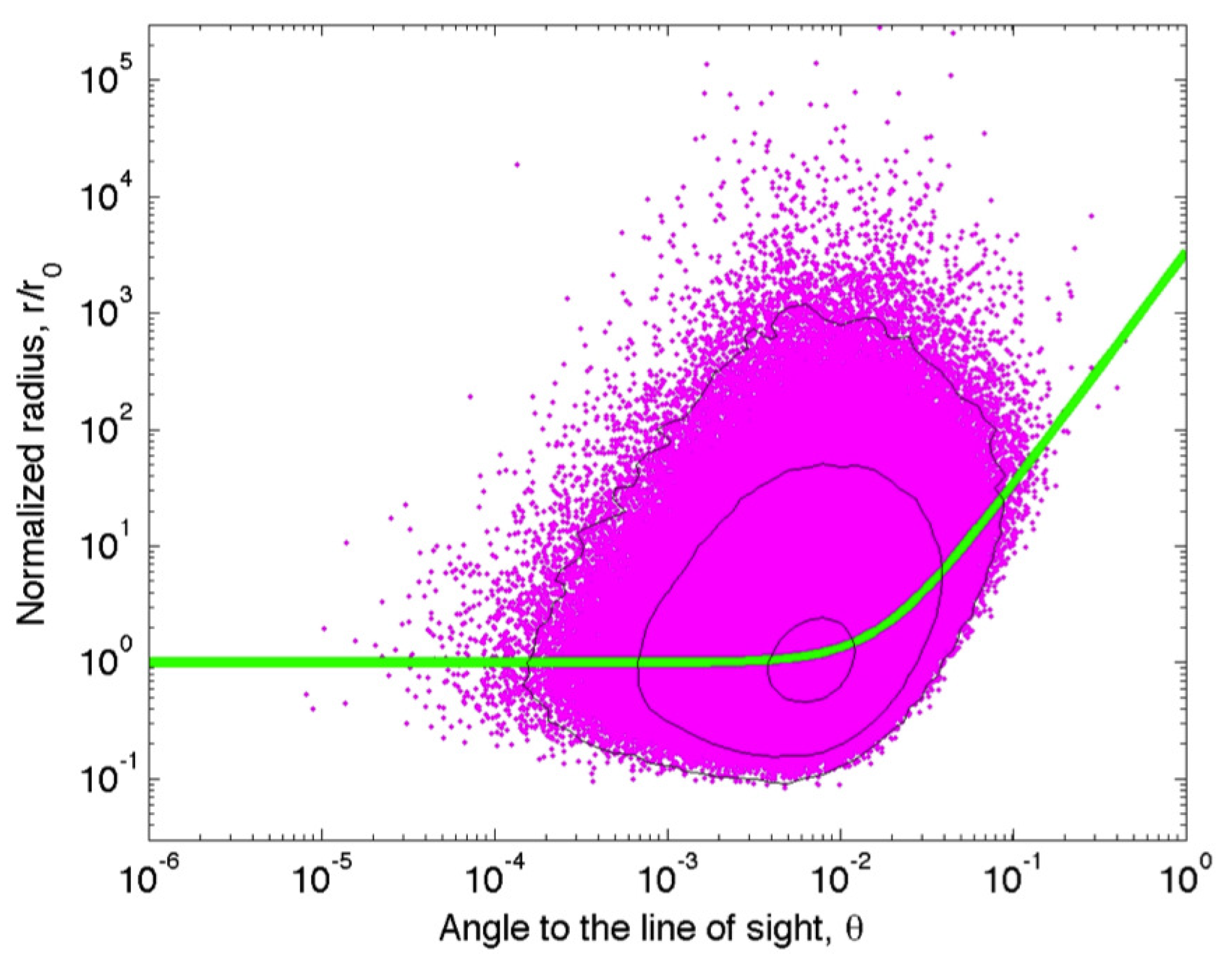
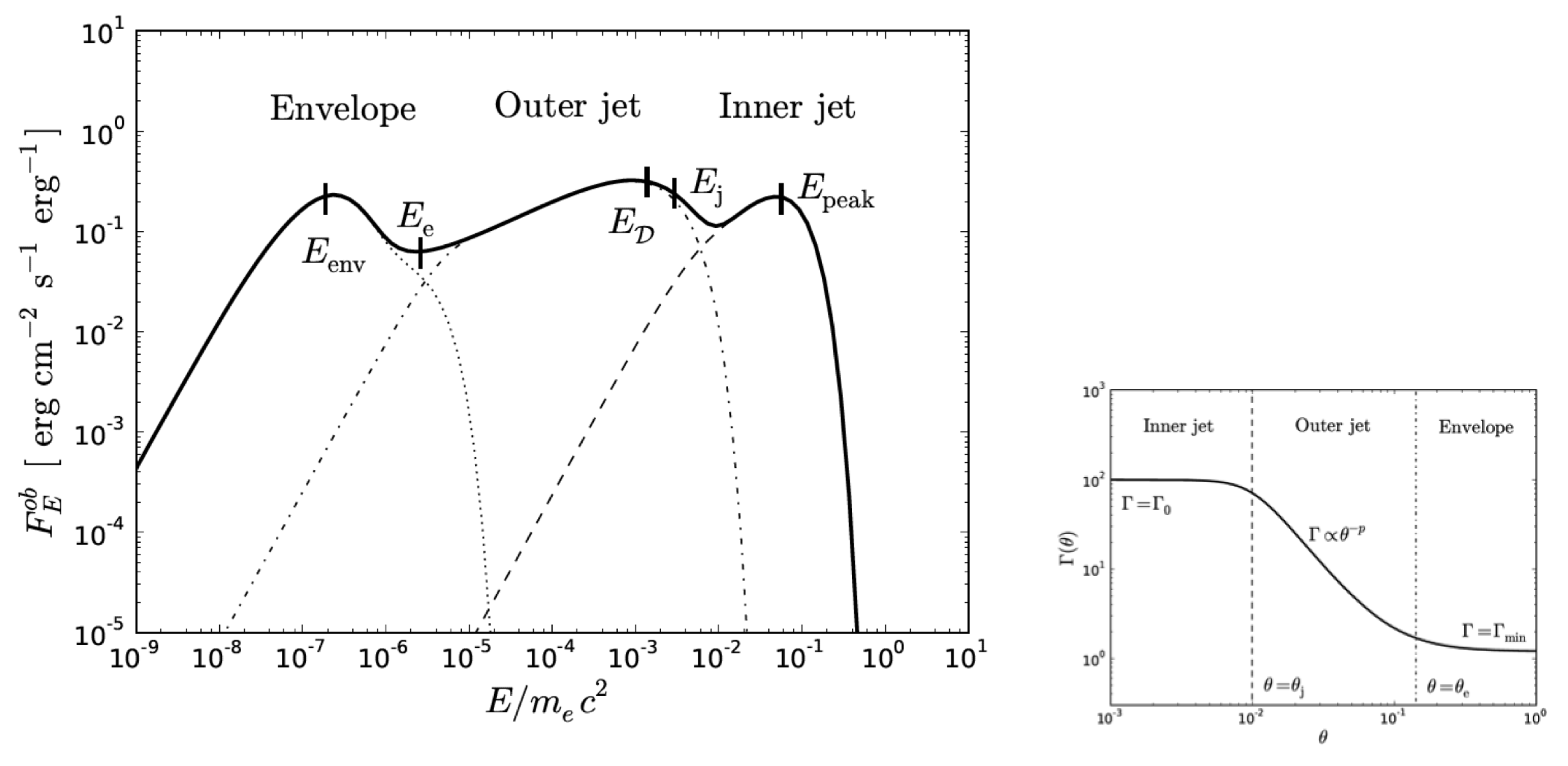
5. GRB Environments and GRB170817a
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdo, A.A.; Ackermann, M.; Arimoto, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. Fermi Observations of High-Energy Gamma-Ray Emission from GRB 080916C. Science 2009, 323, 1688–1693. [Google Scholar] [CrossRef] [PubMed]
- Costa, E.; Frontera, F.; Heise, J.; Feroci, M.; in’t Zand, J.; Fiore, F.; Cinti, M.N.; Dal Fiume, D.; Nicastro, L.; Orlandini, M.; et al. Discovery of an X-ray afterglow associated with the γ-ray burst of 28 February 1997. Nature 1997, 387, 783–785. [Google Scholar] [CrossRef]
- van Paradijs, J.; Groot, P.J.; Galama, T.; Kouveliotou, C.; Strom, R.G.; Telting, J.; Rutten, R.G.M.; Fishman, G.J.; Meegan, C.A.; Pettini, M.; et al. Transient optical emission from the error box of the γ-ray burst of 28 February 1997. Nature 1997, 386, 686–689. [Google Scholar] [CrossRef]
- Frail, D.A.; Kulkarni, S.R.; Nicastro, L.; Feroci, M.; Taylor, G.B. The radio afterglow from the γ-ray burst of 8 May 1997. Nature 1997, 389, 261–263. [Google Scholar] [CrossRef]
- Wijers, R.A.M.J.; Rees, M.J.; Meszaros, P. Shocked by GRB 970228: The afterglow of a cosmological fireball. Mon. Notices R. Astron. Soc. 1997, 288, L51–L56. [Google Scholar] [CrossRef]
- Galama, T.J.; Vreeswijk, P.M.; van Paradijs, J.; Kouveliotou, C.; Augusteijn, T.; Böhnhardt, H.; Brewer, J.P.; Doublier, V.; Gonzalez, J.F.; Leibundgut, B.; et al. An unusual supernova in the error box of the γ-ray burst of 25 April 1998. Nature 1998, 395, 670–672. [Google Scholar] [CrossRef]
- Wijers, R.A.M.J.; Galama, T.J. Physical Parameters of GRB 970508 and GRB 971214 from Their Afterglow Synchrotron Emission. Astrophys. J. 1999, 523, 177–186. [Google Scholar] [CrossRef]
- Blandford, R.D.; McKee, C.F. Fluid dynamics of relativistic blast waves. Phys. Fluids 1976, 19, 1130–1138. [Google Scholar] [CrossRef]
- Galama, T.J.; Wijers, R.A.M.J.; Bremer, M.; Groot, P.J.; Strom, R.G.; Kouveliotou, C.; van Paradijs, J. The Radio-to-X-ray Spectrum of GRB 970508 on 1997 May 21.0 UT. Astrophys. J. 1998, 500, L97–L100. [Google Scholar] [CrossRef]
- Kumar, P.; Panaitescu, A. Afterglow Emission from Naked Gamma-Ray Bursts. Astrophys. J. 2000, 541, L51–L54. [Google Scholar] [CrossRef]
- Santana, R.; Barniol Duran, R.; Kumar, P. Magnetic Fields in Relativistic Collisionless Shocks. Astrophys. J. 2014, 785, 29. [Google Scholar] [CrossRef]
- Atteia, J.L.; Boër, M. Observing the prompt emission of GRBs. C. R. Phys. 2011, 12, 255–266. [Google Scholar] [CrossRef]
- Gehrels, N.; Mészáros, P. Gamma-Ray Bursts. Science 2012, 337, 932. [Google Scholar] [CrossRef] [PubMed]
- Bucciantini, N. Magnetars and Gamma Ray Bursts. In Proceedings of the IAU Symposium: Death of Massive Stars: Supernovae and Gamma-Ray Bursts, Nikko, Japan, 12–16 March 2012; Volume 279, pp. 289–296. [Google Scholar] [CrossRef]
- Gehrels, N.; Razzaque, S. Gamma-ray bursts in the swift-Fermi era. Front. Phys. 2013, 8, 661–678. [Google Scholar] [CrossRef]
- Daigne, F. GRB Prompt Emission and the Physics of Ultra-Relativistic Outflows; EAS Publications Series; Castro-Tirado, A.J., Gorosabel, J., Park, I.H., Eds.; Cambridge University Press: Cambridge, UK, 2013; Volume 61, pp. 185–191. [Google Scholar] [CrossRef]
- Zhang, B. Gamma-Ray Burst Prompt Emission. Int. J. Mod. Phys. D 2014, 23, 30002. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-Ray Bursts. Annu. Rev. Astron. Astrophys. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Gamma-Ray Bursts. arXiv, 2014; arXiv:astro-ph.HE/1401.3012. [Google Scholar]
- Pe’er, A. Physics of Gamma-Ray Bursts Prompt Emission. Adv. Astron. 2015, 2015, 907321. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts and relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar] [CrossRef]
- Granot, J.; Piran, T.; Bromberg, O.; Racusin, J.L.; Daigne, F. Gamma-Ray Bursts as Sources of Strong Magnetic Fields. Space Sci. Rev. 2015, 191, 471–518. [Google Scholar] [CrossRef]
- Zhang, B.; Lü, H.J.; Liang, E.W. GRB Observational Properties. Space Sci. Rev. 2016, 202, 3–32. [Google Scholar] [CrossRef]
- Toma, K.; Yoon, S.C.; Bromm, V. Gamma-Ray Bursts and Population III Stars. Space Sci. Rev. 2016, 202, 159–180. [Google Scholar] [CrossRef]
- Pe’er, A.; Ryde, F. Photospheric emission in gamma-ray bursts. Int. J. Mod. Phys. D 2017, 26, 1730018–1730296. [Google Scholar] [CrossRef]
- Beloborodov, A.M.; Mészáros, P. Photospheric Emission of Gamma-Ray Bursts. Space Sci. Rev. 2017, 207, 87–110. [Google Scholar] [CrossRef]
- Dai, Z.; Daigne, F.; Mészáros, P. The Theory of Gamma-Ray Bursts. Space Sci. Rev. 2017, 212, 409–427. [Google Scholar] [CrossRef]
- van Eerten, H. Gamma-ray burst afterglow blast waves. Int. J. Mod. Phys. D 2018. [Google Scholar] [CrossRef]
- Nagataki, S. Theories of central engine for long gamma-ray bursts. Rep. Prog. Phys. 2018, 81, 026901. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169–1174. [Google Scholar] [CrossRef]
- Fermi, E. Galactic Magnetic Fields and the Origin of Cosmic Radiation. Astrophys. J. 1954, 119, 1. [Google Scholar] [CrossRef]
- Axford, W.I.; Leer, E.; Skadron, G. The acceleration of cosmic rays by shock waves. In Proceedings of the International Cosmic Ray Conference, Plovdiv, Bulgaria, 13–26 August 1977; Volume 11, pp. 132–137. [Google Scholar]
- Blandford, R.D.; Ostriker, J.P. Particle acceleration by astrophysical shocks. Astrophys. J. 1978, 221, L29–L32. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts. I. Mon. Notices R. Astron. Soc. 1978, 182, 147–156. [Google Scholar] [CrossRef]
- Blandford, R.; Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 1987, 154, 1–75. [Google Scholar] [CrossRef]
- Jones, F.C.; Ellison, D.C. The plasma physics of shock acceleration. Space Sci. Rev. 1991, 58, 259–346. [Google Scholar] [CrossRef]
- Malkov, M.A.; Drury, L.O. Nonlinear theory of diffusive acceleration of particles by shock waves. Rep. Prog. Phys. 2001, 64, 429–481. [Google Scholar] [CrossRef]
- Bell, A.R. Turbulent amplification of magnetic field and diffusive shock acceleration of cosmic rays. Mon. Notices R. Astron. Soc. 2004, 353, 550–558. [Google Scholar] [CrossRef]
- Longair, M.S. High Energy Astrophysics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Milgrom, M.; Usov, V. Possible Association of Ultra–High-Energy Cosmic-Ray Events with Strong Gamma-Ray Bursts. Astrophys. J. 1995, 449, L37. [Google Scholar] [CrossRef]
- Waxman, E. Cosmological Gamma-Ray Bursts and the Highest Energy Cosmic Rays. Phys. Rev. Lett. 1995, 75, 386–389. [Google Scholar] [CrossRef] [PubMed]
- Vietri, M. The Acceleration of Ultra–High-Energy Cosmic Rays in Gamma-Ray Bursts. Astrophys. J. 1995, 453, 883. [Google Scholar] [CrossRef]
- Samuelsson, F.; Bégué, D.; Ryde, F.; Pe’er, A. The Limited Contribution of Low- and High-Luminosity Gamma-Ray Bursts to Ultra-High Energy Cosmic Rays. arXiv, 2018; arXiv:astro-ph.HE/1810.06579. [Google Scholar]
- Ackermann, M.; Ajello, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; et al. Fermi-LAT Observations of the Gamma-Ray Burst GRB 130427A. Science 2014, 343, 42–47. [Google Scholar] [CrossRef]
- Tavani, M. A Shock Emission Model for Gamma-Ray Bursts. II. Spectral Properties. Astrophys. J. 1996, 466, 768. [Google Scholar] [CrossRef]
- Crider, A.; Liang, E.P.; Smith, I.A.; Preece, R.D.; Briggs, M.S.; Pendleton, G.N.; Paciesas, W.S.; Band, D.L.; Matteson, J.L. Evolution of the Low-Energy Photon Spectral in Gamma-Ray Bursts. Astrophys. J. 1997, 479, L39–L42. [Google Scholar] [CrossRef]
- Berger, E.; Kulkarni, S.R.; Frail, D.A. A Standard Kinetic Energy Reservoir in Gamma-Ray Burst Afterglows. Astrophys. J. 2003, 590, 379–385. [Google Scholar] [CrossRef]
- Sironi, L.; Keshet, U.; Lemoine, M. Relativistic Shocks: Particle Acceleration and Magnetization. Space Sci. Rev. 2015, 191, 519–544. [Google Scholar] [CrossRef]
- Kirk, J.G.; Heavens, A.F. Particle acceleration at oblique shock fronts. Mon. Notices R. Astron. Soc. 1989, 239, 995–1011. [Google Scholar] [CrossRef]
- Malkov, M.A. Analytic Solution for Nonlinear Shock Acceleration in the Bohm Limit. Astrophys. J. 1997, 485, 638–654. [Google Scholar] [CrossRef]
- Kirk, J.G.; Guthmann, A.W.; Gallant, Y.A.; Achterberg, A. Particle Acceleration at Ultrarelativistic Shocks: An Eigenfunction Method. Astrophys. J. 2000, 542, 235–242. [Google Scholar] [CrossRef]
- Caprioli, D.; Amato, E.; Blasi, P. Non-linear diffusive shock acceleration with free-escape boundary. Astropart. Phys. 2010, 33, 307–311. [Google Scholar] [CrossRef]
- Keshet, U.; Waxman, E. Energy Spectrum of Particles Accelerated in Relativistic Collisionless Shocks. Phys. Rev. Lett. 2005, 94, 111102. [Google Scholar] [CrossRef]
- Keshet, U. Analytic study of 1D diffusive relativistic shock acceleration. J. Cosmol. Astropart. Phys. 2017, 10, 025. [Google Scholar] [CrossRef]
- Kirk, J.G.; Schneider, P. Particle acceleration at shocks—A Monte Carlo method. Astrophys. J. 1987, 322, 256–265. [Google Scholar] [CrossRef]
- Ellison, D.C.; Reynolds, S.P.; Jones, F.C. First-order Fermi particle acceleration by relativistic shocks. Astrophys. J. 1990, 360, 702–714. [Google Scholar] [CrossRef]
- Achterberg, A.; Gallant, Y.A.; Kirk, J.G.; Guthmann, A.W. Particle acceleration by ultrarelativistic shocks: Theory and simulations. Mon. Notices R. Astron. Soc. 2001, 328, 393–408. [Google Scholar] [CrossRef]
- Lemoine, M.; Pelletier, G. Particle Transport in Tangled Magnetic Fields and Fermi Acceleration at Relativistic Shocks. Astrophys. J. 2003, 589, L73–L76. [Google Scholar] [CrossRef]
- Ellison, D.C.; Double, G.P. Diffusive shock acceleration in unmodified relativistic, oblique shocks. Astropart. Phys. 2004, 22, 323–338. [Google Scholar] [CrossRef]
- Summerlin, E.J.; Baring, M.G. Diffusive Acceleration of Particles at Oblique, Relativistic, Magnetohydrodynamic Shocks. Astrophys. J. 2012, 745, 63. [Google Scholar] [CrossRef]
- Ellison, D.C.; Warren, D.C.; Bykov, A.M. Monte Carlo Simulations of Nonlinear Particle Acceleration in Parallel Trans-relativistic Shocks. Astrophys. J. 2013, 776, 46. [Google Scholar] [CrossRef]
- Bykov, A.M.; Ellison, D.C.; Osipov, S.M. Nonlinear Monte Carlo model of superdiffusive shock acceleration with magnetic field amplification. Phys. Rev. E 2017, 95, 033207. [Google Scholar] [CrossRef]
- Riordan, J.D.; Pe’er, A. Pitch-Angle Diffusion and Bohm-type Approximations in Diffusive Shock Acceleration. arXiv, 2018; arXiv:astro-ph.HE/1810.11817. [Google Scholar]
- Silva, L.O.; Fonseca, R.A.; Tonge, J.W.; Dawson, J.M.; Mori, W.B.; Medvedev, M.V. Interpenetrating Plasma Shells: Near-equipartition Magnetic Field Generation and Nonthermal Particle Acceleration. Astrophys. J. 2003, 596, L121–L124. [Google Scholar] [CrossRef]
- Frederiksen, J.T.; Hededal, C.B.; Haugbølle, T.; Nordlund, Å. Magnetic Field Generation in Collisionless Shocks: Pattern Growth and Transport. Astrophys. J. 2004, 608, L13–L16. [Google Scholar] [CrossRef]
- Spitkovsky, A. Particle Acceleration in Relativistic Collisionless Shocks: Fermi Process at Last? Astrophys. J. 2008, 682, L5–L8. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Synthetic Spectra from Particle-In-Cell Simulations of Relativistic Collisionless Shocks. Astrophys. J. 2009, 707, L92–L96. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Frederiksen, J.T.; Nordlund, Å.; Mizuno, Y.; Hardee, P.E.; Niemiec, J.; Gómez, J.L.; Pe’er, A.; Duţan, I.; Meli, A.; et al. Evolution of Global Relativistic Jets: Collimations and Expansion with kKHI and the Weibel Instability. Astrophys. J. 2016, 820, 94. [Google Scholar] [CrossRef]
- Yost, S.A.; Harrison, F.A.; Sari, R.; Frail, D.A. A Study of the Afterglows of Four Gamma-Ray Bursts: Constraining the Explosion and Fireball Model. Astrophys. J. 2003, 597, 459–473. [Google Scholar] [CrossRef]
- Gompertz, B.P.; Fruchter, A.S.; Pe’er, A. The Environments of the Most Energetic Gamma-Ray Bursts. Astrophys. J. 2018, 866, 162. [Google Scholar] [CrossRef]
- Spruit, H.C.; Daigne, F.; Drenkhahn, G. Large scale magnetic fields and their dissipation in GRB fireballs. Astron. Astrophys. 2001, 369, 694–705. [Google Scholar] [CrossRef]
- Drenkhahn, G. Acceleration of GRB outflows by Poynting flux dissipation. Astron. Astrophys. 2002, 387, 714–724. [Google Scholar] [CrossRef]
- Drenkhahn, G.; Spruit, H.C. Efficient acceleration and radiation in Poynting flux powered GRB outflows. Astron. Astrophys. 2002, 391, 1141–1153. [Google Scholar] [CrossRef]
- Vlahakis, N.; Königl, A. Relativistic Magnetohydrodynamics with Application to Gamma-Ray Burst Outflows. I. Theory and Semianalytic Trans-Alfvénic Solutions. Astrophys. J. 2003, 596, 1080–1103. [Google Scholar] [CrossRef]
- Giannios, D. Spectra of black-hole binaries in the low/hard state: From radio to X-rays. Astron. Astrophys. 2005, 437, 1007–1015. [Google Scholar] [CrossRef]
- Giannios, D. Prompt emission spectra from the photosphere of a GRB. Astron. Astrophys. 2006, 457, 763–770. [Google Scholar] [CrossRef]
- Giannios, D.; Spruit, H.C. Spectra of Poynting-flux powered GRB outflows. Astron. Astrophys. 2005, 430, 1–7. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. GeV Emission from Collisional Magnetized Gamma-Ray Bursts. Astrophys. J. 2011, 733, L40. [Google Scholar] [CrossRef]
- Weibel, E.S. Spontaneously Growing Transverse Waves in a Plasma Due to an Anisotropic Velocity Distribution. Phys. Rev. Lett. 1959, 2, 83–84. [Google Scholar] [CrossRef]
- Medvedev, M.V.; Loeb, A. Generation of Magnetic Fields in the Relativistic Shock of Gamma-Ray Burst Sources. Astrophys. J. 1999, 526, 697–706. [Google Scholar] [CrossRef]
- Gruzinov, A.; Waxman, E. Gamma-Ray Burst Afterglow: Polarization and Analytic Light Curves. Astrophys. J. 1999, 511, 852–861. [Google Scholar] [CrossRef]
- Wiersma, J.; Achterberg, A. Magnetic field generation in relativistic shocks. An early end of the exponential Weibel instability in electron-proton plasmas. Astron. Astrophys. 2004, 428, 365–371. [Google Scholar] [CrossRef]
- Lyubarsky, Y.; Eichler, D. Are Gamma-Ray Burst Shocks Mediated by the Weibel Instability? Astrophys. J. 2006, 647, 1250–1254. [Google Scholar] [CrossRef]
- Achterberg, A.; Wiersma, J. The Weibel instability in relativistic plasmas. I. Linear theory. Astron. Astrophys. 2007, 475, 1–18. [Google Scholar] [CrossRef]
- Shaisultanov, R.; Lyubarsky, Y.; Eichler, D. Stream Instabilities in Relativistically Hot Plasma. Astrophys. J. 2012, 744, 182. [Google Scholar] [CrossRef]
- Kumar, R.; Eichler, D.; Gedalin, M. Electron Heating in a Relativistic, Weibel-unstable Plasma. Astrophys. J. 2015, 806, 165. [Google Scholar] [CrossRef]
- Bret, A.; Stockem Novo, A.; Narayan, R.; Ruyer, C.; Dieckmann, M.E.; Silva, L.O. Theory of the formation of a collisionless Weibel shock: Pair vs. electron/proton plasmas. Laser Part. Beams 2016, 34, 362–367. [Google Scholar] [CrossRef]
- Pelletier, G.; Bykov, A.; Ellison, D.; Lemoine, M. Towards Understanding the Physics of Collisionless Relativistic Shocks. Relativistic Collisionless Shocks. Space Sci. Rev. 2017, 207, 319–360. [Google Scholar] [CrossRef]
- Bret, A.; Pe’er, A. On the formation and properties of fluid shocks and collisionless shock waves in astrophysical plasmas. J. Plasma Phys. 2018, 84, 905840311. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Hardee, P.; Richardson, G.; Preece, R.; Sol, H.; Fishman, G.J. Particle Acceleration and Magnetic Field Generation in Electron-Positron Relativistic Shocks. Astrophys. J. 2005, 622, 927–937. [Google Scholar] [CrossRef]
- Kato, T.N. Saturation mechanism of the Weibel instability in weakly magnetized plasmas. Phys. Plasmas 2005, 12, 080705. [Google Scholar] [CrossRef]
- Ramirez-Ruiz, E.; Nishikawa, K.I.; Hededal, C.B. e+/− Pair Loading and the Origin of the Upstream Magnetic Field in GRB Shocks. Astrophys. J. 2007, 671, 1877–1885. [Google Scholar] [CrossRef]
- Spitkovsky, A. On the Structure of Relativistic Collisionless Shocks in Electron-Ion Plasmas. Astrophys. J. 2008, 673, L39–L42. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Niemiec, J.; Hardee, P.E.; Medvedev, M.; Sol, H.; Mizuno, Y.; Zhang, B.; Pohl, M.; Oka, M.; Hartmann, D.H. Weibel Instability and Associated Strong Fields in a Fully Three-Dimensional Simulation of a Relativistic Shock. Astrophys. J. 2009, 698, L10–L13. [Google Scholar] [CrossRef]
- Gruzinov, A. Gamma-Ray Burst Phenomenology, Shock Dynamo, and the First Magnetic Fields. Astrophys. J. 2001, 563, L15–L18. [Google Scholar] [CrossRef]
- Spitkovsky, A. Simulations of relativistic collisionless shocks: Shock structure and particle acceleration. In Astrophysical Sources of High Energy Particles and Radiation; American Institute of Physics Conference Series; Bulik, T., Rudak, B., Madejski, G., Eds.; American Institute of Physics: College Park, MD, USA, 2005; Volume 801, pp. 345–350. [Google Scholar] [CrossRef]
- Milosavljević, M.; Nakar, E. Weibel Filament Decay and Thermalization in Collisionless Shocks and Gamma-Ray Burst Afterglows. Astrophys. J. 2006, 641, 978–983. [Google Scholar] [CrossRef]
- Chang, P.; Spitkovsky, A.; Arons, J. Long-Term Evolution of Magnetic Turbulence in Relativistic Collisionless Shocks: Electron-Positron Plasmas. Astrophys. J. 2008, 674, 378–387. [Google Scholar] [CrossRef]
- Pe’er, A.; Zhang, B. Synchrotron Emission in Small-Scale Magnetic Fields as a Possible Explanation for Prompt Emission Spectra of Gamma-Ray Bursts. Astrophys. J. 2006, 653, 454–461. [Google Scholar] [CrossRef]
- Milosavljević, M.; Nakar, E. The Cosmic-Ray Precursor of Relativistic Collisionless Shocks: A Missing Link in Gamma-Ray Burst Afterglows. Astrophys. J. 2006, 651, 979–984. [Google Scholar] [CrossRef]
- Couch, S.M.; Milosavljević, M.; Nakar, E. Shock Vorticity Generation from Accelerated Ion Streaming in the Precursor of Ultrarelativistic Gamma-Ray Burst External Shocks. Astrophys. J. 2008, 688, 462–469. [Google Scholar] [CrossRef]
- Keshet, U.; Katz, B.; Spitkovsky, A.; Waxman, E. Magnetic Field Evolution in Relativistic Unmagnetized Collisionless Shocks. Astrophys. J. 2009, 693, L127–L130. [Google Scholar] [CrossRef]
- Sironi, L.; Goodman, J. Production of Magnetic Energy by Macroscopic Turbulence in GRB Afterglows. Astrophys. J. 2007, 671, 1858–1867. [Google Scholar] [CrossRef]
- Zhang, W.; MacFadyen, A.; Wang, P. Three-Dimensional Relativistic Magnetohydrodynamic Simulations of the Kelvin-Helmholtz Instability: Magnetic Field Amplification by a Turbulent Dynamo. Astrophys. J. 2009, 692, L40–L44. [Google Scholar] [CrossRef]
- Inoue, T.; Asano, K.; Ioka, K. Three-dimensional Simulations of Magnetohydrodynamic Turbulence Behind Relativistic Shock Waves and Their Implications for Gamma-Ray Bursts. Astrophys. J. 2011, 734, 77. [Google Scholar] [CrossRef]
- Mizuno, Y.; Pohl, M.; Niemiec, J.; Zhang, B.; Nishikawa, K.I.; Hardee, P.E. Magnetic-field Amplification by Turbulence in a Relativistic Shock Propagating Through an Inhomogeneous Medium. Astrophys. J. 2011, 726, 62. [Google Scholar] [CrossRef]
- Mizuno, Y.; Hardee, P.E.; Nishikawa, K.I. Spatial Growth of the Current-driven Instability in Relativistic Jets. Astrophys. J. 2014, 784, 167. [Google Scholar] [CrossRef]
- Mizuno, Y.; Pohl, M.; Niemiec, J.; Zhang, B.; Nishikawa, K.I.; Hardee, P.E. Magnetic field amplification and saturation in turbulence behind a relativistic shock. Mon. Notices R. Astron. Soc. 2014, 439, 3490–3503. [Google Scholar] [CrossRef]
- Nishikawa, K.I.; Mizuno, Y.; Gómez, J.; Duţan, I.; Meli, A.; White, C.; Niemiec, J.; Kobzar, O.; Pohl, M.; Pe’er, A.; et al. Microscopic Processes in Global Relativistic Jets Containing Helical Magnetic Fields: Dependence on Jet Radius. Galaxies 2017, 5, 58. [Google Scholar] [CrossRef]
- Ardaneh, K.; Cai, D.; Nishikawa, K.I. Collisionless Electron-ion Shocks in Relativistic Unmagnetized Jet-ambient Interactions: Non-thermal Electron Injection by Double Layer. Astrophys. J. 2016, 827, 124. [Google Scholar] [CrossRef]
- Piran, T. The physics of gamma-ray bursts. Rev. Mod. Phys. 2004, 76, 1143–1210. [Google Scholar] [CrossRef]
- Mészáros, P. Gamma-ray bursts. Rep. Prog. Phys. 2006, 69, 2259–2321. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Unsteady outflow models for cosmological gamma-ray bursts. Astrophys. J. 1994, 430, L93–L96. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Variability in Gamma-Ray Bursts: A Clue. Astrophys. J. 1997, 485, 270–273. [Google Scholar]
- Ramirez-Ruiz, E.; Fenimore, E.E. Pulse Width Evolution in Gamma-Ray Bursts: Evidence for Internal Shocks. Astrophys. J. 2000, 539, 712–717. [Google Scholar] [CrossRef]
- Kobayashi, S.; Piran, T.; Sari, R. Can Internal Shocks Produce the Variability in Gamma-Ray Bursts? Astrophys. J. 1997, 490, 92. [Google Scholar] [CrossRef]
- Mochkovitch, R.; Maitia, V.; Marques, R. Internal Shocks in a Relativistic Wind as a Source for Gamma-Ray Bursts? Astrophys. Space Sci. 1995, 231, 441–444. [Google Scholar] [CrossRef]
- Panaitescu, A.; Spada, M.; Mészáros, P. Power Density Spectra of Gamma-Ray Bursts in the Internal Shock Model. Astrophys. J. 1999, 522, L105–L108. [Google Scholar] [CrossRef]
- Beloborodov, A.M. On the Efficiency of Internal Shocks in Gamma-Ray Bursts. Astrophys. J. 2000, 539, L25–L28. [Google Scholar] [CrossRef]
- Spada, M.; Panaitescu, A.; Mészáros, P. Analysis of Temporal Features of Gamma-Ray Bursts in the Internal Shock Model. Astrophys. J. 2000, 537, 824–832. [Google Scholar] [CrossRef]
- Guetta, D.; Spada, M.; Waxman, E. Efficiency and Spectrum of Internal Gamma-Ray Burst Shocks. Astrophys. J. 2001, 557, 399–407. [Google Scholar] [CrossRef]
- Pe’er, A.; Long, K.; Casella, P. Dynamical Properties of Internal Shocks Revisited. Astrophys. J. 2017, 846, 54. [Google Scholar] [CrossRef]
- Kobayashi, S.; Sari, R. Ultraefficient Internal Shocks. Astrophys. J. 2001, 551, 934–939. [Google Scholar] [CrossRef]
- Preece, R.D.; Briggs, M.S.; Mallozzi, R.S.; Pendleton, G.N.; Paciesas, W.S.; Band, D.L. The Synchrotron Shock Model Confronts a “Line of Death” in the BATSE Gamma-Ray Burst Data. Astrophys. J. 1998, 506, L23–L26. [Google Scholar] [CrossRef]
- Preece, R.D.; Briggs, M.S.; Giblin, T.W.; Mallozzi, R.S.; Pendleton, G.N.; Paciesas, W.S.; Band, D.L. On the Consistency of Gamma-Ray Burst Spectral Indices with the Synchrotron Shock Model. Astrophys. J. 2002, 581, 1248–1255. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Celotti, A.; Ghisellini, G. Extremely hard GRB spectra prune down the forest of emission models. Astron. Astrophys. 2003, 406, 879–892. [Google Scholar] [CrossRef]
- Axelsson, M.; Borgonovo, L. The width of gamma-ray burst spectra. Mon. Notices R. Astron. Soc. 2015, 447, 3150–3154. [Google Scholar] [CrossRef]
- Woosley, S.E. Gamma-ray bursts from stellar mass accretion disks around black holes. Astrophys. J. 1993, 405, 273–277. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E. Collapsars: Gamma-Ray Bursts and Explosions in “Failed Supernovae”. Astrophys. J. 1999, 524, 262–289. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Notices R. Astron. Soc. 1977, 179, 433–456. [Google Scholar]
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Theory of extragalactic radio sources. Rev. Mod. Phys. 1984, 56, 255–351. [Google Scholar] [CrossRef]
- Wilson, A.S.; Colbert, E.J.M. The difference between radio-loud and radio-quiet active galaxies. Astrophys. J. 1995, 438, 62–71. [Google Scholar] [CrossRef]
- Narayan, R.; McKinney, J.C.; Farmer, A.J. Self-similar force-free wind from an accretion disc. Mon. Notices R. Astron. Soc. 2007, 375, 548–566. [Google Scholar] [CrossRef]
- Usov, V.V. Millisecond pulsars with extremely strong magnetic fields as a cosmological source of gamma-ray bursts. Nature 1992, 357, 472–474. [Google Scholar] [CrossRef]
- Thompson, C. A Model of Gamma-Ray Bursts. Mon. Notices R. Astron. Soc. 1994, 270, 480. [Google Scholar]
- Vlahakis, N.; Königl, A. Magnetohydrodynamics of Gamma-Ray Burst Outflows. Astrophys. J. 2001, 563, L129–L132. [Google Scholar] [CrossRef]
- Lyutikov, M.; Blandford, R. Gamma Ray Bursts as Electromagnetic Outflows. arXiv, 2003; arXiv:astro-ph/031234. [Google Scholar]
- Levinson, A. General Relativistic, Neutrino-assisted Magnetohydrodynamic Winds-Theory and Application to Gamma-Ray Bursts. I. Schwarzschild Geometry. Astrophys. J. 2006, 648, 510–522. [Google Scholar] [CrossRef]
- Giannios, D. Prompt GRB emission from gradual energy dissipation. Astron. Astrophys. 2008, 480, 305–312. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Vlahakis, N.; Königl, A.; Barkov, M.V. Magnetic acceleration of ultrarelativistic jets in gamma-ray burst sources. Mon. Notices R. Astron. Soc. 2009, 394, 1182–1212. [Google Scholar] [CrossRef]
- Beniamini, P.; Giannios, D. Prompt gamma-ray burst emission from gradual magnetic dissipation. Mon. Notices R. Astron. Soc. 2017, 468, 3202–3211. [Google Scholar] [CrossRef]
- Contopoulos, J. A Simple Type of Magnetically Driven Jets: An Astrophysical Plasma Gun. Astrophys. J. 1995, 450, 616. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; McKinney, J.C.; Narayan, R. Simulations of ultrarelativistic magnetodynamic jets from gamma-ray burst engines. Mon. Notices R. Astron. Soc. 2008, 388, 551–572. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Magnetohydrodynamic simulations of gamma-ray burst jets: Beyond the progenitor star. New A. 2010, 15, 749–754. [Google Scholar] [CrossRef]
- Komissarov, S.S.; Vlahakis, N.; Königl, A. Rarefaction acceleration of ultrarelativistic magnetized jets in gamma-ray burst sources. Mon. Notices R. Astron. Soc. 2010, 407, 17–28. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Notices R. Astron. Soc. 2011, 413, 2031–2056. [Google Scholar] [CrossRef]
- Granot, J.; Komissarov, S.S.; Spitkovsky, A. Impulsive acceleration of strongly magnetized relativistic flows. Mon. Notices R. Astron. Soc. 2011, 411, 1323–1353. [Google Scholar] [CrossRef]
- Zhang, B.; Yan, H. The Internal-collision-induced Magnetic Reconnection and Turbulence (ICMART) Model of Gamma-ray Bursts. Astrophys. J. 2011, 726, 90. [Google Scholar] [CrossRef]
- Sironi, L.; Petropoulou, M.; Giannios, D. Relativistic jets shine through shocks or magnetic reconnection? Mon. Notices R. Astron. Soc. 2015, 450, 183–191. [Google Scholar] [CrossRef]
- Kennel, C.F.; Coroniti, F.V. Confinement of the Crab pulsar’s wind by its supernova remnant. Astrophys. J. 1984, 283, 694–709. [Google Scholar] [CrossRef]
- Coroniti, F.V. Magnetically striped relativistic magnetohydrodynamic winds—The Crab Nebula revisited. Astrophys. J. 1990, 349, 538–545. [Google Scholar] [CrossRef]
- Bogovalov, S.V. On the physics of cold MHD winds from oblique rotators. Astron. Astrophys. 1999, 349, 1017–1026. [Google Scholar]
- Sironi, L.; Spitkovsky, A. Particle-in-cell simulations of shock-driven reconnection in relativistic striped winds. Comput. Sci. Discov. 2012, 5, 014014. [Google Scholar] [CrossRef]
- Lyubarsky, Y.; Kirk, J.G. Reconnection in a Striped Pulsar Wind. Astrophys. J. 2001, 547, 437–448. [Google Scholar] [CrossRef]
- Spruit, H.C.; Drenkhahn, G.D. Magnetically powered prompt radiation and flow acceleration in GRB. In Gamma-Ray Bursts in the Afterglow Era; Astronomical Society of the Pacific Conference Series; Feroci, M., Frontera, F., Masetti, N., Piro, L., Eds.; Societá Italiana de Fisica: Bologna, Spain, 2004; Volume 312, p. 357. [Google Scholar]
- Bégué, D.; Pe’er, A.; Lyubarsky, Y. Radiative striped wind model for gamma-ray bursts. Mon. Notices R. Astron. Soc. 2017, 467, 2594–2611. [Google Scholar] [CrossRef]
- Pe’er, A. Constraining Magnetization of Gamma-Ray Bursts Outflows Using Prompt Emission Fluence. Astrophys. J. 2017, 850, 200. [Google Scholar] [CrossRef]
- Lyubarskij, Y.E. Energy release in strongly magnetized relativistic winds. Soviet Astron. Lett. 1992, 18, 356. [Google Scholar]
- Begelman, M.C. Instability of Toroidal Magnetic Field in Jets and Plerions. Astrophys. J. 1998, 493, 291–300. [Google Scholar] [CrossRef]
- Giannios, D.; Spruit, H.C. The role of kink instability in Poynting-flux dominated jets. Astron. Astrophys. 2006, 450, 887–898. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J.; Lyubarsky, Y. 2D Relativistic MHD simulations of the Kruskal-Schwarzschild instability in a relativistic striped wind. Mon. Notices R. Astron. Soc. 2018, 474, 3535–3546. [Google Scholar] [CrossRef]
- Sobacchi, E.; Lyubarsky, Y.E. Instability induced by recollimation in highly magnetized outflows. Mon. Notices R. Astron. Soc. 2018, 480, 4948–4954. [Google Scholar] [CrossRef]
- Riquelme, M.A.; Quataert, E.; Sharma, P.; Spitkovsky, A. Local Two-dimensional Particle-in-cell Simulations of the Collisionless Magnetorotational Instability. Astrophys. J. 2012, 755, 50. [Google Scholar] [CrossRef]
- Melzani, M.; Walder, R.; Folini, D.; Winisdoerffer, C.; Favre, J.M. Relativistic magnetic reconnection in collisionless ion-electron plasmas explored with particle-in-cell simulations. Astron. Astrophys. 2014, 570, A111. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Y.H.; Daughton, W.; Li, H. Particle Acceleration and Plasma Dynamics during Magnetic Reconnection in the Magnetically Dominated Regime. Astrophys. J. 2015, 806, 167. [Google Scholar] [CrossRef]
- Bret, A.; Pe’er, A.; Sironi, L.; Sadowski, A.; Narayan, R. Kinetic inhibition of magnetohydrodynamics shocks in the vicinity of a parallel magnetic field. J. Plasma Phys. 2017, 83, 715830201. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A.; Arons, J. The Maximum Energy of Accelerated Particles in Relativistic Collisionless Shocks. arXiv, 2013; arXiv:astro-ph.HE/1301.5333. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Pair Shocks: Dependence of Shock Acceleration on Magnetic Obliquity. Astrophys. J. 2009, 698, 1523–1549. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Particle Acceleration in Relativistic Magnetized Collisionless Electron-Ion Shocks. Astrophys. J. 2011, 726, 75. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Amano, T.; Kato, T.N.; Hoshino, M. Electron Surfing and Drift Accelerations in a Weibel-Dominated High-Mach-Number Shock. Phys. Rev. Lett. 2017, 119, 105101. [Google Scholar] [CrossRef]
- Romanova, M.M.; Lovelace, R.V.E. Magnetic field, reconnection, and particle acceleration in extragalactic jets. Astron. Astrophys. 1992, 262, 26–36. [Google Scholar]
- Lyutikov, M. Role of reconnection in AGN jets. New Astron. Rev. 2003, 47, 513–515. [Google Scholar] [CrossRef]
- Jaroschek, C.H.; Treumann, R.A.; Lesch, H.; Scholer, M. Fast reconnection in relativistic pair plasmas: Analysis of particle acceleration in self-consistent full particle simulations. Phys. Plasmas 2004, 11, 1151–1163. [Google Scholar] [CrossRef]
- Lyubarsky, Y.E. On the relativistic magnetic reconnection. Mon. Notices R. Astron. Soc. 2005, 358, 113–119. [Google Scholar] [CrossRef]
- Giannios, D. UHECRs from magnetic reconnection in relativistic jets. Mon. Notices R. Astron. Soc. 2010, 408, L46–L50. [Google Scholar] [CrossRef]
- Lazarian, A.; Kowal, G.; Vishniac, E.; de Gouveia Dal Pino, E. Fast magnetic reconnection and energetic particle acceleration. Planet. Space Sci. 2011, 59, 537–546. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Yin, L.; Albright, B.J.; Bowers, K.J.; Liang, E.P. Particle energization in 3D magnetic reconnection of relativistic pair plasmas. Phys. Plasmas 2011, 18, 052105. [Google Scholar] [CrossRef]
- Uzdensky, D.A.; McKinney, J.C. Magnetic reconnection with radiative cooling. I. Optically thin regime. Phys. Plasmas 2011, 18, 042105. [Google Scholar] [CrossRef]
- McKinney, J.C.; Uzdensky, D.A. A reconnection switch to trigger gamma-ray burst jet dissipation. Mon. Notices R. Astron. Soc. 2012, 419, 573–607. [Google Scholar] [CrossRef]
- Bessho, N.; Bhattacharjee, A. Fast Magnetic Reconnection and Particle Acceleration in Relativistic Low-density Electron-Positron Plasmas without Guide Field. Astrophys. J. 2012, 750, 129. [Google Scholar] [CrossRef]
- Cerutti, B.; Werner, G.R.; Uzdensky, D.A.; Begelman, M.C. Beaming and Rapid Variability of High-energy Radiation from Relativistic Pair Plasma Reconnection. Astrophys. J. 2012, 754, L33. [Google Scholar] [CrossRef]
- Cerutti, B.; Werner, G.R.; Uzdensky, D.A.; Begelman, M.C. Simulations of Particle Acceleration beyond the Classical Synchrotron Burnoff Limit in Magnetic Reconnection: An Explanation of the Crab Flares. Astrophys. J. 2013, 770, 147. [Google Scholar] [CrossRef]
- Kagan, D.; Milosavljević, M.; Spitkovsky, A. A Flux Rope Network and Particle Acceleration in Three-dimensional Relativistic Magnetic Reconnection. Astrophys. J. 2013, 774, 41. [Google Scholar] [CrossRef]
- Uzdensky, D.A.; Spitkovsky, A. Physical Conditions in the Reconnection Layer in Pulsar Magnetospheres. Astrophys. J. 2014, 780, 3. [Google Scholar] [CrossRef]
- Kagan, D.; Sironi, L.; Cerutti, B.; Giannios, D. Relativistic Magnetic Reconnection in Pair Plasmas and Its Astrophysical Applications. Space Sci. Rev. 2015, 191, 545–573. [Google Scholar] [CrossRef]
- Sironi, L.; Spitkovsky, A. Relativistic Reconnection: An Efficient Source of Non-thermal Particles. Astrophys. J. 2014, 783, L21. [Google Scholar] [CrossRef]
- Zenitani, S.; Hoshino, M. The Generation of Nonthermal Particles in the Relativistic Magnetic Reconnection of Pair Plasmas. Astrophys. J. 2001, 562, L63–L66. [Google Scholar] [CrossRef]
- Bessho, N.; Bhattacharjee, A. Collisionless Reconnection in an Electron-Positron Plasma. Phys. Rev. Lett. 2005, 95, 245001. [Google Scholar] [CrossRef] [PubMed]
- Zenitani, S.; Hoshino, M. Particle Acceleration and Magnetic Dissipation in Relativistic Current Sheet of Pair Plasmas. Astrophys. J. 2007, 670, 702–726. [Google Scholar] [CrossRef]
- Hesse, M.; Zenitani, S. Dissipation in relativistic pair-plasma reconnection. Phys. Plasmas 2007, 14, 112102. [Google Scholar] [CrossRef]
- Lyubarsky, Y.; Liverts, M. Particle Acceleration in the Driven Relativistic Reconnection. Astrophys. J. 2008, 682, 1436–1442. [Google Scholar] [CrossRef]
- Guo, F.; Li, H.; Daughton, W.; Liu, Y.H. Formation of Hard Power Laws in the Energetic Particle Spectra Resulting from Relativistic Magnetic Reconnection. Phys. Rev. Lett. 2014, 113, 155005. [Google Scholar] [CrossRef] [PubMed]
- Nalewajko, K.; Uzdensky, D.A.; Cerutti, B.; Werner, G.R.; Begelman, M.C. On the Distribution of Particle Acceleration Sites in Plasmoid-dominated Relativistic Magnetic Reconnection. Astrophys. J. 2015, 815, 101. [Google Scholar] [CrossRef]
- Werner, G.R.; Uzdensky, D.A.; Cerutti, B.; Nalewajko, K.; Begelman, M.C. The Extent of Power-law Energy Spectra in Collisionless Relativistic Magnetic Reconnection in Pair Plasmas. Astrophys. J. 2016, 816, L8. [Google Scholar] [CrossRef]
- Sironi, L.; Giannios, D.; Petropoulou, M. Plasmoids in relativistic reconnection, from birth to adulthood: First they grow, then they go. Mon. Notices R. Astron. Soc. 2016, 462, 48–74. [Google Scholar] [CrossRef]
- Zenitani, S.; Hoshino, M. The Role of the Guide Field in Relativistic Pair Plasma Reconnection. Astrophys. J. 2008, 677, 530–544. [Google Scholar] [CrossRef]
- Yin, L.; Daughton, W.; Karimabadi, H.; Albright, B.J.; Bowers, K.J.; Margulies, J. Three-Dimensional Dynamics of Collisionless Magnetic Reconnection in Large-Scale Pair Plasmas. Phys. Rev. Lett. 2008, 101, 125001. [Google Scholar] [CrossRef] [PubMed]
- Cerutti, B.; Werner, G.R.; Uzdensky, D.A.; Begelman, M.C. Three-dimensional Relativistic Pair Plasma Reconnection with Radiative Feedback in the Crab Nebula. Astrophys. J. 2014, 782, 104. [Google Scholar] [CrossRef]
- Werner, G.R.; Uzdensky, D.A. Nonthermal Particle Acceleration in 3D Relativistic Magnetic Reconnection in Pair Plasma. Astrophys. J. 2017, 843, L27. [Google Scholar] [CrossRef]
- Petropoulou, M.; Sironi, L. The steady growth of the high-energy spectral cut-off in relativistic magnetic reconnection. Mon. Notices R. Astron. Soc. 2018, 481, 5687–5701. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Syrovatskii, S.I. Cosmic Magnetobremsstrahlung (synchrotron Radiation). Annu. Rev. Astron. Astrophys. 1965, 3, 297. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Gould, R.J. Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases. Rev. Mod. Phys. 1970, 42, 237–271. [Google Scholar] [CrossRef]
- Rees, M.J.; Meszaros, P. Relativistic fireballs—Energy conversion and time-scales. Mon. Notices R. Astron. Soc. 1992, 258, 41–43. [Google Scholar]
- Meszaros, P.; Rees, M.J. Relativistic fireballs and their impact on external matter—Models for cosmological gamma-ray bursts. Astrophys. J. 1993, 405, 278–284. [Google Scholar] [CrossRef]
- Meszaros, P.; Laguna, P.; Rees, M.J. Gasdynamics of relativistically expanding gamma-ray burst sources—Kinematics, energetics, magnetic fields, and efficiency. Astrophys. J. 1993, 415, 181–190. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J.; Papathanassiou, H. Spectral properties of blast-wave models of gamma-ray burst sources. Astrophys. J. 1994, 432, 181–193. [Google Scholar] [CrossRef]
- Paczynski, B.; Xu, G. Neutrino bursts from gamma-ray bursts. Astrophys. J. 1994, 427, 708–713. [Google Scholar] [CrossRef]
- Papathanassiou, H.; Meszaros, P. Spectra of Unsteady Wind Models of Gamma-Ray Bursts. Astrophys. J. 1996, 471, L91. [Google Scholar] [CrossRef]
- Cohen, E.; Katz, J.I.; Piran, T.; Sari, R.; Preece, R.D.; Band, D.L. Possible Evidence for Relativistic Shocks in Gamma-Ray Bursts. Astrophys. J. 1997, 488, 330. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Cosmological gamma-ray bursts: Internal versus external shocks. Mon. Notices R. Astron. Soc. 1997, 287, 110–116. [Google Scholar]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 497, L17. [Google Scholar] [CrossRef]
- Pilla, R.P.; Loeb, A. Emission Spectra from Internal Shocks in Gamma-Ray Burst Sources. Astrophys. J. 1998, 494, L167–L171. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. Gamma-ray bursts from internal shocks in a relativistic wind: Temporal and spectral properties. Mon. Notices R. Astron. Soc. 1998, 296, 275–286. [Google Scholar] [CrossRef]
- Granot, J.; Sari, R. The Shape of Spectral Breaks in Gamma-Ray Burst Afterglows. Astrophys. J. 2002, 568, 820–829. [Google Scholar] [CrossRef]
- Gao, H.; Lei, W.H.; Zou, Y.C.; Wu, X.F.; Zhang, B. A complete reference of the analytical synchrotron external shock models of gamma-ray bursts. New Astron. Rev. 2013, 57, 141–190. [Google Scholar] [CrossRef]
- Pe’er, A.; Waxman, E. Prompt Gamma-Ray Burst Spectra: Detailed Calculations and the Effect of Pair Production. Astrophys. J. 2004, 613, 448–459. [Google Scholar] [CrossRef]
- Baring, M.G.; Braby, M.L. A Study of Prompt Emission Mechanisms in Gamma-Ray Bursts. Astrophys. J. 2004, 613, 460–476. [Google Scholar] [CrossRef]
- Gupta, N.; Zhang, B. Prompt emission of high-energy photons from gamma ray bursts. Mon. Notices R. Astron. Soc. 2007, 380, 78–92. [Google Scholar] [CrossRef]
- Asano, K.; Inoue, S. Prompt GeV-TeV Emission of Gamma-Ray Bursts Due to High-Energy Protons, Muons, and Electron-Positron Pairs. Astrophys. J. 2007, 671, 645–655. [Google Scholar] [CrossRef]
- Sari, R.; Esin, A.A. On the Synchrotron Self-Compton Emission from Relativistic Shocks and Its Implications for Gamma-Ray Burst Afterglows. Astrophys. J. 2001, 548, 787–799. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. High-Energy Spectral Components in Gamma-Ray Burst Afterglows. Astrophys. J. 2001, 559, 110–122. [Google Scholar] [CrossRef]
- Harrison, F.A.; Yost, S.A.; Sari, R.; Berger, E.; Galama, T.J.; Holtzman, J.; Axelrod, T.; Bloom, J.S.; Chevalier, R.; Costa, E.; et al. Broadband Observations of the Afterglow of GRB 000926: Observing the Effect of Inverse Compton Scattering. Astrophys. J. 2001, 559, 123–130. [Google Scholar] [CrossRef]
- Galli, A.; Piro, L. High energy afterglows and flares from gamma-ray burst by inverse Compton emission. Astron. Astrophys. 2007, 475, 421–434. [Google Scholar] [CrossRef]
- Fan, Y.Z.; Piran, T.; Narayan, R.; Wei, D.M. High-energy afterglow emission from gamma-ray bursts. Mon. Notices R. Astron. Soc. 2008, 384, 1483–1501. [Google Scholar] [CrossRef]
- Fraija, N.; González, M.M.; Lee, W.H. Synchrotron Self-Compton Emission as the Origin of the Gamma-Ray Afterglow Observed in GRB 980923. Astrophys. J. 2012, 751, 33. [Google Scholar] [CrossRef]
- Pe’er, A.; Waxman, E. Time-dependent Numerical Model for the Emission of Radiation from Relativistic Plasma. Astrophys. J. 2005, 628, 857–866. [Google Scholar] [CrossRef]
- Gill, R.; Granot, J. The effect of pair cascades on the high-energy spectral cut-off in gamma-ray bursts. Mon. Notices R. Astron. Soc. 2018, 475, L1–L5. [Google Scholar] [CrossRef]
- Böttcher, M.; Dermer, C.D. High-energy Gamma Rays from Ultra-high-energy Cosmic-Ray Protons in Gamma-Ray Bursts. Astrophys. J. 1998, 499, L131–L134. [Google Scholar] [CrossRef]
- Totani, T. TEV Burst of Gamma-Ray Bursts and Ultra-High-Energy Cosmic Rays. Astrophys. J. 1998, 509, L81–L84. [Google Scholar] [CrossRef]
- Asano, K.; Inoue, S.; Mészáros, P. Prompt High-Energy Emission from Proton-Dominated Gamma-Ray Bursts. Astrophys. J. 2009, 699, 953–957. [Google Scholar] [CrossRef]
- Razzaque, S.; Dermer, C.D.; Finke, J.D. Synchrotron Radiation from Ultra-High Energy Protons and the Fermi Observations of GRB 080916C. Open Astron. J. 2010, 3, 150–155. [Google Scholar] [CrossRef]
- Asano, K.; Mészáros, P. Delayed Onset of High-energy Emissions in Leptonic and Hadronic Models of Gamma-Ray Bursts. Astrophys. J. 2012, 757, 115. [Google Scholar] [CrossRef]
- Crumley, P.; Kumar, P. Hadronic models for Large Area Telescope prompt emission observed in Fermi gamma-ray bursts. Mon. Notices R. Astron. Soc. 2013, 429, 3238–3251. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. 1986, 308, L43–L46. [Google Scholar] [CrossRef]
- Goodman, J. Are gamma-ray bursts optically thick? Astrophys. J. 1986, 308, L47–L50. [Google Scholar] [CrossRef]
- Shemi, A.; Piran, T. The appearance of cosmic fireballs. Astrophys. J. 1990, 365, L55–L58. [Google Scholar] [CrossRef]
- Burgess, J.M.; Bégué, D.; Bacelj, A.; Giannios, D.; Berlato, F.; Greiner, J. Gamma-ray bursts as cool synchrotron sources. arXiv, 2018; arXiv:astro-ph.HE/1810.06965. [Google Scholar]
- Ryde, F. The Cooling Behavior of Thermal Pulses in Gamma-Ray Bursts. Astrophys. J. 2004, 614, 827–846. [Google Scholar] [CrossRef]
- Ryde, F. Is Thermal Emission in Gamma-Ray Bursts Ubiquitous? Astrophys. J. 2005, 625, L95–L98. [Google Scholar] [CrossRef]
- Ryde, F.; Pe’er, A. Quasi-blackbody Component and Radiative Efficiency of the Prompt Emission of Gamma-ray Bursts. Astrophys. J. 2009, 702, 1211–1229. [Google Scholar] [CrossRef]
- McGlynn, S.; Foley, S.; McBreen, B.; Hanlon, L.; McBreen, S.; Clark, D.J.; Dean, A.J.; Martin-Carrillo, A.; O’Connor, R. High energy emission and polarisation limits for the INTEGRAL burst GRB 061122. Astron. Astrophys. 2009, 499, 465–472. [Google Scholar] [CrossRef]
- Larsson, J.; Ryde, F.; Lundman, C.; McGlynn, S.; Larsson, S.; Ohno, M.; Yamaoka, K. Spectral components in the bright, long GRB 061007: Properties of the photosphere and the nature of the outflow. Mon. Notices R. Astron. Soc. 2011, 414, 2642–2649. [Google Scholar] [CrossRef]
- Ackermann, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.; et al. Fermi Observations of GRB 090510: A Short-Hard Gamma-ray Burst with an Additional, Hard Power-law Component from 10 keV TO GeV Energies. Astrophys. J. 2010, 716, 1178–1190. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; et al. Fermi Observations of GRB 090902B: A Distinct Spectral Component in the Prompt and Delayed Emission. Astrophys. J. 2009, 706, L138–L144. [Google Scholar] [CrossRef]
- Ryde, F.; Axelsson, M.; Zhang, B.B.; McGlynn, S.; Pe’er, A.; Lundman, C.; Larsson, S.; Battelino, M.; Zhang, B.; Bissaldi, E.; et al. Identification and Properties of the Photospheric Emission in GRB090902B. Astrophys. J. 2010, 709, L172–L177. [Google Scholar] [CrossRef]
- Ryde, F.; Pe’er, A.; Nymark, T.; Axelsson, M.; Moretti, E.; Lundman, C.; Battelino, M.; Bissaldi, E.; Chiang, J.; Jackson, M.S.; et al. Observational evidence of dissipative photospheres in gamma-ray bursts. Mon. Notices R. Astron. Soc. 2011, 415, 3693–3705. [Google Scholar] [CrossRef]
- Guiriec, S.; Connaughton, V.; Briggs, M.S.; Burgess, M.; Ryde, F.; Daigne, F.; Mészáros, P.; Goldstein, A.; McEnery, J.; Omodei, N.; et al. Detection of a Thermal Spectral Component in the Prompt Emission of GRB 100724B. Astrophys. J. 2011, 727, L33. [Google Scholar] [CrossRef]
- Iyyani, S.; Ryde, F.; Axelsson, M.; Burgess, J.M.; Guiriec, S.; Larsson, J.; Lundman, C.; Moretti, E.; McGlynn, S.; Nymark, T.; Rosquist, K. Variable jet properties in GRB 110721A: Time resolved observations of the jet photosphere. Mon. Notices R. Astron. Soc. 2013, 433, 2739–2748. [Google Scholar] [CrossRef]
- Guiriec, S.; Daigne, F.; Hascoët, R.; Vianello, G.; Ryde, F.; Mochkovitch, R.; Kouveliotou, C.; Xiong, S.; Bhat, P.N.; Foley, S.; et al. Evidence for a Photospheric Component in the Prompt Emission of the Short GRB 120323A and Its Effects on the GRB Hardness-Luminosity Relation. Astrophys. J. 2013, 770, 32. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Steep Slopes and Preferred Breaks in Gamma-Ray Burst Spectra: The Role of Photospheres and Comptonization. Astrophys. J. 2000, 530, 292–298. [Google Scholar] [CrossRef]
- Mészáros, P.; Ramirez-Ruiz, E.; Rees, M.J.; Zhang, B. X-ray-rich Gamma-Ray Bursts, Photospheres, and Variability. Astrophys. J. 2002, 578, 812–817. [Google Scholar] [CrossRef]
- Pe’er, A.; Mészáros, P.; Rees, M.J. Peak Energy Clustering and Efficiency in Compact Objects. Astrophys. J. 2005, 635, 476–480. [Google Scholar] [CrossRef]
- Pe’er, A.; Mészáros, P.; Rees, M.J. The Observable Effects of a Photospheric Component on GRB and XRF Prompt Emission Spectrum. Astrophys. J. 2006, 642, 995–1003. [Google Scholar] [CrossRef]
- Ioka, K.; Murase, K.; Toma, K.; Nagataki, S.; Nakamura, T. Unstable GRB Photospheres and e+/− Annihilation Lines. Astrophys. J. 2007, 670, L77–L80. [Google Scholar] [CrossRef]
- Thompson, C.; Mészáros, P.; Rees, M.J. Thermalization in Relativistic Outflows and the Correlation between Spectral Hardness and Apparent Luminosity in Gamma-Ray Bursts. Astrophys. J. 2007, 666, 1012–1023. [Google Scholar] [CrossRef]
- Lazzati, D.; Morsony, B.J.; Begelman, M.C. Very High Efficiency Photospheric Emission in Long-Duration γ-Ray Bursts. Astrophys. J. 2009, 700, L47–L50. [Google Scholar] [CrossRef]
- Lazzati, D.; Begelman, M.C. Non-thermal Emission from the Photospheres of Gamma-ray Burst Outflows. I. High-Frequency Tails. Astrophys. J. 2010, 725, 1137–1145. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Collisional mechanism for gamma-ray burst emission. Mon. Notices R. Astron. Soc. 2010, 407, 1033–1047. [Google Scholar] [CrossRef]
- Mizuta, A.; Nagataki, S.; Aoi, J. Thermal Radiation from Gamma-ray Burst Jets. Astrophys. J. 2011, 732, 26. [Google Scholar] [CrossRef]
- Lazzati, D.; Morsony, B.J.; Begelman, M.C. High-efficiency Photospheric Emission of Long-duration Gamma-ray Burst Jets: The Effect of the Viewing Angle. Astrophys. J. 2011, 732, 34. [Google Scholar] [CrossRef]
- Toma, K.; Wu, X.F.; Mészáros, P. Photosphere-internal shock model of gamma-ray bursts: Case studies of Fermi/LAT bursts. Mon. Notices R. Astron. Soc. 2011, 415, 1663–1680. [Google Scholar] [CrossRef]
- Bromberg, O.; Mikolitzky, Z.; Levinson, A. Sub-photospheric Emission from Relativistic Radiation Mediated Shocks in GRBs. Astrophys. J. 2011, 733, 85. [Google Scholar] [CrossRef]
- Levinson, A. Observational Signatures of Sub-photospheric Radiation-mediated Shocks in the Prompt Phase of Gamma-Ray Bursts. Astrophys. J. 2012, 756, 174. [Google Scholar] [CrossRef]
- Veres, P.; Zhang, B.B.; Mészáros, P. The Extremely High Peak Energy of GRB 110721A in the Context of a Dissipative Photosphere Synchrotron Emission Model. Astrophys. J. 2012, 761, L18. [Google Scholar] [CrossRef]
- Vurm, I.; Lyubarsky, Y.; Piran, T. On Thermalization in Gamma-Ray Burst Jets and the Peak Energies of Photospheric Spectra. Astrophys. J. 2013, 764, 143. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Regulation of the Spectral Peak in Gamma-Ray Bursts. Astrophys. J. 2013, 764, 157. [Google Scholar] [CrossRef]
- Hascoët, R.; Daigne, F.; Mochkovitch, R. Prompt thermal emission in gamma-ray bursts. Astron. Astrophys. 2013, 551, A124. [Google Scholar] [CrossRef]
- Lazzati, D.; Morsony, B.J.; Margutti, R.; Begelman, M.C. Photospheric Emission as the Dominant Radiation Mechanism in Long-duration Gamma-Ray Bursts. Astrophys. J. 2013, 765, 103. [Google Scholar] [CrossRef]
- Asano, K.; Mészáros, P. Photon and neutrino spectra of time-dependent photospheric models of gamma-ray bursts. J. Cosmol. Astropart. Phys. 2013, 9, 8. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, B. Low Energy Spectral Index and Ep Evolution of Quasi-thermal Photosphere Emission of Gamma-Ray Bursts. Astrophys. J. 2014, 785, 112. [Google Scholar] [CrossRef]
- Cuesta-Martínez, C.; Aloy, M.A.; Mimica, P.; Thöne, C.; de Ugarte Postigo, A. Numerical models of blackbody-dominated gamma-ray bursts—II. Emission properties. Mon. Notices R. Astron. Soc. 2015, 446, 1737–1749. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Sub-photospheric Shocks in Relativistic Explosions. Astrophys. J. 2017, 838, 125. [Google Scholar] [CrossRef]
- Lundman, C.; Beloborodov, A.M.; Vurm, I. Radiation-mediated Shocks in Gamma-Ray Bursts: Pair Creation. Astrophys. J. 2018, 858, 7. [Google Scholar] [CrossRef]
- Lundman, C.; Beloborodov, A. Radiation mediated shocks in gamma-ray bursts: Subshock photon production. arXiv, 2018; arXiv:astro-ph.HE/1804.03053. [Google Scholar]
- Zrake, J.; Beloborodov, A.M.; Lundman, C. Sub-photospheric turbulence as a heating mechanism in gamma-ray bursts. arXiv, 2018; arXiv:astro-ph.HE/1810.02228. [Google Scholar]
- Pe’er, A. Temporal Evolution of Thermal Emission from Relativistically Expanding Plasma. Astrophys. J. 2008, 682, 463–473. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Radiative Transfer in Ultrarelativistic Outflows. Astrophys. J. 2011, 737, 68. [Google Scholar] [CrossRef]
- Pe’er, A.; Ryde, F. A Theory of Multicolor Blackbody Emission from Relativistically Expanding Plasmas. Astrophys. J. 2011, 732, 49. [Google Scholar] [CrossRef]
- Lundman, C.; Pe’er, A.; Ryde, F. A theory of photospheric emission from relativistic, collimated outflows. Mon. Notices R. Astron. Soc. 2013, 428, 2430–2442. [Google Scholar] [CrossRef]
- Ruffini, R.; Siutsou, I.A.; Vereshchagin, G.V. A Theory of Photospheric Emission from Relativistic Outflows. Astrophys. J. 2013, 772, 11. [Google Scholar] [CrossRef]
- Aksenov, A.G.; Ruffini, R.; Vereshchagin, G.V. Comptonization of photons near the photosphere of relativistic outflows. Mon. Notices R. Astron. Soc. 2013, 436, L54–L58. [Google Scholar] [CrossRef]
- Ito, H.; Nagataki, S.; Ono, M.; Lee, S.H.; Mao, J.; Yamada, S.; Pe’er, A.; Mizuta, A.; Harikae, S. Photospheric Emission from Stratified Jets. Astrophys. J. 2013, 777, 62. [Google Scholar] [CrossRef]
- Vereshchagin, G.V. Physics of Nondissipative Ultrarelativistic Photospheres. Int. J. Mod. Phys. D 2014, 23, 30003. [Google Scholar] [CrossRef]
- Lundman, C.; Pe’er, A.; Ryde, F. Polarization properties of photospheric emission from relativistic, collimated outflows. Mon. Notices R. Astron. Soc. 2014, 440, 3292–3308. [Google Scholar] [CrossRef]
- Chang, Z.; Lin, H.N.; Jiang, Y. Gamma-Ray Burst Polarization via Compton Scattering Process. Astrophys. J. 2014, 783, 30. [Google Scholar] [CrossRef]
- Pe’er, A.; Ryde, F.; Wijers, R.A.M.J.; Mészáros, P.; Rees, M.J. A New Method of Determining the Initial Size and Lorentz Factor of Gamma-Ray Burst Fireballs Using a Thermal Emission Component. Astrophys. J. 2007, 664, L1–L4. [Google Scholar] [CrossRef]
- Larsson, J.; Racusin, J.L.; Burgess, J.M. Evidence for Jet Launching Close to the Black Hole in GRB 101219b—A Fermi GRB Dominated by Thermal Emission. Astrophys. J. 2015, 800, L34. [Google Scholar] [CrossRef]
- Pe’er, A.; Barlow, H.; O’Mahony, S.; Margutti, R.; Ryde, F.; Larsson, J.; Lazzati, D.; Livio, M. Hydrodynamic Properties of Gamma-Ray Burst Outflows Deduced from the Thermal Component. Astrophys. J. 2015, 813, 127. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Wang, H.; Zhang, S.; Liang, Y.F.; Jin, Z.P.; He, H.N.; Liao, N.H.; Fan, Y.Z.; Wei, D.M. Evaluating the Bulk Lorentz Factors of Outflow Material: Lessons Learned from the Extremely Energetic Outburst GRB 160625B. Astrophys. J. 2017, 836, 81. [Google Scholar] [CrossRef]
- Zhang, B.; Mészáros, P. An Analysis of Gamma-Ray Burst Spectral Break Models. Astrophys. J. 2002, 581, 1236–1247. [Google Scholar] [CrossRef]
- Daigne, F.; Mochkovitch, R. The expected thermal precursors of gamma-ray bursts in the internal shock model. Mon. Notices R. Astron. Soc. 2002, 336, 1271–1280. [Google Scholar] [CrossRef]
- Zhang, B.; Pe’er, A. Evidence of an Initially Magnetically Dominated Outflow in GRB 080916C. Astrophys. J. 2009, 700, L65–L68. [Google Scholar] [CrossRef]
- Beniamini, P.; Piran, T. The emission mechanism in magnetically dominated gamma-ray burst outflows. Mon. Notices R. Astron. Soc. 2014, 445, 3892–3907. [Google Scholar] [CrossRef]
- Bégué, D.; Pe’er, A. Poynting-flux-dominated Jets Challenged by their Photospheric Emission. Astrophys. J. 2015, 802, 134. [Google Scholar] [CrossRef]
- Meng, Y.Z.; Geng, J.J.; Zhang, B.B.; Wei, J.J.; Xiao, D.; Liu, L.D.; Gao, H.; Wu, X.F.; Liang, E.W.; Huang, Y.F.; Dai, Z.G.; Zhang, B. The Origin of the Prompt Emission for Short GRB 170817A: Photosphere Emission or Synchrotron Emission? Astrophys. J. 2018, 860, 72. [Google Scholar] [CrossRef]
- Paczyński, B. Are Gamma-Ray Bursts in Star-Forming Regions? Astrophys. J. 1998, 494, L45–L48. [Google Scholar] [CrossRef]
- Paczyński, B. Gamma-ray bursts as hypernovae. In Gamma-Ray Bursts, Proceedings of the 4th Hunstville Symposium; Meegan, C.A., Preece, R.D., Koshut, T.M., Eds.; American Institute of Physics: College Park, MD, USA, 1998; Volume 428, pp. 783–787. [Google Scholar] [CrossRef]
- Fryer, C.L.; Woosley, S.E.; Hartmann, D.H. Formation Rates of Black Hole Accretion Disk Gamma-Ray Bursts. Astrophys. J. 1999, 526, 152–177. [Google Scholar] [CrossRef]
- Popham, R.; Woosley, S.E.; Fryer, C. Hyperaccreting Black Holes and Gamma-Ray Bursts. Astrophys. J. 1999, 518, 356–374. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E.; Heger, A. Supernovae, Jets, and Collapsars. Astrophys. J. 2001, 550, 410–425. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Sobacchi, E.; Granot, J.; Bromberg, O.; Sormani, M.C. A common central engine for long gamma-ray bursts and Type Ib/c supernovae. Mon. Notices R. Astron. Soc. 2017, 472, 616–627. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and gamma-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Paczynski, B. Super-Eddington winds from neutron stars. Astrophys. J. 1990, 363, 218–226. [Google Scholar] [CrossRef]
- Narayan, R.; Piran, T.; Shemi, A. Neutron star and black hole binaries in the Galaxy. Astrophys. J. 1991, 379, L17–L20. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Tidal heating and mass loss in neutron star binaries—Implications for gamma-ray burst models. Astrophys. J. 1992, 397, 570–575. [Google Scholar] [CrossRef]
- Narayan, R.; Paczynski, B.; Piran, T. Gamma-ray bursts as the death throes of massive binary stars. Astrophys. J. 1992, 395, L83–L86. [Google Scholar] [CrossRef]
- Hjorth, J.; Sollerman, J.; Møller, P.; Fynbo, J.P.U.; Woosley, S.E.; Kouveliotou, C.; Tanvir, N.R.; Greiner, J.; Andersen, M.I.; Castro-Tirado, A.J.; et al. A very energetic supernova associated with the γ-ray burst of 29 March 2003. Nature 2003, 423, 847–850. [Google Scholar] [CrossRef]
- Stanek, K.Z.; Matheson, T.; Garnavich, P.M.; Martini, P.; Berlind, P.; Caldwell, N.; Challis, P.; Brown, W.R.; Schild, R.; Krisciunas, K.; et al. Spectroscopic Discovery of the Supernova 2003dh Associated with GRB 030329. Astrophys. J. 2003, 591, L17–L20. [Google Scholar] [CrossRef]
- Campana, S.; Mangano, V.; Blustin, A.J.; Brown, P.; Burrows, D.N.; Chincarini, G.; Cummings, J.R.; Cusumano, G.; Della Valle, M.; Malesani, D.; et al. The association of GRB 060218 with a supernova and the evolution of the shock wave. Nature 2006, 442, 1008–1010. [Google Scholar] [CrossRef]
- Pian, E.; Mazzali, P.A.; Masetti, N.; Ferrero, P.; Klose, S.; Palazzi, E.; Ramirez-Ruiz, E.; Woosley, S.E.; Kouveliotou, C.; Deng, J.; et al. An optical supernova associated with the X-ray flash XRF 060218. Nature 2006, 442, 1011–1013. [Google Scholar] [CrossRef]
- Cobb, B.E.; Bloom, J.S.; Perley, D.A.; Morgan, A.N.; Cenko, S.B.; Filippenko, A.V. Discovery of SN 2009nz Associated with GRB 091127. Astrophys. J. 2010, 718, L150–L155. [Google Scholar] [CrossRef]
- Starling, R.L.C.; Wiersema, K.; Levan, A.J.; Sakamoto, T.; Bersier, D.; Goldoni, P.; Oates, S.R.; Rowlinson, A.; Campana, S.; Sollerman, J.; et al. Discovery of the nearby long, soft GRB 100316D with an associated supernova. Mon. Notices R. Astron. Soc. 2011, 411, 2792–2803. [Google Scholar] [CrossRef]
- Cano, Z.; Wang, S.Q.; Dai, Z.G.; Wu, X.F. The Observer’s Guide to the Gamma-Ray Burst Supernova Connection. Adv. Astron. 2017, 2017, 8929054. [Google Scholar] [CrossRef]
- Gehrels, N.; Sarazin, C.L.; O’Brien, P.T.; Zhang, B.; Barbier, L.; Barthelmy, S.D.; Blustin, A.; Burrows, D.N.; Cannizzo, J.; Cummings, J.R.; et al. A short γ-ray burst apparently associated with an elliptical galaxy at redshift z = 0.225. Nature 2005, 437, 851–854. [Google Scholar] [CrossRef] [PubMed]
- Fruchter, A.S.; Levan, A.J.; Strolger, L.; Vreeswijk, P.M.; Thorsett, S.E.; Bersier, D.; Burud, I.; Castro Cerón, J.M.; Castro-Tirado, A.J.; Conselice, C.; et al. Long γ-ray bursts and core-collapse supernovae have different environments. Nature 2006, 441, 463–468. [Google Scholar] [CrossRef]
- Nakar, E. Short-hard gamma-ray bursts. Phys. Rep. 2007, 442, 166–236. [Google Scholar] [CrossRef]
- Gehrels, N.; Ramirez-Ruiz, E.; Fox, D.B. Gamma-Ray Bursts in the Swift Era. Annu. Rev. Astron. Astrophys. 2009, 47, 567–617. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. 2017, 848, L14. [Google Scholar] [CrossRef]
- Alexander, K.D.; Berger, E.; Fong, W.; Williams, P.K.G.; Guidorzi, C.; Margutti, R.; Metzger, B.D.; Annis, J.; Blanchard, P.K.; Brout, D.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. VI. Radio Constraints on a Relativistic Jet and Predictions for Late-time Emission from the Kilonova Ejecta. Astrophys. J. 2017, 848, L21. [Google Scholar] [CrossRef]
- Nysewander, M.; Fruchter, A.S.; Pe’er, A. A Comparison of the Afterglows of Short- and Long-duration Gamma-ray Bursts. Astrophys. J. 2009, 701, 824–836. [Google Scholar] [CrossRef]
- Weaver, R.; McCray, R.; Castor, J.; Shapiro, P.; Moore, R. Interstellar bubbles. II—Structure and evolution. Astrophys. J. 1977, 218, 377–395. [Google Scholar] [CrossRef]
- Pe’er, A.; Wijers, R.A.M.J. The Signature of a Wind Reverse Shock in Gamma-Ray Burst Afterglows. Astrophys. J. 2006, 643, 1036–1046. [Google Scholar] [CrossRef]
- van Eerten, H.J.; Meliani, Z.; Wijers, R.A.M.J.; Keppens, R. No visible optical variability from a relativistic blast wave encountering a wind termination shock. Mon. Notices R. Astron. Soc. 2009, 398, L63–L67. [Google Scholar] [CrossRef]
- Chevalier, R.A.; Li, Z.Y. Gamma-Ray Burst Environments and Progenitors. Astrophys. J. 1999, 520, L29–L32. [Google Scholar] [CrossRef]
- Panaitescu, A.; Kumar, P. Jet Energy and Other Parameters for the Afterglows of GRB 980703, GRB 990123, GRB 990510, and GRB 991216 Determined from Modeling of Multifrequency Data. Astrophys. J. 2001, 554, 667–677. [Google Scholar] [CrossRef]
- Panaitescu, A.; Kumar, P. Properties of Relativistic Jets in Gamma-Ray Burst Afterglows. Astrophys. J. 2002, 571, 779–789. [Google Scholar] [CrossRef]
- Starling, R.L.C.; van der Horst, A.J.; Rol, E.; Wijers, R.A.M.J.; Kouveliotou, C.; Wiersema, K.; Curran, P.A.; Weltevrede, P. Gamma-Ray Burst Afterglows as Probes of Environment and Blast Wave Physics. II. The Distribution of p and Structure of the Circumburst Medium. Astrophys. J. 2008, 672, 433–442. [Google Scholar] [CrossRef]
- Curran, P.A.; Starling, R.L.C.; van der Horst, A.J.; Wijers, R.A.M.J. Testing the blast wave model with Swift GRBs. Mon. Notices R. Astron. Soc. 2009, 395, 580–592. [Google Scholar] [CrossRef]
- Oates, S.R.; Page, M.J.; De Pasquale, M.; Schady, P.; Breeveld, A.A.; Holland, S.T.; Kuin, N.P.M.; Marshall, F.E. A correlation between the intrinsic brightness and average decay rate of Swift/UVOT gamma-ray burst optical/ultraviolet light curves. Mon. Notices R. Astron. Soc. 2012, 426, L86–L90. [Google Scholar] [CrossRef]
- Oates, S.R.; Racusin, J.L.; De Pasquale, M.; Page, M.J.; Castro-Tirado, A.J.; Gorosabel, J.; Smith, P.J.; Breeveld, A.A.; Kuin, N.P.M. Exploring the canonical behaviour of long gamma-ray bursts using an intrinsic multiwavelength afterglow correlation. Mon. Notices R. Astron. Soc. 2015, 453, 4121–4135. [Google Scholar] [CrossRef]
- Li, L.; Wu, X.F.; Huang, Y.F.; Wang, X.G.; Tang, Q.W.; Liang, Y.F.; Zhang, B.B.; Wang, Y.; Geng, J.J.; Liang, E.W.; et al. A Correlated Study of Optical and X-ray Afterglows of GRBs. Astrophys. J. 2015, 805, 13. [Google Scholar] [CrossRef]
- Racusin, J.L.; Oates, S.R.; de Pasquale, M.; Kocevski, D. A Correlation between the Intrinsic Brightness and Average Decay Rate of Gamma-Ray Burst X-ray Afterglow Light Curves. Astrophys. J. 2016, 826, 45. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pe’er, A. Plasmas in Gamma-Ray Bursts: Particle Acceleration, Magnetic Fields, Radiative Processes and Environments. Galaxies 2019, 7, 33. https://doi.org/10.3390/galaxies7010033
Pe’er A. Plasmas in Gamma-Ray Bursts: Particle Acceleration, Magnetic Fields, Radiative Processes and Environments. Galaxies. 2019; 7(1):33. https://doi.org/10.3390/galaxies7010033
Chicago/Turabian StylePe’er, Asaf. 2019. "Plasmas in Gamma-Ray Bursts: Particle Acceleration, Magnetic Fields, Radiative Processes and Environments" Galaxies 7, no. 1: 33. https://doi.org/10.3390/galaxies7010033
APA StylePe’er, A. (2019). Plasmas in Gamma-Ray Bursts: Particle Acceleration, Magnetic Fields, Radiative Processes and Environments. Galaxies, 7(1), 33. https://doi.org/10.3390/galaxies7010033



