Magnetic Fields in Galaxy Clusters and in the Large-Scale Structure of the Universe
Abstract
1. Introduction
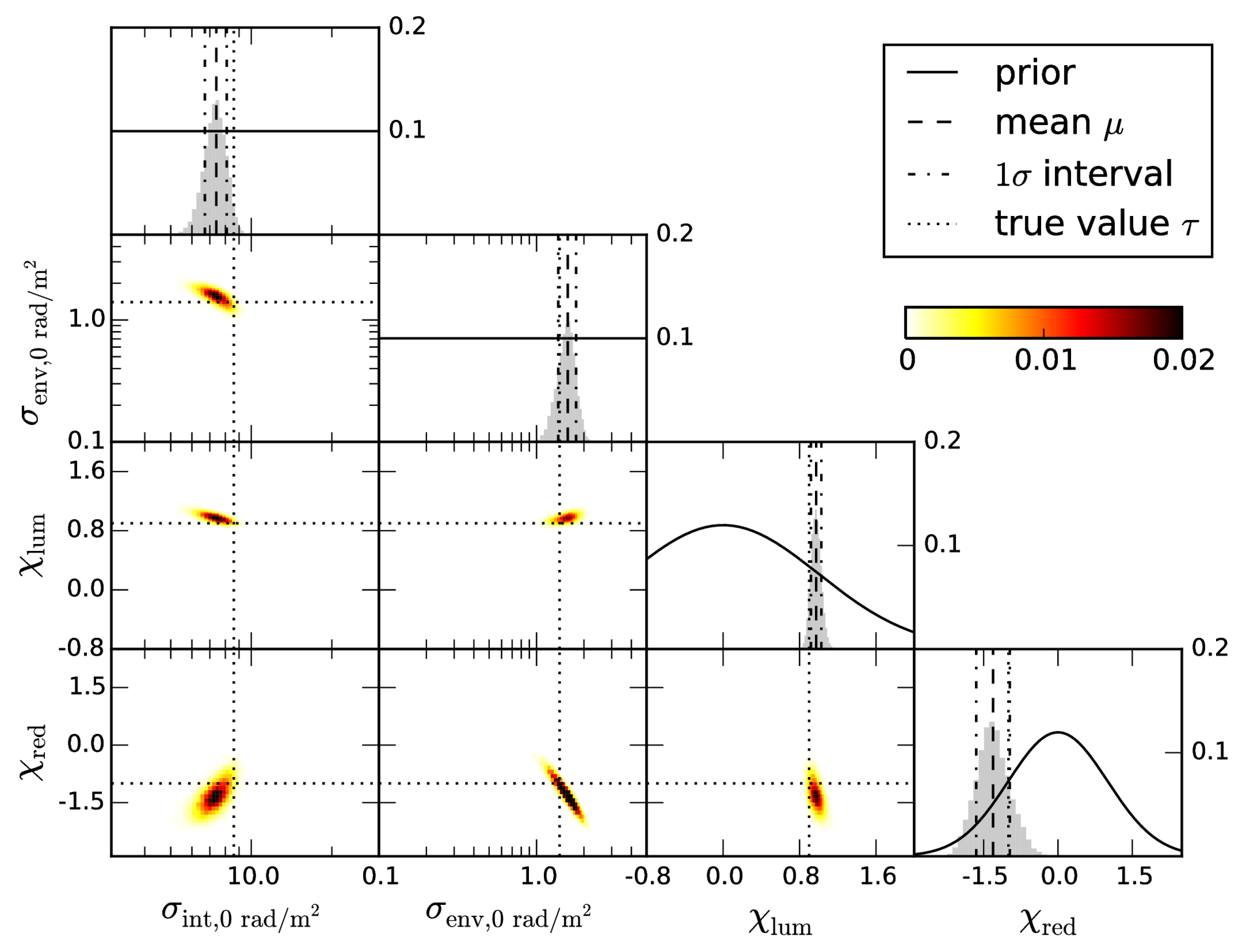
2. Methods
2.1. Diffuse Synchrotron Emission
2.2. Polarimetric Properties of Radio Galaxies
3. Simulations
- a Gaussian intracluster magnetic field with a power law power spectrumfluctuating between a minimum and a maximum spatial scale, where k is the wave-number and n the slope of the power spectrum . The normalization of the power spectrum is fixed by imposing an average magnetic field radial profile proportional to a function of the thermal gas density ,where and are respectively the magnetic field strength and the thermal gas density at the center of the cluster and describes the radial profile;
- a population of relativistic electrons with a power law energy spectrumwith energy between and , index related to the spectral index of the radio halo emission through , isotropic distribution of the pitch angle between the direction of the magnetic field and of their velocity and normalization ;
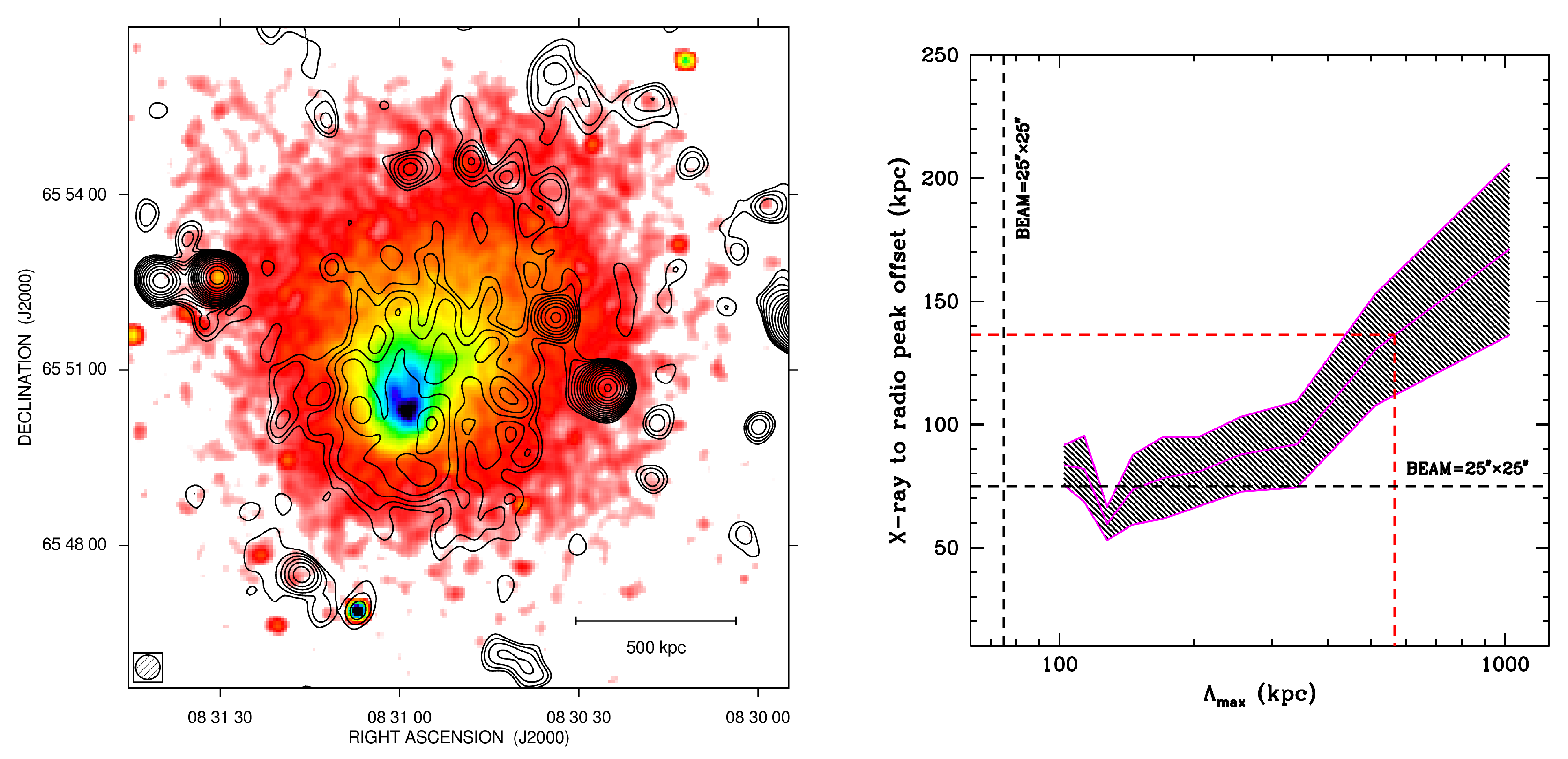
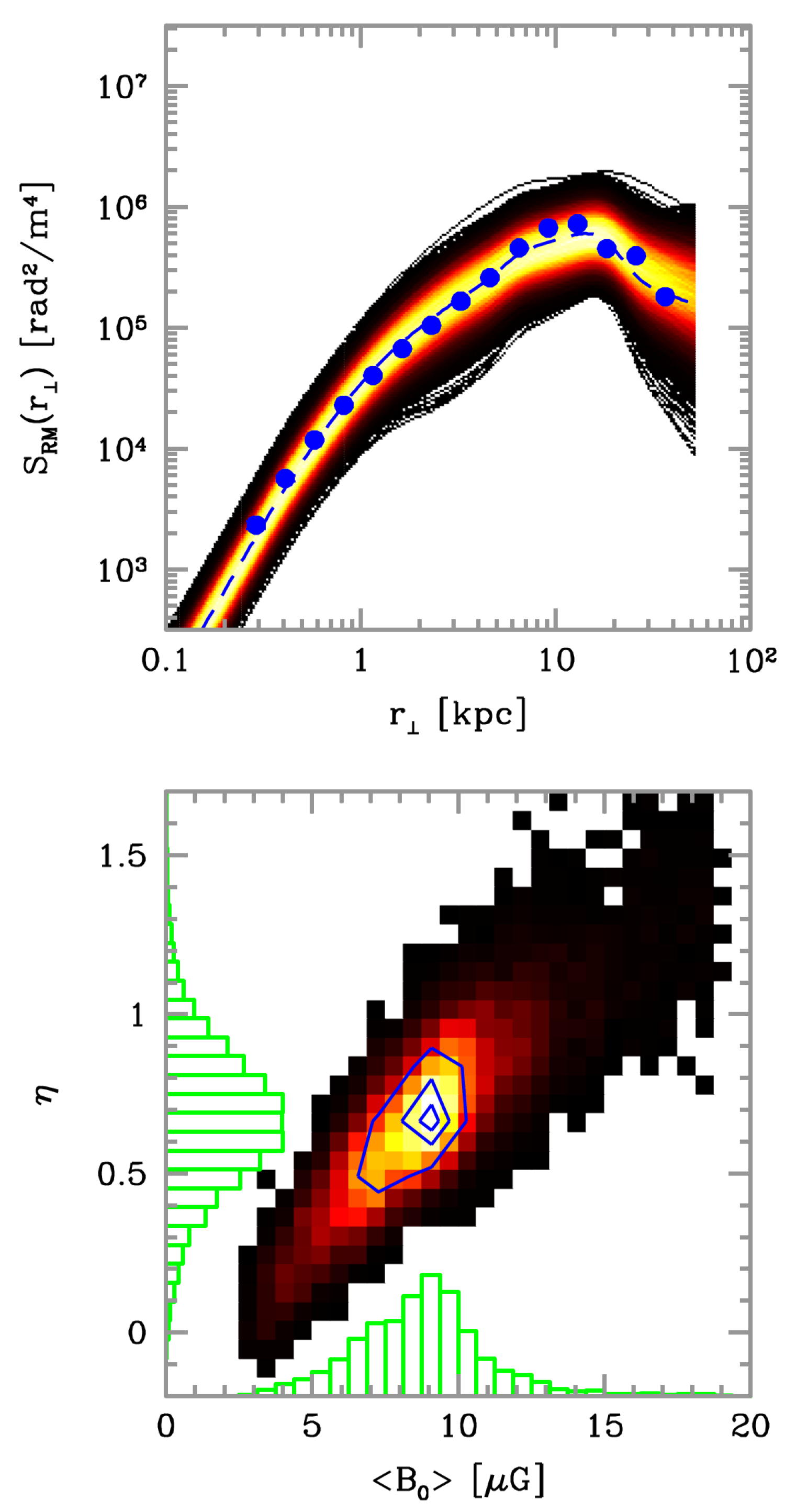
4. Magnetic Fields in Galaxy Clusters
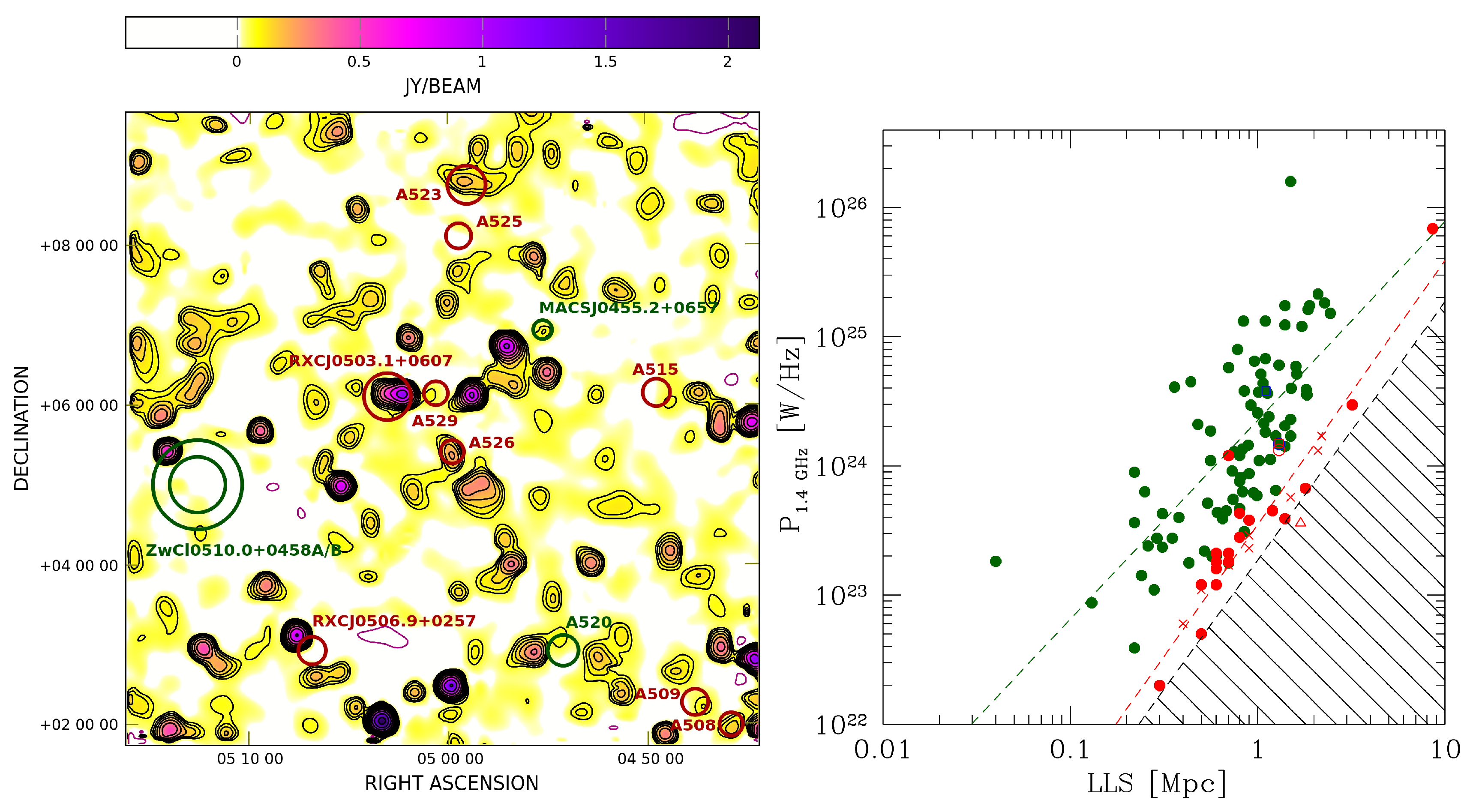
5. Present Results and Perspectives Beyond Galaxy Clusters
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brunetti, G.; Lazarian, A. Acceleration of primary and secondary particles in galaxy clusters by compressible MHD turbulence: From radio haloes to gamma-rays. Mon. Not. R. Astron. Soc. 2011, 410, 127–142. [Google Scholar] [CrossRef]
- Enßlin, T.; Pfrommer, C.; Miniati, F.; Subramanian, K. Cosmic ray transport in galaxy clusters: Implications for radio halos, gamma-ray signatures, and cool core heating. Astron. Astrophys. 2011, 527, A99. [Google Scholar] [CrossRef]
- Govoni, F.; Feretti, L. Magnetic Fields in Clusters of Galaxies. Int. J. Mod. Phys. D 2004, 13, 1549–1594. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Gheller, C.; Wang, P. On the amplification of magnetic fields in cosmic filaments and galaxy clusters. Mon. Not. R. Astron. Soc. 2014, 445, 3706–3722. [Google Scholar] [CrossRef]
- Giovannini, G.; Bonafede, A.; Brown, S.; Feretti, L.; Ferrari, C.; Gitti, M.; Govoni, F.; Murgia, M.; Vacca, V. Mega-parsec scale magnetic fields in low density regions in the SKA era: Filaments connecting galaxy clusters and groups. arXiv, 2015; arXiv:1501.01023. [Google Scholar]
- Brown, S.; Vernstrom, T.; Carretti, E.; Dolag, K.; Gaensler, B.M.; Staveley-Smith, L.; Bernardi, G.; Haverkorn, M.; Kesteven, M.; Poppi, S. Limiting magnetic fields in the cosmic web with diffuse radio emission. Mon. Not. R. Astron. Soc. 2017, 468, 4246–4253. [Google Scholar] [CrossRef]
- Vernstrom, T.; Gaensler, B.M.; Brown, S.; Lenc, E.; Norris, R.P. Low-frequency radio constraints on the synchrotron cosmic web. Mon. Not. R. Astron. Soc. 2017, 467, 4914–4936. [Google Scholar] [CrossRef]
- Akahori, T.; Ryu, D. Faraday Rotation Measure Due to the Intergalactic Magnetic Field. Astrophys. J. 2010, 723, 476–481. [Google Scholar] [CrossRef]
- Feretti, L.; Giovannini, G.; Govoni, F.; Murgia, M. Clusters of galaxies: Observational properties of the diffuse radio emission. Astron. Astrophys. Rev. 2012, 20, 54. [Google Scholar] [CrossRef]
- Eckert, D.; Jauzac, M.; Vazza, F.; Owers, M.S.; Kneib, J.-P.; Tchernin, C.; Intema, H.; Knowles, K. A shock front at the radio relic of Abell 2744. Mon. Not. R. Astron. Soc. 2016, 461, 1302–1307. [Google Scholar] [CrossRef]
- Kronberg, P.P.; Kothes, R.; Salter, C.J.; Perillat, P. Discovery of New Faint Radio Emission on 8° to 3’ Scales in the Coma Field, and Some Galactic and Extragalactic Implications. Astrophys. J. 2007, 659, 267–274. [Google Scholar] [CrossRef]
- Carretti, E.; Brown, S.; Staveley-Smith, L.; Malarecki, J.M.; Bernardi, G.; Gaensler, B.M.; Haverkorn, M.; Kesteven, M.J.; Poppi, S. Detection of a radio bridge in Abell 3667. Mon. Not. R. Astron. Soc. 2013, 430, 1414–1422. [Google Scholar] [CrossRef]
- Vacca, V.; Murgia, M.; Govoni, F.; Feretti, L.; Giovannini, G.; Orrù, E.; Bonafede, A. The intracluster magnetic field power spectrum in Abell 665. Astron. Astrophys. 2010, 514, A71. [Google Scholar] [CrossRef]
- Carilli, C.L.; Taylor, G.B. Cluster Magnetic Fields. Ann. Rev. Astron. Astrophys. 2002, 40, 319–348. [Google Scholar] [CrossRef]
- Burn, B.J. On the depolarization of discrete radio sources by Faraday dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67. [Google Scholar] [CrossRef]
- Tribble, P.C. Depolarization of extended radio sources by a foreground Faraday screen. Mon. Not. R. Astron. Soc. 1991, 250, 726–736. [Google Scholar] [CrossRef]
- Laing, R.A.; Bridle, A.H.; Parma, P.; Murgia, M. Structures of the magnetoionic media around the Fanaroff-Riley Class I radio galaxies 3C31 and Hydra A. Mon. Not. R. Astron. Soc. 2008, 391, 521–549. [Google Scholar] [CrossRef]
- Enßlin, T.A.; Vogt, C. The magnetic power spectrum in Faraday rotation screens. Astron. Astrophys. 2003, 401, 835–848. [Google Scholar] [CrossRef]
- Murgia, M.; Govoni, F.; Feretti, L.; Giovannini, G.; Dallacasa, D.; Fanti, R.; Taylor, G.B.; Dolag, K. Magnetic fields and Faraday rotation in clusters of galaxies. Astron. Astrophys. 2004, 424, 429–446. [Google Scholar] [CrossRef]
- Cavaliere, A.; Fusco-Femiano, R. X-rays from hot plasma in clusters of galaxies. Astron. Astrophys. 1976, 49, 137–144. [Google Scholar]
- Mohr, J.J.; Mathiesen, B.; Evrard, A.E. Properties of the Intracluster Medium in an Ensemble of Nearby Galaxy Clusters. Astrophys. J. 1999, 517, 627–649. [Google Scholar] [CrossRef]
- Vogt, C.; Enßlin, T.A. Measuring the cluster magnetic field power spectra from Faraday rotation maps of Abell 400, Abell 2634 and Hydra A. Astron. Astrophys. 2003, 412, 373–385. [Google Scholar] [CrossRef]
- Vogt, C.; Enßlin, T.A. A Bayesian view on Faraday rotation maps Seeing the magnetic power spectra in galaxy clusters. Astron. Astrophys. 2005, 434, 67–76. [Google Scholar] [CrossRef]
- Kuchar, P.; Enßlin, T.A. Magnetic power spectra from Faraday rotation maps. REALMAF and its use on Hydra A. Astron. Astrophys. 2011, 529, A13. [Google Scholar] [CrossRef]
- Guidetti, D.; Murgia, M.; Govoni, F.; Parma, P.; Gregorini, L.; de Ruiter, H.R.; Cameron, R.A.; Fanti, R. The intracluster magnetic field power spectrum in Abell 2382. Astron. Astrophys. 2008, 483, 699–713. [Google Scholar] [CrossRef]
- Guidetti, D.; Laing, R.A.; Murgia, M.; Govoni, F.; Gregorini, L.; Parma, P. Structure of the magnetoionic medium around the Fanaroff-Riley Class I radio galaxy 3C 449. Astron. Astrophys. 2010, 514, A50. [Google Scholar] [CrossRef]
- Vacca, V.; Murgia, M.; Govoni, F.; Feretti, L.; Giovannini, G.; Perley, R.A.; Taylor, G.B. The intracluster magnetic field power spectrum in A2199. Astron. Astrophys. 2012, 540, A38. [Google Scholar] [CrossRef]
- Bonafede, A.; Feretti, L.; Murgia, M.; Giovannini, G.; Dallacasa, D.; Dolag, K.; Taylor, G.B. The Coma cluster magnetic field from Faraday rotation measures. Astron. Astrophys. 2010, 513, A30. [Google Scholar] [CrossRef]
- Bonafede, A.; Vazza, F.; Brüggen, M.; Murgia, M.; Govoni, F.; Feretti, L.; Giovannini, G.; Ogrean, G. Measurements and simulation of Faraday rotation across the Coma radio relic. Mon. Not. R. Astron. Soc. 2013, 433, 3208–3226. [Google Scholar] [CrossRef]
- Govoni, F.; Murgia, M.; Vacca, V.; Loi, F.; Girardi, M.; Gastaldello, F.; Giovannini, G.; Feretti, L.; Paladino, R.; Carretti, E.; et al. Sardinia Radio Telescope observations of Abell 194. The intra-cluster magnetic field power spectrum. Astron. Astrophys. 2017, 603, A122. [Google Scholar] [CrossRef]
- Govoni, F.; Murgia, M.; Feretti, L.; Giovannini, G.; Dolag, K.; Taylor, G.B. The intracluster magnetic field power spectrum in Abell 2255. Astron. Astrophys. 2006, 460, 425–438. [Google Scholar] [CrossRef]
- Girardi, M.; Boschin, W.; Gastaldello, F.; Giovannini, G.; Govoni, F.; Murgia, M.; Barrena, R.; Ettori, S.; Trasatti, M.; Vacca, V. A multiwavelength view of the galaxy cluster Abell 523 and its peculiar diffuse radio source. Mon. Not. R. Astron. Soc. 2016, 456, 2829–2847. [Google Scholar] [CrossRef]
- Murgia, M.; Eckert, D.; Govoni, F.; Ferrari, C.; Pandey-Pommier, M.; Nevalainen, J.; Paltani, S. GMRT observations of the Ophiuchus galaxy cluster. Astron. Astrophys. 2010, 514, A76. [Google Scholar] [CrossRef]
- Dolag, K.; Bartelmann, M.; Lesch, H. Evolution and structure of magnetic fields in simulated galaxy clusters. Astron. Astrophys. 2002, 387, 383–395. [Google Scholar] [CrossRef]
- Govoni, F.; Murgia, M.; Xu, H.; Li, H.; Norman, M.L.; Feretti, L.; Giovannini, G.; Vacca, V. Polarization of cluster radio halos with upcoming radio interferometers. Astron. Astrophys. 2013, 554, A102. [Google Scholar] [CrossRef]
- Röttgering, H.; Afonso, J.; Barthel, P.; Batejat, F.; Best, P.; Bonafede, A.; Brüggen, M.; Brunetti, G.; Chyzy, K.; Conway, J.; et al. LOFAR and APERTIF Surveys of the Radio Sky: Probing Shocks and Magnetic Fields in Galaxy Clusters. J. Astrophys. Astron. 2011, 32, 557–566. [Google Scholar] [CrossRef]
- Gaensler, B.M.; Landecker, T.L.; Taylor, A.R. Survey Science with ASKAP: Polarization Sky Survey of the Universe’s Magnetism (POSSUM). In Bulletin of the American Astronomical Society; POSSUM Collaboration 2010; American Astronomical Society: Washington, DC, USA, 2010; Volume 42, p. 515. [Google Scholar]
- Johnston-Hollitt, M.; Govoni, F.; Beck, R.; Dehghan, S.; Pratley, L.; Akahori, T.; Heald, G.; Agudo, I.; Bonafede, A.; Carretti, E.; et al. Using SKA Rotation Measures to Reveal the Mysteries of the Magnetised Universe. arXiv, 2015; arXiv:1506.00808. [Google Scholar]
- Bonafede, A.; Vazza, F.; Brüggen, M.; Akahori, T.; Carretti, E.; Colafrancesco, S.; Feretti, L.; Ferrari, C.; Giovannini, G.; Govoni, F.; et al. Unravelling the origin of large-scale magnetic fields in galaxy clusters and beyond through Faraday Rotation Measures with the SKA. arXiv, 2015; arXiv:1501.00321. [Google Scholar]
- Vacca, V.; Murgia, M.; Govoni, F.; Loi, F.; Vazza, F.; Finoguenov, A.; Carretti, E.; Feretti, L.; Giovannini, G.; Concu, R.; et al. Observations of a nearby filament of galaxy clusters with the Sardinia Radio Telescope. Mon. Not. R. Astron. Soc. 2018, 479, 776–806. [Google Scholar] [CrossRef]
- Condon, J.J.; Cotton, W.D.; Greisen, E.W.; Yin, Q.F.; Perley, R.A.; Taylor, G.B.; Broderick, J.J. The NRAO VLA Sky Survey. AJ 1998, 115, 1693–1716. [Google Scholar] [CrossRef]
- Van Eck, C.L.; Haverkorn, M.; Alves, M.I.R.; Beck, R.; Best, P.; Carretti, E.; Chyzy, K.T.; Farnes, J.S.; Ferriére, K.; Hardcastle, M.J.; et al. Polarized point sources in the LOFAR Two-meter Sky Survey: A preliminary catalog. Astron. Astrophys. 2018, 613, A58. [Google Scholar] [CrossRef]
- Taylor, A.R.; Stil, J.M.; Sunstrum, C. A Rotation Measure Image of the Sky. Astrophys. J. 2009, 702, 1230–1236. [Google Scholar] [CrossRef]
- Oppermann, N.; Junklewitz, H.; Greiner, M.; Enßlin, T.A.; Akahori, T.; Carretti, E.; Gaensler, B.M.; Goobar, A.; Harvey-Smith, L.; Johnston-Hollitt, M.; et al. Estimating extragalactic Faraday rotation. Astron. Astrophys. 2015, 575, A118. [Google Scholar] [CrossRef]
- Vacca, V.; Oppermann, N.; Enßlin, T.A.; Selig, M.; Junklewitz, H.; Greiner, M.; Jasche, J.; Hales, C.A.; Reneicke, M.; Carretti, E.; et al. Statistical methods for the analysis of rotation measure grids in large scale structures in the SKA era. arXiv, 2015; arXiv:1501.00415. [Google Scholar]
- Vacca, V.; Oppermann, N.; Enßlin, T.; Jasche, J.; Selig, M.; Greiner, M.; Junklewitz, H.; Reinecke, M.; Brüggen, M.; Carretti, E.; et al. Using rotation measure grids to detect cosmological magnetic fields: A Bayesian approach. Astron. Astrophys. 2016, 591, A13. [Google Scholar] [CrossRef]
- Jasche, J.; Kitaura, F.S.; Li, C.; Enßlin, T.A. Bayesian non-linear large-scale structure inference of the Sloan Digital Sky Survey Data Release 7. Mon. Not. R. Astron. Soc. 2010, 409, 355–370. [Google Scholar] [CrossRef]
- Bolli, P.; Orlati, A.; Stringhetti, L.; Orfei, A.; Righini, S.; Ambrosini, R.; Bartolini, M.; Bortolotti, C.; Buffa, F.; Buttu, M.; et al. Sardinia Radio Telescope: General Description, Technical Commissioning and First Light. J. Astron. Instrum. 2015, 4, 1550008. [Google Scholar] [CrossRef]
- Prandoni, I.; Murgia, M.; Tarchi, A.; Burgay, M.; Castangia, P.; Egron, E.; Govoni, F.; Pellizzoni, A.; Ricci, R.; Righini, S.; et al. The Sardinia Radio Telescope. From a technological project to a radio observatory. Astron. Astrophys. 2017, 608, A40. [Google Scholar] [CrossRef]
- Selig, M.; Bell, M.R.; Junklewitz, H.; Oppermann, N.; Reinecke, M.; Greiner, M.; Pachajoa, C.; Enßlin, T.A. NIFTY—Numerical Information Field Theory. A versatile PYTHON library for signal inference. Astron. Astrophys. 2013, 554, A26. [Google Scholar] [CrossRef]

| Clusters | Observable(s) | Frequency Band(s) | Instrument(s) | Reference |
|---|---|---|---|---|
| A400 | Radio galaxies | C, X band | VLA | [22] |
| A2634 | Radio galaxies | C, X band | VLA | [22] |
| Hydra A | Radio galaxies | X band | VLA | [17,22,23,24] |
| A119 | Radio galaxies | L, C, X band | VLA | [19] |
| A2382 | Radio galaxies | L, C band | VLA | [25] |
| 3C 31 | Radio Galaxies | L, C, X band | VLA | [17] |
| 3C 449 | Radio galaxies | L, C, X band | VLA | [26] |
| A2199 | Radio galaxies | L, C, X band | VLA | [27] |
| A1656 (center) | Radio galaxies | L, C, X band | VLA | [28] |
| A1656 (outskirts) | Radio Galaxies | L, C band | VLA | [29] |
| A194 | Radio galaxies | L, C band | VLA, SRT | [30] |
| A2255 | Radio galaxies and radio halo | C, X band | VLA | [31] |
| A665 | Radio halo | L band | VLA | [13] |
| A523 | Radio halo | L band | VLA | [32] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vacca, V.; Murgia, M.; Govoni, F.; Enßlin, T.; Oppermann, N.; Feretti, L.; Giovannini, G.; Loi, F. Magnetic Fields in Galaxy Clusters and in the Large-Scale Structure of the Universe. Galaxies 2018, 6, 142. https://doi.org/10.3390/galaxies6040142
Vacca V, Murgia M, Govoni F, Enßlin T, Oppermann N, Feretti L, Giovannini G, Loi F. Magnetic Fields in Galaxy Clusters and in the Large-Scale Structure of the Universe. Galaxies. 2018; 6(4):142. https://doi.org/10.3390/galaxies6040142
Chicago/Turabian StyleVacca, Valentina, Matteo Murgia, Federica Govoni, Torsten Enßlin, Niels Oppermann, Luigina Feretti, Gabriele Giovannini, and Francesca Loi. 2018. "Magnetic Fields in Galaxy Clusters and in the Large-Scale Structure of the Universe" Galaxies 6, no. 4: 142. https://doi.org/10.3390/galaxies6040142
APA StyleVacca, V., Murgia, M., Govoni, F., Enßlin, T., Oppermann, N., Feretti, L., Giovannini, G., & Loi, F. (2018). Magnetic Fields in Galaxy Clusters and in the Large-Scale Structure of the Universe. Galaxies, 6(4), 142. https://doi.org/10.3390/galaxies6040142






