The First- and Second-Order Fermi Acceleration Processes in BL Lacertae Objects
Abstract
1. Introduction
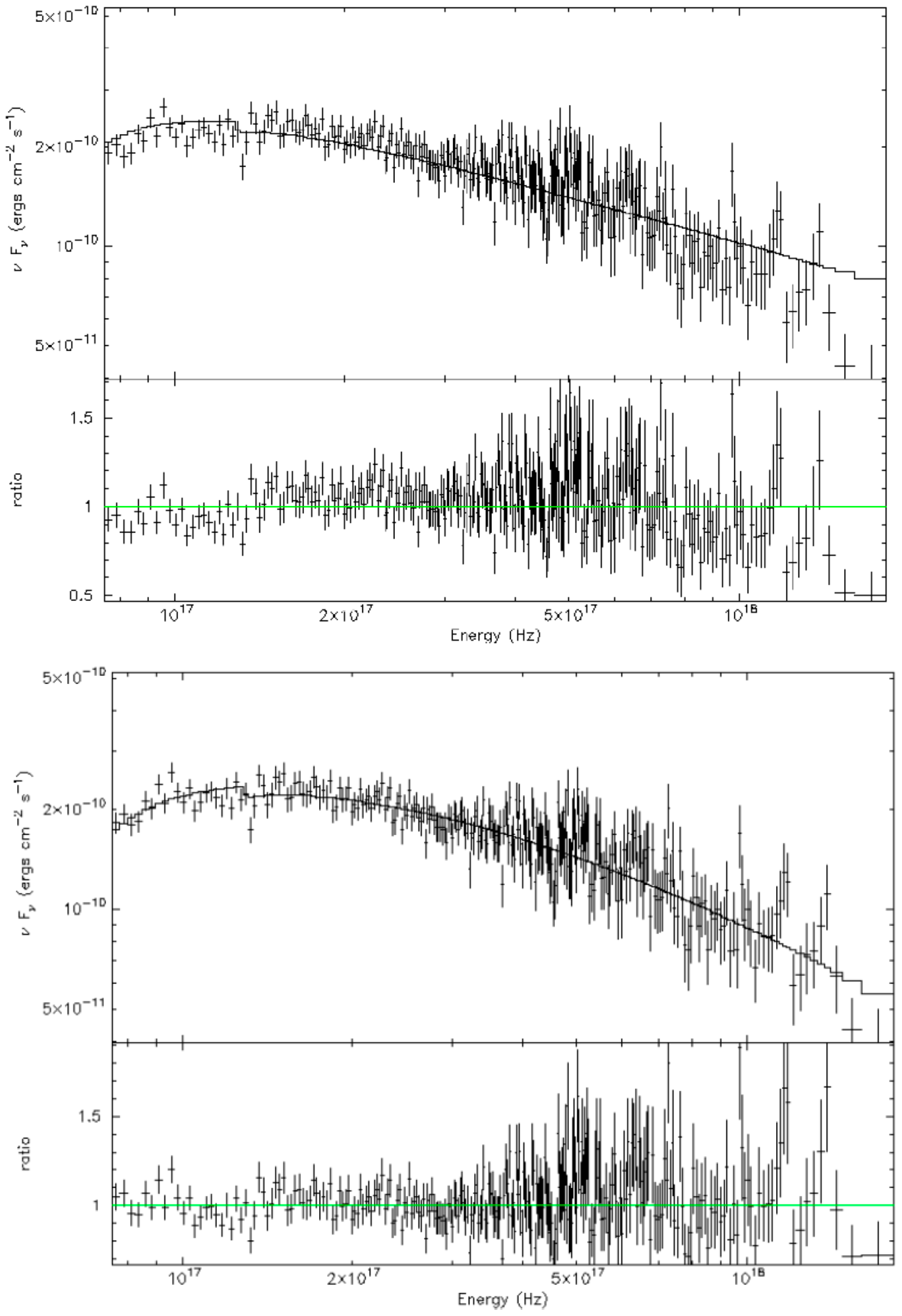
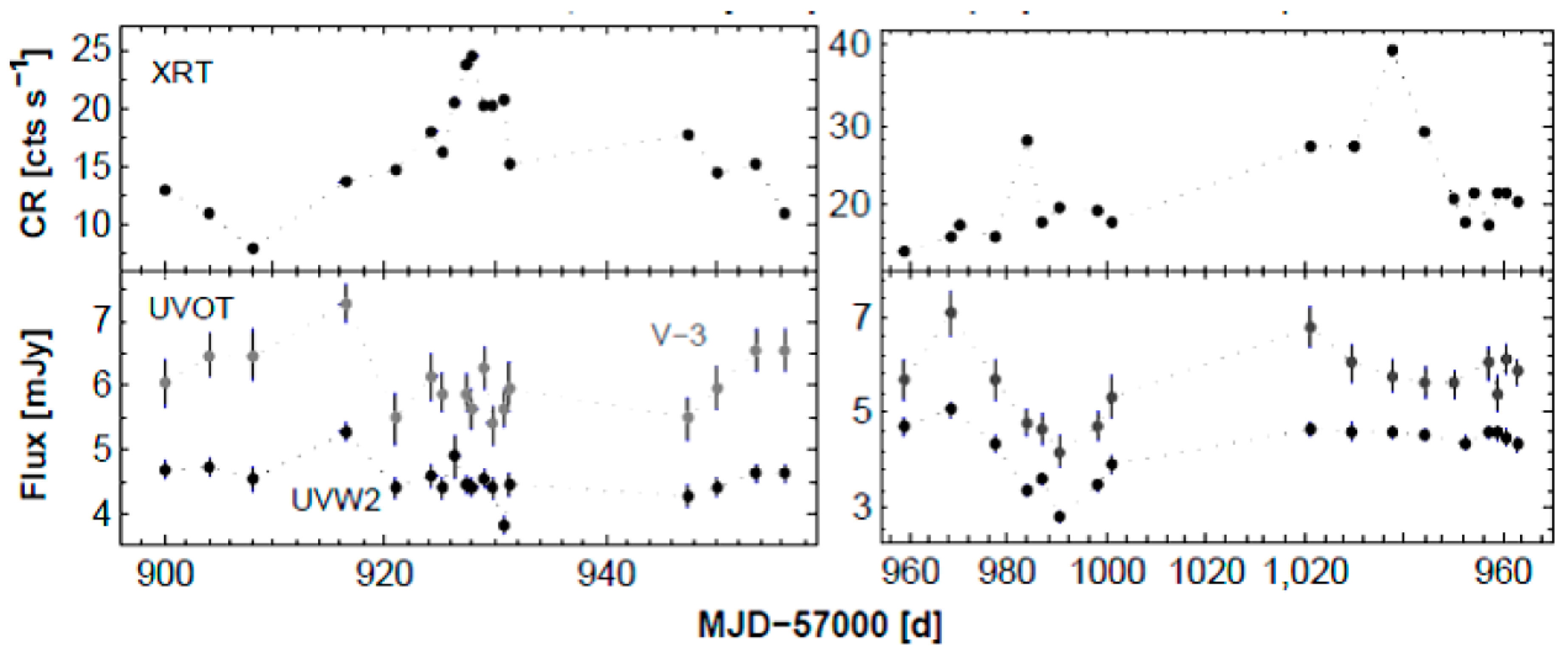
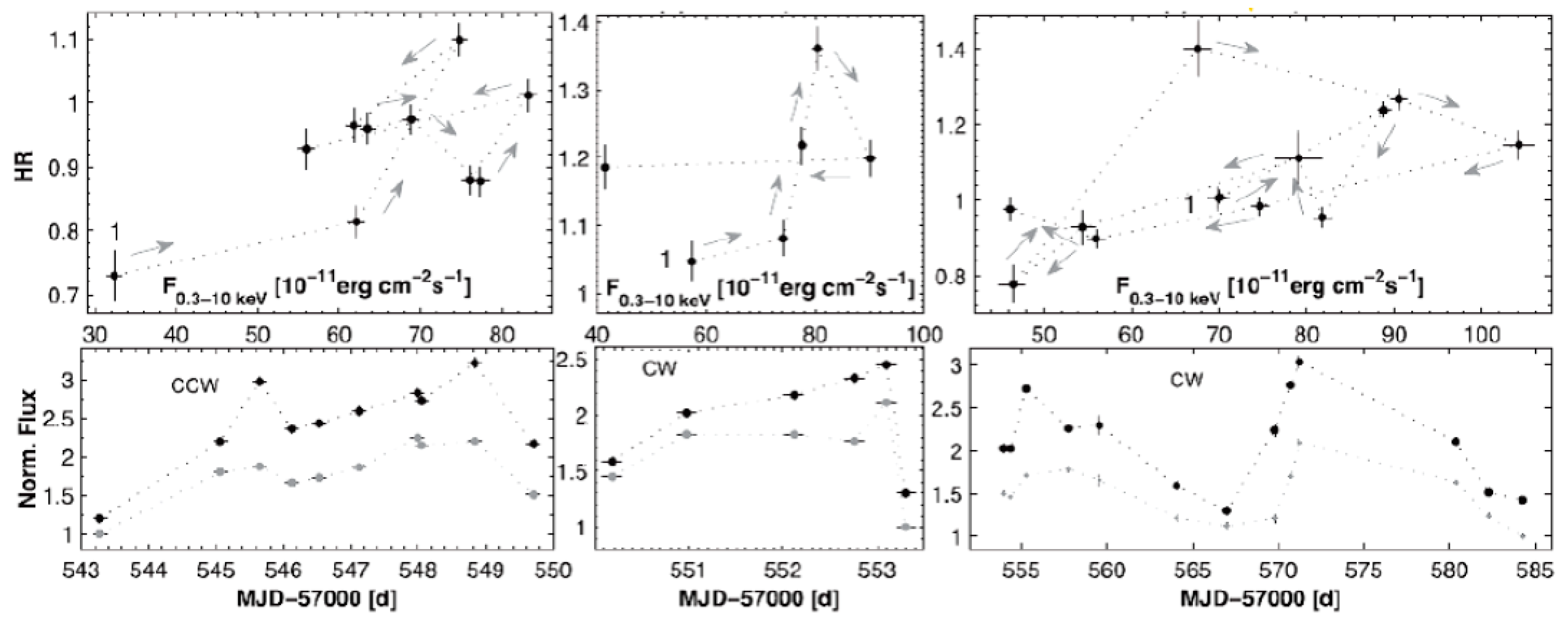
2. The Origin of X-ray Spectral Curvature
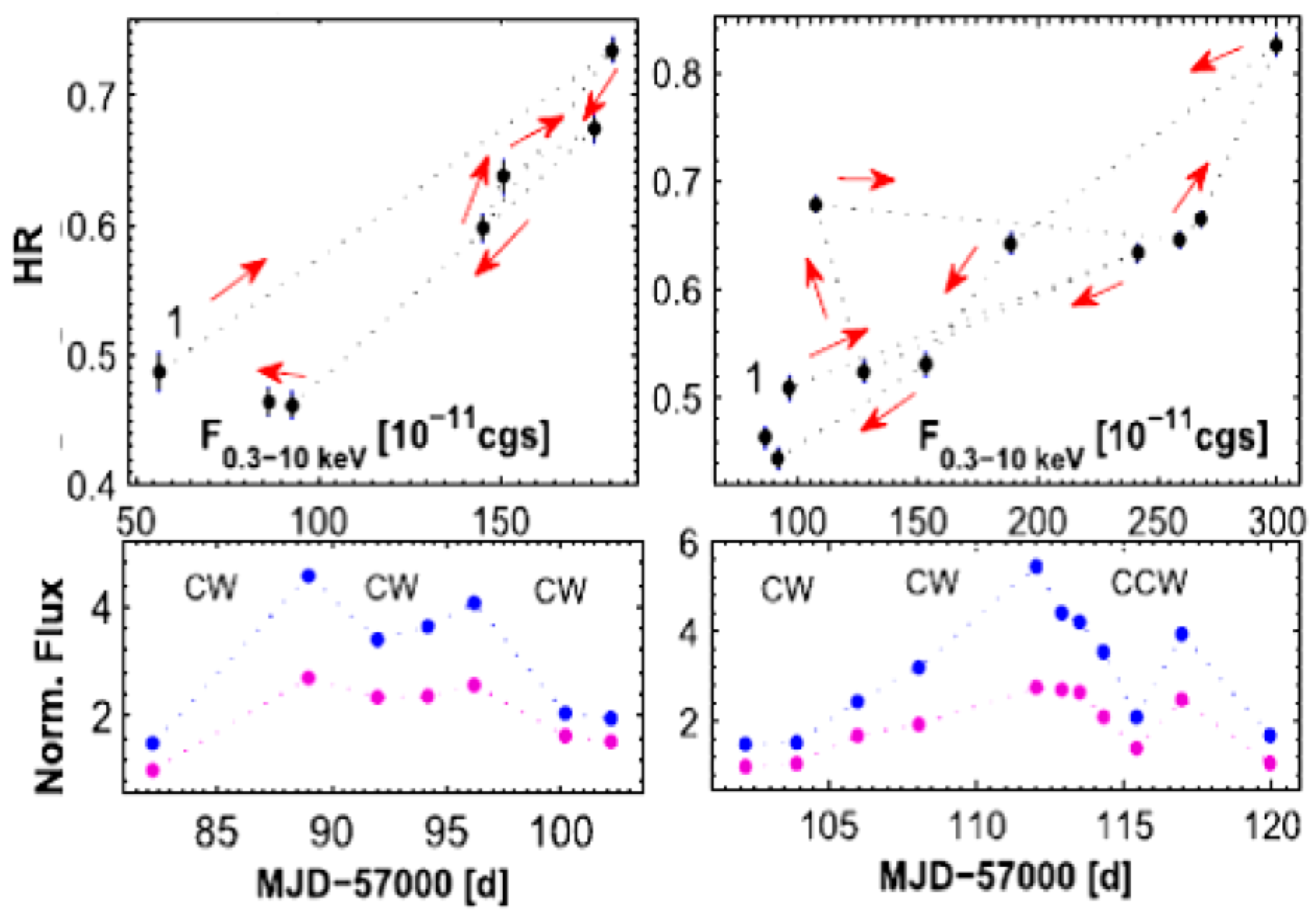
3. Results
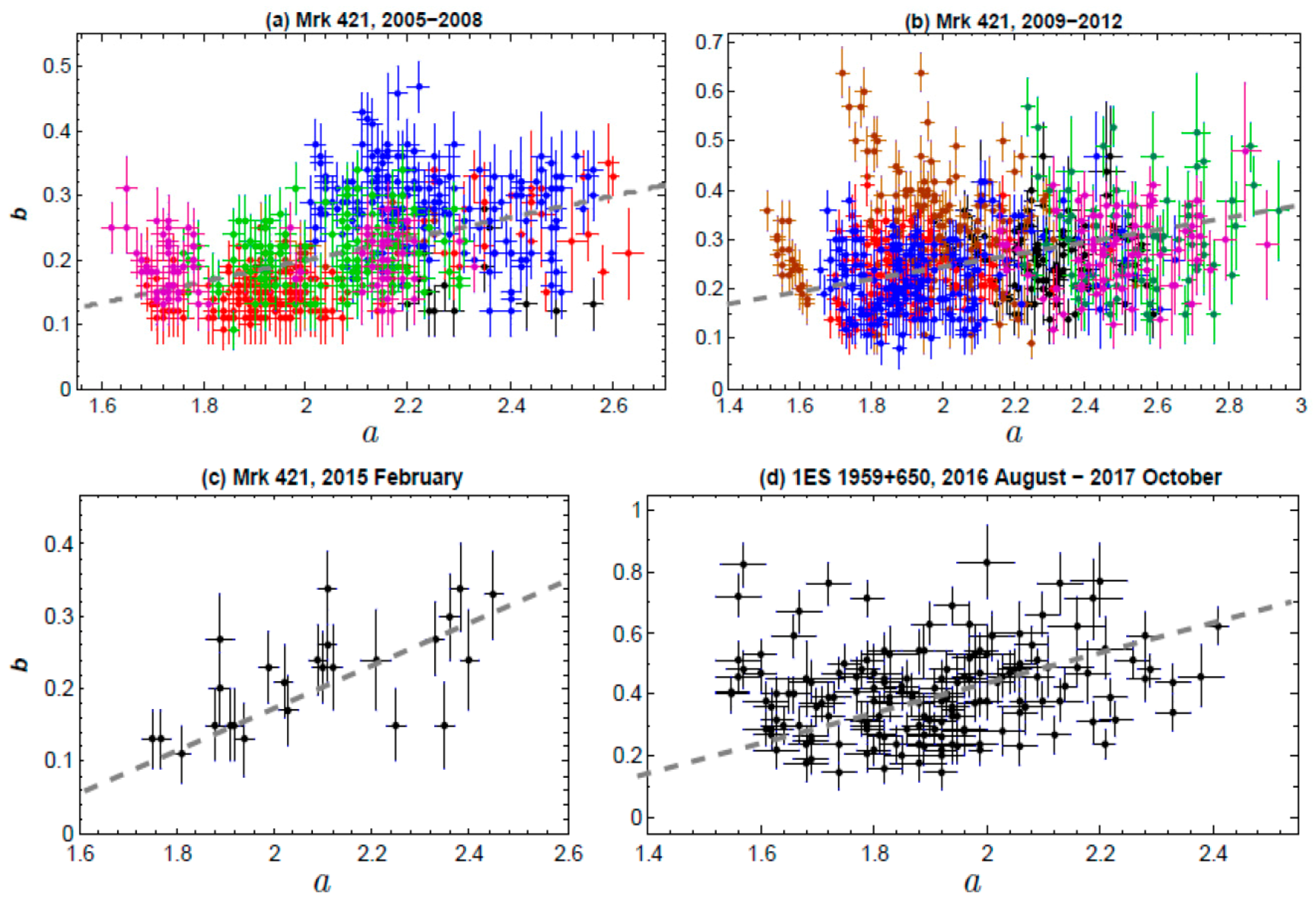
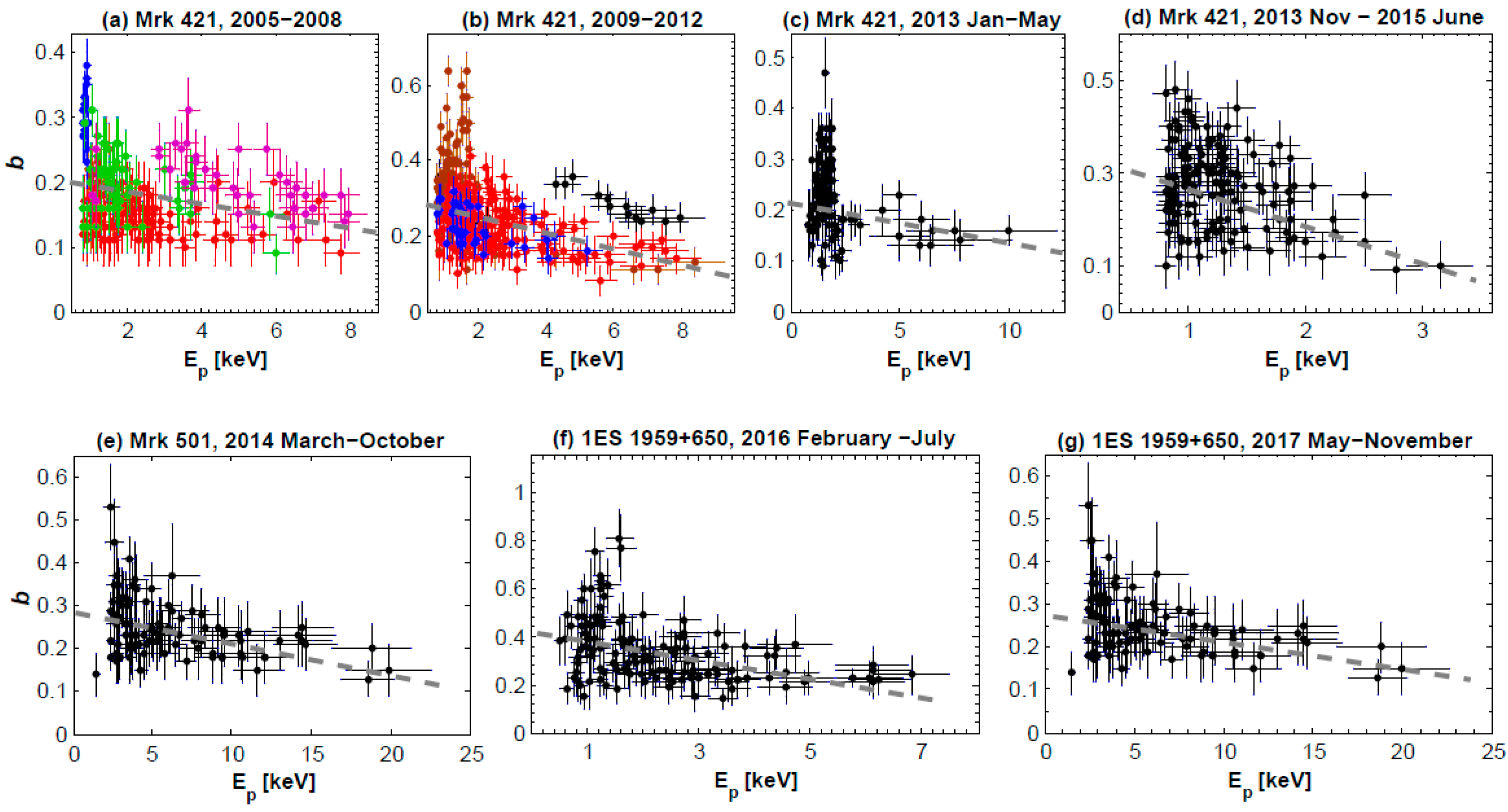
3.1. First-Order Fermi Acceleration
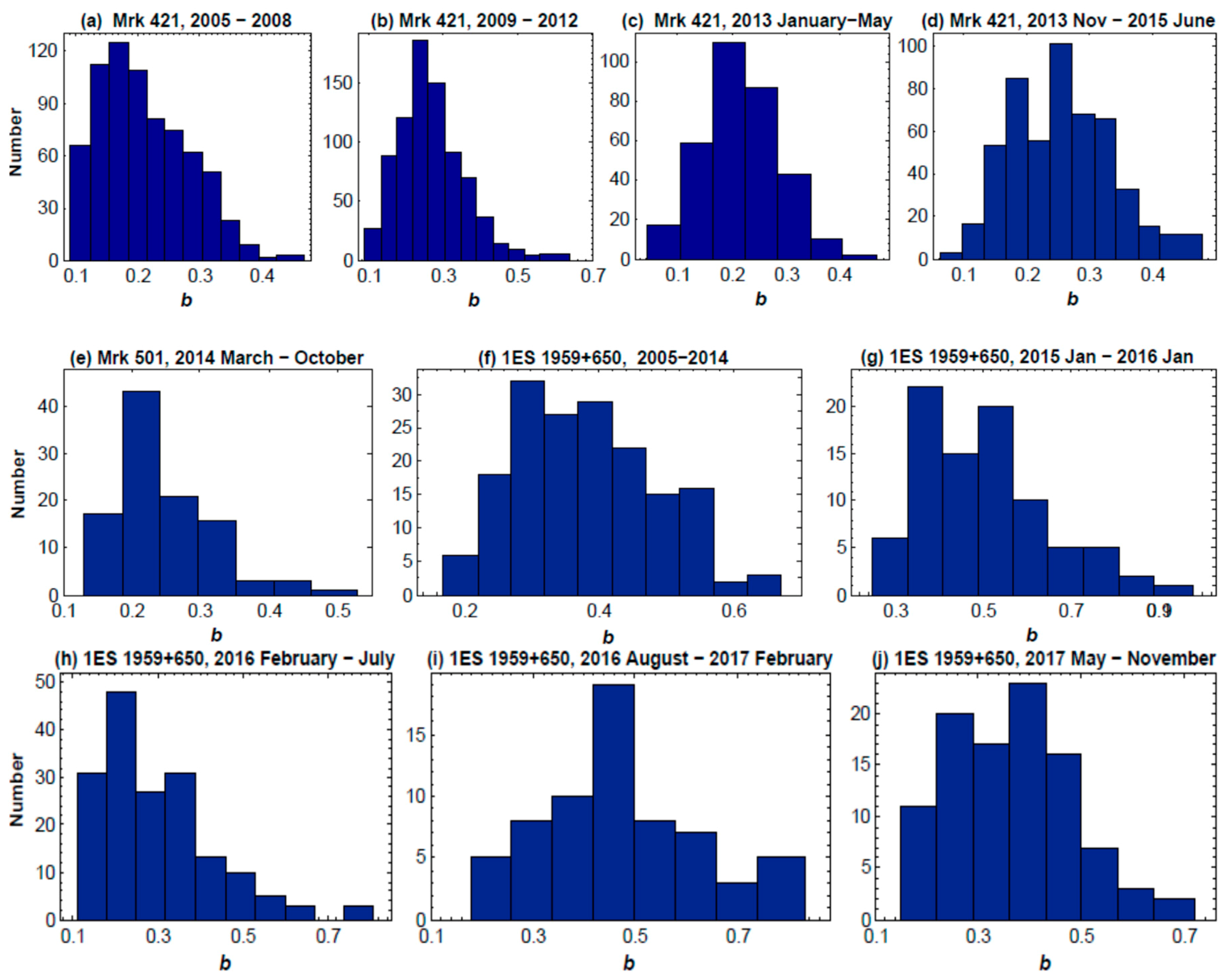
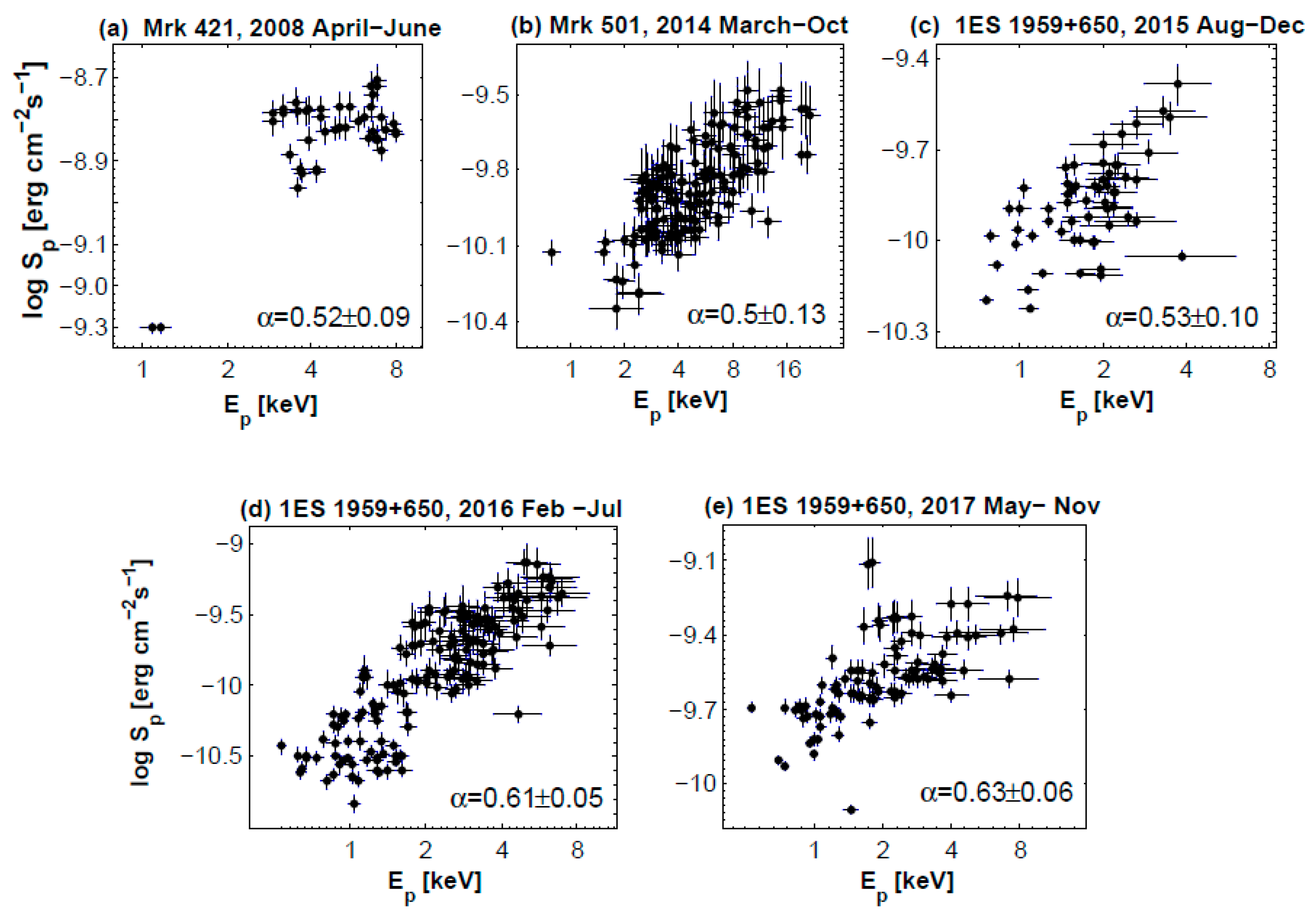
3.2. Stochastic Acceleration
4. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Falomo, R.; Pian, E.; Treves, A. An optical view of BL Lacertae objects. Astron. Astrophys. Rev. 2014, 22, 37. [Google Scholar] [CrossRef]
- Blandford, R.D.; Rees, M.J. Pittsburgh Conference on BL Lac Objects; Wolfe, A.M., Ed.; University Pittsburgh: Pittsburgh, PA, USA, 1978; p. 328. [Google Scholar]
- Marscher, A.P.; Gear, W.K. Models for high-frequency radio outbursts in extragalactic sources, with application to the early 1983 millimeter-to-infrared flare of 3C 273. Astrophys. J. 1985, 298, 114. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R.; Mastichiadis, A. High-energy gamma radiation from extragalactic radio sources. Astron. Astrophys. 1992, 256, L27–L30. [Google Scholar]
- Mannheim, K.; Biermann, P.L. Gamma-ray flaring of 3C 279—A proton-initiated cascade in the jet? Astron. Astrophys. 1992, 253, L21–L24. [Google Scholar]
- Tavecchio, F.; Ghisellini, G. On the magnetization of BL Lac jets. Mon. Not. R. Astron. Soc. 2016, 456, 2374–2382. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; McKinney, J.C.; Narayan, R. Efficiency of Magnetic to Kinetic Energy Conversion in a Monopole Magnetosphere. Astrophys. J. 2009, 699, 1789–1808. [Google Scholar] [CrossRef]
- Massaro, E.; Perri, M.; Giommi, P.; Nesci, R. Log-parabolic spectra and particle acceleration in the BL Lac object Mkn 421: Spectral analysis of the complete BeppoSAX wide band X-ray data set. Astron. Astrophys. 2004, 413, 489–503. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G. The Megaparsec-scale X-ray Jet of The BL Lac Object OJ287. Astrophys. J. 2011, 729, 26. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; et al. An Exceptional Very High Energy Gamma-Ray Flare of PKS 2155-304. Astrophys. J. 2007, 664, L71–L74. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Variable Very High Energy γ-Ray Emission from Markarian 501. Astrophys. J. 2007, 669, 862–883. [Google Scholar] [CrossRef]
- Begelman, M.C.; Fabian, A.C.; Rees, M.J. Implications of very rapid TeV variability in blazars. Mon. Not. R. Astron. Soc. 2008, 384, L19–L23. [Google Scholar] [CrossRef]
- Kirk, J.G.; Rieger, F.M.; Mastichiadis, A. Particle acceleration and synchrotron emission in blazar jets. Astron. Astrophys. 1998, 333, 452–458. [Google Scholar]
- Tramacere, A.; Giommi, P.; Perri, M.; Verrecchia, F.; Tosti, G. Swift observations of the very intense flaring activity of Mrk 421 during 2006. I. Phenomenological picture of electron acceleration and predictions for MeV/GeV emission. Astron. Astrophys. 2009, 501, 879–898. [Google Scholar] [CrossRef]
- Padovani, P.; Giommi, P. The connection between X-ray-and radio-selected BL Lacertae objects. Astrophys. J. 1995, 444, 567. [Google Scholar] [CrossRef]
- Tammi, J.; Duffy, P. Particle-acceleration time-scales in TeVblazar flares. Mon. Not. R. Astron. Soc. 2009, 393, 1063–1069. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 80, 87. [Google Scholar] [CrossRef]
- Mizuno, Y.; Pohl, M.; Niemiec, J.; Zhang, B.; Nishikawa, K.I.; Hardee, P.E. Magnetic field amplification and saturation in turbulence behind a relativistic shock. Mon. Not. R. Astron. Soc. 2014, 439, 3490–3503. [Google Scholar] [CrossRef]
- Virtanen, J.J.P.; Vainio, R. Stochastic Acceleration in Relativistic Parallel Shocks. Astrophys. J. 2005, 621, 313–323. [Google Scholar] [CrossRef]
- Paggi, A.; Massaro, F.; Vittorini, V.; Cavaliere, A.; D’Ammando, F.; Vagnetti, F.; Tavani, M. SSC radiation in BL Lacertae sources, the end of the tether. Astron. Astrophys. 2009, 504, 821–828. [Google Scholar] [CrossRef]
- Tramacere, A.; Massaro, E.; Taylor, A.M. Stochastic Acceleration and the Evolution of Spectral Distributions in Synchro-Self-Compton Sources: A Self-consistent Modeling of Blazars’ Flares. Astrophys. J. 2011, 739, 66. [Google Scholar] [CrossRef]
- Burrows, D.N.; Hill, J.E.; Nousek, J.A.; Kennea, J.A.; Wells, A.; Osborne, J.P.; Abbey, A.F.; Beardmore, A.P.; Mukerjee, K.; Short, A.D.; et al. The Swift X-ray Telescope. Space Sci. Rev. 2005, 120, 165–195. [Google Scholar] [CrossRef]
- Gehrels, N.; Chincarini, G.; Giommi, P.; Mason, K.O.; Nousek, J.A.; Wells, A.A.; White, N.E.; Barthelmy, S.D.; Burrows, D.N.; Cominsky, L.R.; et al. The Swift Gamma-Ray Burst Mission. Astrophys. J. 2004, 611, 1005–1020. [Google Scholar] [CrossRef]
- Kapanadze, B.; Vercellone, S.; Romano, P.; Hughes, P.; Aller, M.; Aller, H.; Kharshiladze, O.; Kapanadze, S.; Tabagari, L. Swift Observations of Mrk 421 in Selected Epochs. I. The Spectral and Flux Variability in 2005–2008. Astrophys. J. 2018, 854, 66. [Google Scholar] [CrossRef]
- Kapanadze, B.; Vercellone, S.; Romano, P.; Hughes, P.; Aller, M.; Aller, H.; Kharshiladze, O.; Tabagari, L. Swift Observations of Mrk 421 in Selected Epochs. II. An Extreme Spectral and Flux Variability in 2009–2012. Astrophys. J. 2018, 858, 68. [Google Scholar] [CrossRef]
- Kapanadze, B.; Dorner, D.; Vercellone, S.; Romano, P.; Aller, H.; Aller, M.; Hughes, P.; Reynolds, M.; Kapanadze, S.; Tabagari, L. X-ray Flaring Activity of MRK 421 in the First Half of 2013. Astrophys. J. 2016, 831, 102. [Google Scholar] [CrossRef]
- Kapanadze, B.; Dorner, D.; Romano, P.; Vercellone, S.; Kapanadze, S.; Tabagari, L. Mrk 421 after the Giant X-ray Outburst in 2013. Astrophys. J. 2017, 848, 103. [Google Scholar] [CrossRef]
- Kapanadze, B.; Dorner, D.; Vercellone, S.; Romano, P.; Hughes, P.; Aller, M.; Aller, H.; Reynolds, M.; Tabagari, L. Strong X-ray and Multiwavelength Flaring Activity for 1ES 1959+650, 2016 August–2017 November. Astrophys. J. Suppl. 2018, 238, 13. [Google Scholar] [CrossRef]
- Kapanadze, B.; Romano, P.; Vercellone, S.; Kapanadze, S.; Mdzinarishvili, T.; Kharshiladze, G. The long-term Swift observations of the high-energy peaked BL Lacertae source 1ES 1959+650. Mon. Not. R. Astron. Soc. 2016, 457, 704–722. [Google Scholar] [CrossRef]
- Kapanadze, B.; Dorner, D.; Vercellone, S.; Romano, P.; Kapanadze, S.; Mdzinarishvili, T. A recent strong X-ray flaring activity of 1ES 1959+650 with possibly less efficient stochastic acceleration. Mon. Not. R. Astron. Soc. 2016, 461, L26–L31. [Google Scholar] [CrossRef]
- Kapanadze, B.; Dorner, D.; Vercellone, S.; Romano, P.; Hughes, P.; Aller, M.; Aller, H.; Reynolds, M.; Kapanadze, S.; Tabagari, L. The second strong X-ray flare and multifrequency variability of 1ES 1959+650 in 2016 January-August. Mon. Not. R. Astron. Soc. 2018, 473, 2542–2564. [Google Scholar] [CrossRef]
- Kapanadze, B.; Dorner, D.; Romano, P.; Vercellone, S.; Mannheim, K.; Lindfors, E.; Nilsson, K.; Reinthal, R.; Takalo, L.; Kapanadze, S.; et al. The prolonged X-ray flaring activity of Mrk 501 in 2014. Mon. Not. R. Astron. Soc. 2017, 469, 1655–1672. [Google Scholar] [CrossRef]
- Kapanadze, B.; Romano, P.; Vercellone, S.; Kapanadze, S. The X-ray behaviour of the high-energy peaked BL Lacertae source PKS 2155-304 in the 0.3-10 keV band. Mon. Not. R. Astron. Soc. 2014, 444, 1077–1094. [Google Scholar] [CrossRef]
- Cui, W. X-ray Flaring Activity of Markarian 421. Astrophys. J. 2004, 605, 662–669. [Google Scholar] [CrossRef]
- Massaro, F.; Paggi, A.; Cavaliere, A. X-ray and TeV Emissions from High-frequency-peaked BL Lac Objects. Astrophys. J. 2011, 742, 662–669. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barres de Almeida, U.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. The 2009 multiwavelength campaign on Mrk 421: Variability and correlation studies. Astron. Astrophys. 2015, 576, L32. [Google Scholar] [CrossRef]
- Katarzyński, K.; Ghisellini, G.; Mastichiadis, A.; Tavecchio, F.; Maraschi, L. Stochastic particle acceleration and synchrotron self-Compton radiation in TeVblazars. Astron. Astrophys. 2006, 453, 47–56. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapanadze, B. The First- and Second-Order Fermi Acceleration Processes in BL Lacertae Objects. Galaxies 2018, 6, 125. https://doi.org/10.3390/galaxies6040125
Kapanadze B. The First- and Second-Order Fermi Acceleration Processes in BL Lacertae Objects. Galaxies. 2018; 6(4):125. https://doi.org/10.3390/galaxies6040125
Chicago/Turabian StyleKapanadze, Bidzina. 2018. "The First- and Second-Order Fermi Acceleration Processes in BL Lacertae Objects" Galaxies 6, no. 4: 125. https://doi.org/10.3390/galaxies6040125
APA StyleKapanadze, B. (2018). The First- and Second-Order Fermi Acceleration Processes in BL Lacertae Objects. Galaxies, 6(4), 125. https://doi.org/10.3390/galaxies6040125




