Strategy to Explore Magnetized Cosmic Web with Forthcoming Large Surveys of Rotation Measure
Abstract
1. Introduction
1.1. Magnetized Cosmic Web
1.2. Faraday Rotation Measure
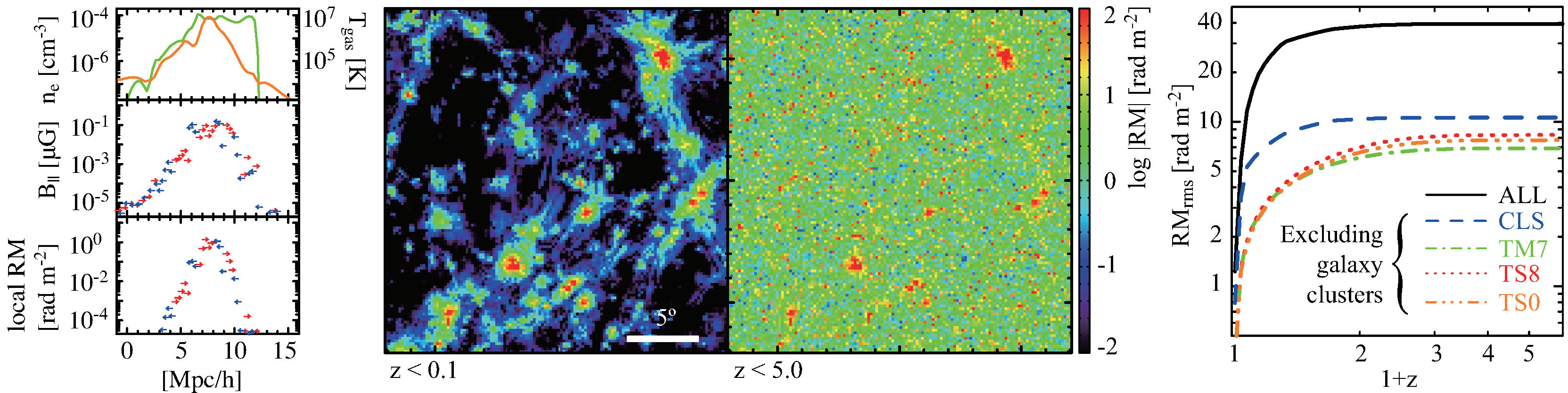
1.3. Prediction of the WHIM’s RM
1.4. Observational Issues
2. The Power of RM Grid
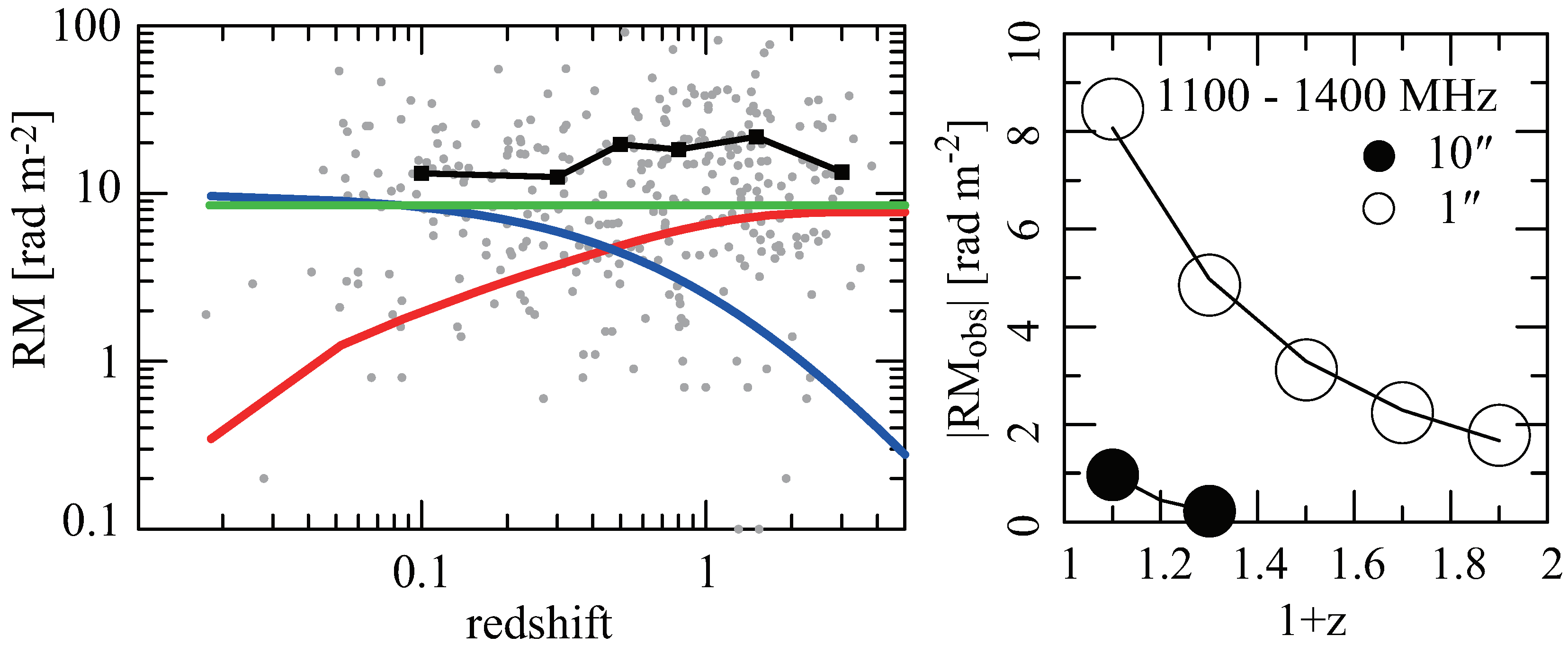
2.1. Intrinsic RM and Cosmological Redshift
2.2. Intervening RM and Faraday Depolarization
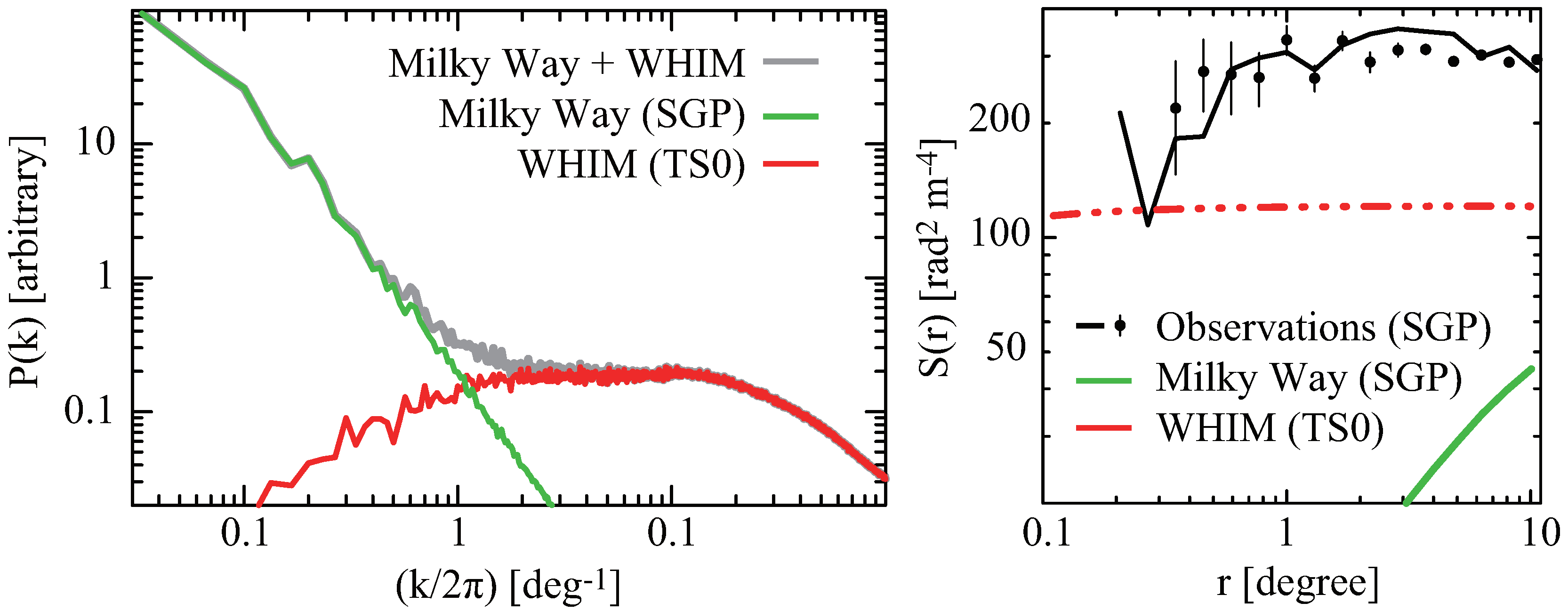
2.3. Galactic RM and Image Processing
2.4. Atmospheric RM and Calibration
3. The Power of Faraday Tomography
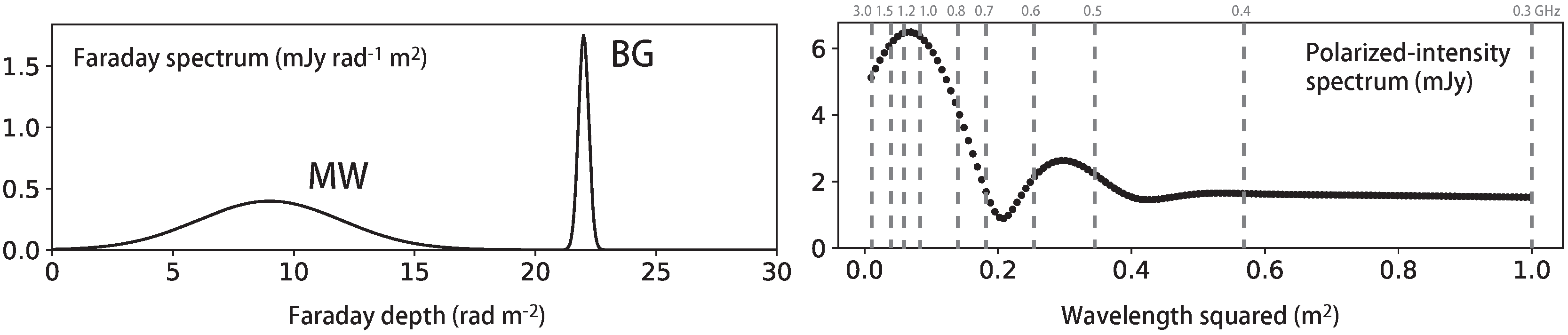
3.1. Find the FDF Gap Caused by the WHIM
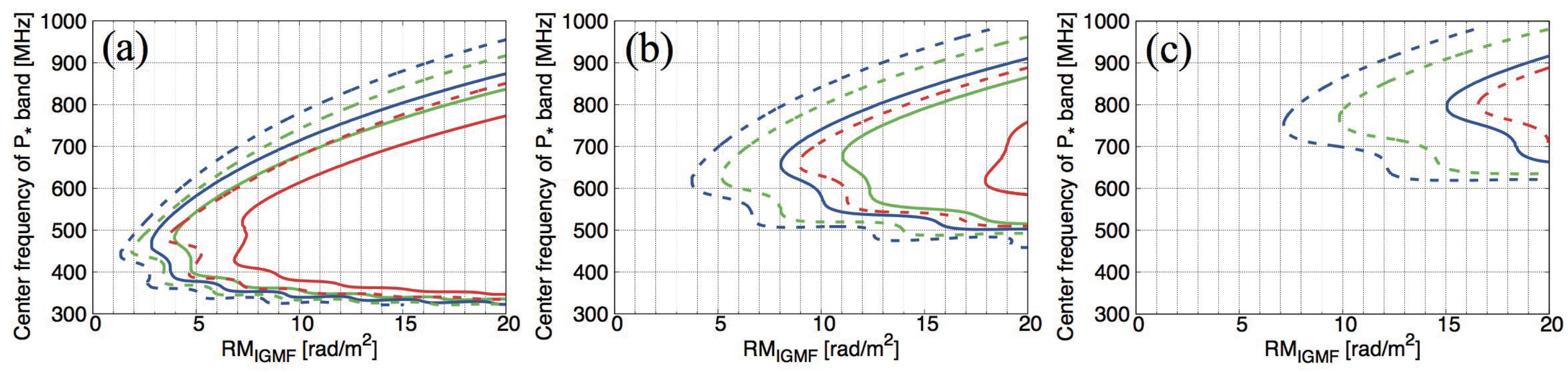
3.2. Optimum Frequency for Exploring the IGMF
4. Concluding Remarks
Funding
Conflicts of Interest
References
- Cen, R.; Ostriker, J.P. Where Are the Baryons? Astrophys. J. 1999, 514, 1–6. [Google Scholar] [CrossRef]
- Fukugita, M.; Hogan, C.J.; Peebles, P.J.E. The Cosmic Baryon Budget. Astrophys. J. 1998, 503, 518–530. [Google Scholar] [CrossRef]
- Nicastro, F.; Kaastra, J.; Krongold, Y.; Borgani, S.; Branchini, E.; Cen, R.; Dadina, M.; Danforth, C.W.; Elvis, M.; Fiore, F.; et al. Observations of the missing baryons in the warm-hot intergalactic medium. Nature 2018, 558, 406–409. [Google Scholar] [CrossRef] [PubMed]
- Ryu, D.; Schleicher, D.R.G.; Treumann, R.A.; Tsagas, C.G.; Widrow, L.M. Magnetic Fields in the Large-Scale Structure of the Universe. Space Sci. Rev. 2012, 166, 1–35. [Google Scholar] [CrossRef]
- Widrow, L.M.; Ryu, D.; Schleicher, D.R.G.; Subramanian, K.; Tsagas, C.G.; Treumann, R.A. The First Magnetic Fields. Space Sci. Rev. 2012, 166, 37–70. [Google Scholar] [CrossRef]
- Ichiki, K.; Takahashi, K.; Ohno, H.; Hanayama, H.; Sugiyama, N. Cosmological Magnetic Field: A Fossil of Density Perturbations in the Early Universe. Science 2006, 311, 827–829. [Google Scholar] [CrossRef] [PubMed]
- Shiromoto, Y.; Susa, H.; Hosokawa, T. Generation of Magnetic Field on the Accretion Disk around a Proto-first-star. Astrophys. J. 2014, 782, 108. [Google Scholar] [CrossRef]
- Xu, H.; O’Shea, B.W.; Collins, D.C.; Norman, M.L.; Li, H.; Li, S. The Biermann Battery in Cosmological MHD Simulations of Population III Star Formation. Astrophys. J. Lett. 2008, 688, L57–L60. [Google Scholar] [CrossRef]
- Gnedin, N.Y.; Ferrara, A.; Zweibel, E.G. Generation of the Primordial Magnetic Fields during Cosmological Reionization. Astrophys. J. 2000, 539, 505–516. [Google Scholar] [CrossRef]
- Langer, M.; Aghanim, N.; Puget, J.L. Magnetic fields from reionisation. Astron. Astrophys. 2005, 443, 367–372. [Google Scholar] [CrossRef]
- Kulsrud, R.M.; Cen, R.; Ostriker, J.P.; Ryu, D. The Protogalactic Origin for Cosmic Magnetic Fields. Astrophys. J. 1997, 480, 481–491. [Google Scholar] [CrossRef]
- Vazza, F.; Brunetti, G.; Brüggen, M.; Bonafede, A. Resolved magnetic dynamo action in the simulated intracluster medium. Mon. Not. R. Astron. Soc. 2018, 474, 1672–1687. [Google Scholar] [CrossRef]
- Donnert, J.; Dolag, K.; Lesch, H.; Müller, E. Cluster magnetic fields from galactic outflows. Mon. Not. R. Astron. Soc. 2009, 392, 1008–1021. [Google Scholar] [CrossRef]
- Miniati, F.; Bell, A.R. Resistive Magnetic Field Generation at Cosmic Dawn. Astrophys. J. 2011, 729, 73. [Google Scholar] [CrossRef]
- Xu, H.; Li, H.; Collins, D.C.; Li, S.; Norman, M.L. Turbulence and Dynamo in Galaxy Cluster Medium: Implications on the Origin of Cluster Magnetic Fields. Astrophys. J. Lett. 2009, 698, L14–L17. [Google Scholar] [CrossRef]
- Akahori, T.; Nakanishi, H.; Sofue, Y.; Fujita, Y.; Ichiki, K.; Ideguchi, S.; Kameya, O.; Kudoh, T.; Kudoh, Y.; Machida, M.; et al. Cosmic magnetism in centimeter- and meter-wavelength radio astronomy. Publ. Astron. Soc. Jpn. 2018, 70, R2. [Google Scholar] [CrossRef]
- Yamazaki, D.G.; Kajino, T.; Mathews, G.J.; Ichiki, K. The search for a primordial magnetic field. Phys. Rep. 2012, 517, 141–167. [Google Scholar] [CrossRef]
- Takami, H.; Nishimichi, T.; Yahata, K.; Sato, K. Cross-correlation between UHECR arrival distribution and large-scale structure. J. Cosmol. Astropart. Phys. 2009, 6, 031. [Google Scholar] [CrossRef]
- Takahashi, K.; Mori, M.; Ichiki, K.; Inoue, S. Lower Bounds on Intergalactic Magnetic Fields from Simultaneously Observed GeV-TeV Light Curves of the Blazar Mrk 501. Astrophys. J. 2012, 744, L7. [Google Scholar] [CrossRef]
- Fujita, Y.; Ohira, Y. Radio mini-halo emission from cosmic rays in galaxy clusters and heating of the cool cores. Mon. Not. R. Astron. Soc. 2013, 428, 599–608. [Google Scholar] [CrossRef]
- Takizawa, M. N-Body + Magnetohydrodynamical Simulations of Merging Clusters of Galaxies: Characteristic Magnetic Field Structures Generated by Bulk Flow Motion. Astrophys. J. 2008, 687, 951–958. [Google Scholar] [CrossRef]
- Akahori, T.; Kato, Y.; Nakazawa, K.; Ozawa, T.; Gu, L.; Takizawa, M.; Fujita, Y.; Nakanishi, H.; Okabe, N.; Makishima, K. ATCA 16 cm observation of CIZA J1358.9-4750: Implication of merger stage and constraint on non-thermal properties. Publ. Astron. Soc. Jpn. 2018, 70, 53. [Google Scholar] [CrossRef]
- Sofue, Y.; Machida, M.; Kudoh, T. The Primordial Origin Model of Magnetic Fields in Spiral Galaxies. Publ. Astron. Soc. Jpn. 2010, 62, 1191–1201. [Google Scholar] [CrossRef]
- Vernstrom, T.; Gaensler, B.M.; Brown, S.; Lenc, E.; Norris, R.P. Low-frequency radio constraints on the synchrotron cosmic web. Mon. Not. R. Astron. Soc. 2017, 467, 4914–4936. [Google Scholar] [CrossRef]
- Hong, S.E.; Kang, H.; Ryu, D. Radio and X-Ray Shocks in Clusters of Galaxies. Astrophys. J. 2015, 812, 49. [Google Scholar] [CrossRef]
- Akahori, T.; Ryu, D.; Gaensler, B.M. Fast Radio Bursts as Probes of Magnetic Fields in the Intergalactic Medium. Astrophys. J. 2016, 824, 105. [Google Scholar] [CrossRef]
- Ryu, D.; Kang, H.; Cho, J.; Das, S. Turbulence and Magnetic Fields in the Large-Scale Structure of the Universe. Science 2008, 320, 909–912. [Google Scholar] [CrossRef] [PubMed]
- Haverkorn, M.; Spangler, S.R. Plasma Diagnostics of the Interstellar Medium with Radio Astronomy. Space Sci. Rev. 2013, 178, 483–511. [Google Scholar] [CrossRef]
- Han, J.L. Observing Interstellar and Intergalactic Magnetic Fields. Annu. Rev. Astron. Astrophys. 2017, 55, 111–157. [Google Scholar] [CrossRef]
- Gaensler, B.M.; Beck, R.; Feretti, L. The origin and evolution of cosmic magnetism. New Astron. Rev. 2004, 48, 1003–1012. [Google Scholar] [CrossRef]
- Feretti, L.; Giovannini, G.; Govoni, F.; Murgia, M. Clusters of galaxies: Observational properties of the diffuse radio emission. Astron. Astrophys. Rev. 2012, 20, 54. [Google Scholar] [CrossRef]
- Vacca, V.; Murgia, M.; Govoni, F.; Feretti, L.; Giovannini, G.; Orra, E.; Bonafede, A. The intracluster magnetic field power spectrum in Abell 665. Astron. Astrophys. 2010, 514, A71. [Google Scholar] [CrossRef]
- Govoni, F.; Dolag, K.; Murgia, M.; Feretti, L.; Schindler, S.; Giovannini, G.; Boschin, W.; Vacca, V.; Bonafede, A. Rotation measures of radio sources in hot galaxy clusters. Astron. Astrophys. 2010, 522, A105. [Google Scholar] [CrossRef]
- Beck, R. Magnetic Visions: Mapping Cosmic Magnetism with Lofar and Ska. In Proceedings of the Conference Magnetic Fields in the Universe II: From Laboratory and Stars to the Primordial Universe, Cozumel, Mexico, 28 January–1 February 2008. [Google Scholar]
- Carilli, C.L.; Taylor, G.B. Cluster Magnetic Fields. Annu. Rev. Astron. Astrophys. 2002, 40, 319–348. [Google Scholar] [CrossRef]
- Akahori, T.; Ryu, D. Faraday Rotation Measure due to the Intergalactic Magnetic Field. II. The Cosmological Contribution. Astrophys. J. 2011, 738, 134. [Google Scholar] [CrossRef]
- Akahori, T.; Ryu, D. Faraday Rotation Measure Due to the Intergalactic Magnetic Field. Astrophys. J. 2011, 723, 476–481. [Google Scholar] [CrossRef]
- Wilman, R.J.; Miller, L.; Jarvis, M.J.; Mauch, T.; Levrier, F.; Abdalla, F.B.; Rawlings, S.; Klöckner, H.-R.; Obreschkow, D.; Olteanu, D.; et al. A semi-empirical simulation of the extragalactic radio continuum sky for next generation radio telescopes. Mon. Not. R. Astron. Soc. 2008, 388, 1335–1348. [Google Scholar] [CrossRef]
- Cho, J.; Ryu, D. Characteristic Lengths of Magnetic Field in Magnetohydrodynamic Turbulence. Astrophys. J. Lett. 2009, 705, L90–L94. [Google Scholar] [CrossRef]
- Akahori, T.; Ryu, D.; Kim, J.; Gaensler, B.M. Simulated Faraday Rotation Measures toward High Galactic Latitudes. Astrophys. J. 2013, 767, 150. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Hinz, P.M.; Wittor, D.; Locatelli, N.; Cheller, C. Probing the origin of extragalactic magnetic fields with Fast Radio Bursts. Mon. Not. R. Astron. Soc. 2018, 480, 3907–3915. [Google Scholar] [CrossRef]
- Akahori, T.; Gaensler, B.M.; Ryu, D. Statistical Techniques for Detecting the Intergalactic Magnetic Field from Large Samples of Extragalactic Faraday Rotation Data. Astrophys. J. 2014, 790, 123. [Google Scholar] [CrossRef]
- Ravi, V.; Shannon, R.M.; Bailes, M.; Bannister, K.; Bhandari, S.; Bhat, N.D.R.; Burke-Spolaor, S.; Caleb, M.; Flynn, C.; Jameson, A.; et al. The magnetic field and turbulence of the cosmic web measured using a brilliant fast radio burst. Science 2016, 354, 1249–1252. [Google Scholar] [CrossRef] [PubMed]
- Johnston-Hollitt, M.; Govoni, F.; Beck, R.; Dehghan, S.; Pratley, L.; Akahori, T.; Heald, G.; Agudo, I.; Bonafede, A.; Carretti, E.; et al. Using SKA Rotation Measures to Reveal the Mysteries of the Magnetised Universe. In Proceedings of the Advancing Astrophysics with the Square Kilometre Array (AASKA14), Giardini Naxos, Italy, 9–13 June 2014. [Google Scholar]
- Taylor, A.R.; Stil, J.M.; Sunstrum, C. A Rotation Measure Image of the Sky. Astrophys. J. 2009, 702, 1230–1236. [Google Scholar] [CrossRef]
- Oppermann, N.; Junklewitz, H.; Greiner, M.; Enßlin, T.A.; Akahori, T.; Carretti, E.; Gaensler, B.M.; Goobar, A.; Harvey-Smith, L.; Johnston-Hollitt, M.; et al. Estimating extragalactic Faraday rotation. Astron. Astrophys. 2015, 575, A118. [Google Scholar] [CrossRef]
- Hammond, A.M.; Robishaw, T.; Gaensler, B.M. A New Catalog of Faraday Rotation Measures and Redshifts for Extragalactic Radio Sources. arXiv, 2012; arXiv:1209.1438. [Google Scholar]
- Beck, A.M.; Lesch, L.; Dolag, K.; Kotarba, H.; Geng, A.; Stasyszyn, F.A. Origin of strong magnetic fields in Milky Way-like galactic haloes. Mon. Not. R. Astron. Soc. 2012, 422, 2152–2163. [Google Scholar] [CrossRef]
- Machida, M.; Akahori, T.; Nakamura, K.E.; Nakanishi, H.; Haverkorn, M. Radio broadband visualization of global three-dimensional magneto-hydrodynamical simulations of spiral galaxies II. Faraday Depolarization from 100 MHz to 10 GHz. arXiv, 2018; arXiv:1811.02829. [Google Scholar]
- Machida, M.; Akahori, T.; Nakamura, K.E.; Nakanishi, H.; Haverkorn, M. Radio broadband visualization of global three-dimensional magnetohydrodynamical simulations of spiral galaxies—I. Faraday rotation at 8 GHz. Mon. Not. R. Astron. Soc. 2018, 480, 17–25. [Google Scholar] [CrossRef]
- Akahori, T.; Kumazaki, K.; Takahashi, K.; Ryu, D. Exploring the intergalactic magnetic field by means of Faraday tomography. Publ. Astron. Soc. Jpn. 2014, 66, 65. [Google Scholar] [CrossRef]
- Farnes, J.S.; O’Sullivan, S.P.; Corrigan, M.E.; Gaensler, B.M. Faraday Rotation from Magnesium II Absorbers toward Polarized Background Radio Sources. Astrophys. J. 2014, 795, 63. [Google Scholar] [CrossRef]
- Zhu, G.; M’enard, B.M. The JHU-SDSS Metal Absorption Line Catalog: Redshift Evolution and Properties of Mg II Absorbers. Astrophys. J. 2013, 770, 130. [Google Scholar] [CrossRef]
- Schnitzeler, D.H.F.M. The latitude dependence of the rotation measures of NVSS sources. Mon. Not. R. Astron. Soc. 2010, 409, L99–L103. [Google Scholar] [CrossRef]
- Mao, S.A.; Gaensler, B.M.; Haverkorn, M.; Zweibel, E.G.; Madsen, G.J.; McClure-Griffiths, N.M.; Shukurov, A.; Kronberg, P.P. A Survey of Extragalactic Faraday Rotation at High Galactic Latitude: The Vertical Magnetic Field of the Milky Way Toward the Galactic Poles. Astrophys. J. 2010, 714, 1170–1186. [Google Scholar] [CrossRef]
- Stil, J.M.; Taylor, A.R.; Sunstrum, C. Structure in the Rotation Measure Sky. Astrophys. J. 2011, 726, 4. [Google Scholar] [CrossRef]
- Sotomayor-Beltran, C.; Sobey, C.; Hessels, J.W.T.; de Bruyn, G.; Noutsos, A.; Alexov, A.; Anderson, J.; Asgekar, A.; Avruch, I.M.; Beck, R.; et al. Calibrating high-precision Faraday rotation measurements for LOFAR and the next generation of low-frequency radio telescopes. Astron. Astrophys. 2013, 552, A58. [Google Scholar] [CrossRef]
- Brentjens, M.A.; de Bruyn, A.G. Faraday rotation measure synthesis. Astron. Astrophys. 2005, 441, 1217–1228. [Google Scholar] [CrossRef]
- Burn, B.J. On the depolarization of discrete radio sources by Faraday dispersion. Mon. Not. R. Astron. Soc. 1966, 133, 67–83. [Google Scholar] [CrossRef]
- Miyashita, Y.; Ideguchi, S.; Takahashi, K. Performance test of RM CLEAN and its evaluation with chi-square value. Publ. Astron. Soc. Jpn. 2016, 68, 44. [Google Scholar] [CrossRef]
- Sun, X.H.; Rudnick, L.; Akahori, T.; Anderson, C.S.; Bell, M.R.; Bray, J.D.; Farnes, J.S.; Ideguchi, S.; Kumazaki, K.; O’Brien, T.; et al. Comparison of Algorithms for Determination of Rotation Measure and Faraday Structure. I. 1100–1400 MHz. Astron. J. 2015, 149, 60. [Google Scholar] [CrossRef]
- Kumazaki, K.; Akahori, T.; Ideguchi, S.; Kurayama, T.; Takahashi, K. Properties of intrinsic polarization angle ambiguities in Faraday tomography. Publ. Astron. Soc. Jpn. 2014, 66, 61. [Google Scholar] [CrossRef]
- Fransworth, D.; Rudnick, L.; Brown, S. Integrated Polarization of Sources at λ ∼ 1 m and New Rotation Measure Ambiguities. Astron. J. 2011, 141, 191. [Google Scholar] [CrossRef]
- Heald, G.; Braun, R.; Edmonds, R. The Westerbork SINGS survey. II Polarization, Faraday rotation, and magnetic fields. Astron. Astrophys. 2009, 503, 409–435. [Google Scholar] [CrossRef]
- Akahori, T.; Ideguchi, S.; Aoki, T.; Takefuji, K.; Ujihara, H.; Takahashi, K. Optimum Frequency of Faraday Tomography to Explore the Inter-Galactic Magnetic Field in Filaments of Galaxies. arXiv, 2018; arXiv:1808.10546. [Google Scholar]
- Ideguchi, S.; Takahashi, K.; Akahori, T.; Kumazaki, K.; Ryu, D. Fisher analysis on wide-band polarimetry for probing the intergalactic magnetic field. Publ. Astron. Soc. Jpn. 2014, 66, 5. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akahori, T. Strategy to Explore Magnetized Cosmic Web with Forthcoming Large Surveys of Rotation Measure. Galaxies 2018, 6, 118. https://doi.org/10.3390/galaxies6040118
Akahori T. Strategy to Explore Magnetized Cosmic Web with Forthcoming Large Surveys of Rotation Measure. Galaxies. 2018; 6(4):118. https://doi.org/10.3390/galaxies6040118
Chicago/Turabian StyleAkahori, Takuya. 2018. "Strategy to Explore Magnetized Cosmic Web with Forthcoming Large Surveys of Rotation Measure" Galaxies 6, no. 4: 118. https://doi.org/10.3390/galaxies6040118
APA StyleAkahori, T. (2018). Strategy to Explore Magnetized Cosmic Web with Forthcoming Large Surveys of Rotation Measure. Galaxies, 6(4), 118. https://doi.org/10.3390/galaxies6040118




