Reverse Shock Emission from Short GRBs
Abstract
1. Introduction
2. Materials and Methods
2.1. Jet Reverse Shock
2.1.1. Self-Absorbed Reverse Shock
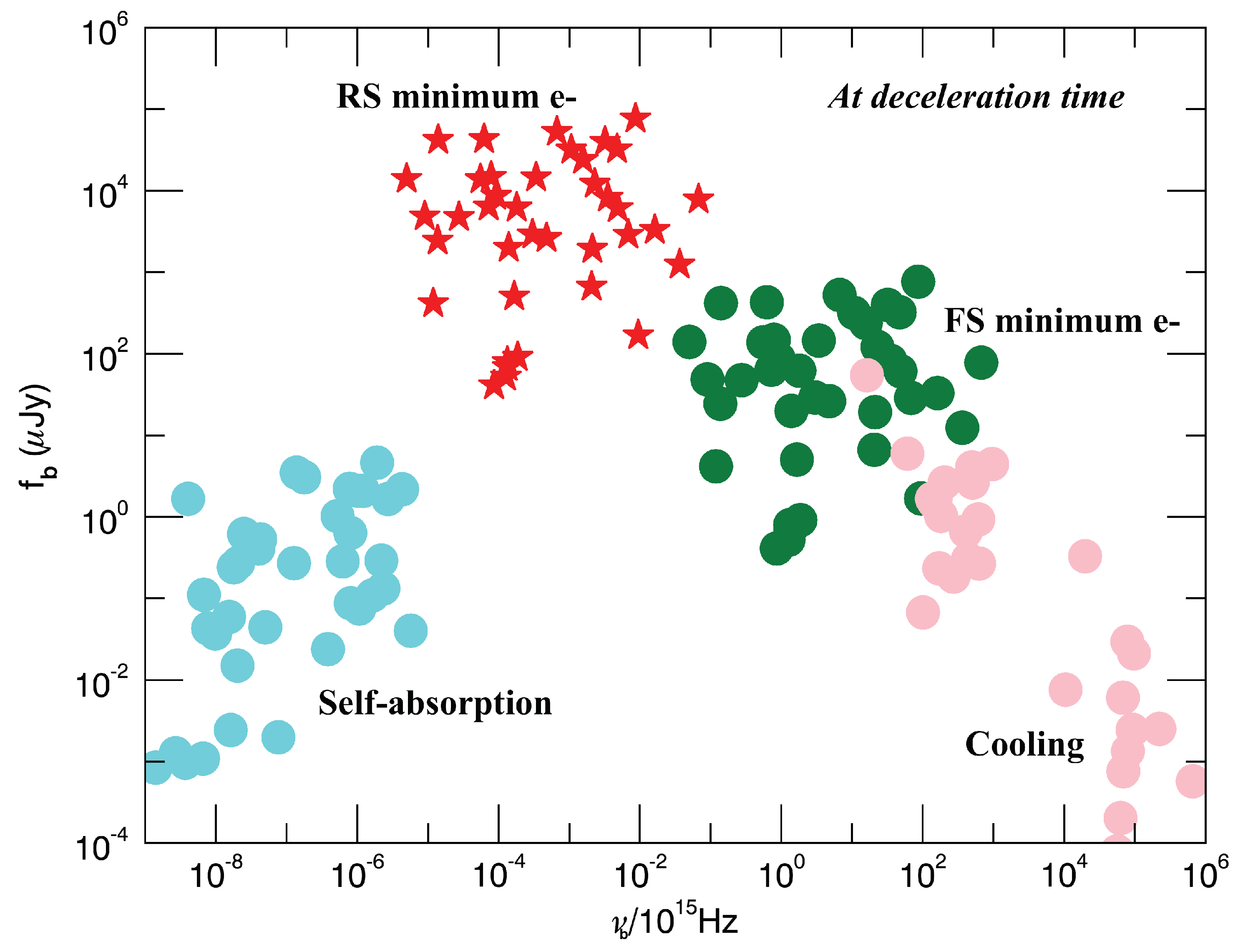
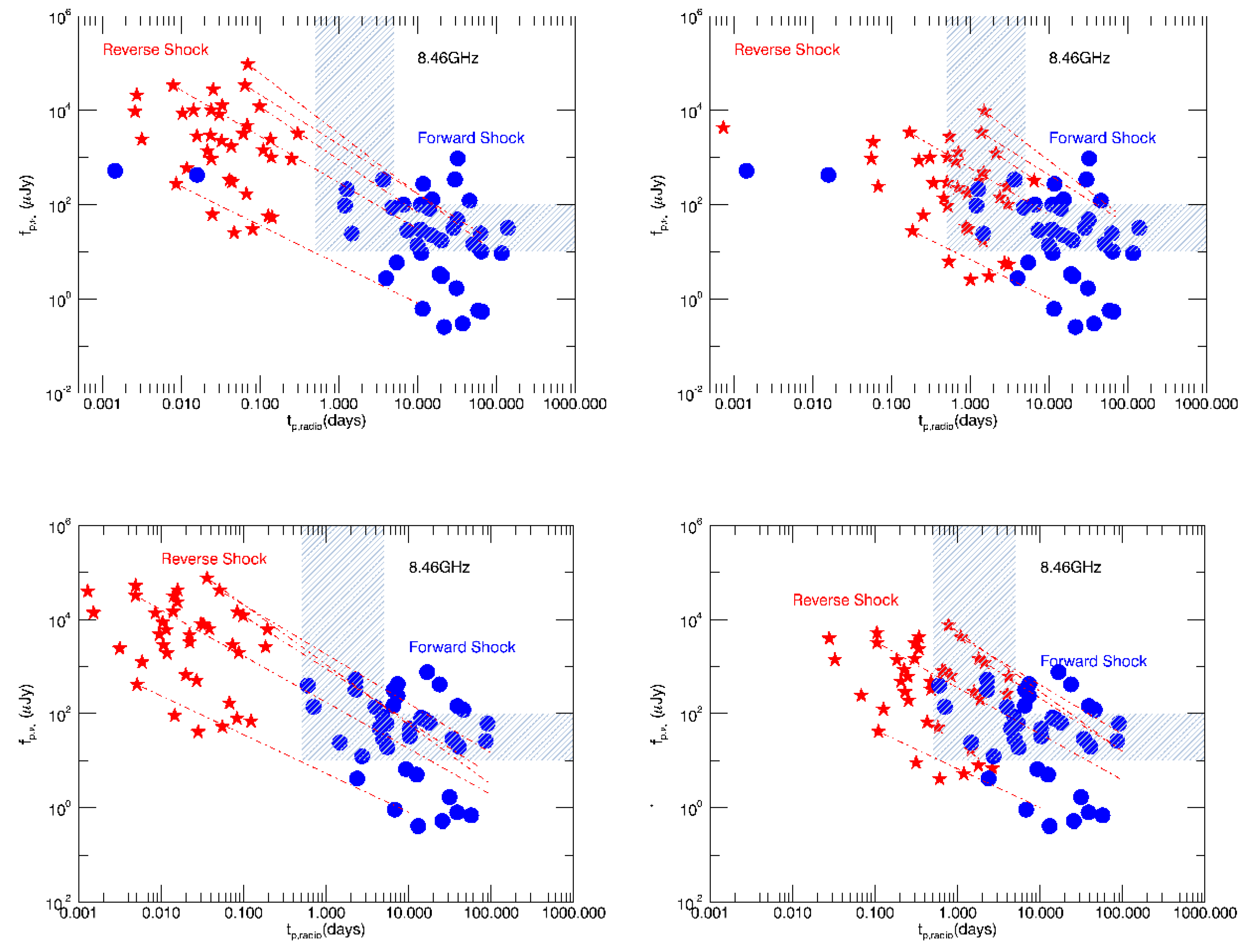
3. Results
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. A Spectacular Radio Flare from XRF 050416a at 40 Days and Implications for the Nature of X-ray Flashes. Nature 1989, 240, 126. [Google Scholar] [CrossRef]
- Narayan, R.; Paczynski, B.; Piran, T. Using the Active Collimator and Shield Assembly of an EXIST-Type Mission as a Gamma-Ray Burst Spectrometer. Astrophys. J. 1992, 395, L83. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observationso of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 1101. [Google Scholar] [CrossRef] [PubMed]
- Fox, D.B.; Frail, D.A.; Hurley, J.C. The afterglow of GRB 050709 and the nature of the short-hard gamma-ray bursts. Nature 2005, 437, 845–850. [Google Scholar] [CrossRef] [PubMed]
- Soderberg, A.; Nakar, E.; Berger, E.; Kulkarni, S.R. Late-time radio observations of 68 type Ibc supernovae: Strong constraints on off-axis gamma-ray bursts. Astrophys. J. 2006, 638, 930. [Google Scholar] [CrossRef]
- Berger, E.; Cenko, S.B.; Fox, D.B.; Cucchiara, A. Discovery of the very red near-infrared and optical afterglow of the short-duration GRB 070724A. Astrophys. J. 2009, 704, 877. [Google Scholar] [CrossRef]
- Kocevski, D.; Thöne, C.C.; Ramirez-Ruiz, E.; Bloom, J.S.; Granot, J.; Butler, N.R.; Perley, D.A.; Modjaz, M.; Lee, W.H.; Cobb, B.E. Limits on radioactive powered emission associated with a short-hard GRB 070724A in a star-forming galaxy. Mon. Not. R. Astron. Soc. 2010, 404, 963–974. [Google Scholar] [CrossRef]
- Leibler, C.N.; Berger, E. The stellar ages and masses of short gamma-ray burst host galaxies: Investigating the progenitor delay time distribution and the role of mass and star formation in the short gamma-ray burst rate. Astrophys. J. 2010, 725, 1202. [Google Scholar] [CrossRef]
- Fong, W.; Berger, E.; Fox, D.B. Hubble space telescope observations of short gamma-ray burst host galaxies: Morphologies, offsets, and local environments. Astrophys. J. 2010, 708, 9. [Google Scholar] [CrossRef]
- Berger, E. A short gamma-ray burst “No-host” problem? Investigating large progenitor offsets for short GRBs with optical afterglows. Astrophys. J. 2010, 722, 1946. [Google Scholar] [CrossRef]
- Fong, W.; Berger, E.; Chornock, R.; Margutti, R.; Levan, A.J.; Tanvir, N.R.; Tunnicliffe, R.L.; Czekala, I.; Fox, D.B.; Perley, D.A. Demographics of the galaxies hosting short-duration gamma-ray bursts. Astrophys. J. 2013, 769, 56. [Google Scholar] [CrossRef]
- Fong, W.; Berger, E.; Metzger, B.D.; Margutti, R.; Chornock, R.; Migliori, G.; Foley, R.J.; Zauderer, B.A.; Lunnan, R.; Laskar, T. Short GRB 130603B: Discovery of a jet break in the optical and radio afterglows, and a mysterious late-time X-ray excess. Astrophys. J. 2014, 780, 118. [Google Scholar] [CrossRef]
- Berger, E. Short-duration gamma-ray bursts. Annu. Rew. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Fong, W.; Berger, E.; Margutti, R.; Zauderer, B.A. A decade of short-duration gamma-ray burst broadband afterglows: Energetics, circumburst densities, and jet opening angles. Astrophys. J. 2015, 815, 102. [Google Scholar] [CrossRef]
- Lloyd-Ronning, N.M.; Fryer, C.L. On the lack of a radio afterglow from some gamma-ray bursts–insight into their progenitors? Mon. Not. R. Astron. Soc. 2017, 467, 3413–3423. [Google Scholar] [CrossRef]
- Laskar, T.; Berger, E.; Zauderer, B.A.; Margutti, R.; Soderberg, A.M.; Chakraborti, S.; Lunnan, R.; Chornock, R.; Chandra, P.; Ray, A. A reverse shock in GRB 130427A. Astrophys. J. 2013, 776, 119. [Google Scholar] [CrossRef]
- Laskar, T.; Alexander, K.D.; Berger, E.; Fong, We.; Margutti, R.; Shivvers, I.; Williams, P.K.G.; Kopač, D.; Kobayashi, S.; Mundell, C. A Reverse Shock in Grb 160509a. Astrophys. J. 2016, 833, 88. [Google Scholar] [CrossRef]
- Alexander, K.D. Radio Emission from Short Gamma-ray Bursts in the Multi-Messenger Era. arXiv, 2017; arXiv:1705.08455. [Google Scholar]
- Blandford, R.D.; McKee, C.F. Fluid dynamics of relativistic blast waves. Phys. Fluids 1976, 19, 1130. [Google Scholar] [CrossRef]
- Granot, J.; Sari, R. The shape of spectral breaks in gamma-ray burst afterglows. Astrophys. J. 2002, 568, 820. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and light curves of gamma-ray burst afterglows. Astrophys. J. 1998, 497, L17. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Optical and Long-wavelength Afterglow from Gamma-ray Bursts. Astrophys. J. 1997, 476, 231. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Predictions for the very early afterglow and the optical flash. Astrophys. J. 1999, 520, 641. [Google Scholar] [CrossRef]
- Kobayashi, S. Light curves of gamma-ray burst optical flashes. Astrophys. J. 2000, 545, 807. [Google Scholar] [CrossRef]
- Zhang, B.; Kobayashi, S.; Meszaros, P. Gamma-ray burst early optical afterglows: Implications for the initial Lorentz factor and the central engine. Astrophys. J. 2003, 595, 950. [Google Scholar] [CrossRef]
- Kobayashi, S.; Zhang, B. Early optical afterglows from wind-type gamma-ray bursts. Astrophys. J. 2003, 597, 455. [Google Scholar] [CrossRef]
- Zou, Y.C.; Wu, X.F.; Dai, Z.G. Early afterglows in wind environments revisited. Mon. Not. R. Astron. Soc. 2005, 363, 93–106. [Google Scholar] [CrossRef]
- Kulkarni, S.; Frail, D.A.; Sari, R. Discovery of a radio flare from GRB 990123. Astrophys. J. 1999, 522, L97. [Google Scholar] [CrossRef]
- Nakar, E.; Piran, T. GRB 990123 revisited: Further evidence of a reverse shock. Astrophys. J. 2005, 619, L147. [Google Scholar] [CrossRef]
- Soderberg, A.; Ramirez-Ruiz, E. Flaring up: Radio diagnostics of the kinematic, hydrodynamic and environmental properties of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2003, 345, 854–864. [Google Scholar] [CrossRef]
- Kopac, D. Radio flares from gamma-ray bursts. Astrophys. J. 2015, 806, 179. [Google Scholar] [CrossRef]
- Resmi, L.; Zhang, B. Gamma-ray burst reverse shock emission in early radio afterglows. Astrophys. J. 2016, 825, 48. [Google Scholar] [CrossRef]
- Lithwick, Y.; Sari, R. Lower limits on Lorentz factors in gamma-ray bursts. Astrophys. J. 2001, 555, 540L. [Google Scholar] [CrossRef]
- Burgess, J.M.; Greiner, J.; Bégué, D.; Berlato, F. A Bayesian Fermi-GBM Short GRB Spectral Catalog. arXiv, 2017; arXiv:1710.08362. [Google Scholar]
| GRB | (Days) | Flux (Jy) |
|---|---|---|
| 150724A | 0.57, 1.68 | 173, 465 |
| 051221A | 0.91 | 155 |
| 130603B | 0.37, 1.43 | 125, 65 |
| 140903A | 0.4, 2.4, 9.2 | 110, 187, 81 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lloyd-Ronning, N. Reverse Shock Emission from Short GRBs. Galaxies 2018, 6, 103. https://doi.org/10.3390/galaxies6040103
Lloyd-Ronning N. Reverse Shock Emission from Short GRBs. Galaxies. 2018; 6(4):103. https://doi.org/10.3390/galaxies6040103
Chicago/Turabian StyleLloyd-Ronning, Nicole. 2018. "Reverse Shock Emission from Short GRBs" Galaxies 6, no. 4: 103. https://doi.org/10.3390/galaxies6040103
APA StyleLloyd-Ronning, N. (2018). Reverse Shock Emission from Short GRBs. Galaxies, 6(4), 103. https://doi.org/10.3390/galaxies6040103





