Towards Exascale Simulations of the ICM Dynamo with WENO-Wombat
Abstract
1. Introduction
2. WENO-Wombat
2.1. WENO Algorithm
2.2. Wombat Implementation
3. Results
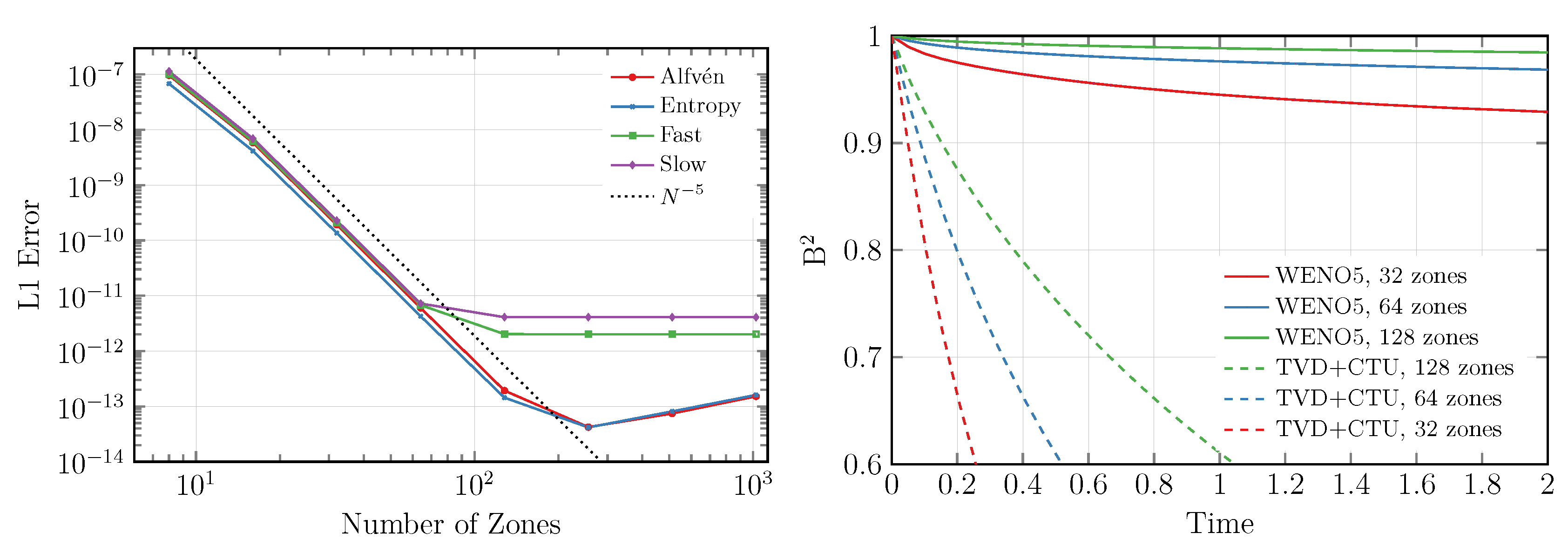
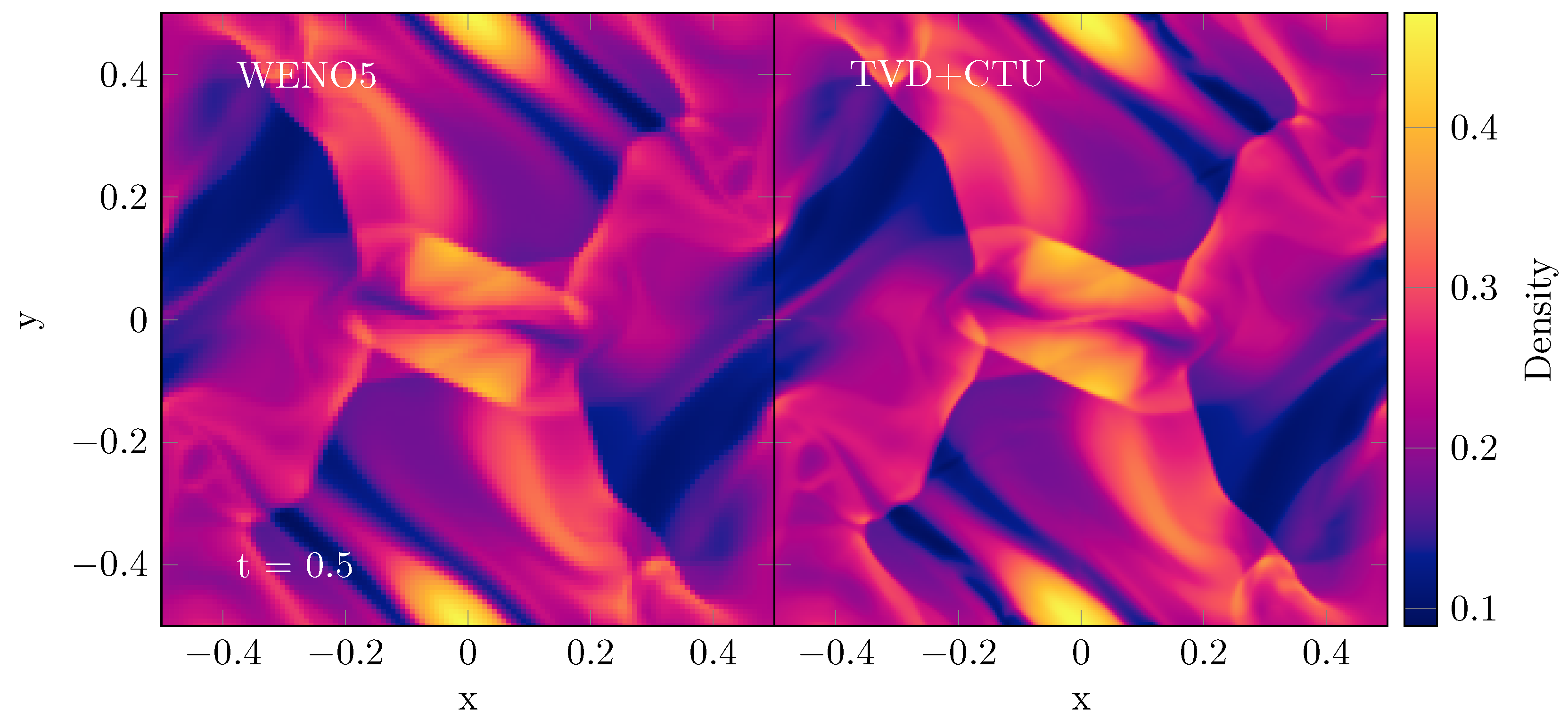
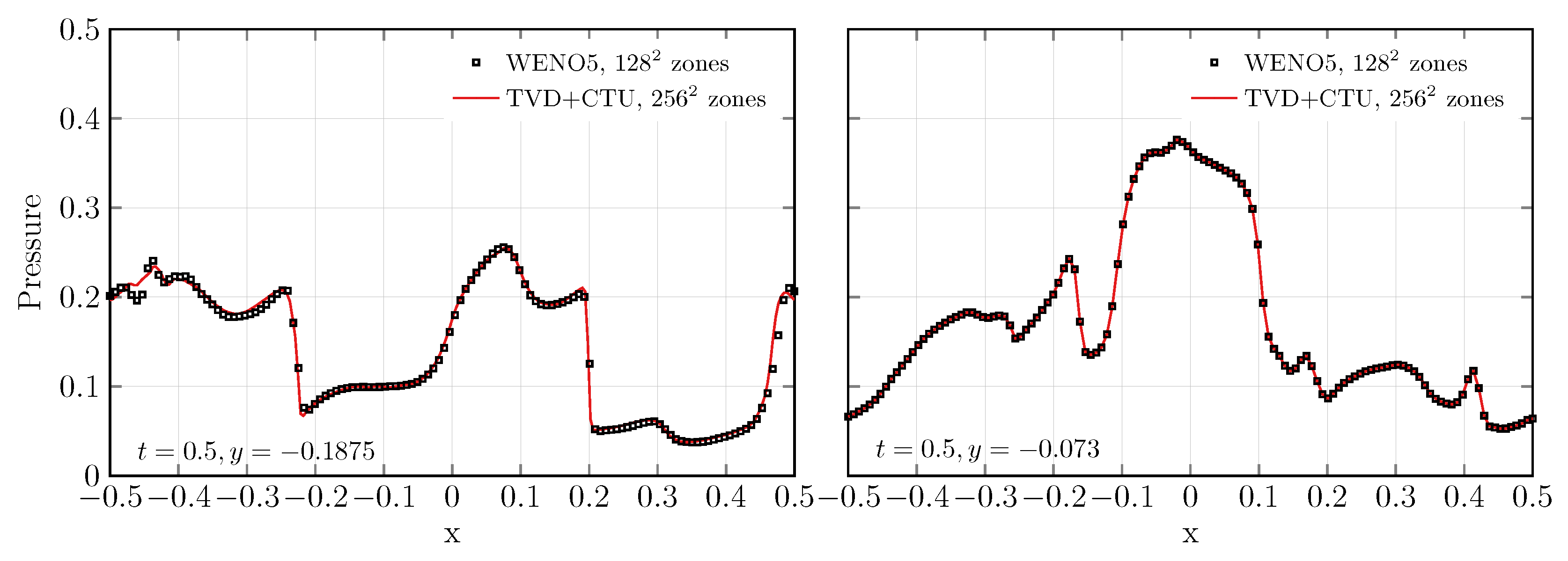
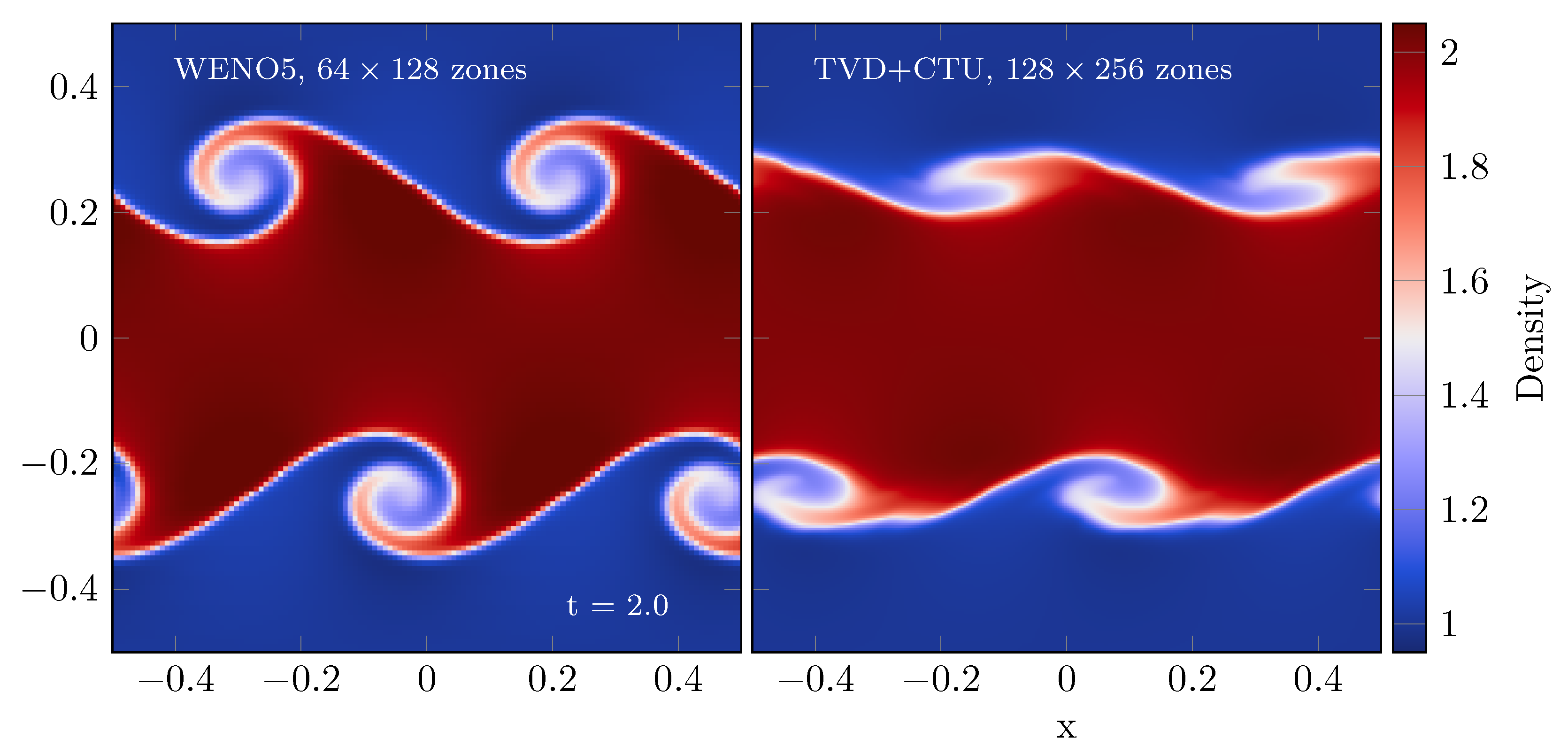
3.1. Fidelity
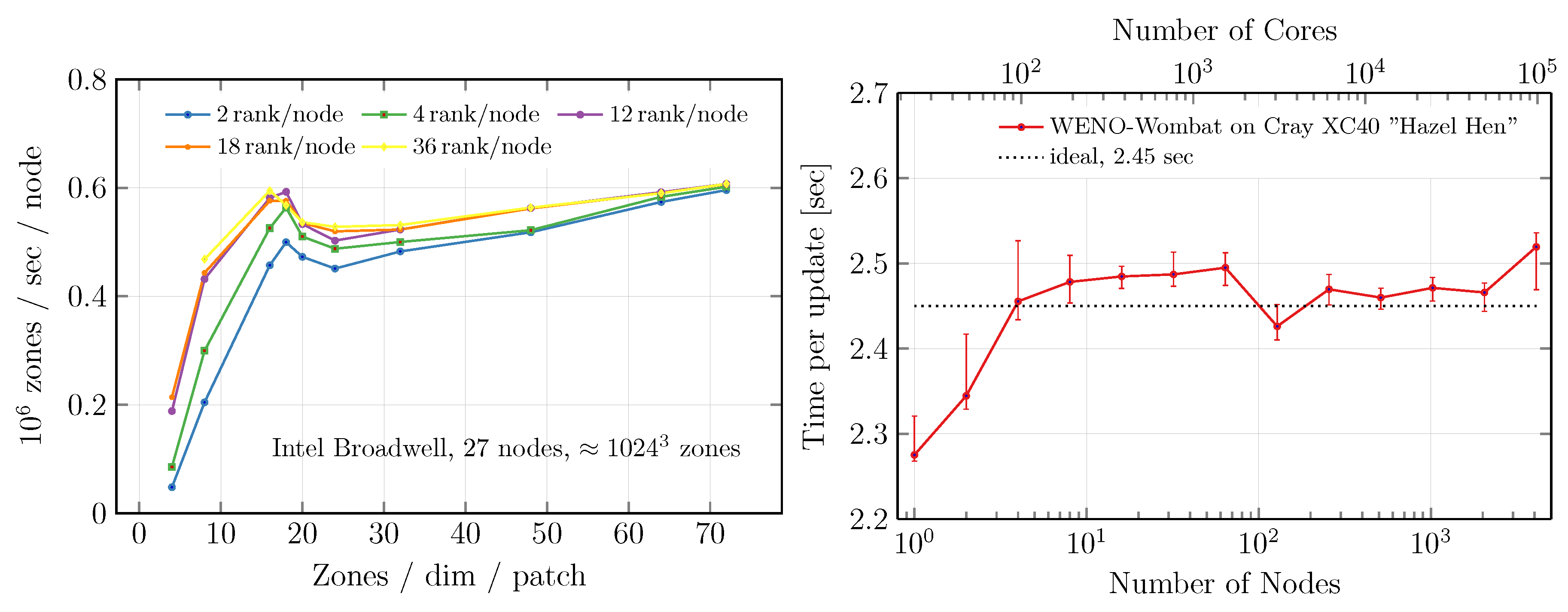
3.2. Efficiency
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schekochihin, A.A.; Cowley, S.C. Turbulence and Magnetic Fields in Astrophysical Plasmas. In Magnetohydrodynamics: Historical Evolution and Trends; Molokov, S., Moreau, R., Moffatt, H.K., Eds.; Springer: Berlin, Germany, 2007; p. 85. [Google Scholar]
- Brunetti, G.; Lazarian, A. Compressible turbulence in galaxy clusters: Physics and stochastic particle re-acceleration. Mon. Not. R. Astron. Soc. 2007, 378, 245–275. [Google Scholar] [CrossRef]
- Schekochihin, A.A.; Cowley, S.C.; Kulsrud, R.M.; Hammett, G.W.; Sharma, P. Plasma Instabilities and Magnetic Field Growth in Clusters of Galaxies. Astrophys. J. 2005, 629, 139–142. [Google Scholar] [CrossRef]
- Porter, D.H.; Jones, T.W.; Ryu, D. Vorticity, Shocks, and Magnetic Fields in Subsonic, ICM-like Turbulence. Astrophys. J. 2015, 810, 93. [Google Scholar] [CrossRef]
- Goldreich, P.; Sridhar, S. Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence. Astrophys. J. 1995, 438, 763–775. [Google Scholar] [CrossRef]
- Beresnyak, A.; Miniati, F. Turbulent Amplification and Structure of the Intracluster Magnetic Field. Astrophys. J. 2016, 817, 127. [Google Scholar] [CrossRef]
- Miniati, F. The Matryoshka Run: A Eulerian Refinement Strategy to Study the Statistics of Turbulence in Virialized Cosmic Structures. Astrophys. J. 2014, 782, 21. [Google Scholar] [CrossRef]
- Mendygral, P.J.; Radcliffe, N.; Kandalla, K.; Porter, D.; O’Neill, B.J.; Nolting, C.; Edmon, P.; Donnert, J.M.F.; Jones, T.W. WOMBAT: A Scalable and High-performance Astrophysical Magnetohydrodynamics Code. Astrophys. J. Suppl. Ser. 2017, 228, 23. [Google Scholar] [CrossRef]
- Liu, X.D.; Osher, S.; Chan, T. Weighted Essentially Non-oscillatory Schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S.R. Uniformly High Order Accurate Essentially Non-oscillatory Schemes III. J. Comput. Phys. 1987, 71, 231–303. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient Implementation of Essentially Non-oscillatory Shock-Capturing Schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- Balsara, D.S. Higher-order accurate space-time schemes for computational astrophysics-Part I: Finite volume methods. Living Rev. Comput. Astrophys. 2017, 3, 2. [Google Scholar] [CrossRef]
- Shu, C. High Order Weighted Essentially Nonoscillatory Schemes for Convection Dominated Problems. SIAM Rev. 2009, 51, 82–126. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient Implementation of Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Jiang, G.S.; Wu, C.C. A High-Order WENO Finite Difference Scheme for the Equations of Ideal Magnetohydrodynamics. J. Comput. Phys. 1999, 150, 561–594. [Google Scholar] [CrossRef]
- Roe, P. Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes. J. Comput. Phys. 1997, 135, 250–258. [Google Scholar] [CrossRef]
- Borges, R.; Carmona, M.; Costa, B.; Don, W.S. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. J. Comput. Phys. 2008, 227, 3191–3211. [Google Scholar] [CrossRef]
- Ryu, D.; Miniati, F.; Jones, T.W.; Frank, A. A Divergence-free Upwind Code for Multidimensional Magnetohydrodynamic Flows. Astrophys. J. 1998, 509, 244–255. [Google Scholar] [CrossRef]
- Gardiner, T.A.; Stone, J.M. An unsplit Godunov method for ideal MHD via constrained transport in three dimensions. J. Comput. Phys. 2008, 227, 4123–4141. [Google Scholar] [CrossRef]
- Orzang, S.A.; Tang, C.-M. Small-scale structure of two-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 1979, 90, 129–143. [Google Scholar]
- Tóth, G. The ∇·B = 0 Constraint in Shock-Capturing Magnetohydrodynamics Codes. J. Comput. Phys. 2000, 161, 605–652. [Google Scholar] [CrossRef]
- Stone, J.M.; Gardiner, T.A.; Teuben, P.; Hawley, J.F.; Simon, J.B. Athena: A New Code for Astrophysical MHD. Astrophys. J. Suppl. Ser. 2008, 178, 137–177. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Shi, J.; Shu, C.W.; Zhou, Y. Numerical viscosity and resolution of high-order weighted essentially nonoscillatory schemes for compressible flows with high Reynolds numbers. Phys. Rev. E 2003, 68, 046709. [Google Scholar] [CrossRef] [PubMed]
- Lecoanet, D.; McCourt, M.; Quataert, E.; Burns, K.J.; Vasil, G.M.; Oishi, J.S.; Brown, B.P.; Stone, J.M.; O’Leary, R.M. A validated non-linear Kelvin-Helmholtz benchmark for numerical hydrodynamics. Mon. Not. R. Astron. Soc. 2016, 455, 4274–4288. [Google Scholar] [CrossRef]
- Amdahl, G.M. Validity of the Single Processor Approach to Achieving Large Scale Computing Capabilities. In Proceedings of the Spring Joint Computer Conference, Atlantic City, NJ, USA, 18–20 April 1967; ACM: New York, NY, USA, 1967; pp. 483–485. [Google Scholar]
| 1 | The scale where magnetic and turbulent pressure are comparable, i.e., where the Lorentz force becomes important [5]. |
| 2 | |
| 3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Donnert, J.; Jang, H.; Mendygral, P.; Brunetti, G.; Ryu, D.; Jones, T. Towards Exascale Simulations of the ICM Dynamo with WENO-Wombat. Galaxies 2018, 6, 104. https://doi.org/10.3390/galaxies6040104
Donnert J, Jang H, Mendygral P, Brunetti G, Ryu D, Jones T. Towards Exascale Simulations of the ICM Dynamo with WENO-Wombat. Galaxies. 2018; 6(4):104. https://doi.org/10.3390/galaxies6040104
Chicago/Turabian StyleDonnert, Julius, Hanbyul Jang, Peter Mendygral, Gianfranco Brunetti, Dongsu Ryu, and Thomas Jones. 2018. "Towards Exascale Simulations of the ICM Dynamo with WENO-Wombat" Galaxies 6, no. 4: 104. https://doi.org/10.3390/galaxies6040104
APA StyleDonnert, J., Jang, H., Mendygral, P., Brunetti, G., Ryu, D., & Jones, T. (2018). Towards Exascale Simulations of the ICM Dynamo with WENO-Wombat. Galaxies, 6(4), 104. https://doi.org/10.3390/galaxies6040104




