Relieving Tensions Related to the Dark Matter Interpretation of the Fermi-LAT Data
Abstract
1. Introduction
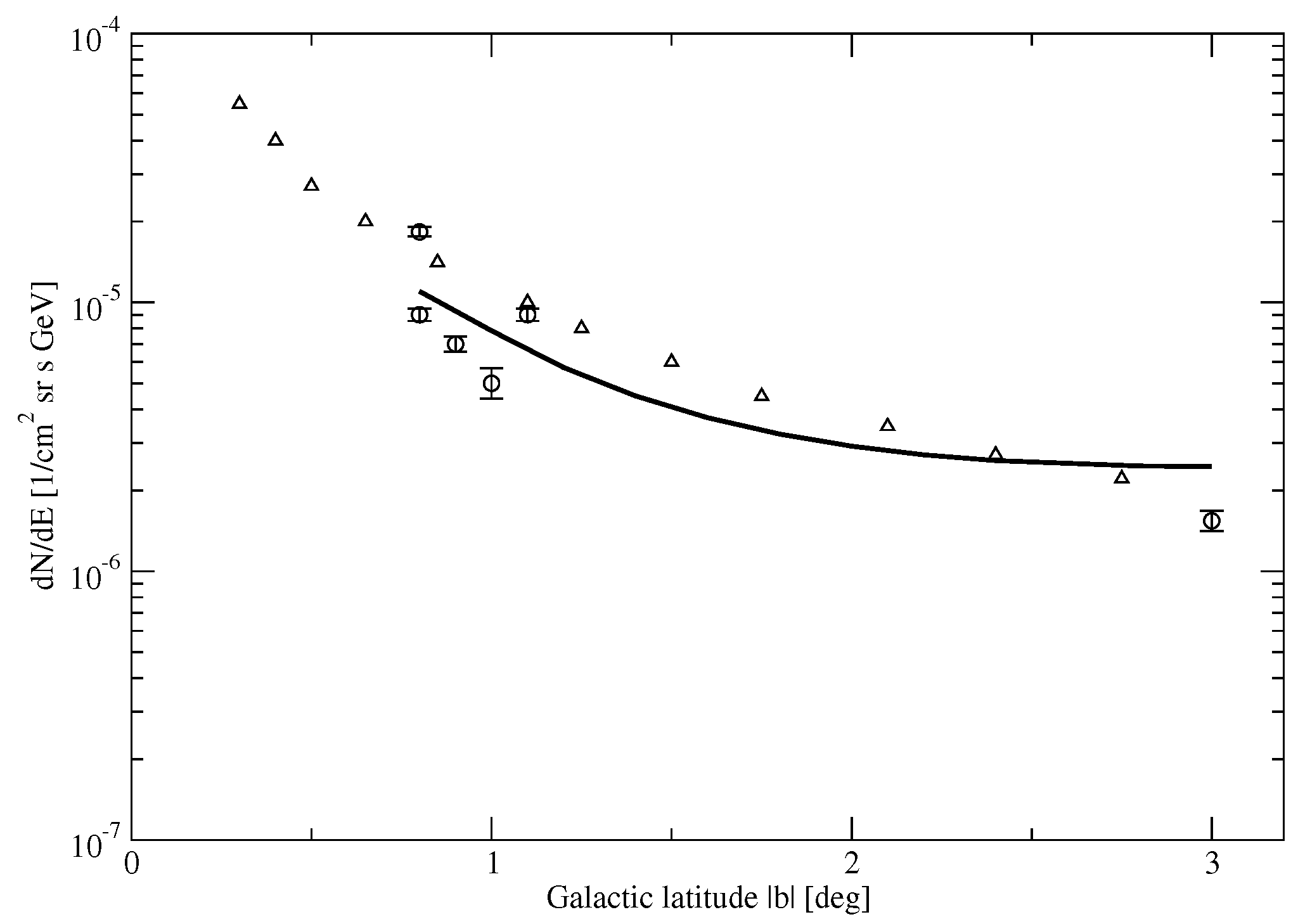
2. The Spike Structure and the Synchrotron Radiation Constraint
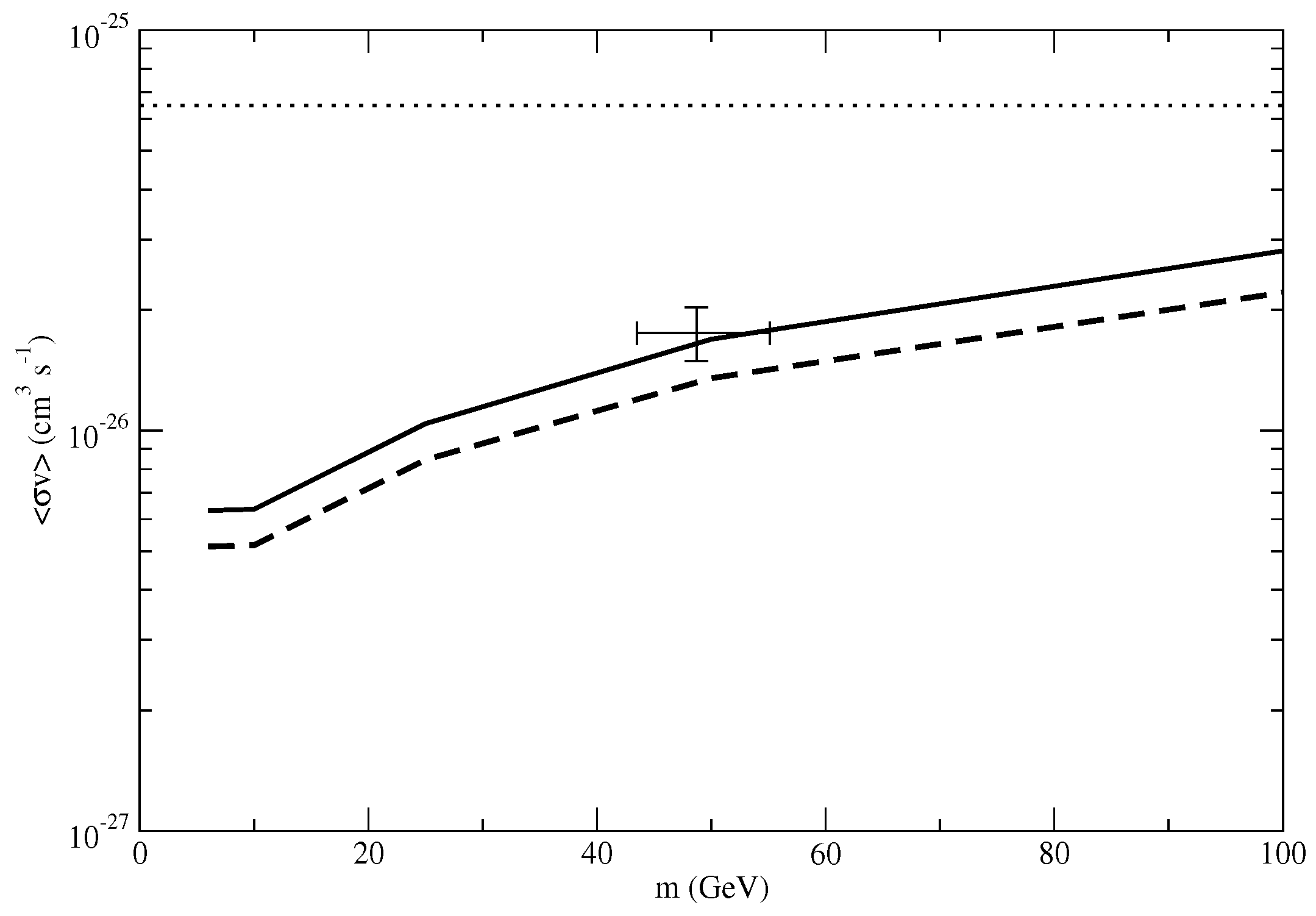
3. Constraints for Milky Way Dwarf Spheroidal Galaxies
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Hooper, D.; Slatyer, T.R. Two emission mechanisms in the Fermi Bubbles: A possible signal of annihilating dark matter. Phys. Dark Universe 2013, 2, 118–138. [Google Scholar] [CrossRef]
- Huang, W.-C.; Urbano, A.; Xue, W. Fermi Bubbles under dark matter scritiny. Part I: Astrophysical analysis. arXiv. 2013. Available online: https://arxiv.org/pdf/1307.6862.pdf (accessed on 22 August 2018).
- Hooper, D.; Cholis, I.; Linden, T.; Siegal-Gaskins, J.; Slatyer, T. Millisecond pulsars cannot account for the inner Galaxy’s GeV excess. Phys. Rev. D 2013, 88, 083009. [Google Scholar] [CrossRef]
- Daylan, T.; Finkbeiner, D.P.; Hooper, D.; Linden, T.; Portillo, S.K.N.; Rodd, N.L.; Slatyer, T.R. The charaterization of the gamma-ray signal from the central Milky Way: A case for annihilating dark matter. Phys. Dark Universe 2016, 12, 1–23. [Google Scholar] [CrossRef]
- Calore, F.; Cholis, I.; Weniger, C. Background model systematics for the Fermi GeV excess. J. Cosmol. Astropart. Phys. 2015, 2015, 038. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, B. Millisecond pulsar interpretation of the Galactic center gamma-ray excess. J. High Energy Astrophys. 2014, 3, 1–8. [Google Scholar] [CrossRef]
- Petrović, J.; Serpico, P.D.; Zaharijas, G. Millisecond pulsars and the Galactic Center gamma-ray excess: The importance of luminosity function and secondary emission. J. Cosmol. Astropart. Phys. 2015, 2015, 023. [Google Scholar] [CrossRef]
- Gaggero, D.; Taoso, M.; Urbano, A.; Valli, M.; Ullio, P. Towards a realistic astrophysical interpretation of the gamma-ray Galactic center excess. J. Cosmol. Astropart. Phys. 2015, 2015, 056. [Google Scholar] [CrossRef]
- Brandt, T.D.; Kocsis, B. Disrupted globular clusters can explain the Galactic Center gamma-ray excess. Astrophys. J. 2015, 812, 15. [Google Scholar] [CrossRef]
- Bartels, R.; Krishnamurthy, S.; Weniger, C. Strong support for the millisecond pulsar origin of the Galactic Center GeV excess. Phys. Rev. Lett. 2016, 116, 051102. [Google Scholar] [CrossRef] [PubMed]
- Gordon, C.; Macias, O. Dark matter and pulsar model constraints from Galactic Center Fermi-LAT gamma-ray observations. Phys. Rev. D 2013, 88, 083521. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Canac, N.; Horiuchi, S.; Kaplinghat, M. Astrophysical and dark matter interpretations of extended gamma-ray emission from the Galactic Center. Phys. Rev. D 2014, 90, 023526. [Google Scholar] [CrossRef]
- Izaguirre, E.; Krnjaic, G.; Shuve, B. Bottom-up approach to the Galactic Center excess. Phys. Rev. D 2014, 90, 055002. [Google Scholar] [CrossRef]
- Calore, F.; Cholis, I.; McCabe, C.; Weniger, C. A tale of tails: Dark matter interpretations of the Fermi GeV excess in light of background model systematics. Phys. Rev. D 2015, 91, 063003. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A universal density profile from hierarchical clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- Moore, B.; Quinn, T.; Governato, F.; Stadel, J.; Lake, G. Cold collapse and the core catastrophe. Mon. Not. R. Astron. Soc. 1999, 310, 1147–1152. [Google Scholar] [CrossRef]
- Hayashi, E.; Navarro, J.F.; Power, C.; Jenkins, A.; Frenk, C.S.; White, S.D.M.; Springel, V.; Stadel, J.; Quinn, T.R. The inner structure of ΛCDM haloes—II. Halo mass profiles and low surface brightness galaxy rotation curves. Mon. Not. R. Astron. Soc. 2004, 355, 794–812. [Google Scholar] [CrossRef]
- Diemand, J.; Moore, M.Z.B.; Stadel, J.; Carollo, C.M. Cusps in cold dark matter haloes. Mon. Not. R. Astron. Soc. 2005, 364, 665–673. [Google Scholar] [CrossRef]
- Ackermann, M.; Albert, A.; Anderson, B.; Atwood, W.B.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Bissaldi, E.; et al. Searching for dark matter annihilation from Milky Way dwarf spheroidal galaxies with six years of Fermi Large Area Telescope data. Phys. Rev. Lett. 2015, 115, 231301. [Google Scholar] [CrossRef] [PubMed]
- Abazajian, K.N.; Keeley, R.E. Bright gamma-ray Galactic Center excess and dark dwarfs: Strong tension for dark matter annihilation despite Milky Way halo profile and diffuse emission uncertainties. Phys. Rev. D 2016, 93, 083514. [Google Scholar] [CrossRef]
- Davies, R.D.; Walsh, D.; Booth, R.S. The radio source at the galactic nucleus. Mon. Not. R. Astron. Soc. 1976, 177, 319–333. [Google Scholar] [CrossRef]
- Cholis, I.; Hooper, D.; Linden, T. A critical reevaluation of radio constraints on annihilating dark matter. Phys. Rev. D 2015, 91, 083507. [Google Scholar] [CrossRef]
- Gondolo, P.; Silk, J. Dark matter annihilation at the Galactic Center. Phys. Rev. Lett. 1999, 83, 1719. [Google Scholar] [CrossRef]
- Fields, B.D.; Shapiro, S.L.; Shelton, J. Galactic Center gamma-ray excess from dark matter annihilation: Is there a black hole spike? Phys. Rev. Lett. 2014, 113, 151302. [Google Scholar] [CrossRef] [PubMed]
- Pontzen, A.; Governato, F. Cold dark matter heats up. Nature 2014, 506, 171–178. [Google Scholar] [CrossRef] [PubMed]
- De Blok, W.J.G. The core-cusp problem. Adv. Astron. 2010, 2010, 789293. [Google Scholar] [CrossRef]
- Governato, F.; Zolotov, A.; Pontzen, A.; Christensen, C.; Oh, S.H.; Brooks, A.M.; Quinn, T.; Shen, S.; Wadsley, J. Cuspy no more: How outflows affect the central dark matter and baryon distribution in Λ cold dark matter galaxies. Mon. Not. R. Astron. Soc. 2012, 422, 1231–1240. [Google Scholar] [CrossRef]
- Salucci, P.; Burkert, A. Dark matter scaling relations. Astrophys. J. 2000, 537, L9. [Google Scholar] [CrossRef]
- Oh, S.-H.; de Blok, W.J.G.; Brinks, E.; Walter, F.; Kennicutt, R.C. Dark and luminous matter in THINGS dwarf galaxies. Astron. J. 2011, 141, 193. [Google Scholar] [CrossRef]
- Loeb, A.; Weiner, N. Cores in dwarf galaxies from dark matter with a Yukawa potential. Phys. Rev. Lett. 2011, 106, 171302. [Google Scholar] [CrossRef] [PubMed]
- Binney, J.; Piffl, T. The distribution function of the Galaxy’s dark halo. Mon. Not. R. Astron. Soc. 2015, 454, 3653–3663. [Google Scholar] [CrossRef]
- Calore, F.; Bozorgnia, N.; Lovell, M.; Bertone, G.; Schaller, M.; Frenk, C.S.; Crain, R.A.; Schaye, J.; Theuns, T.; Trayford, J.W. Simulated Milky Way analogues: Implications for dark matter indirect searches. J. Cosmol. Astropart. Phys. 2015, 2015, 053. [Google Scholar] [CrossRef]
- Schaller, M.; Frenk, C.S.; Theuns, T.; Calore, F.; Bertone, G.; Bozorgnia, N.; Crain, R.A.; Fattahi, A.; Navarro, J.F.; Sawala, T.; et al. Dark matter annihilation radiation in hydrodynamic simulations of Milky Way haloes. Mon. Not. R. Astron. Soc. 2015, 455, 4442–4451. [Google Scholar] [CrossRef]
- Profumo, S.; Ullio, P. Multi-wavelength studies. In Particle Dark Matter: Observations, Models and Searches; Bertone, G., Ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bertone, G.; Cirelli, M.; Strumia, A.; Taoso, M. Gamma-ray and radio tests of the e± excess from DM annihilations. J. Cosmol. Astropart. Phys. 2009, 2009, 009. [Google Scholar] [CrossRef]
- Salucci, P.; Wilkinson, M.I.; Walker, M.G.; Gilmore, G.F.; Grebel, E.K.; Koch, A.; Martins, C.F.; Wyse, R.F.G. Dwarf spheroidal galaxy kinematics and spiral galaxy scaling laws. Mon. Not. R. Astron. Soc. 2012, 420, 2034–2041. [Google Scholar] [CrossRef]
- Burkert, A. The structure and dark halo core properties of dwarf spheroidal galaxies. Astrophys. J. 2015, 808, 158. [Google Scholar] [CrossRef]
- Bringmann, T.; Doro, M.; Fornasa, M. Dark matter signals from Draco and Willman 1: Prospects for MAGIC II and CTA. J. Cosmol. Astropart. Phys. 2009, 2009, 016. [Google Scholar] [CrossRef]
- Martinez, G.D. A robust determination of Milky Way satellite properties using hierarchical mass modelling. Mon. Not. R. Astron. Soc. 2015, 451, 2524–2535. [Google Scholar] [CrossRef]
- Gonzalez-Morales, A.X.; Profumo, S.; Queiroz, F.S. Effect of black holes in local dwarf spheroidal galaxies on gamma-ray constraints on dark matter annihilation. Phys. Rev. D 2014, 90, 103508. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chan, M.H. Relieving Tensions Related to the Dark Matter Interpretation of the Fermi-LAT Data. Galaxies 2018, 6, 92. https://doi.org/10.3390/galaxies6030092
Chan MH. Relieving Tensions Related to the Dark Matter Interpretation of the Fermi-LAT Data. Galaxies. 2018; 6(3):92. https://doi.org/10.3390/galaxies6030092
Chicago/Turabian StyleChan, Man Ho. 2018. "Relieving Tensions Related to the Dark Matter Interpretation of the Fermi-LAT Data" Galaxies 6, no. 3: 92. https://doi.org/10.3390/galaxies6030092
APA StyleChan, M. H. (2018). Relieving Tensions Related to the Dark Matter Interpretation of the Fermi-LAT Data. Galaxies, 6(3), 92. https://doi.org/10.3390/galaxies6030092



