Multi-Wavelength Observations and Modeling of Loop I †
Abstract
1. Introduction
- Energetics: whether the underlying star formation and supernova (SN) rates during the history of Loop I formation are sufficient to feed it?
- Mass budget: whether the gas mass confined into Loop I (accounting in particular, X-ray gas in the NPS) is consistent with the overall evolutionary scenario? (see also [18]).
- Dust mass budget: whether the dust mass as inferred from infrared observations fits this evolutionary path, particularly when the morphology of dust distribution and its temperature with possible dust sputtering in high temperature environment of the NPS are accounted for?
- HI and its kinematics: what would be the fraction of atomic hydrogen in the expanding shell associated with Loop I and whether it is consistent with observational data? Whether the velocity field in 21 cm toward the Galactic center adequately displays the expanding supershell associated with Loop I? (see also [19]).
- Synchrotron: are characteristics of synchrotron emission in Loop I (spectral index, magnetic field) are compatible with its evolutionary scenario? (see also [20]).
- Time scales: whether typical time scales: dynamical, radiative cooling, and dust destruction, do fit the evolutionary scenario?
- Morphology and asymmetry: is Loop I (and the X-ray NPS) physically and genetically connected to the Fermi Bubbles?
2. Evolution of Loop I and Its Driving Engine
2.1. Energetics
2.1.1. Local Hot Bubble and the Supershell from Sco-Cen
2.1.2. Stellar Activity in the Central Molecular Zone and Loop I
2.1.3. Continuous Wind vs. Instant Implosions
2.2. Mass Budget
2.2.1. —The Hot Gas Mass in the NPS
2.2.2. NPS Morphology
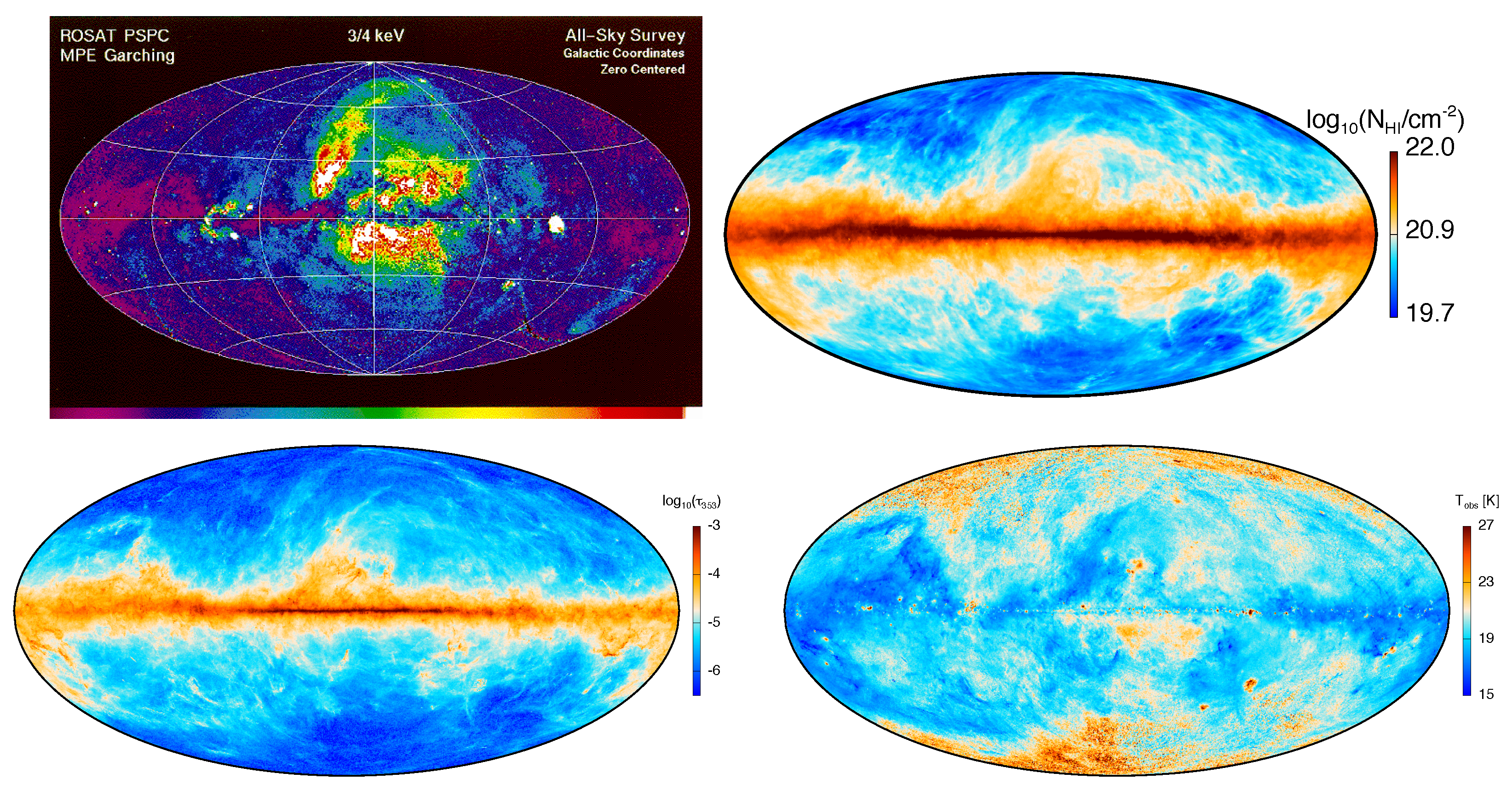
2.3. HI Around NPS
Abundance Pattern in the NPS
2.4. Dust
2.4.1. Dust Mass in Filament
2.4.2. Dust Temperature
2.5. Synchrotron
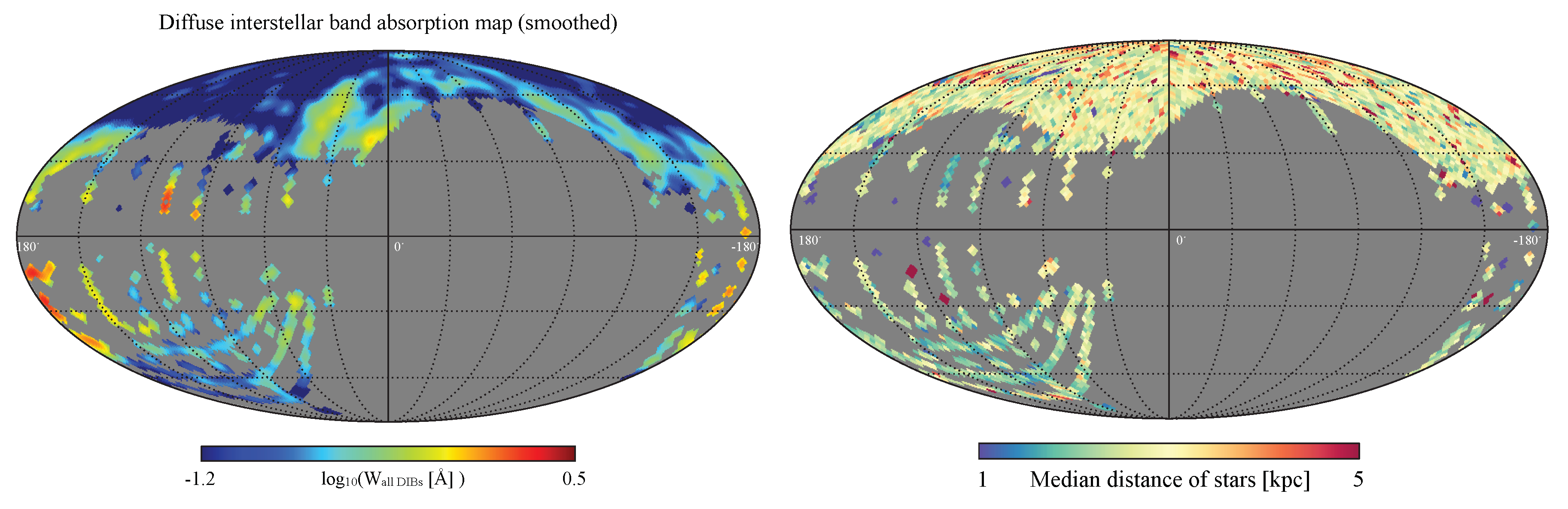
2.6. DIBs in the NPS
3. Conclusions
- Energetic events in the Galactic center and the very existence of the Fermi-bubbles make it very attractive to think, that all this is produced by a collective SN activity in the center. The conclusion of whether a weak central SF rate—SRF ≲ yr is sufficient for maintaining these structures, crucially depends on the numerical model: luminosity-driven wind scenarios require an order of magnitude higher SFR, while randomly spread isolated SNe can apparently do the work with a lower SFR.
- The mass of HI filament inferred from 21 cm column density, and the gas mass of a coincidental filament north-east of the X-ray component of NPS are nearly equal, which would mean that they are physically connected. However, their position with respect to the X-ray NPS indicates most likely that they represent warm gas isolated of the X-ray gas.
- Mass budget and energetics of the X-ray gas of NPS can be maintained by the central star formation of SFR yr during ∼ Myr, within the model of randomly positioned isolated SN explosions as the energy source. However, the dust mass in the X-ray NPS as inferred from far infrared emission at 353 GHz is factor of 3 higher than would be expected from a more than 30 Myr old NPS.
- An enhanced N/O ratio in the NPS reported by Miller et al. [59] does not look to match conditions in the Galacto-centric model. It is easer understood within the Sco-Cen scenario.
- Loop I synchrotron emission and, in particular, softening of its spectrum toward lower frequencies (10 to 820 MHz) in comparison to higher ones (1.4 to 2.3 GHz) is consistent most likely with the galacto-centric scenario.
- On the other hand, discovery of DIB SDSS absorptions in spectra of stars within 2 to 3 kpc sheds a new light on the problem, because the most strong DIB absorptions seem to outline the same regions on sky containing the Loop I and related HI, and the X-ray structures. This may indicate that either these structures are all placed relatively locally, within 2–3 kpc, or otherwise one has to conclude that not all of them are physically connected. For instance, synchrotron Loop I and X-ray NPS gas might arise due to SN activity in the GC, while HI and filaments and plumes along with DIB absorptions represent frontside structures within 2–3 kpc.
Acknowledgments
Conflicts of Interest
References
- Hanbury Brown, R.; Davies, R.D.; Hazard, C. A curious feature of the radio sky. Observatory 1960, 80, 191–198. [Google Scholar]
- Large, M.I.; Quigley, M.J.; Haslam, C.G. A radio study of the North Polar Spur. Mon. Not. R. Astron. Soc. 1964, 127, 273–285. [Google Scholar]
- Landecker, T.L.; Wielebinski, R. The galactic metre wave radiation. Aust. J. Phys. Astrophys. 1970, 16, 1–31. [Google Scholar]
- Berkhuijsen, E.M. The survey of the continuum radiation at 820 MHz between declinations -7∘ and +85∘. Astron. Astrophys. 1971, 14, 359–386. [Google Scholar]
- Haslam, C.G.T.; Salter, C.J.; Stoffel, H.; Wilson, W.E. A 408 MHz all-sky continuum survey. II—The atlas of contour maps. Astron. Astrophys. Suppl. Ser. 1982, 47, 1–142. [Google Scholar]
- Heiles, C. HI shells and supershells. Astrophys. J. 1979, 229, 533–537. [Google Scholar] [CrossRef]
- Heiles, C. HI shells, supershells, shell-like objects, and ‘worms’. Astrophys. J. Suppl. Ser. 1984, 55, 585–595. [Google Scholar] [CrossRef]
- Smith, R.K.; Cox, D.P. Modeling the Local Bubble using multiple supernova remnants. In The Local Bubble and Beyond Lyman-Spitzer-Colloquium; Springer: Berlin/Heidelberg, Germany, 1998; pp. 133–136. [Google Scholar]
- Breitschwerdt, D.; de Avillez, M.A. The history and future if the local and Loop I bubbles. Astron. Astrophys. 2006, 452, L1–L5. [Google Scholar] [CrossRef]
- Preibisch, T.; Mamajek, E. The nearest OB association: Scorpius-Centaurus OB2. In Handbook of Star Forming Regions, Volume II: The Southern Sky; Reipurth, B., Ed.; ASP Monograph: San Francisco, CA, USA, 2008. [Google Scholar]
- Sofue, Y.; Handa, T. A radio lobe over the Galactic center. Nature 1984, 310, 568–569. [Google Scholar] [CrossRef]
- Sofue, Y. The relation of Galactic radio spurs to spiral arms. Astron. Astrophys. 1976, 48, 1–10. [Google Scholar]
- Sofue, Y. Propagation of magnetohydrodynamic waves from the Galactic center. Astron. Astrophys. 1977, 60, 327–336. [Google Scholar]
- Martos, M.A.; Cox, D.P. Magnetohydrodynamic modeling of a galactic spiral arm as a combination shock and hydraulic jump. Astrophys. J. 1998, 509, 703–716. [Google Scholar] [CrossRef]
- Gómez, G.C.; Cox, D.P. Three-dimensional magnetohydrodynamic modeling of the gaseous structure of the Galaxy: description of the simulations. Astrophys. J. 2004, 615, 744–757. [Google Scholar] [CrossRef]
- Lallement, R.; Snowden, S.; Kuntz, K.D.; Dame, T.M.; Koutroumpa, D.; Grenier, I.; Casandjian, J.M. On the distance to the North Polar Spur and the local CO-H2 factor. Astron. Astrophys. 2016, 595, A131–A147. [Google Scholar] [CrossRef]
- Green, G.M.; Schlafly, E.F.; Finkelbeiner, D.P.; Rix, H.W.; Martin, N.; Burgett, W.; Draper, P.W.; Flewelling, H.; Hodapp, K.; Kaiser, N.; et al. A Three-dimensional map of Milky Way dust. Astrophys. J. 2015, 810, 25. [Google Scholar] [CrossRef]
- Kataoka, J.; Sofue, Y.; Inoue, Y.; Akita, M.; Nakashima, S.; Totani, T. X-ray and Gamma-ray observations of the Fermi Bubbles and NPS/Loop I structures. Galaxies 2018, 6, 27. [Google Scholar] [CrossRef]
- McClure-Griffits, N. HI in the direction of the Galactic centre. In Proceedings of the Talk Presented at This Meeting, Stanford, CA, USA, 31 March–1 April 2017. [Google Scholar]
- Dickinson, C. Overview of large-scale features in the radio sky. In Proceedings of the Talk Presented at This Meeting, Stanford, CA, USA, 31 March–1 April 2017. [Google Scholar]
- Weaver, H. Large supernova remnants as common features of the disk. In Symposium-International Astronomical Union; Cambridge University Press: Cambridge, UK, 1974; pp. 295–300. [Google Scholar]
- Egger, R.J.; Aschenbach, B. Interaction of the Loop I supershell with the Local Hot Bubble. Astron. Astrophys. 1995, 294, L25–L28. [Google Scholar]
- Karberla, P.M.W.; Dedes, L. Global properties of the HI distribution in the outer Milky Way. Planar and extraplanar gas. Astron. Astrophys. 2008, 487, 951–963. [Google Scholar] [CrossRef]
- Marasco, A.; Fraternali, F.; van der Hulst, J.M.; Oosterloo, T. Distribution and kinematics of atomic and molecular gas inside the solar circle. Astron. Astrophys. 2017, 607, A106. [Google Scholar] [CrossRef]
- Zhu, H.; Tian, W.; Li, A.; Zhang, M. The gas-to-extinction ratio and the gas distribution in the Galaxy. Mon. Not. R. Astron. Soc. 2017, 471, 3494–3528. [Google Scholar] [CrossRef]
- Schulreich, M.M.; Breitschwerdt, D.; Feige, J.; Dettbarn, C. Numerical studies on the link between radioisotopic signatures on Earth and the formation of the Local Bubble. I. 60Fe transport to the solar system by turbulent mixing of ejecta from nearby supernovae into a locally homogeneous interstellar medium. Astron. Astrophys. 2017, 604, A81. [Google Scholar] [CrossRef]
- Korolev, V.V.; Vasiliev, E.O.; Kovalenko, I.G.; Shchekinov, Y.A. Dynamics of a supernova shell in a cloudy interstellar medium. Astron. Rep. 2015, 59, 690–708. [Google Scholar] [CrossRef]
- Santos, F.P.; Corradi, W.; Reis, W. Optical polarization mapping toward the interface between the Local Cavity and Loop I. Astrophys. J. 2011, 728, 104. [Google Scholar] [CrossRef]
- Pecaut, M.J.; Mamajek, E.E.; Bubar, E.J. A revised age for Upper Scorpius and the star formation history among the F-type members of the Scorpius-Centaurus OB—Association. Astrophys. J. 2012, 746, 154–176. [Google Scholar] [CrossRef]
- Donaldson, J.K.; Weinberger, A.J.; Gagné, J.; Boss, A.P.; Keiser, S.A. New parralaxes for the Upper Scorpius OB association. Astrophys. J. 2017, 850, 11. [Google Scholar] [CrossRef]
- Hyde, M.; Pecaut, M.J. Supernova Ejecta in ocean cores used as time constraints for nearby stellar groups. arXiv, 2017; arXiv:1712.05466. [Google Scholar]
- Sofue, Y. The North Polar Spur and Aquila Rift. Mon. Not. R. Astron. Soc. 2015, 447, 3824–3831. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Aniano, G.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck intermediate results. XXVIII. Interstellar gas and dust in the Chamaeleon clouds as seen by Fermi LAT and Planck. Astron. Astrophys. 2015, 582, A31. [Google Scholar]
- Sun, X.H.; Gaensler, B.M.; Carretti, E.; Purcell, C.R.; Staveley-Smith, L.; Bernardi, G.; Haverkorn, M. Absolutely calibrated radio polarimetry of the inner Galaxy at 2.3 and 4.8 GHz. Not. R. Astron. Soc. 2014, 437, 2936–2947. [Google Scholar] [CrossRef]
- Vasiliev, E.O.; Nath, B.B.; Shchekinov, Y.A. Evolition of multiple supernovae remnants. Mon. Not. R. Astron. Soc. 2015, 446, 1703–1715. [Google Scholar] [CrossRef]
- Sofue, Y. Galactic center shells and a reccurent starburst model. Publ. Astron. Soc. Jpn. 2003, 55, 445–450. [Google Scholar] [CrossRef]
- Oort, J. The galactic center. Astron. Astrophys. 1977, 15, 295–362. [Google Scholar] [CrossRef]
- Sofue, Y. Giant explosion in the Galactic Center and huge shocked shells in the halo. Astrophys. J. 1994, 431, L91–L93. [Google Scholar] [CrossRef]
- Bland-Hawthorn, J.; Cohen, M. The largescale bipolar wind in the Galactic center. Astrophys. J. 2003, 582, 246–256. [Google Scholar] [CrossRef]
- Serabyn, E.; Morris, M. Sustained star formation in the central stellar cluster of the Milky Way. Nature 1996, 382, 602–604. [Google Scholar] [CrossRef]
- Yusef-Zadeh, F.; Hewitt, J.W.; Arendt, R.G.; Whitney, B.; Rieke, G.; Wardle, M.; Hinz, J.L.; Stolovy, S.; Lang, C.C.; Burton, M.G.; et al. Star formation in the central 400 pc of the Milky Way: Evidence for a population of massive young stellar objects. Astrophys. J. 2009, 702, 178–225. [Google Scholar] [CrossRef]
- Sarkar, K.C.; Nath, B.B.; Sharma, P. Multiwavelength features of Fermi bubbles as signatures of a Galactic wind. Mon. Not. R. Astron. Soc. 2015, 453, 3827–3838. [Google Scholar] [CrossRef]
- Koepferl, C.M.; Robitaille, T.P.; Morales, E.F.E.; Johnston, K.G. Main-sequence stars masquerading as young stellar objects in the Central Molecular Zone. Astrophys. J. 2015, 799, 53. [Google Scholar] [CrossRef]
- Barnes, A.T.; Longmore, S.N.; Battersby, C.; Bally, J.; Kruijssen, J.M.; Henshaw, J.D.; Walker, D.L. Star formation rates and efficiencies in the Galactic center. Mon. Not. R. Astron. Soc., 2017, 469, 2263–2285. [Google Scholar] [CrossRef]
- Crocker, R. Nonthermal insights on mass and energy flows through the Galactic centre and into the Fermi bubbles. Mon. Not. R. Astron. Soc. 2012, 423, 3512–3539. [Google Scholar] [CrossRef]
- Nath, B.B.; Shchekinov, Y.A. Conditions for supernova-driven galactic winds. Astrophys. J. Lett. 2013, 777, L12. [Google Scholar] [CrossRef]
- Roy, A.; Nath, B.B.; Sharma Shchekinov, Y.A. Superbubble breakout and galactic widns from disc galaxies. Mon. Not. R. Astron. Soc. 2013, 434, 3572–3581. [Google Scholar] [CrossRef]
- Sharma, P.; Roy, A.; Nath, B.B.; Shchekinov, Y.A. In a hot bubble: why does superbubble feedback work, but isolated supernovae do not. Mon. Not. R. Astron. Soc. 2014, 443, 3463–3476. [Google Scholar] [CrossRef]
- Chevalier, R.A.; Clegg, A.W. Wind from a starburst galaxy nucleus. Nature 1985, 317, 44–45. [Google Scholar] [CrossRef]
- Vasiliev, E.O.; Shchekinov, Y.A.; Nath, B.B. Growing superbubbles in a stratified ISM. Mon. Not. R. Astron. Soc. 2018. submitted. [Google Scholar]
- Mac Low, M.M.; McCray, R.; Norman, M.L. Superbubble blowout dynamics. Astrophys. J. 1989, 337, 141–154. [Google Scholar] [CrossRef]
- Sofue, Y. Giant HI hole inside the 3-kpc ring and the North Polar Spur—The Galactic crater. Publ. Astron. Soc. Jpn. 2017, 69, L8. [Google Scholar] [CrossRef]
- Sofue, Y. The 200-pc molecular cylinder in the Galactic center. Mon. Not. R. Astron. Soc. 2017, 470, 1982–1990. [Google Scholar] [CrossRef]
- Sofue, Y.; Habe, A.; Kataoka, J.; Totani, T.; Inoue, Y.; Nakashima, S.; Matsui, H.; Akita, M. Galactic-center hyper-shell model for the North Polar Spurs. Mon. Not. R. Astron. Soc. 2017, 459, 108–120. [Google Scholar] [CrossRef]
- Willingale, R.; Hands, A.D.; Warwick, R.S.; Snowden, S.L.; Burrows, D.N. The X-ray spectrum of the North Polar Spur. Mon. Not. R. Astron. Soc. 2003, 343, 995–1001. [Google Scholar] [CrossRef]
- Cooper, J.L.; Bicknell, G.V.; Sutherland, R.S.; Bland-Hawthorn, J. Three-dimensional simulations of a starburst-driven galactic wind. Astrophys. J. 2008, 674, 157–171. [Google Scholar] [CrossRef]
- Tanner, R.; Cecil, G.; Heitsch, F. Starburst-driven galactic superbubbles radiating to 10 K. Astrophys. J. 2016, 821, 7–13. [Google Scholar] [CrossRef]
- Oka, T.; Hasegawa, T.; Sato, F.; Tsuboi, M.; Miyazaki, A. A Large-SCale CO survey of the Galactic Center. Astrophys. J. Suppl. Ser. 1998, 118, 455–515. [Google Scholar] [CrossRef]
- Miller, E.D.; Tsunemi, H.; Bautz, M.W.; McCammon, D.; Fujimoto, R.; Hughes, J.P.; Katsuda, S.; Kokubun, M.; Mitsuda, K.; Porter, F.S.; et al. Suzaku observations of the North Polar Spur: Evidence for Nitrigen enhancement. Publ. Astron. Soc. Jpn. 2008, 60, S95–S106. [Google Scholar] [CrossRef]
- Walter, F.; Weiss, A.; Scoville, N. Molecular gas in M82: Resolving the outflow and streamers. Astrophys. J. 2002, 580, L21–L25. [Google Scholar] [CrossRef]
- Snowden, S.L.; Freyberg, M.J.; Plucinsky, P.P.; Schmitt, J.H.; Trümper, J.; Voges, W.; Edgar, R.J.; McCammon, D.; Sanders, W.T. First maps of the soft X-ray diffuse background from the ROSAT XRT/PSPC all-sky survey. Astrophys. J. 1995, 454, 643–653. [Google Scholar] [CrossRef]
- Abergel, A.; Ade, P.A.; Aghanim, N.; Alves, M.I.; Aniano, G.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; et al. Planck 2013 results. XI. All-sky model of thermal dust emission. Astron. Astrophys. 2014, 571, A11. [Google Scholar]
- Kalberla, P.M.; Burton, W.B.; Hartmann, D.; Arnal, E.M.; Bajaja, E.; Morras, R.; Pöppel, W.G. The Leiden/Argentine/Bonn (LAB) survey of galactic HI. Final data release of the combined LDS and IAR surveys with improved stray-radiation correction. Astron. Astrophys. 2005, 440, 775–782. [Google Scholar] [CrossRef]
- Reynolds, R.J.; Tufte, S.L.; Kung, D.T.; McCullough, P.R.; Heiles, C. A comparison of diffuse ionized and neutral hydrogen away from the Galactic plane: Hα-emitting HI clouds. Astrophys. J. 1995, 448, 715–726. [Google Scholar] [CrossRef]
- Haffner, L.M.; Dettmar, R.J.; Beckman, J.E.; Wood, K.; Slavin, J.D.; Giammanco, C.; Madsen, G.J.; Zurita, A.; Reynolds, R.J. The warm ionized medium in spiral galaxies. Rev. Mod. Phys. 2009, 81, 969–997. [Google Scholar] [CrossRef]
- Finkbeiner, D.P. A Full-Sky Hα Template for Microwave Foreground Prediction. Astron. Astrophys. 2003, 146, 407–415. [Google Scholar] [CrossRef]
- Hill, A.S.; Reynolds, R.J.; Benjamin, R.A.; Haffner, L.M. Density distribution of the warm ionized medium. Astrophysics 2007, 365, 250–253. [Google Scholar]
- Witt, A.N.; Gold, B.; Barnes, F.S.; DeRoo, C.T.; Vijh, U.P.; Madsen, G.J. On the origins of the high-latitude Hα background. Astrophys. J. 2010, 724, 1551–1560. [Google Scholar] [CrossRef]
- Woosley, S.E.; Waever, T.A. The Evolution and Explosion of Massive Stars. II. Explosive Hydrodynamics and Nucleosynthesis. Astron. Astrophys. 1995, 101, 181–235. [Google Scholar]
- Compiègne, M.; Verstraete, L.; Jones, A.; Bernard, J.P.; Boulanger, F.; Flagey, N.; Le Bourlot, J.; Paradis, D.; Ysard, N. The global dust SED: Tracing the nature and evolution of dust with DustEM. Astron. Astrophys. 2011, 525, A103. [Google Scholar] [CrossRef]
- Berezhko, E.G. Gamma-ray astronomy and cosmic ray origin problem. Adv. Space Res. 2005, 35, 1031–1040. [Google Scholar] [CrossRef]
- Dubner, G.; Giacani, E. Radio emission from supernova remnants. Astron. Astrophys. Rev. 2015, 23, 3. [Google Scholar] [CrossRef]
- Vidal, M.; Dickinson, C.; Davies, R.D.; Leahy, J.P. Polarised radio filaments outside the Galactic plane. Mon. Not. R. Astron. Soc. 2015, 452, 656–675. [Google Scholar] [CrossRef]
- Dettmar, R.-J.; Shchekinov, Y.A. Nonthermal radio-continuum from blow-outs and magnetic Parker loops. In Proceedings of the 27th International Cosmic Ray Conference, Hamburg, Germany, 7–15 August 2001. [Google Scholar]
- Zheng, H.; Tegmark, M.; Dillon, J.S.; Kim, D.A.; Liu, A.; Neben, A.R.; Jonas, J.; Reich, P.; Reich, W. An improved model of diffuse galactic radio emission from 10 MHz to 5 THz. Mon. Not. R. Astron. Soc. 2017, 464, 3486–3497. [Google Scholar] [CrossRef]
- Adebahr, B.; Krause, M.; Klein, U.; Weżgowiec, M.; Bomans, D.J.; Dettmar, R.J. M 82—A radio continuum and polarisation study. I. Data reduction and cosmic ray propagation. Astron. Astrophys. 2013, 555, A23. [Google Scholar] [CrossRef]
- Heesen, V.; Dettmar, R.J.; Krause, M.; Beck, R.; Stein, Y. Advective and diffusive cosmic ray transport in galactic haloes. Mon. Not. R. Astron. Soc. 2016, 458, 332–353. [Google Scholar] [CrossRef]
- Lan, T.-W.; Ménard, B.; Zhu, G. Exploring the diffuse interstellar bands with the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2015, 452, 3629–3649. [Google Scholar] [CrossRef]
| 1 | Similar estimate is obtained recently from a detailed analysis of Sco-Cen star formation history [31]. |
| 2 | An alternative energy source for the NPS—two subsequent huge explosions not necessarily connected with a starbursts is advocated in the review by Kataoka et al. [18] based on a systematic analysis of available X-ray data. |
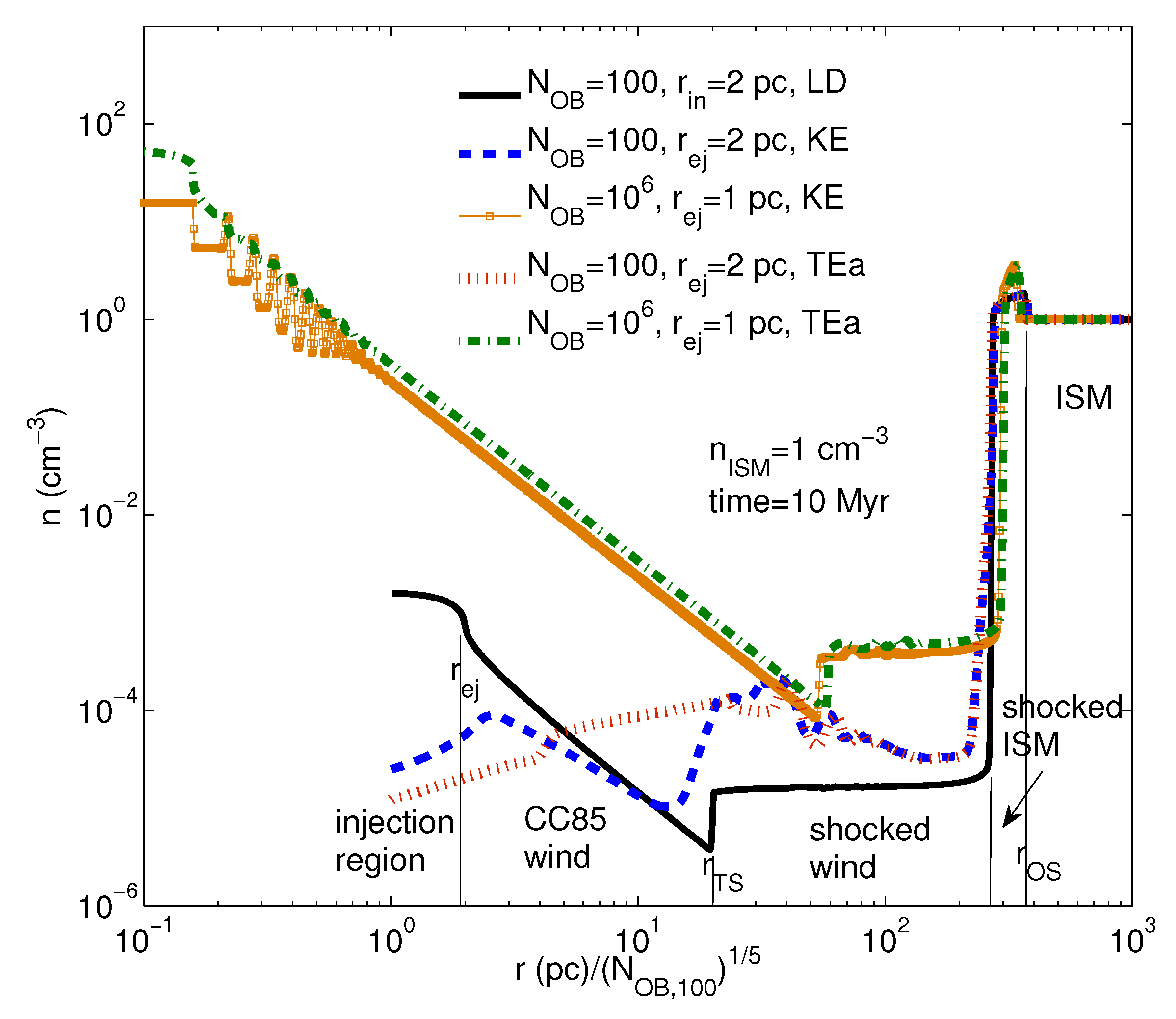
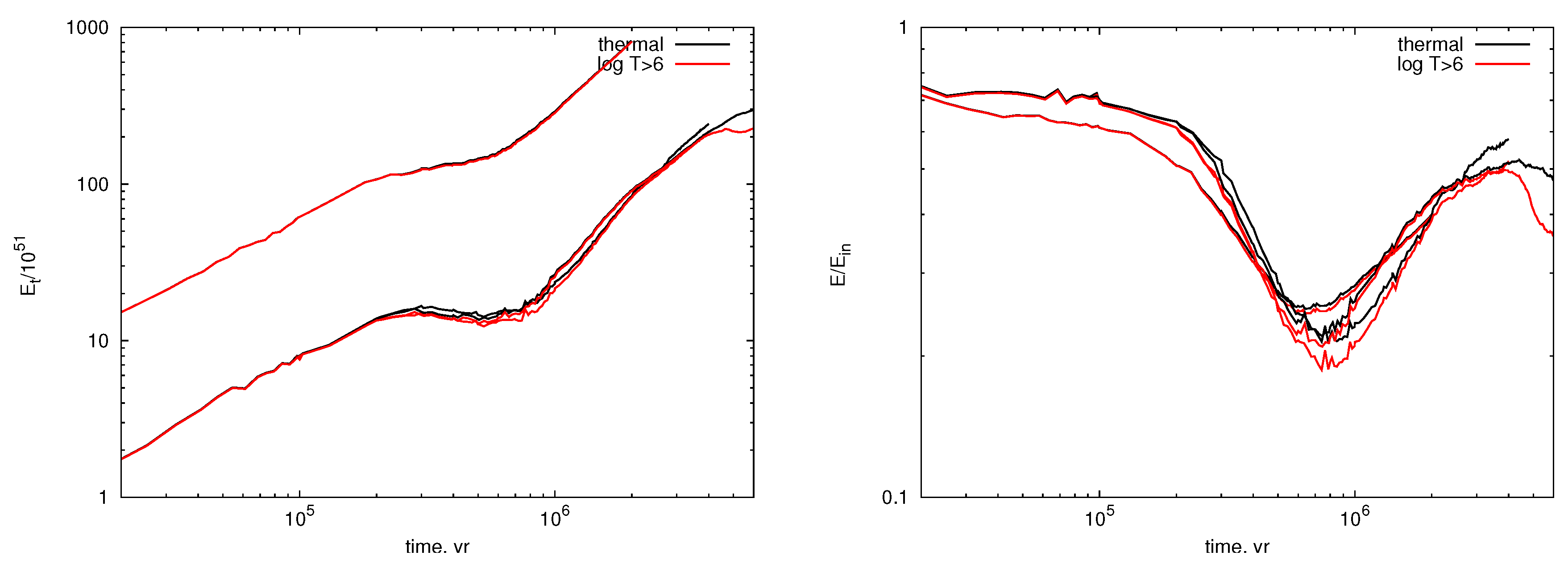
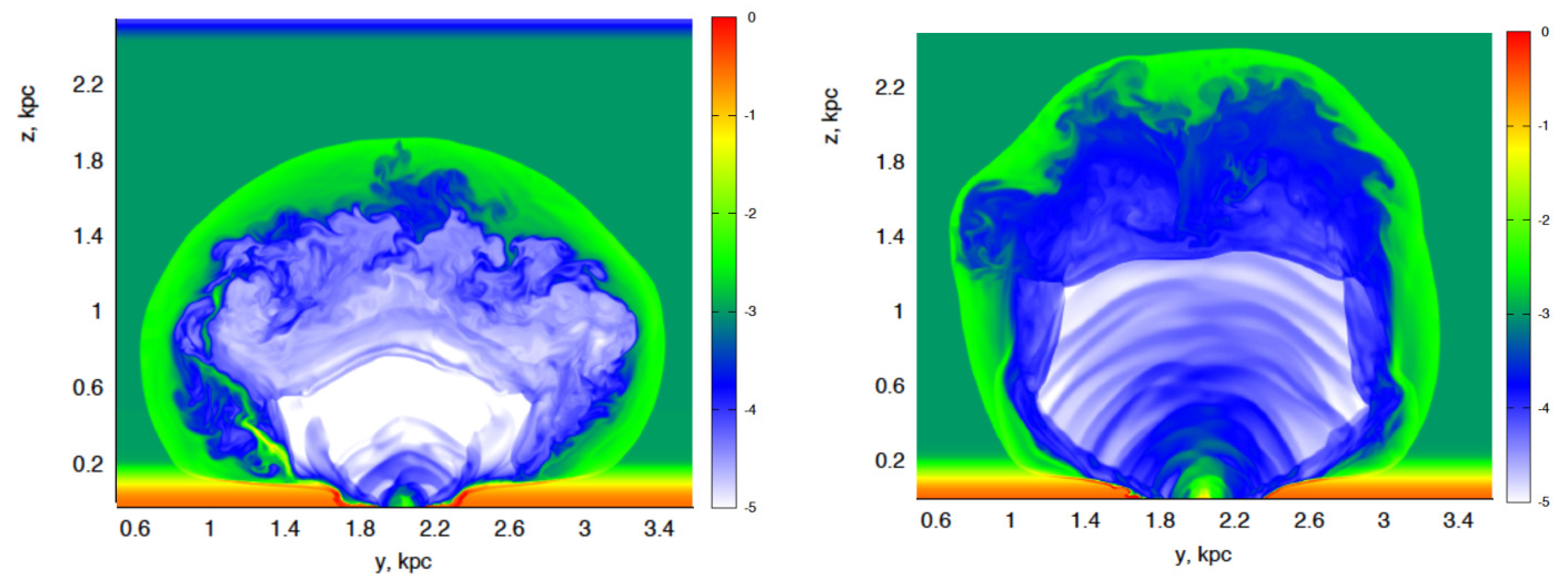
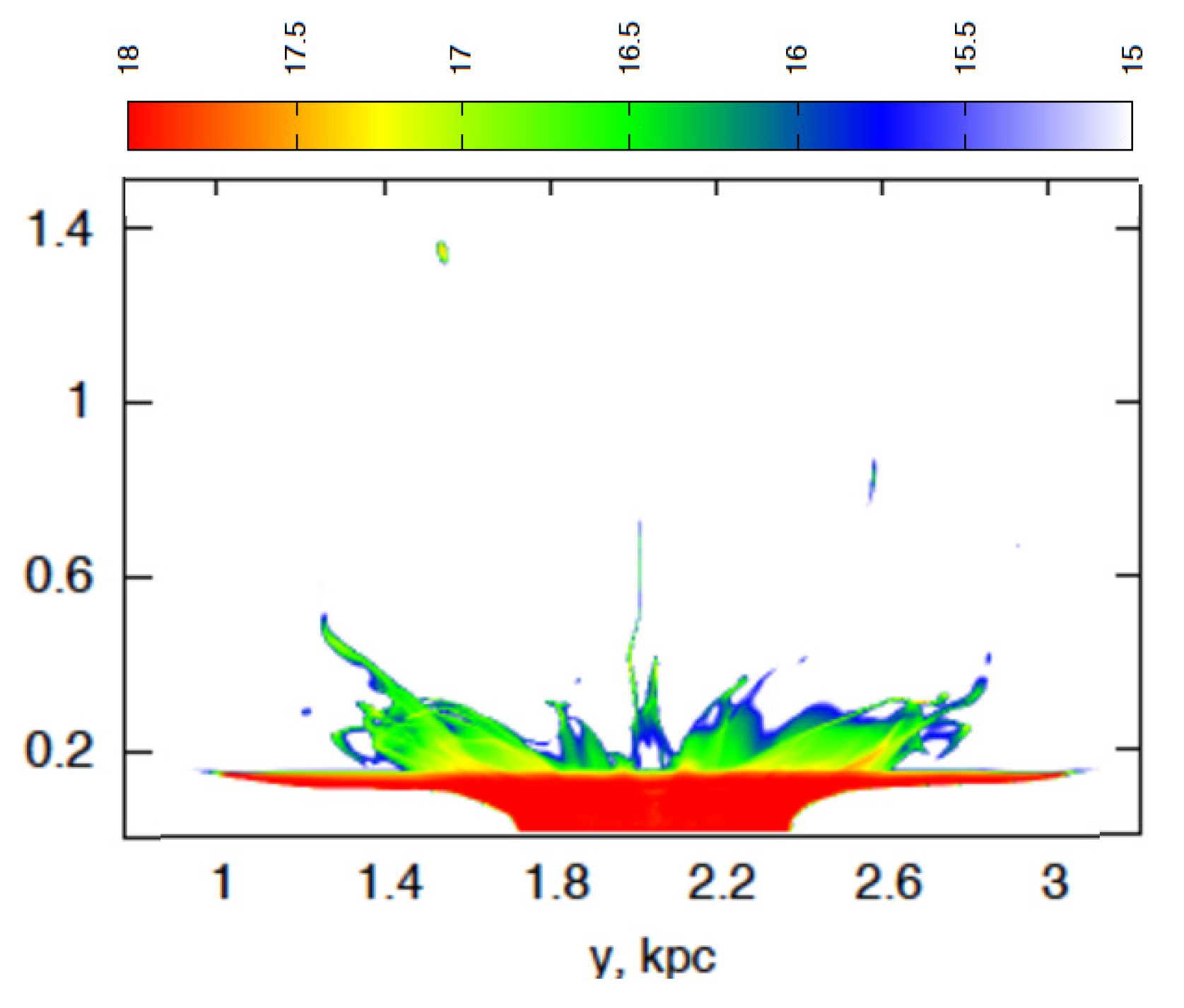
| 3 | It is important to stress that such energy input suggests concerted SN explosions, in which case radiative energy loss in interacting overlapping remnants might be severely enhanced [35]. As a result, the required injected energy should be at least factor of 10 higher than estimated in [38,39], see Figure 1. |
| 4 | For the specific SN rate of SN per |
| 5 | |
| 6 | For this estimate we used dust extinction model cm per H atom at mm, as accepted for the diffuse ISM at high galactic latitudes in [70]. |

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shchekinov, Y. Multi-Wavelength Observations and Modeling of Loop I. Galaxies 2018, 6, 62. https://doi.org/10.3390/galaxies6020062
Shchekinov Y. Multi-Wavelength Observations and Modeling of Loop I. Galaxies. 2018; 6(2):62. https://doi.org/10.3390/galaxies6020062
Chicago/Turabian StyleShchekinov, Yuri. 2018. "Multi-Wavelength Observations and Modeling of Loop I" Galaxies 6, no. 2: 62. https://doi.org/10.3390/galaxies6020062
APA StyleShchekinov, Y. (2018). Multi-Wavelength Observations and Modeling of Loop I. Galaxies, 6(2), 62. https://doi.org/10.3390/galaxies6020062




