Relativistic Motion of Stars near Rotating Black Holes
Abstract
1. Introduction
2. Space–Time near Rotating Black Holes
2.1. The Metric: A Refresher
2.2. The Carter Solution
3. Action, Lagrangian and Equations of Motion
3.1. Principle of Least Action
3.2. The Equivalence Principle
4. Euler–Lagrange Equations of Motion
4.1. Extremum of Action
4.2. Equations of Motion for Test Particle
4.3. Hidden Symmetry
4.4. Trajectory
4.5. Trajectory in Equatorial Surface
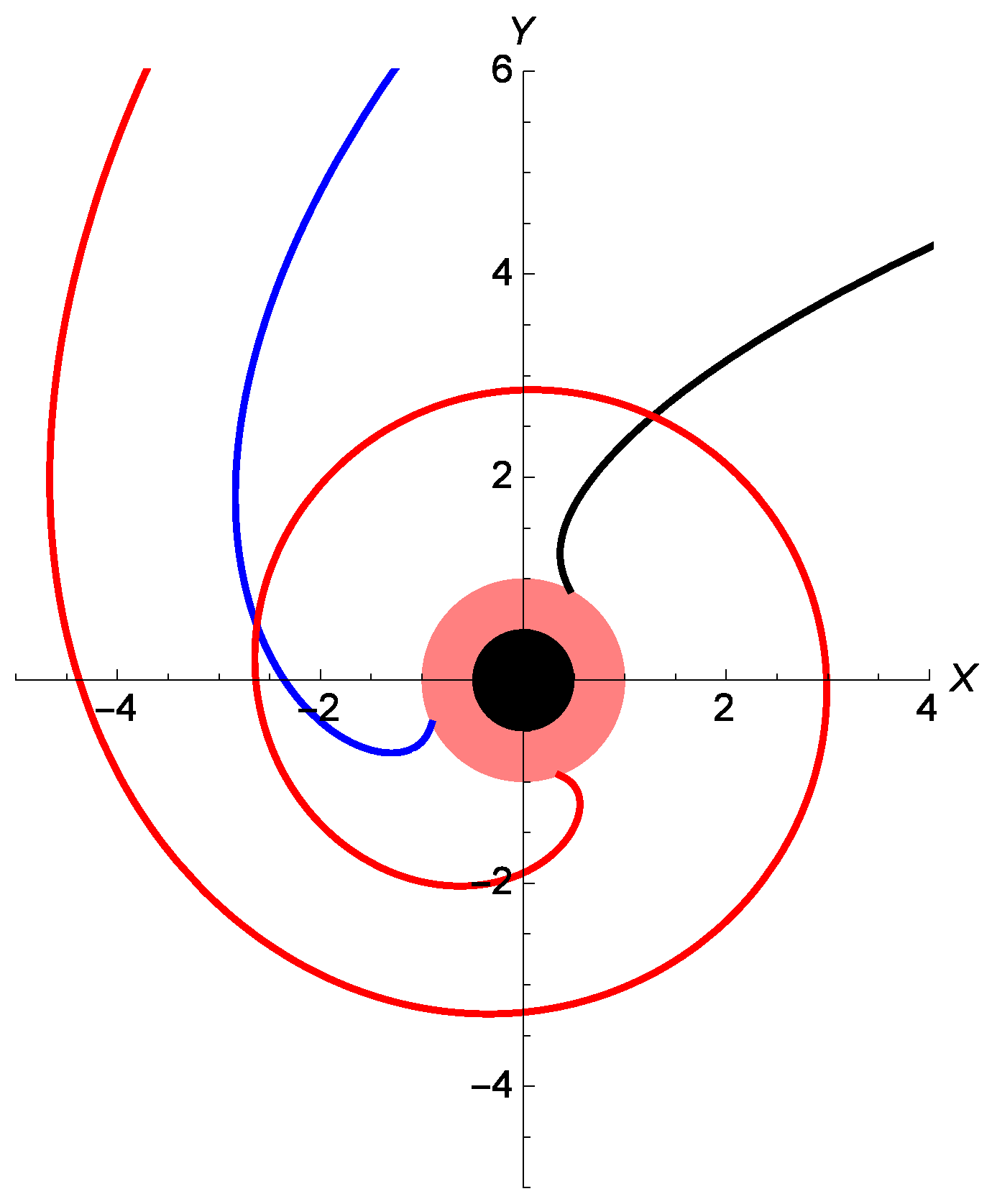
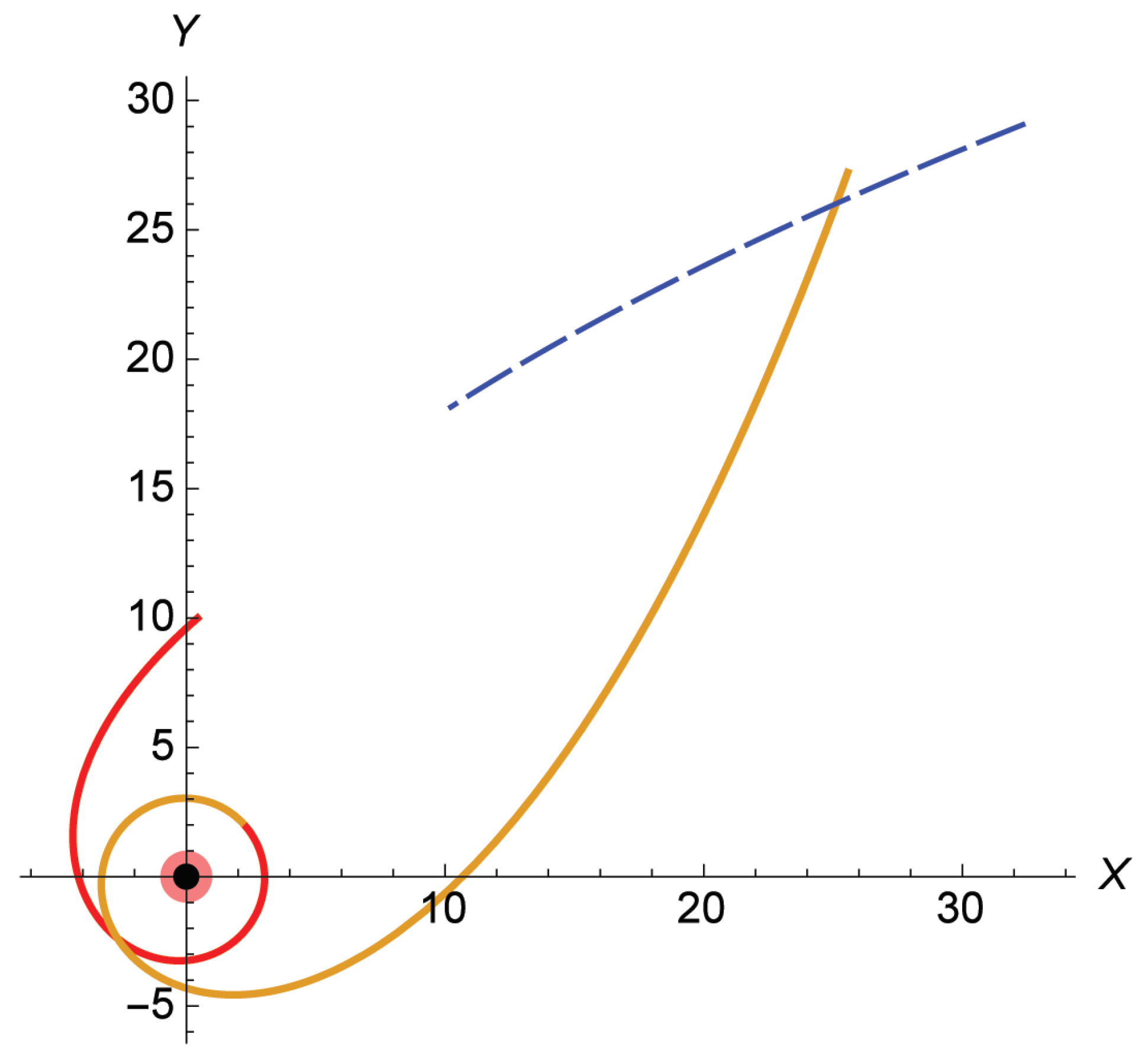
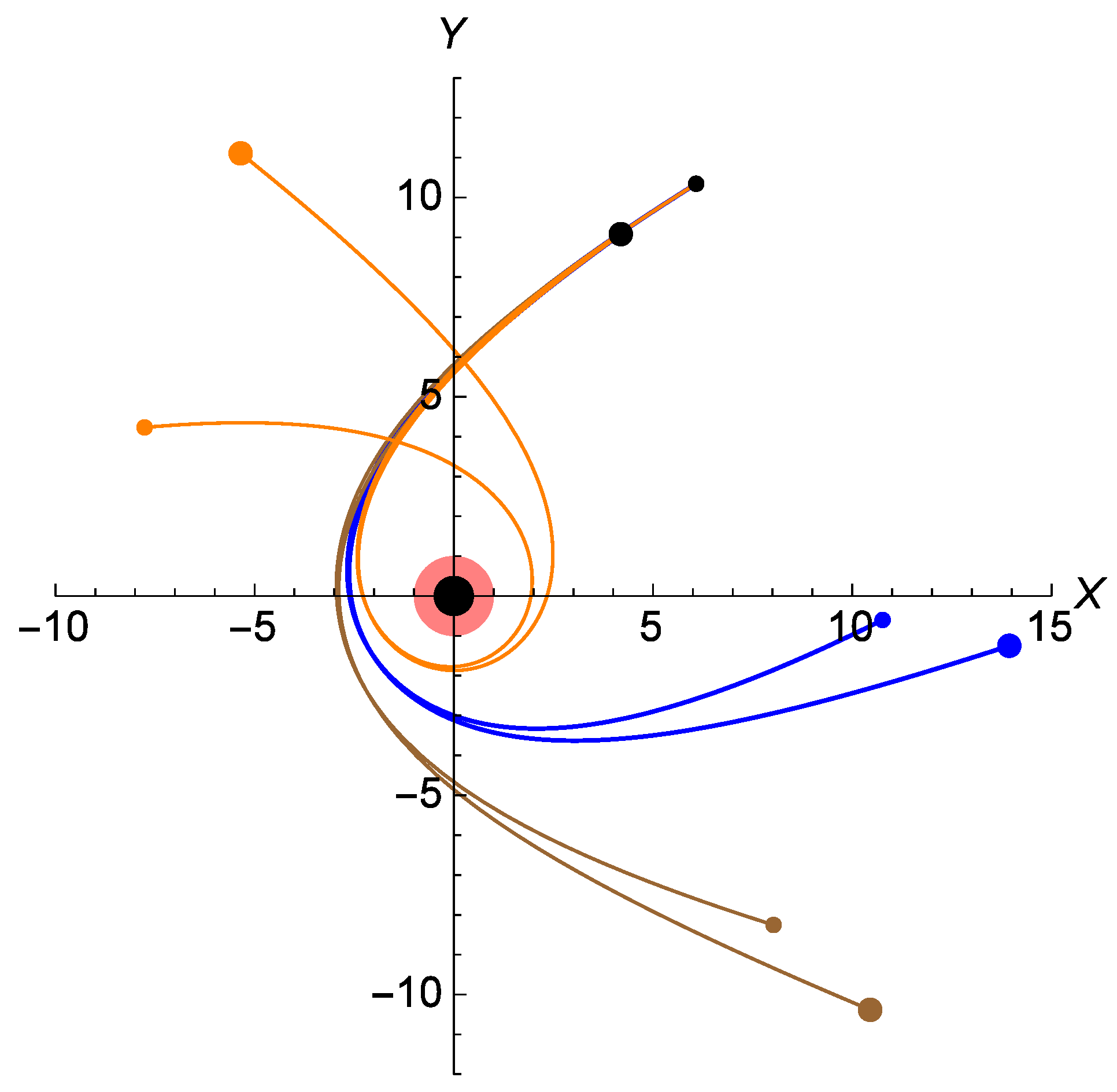
5. Parabolic Trajectory
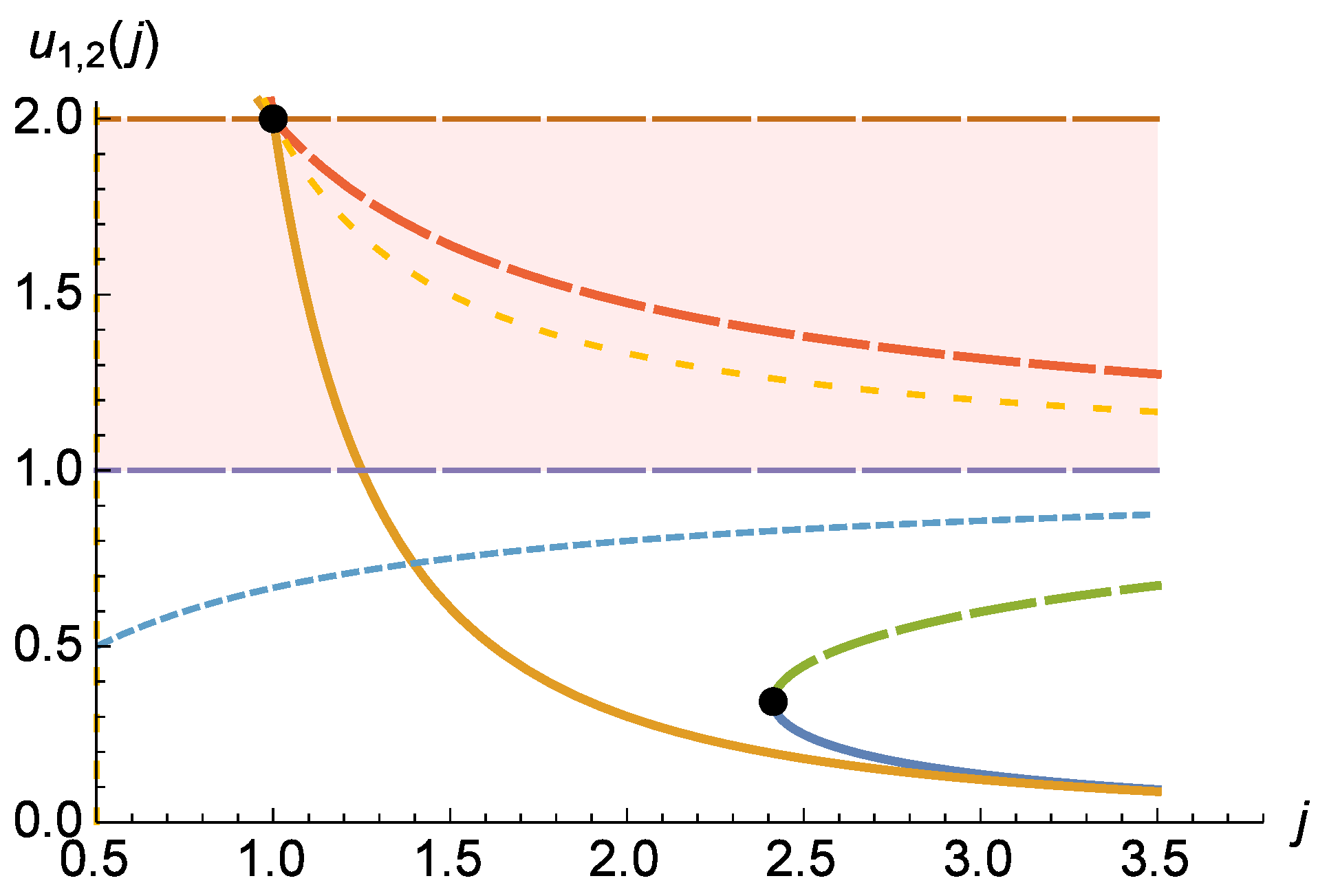
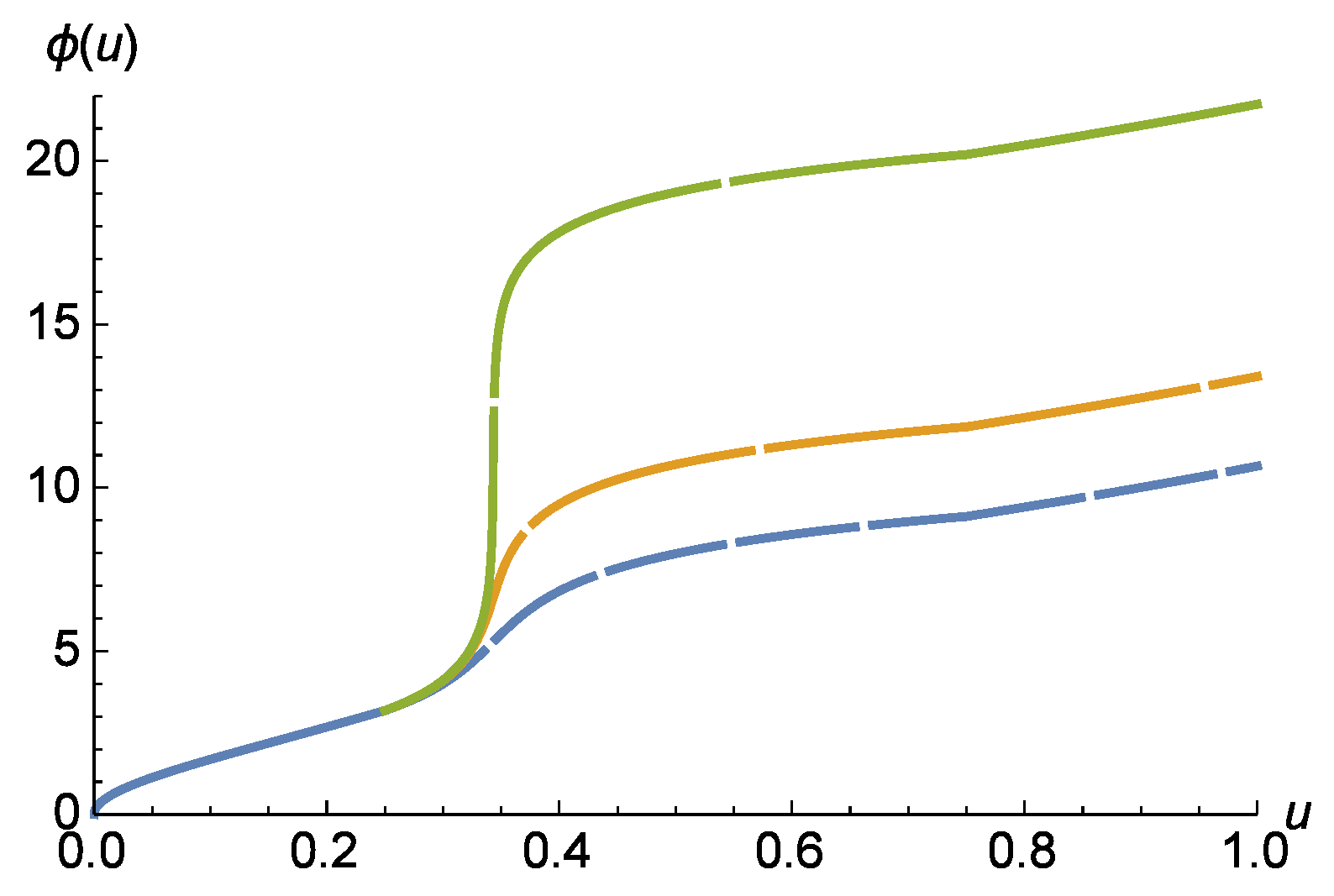
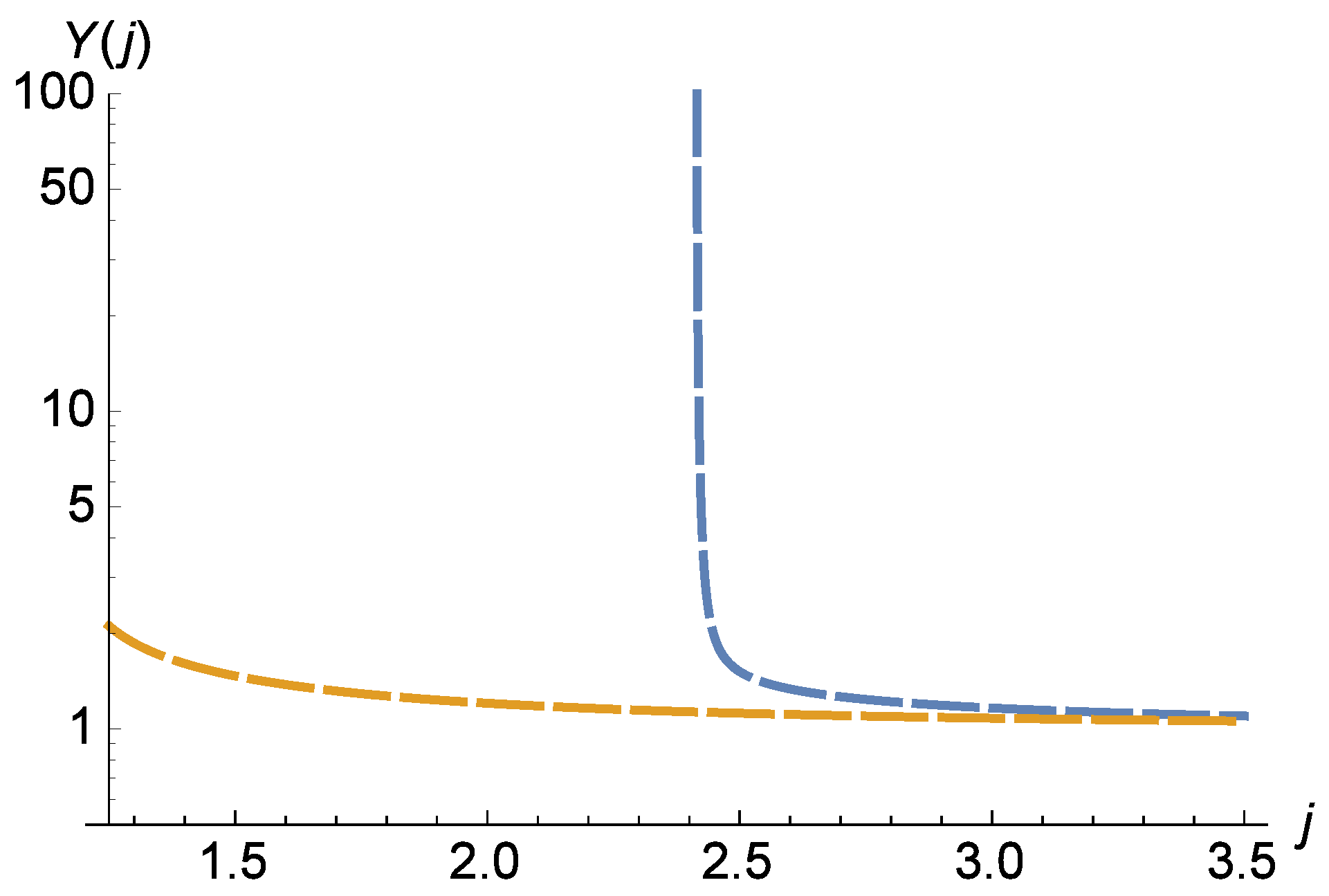
5.1. Classification of Regimes
5.2. At What Angle Does the Body Come Closest to the Black Hole?
5.3. How Many Rotations Does the Body Complete before Departing towards Infinity?
6. Explicit Lagrangian in Post-Newtonian Approximation
7. Conclusions
Author Contributions
Conflicts of Interest
References
- UCLA Galactic Center Group—W.M. Keck Observatory Laser Team, Stellar Orbits in the Central Arcsec. Available online: http://www.galacticcenter.astro.ucla.edu/images.html (accessed on 20 April 2018).
- Reid, M. Is there a supermassive black hole at the center of Milky Way? arXiv, 2008; arXiv:0808.2624. [Google Scholar]
- Thorne, K. The Science of Interstellar; W. W. Norton & Company: New York, NY, USA, 2017; p. 52. [Google Scholar]
- Diener, P.; Frolov, V.P.; Khokhlov, A.M.; Novikov, I.D.; Pethick, C.J. Relativistic Tidal Interaction of Stars with a Rotating Black Hole. Astrophys. J. 1997, 479, 164–178. [Google Scholar] [CrossRef]
- Frolov, V.P.; Zelnikov, A. Introduction to Black Hole Physics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs and Neutron Stars; Willey-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004. [Google Scholar]
- Thorne, K.S.; Blandford, R.D. Modern Classical Physics; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Visser, M. The Kerr Spacetime: A Brief Introduction. arXiv, 2008; arXiv:0706.0622v3. [Google Scholar]
- Neves, J.C.S. Deforming regular black holes. arXiv, 2017; arXiv:1508.06701. [Google Scholar]
- Sharif, M.; Sadiq, S. Tidal effects in some regular black holes. JETP 2018, 153, 232–239. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Physique Théorique I, Mécanique; II Theory of Fields; Mir PublishersMir: Moscow, Russia, 1969. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Carter, B. Solution on a geodesic with the Carter’s constant. Phys. Rev. 1968, 174, 1559. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347. [Google Scholar] [CrossRef]
- Cardoso, V.; Miranda, A.S.; Berti, E.; Witek, H.; Zanchin, V.T. Geodesic stability, Lyapunov exponents, and quasinormal modes. Phys. Rev. D 2009, 79, 064016. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Dymnikova, I.G. Motion of particles and photons in the gravitational field of a rotating body (In memory of Vladimir Afanas’evich Ruban). Sov. Phys. Usp. 1986, 29, 215–237. [Google Scholar] [CrossRef]
- Hackmann, E.; Hartmann, B.; LLäemmerzahl, C.; Sirimachan, P. Test particle motion in the space–time of a Kerr black hole pierced by a cosmic string. Phys. Rev. D 2010, 82, 238–261. [Google Scholar] [CrossRef]
- Hod, S.H. Spherical null geodesics of rotating Kerr black holes. arXiv, 2012; arXiv:1210.2486. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Sharif, M.; Shahzadi, M. Particle dynamics near Kerr-MOG black hole. Eur. Phys. J. C 2017, 77, 363. [Google Scholar] [CrossRef]
- Teo, E. Spherical photon orbits around a Kerr black hole. Gen. Relat. Grav. 2003, 35, 1909–1926. [Google Scholar] [CrossRef]
- Will, C.M. Capture of non-relativistic particles in eccentric orbits by a Kerr black hole. arXiv, 2012; arXiv:10.1088/0264-9381/29/21/217001. [Google Scholar]
- Ritus, V.I. Lagrange equations of motion of particles and photons in the Schwarzschild field. Phys. Usp. 2015, 58, 1118–1123. [Google Scholar] [CrossRef]
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Addison Wesley: Boston, MA, USA, 2018. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Poe, E.A. A Descent into the Maelström. Graham’s Magazine. 1841. Available online: https://archive.org/details/ADescentIntoTheMaelstrom (accessed on 20 April 2018).
- Landau, L.D. A Method Is More Important Than a Discovery, Since the Right Method Will Lead to New and Even More Important Discoveries. Available online: http://www.azquotes.com/quote/1263664 (accessed on 20 April 2018).
- Tito, E.P.; Pavlov, V.I. Hydrodynamical instability of dark matter: Analytical solution for the flat expanding universe. Phys. Rev. D 2012, 85, 96–106. [Google Scholar]
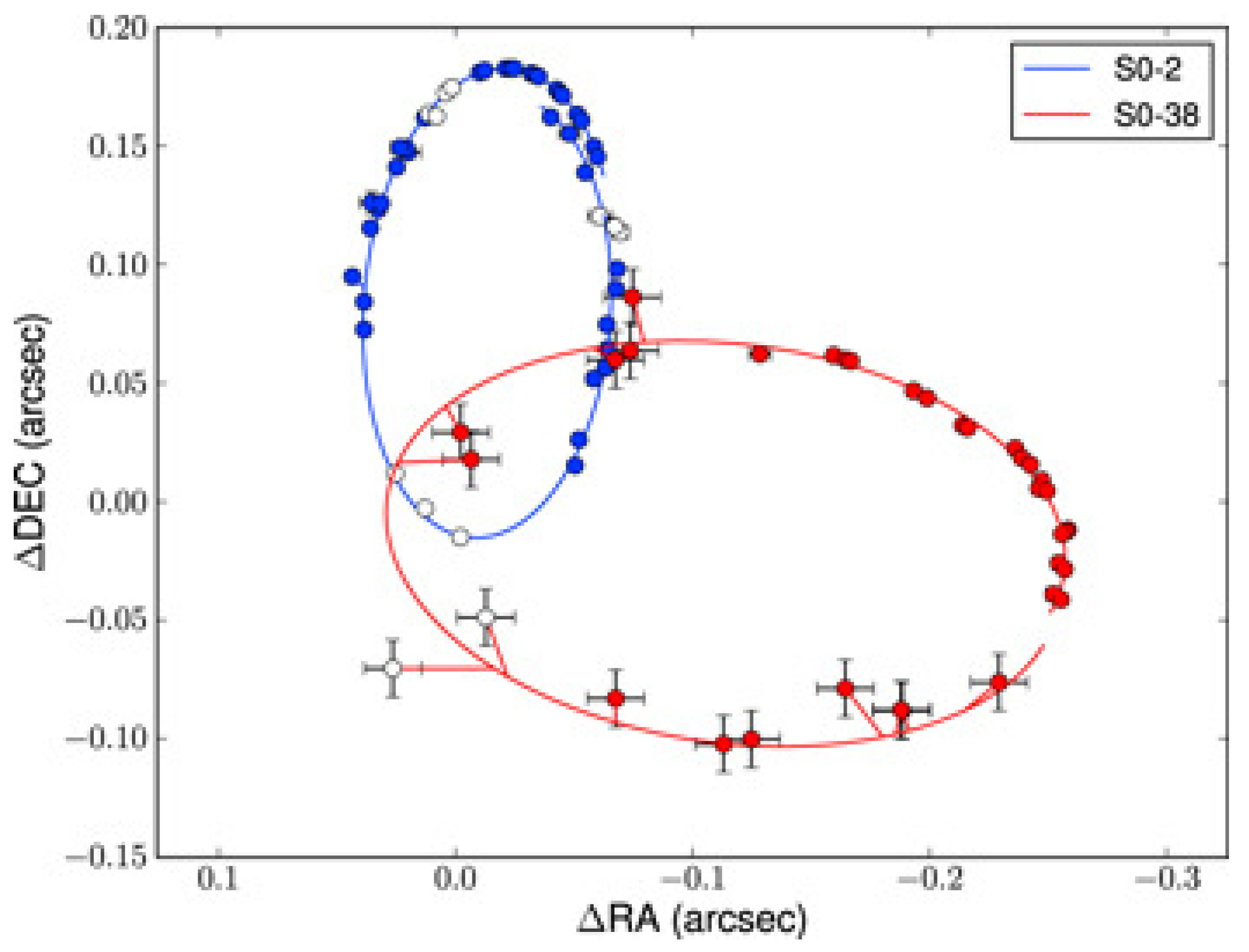
- Gillessen, S.; Plewa, P.M.; Eisenhauer, F.; Sari, R.; Waisberg, I.; Habibi, M.; Pfuhl, O.; George, E.; Dexter, J.; von Fellenberg, S.; et al. An Update on Monitoring Stellar Orbits in the Galactic Center. Astrophys. J. 2017, 837, 30. [Google Scholar] [CrossRef]
- Hees, A.; Do, T.; Ghez, A.M.; Martinez, G.D.; Naoz, S.; Becklin, E.E.; Boehle, A.; Chappell, S.; Chu, D.; Dehghanfar, A.; et al. Testing General Relativity with Stellar Orbits around the Supermassive Black Hole in Our Galactic Center. Phys. Rev. Lett. 2017, 118, 211101. [Google Scholar] [CrossRef] [PubMed]
- Parsa, M.; Eckart, A.; Shahzamanian, B.; Karas, V.; Zajacek, M.; Zensus, J.A.; Straubmeier, C. Investigating the relativistic motion of the stars near the supermassive black hole in the galactic center. Astrophys. J. 2017, 845, 22. [Google Scholar] [CrossRef]
- Zhang, F.; Lu, Y.; Yu, Q. On testing the Kerr metric of the massive black hole in the galactic center via stellar orbital motion: full general relativistic treatment. Astrophys. J. 2015, 809, 127. [Google Scholar] [CrossRef]
- Boehle, A.; Ghez, A.M.; Schödel, R.; Meyer, L.; Yelda, S.; Albers, S.; Martinez, G.D.; Becklin, E.E.; Do, T.; Lu, J.R.; et al. An improved distance and mass estimate for SgrA* from a multistar orbit analysis. Astrophys. J. 2016, 830, 17. [Google Scholar] [CrossRef]
| 1 | In general, parameter is not small in value for many physically interesting situations. For example, J of the Sun (assuming uniform rotation) is of order resulting in —not negligibly small. |
| 2 | |
| 3 | From the definition of interval , it follows that when and (i.e., the non-moving observer is at the infinity), the interval . For a clock located at the point and , the same interval is . It follows then that . This simply shows the well–known red–shift for a clock in the gravitational field compared with a clock at infinity where the gravitational field is absent, is . |
| 4 | Let us remind that the location of the event horizon is determined by the larger of the two roots of When (i.e., in the usual units, ), there are no real-value solutions to this equation, and there is no event horizon. With no event horizons to hide it from the rest of the universe, the black hole ceases to be a black hole and will instead be a “naked” singularity. |
| 5 | This is already evident from the fact that the determinant of , , has no singularity at . In addition, making a transformation of the 4-coordinates of the form and , for which , the element of interval at the Schwarzschild metric becomes . Thus, in the coordinates , the singularity at the Schwarzschild surface, where , is absent, but the metric is nonstationary (see [13], §102). |
| 6 | |
| 7 | Geometrically, geodesics are the curves of extremal length between two points in space–time. The geodesics of Minkowski space–time governed by the special theory of relativity, are 4–dimensional straight lines. The case with describes time-like geodesics, the world–lines of free material particles. Photons-massless particles-travel at the speed of light along the null geodesics (). Within the general relativity theory, free particles travel along geodesics of the curved space–time. |
| 8 | |
| 9 | A whirlpool is a rotating current of water that creates a characteristic vortex. In nature, there exists a number of consistent and frequently occurring whirlpools that have become legendary. Many sea myths have featured whirlpools, typically in situations involving great peril to ships. An especially powerful whirlpool is known as a maelström—one of the more notable maelströms is the Moskstraumen, an immense network of eddies and whirlpools off the coast of Norway. |
| 10 | “Simplicity”, of course, is a relative concept, on par with “large”, “small” and “all we need”, as humored by Mark Twain, a titan of the American literature: “... My friend, take an old man’s advice, and don’t encumber yourself with a large family–mind, I tell you, don’t do it. In a small family, and in a small family only, you will find that comfort and that peace of mind which are the best at last of the blessings this world is able to afford us, and for the lack of which no accumulation of wealth, and no acquisition of fame, power, and greatness can ever compensate us. Take my word for it, ten or eleven wives is all you need–never go over it”. |
| 11 | L. Landau: “A method is more important than a discovery, since the right method will lead to new and even more important discoveries.” [29] |
| 12 | In general, however, the possibility that “dark matter” may have an impact on the motion of stars in the central zone of our Galaxy should also be noted and considered (see, for example, [30] and references therein). |


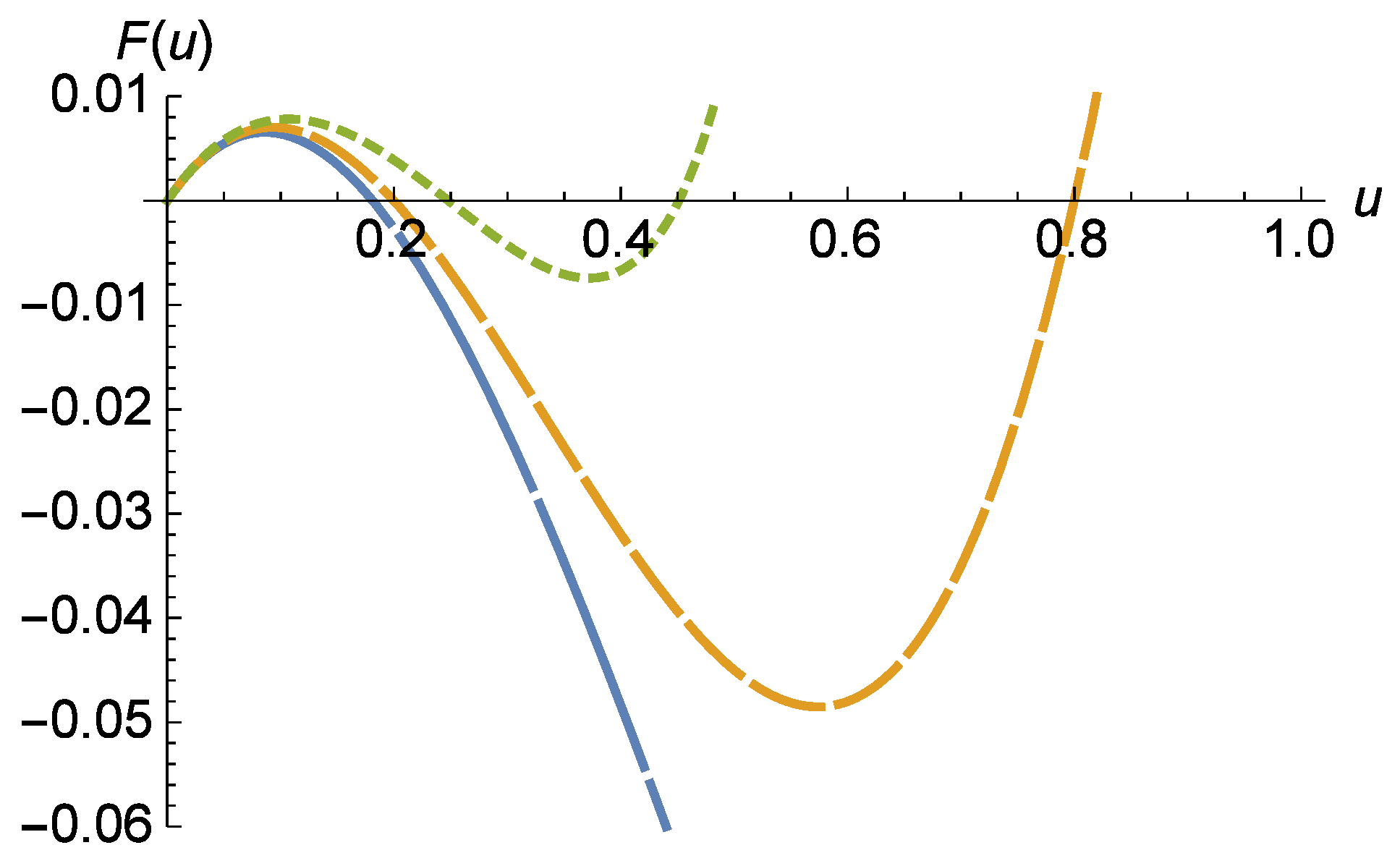
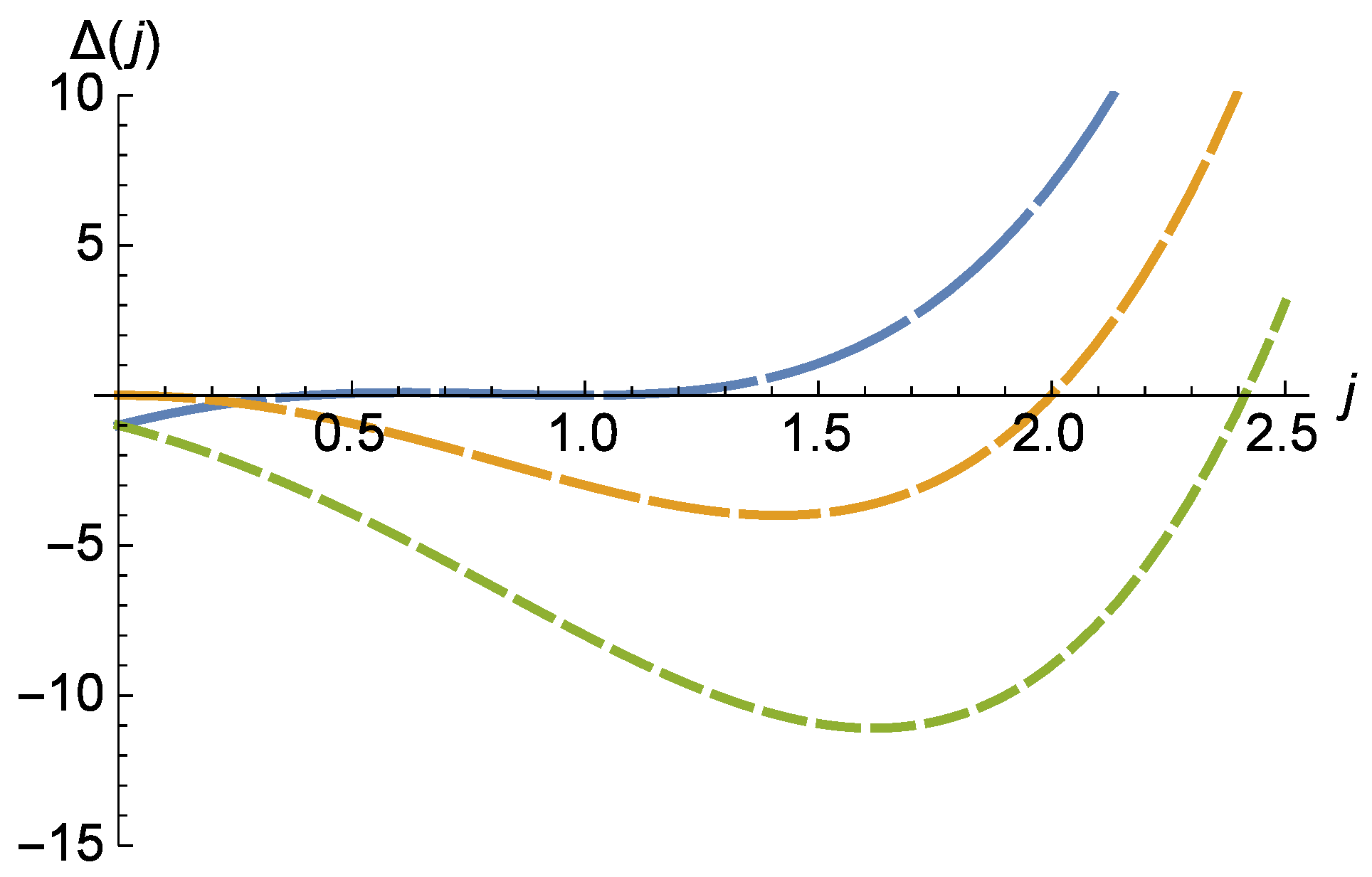
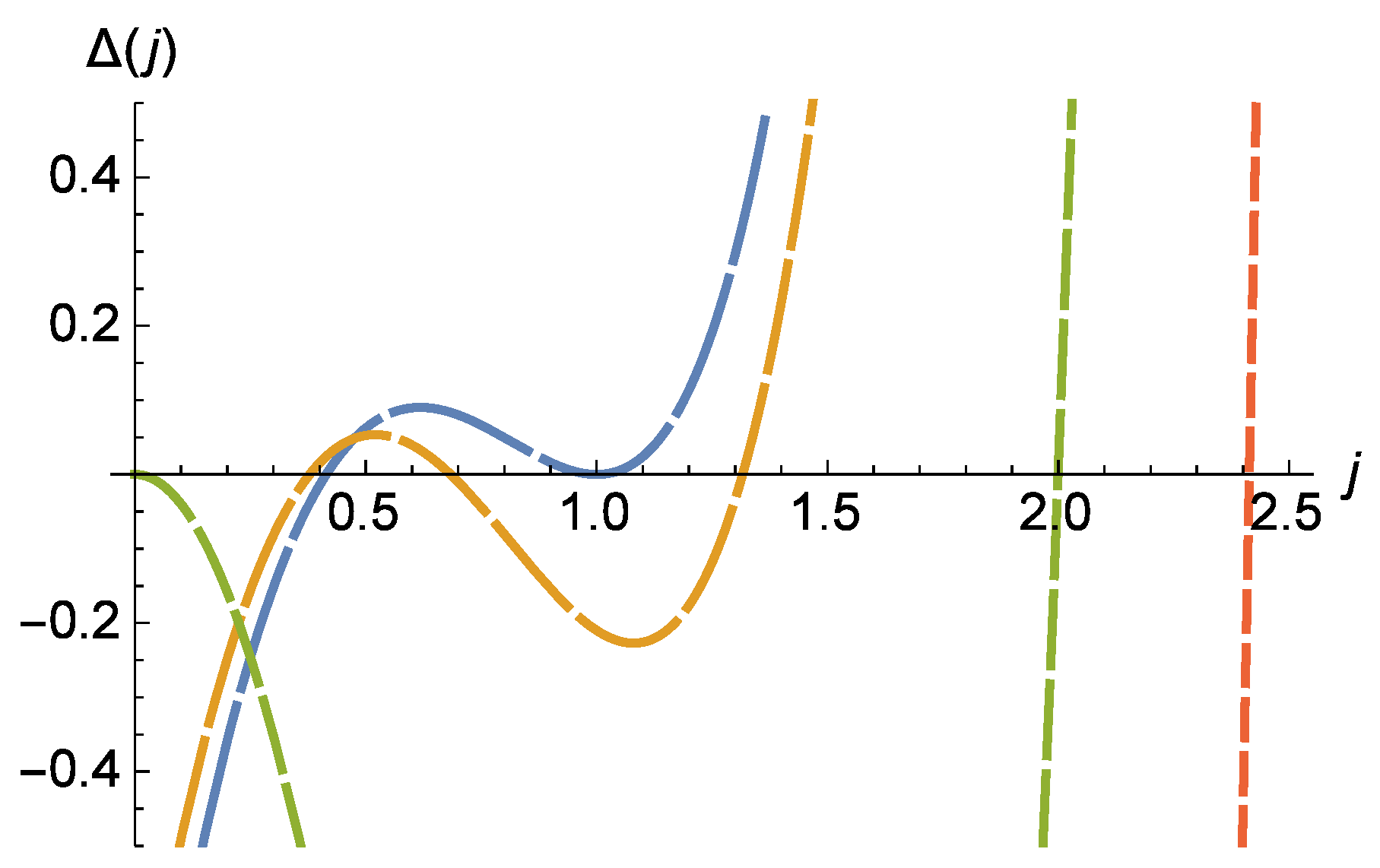


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tito, E.P.; Pavlov, V.I. Relativistic Motion of Stars near Rotating Black Holes. Galaxies 2018, 6, 61. https://doi.org/10.3390/galaxies6020061
Tito EP, Pavlov VI. Relativistic Motion of Stars near Rotating Black Holes. Galaxies. 2018; 6(2):61. https://doi.org/10.3390/galaxies6020061
Chicago/Turabian StyleTito, Elizabeth P., and Vadim I. Pavlov. 2018. "Relativistic Motion of Stars near Rotating Black Holes" Galaxies 6, no. 2: 61. https://doi.org/10.3390/galaxies6020061
APA StyleTito, E. P., & Pavlov, V. I. (2018). Relativistic Motion of Stars near Rotating Black Holes. Galaxies, 6(2), 61. https://doi.org/10.3390/galaxies6020061




