Towards New Constraints in Extended Theories of Gravity: Cosmography and Gravitational-Wave Signals from Neutron Stars
Abstract
1. Introduction
2. Cosmography
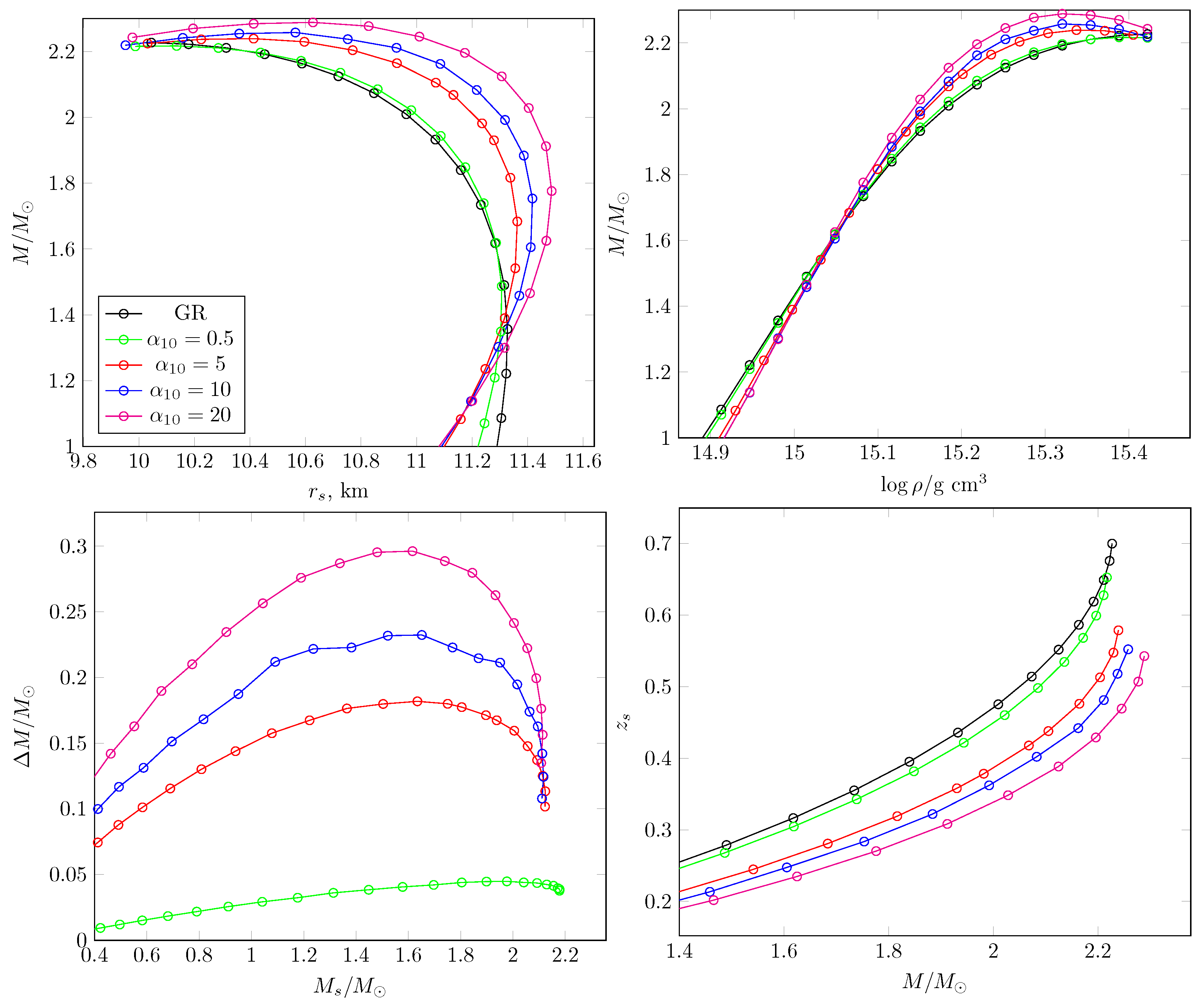
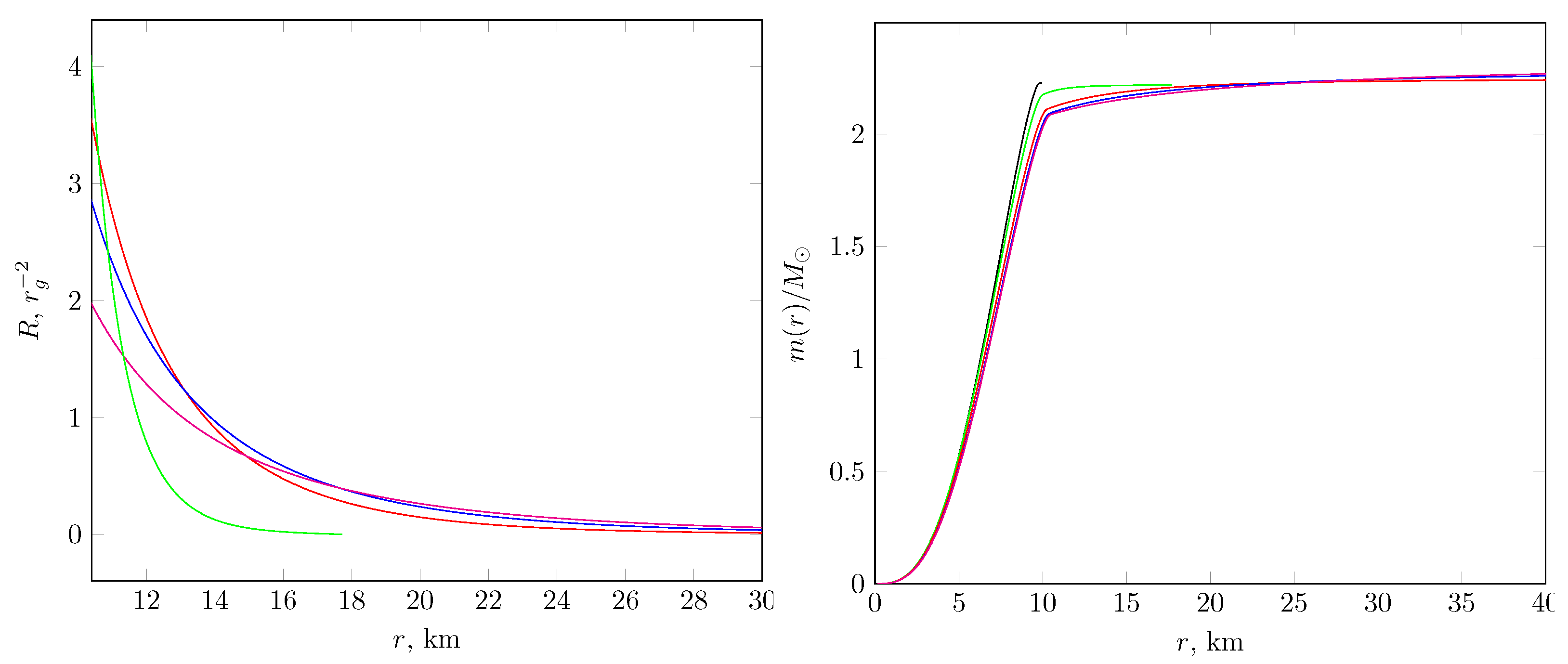
3. Spherical Configurations: Neutron Stars
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia Supernova Discoveries at z > 1 from the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution. Astrophys. J. 2004, 607, 665. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Gooba, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of general relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101. [Google Scholar] [CrossRef] [PubMed]
- Racusin, J.L.; Burns, E.; Goldstein, A.; Connaughton, V.; Wilson-Hodge, C.A.; Jenke, P.; Blackburn, L.; Briggs, M.S.; Broida, J.; Camp, J. Searching the Gamma-ray sky for Counterparts to Gravitational Wave Sources: Fermi Gamma-ray Burst Monitor and Large Area Telescope Observations of LVT151012 and GW151226. Astrophys. J. 2017, 835, 82. [Google Scholar] [CrossRef]
- Hughey, B.; Zanolin, M.; Szczepanczyk, M.; Gill, K. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. 2017, 851, L35. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Clarkson, C.; Ellis, G.; Larena, J.; Umeh, O. Does the growth of structure affect our dynamical models of the universe? The averaging, backreaction and fitting problems in cosmology. Rept. Prog. Phys. 2011, 74, 112901. [Google Scholar] [CrossRef]
- Raccanelli, A.; Bertacca, D.; Pietrobon, D.; Schmidt, F.; Samushia, L.; Bartolo, N.; Doré, O.; Matarrese, S.; Percival, W.J. Testing Gravity Using Large-Scale Redshift-Space Distortions. Mon. Not. Roy. Astron. Soc. 2013, 436, 89–100. [Google Scholar] [CrossRef]
- Tsagas, C.G.; Challinor, A.; Maartens, R. Relativistic cosmology and large-scale structure. Phys. Rep. 2008, 465, 61–147. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Dobado, A.; Maroto, A.L. On the evolution of density perturbations in f(R) theories of gravity. Phys. Rev. D 2008, 77, 123515. [Google Scholar] [CrossRef]
- Capozziello, S.; Carloni, S.; Troisi, A. Quintessence without scalar fields. Recent Res. Dev. Astron. Astrophys. 2003, 1, 625. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Dobado, A. A f(R) gravity without cosmological constant. Phys. Rev. D 2006, 74, 087501. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, Á.; Dunsby, P.K.S.; Kandhai, S.; Sáez-Gómez, D. Theoretical and observational constraints of viable f(R) theories of gravity. Phys. Rev. D 2016, 93, 084016. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A. Towards Degeneracy Problem Breaking by Large Scale Structures Methods. In Progress in Mathematical Relativity, Gravitation and Cosmology; Springer: Berlin, Germany, 2014; pp. 243–247. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F (R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115–146. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity; Springer: New York, NY, USA, 2010. [Google Scholar]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Sáez-Gómez, D. Black holes, cosmological solutions, future singularities, and their thermodynamical properties in modified gravity theories. Entropy 2012, 14, 1717. [Google Scholar] [CrossRef]
- Hehl, F.W.; Von Der Heyde, P.; Kerlick, G.D.; Nester, J.M. General Relativity with Spin and Torsion: Foundations and Prospects. Rev. Mod. Phys. 1976, 48, 393. [Google Scholar] [CrossRef]
- Hayashi, K.; Shirafuji, T. New General Relativity. Phys. Rev. D 1979, 19, 3524. [Google Scholar] [CrossRef]
- Wilczek, F. Riemann-Einstein structure from volume and gauge symmetry. Phys. Rev. Lett. 1998, 80, 4851. [Google Scholar] [CrossRef]
- Obukhov, Y.N. Spectral Geometry of the Riemann-cartan Space-time. Nucl. Phys. B 1983, 212, 237. [Google Scholar] [CrossRef]
- Benn, I.M.; Dereli, T.; Tucker, R.W. Gauge Field Interactions in Spaces with Arbitrary Torsion. Phys. Lett. 1980, 96, 100. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Pereira, J.G. Teleparallel Gravity: An Introduction; Springer: Berlin, Germany, 2013; Volume 173. [Google Scholar]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without inflaton. Phys. Rev. D 2007, 75, 084031. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s Other Gravity and the Acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Myrzakulov, R. Accelerating universe from F(T) gravity. Eur. Phys. J. C 2011, 71, 1752. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, Á.; Farrugia, G.; Said, J.L.; Sáez-Gómez, D. Cosmological reconstructed solutions in extended teleparallel gravity theories with a teleparallel Gauss? Bonnet term. Class. Quant. Grav. 2017, 34, 235011. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, Á.; Dunsby, P.K.S.; Sáez-Gómez, D. Junction conditions in extended Teleparallel gravities. J. Cosmol. Astropart. P. 2014, 1412, 048. [Google Scholar] [CrossRef]
- Dunsby, P.K.S.; Luongo, O. On the theory and applications of modern cosmography. Int. J. Geom. Meth. Mod. Phys. 2016, 13, 1630002. [Google Scholar] [CrossRef]
- Busti, V.C.; de la Cruz-Dombriz, Á.; Dunsby, P.K.S.; Sáez-Gómez, D. Is cosmography a useful tool for testing cosmology? Phys. Rev. D 2015, 92, 123512. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, Á. Limitations of cosmography in extended theories of gravity. PoS DSU 2016, 2015, 007. [Google Scholar]
- Nair, R.; Jhingan, S.; Jain, D. Exploring scalar field dynamics with Gaussian processes. J. Cosmol. Astropart. Phys. 2014, 1401, 5. [Google Scholar] [CrossRef]
- Capozziello, S.; Farooq, O.; Luongo, O.; Ratra, B. Cosmographic bounds on the cosmological deceleration- acceleration transition redshift in f(R) gravity. Phys. Rev. D 2014, 90, 044016. [Google Scholar] [CrossRef]
- Aviles, A.; Bravetti, A.; Capozziello, S.; Luongo, O. Updated constraints on f(R) gravity from cosmography. Phys. Rev. D 2013, 87, 044012. [Google Scholar] [CrossRef]
- Capozziello, S.; Luongo, O.; Saridakis, E.N. Transition redshift in f(T) cosmology and observational constraints. Phys. Rev. D 2015, 91, 124037. [Google Scholar] [CrossRef]
- De la Cruz-Dombriz, A.; Dunsby, P.K.S.; Luongo, O.; Reverberi, L. Model-independent limits and constraints on extended theories of gravity from cosmic reconstruction techniques. J. Cosmol. Astropart. Phys. 2016, 1612, 042. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive neutron cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364. [Google Scholar] [CrossRef]
- Dobado, A.; Llanes-Estrada, F.J.; Oller, J.A. The existence of a two-solar mass neutron star constrains the gravitational constant G_N at strong field. Phys. Rev. C 2012, 85, 012801. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081. [Google Scholar] [CrossRef] [PubMed]
- Barziv, O.; Kaper, L.; van Kerkwijk, M.H.; Telting, J.H.; van Paradijs, J. The mass of the neutron star in vela x-1. Astron. Astrophys. 2001, 377, 925–944. [Google Scholar] [CrossRef]
- Rawls, M.L.; Orosz, J.A.; McClintock, J.E.; Torres, M.A.P.; Bailyn, C.D.; Buxton, M.M. Refined Neutron-Star Mass Determinations for Six Eclipsing X-Ray Pulsar Binaries. Astrophys. J. 2011, 730, 25. [Google Scholar] [CrossRef]
- Munoz-Darias, T.; Casares, J.; Martinez-Pais, I.G. The k-correction for irradiated emission lines in lmxbs: Evidence for a massive neutron star in x1822-371 (v691 cra). Astrophys. J. 2005, 635, 502. [Google Scholar] [CrossRef]
- Nice, D.J.; Splaver, E.M.; Stairs, I.H.; Loehmer, O.; Jessner, A.; Kramer, M., II; Cordes, J.M. A 2.1 solar mass pulsar measured by relativistic orbital decay. Astrophys. J. 2005, 634, 1242. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef] [PubMed]
- Dexheimer, V.A.; Vasconcellos, C.A.Z.; Bodmann, B.E.J. On the Density Dependent Nuclear Matter Compressibility. Phys. Rev. C 2008, 77, 065803. [Google Scholar] [CrossRef]
- Kobayashi, T.; Maeda, K.I. Relativistic stars in f(R) gravity, and absence thereof. Phys. Rev. D 2008, 78, 064019. [Google Scholar] [CrossRef]
- Upadhye, A.; Hu, W. Existence of relativistic stars in f(R) gravity. Phys. Rev. D 2009, 80, 064002. [Google Scholar] [CrossRef]
- Feng, W.X.; Geng, C.Q.; Kao, W.F.; Luo, L.W. Equation of State of Neutron Stars with Junction Conditions in the Starobinsky Model. Int. J. Modern Phys. 2018, 27, 1750186. [Google Scholar] [CrossRef]
- Teppa Pannia, F.A.; GarcAa, F.; Perez Bergliaffa, S.E.; Orellana, M.; Romero, G.E. Structure of Compact Stars in R-squared Palatini Gravity. Gen. Rel. Grav. 2017, 49, 25. [Google Scholar] [CrossRef]
- Wojnar, A.; Velten, H. Equilibrium and stability of relativistic stars in extended theories of gravity. Eur. Phys. J. C 2016, 76, 697. [Google Scholar] [CrossRef]
- Arapoǧlu, S.; Çikintoǧlu, S.; Yavuz Ekşi, K. Relativistic Stars in Starobinsky gravity with matched asymptotic expansion. Phys. Rev. D 2017, 96, 084040. [Google Scholar] [CrossRef]
- Katsuragawa, T.; Nojiri, S.; Odintsov, S.D.; Yamazaki, M. Relativistic stars in de Rham-Gabadadze-Tolley massive gravity. Phys. Rev. D 2016, 93, 124013. [Google Scholar] [CrossRef]
- Fiziev, P.P. A Realistic Model of a Neutron Star in Minimal Dilatonic Gravity. arXiv, 2015; arXiv:1506.08585. [Google Scholar]
- Hendi, S.H.; Bordbar, G.H.; Eslam Panah, B.; Najafi, M. Dilatonic Equation of Hydrostatic Equilibrium and Neutron Star Structure. Astrophys. Space Sci. 2015, 358, 30. [Google Scholar] [CrossRef]
- Momeni, D.; Gholizade, H.; Raza, M.; Myrzakulov, R. Tolman–Oppenheimer–Volkoff equations in nonlocal f(R) gravity. Int. J. Mod. Phys. A 2015, 30, 1550093. [Google Scholar]
- Zubair, M.; Abbas, G. Some interior models of compact stars in f(R) gravity. Astrophys. Space Sci. 2016, 361, 342. [Google Scholar] [CrossRef]
- Bakirova, E.; Folomeev, V. Dipole magnetic field of neutron stars in f(R) gravity. Gen. Rel. Grav. 2016, 48, 135. [Google Scholar] [CrossRef]
- Aparicio Resco, M.; de la Cruz-Dombriz, Á.; Llanes Estrada, F.J.; Zapatero Castrillo, V. On neutron stars in f(R) theories: Small radii, large masses and large energy emitted in a merger. Phys. Dark Univ. 2016, 13, 147–164. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Arbañil, J.D.V.; Malheiro, M. Stellar equilibrium configurations of compact stars in f(R,T) gravity. J. Cosmol. Astropart. Phys. 2016, 1606, 005. [Google Scholar] [CrossRef]
- Sharif, M.; Yousaf, Z. Dynamics of spherical stars with structure scalars and R + ϵRn cosmology. Can. J. Phys. 2015, 93, 905–911. [Google Scholar] [CrossRef]
- Sotani, H.; Kokkotas, K.D. Maximum mass limit of neutron stars in scalar-tensor gravity. Phys. Rev. D 2017, 95, 044032. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Odintsov, S.D.; de la Cruz-Dombriz, A. The realistic models of relativistic stars in f(R) = R + αR2 gravity. Class. Quant. Grav. 2017, 34, 205008. [Google Scholar] [CrossRef]
- Clifton, T.; Dunsby, P.; Goswami, R.; Nzioki, A.M. On the absence of the usual weak-field limit, and the impossibility of embedding some known solutions for isolated masses in cosmologies with f(R) dark energy. Phys. Rev. D 2013, 87, 063517. [Google Scholar] [CrossRef]
- Nzioki, A.M.; Goswami, R.; Dunsby, P.K.S. Jebsen-Birkhoff theorem and its stability in f(R) gravity. Phys. Rev. D 2014, 89, 064050. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farese, G. Tensor—Scalar gravity and binary pulsar experiments. Phys. Rev. D 1996, 54, 1474. [Google Scholar] [CrossRef]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stei, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al. Testing General Relativity with Present and Future Astrophysical Observations. Class. Quant. Grav. 2015, 32, 243001. [Google Scholar] [CrossRef]
- Koyama, K.; Niz, G.; Tasinato, G. Analytic solutions in non-linear massive gravity. Phys. Rev. Lett. 2011, 107, 131101. [Google Scholar] [CrossRef] [PubMed]
- Sibandze, D.B.; Goswami, R.; Maharaj, S.D.; Nzioki, A.M.; Dunsby, P.K.S. Scalar Wave Scattering from Schwarzschild Black Holes in Modified Gravity. arXiv, 2016; arXiv:1611.06043. [Google Scholar]
- Sibandze, D.B.; Goswami, R.; Maharaj, S.D.; Dunsby, P.K.S. Echoes from the Black Holes: Evidence of Higher Order Corrections to General Relativity in Strong Gravity Regime. arXiv, 2017; arXiv:1702.04926. [Google Scholar]
- Beltran Jimenez, J.; Heisenberg, L.; Olmo, G.J.; Rubiera-Garcia, D. Born-Infeld Inspired Modifications of Gravity. arXiv, 2017; arXiv:1704.03351. [Google Scholar]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy After GW170817: Dead Ends and the Road Ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef] [PubMed]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef] [PubMed]
| 1. | with the exception of , in which a Gaussian prior was used and set at Planck’s best values [46]. |
| 2. | This does not apply to BAO measurements, since all data points are confined inside . Hence, the same data were used for both fits [46]. |
| 3. | c.f. [25] for a review about the existence and main features of black holes in theories beyond GR. |
| 4. | |
| 5. | c.f. [68] for a thorough analysis regarding the so-called Hu-Sawicki model. |
| 6. | For , results in [72] concluded that, although outside the star the Ricci scalar shows damped oscillations, the total gravitational mass would increase with the radial distance, showing the lack of realism of such an parameter space. |


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De la Cruz Dombriz, Á. Towards New Constraints in Extended Theories of Gravity: Cosmography and Gravitational-Wave Signals from Neutron Stars. Galaxies 2018, 6, 28. https://doi.org/10.3390/galaxies6010028
De la Cruz Dombriz Á. Towards New Constraints in Extended Theories of Gravity: Cosmography and Gravitational-Wave Signals from Neutron Stars. Galaxies. 2018; 6(1):28. https://doi.org/10.3390/galaxies6010028
Chicago/Turabian StyleDe la Cruz Dombriz, Álvaro. 2018. "Towards New Constraints in Extended Theories of Gravity: Cosmography and Gravitational-Wave Signals from Neutron Stars" Galaxies 6, no. 1: 28. https://doi.org/10.3390/galaxies6010028
APA StyleDe la Cruz Dombriz, Á. (2018). Towards New Constraints in Extended Theories of Gravity: Cosmography and Gravitational-Wave Signals from Neutron Stars. Galaxies, 6(1), 28. https://doi.org/10.3390/galaxies6010028




