Abstract
In this conference contribution, we discuss and interpret the time variable rotation measure (RM) detected in the core region of the TeV blazar Markarian 421 (Mrk 421). We monitored Mrk 421 during 2011 with one observing run per month at 15, 24, and 43 GHz with the American Very Long Baseline Array. We explore the possible connection between the RM and the accretion rate, and we investigate the Faraday screen properties and its location with respect to the jet emitting region. Among the various scenarios, the jet sheath is the most promising candidate for being the main source of Faraday rotation. We interpret the RM sign reversals observed during the one-year monitoring within the context of the magnetic tower models by invoking the presence of two nested helical magnetic fields in the relativistic jet with opposite helicities, originating through the Poynting–Robertson cosmic battery effect. The net observed RM values result from the relative contribution of both inner and outer helical fields.
1. Introduction
The study of the polarized emission from active galactic nuclei (AGN) jets is the most powerful tool for investigating the magnetic field structure. When a polarized wave passes through a magnetized non-relativistic plasma, the observed polarization angle is rotated with respect to the intrinsic one. This is known as the Faraday rotation effect, and we need to take it into account in order to properly characterize the source polarization properties. When the Faraday rotating medium (Faraday screen) is external to the emitting region, this effect is described by the linear relationship , where is the observing wavelength and RM represents the rotation measure [1]:
In Equation (1), , , and dl represent the electron number density (cm), the parallel to the line-of-sight magnetic field component (milligauss), and the path length (parsecs), respectively.
Due to the linear dependence of and , by measuring the electric vector position angle (EVPA) as a function of the wavelength it is possible to estimate both the RM and values. For the RM estimate, multi-frequency polarimetric observations with the Very Long Baseline Interferometry (VLBI) technique represent the best tool, allowing us to investigate the magnetic field configuration in the innermost regions of the AGN jets (e.g., [2,3,4,5,6,7,8]).
While the RM has found to be stable over several years in some extragalactic radio sources (e.g., in 3C 84, see [9]), in other sources the RM shows a variable behavior. For example, in the jet region of the radio source 3C273, Asada et al. (2008) [10] found a time-variable RM, and in some cases RM sign reversals are observed with distance from the radio core and within different frequency intervals [4,5,11]. Another important finding is the detection of RM gradient transverse to the jet axis, suggesting the presence of helical magnetic fields in relativistic jets (e.g., [5,11,12,13]).
In this conference contribution, we discuss the time-variable RM observed in the core region of the TeV blazar Markarian 421 (Mrk 421) reported in ([6] hereafter L14), based on a one-year multi-frequency Very Long Baseline Array (VLBA) monitoring in the year 2011. Our goal is to constrain the location of the Faraday screen producing the observed RM. We mainly consider two scenarios for the Faraday screen location: (1) the accretion flow around the black hole and (2) the jet sheath region. In the first case, we explore the possibility in which the RM is related to the mass accretion rate; in the second case we interpret the observed RM time evolution within the context of the magnetic tower models.
2. Results: RM and 43 GHz Flux Density Time Evolution
The model and the discussion presented in this contribution are based on a multi-frequency (15, 24, and 43 GHz) VLBA monitoring campaign with monthly observations conducted during 2011. The observations were carried out in both total and polarized intensity. The complete data analysis and the results of this observing campaign are reported in [6,14,15]. In this work, we mainly focus on the results presented in [6] about the RM values found in the core region of Mrk 421.
Figure 1 is adapted from Figures 2 and 5 reported in L14. In the upper frame of Figure 1, we show the RM time evolution obtained from the linear fits of EVPAs versus . All of the details about the RM values shown in Figure 1 are presented in L14. The RM is variable during the one year observing period, assuming negative values for most of the epochs except for the 3rd and 4th epochs, when the RM is positive. Regarding the intrinsic polarization angle in the source core region, we find that it is roughly parallel to the jet axis () during the entire observing period.
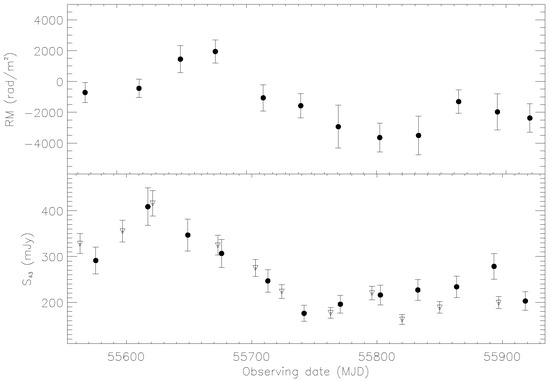
Figure 1.
Upper frame: rotation measure (RM) time evolution in the core region of Mrk 421 (see Section 2 for details). Lower frame: time evolution of the 43 GHz total intensity emission in the core region of Mrk 421. This image is adapted from Figures 2 and 5 presented in L14. Filled circle symbols represent data from L14; the empty triangle symbols in the lower frame are data provided by the VLBA-BU-BLAZAR monitoring program1 .
In the lower frame of Figure 1, we show the core region 43 GHz total intensity light curve, from which it clearly emerges that an enhanced activity is occurring during the first half of 2011.
3. Discussion
In this section, we will consider and investigate the two scenarios in which the Faraday screen is located in the accretion flow region or in the jet sheath.
Given that the EVPAs vs. trend is reasonably represented by linear fits (see L14), we assume that the Faraday screen producing the observed RM is mostly external to the emitting region. Moreover, we assume that most of the observed RM is produced by thermal electrons, mainly because the relativistic mass correction reduces the contribution of relativistic electrons to the Faraday rotation by a factor [16,17,18].
3.1. Faraday Screen in the Accretion Flow
By a visual inspection of Figure 1 it emerges that the RM and the 43 GHz flux density have a similar trend in their time evolution. Given that the RM is related to (see Equation 1) it is reasonable to consider that the RM could be connected with the mass accretion rate . We will now consider this possibility by assuming that the Faraday screen is located in the accretion flow region. By making some simplifying assumptions on the accretion flow geometry, electron density distribution, and magnetic field configuration, in principle, it is possible to estimate from the observed RM values. This approach was proposed by [19] for the case of the radio source Sgr A, and then also used for M87 [20] and 3C 84 [9]. In particular, we assume (1) a roughly spherical accretion flow; (2) a power-law radial density profile ( ), with r being the accretion flow radius and ranging from 3/2 for advection-dominated accretion flow (ADAF, [21]) to 1/2 for convection-dominated accretion flow (CDAF, [22]) models; (3) a radial, ordered, and of equipartition strength magnetic field.
By using the formula presented in Section 4.1 in [20], we estimate a mass accretion rate of M/yr (for details see [23]). For comparison, we make an independent estimate by using the bolometric luminosity (L) with a radiative efficiency of 10% (∼L/(), and we obtain an accretion rate of Myr, which is significantly different from the value obtained with the previous method. A similar discrepancy was obtained for the case of 3C 84 by [9]. Several strong assumptions are made to estimate from the observed RM with the above-mentioned approach, and possibly one or more assumptions are not suitable for the case of Mrk 421. For example, the accretion flow is not necessary spherical and could be disc- or torus-like, and the magnetic field could be weaker than the equipartition value. Moreover, we find sign reversals in the RM values which can only be ascribed to a variation in the term in Equation (1), indicating the presence of a tangled component in the magnetic field.
We conclude that in the specific case of the blazar Mrk 421, the observed RM cannot be used as a reliable tool for estimating the accretion rate and for tracing the accretion flow.
3.2. Faraday Screen in the Jet Sheath
Another good candidate for the Faraday screen location is the jet sheath, located between the emitting region and the observer (e.g., [12,13]). Thermal electrons within the jet sheath can act as a foreground Faraday screen. In this framework, we interpret the observed RM sign reversals reported in the upper panel of Figure 1 within the context of the magnetic tower models (e.g., [24,25]) by means of the Poynting–Robertson (PR) cosmic battery effect [26,27,28,29]. Because of the accretion disc differential rotation, through the PR effect, two nested helical fields are produced in the jet, anchored to the inner and outer accretion disk. The inner magnetic field component originates close to the disk symmetry axis and has the same helicity as the disc rotation, while the outer one (the return field) threads the disk further away from the axis with opposite helicity. In more detail, this model predicts that the poloidal field component () in the inner helical field is parallel to the angular velocity vector (), while in the outer field is antiparallel to . With this configuration, the observed RM results from the relative contribution from both helical field components (e.g., [30,31]).
Our goal is to adapt this general model to the specific case of Mrk 421. We use the numerical model described in [32,33] (see also the conference proceeding by Antonio Fuentes) by performing simulations of a jet threaded by a helical magnetic field for different pitch angle () values, a source viewing angle , and a bulk flow Lorentz factor (for more details on these values, see [14]).
In Figure 2, we show a schematic representation of the proposed model, with the inner helical field represented in blue colour and the outer field in green. The inner helical field, extending over the jet emitting region (solid black line), has in the observer’s direction and produces a positive RM. Conversely, the outer helical field, with in the opposite observer’s direction, produces a negative RM and has the dominant contribution to the observed RM. With this magnetic field configuration and the above-mentioned values for and , we find that the direction of helical field toroidal component () does not affect the RM sign; it only affects the direction of the RM gradient transverse to the jet. Moreover, to obtain an intrinsic polarization angle in the source core region which is parallel to the jet axis (see Section 2), a pitch angle is required.
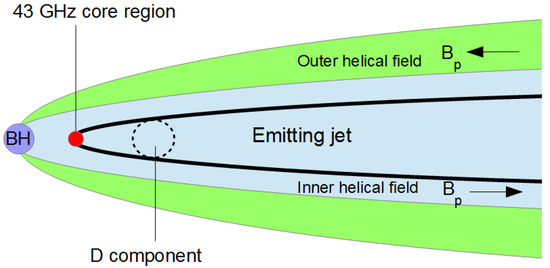
Figure 2.
In this jet cartoon, the blue and green colors represent the inner (RM > 0 and in the observer’s direction) and outer (RM < 0 and in the opposite observer’s direction), respectively. The solid black line and the violet circle mark the emitting jet and the black hole (BH) regions, respectively.
Within this specific magnetic field configuration, an RM sign change from negative to positive can be produced when the inner helical field temporarily dominates the contribution to the observed RM. This behavior can be ascribed to an increased activity in the central region, possibly accompanied by the ejection of a new jet component expanding in the neighboring regions (e.g., [33,34]). This scenario is in agreement with the core region’s enhanced activity observed both at radio and -ray frequencies occurring during the previous observing epoch with respect to the one in which the RM sign reversal is observed. At the same time, a new modelfit component at pc from the core region is detected at 43 GHz [15]. For a more quantitative interpretation of the RM sign changes related to the enhanced core region activity and the new component ejection, further dedicated relativistic MHD simulations and models are required, which fall outside the scope of this work.
As mentioned earlier, within the PR effect mechanism, the polarity of is univocally determined by the direction of the disc rotation. Having assumed in the observer’s direction in the inner helical field, by using the right hand rule, we can infer that the disk of Mrk 421 is rotating counter-clockwise, as seen by an observer looking at the relativistic jet which is closely aligned to the line-of-sight.
4. Concluding Remarks
In this work we tried to identify the most reliable location for the Faraday screen in Mrk 421. We favor the scenario in which the Faraday screen is located in the jet sheath region. We invoke the presence within the jet of two nested helical fields with opposite helicities, originated through the PR cosmic battery effect, both contributing to the observed RM.
In general, the identification of the Faraday screen location is not an easy and straightforward task. In addition to the model that we propose, there are different scenarios explaining RM sign reversals. For example, in [11] the authors show how small changes in the jet speed and/or slight bends of the parsec-scale jet can easily produce a change in RM sign. In [35], the authors show how RM sign reversals can be produced in the transition regions between ultra-relativistic and moderately relativistic helical motion in the innermost AGN regions. Another possibility is that an RM sign reversal can be ascribed to the presence of a blend of multiple sub-components within the beam with different polarization properties [5,8].
Acknowledgments
R.L. gratefully acknowledges the financial support and the kind hospitality from the Instituto de Astrofísica de Andalucia (IAA-CSIC) in Granada. This work is based on observations obtained through the BG207 VLBA project, which makes use of the Swinburne University of Technology software correlator, developed as part of the Australian Major National Research Facilities Programme and operated under license [36]. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We acknowledge financial support from grants PRIN-INAF-2014 and AYA2013-40825-P. This study makes use of 43 GHz VLBA data from the VLBA-BU Blazar Monitoring Program (VLBA-BU-BLAZAR; http://www.bu.edu/blazars/VLBAproject.html), funded by NASA through the Fermi Guest Investigator Program. The VLBA is an instrument of the Long Baseline Observatory. The Long Baseline Observatory is a facility of the National Science Foundation operated by Associated Universities, Inc.
Author Contributions
This work was led by R.L. with the active and needful collaboration of all three co-authors. In particular, the contribution of J.L.G. was essential for the discussion and the model presented in Section 3.2; K.A. contributed to the discussion presented in Section 3.1; A.F. performed the simulations for Section 3.2.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gardner, F.F.; Whiteoak, J.B. The Polarization of Cosmic Radio Waves. Annu. Rev. Astron. Astrophys. 1966, 4, 245–292. [Google Scholar] [CrossRef]
- Zavala, R.T.; Taylor, G.B. A View through Faraday’s Fog: Parsec-Scale Rotation Measures in Active Galactic Nuclei. Astrophys. J. 2003, 589, 126–146. [Google Scholar] [CrossRef]
- Asada, K.; Nakamura, M.; Inoue, M.; Kameno, S.; Nagai, H. Multi-frequency Polarimetry toward S5 0836+710: A Possible Spine-Sheath Structure for the Jet. Astrophys. J. 2010, 720, 41–45. [Google Scholar] [CrossRef]
- Gómez, J.L.; Roca-Sogorb, M.; Agudo, I.; Marscher, A.P.; Jorstad, S.G. On the Source of Faraday Rotation in the Jet of the Radio Galaxy 3C 120. Astrophys. J. 2011, 733, 11. [Google Scholar] [CrossRef]
- Hovatta, T.; Lister, M.L.; Aller, M.F.; Aller, H.D.; Homan, D.C.; Kovalev, Y.Y.; Pushkarev, A.B.; Savolainen, T. MOJAVE: Monitoring of Jets in Active Galactic Nuclei with VLBA Experiments. VIII. Faraday Rotation in Parsec-scale AGN Jets. Astrophys. J. 2012, 144, 105. [Google Scholar] [CrossRef]
- Lico, R.; Giroletti, M.; Orienti, M.; Gómez, J.L.; Casadio, C.; D’Ammando, F.; Blasi, M.G.; Cotton, W.; Edwards, P.G.; Fuhrmann, L.; et al. Very Long Baseline polarimetry and the γ-ray connection in Markarian 421 during the broadband campaign in 2011. Astron. Astrophys. 2014, 571, A54–A66. [Google Scholar] [CrossRef]
- Gómez, J.L.; Lobanov, A.P.; Bruni, G.; Kovalev, Y.Y.; Marscher, A.P.; Jorstad, S.G.; Mizuno, Y.; Bach, U.; Sokolovsky, K.V.; Anderson, J.M.; et al. Probing the Innermost Regions of AGN Jets and Their Magnetic Fields with RadioAstron. I. Imaging BL Lacertae at 21 Microarcsecond Resolution. Astrophys. J. 2016, 817, 96. [Google Scholar] [CrossRef]
- Kravchenko, E.V.; Kovalev, Y.Y.; Sokolovsky, K.V. Parsec-scale Faraday rotation and polarization of 20 active galactic nuclei jets. Mon. Not. R. Astron. Soc. 2017, 467, 83–101. [Google Scholar] [CrossRef][Green Version]
- Plambeck, R.L.; Bower, G.C.; Rao, R.; Marrone, D.P.; Jorstad, S.G.; Marscher, A.P.; Doeleman, S.S.; Fish, V.L.; Johnson, M.D. Probing the Parsec-scale Accretion Flow of 3C 84 with Millimeter Wavelength Polarimetry. Astrophys. J. 2014, 797, 66. [Google Scholar] [CrossRef]
- Asada, K.; Inoue, M.; Kameno, S.; Nagai, H. Time Variation of the Rotation Measure Gradient in the 3C 273 Jet. Astrophys. J. 2008, 675, 79–82. [Google Scholar] [CrossRef]
- O’Sullivan, S.P.; Gabuzda, D.C. Three-dimensional magnetic field structure of six parsec-scale active galactic nuclei jets. Mon. Not. R. Astron. Soc. 2009, 393, 429–456. [Google Scholar] [CrossRef]
- Asada, K.; Inoue, M.; Uchida, Y.; Kameno, S.; Fujisawa, K.; Iguchi, S.; Mutoh, M. A Helical Magnetic Field in the Jet of 3C 273. Publ. Astron. Soc. Jpn. 2002, 54, L39–L43. [Google Scholar] [CrossRef]
- Zavala, R.T.; Taylor, G.B. A View through Faraday’s Fog. II. Parsec-Scale Rotation Measures in 40 Active Galactic Nuclei. Astrophys. J. 2004, 612, 749–779. [Google Scholar] [CrossRef]
- Lico, R.; Giroletti, M.; Orienti, M.; Giovannini, G.; Cotton, W.; Edwards, P.G.; Fuhrmann, L.; Krichbaum, T.P.; Sokolovsky, K.V.; Kovalev, Y.Y.; et al. VLBA monitoring of Mrk 421 at 15 GHz and 24 GHz during 2011. Astron. Astrophys. 2012, 545, A117. [Google Scholar] [CrossRef]
- Blasi, M.G.; Lico, R.; Orienti, M.; Giovannini, G.; Giroletti, M.; Cotton, W.; Edwards, P.G.; Fuhrmann, L.; Krichbaum, T.P.; Sokolovsky, K.V.; et al. The TeV blazar Markarian 421 at the highest spatial resolution. Astron. Astrophys. 2013, 559, A75–A85. [Google Scholar] [CrossRef]
- Jones, T.W.; Odell, S.L. Transfer of polarized radiation in self-absorbed synchrotron sources. I. Results for a homogeneous source. Astrophys. J. 1977, 214, 522–539. [Google Scholar] [CrossRef]
- Wardle, J.F.C.; Homan, D.C. Theoretical Models for Producing Circularly Polarized Radiation in Extragalactic Radio Sources. Astrophys. Space Sci. 2003, 288, 143–153. [Google Scholar] [CrossRef]
- Celotti, A.; Kuncic, Z.; Rees, M.J.; Wardle, J.F.C. Thermal material in relativistic jets. Mon. Not. R. Astron. Soc. 1998, 293, 288–298. [Google Scholar] [CrossRef]
- Marrone, D.P.; Moran, J.M.; Zhao, J.-H.; Rao, R. Interferometric Measurements of Variable 340 GHz Linear Polarization in Sagittarius A. Astrophys. J. 2006, 640, 308–318. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Asada, K.; Rao, R.; Nakamura, M.; Algaba, J.C.; Liu, H.B.; Inoue, M.; Koch, P.M.; Ho, P.T.P.; Matsushita, S.; et al. Measuring Mass Accretion Rate onto the Supermassive Black Hole in M87 Using Faraday Rotation Measure with the Submillimeter Array. Astrophys. J. Lett. 2014, 783, L33. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated accretion: A self-similar solution. Astrophys. J. 1994, 428, L13–L16. [Google Scholar] [CrossRef]
- Quataert, E.; Gruzinov, A. Convection-dominated Accretion Flows. Astrophys. J. 2000, 539, 809–814. [Google Scholar] [CrossRef]
- Lico, R.; Gómez, J.L.; Asada, K.; Fuentes, A. Interpreting the time variable RM observed in the core region of the TeV blazar Mrk 421. Mon. Not. R. Astron. Soc. 2017, 469, 1612–1616. [Google Scholar] [CrossRef]
- Lynden-Bell, D. Magnetic collimation by accretion discs of quasars and stars. Mon. Not. R. Astron. Soc. 1996, 279, 389–401. [Google Scholar] [CrossRef]
- Kato, Y.; Mineshige, S.; Shibata, K. Magnetohydrodynamic Accretion Flows: Formation of Magnetic Tower Jet and Subsequent Quasi-Steady State. Astrophys. J. 2004, 605, 307–320. [Google Scholar] [CrossRef]
- Contopoulos, I.; Kazanas, D. A Cosmic Battery. Astrophys. J. 1998, 508, 859–863. [Google Scholar] [CrossRef]
- Contopoulos, I.; Christodoulou, D.M.; Kazanas, D.; Gabuzda, D.C. The Invariant Twist of Magnetic Fields in the Relativistic Jets of Active Galactic Nuclei. Astrophys. J. Lett. 2009, 702, L148–L152. [Google Scholar] [CrossRef]
- Contopoulos, I.; Nathanail, A.; Sadowski, A.; Kazanas, D.; Narayan, R. Numerical simulations of the Cosmic Battery in accretion flows around astrophysical black holes. arXiv 2017, arXiv:1705.11021. [Google Scholar]
- Christodoulou, D.M.; Gabuzda, D.C.; Knuettel, S.; et al. Dominance of outflowing electric currents on decaparsec to kiloparsec scales in extragalactic jets. Astron. Astrophys. 2016, 591, A61–A71. [Google Scholar] [CrossRef]
- Mahmud, M.; Gabuzda, D.C.; Bezrukovs, V. Surprising evolution of the parsec-scale Faraday Rotation gradients in the jet of the BL Lac object B1803+784. Mon. Not. R. Astron. Soc. 2009, 400, 2–12. [Google Scholar] [CrossRef]
- Mahmud, M.; Coughlan, C.P.; Murphy, E.; Gabuzda, D.C.; Hallahan, D.R. Connecting magnetic towers with Faraday rotation gradients in active galactic nuclei jets. Mon. Not. R. Astron. Soc. 2013, 431, 695–709. [Google Scholar] [CrossRef]
- Gómez, J.L.; Marti, J.M.A.; Marscher, A.P.; Ibanez, J.M.A.; Marcaide, J.M. Parsec-Scale Synchrotron Emission from Hydrodynamic Relativistic Jets in Active Galactic Nuclei. Astrophys. J. Lett. 1995, 449, L19. [Google Scholar] [CrossRef]
- Gómez, J.L.; Martí, J.M.; Marscher, A.P.; Ibáñez, J.M.; Alberdi, A. Hydrodynamical Models of Superluminal Sources. Astrophys. J. Lett. 1997, 482, L33–L36. [Google Scholar] [CrossRef]
- Fromm, C.M.; Perucho, M.; Mimica, P.; Ros, E. Spectral evolution of flaring blazars from numerical simulations. Astron. Astrophys 2016, 588, A101–A115. [Google Scholar] [CrossRef]
- Broderick, A.E.; Loeb, A. Signatures of Relativistic Helical Motion in the Rotation Measures of Active Galactic Nucleus Jets. Astrophys. J. Lett. 2009, 703, L104–L108. [Google Scholar] [CrossRef]
- Deller, A.T.; Brisken, W.F.; Phillips, C.J.; Morgan, J.; Alef, W.; Cappallo, R.; Middelberg, E.; Romney, J.; Rottmann, H.; Tingay, S.J.; et al. DiFX-2: A More Flexible, Efficient, Robust, and Powerful Software Correlator. Publ. Astron. Soc. Pac. 2011, 123, 275. [Google Scholar] [CrossRef]
| 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).