Exoplanet Predictions Based on Harmonic Orbit Resonances
Abstract
1. Introduction
2. Observations and Data Analysis Method
2.1. Data Set Statistics
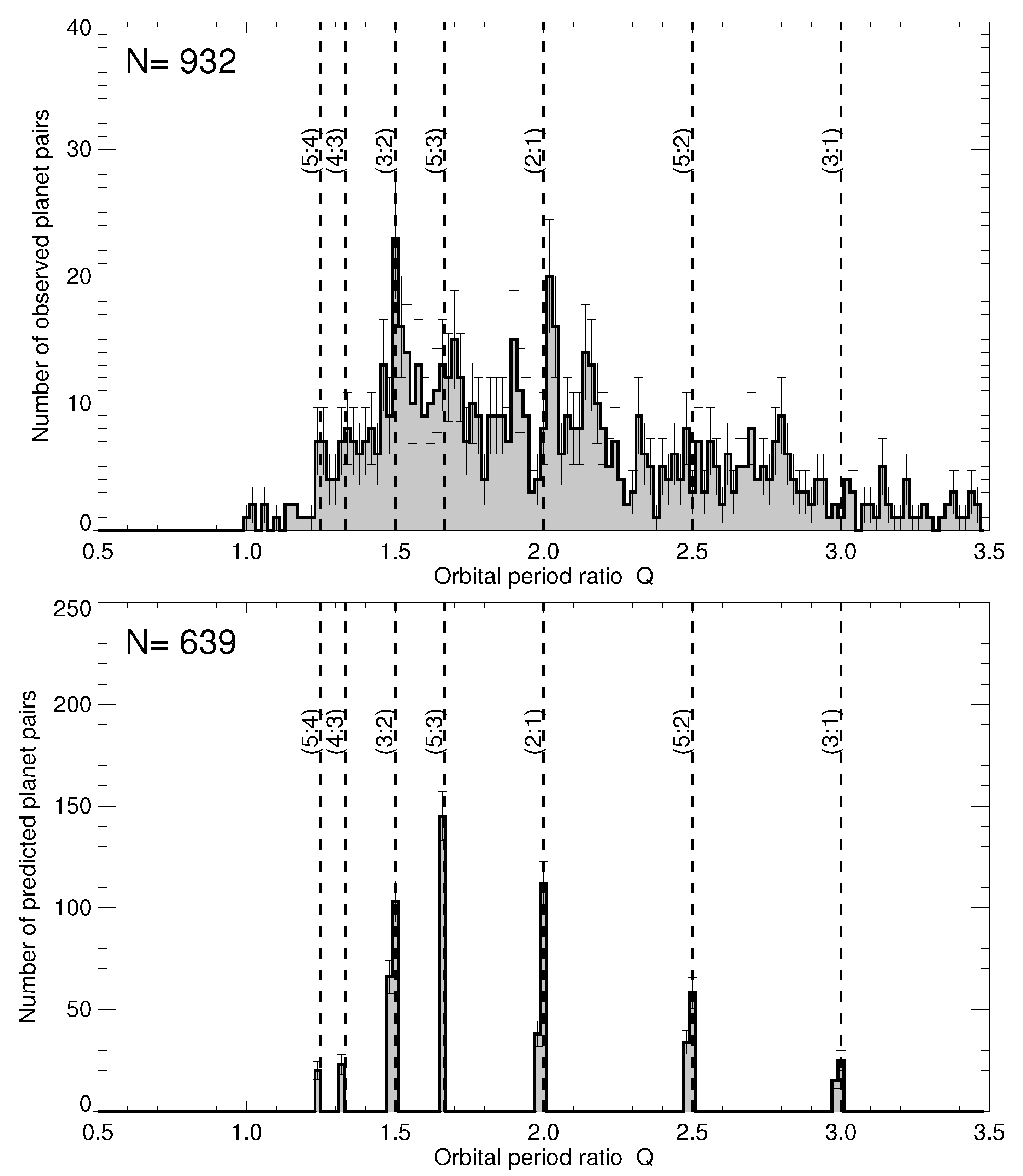
2.2. Orbital Period Ratio Distribution
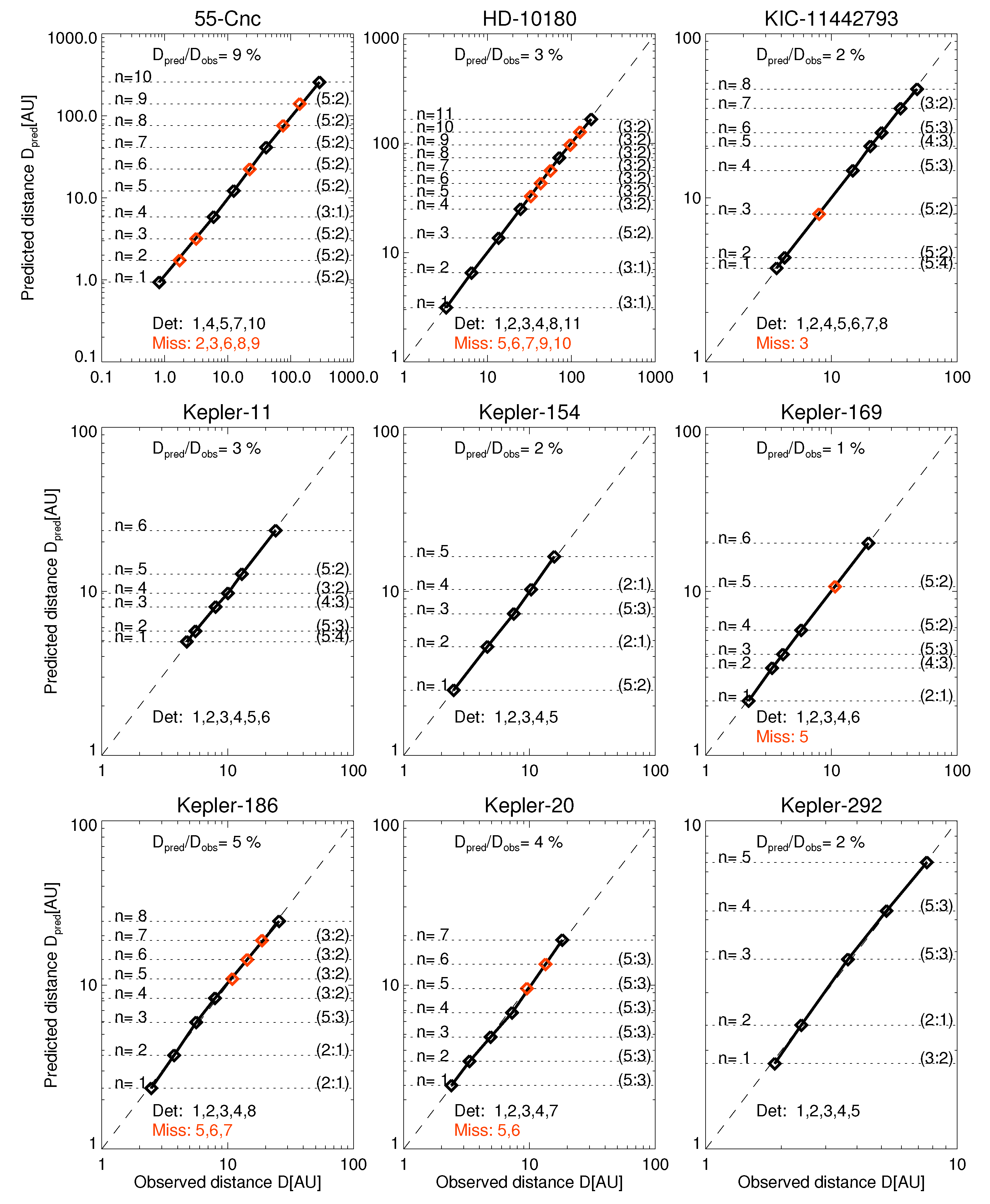
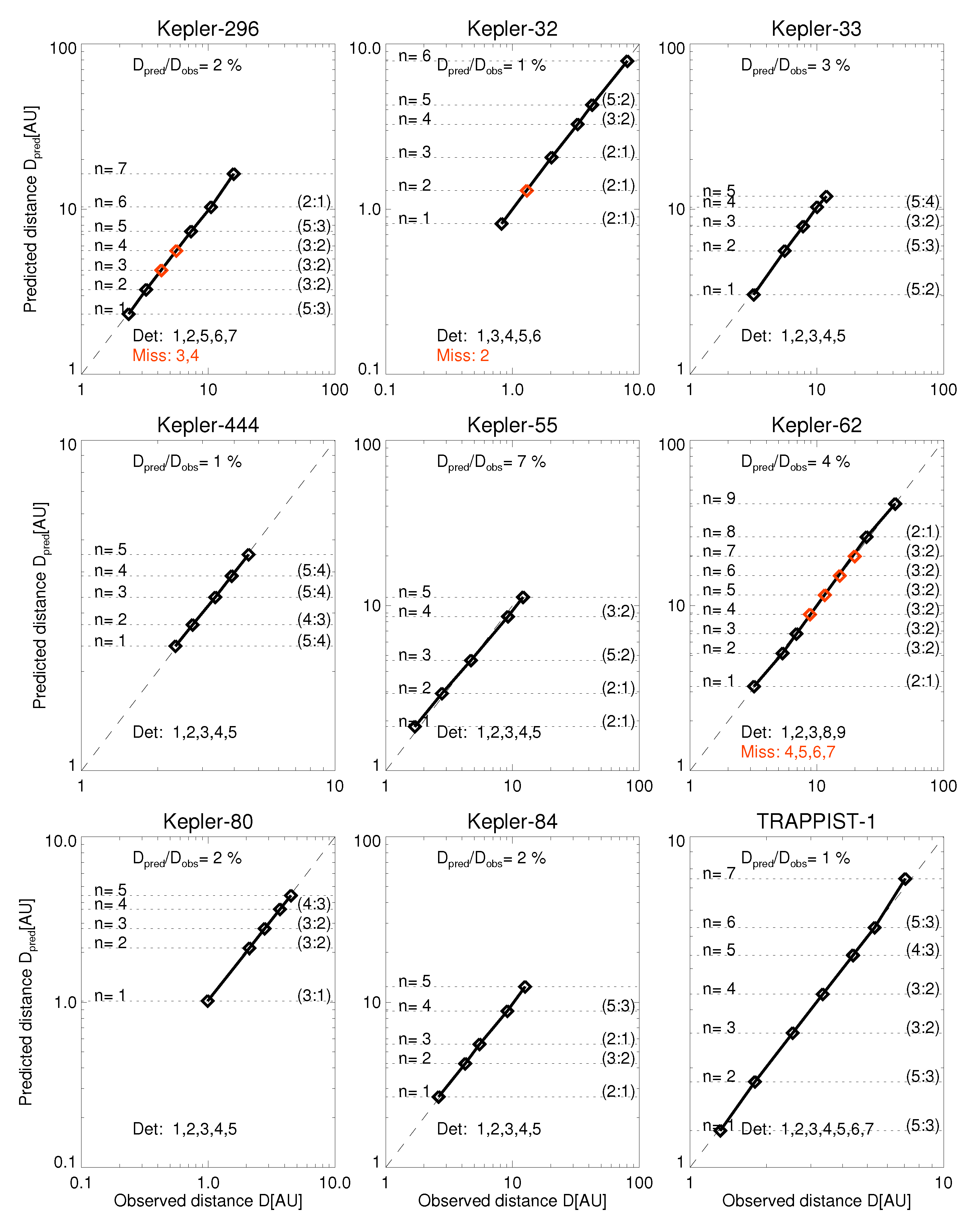
2.3. Orbital Period Ratios of Large Planet Systems
2.4. Strategy for Predicting Missing Exoplanets
2.5. Statistical Probability of Quantized Periods
2.6. Catalog of Exoplanet Predictions
3. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
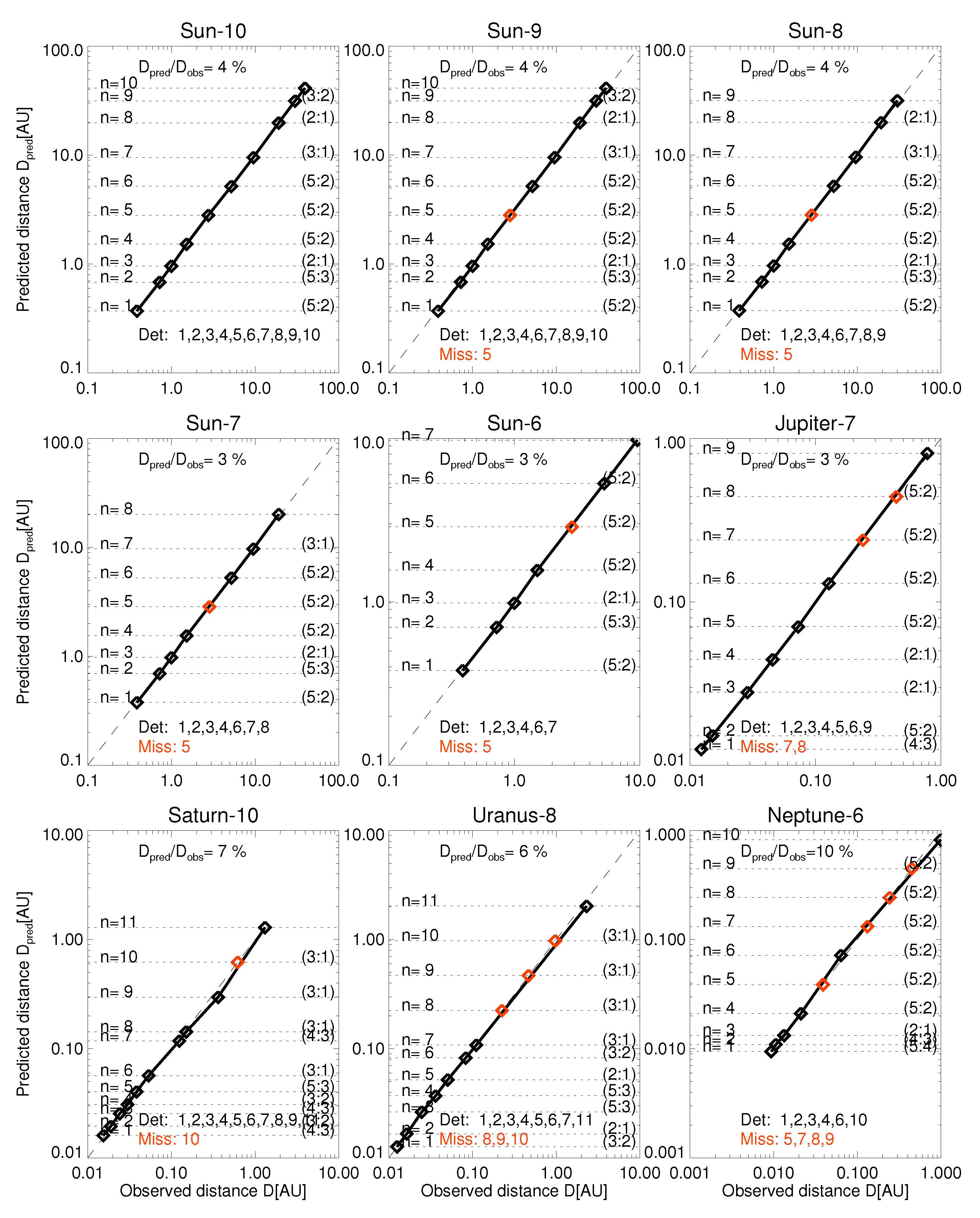
Appendix A. Solar System and Planetary Moon Systems
References
- Han, E.; Wang, S.; Wright, J.T.; Feng, Y.K.; Zhao, M.; Fakhouri, O.; Brown, J.I.; Hancock, C. Exoplanet Orbit Database. II. Updates to Exoplanets.org. Pubs. Astron. Soc. Pac. 2014, 126, 827. [Google Scholar] [CrossRef]
- Malhotra, R. Solar System Formation and Evolution; Lazarro, D., Vieira Martins, R., Ferraz-Mello, S., Fernandez, J., Eds.; Astronomical Society of the Pacific: California, CA, USA, 1998; Volume 149, p. 37. [Google Scholar]
- Peale, S.J. Orbital resonances in the solar system. Annu. Rev. Astron. Astrophys. 1976, 14, 215–246. [Google Scholar] [CrossRef]
- Laplace, P.S. Mécanique Céleste; Hillard, Gray, Little and Wilkins: Boston, MA, USA, 1829. [Google Scholar]
- Brown, E.W.; Shook, C.A. Planetary Theory; Dover: New York, NY, USA, 1933. [Google Scholar]
- Aschwanden, M.J. Self-organizing systems in planetary physics: harmonic resonances of planet and moon orbits. New Astron. 2018, 58, 107–123. [Google Scholar] [CrossRef]
- Armellini, G. Sopra le distanze dei pianeti dal Sole. Astr. Nachr. 1921, 215, 263–264. [Google Scholar] [CrossRef]
- Basano, L.; Hughes, D.W. A modified titius-bode law for planetary orbits. Il Nuovo Cimento 1979, 2, 505–510. [Google Scholar] [CrossRef]
- Cuntz, M. Application of the Titius–Bode Rule to the 55 Cancri System: Tentative Prediction of a Possibly Habitable Planet. Publ. Astron. Soc. Jpn. 2012, 64, 73. [Google Scholar] [CrossRef]
- Poveda, A.; Lara, P. Revista mexicana de astronomía y astrofísica. Rev. Mex. Astron. Astrofisica 2008, 44, 243–246. [Google Scholar]
- Qian, S.B.; Liu, L.; Liao, W.P.; Li, J.; Zhu, L.Y.; Dai, Z.B.; He, J.J.; Zhao, E.G.; Zhang, J.; Li, K. Detection of a planetary system orbiting the eclipsing polar HU Aqr. Mon. Not. R. Astron. Soc. 2011, 414, L16–L20. [Google Scholar] [CrossRef]
- Bovaird, T.; Lineweaver, C.H. Exoplanet predictions based on the generalized Titius-Bode relation. Mon. Not. R. Astron. Soc. 2013, 435, 1126–1138. [Google Scholar] [CrossRef]
- Bovaird, T.; Lineweaver, C.H.; Jacobsen, S.K. Using the inclinations of Kepler systems to prioritize new Titius–Bode-based exoplanet predictions. Mon. Not. R. Astron. Soc. 2015, 448, 3608–3627. [Google Scholar] [CrossRef]
- Huang, C.X.; Bakos, G.A. Testing the Titius–Bode law predictions for Kepler multiplanet systems. Mon. Not. R. Astron. Soc. 2014, 442, 674–681. [Google Scholar] [CrossRef]
- Lovis, C.; Segransan, D.; Mayor, M.; Udry, S.; Benz, W.; Bertaux, J.L.; Bouchy, F.; Correia, A.C.M.; Laskar, J.; Curto, G.L. The HARPS search for southern extra-solar planets-XXVIII. Up to seven planets orbiting HD 10180: probing the architecture of low-mass planetary systems. Astron. Astrophys. 2011, 528, A112. [Google Scholar] [CrossRef]
- Pletser, V. Exponential distance laws for satellite systems. Earth Moon Planets 1986, 36, 193–210. [Google Scholar] [CrossRef]
- Pletser, V. Exponential distance relations in planetary-like systems generated at random. Earth Moon Planets 1988, 42, 1–18. [Google Scholar] [CrossRef]
- Scholkmann, F. A prediction of an additional planet of the extrasolar planetary system Kepler-62 based on the planetary distances’ long-range order. Prog. Phys. 2013, 4, 85–89. [Google Scholar]
- Ghilea, M.C. Statistical distributions of mean motion resonances and near-resonances in multiplanetary systems. arXiv, 2014; arXiv:1410.2478v3. [Google Scholar]
- Gomes, R.; Levison, H.F.; Tsiganis, K.; Morbidelli, A. Origin of the cataclysmic Late Heavy Bombardment period of the terrestrial planets. Nature 2005, 435, 466. [Google Scholar] [CrossRef] [PubMed]
- Minton, D.A.; Malhotra, R. A record of planet migration in the Main Asteroid Belt. Nature 2009, 457, 1109–1111. [Google Scholar] [CrossRef] [PubMed]
- Tsiganis, K.; Gomes, R.; Morbidelli, A.; Levison, H.F. Origin of the orbital architecture of the giant planets of the Solar System. Nature 2005, 435, 459–461. [Google Scholar] [CrossRef] [PubMed]
- Gillon, M.; Triaud, A.H.M.J.; Demory, B.O.; Jehin, E.; Agol, E.D.; Katherine, M.; Lederer, S.M.; De Wit, J.; Burdanov, A.; Ingalls, J. GSeven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1. Nature 2017, 542, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Pletser, V.; Basano, L. Exponential distance relation and near resonances in the Trappist-1 Planetary System. Adv. Space Sci. 2017, in press. [Google Scholar]
- Scholkmann, F. Harmonic Orbital Resonances and Orbital Long-Range Order of the TRAPPIST-1 Exoplanetary System. Prog. Phys. 2017, 9, 85–89. [Google Scholar]
- Chandler, C.O.; McDonald, I.; Kane, S.R. The Catalog of Earth-Like Exoplanet Survey Targets (CELESTA): A Database of Habitable Zones Around Nearby Stars. Astron. J. 2016, 151, 59. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381. [Google Scholar] [CrossRef] [PubMed]
- Aschwanden, M.J.; Crosby, N.; Dimitropoulou, M.; Georgoulis, M.K.; Hergarten, S.; McAteer, J.; Milovanov, A.; Mineshige, S.; Morales, L.; Nishizuka, N.; et al. 25 Years of Self-Organized Criticality: Solar and Astrophysics. Sp. Sc. Rev. 2016, 198, 47–166. [Google Scholar] [CrossRef]
| Data Set | Number |
|---|---|
| Number of detected exoplanets | 5454 |
| Number of exoplanet-associated stars | 4522 |
| Number of stars with one exoplanet | 3860 |
| Number of stars with two exoplanets | 472 |
| Number of stars with three exoplanets | 128 |
| Number of stars with four exoplanets | 44 |
| Number of stars with five exoplanets | 14 |
| Number of stars with six exoplanets | 2 |
| Number of stars with seven exoplanets | 2 |
| Number of planet-pair orbit ratios | 932 |
| Star | Planet Distances (in Units of AU) |
|---|---|
| 55-Cnc | 0.82, (1.50), (2.77), 5.10, 10.60, (19.53), 35.98, (66.27), (122.07), 224.85 |
| 61-Vir | 2.61, (5.43), 11.29, 23.48 |
| GJ-163 | 4.21, 8.75, (12.30), (17.29), (24.31), (34.18), (48.04), 67.53 |
| GJ-581 | 2.15, 3.02, 5.56 |
| GJ-876 | 1.55, (2.86), (5.27), 9.71, 15.42, 24.48 |
| HD-10180 | 3.21, 6.68, 13.90, 25.61, (33.56), (43.97), (57.62), 75.50, (98.94), (129.64), 169.88 |
| HD-181433 | 4.45, (8.19), (15.09), (27.79), (51.18), 94.28, 173.67 |
| HD-20794 | 6.95, 11.03, 20.32 |
| HD-37124 | 28.78, (53.01), 97.64, 155.00 |
| HD-40307 | 2.65, 4.21, 6.68 |
| HD-69830 | 4.22, (5.53), (7.24), 9.49, (12.44), (16.30), (21.36), (27.99), 36.68 |
| HD-7924 | 3.08, 6.40, 9.00 |
| HIP-14810 | 3.54, (4.98), (7.00), (9.85), (13.84), (19.46), 27.35, (38.45), (54.05), (75.98), 106.80 |
| HIP-57274 | 4.04, (5.69), (7.99), 11.24, (15.79), (22.20), (31.21), (43.87), 61.67 |
| HR-8799 | 646.08, 1190.08, 1889.14, 2998.82 |
| K2-3 | 4.66, 8.58, 12.06 |
| KIC-11442793 | 3.66, 4.25, (7.83), 14.42, 20.27, 24.55, 34.52, 45.23 |
| KOI-1082 | 2.56, 3.60, 4.72 |
| KOI-1358 | 1.77, 2.31, 3.03, 3.97 |
| KOI-1475 | 1.37, 2.86, 4.53 |
| KOI-1563 | 2.17, 3.06, 4.00 |
| KOI-1576 | 4.77, 5.53, 7.78 |
| KOI-1590 | 1.77, 2.81, 5.18 |
| KOI-1681 | 1.58, 2.23, 3.53, (4.63), (6.07), 7.95 |
| KOI-1860 | 2.12, 3.36, 5.33, 8.46 |
| KOI-2037 | 3.11, 4.07, (8.47), 17.62 |
| KOI-2093 | 0.99, 1.83, 3.38 |
| KOI-2169 | 1.69, 2.21, 2.68 |
| KOI-2174 | 3.55, 4.12, (6.54), 10.39 |
| KOI-2248 | 1.91, 2.22, 4.62 |
| KOI-2433 | 3.33, (4.67), (6.57), 9.24, 14.66, 19.21 |
| KOI-2579 | 1.95, 2.37, 4.92 |
| KOI-279 | 3.84, 6.09, 9.67 |
| KOI-285 | 5.74, 9.11, 14.46 |
| KOI-2859 | 2.04, 2.67, 3.10 |
| KOI-3083 | 3.39, 4.10, 4.76 |
| KOI-3425 | 2.15, 3.96, 7.30 |
| KOI-3444 | 1.91, (3.03), 4.81, 5.58, (8.86), 14.06 |
| KOI-353 | 4.99, 9.20, (12.06), (15.80), (20.70), 27.13 |
| KOI-4524 | 2.23, 2.71, 3.80 |
| KOI-6242 | 18.07, 20.97, 38.63 |
| KOI-85 | 1.67, 3.07, 3.72 |
| KOI-94 | 2.41, 5.01, 7.96, 14.66 |
| KOI-945 | 8.74, 11.46, 16.10 |
| Kepler-102 | 3.03, 4.82, 6.31, 8.87 |
| Kepler-106 | 3.36, 5.34, (6.99), (9.16), 12.01 |
| Kepler-107 | 2.16, 2.83, 3.98, 6.32 |
| Kepler-11 | 4.74, 5.49, 7.72, 9.36, 12.26, 22.59 |
| Kepler-122 | 3.22, 5.10, 7.18, 10.09 |
| Kepler-124 | 2.27, (3.60), 5.71, 9.06 |
| Kepler-1254 | 2.35, 3.30, 4.64 |
| Kepler-126 | 4.79, 7.61, (10.70), (15.04), 21.14 |
| Kepler-127 | 5.93, 9.41, 13.23 |
| Kepler-132 | 3.37, 3.91, 8.13, (10.65), (13.95), (18.29), 23.96 |
| Kepler-1388 | 3.13, 4.97, 6.98, 9.82 |
| Kepler-142 | 1.60, 2.95, (6.13), 12.75 |
| Kepler-148 | 1.44, 2.65, (3.73), (5.24), (7.37), (10.36), 14.57 |
| Kepler-149 | 9.48, 15.05, 31.31 |
| Kepler-150 | 2.27, 3.61, 5.07, 9.34 |
| Kepler-154 | 2.49, 4.59, 7.29, 10.24, 16.26 |
| Kepler-1542 | 2.03, 2.46, 2.85, 3.31 |
| Kepler-157 | 1.44, (2.29), 3.63, 5.77 |
| Kepler-164 | 2.94, 4.66, 8.59 |
| Kepler-166 | 1.34, (1.89), (2.65), 3.73, (5.24), (7.36), 10.35 |
| Kepler-169 | 2.19, 3.48, 4.22, 5.93, (10.93), 20.13 |
| Kepler-171 | 2.59, 5.39, (7.06), (9.25), 12.12 |
| Kepler-172 | 2.05, 3.26, 6.00, 11.05 |
| Kepler-174 | 5.80, (7.61), (9.97), 13.06, (17.11), (22.42), (29.38), 38.50 |
| Kepler-176 | 3.09, 5.69, 9.04, 14.34 |
| Kepler-178 | 4.51, 7.16, (9.38), (12.29), (16.11), 21.11 |
| Kepler-18 | 2.31, 3.66, 5.81 |
| Kepler-184 | 4.85, 7.70, 10.09 |
| Kepler-186 | 2.47, 3.92, 6.23, 8.76, (11.47), (15.04), (19.70), 25.82 |
| Kepler-191 | 3.28, 4.61, 6.48 |
| Kepler-192 | 3.47, 4.55, 7.22 |
| Kepler-194 | 1.64, (2.60), (4.12), 6.54, 13.61 |
| Kepler-197 | 3.15, 5.01, 6.56, 9.22 |
| Kepler-198 | 1.20, (1.68), (2.37), (3.33), (4.68), 6.58, 13.68 |
| Kepler-20 | 2.39, 3.36, 4.72, 6.64, (9.33), (13.12), 18.45 |
| Kepler-203 | 2.15, 3.03, 4.81 |
| Kepler-206 | 3.93, 5.52, 7.76 |
| Kepler-207 | 1.37, 2.18, 3.46 |
| Kepler-208 | 2.61, 3.68, 4.82, 6.31 |
| Kepler-215 | 4.44, 5.82, 9.24, 14.67 |
| Kepler-217 | 2.47, 2.99, 4.21 |
| Kepler-218 | 2.36, (3.09), (4.05), (5.30), (6.95), (9.11), 11.93, 24.82 |
| Kepler-219 | 2.76, (3.62), (4.74), (6.21), 8.14, 12.92 |
| Kepler-220 | 2.59, 4.11, (5.38), (7.05), 9.24, 12.99 |
| Kepler-221 | 1.98, 3.15, 4.43, 6.23 |
| Kepler-222 | 2.49, 4.59, 9.55 |
| Kepler-223 | 3.79, 4.59, 6.02, 7.29 |
| Kepler-224 | 2.14, 3.40, 5.40, 7.58 |
| Kepler-226 | 2.50, 3.02, 3.96 |
| Kepler-228 | 1.87, 2.64, 4.85 |
| Kepler-229 | 3.39, 6.25, 11.52 |
| Kepler-23 | 3.70, 4.84, 6.35 |
| Kepler-235 | 2.23, 4.12, 7.58, 13.97 |
| Kepler-238 | 1.64, 3.40, 5.40 |
| Kepler-24 | 2.62, 5.45, 7.15 |
| Kepler-244 | 2.65, 4.88, 7.75 |
| Kepler-245 | 2.18, 4.02, 7.40, 11.74 |
| Kepler-247 | 2.23, 4.64, 7.37 |
| Kepler-249 | 2.22, 3.52, 5.59 |
| Kepler-250 | 2.58, 3.63, 6.68 |
| Kepler-251 | 2.84, (3.72), (4.88), 6.39, 8.99, (11.78), (15.43), 20.22 |
| Kepler-253 | 2.43, 4.47, 6.29 |
| Kepler-254 | 3.24, 5.14, 6.74 |
| Kepler-255 | 1.03, (1.35), (1.77), (2.32), 3.04, 4.27 |
| Kepler-256 | 1.38, 2.19, 3.08, 4.33 |
| Kepler-257 | 1.78, 3.71, (4.86), (6.37), 8.35 |
| Kepler-26 | 2.32, (3.69), 5.86, 7.10, 13.07 |
| Kepler-265 | 3.61, 6.64, 12.23, 16.03 |
| Kepler-267 | 2.24, 3.56, (5.65), 8.96 |
| Kepler-271 | 3.01, 3.49, 4.23 |
| Kepler-272 | 2.07, 3.28, 4.61 |
| Kepler-275 | 4.73, 6.20, 9.85 |
| Kepler-286 | 1.48, 2.35, 3.30, (4.32), (5.66), (7.42), 9.72 |
| Kepler-288 | 3.34, 6.94, 14.44 |
| Kepler-289 | 10.61, 16.84, 26.73 |
| Kepler-292 | 1.88, 2.47, 3.91, 5.50, 7.73 |
| Kepler-295 | 5.43, 7.63, 10.00 |
| Kepler-296 | 2.36, 3.32, (4.34), (5.69), 7.46, 10.49, 16.64 |
| Kepler-298 | 4.79, 7.60, (9.96), (13.05), 17.10 |
| Kepler-299 | 2.05, 3.77, 5.98, 11.02 |
| Kepler-30 | 9.51, 15.10, 27.81 |
| Kepler-301 | 1.85, 2.93, 5.40 |
| Kepler-304 | 1.31, 2.08, 2.92, 4.11 |
| Kepler-306 | 2.78, 3.65, 6.72, 12.38 |
| Kepler-31 | 7.58, 12.03, 19.10 |
| Kepler-310 | 5.79, (9.19), 14.59, 20.51 |
| Kepler-319 | 2.67, 3.75, (5.28), (7.42), 10.43 |
| Kepler-32 | 0.82, (1.30), 2.07, 3.28, 4.30, 7.92 |
| Kepler-325 | 2.74, 5.71, 11.87 |
| Kepler-326 | 1.72, 2.72, 3.57 |
| Kepler-327 | 1.87, 2.96, 5.46 |
| Kepler-33 | 3.18, 5.86, 8.23, 10.79, 12.52 |
| Kepler-331 | 4.15, 6.59, 10.46 |
| Kepler-332 | 3.87, 6.15, 9.76 |
| Kepler-334 | 3.10, 5.72, 9.08 |
| Kepler-336 | 1.60, (2.10), (2.75), (3.60), 4.72, 7.49 |
| Kepler-338 | 5.73, 8.06, 11.33 |
| Kepler-339 | 2.92, 3.53, 4.63 |
| Kepler-341 | 3.00, 3.93, (5.15), (6.75), 8.84, 11.59 |
| Kepler-342 | 1.39, (2.90), 6.03, 8.47, 11.10 |
| Kepler-351 | 11.11, 14.56, 26.83 |
| Kepler-354 | 3.11, 6.46, 8.47 |
| Kepler-357 | 3.47, 6.40, 13.31 |
| Kepler-359 | 8.68, 15.98, 19.36 |
| Kepler-363 | 2.36, 3.74, 4.90 |
| Kepler-37 | 5.63, 7.92, 12.57 |
| Kepler-372 | 3.61, 7.50, 9.83 |
| Kepler-374 | 1.53, 2.15, 2.82 |
| Kepler-398 | 2.55, 3.59, 5.05 |
| Kepler-399 | 5.93, 9.41, 14.93 |
| Kepler-401 | 5.91, (7.75), (10.16), 13.31, (17.44), (22.85), 29.94 |
| Kepler-402 | 2.53, 3.32, 4.35, 5.04 |
| Kepler-403 | 3.67, 5.83, (9.25), 14.68 |
| Kepler-42 | 0.59, 1.09, 1.42 |
| Kepler-431 | 3.59, 4.17, 5.05 |
| Kepler-444 | 2.35, 2.73, 3.30, 3.83, 4.45 |
| Kepler-445 | 2.07, 2.91, 4.10 |
| Kepler-446 | 1.35, 2.14, 3.01 |
| Kepler-48 | 2.84, 4.50, (6.33), (8.90), 12.51 |
| Kepler-49 | 1.88, 3.91, 5.12, 7.20 |
| Kepler-52 | 3.96, 6.28, 9.98 |
| Kepler-53 | 4.56, 7.25, 11.50 |
| Kepler-54 | 4.00, 5.25, 7.37 |
| Kepler-55 | 1.70, 2.69, 4.28, 7.88, 10.32 |
| Kepler-58 | 4.71, 6.17, 11.37 |
| Kepler-60 | 3.71, 4.30, 5.21 |
| Kepler-603 | 3.38, (4.43), (5.81), 7.61, (9.97), (13.06), (17.12), 22.43 |
| Kepler-62 | 3.20, 5.07, 6.65, (8.71), (11.42), (14.96), (19.60), 25.69, 40.78 |
| Kepler-68 | 3.08, 4.33, (6.87), (10.90), (17.30), (27.47), (43.60), 69.22 |
| Kepler-758 | 2.83, 3.98, 5.21, 7.32 |
| Kepler-770 | 1.30, 2.70, (3.79), (5.33), 7.49 |
| Kepler-79 | 5.67, 8.99, 14.28, 18.71 |
| Kepler-80 | 0.99, 2.06, 2.70, 3.54, 4.29 |
| Kepler-81 | 3.29, 5.22, 7.33 |
| Kepler-82 | 1.78, 3.29, (4.62), (6.49), 9.13, 14.49 |
| Kepler-83 | 2.99, 4.75, 7.53 |
| Kepler-84 | 2.61, 4.15, 5.44, 8.63, 12.13 |
| Kepler-85 | 4.10, 5.37, 7.04, 8.53 |
| Kepler-89 | 2.41, 5.01, 7.96, 14.66 |
| Kepler-9 | 1.36, (1.92), (2.70), (3.79), (5.33), 7.49, 11.88 |
| PSR-B1257+12 | 8.61, 15.86, 20.78 |
| TRAPPIST-1 | 1.32, 1.85, 2.60, 3.41, 4.47, 5.41, 7.09 |
| WASP-47 | 2.59, 4.11, (6.52), (10.34), (16.42), (26.07), (41.38), 65.69 |
| mu-Ara | 4.53, (8.34), (15.37), (28.31), 52.14, 82.77, (152.46), 280.84 |
| upsilon-And | 2.77, (5.11), (9.41), (17.33), 31.92, (58.80), 108.31 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aschwanden, M.J.; Scholkmann, F. Exoplanet Predictions Based on Harmonic Orbit Resonances. Galaxies 2017, 5, 56. https://doi.org/10.3390/galaxies5040056
Aschwanden MJ, Scholkmann F. Exoplanet Predictions Based on Harmonic Orbit Resonances. Galaxies. 2017; 5(4):56. https://doi.org/10.3390/galaxies5040056
Chicago/Turabian StyleAschwanden, Markus J., and Felix Scholkmann. 2017. "Exoplanet Predictions Based on Harmonic Orbit Resonances" Galaxies 5, no. 4: 56. https://doi.org/10.3390/galaxies5040056
APA StyleAschwanden, M. J., & Scholkmann, F. (2017). Exoplanet Predictions Based on Harmonic Orbit Resonances. Galaxies, 5(4), 56. https://doi.org/10.3390/galaxies5040056







