Modeling Polarized Emission from Black Hole Jets: Application to M87 Core Jet
Department of Astrophysics, The Institute for Mathematics, Astrophysics and Particle Physics, Radboud University, P.O. Box 9010, 6500 GL Nijmegen, The Netherlands
Academic Editors: Emmanouil Angelakis and Jose L. Gómez
Galaxies 2017, 5(3), 54; https://doi.org/10.3390/galaxies5030054
Received: 18 August 2017 / Revised: 11 September 2017 / Accepted: 13 September 2017 / Published: 19 September 2017
(This article belongs to the Special Issue Polarised Emission from Astrophysical Jets)
We combine three-dimensional general-relativistic numerical models of hot, magnetized Advection Dominated Accretion Flows around a supermassive black hole and the corresponding outflows from them with a general relativistic polarized radiative transfer model to produce synthetic radio images and spectra of jet outflows. We apply the model to the underluminous core of M87 galaxy. The assumptions and results of the calculations are discussed in context of millimeter observations of the M87 jet launching zone. Our ab initio polarized emission and rotation measure models allow us to address the constrains on the mass accretion rate onto the M87 supermassive black hole.
View Full-Text
Keywords:
black holes; jets; polarized emission; GRMHD simulations
▼
Show Figures
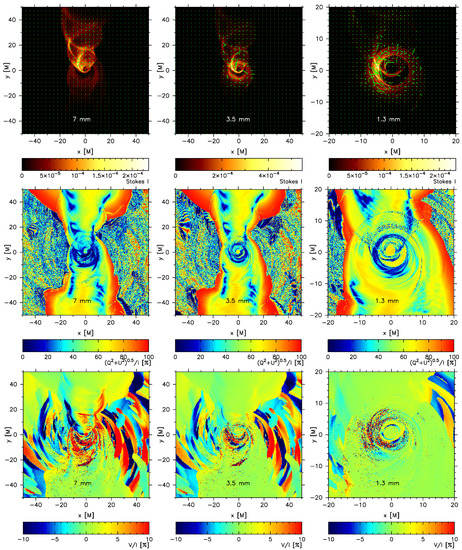
Figure 1
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited
MDPI and ACS Style
Mościbrodzka, M. Modeling Polarized Emission from Black Hole Jets: Application to M87 Core Jet. Galaxies 2017, 5, 54.
Show more citation formats
Note that from the first issue of 2016, MDPI journals use article numbers instead of page numbers. See further details here.
