Estimation of Host Galaxy Extinction for SNe Ia
Abstract
1. Introduction
2. Description of the Model
2.1. Distribution of Interstellar Medium in A Galaxy
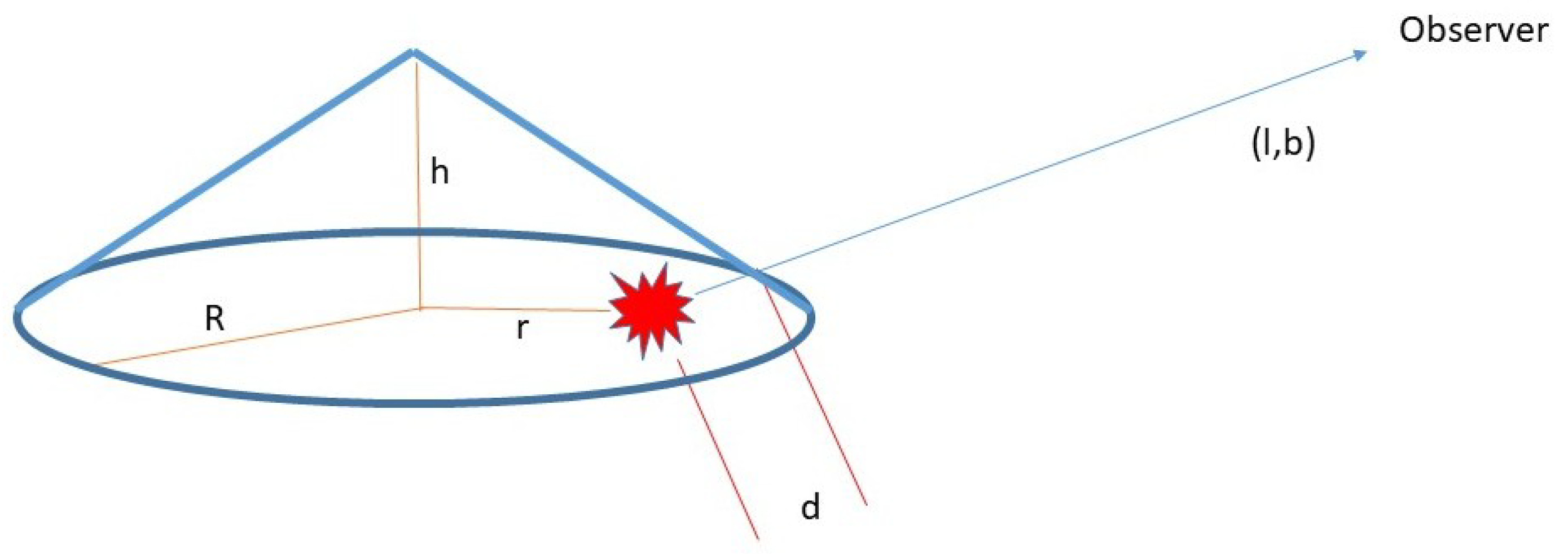
2.2. Estimating the Interstellar Extinction of Light from a Star in a Distant Galaxy
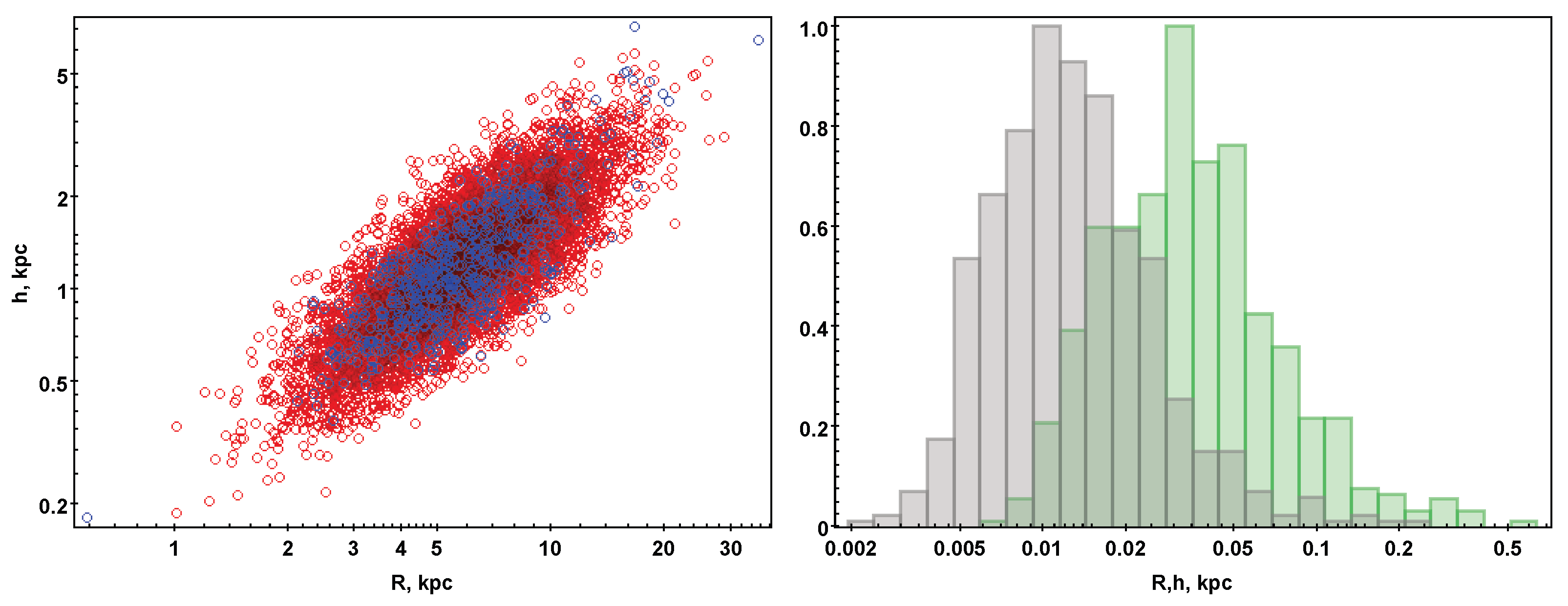
2.3. The Distribution of Spiral Galaxy Radii and Heights from Observational Survey and Numerical Simulations
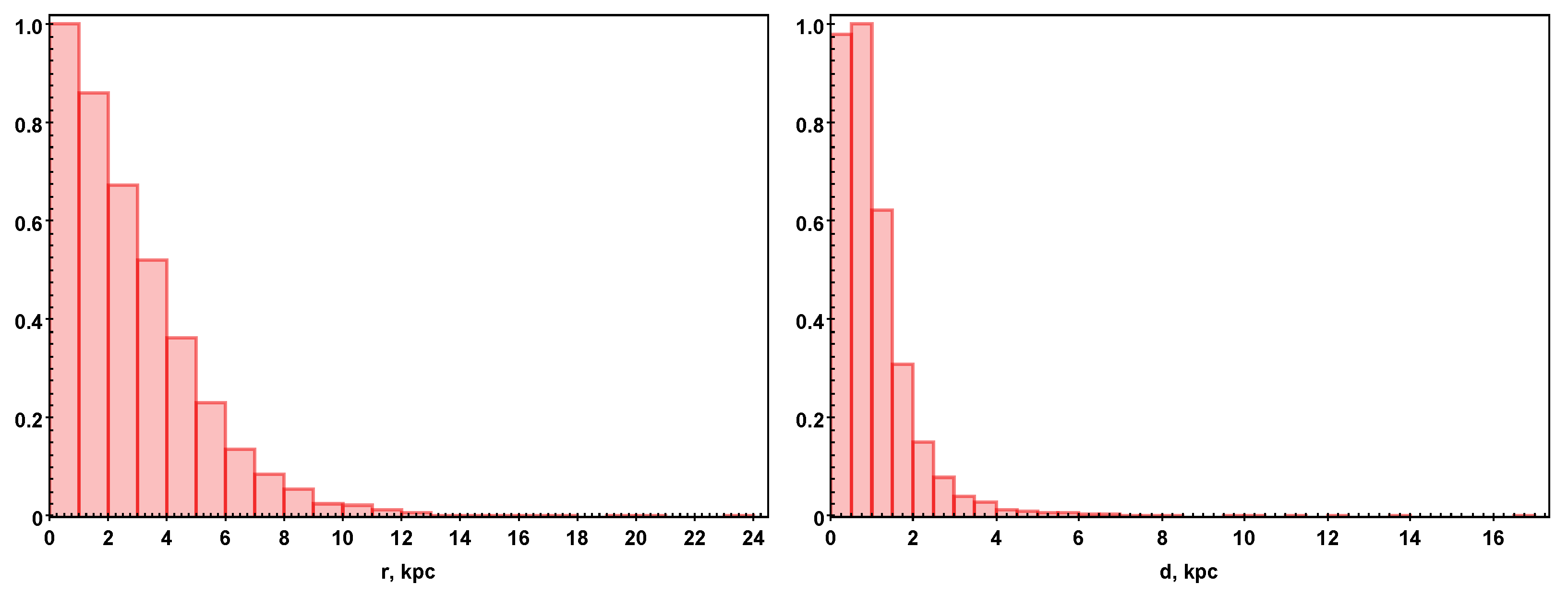
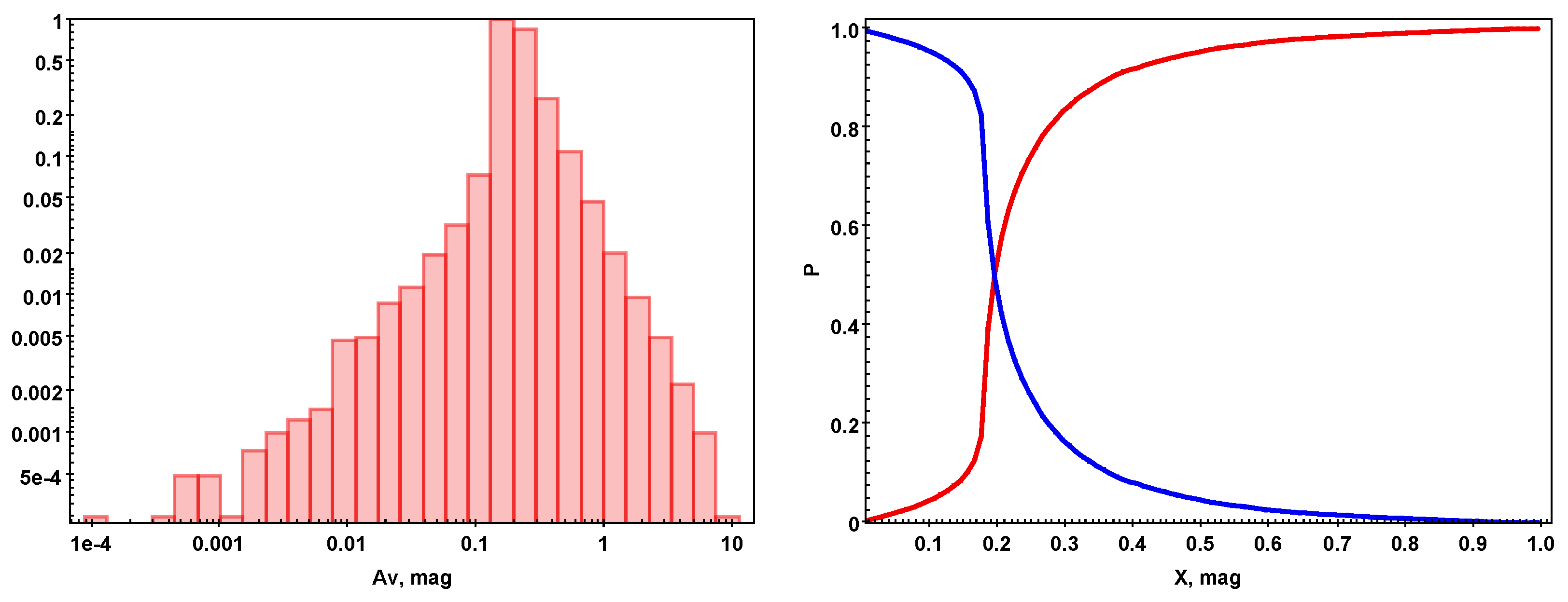
3. Results
- mag) = 0.95;
- mag) = 0.90;
- mag) = 0.46;
- mag) = 0.25;
- mag) = 0.11.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Livio, M.; Mazzali, P. On the progenitors of Type Ia supernovae. Phys. Rep. 2018, 736, 1–23. [Google Scholar] [CrossRef]
- Li, W.; Chornock, R.; Leaman, J.; Filippenko, A.V.; Poznanski, D.; Wang, X.; Ganeshalingam, M.; Mannucci, F. Nearby supernova rates from the Lick Observatory Supernova Search—III. The rate-size relation, and the rates as a function of galaxy Hubble type and colour. Mon. Not. R. Astron. Soc. 2011, 412, 1473–1507. [Google Scholar] [CrossRef]
- Palicio, P.A.; Matteucci, F.; Della Valle, M.; Spitoni, E. Cosmic Type Ia supernova rate and constraints on supernova Ia progenitors. Astron. Astrophys. 2024, 689, A203. [Google Scholar] [CrossRef]
- Rigault, M.; Smith, M.; Goobar, A.; Maguire, K.; Dimitriadis, G.; Johansson, J.; Nordin, J.; Burgaz, U.; Dhawan, S.; Sollerman, J.; et al. ZTF SN Ia DR2: Overview. Astron. Astrophys. 2025, 694, A1. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Guy, J.; Astier, P.; Baumont, S.; Hardin, D.; Pain, R.; Regnault, N.; Basa, S.; Carlberg, R.G.; Conley, A.; Fabbro, S.; et al. SALT2: Using distant supernovae to improve the use of type Ia supernovae as distance indicators. Astron. Astrophys. 2007, 466, 11–21. [Google Scholar] [CrossRef]
- Taylor, G.; Lidman, C.; Tucker, B.E.; Brout, D.; Hinton, S.R.; Kessler, R. A revised SALT2 surface for fitting Type Ia supernova light curves. Mon. Not. R. Astron. Soc. 2021, 504, 4111–4122. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Kenworthy, W.D.; Jones, D.O.; Dai, M.; Kessler, R.; Scolnic, D.; Brout, D.; Siebert, M.R.; Pierel, J.D.R.; Dettman, K.G.; Dimitriadis, G.; et al. SALT3: An Improved Type Ia Supernova Model for Measuring Cosmic Distances. Astrophys. J. 2021, 923, 265. [Google Scholar] [CrossRef]
- DES Collaboration; Abbott, T.M.C.; Acevedo, M.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; et al. The Dark Energy Survey: Cosmology Results with ∼1500 New High-redshift Type Ia Supernovae Using the Full 5 yr Data Set. Astrophys. J. Lett. 2024, 973, L14. [Google Scholar] [CrossRef]
- Seifert, A.; Lane, Z.G.; Galoppo, M.; Ridden-Harper, R.; Wiltshire, D.L. Supernovae evidence for foundational change to cosmological models. Mon. Not. R. Astron. Soc. 2025, 537, L55–L60. [Google Scholar] [CrossRef]
- Foley, R.J.; Kasen, D. Measuring Ejecta Velocity Improves Type Ia Supernova Distances. Astrophys. J. 2011, 729, 55. [Google Scholar] [CrossRef]
- Wang, L. Dust around Type Ia Supernovae. Astrophys. J. Lett. 2005, 635, L33–L36. [Google Scholar] [CrossRef]
- Goobar, A. Low RV from Circumstellar Dust around Supernovae. Astrophys. J. Lett. 2008, 686, L103. [Google Scholar] [CrossRef]
- Maeda, K.; Leloudas, G.; Taubenberger, S.; Stritzinger, M.; Sollerman, J.; Elias-Rosa, N.; Benetti, S.; Hamuy, M.; Folatelli, G.; Mazzali, P.A. Effects of the explosion asymmetry and viewing angle on the Type Ia supernova colour and luminosity calibration. Mon. Not. R. Astron. Soc. 2011, 413, 3075–3094. [Google Scholar] [CrossRef]
- Chotard, N.; Gangler, E.; Aldering, G.; Antilogus, P.; Aragon, C.; Bailey, S.; Baltay, C.; Bongard, S.; Buton, C.; Canto, A.; et al. The reddening law of type Ia supernovae: Separating intrinsic variability from dust using equivalent widths. Astron. Astrophys. 2011, 529, L4. [Google Scholar] [CrossRef]
- Meldorf, C.; Palmese, A.; Brout, D.; Chen, R.; Scolnic, D.; Kelsey, L.; Galbany, L.; Hartley, W.G.; Davis, T.M.; Drlica-Wagner, A.; et al. The Dark Energy Survey Supernova Program results: Type Ia supernova brightness correlates with host galaxy dust. Mon. Not. R. Astron. Soc. 2023, 518, 1985–2004. [Google Scholar] [CrossRef]
- Smadja, G.; Copin, Y.; Hillebrandt, W.; Saunders, C.; Tao, C. Intrinsic and extinction colour components in SNe Ia and the determination of RV. Astron. Astrophys. 2024, 682, A121. [Google Scholar] [CrossRef]
- Gontcharov, G.A.; Marchuk, A.A.; Khovrichev, M.Y.; Mosenkov, A.V.; Savchenko, S.S.; Il’in, V.B.; Poliakov, D.M.; Smirnov, A.A. New Interstellar Extinction Maps Based on Gaia and Other Sky Surveys. Astron. Lett. 2023, 49, 673–696. [Google Scholar] [CrossRef]
- Malkov, O.; Avdeeva, A.; Kovaleva, D. LAMOST Spectroscopy and Gaia Photo-Astrometry for an Interstellar Extinction Study. Galaxies 2024, 12, 65. [Google Scholar] [CrossRef]
- Zhang, X.; Green, G.M. Three-dimensional maps of the interstellar dust extinction curve within the Milky Way galaxy. Science 2025, 387, 1209–1214. [Google Scholar] [CrossRef]
- Parenago, P.P. On interstellar extinction of light. Astron. Zh. 1940, 13, 3. [Google Scholar]
- Fitzgerald, M.P. The Distribution of Interstellar Reddening Material. Astron. J. 1968, 73, 983. [Google Scholar] [CrossRef]
- Neckel, T.; Klare, G. The spatial distribution of the interstellar extinction. Astronomy and Astrophysics Supplement Series 1980, 42, 251. [Google Scholar]
- Pandey, A.K.; Mahra, H.S. Interstellar extinction and Galactic structure. Mon. Not. R. Astron. Soc. 1987, 226, 635–643. [Google Scholar] [CrossRef]
- Arenou, F.; Grenon, M.; Gomez, A. 16. A tridimensional model of the galactic interstellar extinction. Astron. Astrophys. 1992, 258, 104–111. [Google Scholar]
- Sale, S.E.; Drew, J.E.; Barentsen, G.; Farnhill, H.J.; Raddi, R.; Barlow, M.J.; Eislöffel, J.; Vink, J.S.; Rodríguez-Gil, P.; Wright, N.J. A 3D extinction map of the northern Galactic plane based on IPHAS photometry. Mon. Not. R. Astron. Soc. 2014, 443, 2907–2922. [Google Scholar] [CrossRef]
- Green, G.M.; Schlafly, E.F.; Finkbeiner, D.P.; Rix, H.-W.; Martin, N.; Burgett, W.; Draper, P.W.; Flewelling, H.; Hodapp, K.; Kaiser, N. A Three-dimensional Map of Milky Way Dust. Astrophys. J. 2015, 810, 25. [Google Scholar] [CrossRef]
- Lallement, R.; Babusiaux, C.; Vergely, J.L.; Katz, D.; Arenou, F.; Valette, B.; Hottier, C.; Capitanio, L. Gaia-2MASS 3D maps of Galactic interstellar dust within 3 kpc. Astron. Astrophys. 2019, 625, A135. [Google Scholar] [CrossRef]
- Hakkila, J.; Myers, J.M.; Stidham, B.J.; Hartmann, D.H. A Computerized Model of Large-Scale Visual Interstellar Extinction. Astron. J. 1997, 114, 2043. [Google Scholar] [CrossRef]
- Bundy, K.; Bershady, M.A.; Law, D.R.; Yan, R.; Drory, N.; MacDonald, N.; Wake, D.A.; Cherinka, B.; Sánchez-Gallego, J.R.; Weijmans, A.M.; et al. Overview of the SDSS-IV MaNGA Survey: Mapping nearby Galaxies at Apache Point Observatory. Astrophys. J. 2015, 798, 7. [Google Scholar] [CrossRef]
- Sánchez, S.F.; Barrera-Ballesteros, J.K.; Lacerda, E.; Mejía-Narvaez, A.; Camps-Fariña, A.; Bruzual, G.; Espinosa-Ponce, C.; Rodríguez-Puebla, A.; Calette, A.R.; Ibarra-Medel, H.; et al. SDSS-IV MaNGA: PyPipe3D Analysis Release for 10,000 Galaxies. Astrophys. J. Suppl. Ser. 2022, 262, 36. [Google Scholar] [CrossRef]
- Fischer, J.L.; Domínguez Sánchez, H.; Bernardi, M. SDSS-IV MaNGA PyMorph Photometric and Deep Learning Morphological Catalogues and implications for bulge properties and stellar angular momentum. Mon. Not. R. Astron. Soc. 2019, 483, 2057–2077. [Google Scholar] [CrossRef]
- Domínguez Sánchez, H.; Margalef, B.; Bernardi, M.; Huertas-Company, M. SDSS-IV DR17: Final release of MaNGA PyMorph photometric and deep-learning morphological catalogues. Mon. Not. R. Astron. Soc. 2022, 509, 4024–4036. [Google Scholar] [CrossRef]
- Sharov, A.S. A Reappraisal of Interstellar Light Absorption in the Galaxy. Astron. Rep. 1963, 40, 900. [Google Scholar]
- Riello, M.; Patat, F. Extinction correction for Type Ia supernova rates - I. The model. Mon. Not. R. Astron. Soc. 2005, 362, 671–680. [Google Scholar] [CrossRef]
- Holwerda, B.W.; Reynolds, A.; Smith, M.; Kraan-Korteweg, R.C. SN Ia host galaxy properties and the dust extinction distribution. Mon. Not. R. Astron. Soc. 2015, 446, 3768–3775. [Google Scholar] [CrossRef]
- Ménard, B.; Kilbinger, M.; Scranton, R. On the impact of intergalactic dust on cosmology with Type Ia supernovae. Mon. Not. R. Astron. Soc. 2010, 406, 1815–1820. [Google Scholar] [CrossRef]
- Hakobyan, A.A.; Barkhudaryan, L.V.; Karapetyan, A.G.; Mamon, G.A.; Kunth, D.; Adibekyan, V.; Aramyan, L.S.; Petrosian, A.R.; Turatto, M. Supernovae and their host galaxies - V. The vertical distribution of supernovae in disc galaxies. Mon. Not. R. Astron. Soc. 2017, 471, 1390–1400. [Google Scholar] [CrossRef]
- Santos-Santos, I.M.E.; Frenk, C.S.; Navarro, J.F.; Cole, S.; Helly, J. The unabridged satellite luminosity function of Milky Way-like galaxies in ΛCDM: The contribution of ’orphan’ satellites. Mon. Not. R. Astron. Soc. 2025, 540, 1107–1123. [Google Scholar] [CrossRef]
- Taylor, M.B. TOPCAT & STIL: Starlink Table/VOTable Processing Software. In Proceedings of the Astronomical Data Analysis Software and Systems XIV; Astronomical Society of the Pacific Conference Series; Shopbell, P., Britton, M., Ebert, R., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2005; Volume 347, p. 29. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malkov, O.; Sytov, A.; Zhao, G.; Zhong, Z. Estimation of Host Galaxy Extinction for SNe Ia. Galaxies 2025, 13, 129. https://doi.org/10.3390/galaxies13060129
Malkov O, Sytov A, Zhao G, Zhong Z. Estimation of Host Galaxy Extinction for SNe Ia. Galaxies. 2025; 13(6):129. https://doi.org/10.3390/galaxies13060129
Chicago/Turabian StyleMalkov, Oleg, Alexey Sytov, Gang Zhao, and Zehao Zhong. 2025. "Estimation of Host Galaxy Extinction for SNe Ia" Galaxies 13, no. 6: 129. https://doi.org/10.3390/galaxies13060129
APA StyleMalkov, O., Sytov, A., Zhao, G., & Zhong, Z. (2025). Estimation of Host Galaxy Extinction for SNe Ia. Galaxies, 13(6), 129. https://doi.org/10.3390/galaxies13060129







