Testing CCC+TL Cosmology with Galaxy Rotation Curves
Abstract
1. Introduction
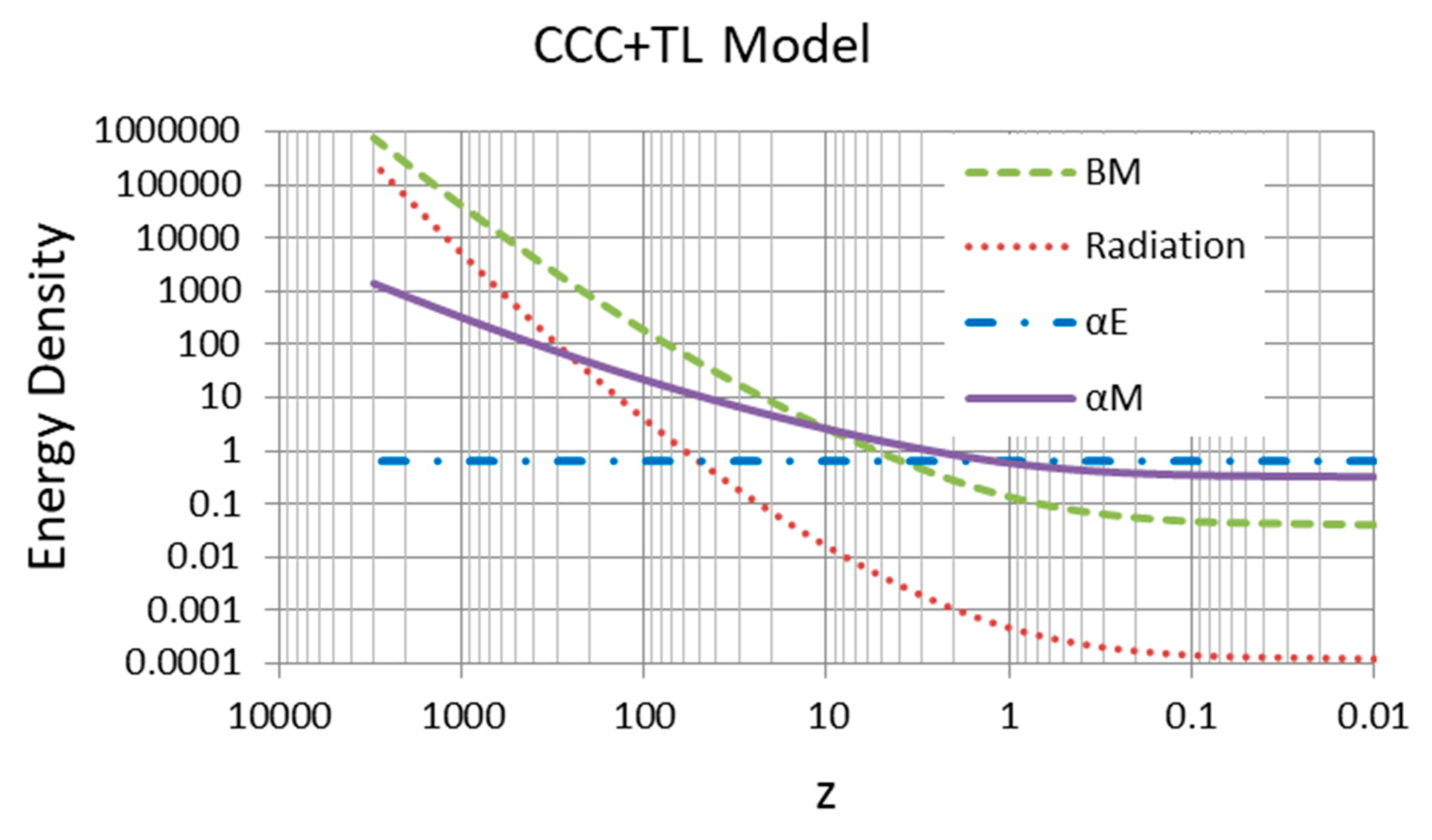
2. Theoretical Background
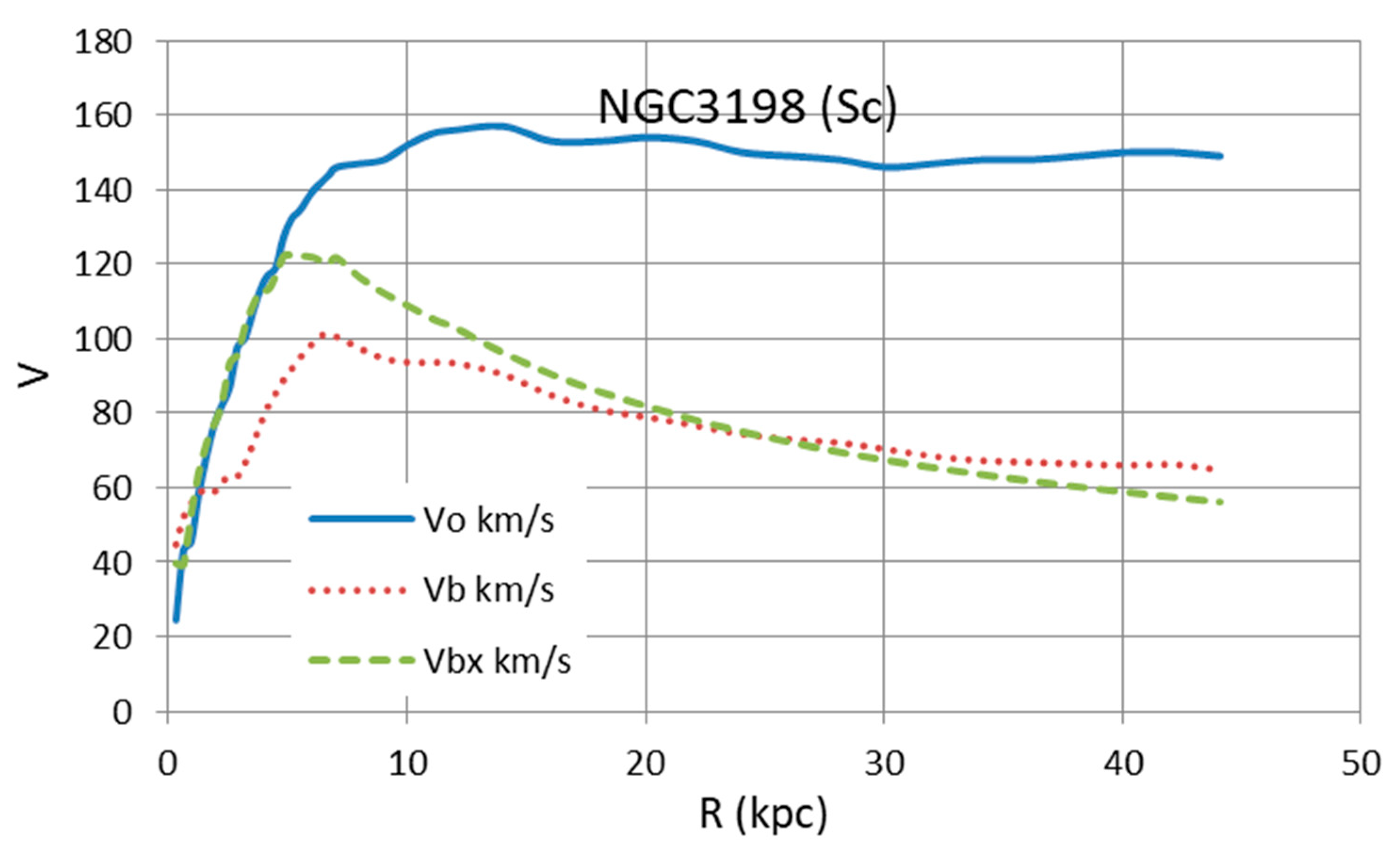
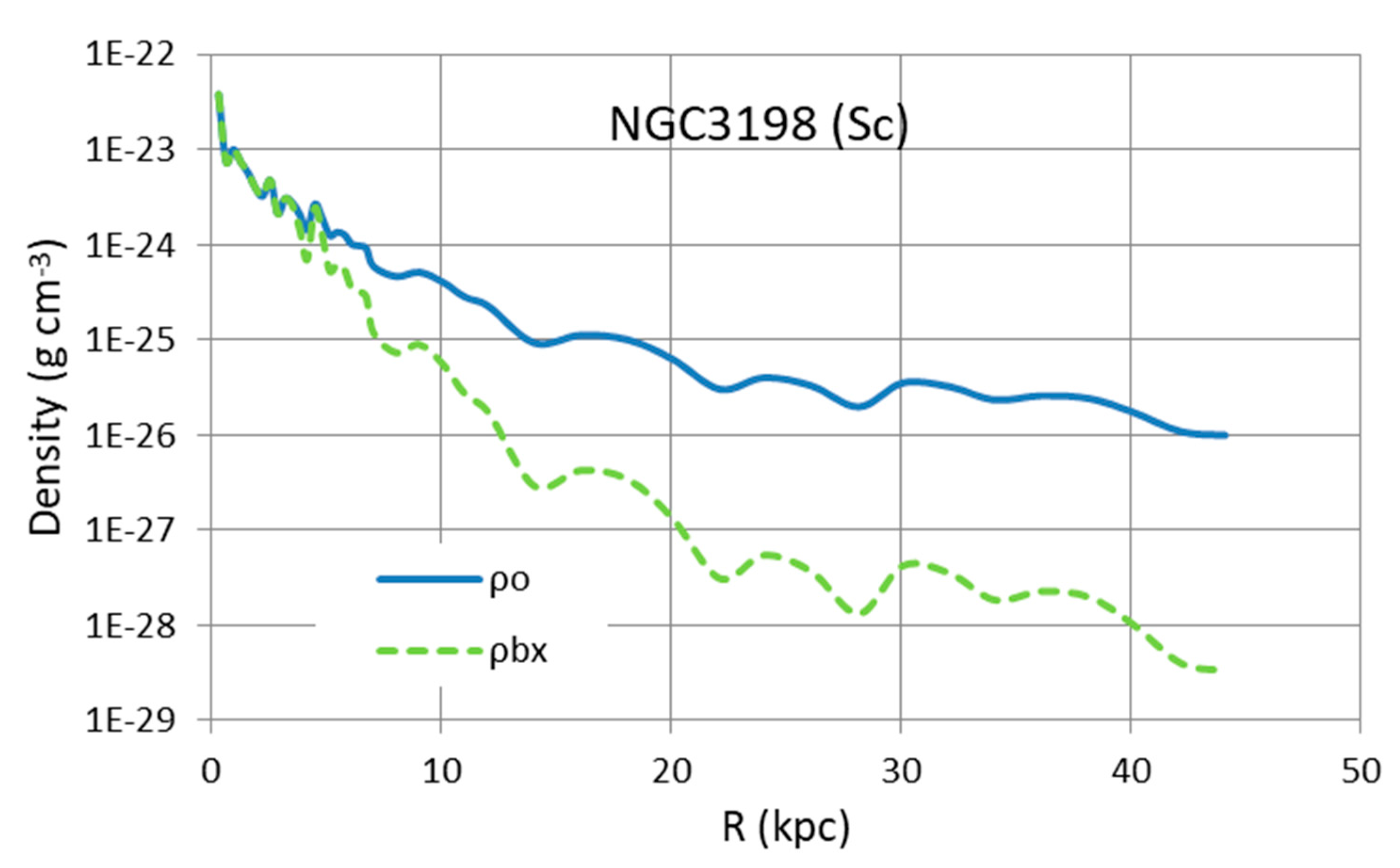
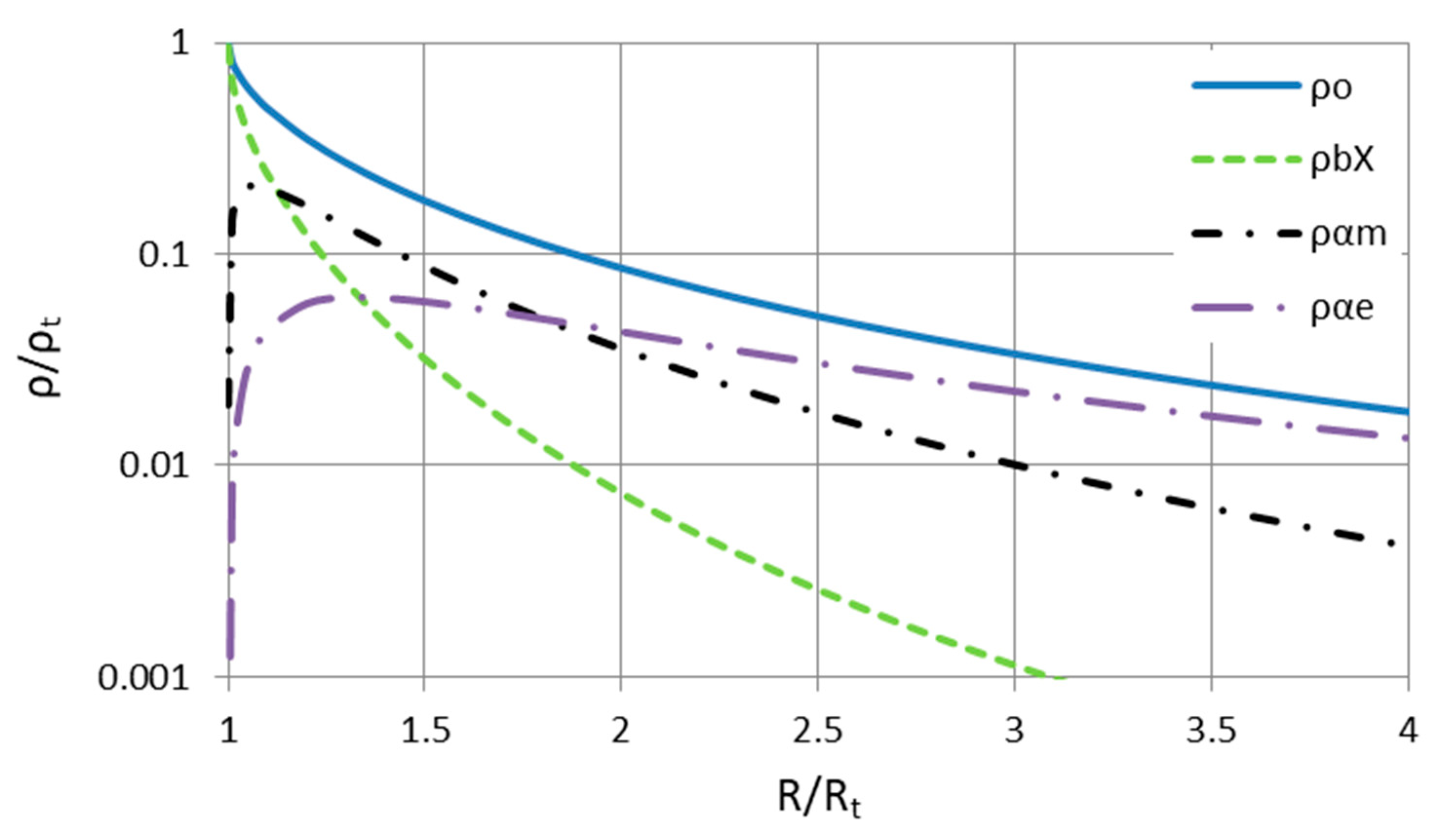
3. Galaxy Rotation Curves
4. Discussion
5. Conclusions
- Dark matter and dark energy of the ΛCDM model may be considered emerging from the weakening of the forces of nature in an expanding Universe determined by a dimensionless covarying coupling constant function. For simplicity, we have defined the function as , with as a constant.
- The observed galaxy rotation curves can be used to derive the baryonic matter distribution in a galaxy. One may not need to bring in new physics, such as modified gravity, Modified Newtonian Dynamics, etc., to explain the observed flat rotation curves of galaxies. The CCC approach is thus cosmologically and astrophysically consistent.
- The emergent -matter and -energy can, in principle, replace dark matter in galaxy clusters and assist in galaxy formation. However, unlike in the ΛCDM cosmology, -matter is not something physical.
- The simplified spherical galaxy approach we have used in this paper needs correction to account for the observed galaxy morphologies to obtain a better data fit.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | It should be mentioned that the metric, Equation (1), can be transformed into the standard FLRW metric by redefining and a new scale factor , thus yielding the standard Einstein tensor. However, when we write the complete Einstein equations [58], we find that we cannot eliminate from the right-hand side, i.e., the right-hand side cannot be transformed into the standard form. |
References
- Chae, K.H.; Lelli, F.; Desmond, H.; McGaugh, S.S.; Li, P.; Schombert, J.M. Testing the Strong Equivalence Principle: Detection of the External Field Effect in Rotationally Supported Galaxies. Astrophys. J. 2020, 904, 51. [Google Scholar] [CrossRef]
- Genzel, R.; Schreiber, N.F.; Übler, H.; Lang, P.; Naab, T.; Bender, R.; Tacconi, L.J.; Wisnioski, E.; Wuyts, S.; Alexander, T.; et al. Strongly baryon-dominated disk galaxies at the peak of galaxy formation ten billion years ago. Nature 2017, 543, 397. [Google Scholar] [CrossRef] [PubMed]
- Lang, P.; Schreiber, N.M.F.; Genzel, R.; Wuyts, S.; Wisnioski, E.; Beifiori, A.; Belli, S.; Bender, R.; Brammer, G.; Burkert, A.; et al. Falling Outer Rotation Curves of Star-forming Galaxies at 0.6 ≲ z ≲ 2.6 Probed with KMOS3D and SINS/zC-SINF. Astrophys. J. 2017, 840, 92. [Google Scholar] [CrossRef]
- Nadler, E.O.; Yang, D.; Yu, H.-B. A Self-interacting Dark Matter Solution to the Extreme Diversity of Low-mass Halo Properties. Astrophys. J. Lett. 2023, 958, L39. [Google Scholar] [CrossRef]
- Nelson, A.H.; Williams, P.R. Recent observations of the rotation of distant galaxies and the implication for dark matter. Astron. Astrophys. 2024, 687, A261. [Google Scholar] [CrossRef]
- Adhikari, P.; Ajaj, R.; Alpízar-Venegas, M.; Auty, D.J.; Benmansour, H.; Bina, C.E.; Bonivento, W.; Boulay, M.G.; Cadeddu, M.; Cai, B.; et al. First Direct Detection Constraints on Planck-Scale Mass Dark Matter with Multiple-Scatter Signatures Using the DEAP-3600 Detector. Phys. Rev. Lett. 2022, 128, 011801. [Google Scholar] [CrossRef]
- Kane, G.; Watson, S. Dark Matter and LHC: What is the Connection? Mod. Phys. Lett. A 2008, 23, 2103. [Google Scholar] [CrossRef]
- Fox, P.J.; Harnik, R.; Kopp, J.; Tsai, Y. LEP Shines Light on Dark Matter. Phys. Rev. D 2011, 84, 014028. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. The physics of galactic spin. Can. J. Phys. 2017, 95, 156–166. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Debate on the Physics of Galactic Rotation and the Existence of Dark Matter. Galaxies 2020, 8, 54. [Google Scholar] [CrossRef]
- Maoz, D. Astrophysics in a Nutshell, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Slipher, V.M. The detection of nebular rotation. Lowell Obs. Bull. 1914, 2, 66. [Google Scholar]
- Page, T. Radial Velocities and Masses of Double Galaxies. Astrophys. J. 1952, 116, 63. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R. Motions in Barred Spiral Galaxies. I. The Nuclei of NGC 1097 and NGC 1365. Astrophys. J. 1960, 132, 30. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 150, 379. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Extended rotation curves of high-luminosity spiral galaxies. IV. Systematic dynamical properties, Sa -> Sc. Astrophys. J. 1978, 225, L107. [Google Scholar] [CrossRef]
- Bosma, A. 21-cm line studies of spiral galaxies. II. The distribution and kinematics of neutral hydrogen in spiral galaxies of various morphological types. Astrophys. J. 1981, 86, 1825. [Google Scholar] [CrossRef]
- Trimble, V. Existence and Nature of Dark Matter in the Universe. Annu. Rev. Astron. Astrophys. 1987, 25, 425. [Google Scholar] [CrossRef]
- Ashman, K.M. Dark Matter in Galaxies. PASP. Astrophys. J. 1992, 104, 1109. [Google Scholar] [CrossRef][Green Version]
- Persic, M.; Salucci, P.; Stel, F. The universal rotation curve of spiral galaxies—I. The dark matter connection. Mon. Not. R. Astron. Soc. 1996, 281, 27. [Google Scholar] [CrossRef]
- Sofue, Y.; Rubin, V. Rotation Curves of Spiral Galaxies. An. Rev. Astron. Astrophys. 2001, 39, 137–174. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry and Accurate Rotation Curves. Astron. J. 2016, 152, 157. [Google Scholar] [CrossRef]
- Tiley, A.L.; Swinbank, A.M.; Harrison, C.M.; Smail, I.; Turner, O.J.; Schaller, M.; Stott, J.P.; Sobral, D.; Theuns, T.; Sharples, R.M.; et al. The shapes of the rotation curves of star-forming galaxies over the last ≈10 Gyr. MNRAS 2019, 485, 934–960. [Google Scholar] [CrossRef]
- Sharma, G.; Salucci, P.; Harrison, C.M.; van de Ven, G.; Lapi, A. Flat rotation curves of z ∼ 1 star-forming galaxies. MNRAS 2021, 503, 1753. [Google Scholar] [CrossRef]
- Teklu, A.F.; Remus, R.S.; Dolag, K.; Arth, A.; Burkert, A.; Obreja, A.; Schulze, F. Declining Rotation Curves at z = 2 in ΛCDM Galaxy Formation Simulations. Astrophys. J. Lett. 2018, 854, L28. [Google Scholar] [CrossRef]
- Fei, Q.; Silverman, J.D.; Fujimoto, S.; Wang, R.; Ho, L.C.; Bischetti, M.; Carniani, S.; Ginolfi, M.; Jones, G.C.; Maiolino, R.; et al. Assessing the dark matter content of two quasar host galaxies at z~6 through gas kinematics. arXiv 2025, arXiv:2501.09077. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E.; Chou, H. Baryonic Mass Inventory for Galaxies and Rarefied Media from Theory and Observations of Rotation and Luminosity. Galaxies 2023, 11, 100. [Google Scholar] [CrossRef]
- Ogle, P.M.; Jarrett, T.; Lanz, L.; Cluver, M.; Alatalo, K.; Appleton, P.N.; Mazzarella, J.M. A Break in Spiral Galaxy Scaling Relations at the Upper Limit of Galaxy Mass. Astrophys. J. Lett. 2019, 884, L11. [Google Scholar] [CrossRef]
- Wiegert, T.; English, J. Kinematic Classification of Non-Interacting Spiral Galaxies. New Astron. 2014, 26, 40–61. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365. [Google Scholar] [CrossRef]
- Milgrom, M. Universal Modified Newtonian Dynamics Relation between the Baryonic and “Dynamical” Central Surface Densities of Disc Galaxies. Phys. Rev. Lett. 2016, 117, 141101. [Google Scholar] [CrossRef]
- Milgrom, M. MOND in galaxy groups: A superior sample. Phys. Rev. D 2019, 99, 044041. [Google Scholar] [CrossRef]
- Milgrom, M. MOND vs. dark matter in light of historical parallels. Stud. Hist. Philos. Mod. Phys. 2020, 71, 170. [Google Scholar] [CrossRef]
- Kroupa, P. A modern view of galaxies and their stellar populations. arXiv 2023, arXiv:2310.01473. [Google Scholar] [CrossRef]
- Milgrom, M. MOND as manifestation of modified inertia. arXiv 2023, arXiv:2310.14334. [Google Scholar] [CrossRef]
- Kroupa, P.; Pawlowski, M.; Milgrom, M. The failures of the standard model of cosmology require a new paradigm. Int. J. Mod. Phys. D 2012, 21, 1230003. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. The dark matter problem from f(R) gravity viewpoint. Ann. Physik. 2012, 524, 545. [Google Scholar] [CrossRef]
- Farnes, J.S. A unifying theory of dark energy and dark matter: Negative masses and matter creation within a modified ΛCDM framework. Astron. Astrophys. 2018, 620, A92, arXiv:1712.07962. [Google Scholar] [CrossRef]
- Verlinde, E.P. On the Origin of Gravity and the Laws of Newton. JHEP 2011, 1104, 029. [Google Scholar] [CrossRef]
- Gonzalo, E.; Montero, M.; Obied, G.; Vafa, C. Dark Dimension Gravitons as Dark Matter. arXiv 2022, arXiv:2209.09249. [Google Scholar] [CrossRef]
- Yahalom, A. The Geometrical Meaning of Time. Found. Phys. 2008, 38, 489. [Google Scholar] [CrossRef]
- Yahalom, A. The Effect of Retardation on Galactic Rotation Curves. J. Phys. Conf. Ser. 2019, 1239, 012006. [Google Scholar] [CrossRef]
- Wagman, M.; Horwitz, L.P.; Yahalom, A. Applying Retardation Theory to Galaxies. J. Phys. Conf. Ser. 2023, 2482, 012005. [Google Scholar] [CrossRef]
- Mannheim, P.D. Alternatives to dark matter and dark energy. Prog. Part. Nucl. Phys. 2006, 56, 340–445. [Google Scholar] [CrossRef]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the Cosmological Standard Model. Phys. Rep. 2015, 568, 1. [Google Scholar] [CrossRef]
- Skordis, C.; Złośnik, T. New Relativistic Theory for Modified Newtonian Dynamics. Phys. Rev. Lett. 2021, 127, 161302. [Google Scholar] [CrossRef]
- Roberts, M.G.; Kapalinghat, M.; Valli, M.; Yu, H.-B. Gravothermal collapse and the diversity of galactic rotation curves. arXiv 2024, arXiv:2407.15005. [Google Scholar] [CrossRef]
- Mistele, T.; McGaugh, S.; Lelli, F.; Schombert, J.; Li, P. Indefinitely Flat Circular Velocities and the Baryonic Tully–Fisher Relation from Weak Lensing. Astrophys. J. Lett. 2024, 969, L3. [Google Scholar] [CrossRef]
- Brouwer, M.M.; Oman, K.A.; Valentijn, E.A.; Bilicki, M.; Heymans, C.; Hoekstra, H.; Napolitano, N.R.; Roy, N.; Tortora, C.; Wright, A.H.; et al. The weak lensing radial acceleration relation: Constraining modified gravity and cold dark matter theories with KiDS-1000. Astron. Astrophys. 2021, 650, A113. [Google Scholar] [CrossRef]
- Hoeneisen, B. Why do galaxies have extended flat rotation curves? arXiv 2024, arXiv:2412.17869. [Google Scholar] [CrossRef]
- Buzzo, M.L.; Forbes, D.A.; Romanowski, A.J.; Haacke, L.; Gannon, J.S.; Tang, Y.; Hilker, M.; Ferré-Mateu, A.; Janssens, S.R.; Brodie, J.P.; et al. A new class of dark matter-free dwarf galaxies? I. Clues from FCC 224, NGC 1052-DF2 and NGC 1052-DF4. arXiv 2025, arXiv:2502.05405. [Google Scholar]
- Sipols, A.; Pavlovich, A. Dark Matter Dogma: A Study of 214 Galaxies. Galaxies 2020, 8, 36. [Google Scholar] [CrossRef]
- Feng, J.Q. Rotating Disk Galaxies without Dark Matter Based on Scientific Reasoning. Galaxies 2020, 8, 9. [Google Scholar] [CrossRef]
- Feng, J.Q.; Gallo, C.F. Deficient reasoning for dark matter in galaxies. Phys. Int. 2015, 6, 11–22. [Google Scholar] [CrossRef]
- McGaugh, S. Predictions and Outcomes for the Dynamics of Rotating Galaxies. Galaxies 2020, 8, 35. [Google Scholar] [CrossRef]
- Marr, J.H. Entropy and Mass Distribution in Disc Galaxies. Galaxies 2020, 8, 12. [Google Scholar] [CrossRef]
- Gupta, R.P. JWST early Universe observations and ΛCDM cosmology. MNRAS 2023, 524, 3385. [Google Scholar] [CrossRef]
- Gupta, R.P. Testing CCC+TL Cosmology with Observed BAO Features. Astrophys. J. 2024, 964, 55. [Google Scholar] [CrossRef]
- Gupta, R.P. On Dark Matter and Dark Energy in CCC+TL Cosmology. Universe 2024, 10, 266. [Google Scholar] [CrossRef]
- Gupta, R.P. Varying coupling constants and their interdependence. Mod. Phys. Lett. A 2022, 37, 2250155. [Google Scholar] [CrossRef]
- Cuzinatto, R.R.; Gupta, R.P.; Pompeia, P.J. Covarying-Bi-Scalar Theory: A model with covarying G and c and a natural screening mechanism. Ann. Phys. 2025, 479, 170039. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Daod, N.A.; Zeki, M.K. Density and Mass Distribution of Spiral Galaxy NGC 3198. Astrophys. J. 2019, 870, 107. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. Stellar Mass-to-light Ratios: Composite Bulge+Disk Models and the Baryonic Tully–Fisher Relation. Astrophys. J. 2022, 870, 154. [Google Scholar] [CrossRef]
- Criss, R.E.; Hofmeister, A.M. Density Profiles of 51 Galaxies from Parameter-Free Inverse Models of Their Measured Rotation Curves. Galaxies 2020, 8, 19. [Google Scholar] [CrossRef]
- Hernquist, L. An Analytical Model for Spherical Galaxies and Bulges. Astrophys. J. 1990, 356, 359. [Google Scholar] [CrossRef]
- Sanders, R.H. The Dark Matter Problem: A Historical Perspective; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- McGaugh, S. The Baryonic TullyY–Fisher Relation of Gas-rich Galaxies as a Test of ΛCDM and MOND. Astron. J. 2012, 143, 40. [Google Scholar] [CrossRef]
- Rowland, L.E.; Hodge, J.; Bouwens, R.; Mancera Pina, P.E.; Hygate, A.; Algera, H.; Aravena, M.; Bowler, R.; da Cunha, E.; Dayal, P.; et al. REBELS-25: Discovery of a dynamically cold disc galaxy at z = 7.31. MNRAS 2024, 535, 2068. [Google Scholar] [CrossRef]
- Mandelbaum, R.; Seljak, U.; Cool, R.J.; l Blanton, M.; Hirata, C.M.; Brinkmann, J. Density profiles of galaxy groups and clusters from SDSS galaxy–galaxy weak lensing. MNRAS 2006, 372, 758. [Google Scholar] [CrossRef]
- Costa, R.; Cuzinatto, R.R.; Ferreira, E.G.M.; Franzmann, G. Covariant c-flation: A variational approach. Int. J. Mod. Phys. D 2019, 28, 1950119. [Google Scholar] [CrossRef]
- Gupta, R.P. Cosmology with relativistically varying physical constants. MNRAS 2020, 498, 4481. [Google Scholar] [CrossRef]
- Cuzinatto, R.R.; Gupta, R.P.; Pompeia, P.J. Dynamical Analysis of the Covarying Coupling Constants in Scalar–Tensor Gravity. Symmetry 2023, 15, 709. [Google Scholar] [CrossRef]
- Albrecht, A.; Magueijo, J. Time varying speed of light as a solution to cosmological puzzles. Phys. Rev. D 1999, 59, 043516. [Google Scholar] [CrossRef]
- Faraoni, V. Cosmology in Scalar-Tensor Gravity; Springer: Berlin/Heidelberg, Germany, 2004; Chapter 2. [Google Scholar]


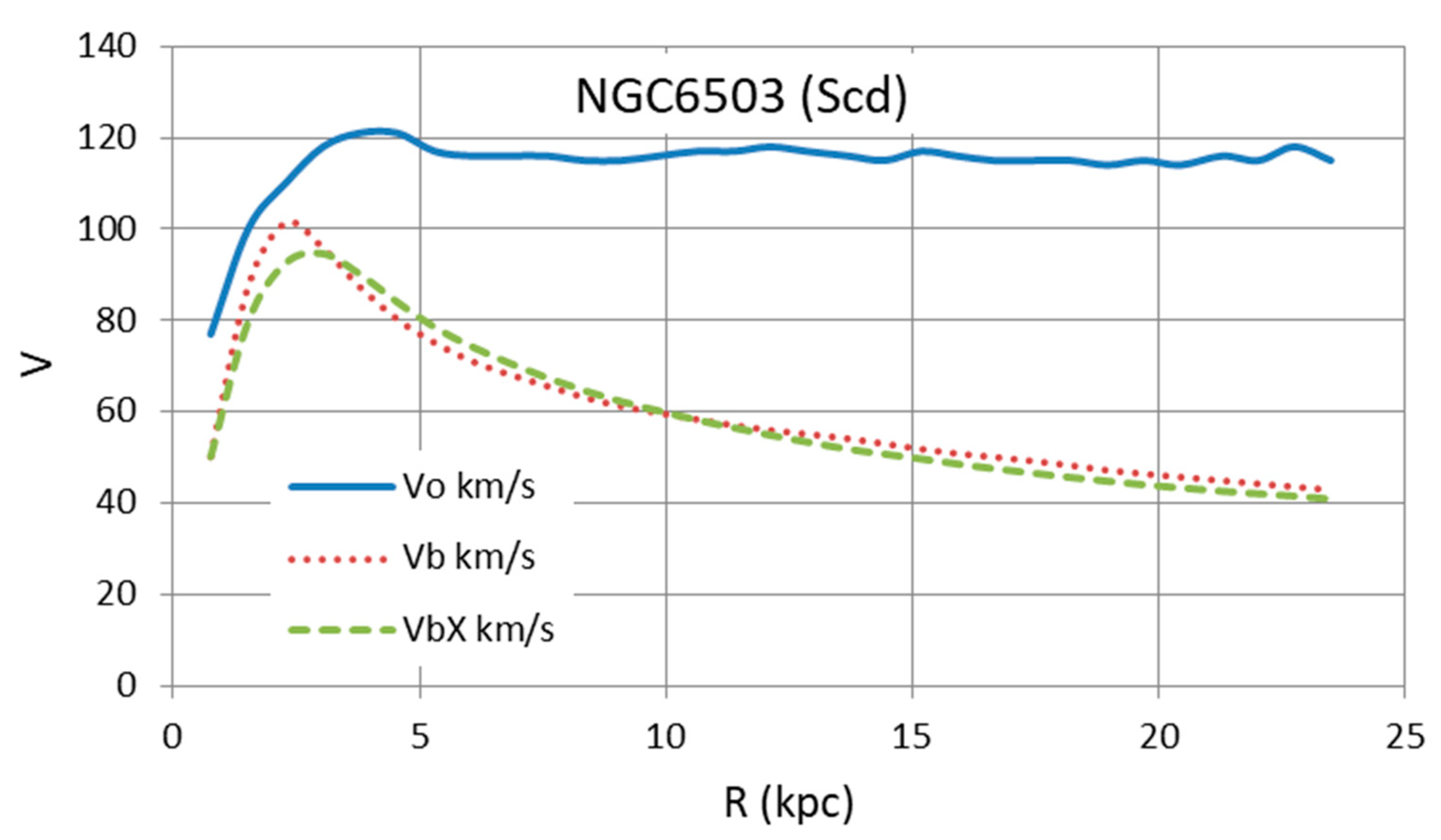
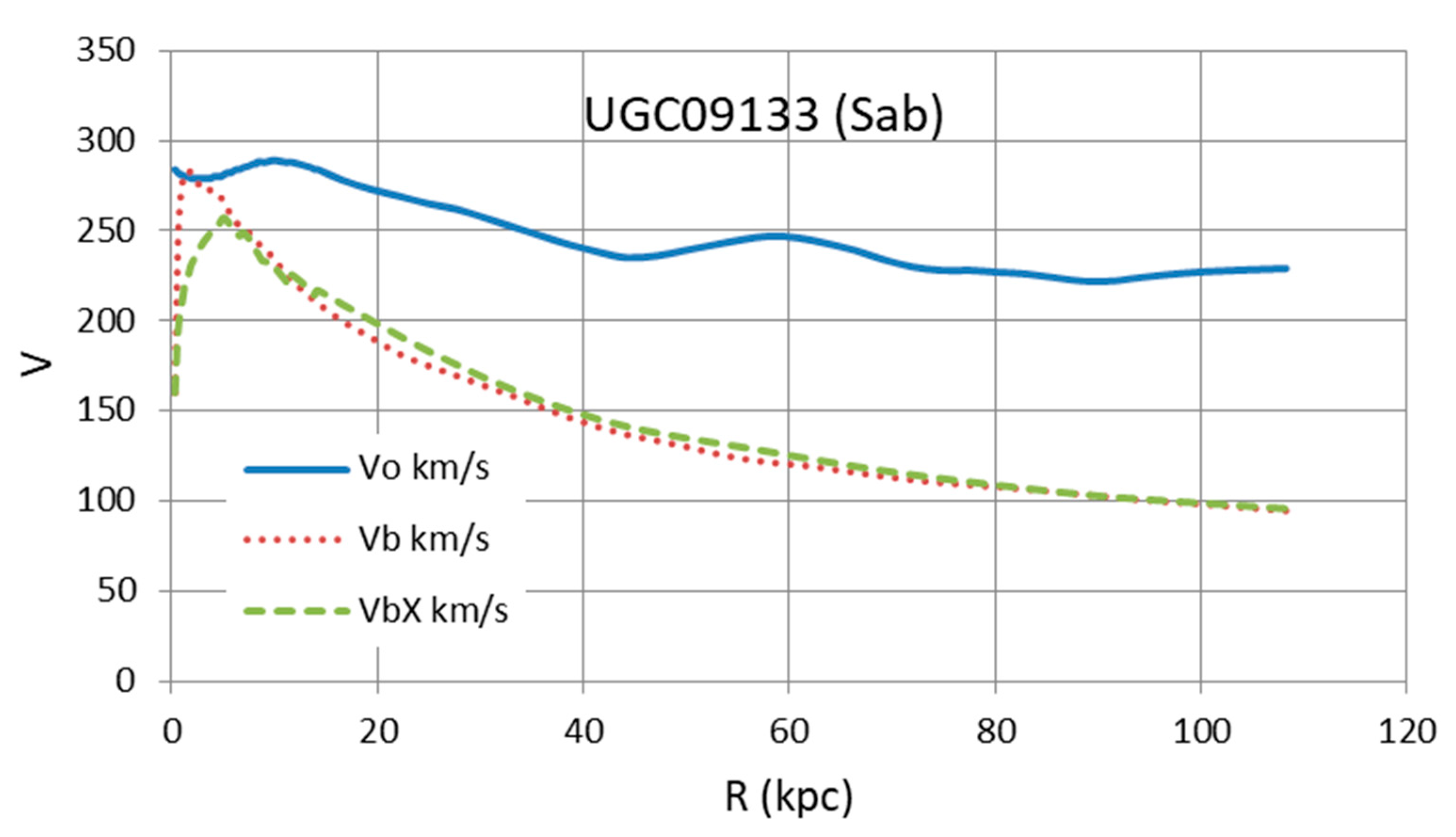
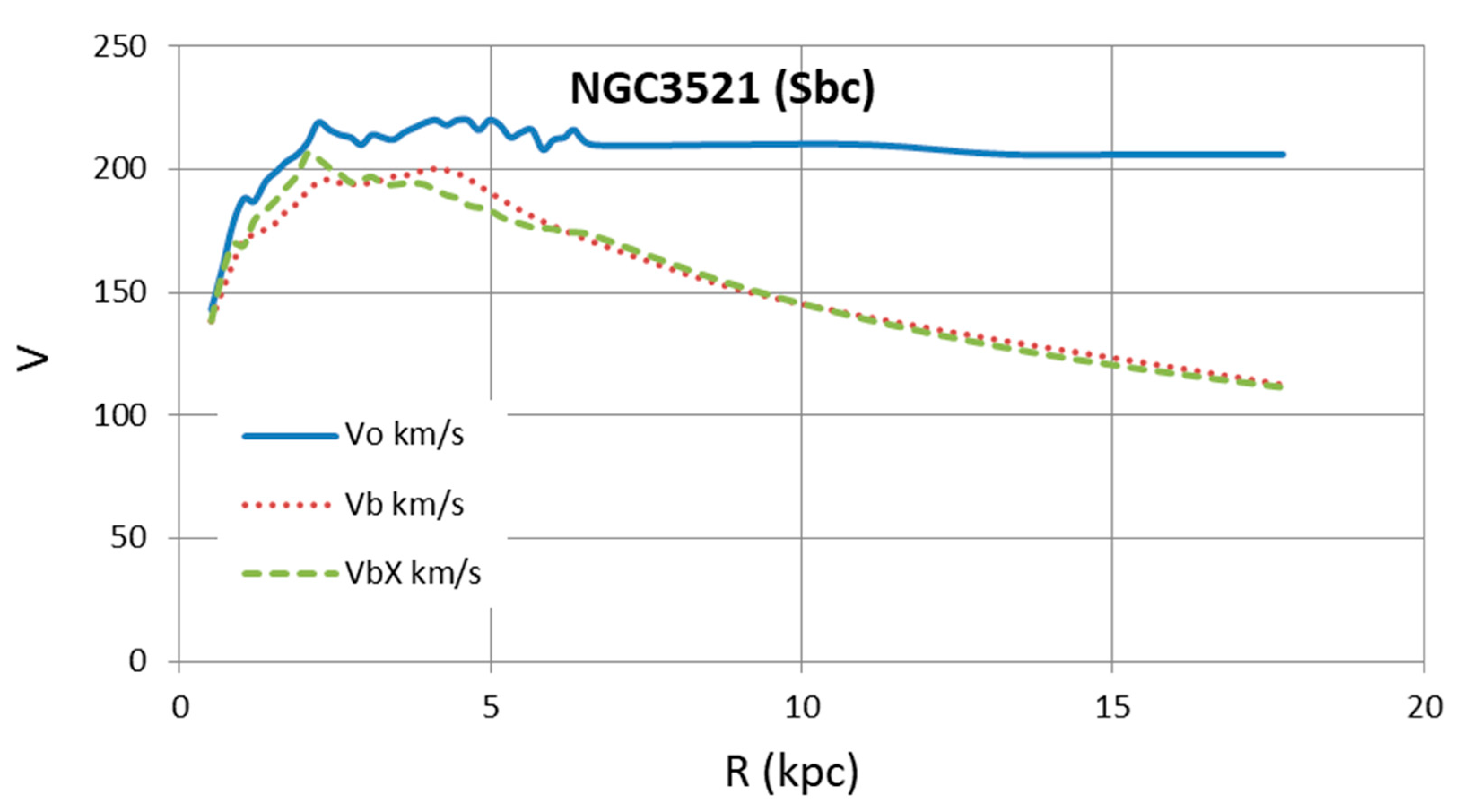
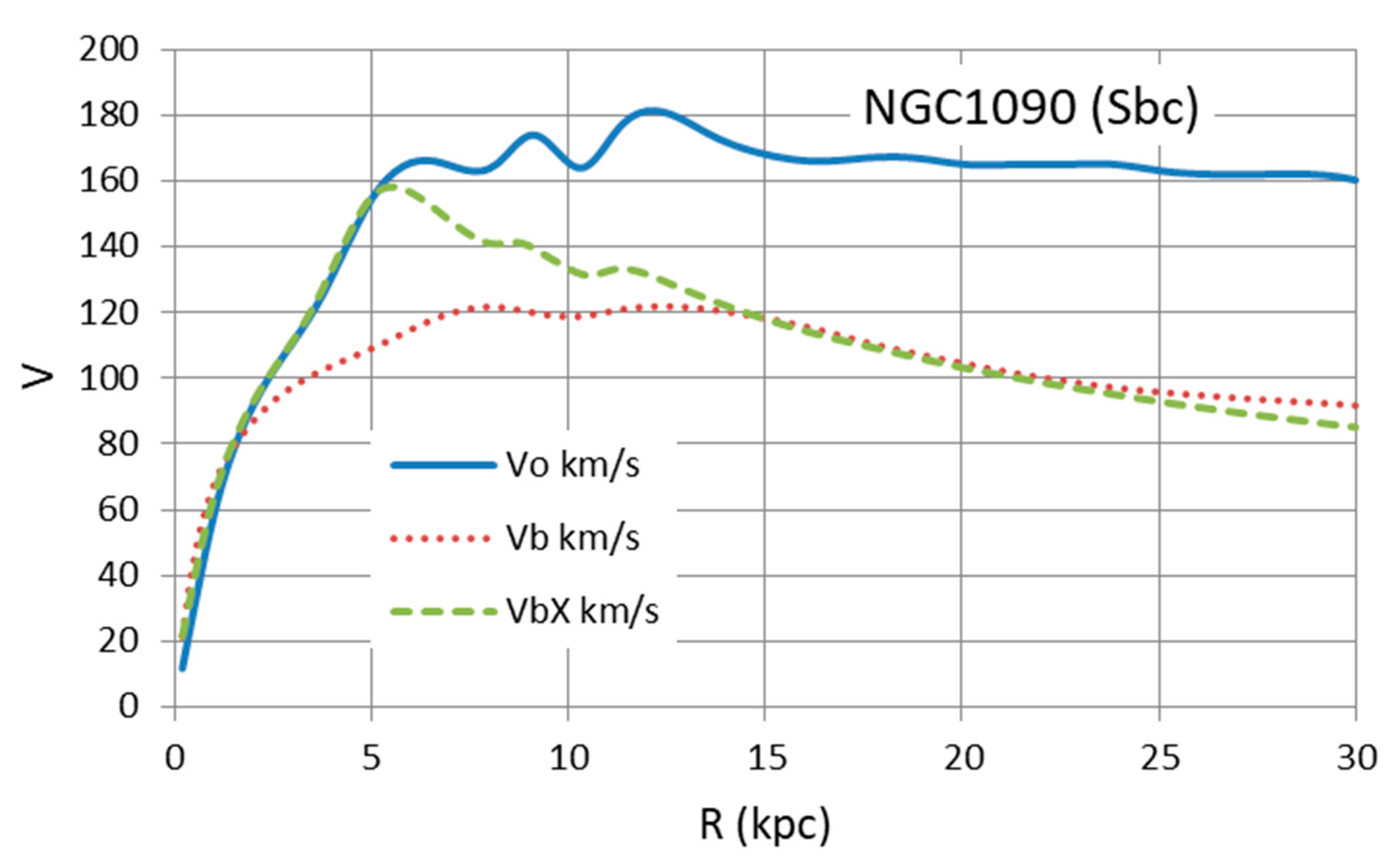
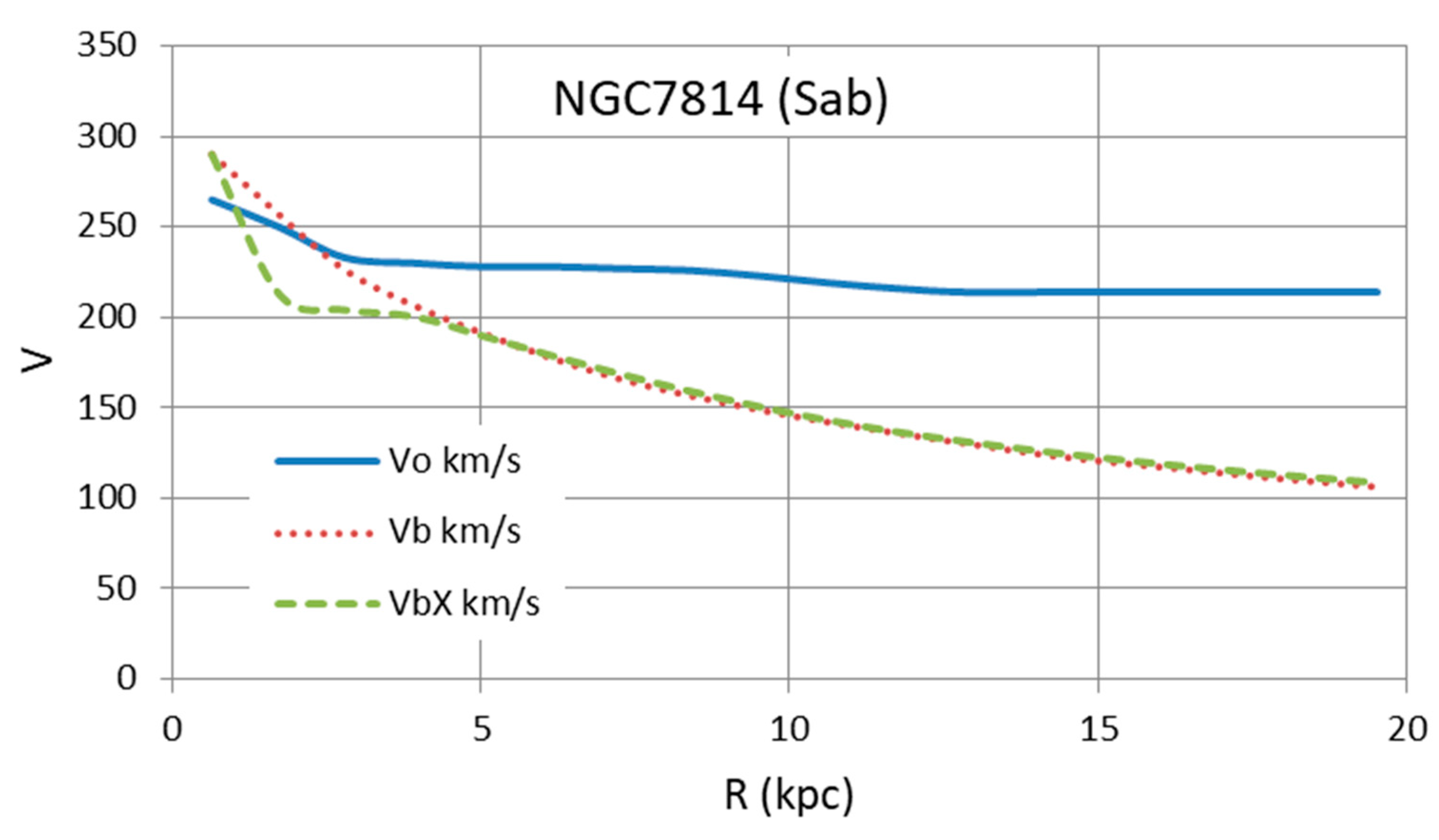
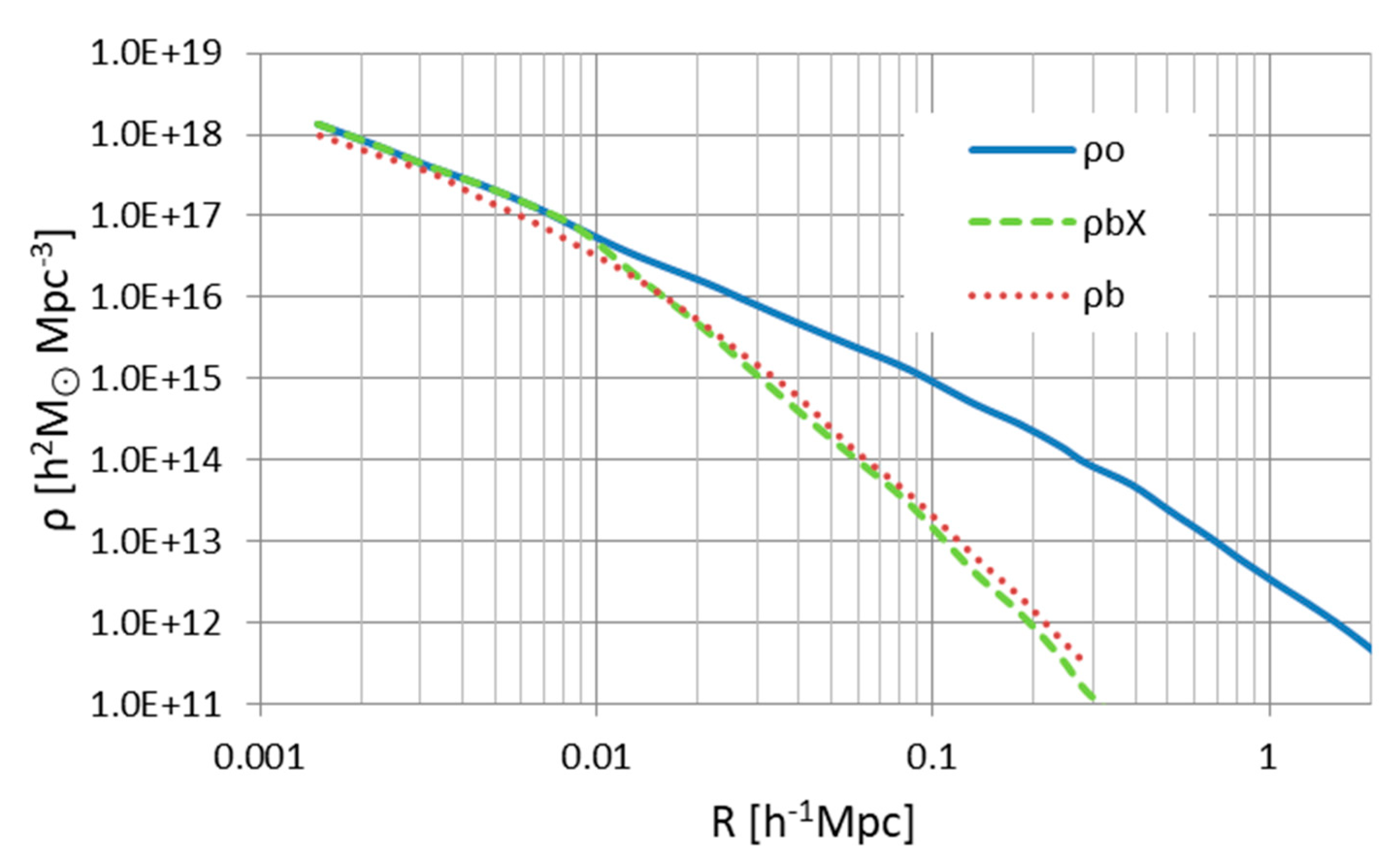
| Galaxy | Type | Distance | Size | Remarks | |||
|---|---|---|---|---|---|---|---|
| Mpc | kpc | kpc | |||||
| D631-7 A | Im | 7.72 | 1.22 | 0.35 | 2.79 | 3.10 | Good overall fit |
| NGC1090 | Sbc | 37.00 | 6.36 | 4.7 | 2.23 | 1.76 | Not a good fit for |
| NGC3198 | Sc | 13.80 | 5.84 | 3.37 | 2.09 | 2.15 | OK overall fit |
| NGC3521 | Sbc | 7.70 | 2.45 | 2.15 | 7.96 | 6.43 | Good fit |
| NGC6503 | Scd | 6.26 | 1.62 | 1.9 | 5.17 | 2.25 | Good fit |
| NGC7814 | Sab | 14.40 | 2.08 | 2.8 | 5.01 | 5.33 | Good fit |
| UGC09133 | Sab | 57.10 | 5.92 | 4.9 | 3.98 | 3.33 | Good overall fit |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, R.P. Testing CCC+TL Cosmology with Galaxy Rotation Curves. Galaxies 2025, 13, 108. https://doi.org/10.3390/galaxies13050108
Gupta RP. Testing CCC+TL Cosmology with Galaxy Rotation Curves. Galaxies. 2025; 13(5):108. https://doi.org/10.3390/galaxies13050108
Chicago/Turabian StyleGupta, Rajendra P. 2025. "Testing CCC+TL Cosmology with Galaxy Rotation Curves" Galaxies 13, no. 5: 108. https://doi.org/10.3390/galaxies13050108
APA StyleGupta, R. P. (2025). Testing CCC+TL Cosmology with Galaxy Rotation Curves. Galaxies, 13(5), 108. https://doi.org/10.3390/galaxies13050108







