One-Dimensional Analytical Solutions of the Transport Equations for Incompressible Magnetohydrodynamic (MHD) Turbulence
Abstract
1. Introduction
2. 1D Analytical Solutions of the Turbulence Transport Equations
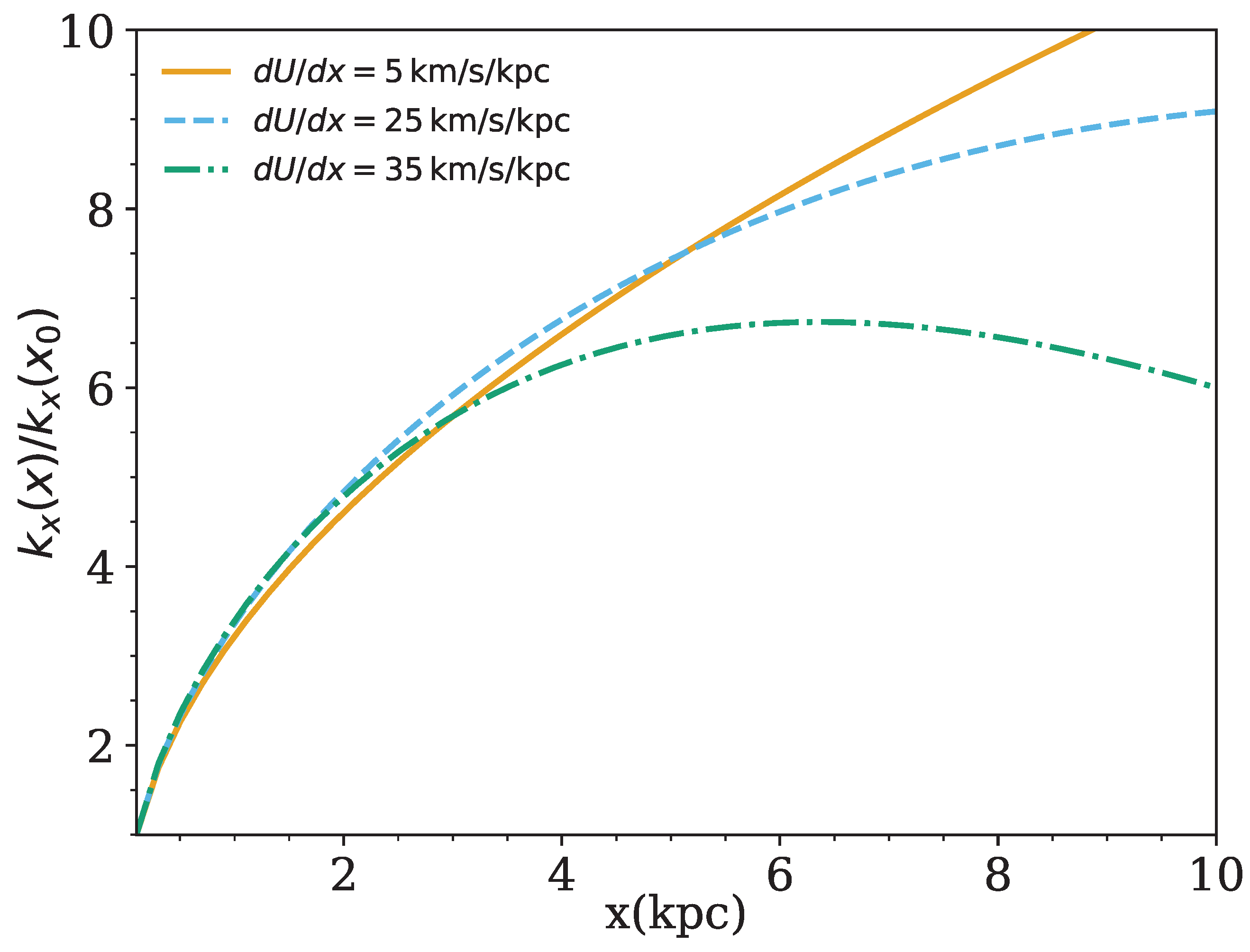
3. A Toy Model for Cosmic Ray Diffusion Coefficient in the Halo
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MHD | Magnetohydrodynamic |
| 1D | One-Dimensional |
References
- Parker, E.N. Dynamical Theory of the Solar Wind. Space Sci. Rev. 1965, 4, 666–708. [Google Scholar] [CrossRef]
- Hollweg, J.V. Alfvén waves in the solar wind: Wave pressure, poynting flux, and angular momentum. J. Geophys. Res. 1973, 78, 3643. [Google Scholar] [CrossRef]
- Zank, G.P.; Matthaeus, W.H.; Smith, C.W. Evolution of turbulent magnetic fluctuation power with heliospheric distance. J. Geophys. Res. 1996, 101, 17093–17108. [Google Scholar] [CrossRef]
- Zank, G.P.; Dosch, A.; Hunana, P.; Florinski, V.; Matthaeus, W.H.; Webb, G.M. The Transport of Low-frequency Turbulence in Astrophysical Flows. I. Governing Equations. Astrophys. J. 2012, 745, 35. [Google Scholar] [CrossRef]
- Adhikari, L.; Zank, G.P.; Wang, B.; Zhao, L.; Telloni, D.; Pitna, A.; Opher, M.; Shrestha, B.; McComas, D.J.; Nykyri, K. Theory and Transport of Nearly Incompressible Magnetohydrodynamic Turbulence: High Plasma Beta Regime. Astrophys. J. 2023, 953, 44. [Google Scholar] [CrossRef]
- Adhikari, L.; Zank, G.P.; Hunana, P.; Hu, Q. The Interaction of Turbulence with Parallel and Perpendicular Shocks: Theory and Observations at 1 au. Astrophys. J. 2016, 833, 218. [Google Scholar] [CrossRef]
- Wang, B.B.; Zank, G.P.; Zhao, L.L.; Adhikari, L. Turbulent Cosmic Ray-Mediated Shocks in the Hot Ionized Interstellar Medium. Astrophys. J. 2022, 932, 65. [Google Scholar] [CrossRef]
- Zank, G.P.; Adhikari, L.; Hunana, P.; Shiota, D.; Bruno, R.; Telloni, D. Theory and Transport of Nearly Incompressible Magnetohydrodynamic Turbulence. Astrophys. J. 2017, 835, 147. [Google Scholar] [CrossRef]
- Adhikari, L.; Zank, G.P.; Telloni, D.; Zhao, L.; Wang, B.; Webb, G.; Tang, B.; Nykyri, K. Turbulence, and Proton and Electron Heating Rates in the Solar Corona: Analytical Approach. Astrophys. J. 2024, 966, 52. [Google Scholar] [CrossRef]
- Moskalenko, I.V.; Strong, A.W.; Ormes, J.F.; Potgieter, M.S. Secondary Antiprotons and Propagation of Cosmic Rays in the Galaxy and Heliosphere. Astrophys. J. 2002, 565, 280–296. [Google Scholar] [CrossRef]
- Porter, T.A.; Jóhannesson, G.; Moskalenko, I.V. The GALPROP Cosmic-ray Propagation and Nonthermal Emissions Framework: Release v57. Astrophys. J. 2022, 262, 30. [Google Scholar] [CrossRef]
- Zank, G.P.; Matthaeus, W.H.; Bieber, J.W.; Moraal, H. The radial and latitudinal dependence of the cosmic ray diffusion tensor in the heliosphere. J. Geophys. Res. 1998, 103, 2085–2098. [Google Scholar] [CrossRef]
- Yuan, Q.; Lin, S.J.; Fang, K.; Bi, X.J. Propagation of cosmic rays in the AMS-02 era. Phys. Rev. D 2017, 95, 083007. [Google Scholar] [CrossRef]
- Maurin, D.; Taillet, R.; Donato, F.; Salati, P.; Barrau, A.; Boudoul, G. Galactic Cosmic Ray Nuclei as a Tool for Astroparticle Physics. arXiv 2002, arXiv:astro-ph/0212111. [Google Scholar] [CrossRef]
- Wiener, J.; Oh, S.P.; Guo, F. Cosmic ray streaming in clusters of galaxies. Mon. Not. R. Astron. Soc. 2013, 434, 2209–2228. [Google Scholar] [CrossRef]
- Wiener, J.; Pfrommer, C.; Oh, S.P. Cosmic ray-driven galactic winds: Streaming or diffusion? Mon. Not. R. Astron. Soc. 2017, 467, 906–921. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zank, G.P.; Adhikari, L.; Sharma, S. One-Dimensional Analytical Solutions of the Transport Equations for Incompressible Magnetohydrodynamic (MHD) Turbulence. Galaxies 2025, 13, 104. https://doi.org/10.3390/galaxies13050104
Wang B, Zank GP, Adhikari L, Sharma S. One-Dimensional Analytical Solutions of the Transport Equations for Incompressible Magnetohydrodynamic (MHD) Turbulence. Galaxies. 2025; 13(5):104. https://doi.org/10.3390/galaxies13050104
Chicago/Turabian StyleWang, Bingbing, Gary P. Zank, Laxman Adhikari, and Swati Sharma. 2025. "One-Dimensional Analytical Solutions of the Transport Equations for Incompressible Magnetohydrodynamic (MHD) Turbulence" Galaxies 13, no. 5: 104. https://doi.org/10.3390/galaxies13050104
APA StyleWang, B., Zank, G. P., Adhikari, L., & Sharma, S. (2025). One-Dimensional Analytical Solutions of the Transport Equations for Incompressible Magnetohydrodynamic (MHD) Turbulence. Galaxies, 13(5), 104. https://doi.org/10.3390/galaxies13050104







