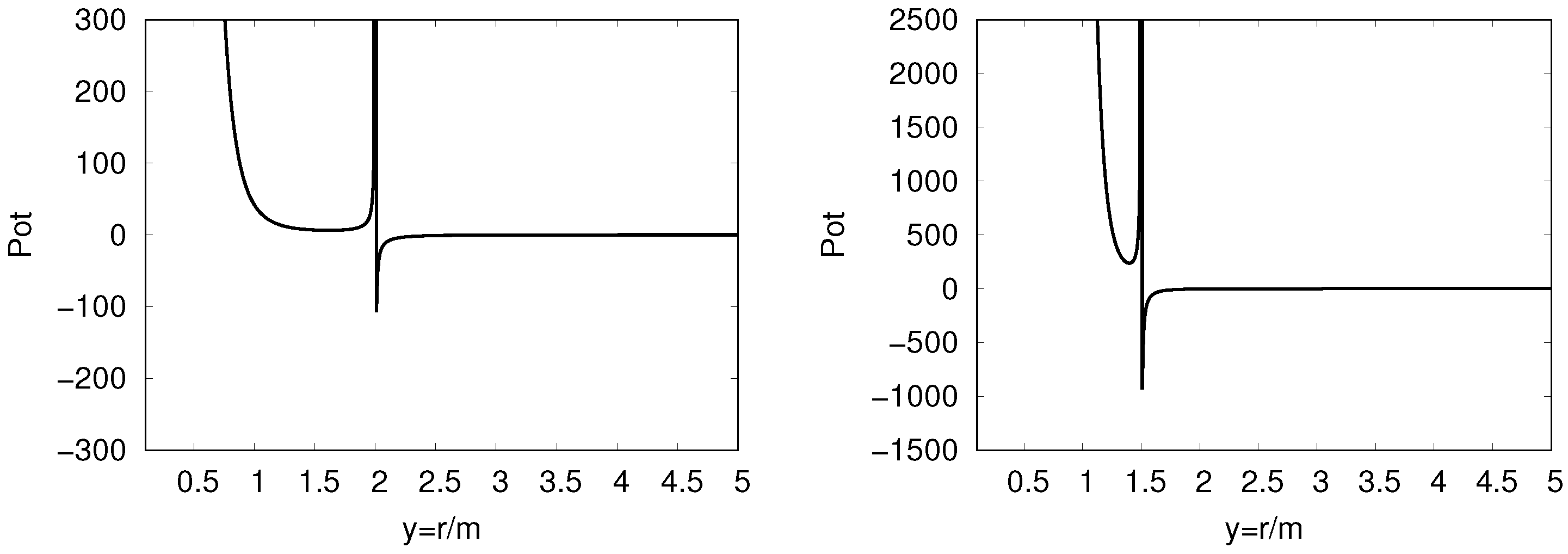The pcGR Within the Hořava-Lifshitz Gravity and the Wheeler-deWitt Quantization

Abstract

We investigate pseudo-complex General Relativity (pcGR)—a coordinate-extended formulation of General Relativity (GR)—within the framework of Hořava-Lifshitz gravity, a regularized theory featuring anisotropic scaling. The pcGR framework bridges GR with modified gravitational theories through the introduction of a minimal length scale. Focusing on Schwarzschild black holes, we derive the Wheeler-deWitt equation, obtaining a quantized description of pcGR. Using perturbative methods and semi-classical approximations, we analyze the solutions of the equations and their physical implications. A key finding is the avoidance of the central singularity due to nonlinear interaction terms in the Hořava-Lifshitz action. Notably, extrinsic curvature (kinetic energy) contributions prove essential for singularity resolution, even in standard GR. Furthermore, the theory offers new perspectives on dark energy, proposing an alternative mechanism for its accumulation.

1. Introduction

General relativity (GR) is one of the most successful theories in physics, with its predictions consistently validated by numerous observations [1]. However, in extreme situations such as strong gravitational fields near the event horizon of a black hole, the limitations of GR become apparent.

The formation of singularities at the center of black holes is a long-standing issue, which is expected to be resolved in a quantum gravity framework where the ultraviolet completion of gravity could introduce a minimal length scale or modify the spacetime geometry in such a way that the singularity is avoided. An alternative approach to addressing singularities is pseudocomplex General Relativity (pcGR) [2,3], an algebraic extension of GR modeled by a parameter b that characterizes deviations of the standard theory. pcGR has been applied to black hole physics, predicting the existence of stable “dark stars” and a continuous transition from neutron stars to black holes [4]. Notably, pcGR maintains Lorentz invariance while incorporating a minimal length parameter, unaffected by Lorentz contraction.

Despite its merits, this study explores a unified framework combining pcGR with Hořava-Lifshitz gravity [5,6]—a regularized modification of general relativity that employs Lifshitz-type anisotropic scaling between time and space. This scaling asymmetry alters the ultraviolet behavior of the theory, potentially ensuring renormalizability. The resulting unification of pcGR with Hořava-Lifshitz gravity opens a promising avenue for a consistent ultraviolet completion of gravity. While certain aspects of this approach remain speculative, the proposed mathematical formulation provides a coherent description of quantum gravitational effects in primordial cosmology and black hole dynamics.

As a result of the combination of pcGR with the Hořava-Lifshitz gravity [5], which introduces higher-order terms in the Riemann tensor, the anisotropic scaling of HL gravity can be used to modify the UV behavior of the pseudo-complex metric, potentially leading to a theory that is both renormalizable and consistent with the algebraic properties of spacetime. The potential effectiveness of this approach has been demonstrated in recent studies on complexified cosmological theories, where Hořava-Lifshitz gravity yields a Wheeler-DeWitt equation that was successfully applied to resolve cosmological singularities and offers a new perspective on explaining the rate of accelerating cosmic expansion and the inflationary period [7].

Contemporary theoretical work has demonstrated that algebraic extensions of General Relativity can address both UV completion and infrared consistency challenges. In particular, the pseudo-complex formulation provides a mathematically rigorous framework for introducing a minimal length scale while preserving Lorentz invariance, as shown in [2,3]. Our unification with Hořava-Lifshitz gravity, as emphasized, builds on this foundation by incorporating the anisotropic scaling that characterizes the renormalizability properties of HL gravity [6]. This combination offers distinct advantages: the pcGR structure maintains the successful low-energy predictions of General Relativity, while the HL terms regulate the high-energy behavior through their intrinsic momentum-dependent scaling.

Notably, this unification could lead to distinct signatures in the gravitational wave signal from binary black hole mergers, potentially observable by future gravitational wave detectors such as LISA [8] or the Einstein Telescope [9]. The potential effectiveness of this approach was demonstrated once again in a recent study [10] involving Hořava-Lifshitz gravity incorporated into a complex cosmological theory which reveals a high sensitivity of relic gravitational wave amplitudes to the primordial matter and energy content of the universe. Moreover, this formulation predicts stochastic homogeneous distributions of gravitational wave intensities arising from the interplay of short- and long-spacetime effects within a non-commutative algebraic framework. The results of this formulation [10] align with the future expected observations of relic gravitational waves, predicted to pervade the universe as a stochastic, homogeneous background [11,12,13,14,15,16].

The unification of pcGR and HL gravity offers a promising approach to resolving the singularity problem by introducing a minimal length scale, the Planck length ($l_P=\sqrt{\hslash G/c^3}\approx 1.62\times {10}^{-35}$ m), where the effects of quantum gravity become significant [17,18,19,20]. This synergy leverages the anisotropic scaling of HL gravity to modify the pseudo-complex metric, preventing singularity formation. The pseudo-complex structure of pcGR provides a mathematical framework for spacetime geometry, althought the Hořava-Lifshitz gravity terms not only regulate the metric near the classical singularity but also enable a consistent resolution of black hole singularities.

The unification of pcGR and Hořava-Lifshitz gravity could explain dark energy as an emergent effect of modified gravity. The anisotropic scaling in HL gravity alters the pseudo-complex metric, inducing an infrared phase that reproduces dark energy behavior. Interestingly, this framework could also lead to novel predictions for the large-scale structure of the universe, potentially testable against observations from upcoming surveys such as Euclid [21] or LSST [22]. In this context, the pseudocomplex structure of pcGR provides a mathematical framework for describing the spacetime geometry, while the HL gravity terms regulate the behavior of the metric at large distances.

Finally, the unification of pcGR and HL gravity allows exploration of the UV completion of gravity. This combination enables the construction of a UV-complete theory of gravity, where the anisotropic scaling of HL gravity modifies the UV behavior of the pseudo-complex metric. Once again, despite its speculative nature, the unification may lead to a theory that is renormalizable, consistent with the algebraic properties of spacetime, and predictive at all energy scales, including the ultraviolet regime, where quantum gravity effects dominate. The resulting theory could have implications for our understanding of cosmic microwave background radiation, particularly in the context of inflationary models that rely on modified gravity theories. For example, the modified UV behavior of the theory could lead to changes in the predicted power spectrum of primordial fluctuations.

In hybrid theory combining pcGR and HL gravity, the Lorentz invariance of pcGR is modified by the anisotropic scaling introduced by HL gravity. Specifically, the ultraviolet behavior of the theory is governed by the HL gravity terms, which break Lorentz invariance, whereas the infrared behavior is expected to be dominated by the pcGR framework, which preserves Lorentz invariance. This dichotomy suggests that the hybrid theory may exhibit a transition from Lorentz-breaking behavior at high energies to approximate Lorentz invariance at larger distances or lower energies. The implications of this merger for the Lorentz invariance of the hybrid theory require careful consideration, and a detailed analysis of this issue is beyond the scope of the present study. However, it is worth noting that the potential consequences of Lorentz invariance breaking in hybrid theory could have significant implications for our understanding of gravity and its relationship to other fundamental interactions. Further investigation of this issue is warranted and will be pursued in a separate study.

In short, while the combination of pcGR and HL gravity may seem unconventional, our proposal leverages the strengths of both frameworks to provide a potentially renormalizable and consistent theory of gravity. This unification not only offers a new perspective on resolving black hole singularities and addressing the dark energy problem, but also provides a framework for exploring the UV completion of gravity and making novel predictions for large-scale structure observations. More research is needed to fully explore the implications of this unification, and we will address some of these issues in the following sections of this paper.

The paper is organized as follows. Section 2 reviews the Schwarzschild metric and presents the Hořava-Lifshitz action. Section 3 derives the Lagrangian and Hamiltonian formulations and obtains the Wheeler-deWitt equation. Section 4 presents the results and Section 5 draws conclusions.

2. pcGR and the Hořava-Lifshitz Hamiltonian

For a detailed introduction to pcGR, we refer the reader to [2,3,23]. Here, we focus on the spatial metric components, which are the only terms contributing to the Hořava-Lifshitz formulation due to its foliation of 4-dimensional spacetime into 3-dimensional spatial sheets.

The adopted 3-d line element is [3,23]

$$\begin{array}{ccc}\hfill d{s}^2& =& {\tilde{g}}_{11}d{r}^2+{\tilde{g}}_{22}d{\vartheta }^2+{\tilde{g}}_{33}d{\phi }^2,\hfill \end{array}$$

(1)

with ($r,\vartheta ,\phi$) representing respectively the radial, colatitude, and latitude coordinates respectively.

The Schwarzschild metric $g_{ij}$ is defined on a 3-dimensional spatial hypersurface, with $i=1,2,3$ corresponding to r, $\vartheta$, and $\phi$, respectively, whose components are [3,23]

$$\begin{array}{ccc}\hfill {\tilde{g}}_{11}& =& \left(1-{\displaystyle \frac{2m}{r}}+{\displaystyle \frac{B}{6r^4}}\right),\hfill \\ \hfill {\tilde{g}}_{22}& =& r^2,\hfill \\ \hfill {\tilde{g}}_{33}& =& r^2{\sin }^2\left(\vartheta \right).\hfill \end{array}$$

(2)

In pcGR, the parameter B models the accumulation of dark energy around a star. For $B=0$, the metric reduces to the Schwarzschild solution of General Relativity. The dark energy contribution introduces an additional term in the metric, proportional to $B=C/r^n$, where $n>3$ [23]. Although we restrict the r-dependence on $n=4$ for concreteness, higher-order dependencies ($n>4$) have been explored in Ref. [23] with minimal qualitative impact.

Before we proceed, for simplicity, alternative parameterizations are introduced, namely

$$\begin{array}{ccc}\hfill y& \equiv & {\displaystyle \frac{r}{m}},b\equiv {\displaystyle \frac{\mathit{B}}{m^4}},\hfill \end{array}$$

(3)

where y and b correspond respectively to the reparameterization of the radial distance and the accumulation of dark energy around a star.

In terms of the new variables, the metric components transform as ${\tilde{g}}_{11}\to m^{2}d{y}^2$, ${\tilde{g}}_{22}\to m^2{y}^2$, and ${\tilde{g}}_{33}\to m^2{y}^{2}sin\left(\vartheta \right)$. In particular, the common factor $m^2$ can be factored in these expressions, allowing us to define a rescaled line element $d{\tilde{s}}^2=d{s}^2/m^2$ that is manifestly independent of m.

With these new characterizations, the line element (1) becomes

$$\begin{array}{ccc}\hfill d{\tilde{s}}^2& =& g_{11}d{y}^2+g_{22}d{\vartheta }^2+g_{33}d{\phi }^2,\hfill \end{array}$$

(4)

where the $g_{ij}$ are pure functions of y:

$$\begin{array}{ccc}\hfill g_{11}& =& \left(1-{\displaystyle \frac{2}{y}}+{\displaystyle \frac{b}{6y^4}}\right);\hfill \\ \hfill g_{22}& =& y^2;\hfill \\ \hfill g_{33}& =& y^2{\sin }^2\left(\vartheta \right).\hfill \end{array}$$

(5)

This reparameterization eliminates any explicit dependence on the mass parameter m. Furthermore, we restricted our analysis to the orbital plane by setting $\vartheta =\pi /2$, treating it as a static variable. Although our study focuses on theoretical implications, further investigation of parameter b and observational constraints is warranted. Parameter b, as stressed before, governs the accumulation of dark energy around a star, and its value could potentially be constrained by observations of stellar dynamics or other astrophysical phenomena. We treat b as a free parameter due to the speculative nature of dark energy. In particular, previous studies have considered a specific value of b = 81/8, which eliminates the event horizon and predicts a distinct ring structure in the accretion disk near a black hole. Observing this ring structure could provide a direct measurement of b. Although current telescope resolutions are insufficient to resolve this feature, our analysis remains general by not fixing b to a specific value, allowing for a broader exploration of its implications.

The Hořava-Lifshitz action, for the quantization of pcGR, is given by [5,24]:

$$\begin{array}{ccc}\hfill {\mathcal{S}}_{HL}& =& \int d^{3}xdt\mathcal{L}={\displaystyle \frac{M_P^2}{2}}\int d^{3}xdtN\sqrt{g}(K_{ij}{K}^{ij}-\lambda K^2-g_0{M}_P^2-g_1\mathcal{R}\hfill \\ & & -g_2{M}_P^{-2}{\mathcal{R}}^2-g_3{M}_P^{-2}{\mathcal{R}}_{ij}{\mathcal{R}}^{ij}-g_4{M}_P^{-4}{\mathcal{R}}^3-g_5{M}_P^{-4}\mathcal{R}\left({\mathcal{R}}_j^i{\mathcal{R}}_i^j\right)\hfill \\ & & -g_6{M}_P^{-4}{\mathcal{R}}_j^i{\mathcal{R}}_k^j{\mathcal{R}}_i^k-g_7{M}_P^{-4}\mathcal{R}{\nabla }^2\mathcal{R}-g_8{M}_P^{-4}{\nabla }_i{\mathcal{R}}_{jk}{\nabla }^i{R}^{jk}).\hfill \end{array}$$

(6)

In this expression, $M_P$ denotes the Planck mass and ${\nabla }_i$ is the covariant derivative in 3-dimensions. The action comprises kinetic and potential terms, the kinetic term involves the extrinsic curvature tensor $K_{ij}$ and the potential term depends on the Ricci tensor. Within the perturbative framework, we truncate the potential to fourth-order terms ($g_4$) and set $\lambda =1$, which is a natural choice in the context of general relativity, where $\lambda$ represents a parameter that measures the deviation from the standard diffeomorphism invariance that preserves folliation. By setting $\lambda =1$, we effectively recover the standard gravitational action in the infrared limit. Furthermore, the truncation of higher-order terms is motivated by the assumption that their contributions are suppressed by powers of the relevant energy scale, rendering them negligible in the context of our analysis. Although these approximations may limit the precision of our results, they enable us to capture the essential features of the system and provide a tractable framework for exploring the Wheeler-deWitt equation. For a more comprehensive discussion of the implications of $\lambda$ and its potential values, we refer the reader to [5].

The contribution of kinetic energy is defined in terms of the extrinsic metric covariant and contravariant tensors $K_{ij}$ and $K^{ij}$:

$$K_{ij}={\displaystyle \frac{1}{2\sigma N}}\left(-{\displaystyle \frac{\partial g_{ij}}{\partial t}}+{\nabla }_i{N}_j+{\nabla }_j{N}_i\right)\mathrm{and}{K}^{ij}={\displaystyle \frac{1}{2\sigma N}}\left({\displaystyle \frac{\partial g^{ij}}{\partial t}}+{\nabla }^i{N}^j+{\nabla }^j{N}^i\right),$$

(7)

where $N_i$ is the Arnowitt-Deser-Misner (ADM) shift vector and where the extrinsic metric scalar is represented by K.

The potential contribution is in turn defined in terms of the Ricci curvature scalar. This theory is based on the ADM foliation of the 4-dimensional space, partitioning the space-time into 3-dimensional space sheets and a perpendicular-time parameter vector. The action in (6) produces propagators that make the theory renormalizable in the UV limit and recover the GR in the IR limit [5]. The deviation from the Lorentz symmetry implies that a minimal length is effectively introduced.

In this contribution we will, for simplicity, restrict the Hořava-Lifshitz action to up to third order terms and also exclude derivative terms. In most sample calculations, we apply the naturalness condition, which means that all parameters are set to 1, except explicitly stated differently, assuming an equal contribution at all scales. The naturalness condition, which requires all dimensionless parameters to be of order unity, is motivated by the expectation that the theory should not rely on fine tuning to reproduce observed physics [25,26]. This principle is widely adopted in effective field theories, as parameters are generically expected to be natural in size unless a symmetry or other mechanism (e.g., decoupling) explicitly suppresses them [27]. Imposing the naturalness condition eliminates fine-tuned parameters and prevents unphysical hierarchies or instabilities, while simultaneously revealing possible fixed points or physically meaningful regimes.

In summary, this section has outlined the theoretical framework for pcGR and its unification with Hořava-Lifshitz gravity, the choice $\lambda =1$ have been justified, and the naturalness condition has been imposed to minimize fine-tuned parameters. This framework will serve as the basis for our subsequent analysis of the Wheeler-deWitt equation and the implications for black hole physics.

3. The Lagrangian of pcGR Within the Hořava-Lifshitz Action

The Lagrange density of this theory ($\mathcal{L}$), the kinetic energy density ($\mathcal{T}$) and the potential ($\mathcal{V}$) can be recovered from the action (6), with the following definitions:

$$\begin{array}{ccc}\mathcal{L}\hfill & =& \mathcal{T}-\mathcal{V},\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\mathcal{T}\hfill & =& (K_{ij}{K}^{ij}-\lambda K^2),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\mathcal{V}\hfill & =& G_0+G_{1}R+G_2{R}^2+G_3{R}_{ij}{R}^{ij}+G_4{R}^3,\hfill \end{array}$$

(10)

where the rescaled parameter $G_k$ is set as ${\displaystyle \frac{g_k}{M_P^d}}$, expressed in terms of the original interaction parameters $g_k$, defined in (6).

3.1. Kinetic Energy

In Hořava-Lifshitz gravity, foliation-preserving diffeomorphism invariance constrains the lapse function N to be spatially constant. We therefore adopt the gauge choice $N=1$ and $N_i=0$ for the lapse function and the shift vector, respectively. This gauge-fixing simplifies the kinetic term, as demonstrated in [24]. From

$$\begin{array}{cc}\hfill K_{ij}& =K^{ij}=g^{ip}{g}^{jq}{K}_{pq}\end{array}$$

(11)

and (7), we obtain after a lengthy calculation the expression for $K_{ij}{K}^{ij}$:

$$\begin{array}{ccc}\hfill K_{ij}{K}^{ij}& =& {\displaystyle \frac{6\left(b^2+2y^3\left(2by-6b+6y^5-24y^4+27y^3\right)\right){\dot{y}}^2}{y^2{\left(b+6(y-2)y^3\right)}^2}};\hfill \end{array}$$

(12)

K, which represents the trace of $K_{ij}$, in the second term of the kinetic energy term (9), then becomes

$$\begin{array}{ccc}\hfill K& =& -{\displaystyle \frac{2\left(2b+3(2y-5)y^3\right)\dot{y}}{y\left(b+6(y-2)y^3\right)}}.\hfill \end{array}$$

(13)

The time derivative of y is denoted by $\dot{y}$. Setting $\lambda =1$ [24], we arrive at the following expression for the kinetic energy:

$$\begin{array}{ccc}\hfill \mathcal{T}& =& K_{ij}{K}^{ij}-K^2\hfill \\ & =& -{\displaystyle \frac{2\left(5b+6(y-4)y^3\right)}{y^2\left(b+6(y-2)y^3\right)}}{\dot{y}}^2\hfill \\ & =& -\mathrm{\Theta }\left(y\right){\dot{y}}^2,\hfill \end{array}$$

(14)

where $\mathrm{\Theta }\left(y\right)$, given by

$$\begin{array}{ccc}\hfill \mathrm{\Theta }\left(y\right)& =& {\displaystyle \frac{2\left(5b+6(y-4)y^3\right)}{y^2\left(b+6(y-2)y^3\right)}},\hfill \end{array}$$

(15)

captures the properties of inertia of the system under changes in y.

3.2. Potential Energy

The building blocks of the interaction are expressed in terms of the variables and parameters of the pcGR, specifically for the Schwarzschild case. While Mathematica [28] was used to verify the results, all calculations were carefully performed by hand to ensure precision. For brevity and focus on novel results, we omit detailed derivations of standard quantities such as metric components, extrinsic curvature, Christoffel symbols, and Ricci tensor, as these can be found in classical texts on general relativity [1,29]. Our emphasis is on the application of pcGR to the Schwarzschild case and the resulting implications for quantum gravity. The potential energy contains many different terms, and it is not very illustrative to describe them all at once. Alternatively, we can use Equation (10) and list the building blocks of potential energy, which are:

(a)

The Ricci scalar

$$\begin{array}{ccc}\hfill R& =& b/y^6;\hfill \end{array}$$

(16)

(b)

The interaction $R_{ij}{R}^{ji}$

$$\begin{array}{ccc}\hfill R_{ij}{R}^{ji}& =& {\displaystyle \frac{4{(b-3y^3)}^2}{9y^{12}}}+2{\displaystyle \frac{{(b+6y^3)}^2}{36y^{12}}}.\hfill \end{array}$$

(17)

We finally arrive at

$$\begin{array}{ccc}\hfill \mathcal{V}& =& G_0+G_1{\displaystyle \frac{b}{y^6}}+G_2{\displaystyle \frac{b^2}{y^{12}}}+G_3\left({\displaystyle \frac{4{(b-3y^3)}^2}{9y^{12}}}+2{\displaystyle \frac{{(b+6y^3)}^2}{36y^{12}}}\right)+G_4{\displaystyle \frac{b^3}{y^{18}}}.\hfill \end{array}$$

(18)

3.3. Hamiltonian and the Wheeler-deWitt Equation

The canonical quantization procedure is applied to the variable y. To achieve this, we first define the canonical momentum ${\mathrm{\Pi }}_y$ as the derivative of the Lagrange density $\mathcal{L}$ with respect to the parametric “velocity” $\dot{y}$, yielding

$${\mathrm{\Pi }}_y={\displaystyle \frac{\partial \mathcal{L}}{\partial \dot{y}}}=-2\mathrm{\Theta }\left(y\right)\dot{y}.$$

(19)

This definition of the canonical momentum is a crucial step in the quantization process, where the momentum is subsequently promoted to an operator. The time parameter in this context is defined within the Arnowitt-Deser-Misner (ADM) foliation of spacetime, providing a framework for describing the dynamics of the system.

Resolving for $\dot{y}$, we get

$$\begin{array}{ccc}\hfill \dot{y}& =& -{\displaystyle \frac{1}{2\mathrm{\Theta }\left(y\right)}}{\mathrm{\Pi }}_y,\hfill \end{array}$$

(20)

which results for the kinetic energy (14) into

$$\begin{array}{ccc}\hfill \mathcal{T}& =& -{\displaystyle \frac{{\mathrm{\Pi }}_y^2}{4\mathrm{\Theta }\left(y\right)}}.\hfill \end{array}$$

(21)

Combining Equations (18) and (21), the Hamiltonian density can be written as

$$\begin{array}{ccc}\hfill \mathcal{H}& =& \mathcal{T}+\mathcal{V}\hfill \\ & =& -{\displaystyle \frac{{\mathrm{\Pi }}_y^2}{4\mathrm{\Theta }\left(y\right)}}+\mathcal{V}.\hfill \end{array}$$

(22)

The canonical quantization procedure follows DeWitt’s original prescription [30] for constrained Hamiltonian systems, promoting classical constraints to operators that annihilate physical states. In our framework, the Hamiltonian constrain

$$\mathcal{H}\mathrm{\Psi }=0$$

(23)

generates the Wheeler-DeWitt-equation—a timeless Schrödinger equation governing quantum spacetime geometry. The pseudo-complex (pcGR) metric structure naturally introduces a minimal length scale, while the Hořava-Lifshitz terms provide ultraviolet regularization. The momentum ${\mathrm{\Pi }}_y$ is quantized through the operator prescription.

$${\mathrm{\Pi }}_y\to {\widehat{\mathrm{\Pi }}}_y=-i\hslash {\displaystyle \frac{\partial }{\partial y}},$$

(24)

which transforms the Wheeler-DeWitt equation into

$$\mathcal{H}\left(y,-i\hslash {\displaystyle \frac{\partial }{\partial y}}\right)\mathrm{\Psi }\left(y\right)={\displaystyle \frac{d^2\mathrm{\Psi }\left(y\right)}{d{y}^2}}+4\mathrm{\Theta }\left(y\right)\mathcal{V}=0.$$

(25)

The following expression is used

$$\mathrm{Pot}\left(y\right)\equiv 4\mathrm{\Theta }\left(y\right)\mathcal{V},$$

(26)

defines an effective potential where the inertia function $\mathrm{\Theta }\left(y\right)$ modulates $\mathcal{V}$ by encoding the “resistance” of the system to y-variations. This modulation critically determines the dynamical evolution. The repulsive core of the potential at small y manifests the singularity resolution in our pcGR-HL framework, analogous to bounce phenomena in loop quantum cosmology [31]. Key distinctions emerge from: (i) the pseudocomplex algebraic structure modifying the metric at fundamental level; (ii) Hořava-Lifshitz nonlinearities generating a stabilizing potential barrier ($\mathrm{Pot}\left(y\right)\to +\infty$ as $y\to 0$).

4. Results

The behavior of the potential $Pot\left(y\right)$ shown in the left panel of Figure 1, is analyzed in the context of the Hořava-Lifshitz action for $b=0$, which reduces to the standard Schwarzschild solution in General Relativity. The potential exhibits a pocket structure with infinite walls in the region $y<2$, indicative of a confined system. At $y=2$, the results indicate the position of the event horizon, where the black hole wave function is concentrated. The repulsive potential towards $r=my=0$ can be attributed to the non-linear terms in the Hořava-Lifshitz action, which dominate the behavior of the potential in this region and prevent the formation of a singularity.

The right panel of Figure 1 corresponds to $b={\displaystyle \frac{81}{8}}$, a limiting value above which there is no event horizon. The potential tends to $-\infty$ at $y={\displaystyle \frac{3}{2}}$, signaling the disappearance of the event horizon above this value of b. However, the potential remains repulsive towards $r=0$, suggesting that nonlinear terms continue to play a crucial role in avoiding the formation of a singularity.

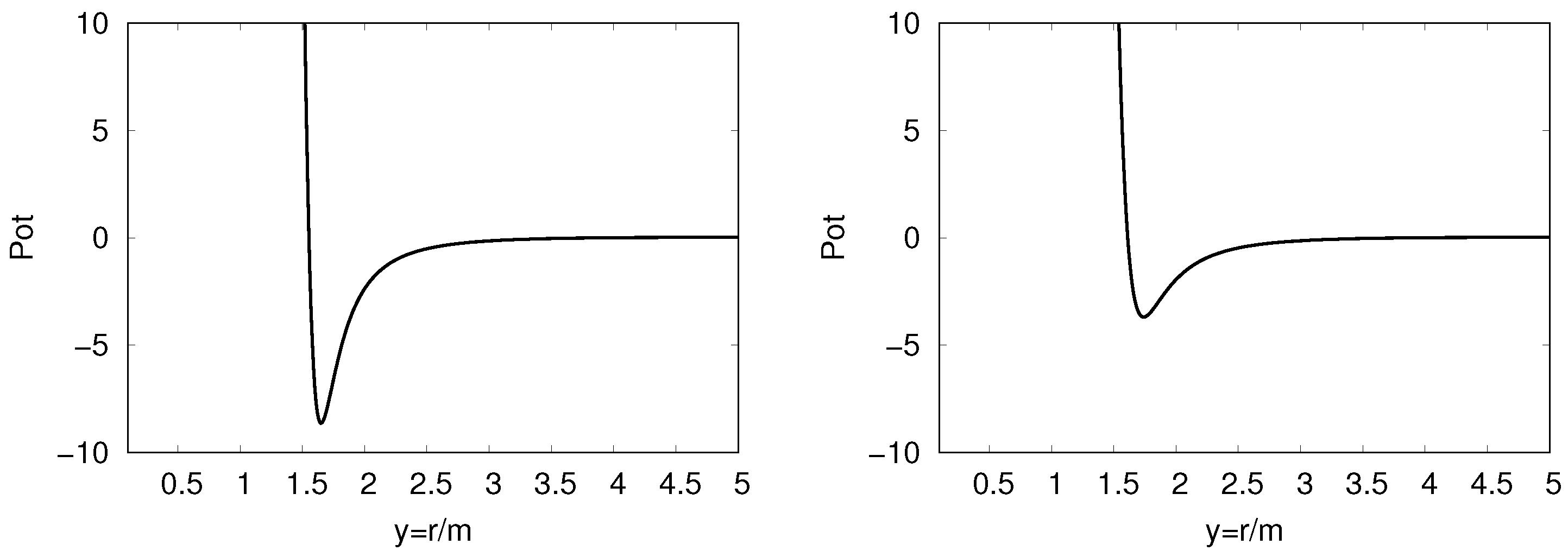
For parameter values $b>{\displaystyle \frac{81}{8}}$ (Figure 2), increasing b produces three key effects: the potential minimum becomes broader and shallower, the black hole wave function $\psi \left(y\right)$ exhibits stronger spatial localization, and the system stabilizes at a fixed radial position $y_{\min }$. This enhanced localization facilitates the numerical solution of the wave equation, while the constant minimum position $y_{\min }$ corresponds to a stable stellar configuration with fixed radius $R=y_{\min }$. This reflects the result obtained in previous publications on pcGR. Even when an event horizon exists, the higher-order terms of the Hořava-Lifshitz action prevent the colapse of the star to a singularity.

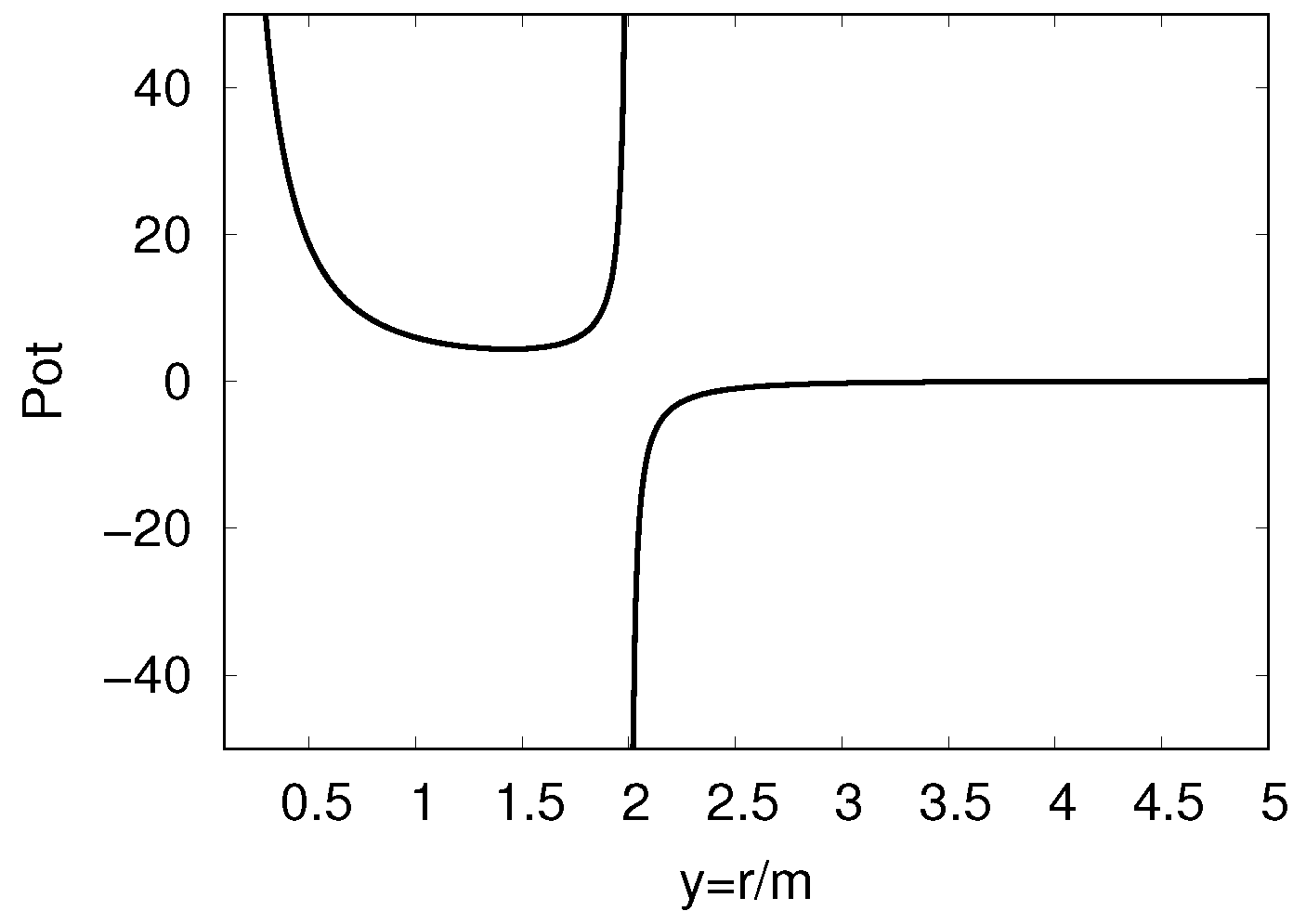
In contrast, when higher-order terms are skipped, as shown in Figure 3 ($\mathcal{V}=1$), all information is contained in the inertia function $\mathrm{\Theta }\left(y\right)$. In this case, the inertia effect of the kinetic energy plays the dominant role and still localizes the wave function in $r=my>0$, indicating that the system flexes resistance to contracting to the center, even in GR.

The features of the potential can be understood in terms of the competition between the gravitational and kinetic terms in the Hořava-Lifshitz action. The former tends to create a singularity, while the latter provides a repulsive contribution that prevents the collapse of the system. Our analysis suggests that this interplay is responsible for the emergence of the event horizon and the avoidance of singularities in the system.

In particular, we anticipate that a detailed analysis of the eigenvalues and masses will provide further insight into the properties of black holes in the context of HL gravity and may even shed light on the potential observational signatures of these systems. Our work provides a first step in exploring the connection between pcGR and HL gravity and lays the groundwork for further investigation of the relationship between these approaches.

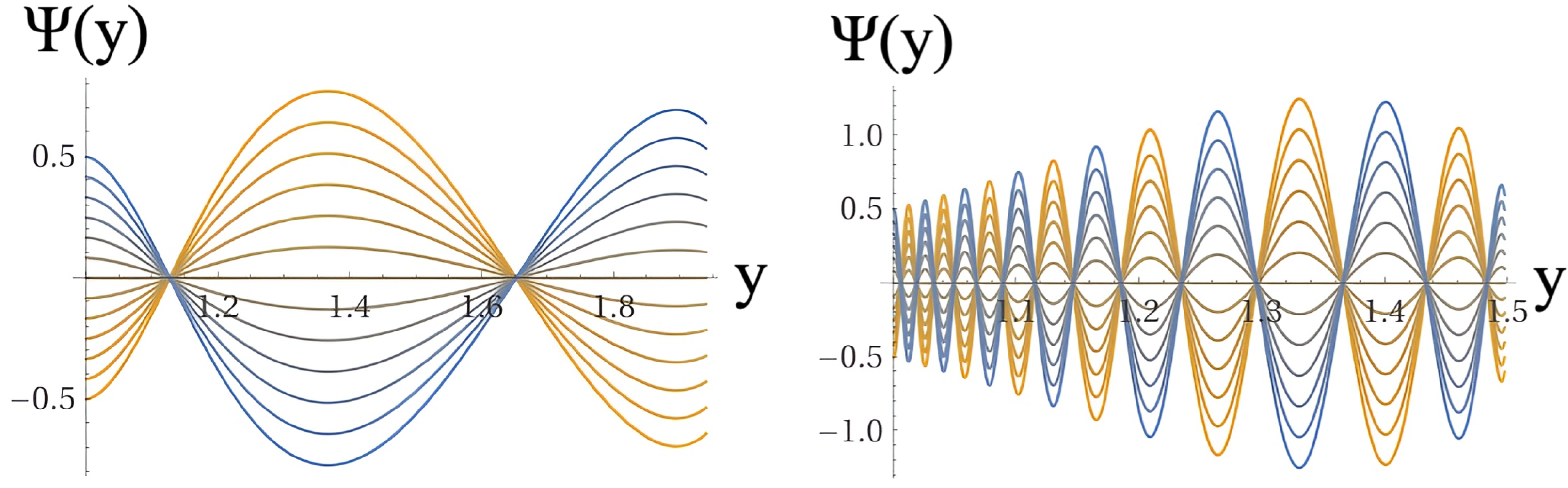
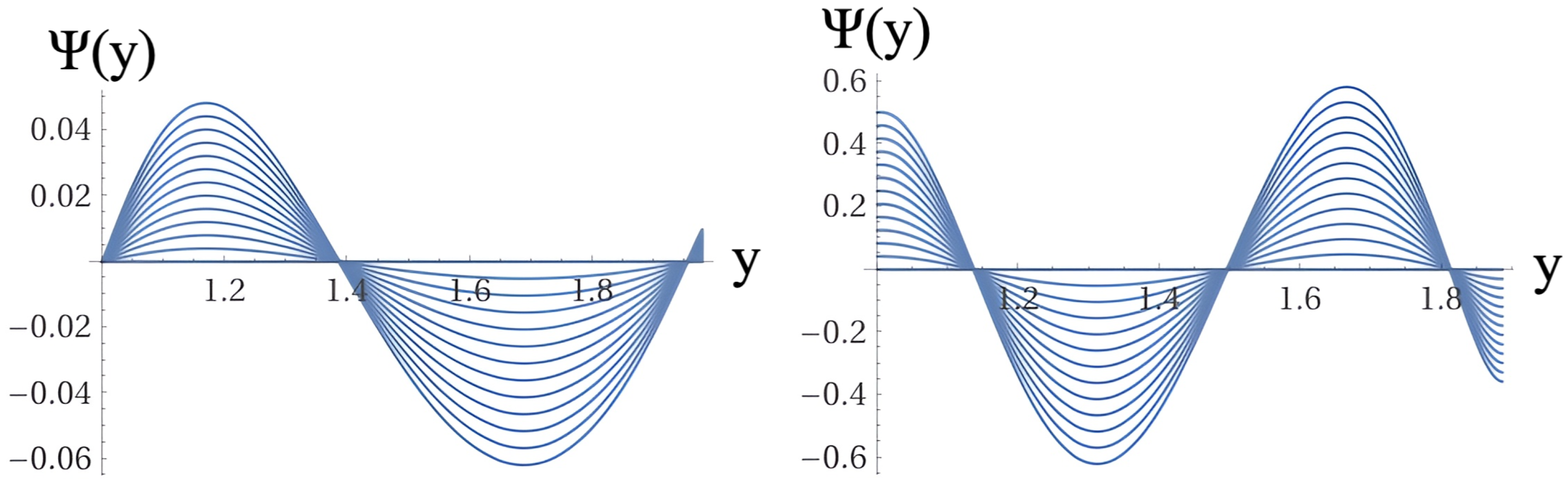
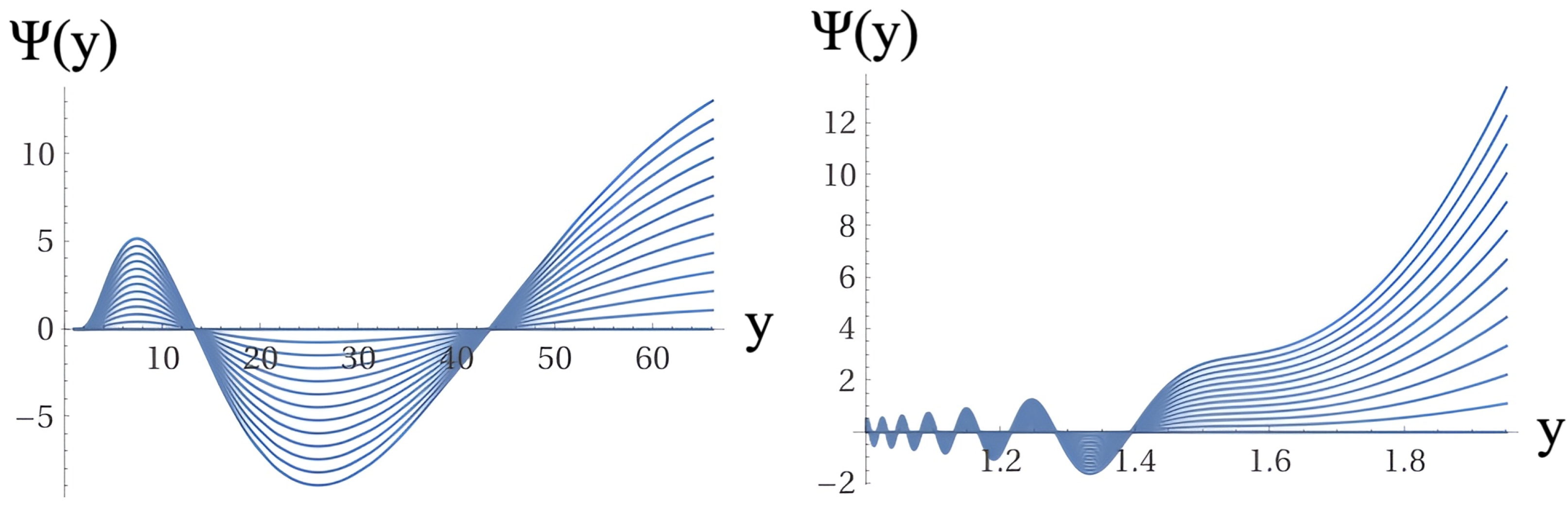
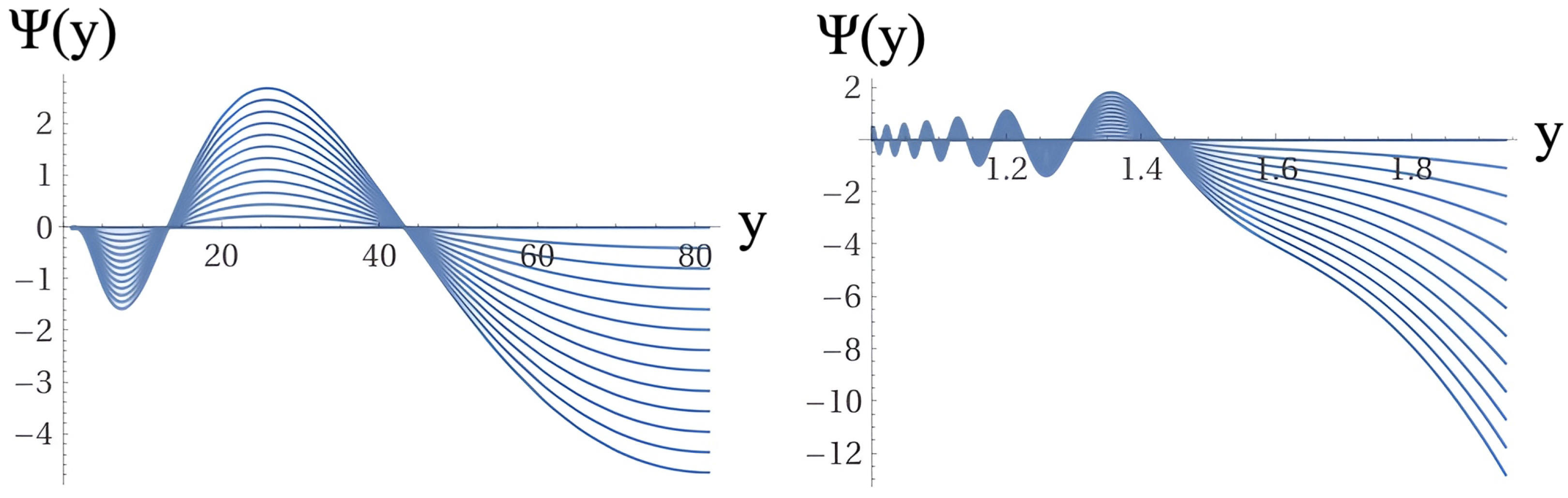
We have selected several values of the parameter b to illustrate the dependence of the wave function $\mathrm{\Psi }\left(y\right)$ on this parameter. The values of b were chosen to demonstrate the varying effects of the potential $\mathcal{V}$ on the solution of the Wheeler-deWitt equation. Specifically, the different values of b modify the shape and amplitude of the potential, leading to distinct profiles of wave functions. This range of solutions showcases the sensitivity of the wave function to changes in potential $\mathcal{V}$, as depicted in the figures for various values of b.

Figure 4, Figure 5, Figure 6 and Figure 7 depict quantum solutions of the Wheeler-deWitt Equation (25) for a regularized black hole (i.e., without a central singularity). The results of Figure 4 show the sample solution family of the black hole wave function and resemble the typical evolutionary behavior of a quantum-mechanical wave packet with an envelope containing transverse-wave solutions inside. The plots in Figure 5, Figure 6 and Figure 7 show samples of individual solutions of the black hole wave function.

The interpretation of an oscillating quantum wave packet of a regularized black hole and the corresponding individual solutions requires a quantum-mechanical appreciation of the modified space- time structure near the black hole core. Based on the following references (see [32,33,34,35,36,37]), we address some interpretative conjectural aspects. It is important to remember that, in classical general relativity, black holes contain a singularity at the center, where the curvature diverges. Quantum gravity models, in turn, often regularize the singularity by replacing it with a high-density quantum nucleus or a Planck-scale structure (such as a quantum jump, for example), resulting in an effective metric near the center that may resemble a de Sitter-type geometry or other nonsingular geometry. From a quantum-mechanical perspective, the corresponding wave functions describe the probability amplitude of finding quantum gravitational degrees of freedom (or matter fields) in a given state. In the case where the wave function oscillates, this suggests a dynamical evolution, which could be due to quantum fluctuations of the black hole’s internal geometry, a gravitational backlash from matter entering or leaving the black hole composing Hawking radiation, or even quasi- normal mode oscillations of the horizon or core that are quantumly corrected. In our analysis, the Wheeler-DeWitt equation yields wave functions that exhibit oscillatory behavior, which may seem counterintuitive given the static nature of spacetime. However, this apparent paradox can be resolved by considering the quantum nature of the system. In quantum gravity, the wave function describes the probability amplitude of finding the system in a particular state. The oscillations in the wave function can be attributed to quantum fluctuations of the black hole’s internal geometry or quasi-normal mode oscillations of the horizon/core that are quantum-corrected. These oscillations do not necessarily imply a dynamical evolution of the spacetime itself, but rather reflect the quantum nature of the system. Our results suggest that the oscillating wave functions describe a quantum black hole with a non-singular core, where the classical singularity is replaced by a high-density quantum nucleus. The oscillations may encode information about the quantum structure of the black hole, such as the discreteness of the area spectrum or the unitary propagation of information. In this context, the statement refering to the oscillation of wave function as suggesting a dynamical evolution should be understood as referring to the quantum dynamics of the system, rather than a classical dynamical evolution of the spacetime.

Concerning interpreting the oscillations, we could consider radial and temporal components. Radial oscillations may represent a superposition of states in which the black hole core pulses between expanded and contracted phases (such as a branch cut or a quantum bounce scenario) [7,38]. Temporal oscillations, in turn, could indicate energy eigenstates of the quantum black hole (e.g., discrete mass/area spectra). The physical implications of these scenarios indicate for instance a singularity resolution in which the oscillations may encode how quantum effects smear out the classical singularity into a finite-sized, dynamic core. Alternatively, it may indicate information preservation, in the sense that nonsingular evolution could unitarily propagate information (with no loss to a singularity), with oscillations reflecting interference or revival effects. With respect to observable signatures, if the oscillations couple to the outgoing Hawking radiation, they can impart modulations to the emission spectrum; and as a result gravitational wave echoes from the quantum nucleus can arise if the oscillations excite quasi-normal modes.

The boundary conditions adopted in this work follow the conventional canons of convergence, as well as stability and continuity of the solutions of differential equations, and are in tune with the Bekenstein criterion [32]. Considering spatially connected regions within the particle horizon of a given observer, locus of the most distant points that can be observed at a specific time $t_0$ in an event, made Bekenstein’s conjecture an upper bound for the entropy of a black hole. According to the criterion, the entropy S is proportional to the number of Planck areas to cover the black hole’s event horizon. Taking in a simplified way the proper distance $d\left(t\right)$ of a pair of objects, at an arbitrary time t and its relation to the proper distance $d\left(t_0\right)$ at a reference time $t_0$, results in $d\left(t\right)=u\left(t\right)d\left(t_0\right)$, this implies that for $t=t_0$, $u\left(t_0\right)=1$. We consider the boundary condition $\left|u\right(t_0)=1|$, assuming that time $t_0$ is the location of the most distant points that can be observed, in line with the Bekenstein criterion. These boundary conditions lead to $\mathrm{\Psi }\left(u\right(t\left)\right)\to \mathrm{\Psi }\left(1\right)=1\mathrm{and}\mathrm{\Psi }\left(1\right)=0$. Regarding possible interpretations involving amplitude variations, the possible causes of an increase, decrease, or stability of the amplitudes may be due to several factors. Among the possible causes for the increase in amplitudes, resonance effects, instability in quantum geometry, and energy influx stand out, signaling an indefinite transition or jump, such as the formation of a white hole, or indicating a quantum revitalization. Decreasing amplitudes are generally associated with decoherence effects, dispersive effects, or even absorption effects by an effective horizon, implying ’information leakage’ or even temporary suppression, as in a collapse-rebound scenario. Finally, the stability of the amplitudes would possibly indicate stationary or quasi-stationary configurations or even an equilibrium between the expansion and contraction phases, indicating a metastable quantum black hole or a quasi-classical regime where quantum fluctuations are suppressed.

As a final comment, the oscillating wave functions reflect the dynamical non-singular quantum geometry of the black hole interior. Its interpretation is based on the predictions of the underlying theory for how spacetime and matter behave at Planckian densities. Probing these oscillations theoretically could bridge quantum gravity with observable phenomena such as gravitational waves or modified Hawking radiation.

5. Conclusions

This work develops a unified framework combining Hořava-Lifshitz gravity with pseudo-complex General Relativity (pcGR), which generalizes Einstein’s theory through two fundamental modifications: (i) the introduction of a minimal length scale, and (ii) the natural emergence of dark energy effects in strong gravitational fields near black holes. Our analysis yields four key insights. First, the Wheeler-DeWitt quantization of pcGR demonstrates that nonlinear Hořava-Lifshitz interaction terms prevent singularity formation independently of dark-energy effects. Second, the kinetic energy terms—particularly the inertia contribution—play an essential role in this singularity resolution mechanism. Third, systems with large dark-energy parameters ($b>81/8$) exhibit strongly localized wave functions, while smaller values correspond to stable stellar configurations with radii determined by potential minima. Finally, quantum corrections manifest as wave function oscillations that effectively smear the classical singularity.

These quantum gravity predictions may produce observable signatures in gravitational wave signals from compact binary mergers. Current LIGO-Virgo observations [39] have constrained deviations from classical general relativity, with our model remaining consistent with these bounds while predicting distinctive features in the kHz regime. Future third-generation detectors like the Einstein Telescope [40] will provide the sensitivity required to test these predictions, particularly through precision measurements of the ringdown phase, where quantum horizon fluctuations become significant.

Our results establish a concrete connection between three fundamental aspects of modified gravity: (1) the regularization of singularities through nonlinear interactions, (2) the critical role of kinetic terms in quantum gravity, and (3) the interplay between minimal length scales and dark energy in strong field regimes. This framework opens new avenues for investigating quantum gravitational effects in both theoretical and observational contexts.