Looking for Signs of Unresolved Binarity in the Continuum of LAMOST Stellar Spectra
Abstract
1. Introduction
2. Data: LAMOST Spectra
3. Data: Known Single and Binary Stars
3.1. Reliable Unresolved Binary Stars
3.2. Reliable Single Stars
- Compilation of spectra of single stars, mostly Praesepe and M67 spectral standards [52]. There is = 1 star overlapping with the LAMOST DR5 catalog.
- ELODIE.3.1—an updated release of the library published in Prugniel et al. [53]. = 15.
- The Indo-US Library of Coudé Feed Stellar Spectra [54] containing spectra of 1273 stars obtained using the 0.9 m Coudé feed telescope at Kitt Peak National Observatory. = 30.
- LCO-SL, the Las Campanas Observatory Stellar Library 3, which is the most comprehensive near-infrared spectral library with 1300+ spectra obtained between 2013 and 2017 using the Folded-port InfraRed Echellette (FIRE) spectrograph operated using the 6.5 m Magellan Baade telescope. = 12.
- MILES—the library of spectra obtained by the 2.5 m Isaac Newton Telescope used, in particular, for stellar population synthesis [55]. = 25.
- The Tian Shan (Alma-Ata) Sternberg Astronomical Institute photometric catalog of 13,586 bright northern-sky stars [57]. The catalog contains both single stars and double (multiple) systems. For single stars, .
- The latest issue of the astrometric fundamental star catalog, FK6 [58], a combination of results from ground-based observations and from the Hipparcos project of space astrometry. .
3.3. Presumably Single and Unresolved Binary Stars
3.3.1. Presumably Single Stars
3.4. Gaia Non-Single Stars
4. The Method for Comparing Model Spectra with the LAMOST Spectrum in the Terms of Their Continua
4.1. Description of the Method in General
4.2. The Library of Synthetic Spectra
- takes 76 values from 3500 K to 50,000 K. The increment in is not uniform: it increases from K for low temperatures to K for high temperatures;
- takes 11 values, from 0 to 5, with the uniform increment ;
- Not every combination of these two parameters is possible; the allowed combinations form a triangle in the — plane. See Castelli and Kurucz [49] for details;
- takes values from to , with a uniform increment .
4.3. Removal of the Outliers at the Edges of LAMOST Spectra
- We check whether there is an outlier in the Å range. This value is chosen based on the results of visual analysis of the spectra.
- We search a data point in the spectrum, closest to at longer . For most LAMOST spectra, the corresponding wavelength is Å. The flux at this is .
- If at any point of the LAMOST spectrum with , the deviation of the flux from exceeds the pre-selected value, , i.e., mod, we assume that an outlier is present. In this study, we accept .
4.4. Interpolation and Normalization of the Spectra
4.5. Four-Parameter Representation of Stellar Synthetic Spectra Taking into Account Interstellar Reddening
- For every star, we subdivided the range of possible values of interstellar absorption into intervals, and for every input synthetic spectrum from the CKL library we computed 21 spectra with different values of .
- Next, we formed the relative absorption line, i.e., for all 270 wavelengths of CKL spectra that were within the LAMOST range (see Section 4.2) we computed using Equation (3) with .
- For a particular star, we found the acceptable range of interstellar absorption, . The edges of this interval depended on stellar coordinates , , which were well known and presented in the LAMOST catalog, and on the distance to the star d absent in the catalog.To determine the distance d, we used several approaches:
- (a)
- The majority of stars from the LAMOST catalog could be identified with the stars from the Gaia DR3 catalog [12,73] that currently contains the most accurate stellar parallaxes and their uncertainties . Using them, we computed possible limits for the distance to the star:If the computed turned out to be negative, we set .
- (b)
- If a LAMOST star had no identification in the Gaia DR3 catalog, then, for some single stars, we took information on the distance or interstellar absorption directly from the original catalogs (see Section 3.2).
- (c)
- If identification of a LAMOST star with the Gaia DR3 catalog and any information on the distance to it were lacking, we assumed
- The values of and together with the stellar coordinates and were uploaded to the site http://stilism.obspm.fr (accessed on 5 December 2024), where an interactive procedure permitting us to determine the interstellar reddening from a 3D map of interstellar absorption described in Lallement et al. [74], Capitanio et al. [75], Lallement et al. [76] is possible. This procedure returns the limits of interstellar reddening, , , possible for the star, with corresponding distances and and the limiting distance covered by the interactive interstellar absorption map on the site. When , we assumed , having in mind that factor 2 results in the maximum possible absorption for barometric dependence of the latter on the z-coordinate.
- We recomputed the derived limits of the interstellar reddening into the limits of the interstellar absorption and .
- For every spectrum from the CKL library defined by the parameters , , and , and for all wavelengths in the sensitivity range of the LAMOST survey, we computed reddened spectra for the following values of interstellar absorption:where the index i takes the values and where is the number of intervals into which the range of interstellar absorption is split. To compute the intensity of light for the reddened synthetic spectrum, we used the Pogson [77] formula , where are intensities of stellar light given in the CKL library without account of the interstellar absorption.
4.6. The Search for Optimal Synthetic Spectrum in the Four-Parameter Set of the Reddened Synthetic Spectra
4.6.1. The Search for a Spectrum with the Lowest Rms Deviations in the 4-Parameter Set of Synthetic Spectra
- For a selected LAMOST spectrum, we found in the CKL library a spectrum with the parameters , , and , closest to the catalog parameters , , and . For the initial value of interstellar absorption , we selected the value from the sequence of acceptable values provided by Formula (5) that was either the closest to the interstellar absorption corresponding to the star’s mean parallax (if the star was identified with the Gaia catalog) or the closest to the mean interstellar absorption known from the other sources (see Section 4.5).
- The so-called “current spectrum”, containing intermediate optimization results, is introduced. We designate parameters of the current spectrum as , , , and for the spectrum used at the first step of the optimization procedure .
- The deviation is computed for the current spectrum: .
- We compute deviations for eight adjacent spectra, , that differ from the current spectrum by their value of one of the parameters in the 4-parameter set of synthetic spectra. For example, is the deviation for the spectrum with , , and similar to those of the current spectrum, but is the closest one, exceeding . If the parameters of the current spectrum are at the edge of the 4D set, i.e., are at the maximum or minimum possible level, then the current spectrum will have only one neighbor in this direction.
- If the deviation for one of these neighbor spectra is lower than that for the current spectrum, , then the spectrum with the lowest deviation is chosen as the current spectrum, and the minimization procedure returns to step 3.
- If , we additionally calculate deviations for 72 adjacent spectra, , so that these spectra simultaneously have from 2 to 4 parameters differing from the current spectrum by one step. Similarly to calculating deviations , if the current point is at the edge of the 4D distribution of the parameters, it will have less than 72 additional neighbors. If the deviation for one of adjacent spectra of the additional set is lower than that for the current spectrum, , then we select the spectrum with the lowest deviation as the current spectrum. The minimization procedure returns to step 3.
- If , the procedure of the search for the spectrum with the minimum rms deviation in the 4-parameter set is completed, and the desired spectrum is contained in the current spectrum.
4.6.2. Comparison of the Methods
4.7. Improving the Optimal Spectrum by Interpolation Between Adjacent Spectra
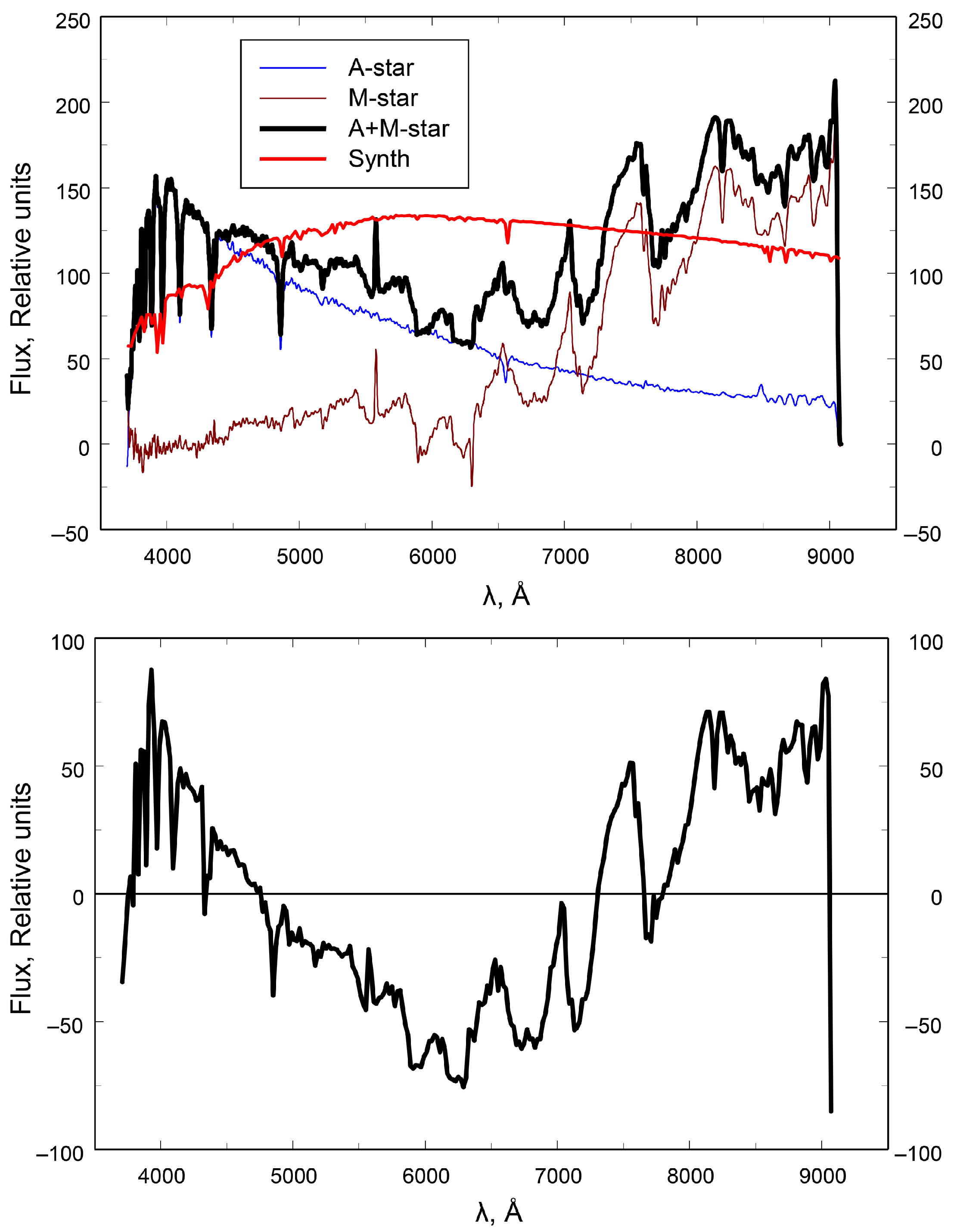
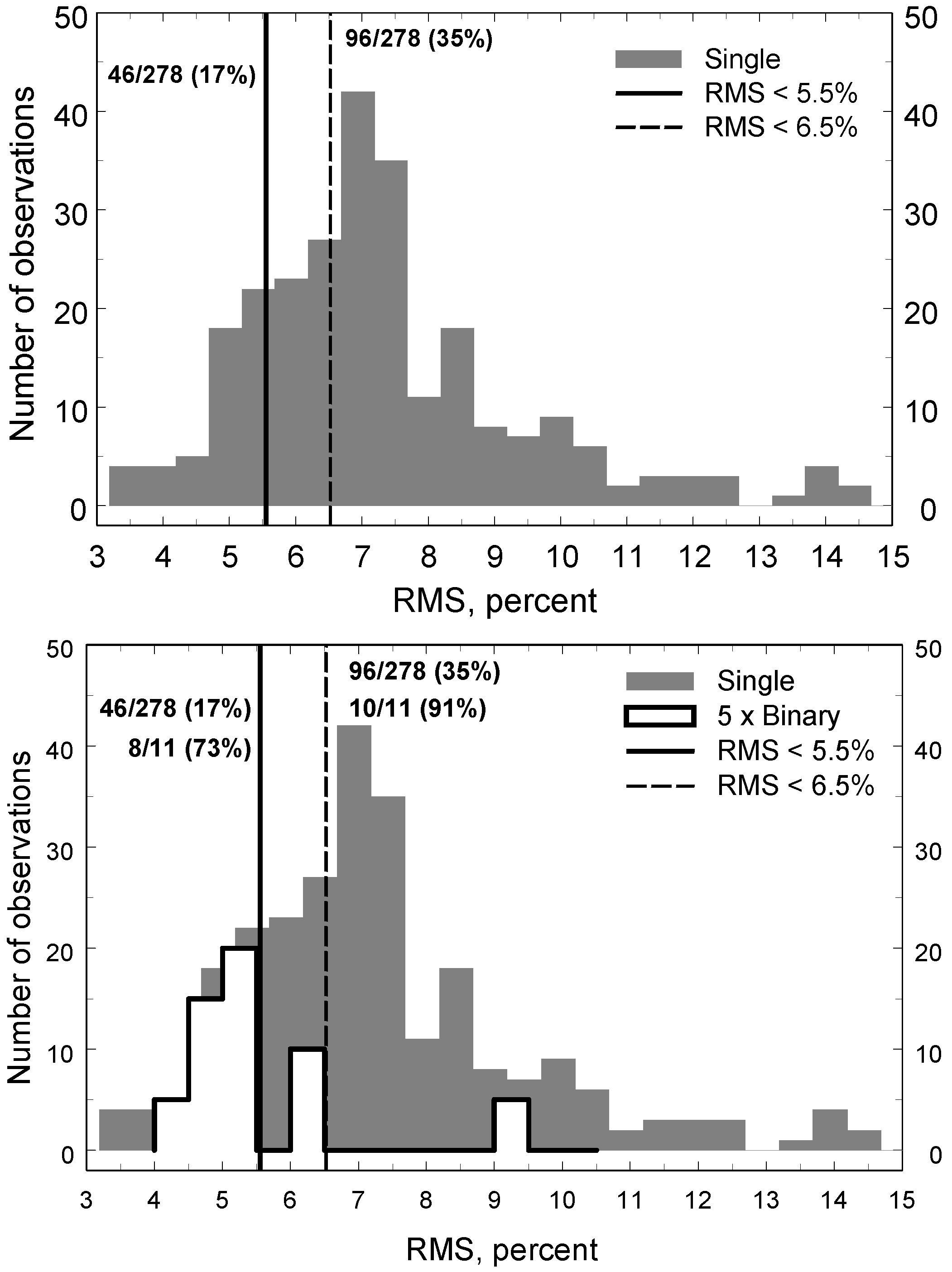
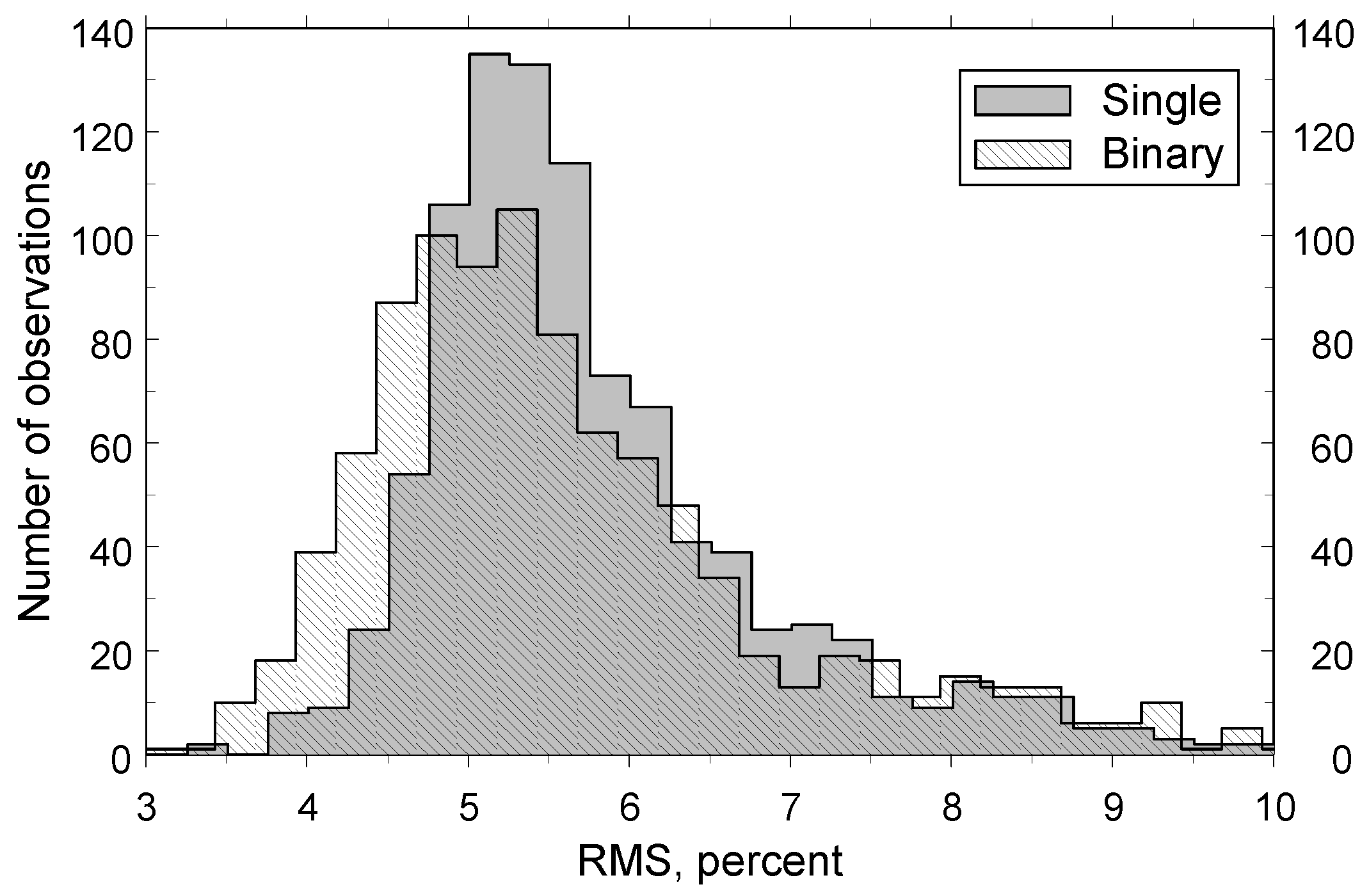
5. Presentation of Results of Comparison Between Synthetic and LAMOST Spectra for Single and Binary Stars
6. Conclusions
- Compilation of a special version of the CKL synthetic spectra library, with wavelengths exactly coinciding with those in the LAMOST spectra. Using such spectra would eliminate procedures of smoothing and interpolation, leading to lower rms deviations between the observed and synthetic spectra and to better sensitivity of the method. However, computation of stellar spectra library is a stand-alone problem.
- Switching to a method based on a comparison of intensities for pairs of spectral lines or intensities for individual lines. The first of these methods is currently the most widely used approach for high-accuracy spectral classification of stars. The second approach is used for spectral classification of stars in the LAMOST project proper. However, the LAMOST survey provides low-resolution stellar spectra, and such methods can also turn out to be not sensitive to stellar binarity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | An estimate exceeding 100% means that binaries are components of triples. |
| 2 | Ref. [51] (http://sb9.astro.ulb.ac.be, accessed on 24 July 2025). |
| 3 | https://sl.voxastro.org/ (accessed on 24 July 2025) |
| 4 | http://archive.stsci.edu/prepds/stisngsl/ (accessed on 24 July 2025). |
| 5 | Both spectra are taken from the LAMOST DR5 site. |
References
- Duchêne, G.; Kraus, A. Stellar Multiplicity. Annu. Rev. Astron. Astrophys. 2013, 51, 269–310. [Google Scholar] [CrossRef]
- Moe, M.; Di Stefano, R. Mind Your Ps and Qs: The Interrelation between Period (P) and Mass-ratio (Q) Distributions of Binary Stars. Astrophys. J. Suppl. Ser. 2017, 230, 15. [Google Scholar] [CrossRef]
- Merle, T. Dancing with the Stars: A Review on Stellar Multiplicity. Bull. Soc. R. Sci. Liege 2024, 93, 170–214. [Google Scholar] [CrossRef]
- Cifuentes, C.; Caballero, J.A.; González-Payo, J.; Amado, P.J.; Béjar, V.J.S.; Burgasser, A.J.; Cortés-Contreras, M.; Lodieu, N.; Montes, D.; Quirrenbach, A.; et al. CARMENES input catalogue of M dwarfs: IX. Multiplicity from close spectroscopic binaries to ultra-wide systems. Astron. Astrophys. 2025, 693, A228. [Google Scholar] [CrossRef]
- Tutukov, A.V.; Yungelson, L.R. Evolutionary Scenario for Close Binary Systems of Low and Moderate Masses. Nauchnye Informatsii 1981, 49, 3. [Google Scholar]
- Kroupa, P.; Tout, C.A.; Gilmore, G. The effects of unresolved binary stars on the determination of the stellar mass function. Mon. Not. RAS 1991, 251, 293–302. [Google Scholar] [CrossRef]
- Kroupa, P. On the variation of the initial mass function. Mon. Not. RAS 2001, 322, 231–246. [Google Scholar] [CrossRef]
- El-Badry, K.; Rix, H.W.; Ting, Y.S.; Weisz, D.R.; Bergemann, M.; Cargile, P.; Conroy, C.; Eilers, A.C. Signatures of unresolved binaries in stellar spectra: Implications for spectral fitting. Mon. Not. RAS 2018, 473, 5043–5049. [Google Scholar] [CrossRef]
- Borodina, O.I.; Seleznev, A.F.; Carraro, G.; Danilov, V.M. Unresolved Binaries and Galactic Clusters’ Mass Estimates. Astrophys. J. 2019, 874, 127. [Google Scholar] [CrossRef]
- Sullivan, K.; Kraus, A.L. Undetected Binary Stars Cause an Observed Mass-dependent Age Gradient in Upper Scorpius. Astrophys. J. 2021, 912, 137. [Google Scholar] [CrossRef]
- Prusti, T. et al. [Gaia Collaboration] The Gaia mission. Astron. Astrophys. 2016, 595, A1. [Google Scholar] [CrossRef]
- Vallenari, A. et al. [Gaia Collaboration] Gaia Data Release 3. Summary of the content and survey properties. Astron. Astrophys. 2023, 674, A1. [Google Scholar] [CrossRef]
- Almeida, A.; Anderson, S.F.; Argudo-Fernández, M.; Badenes, C.; Barger, K.; Barrera-Ballesteros, J.K.; Bender, C.F.; Benitez, E.; Besser, F.; Bird, J.C.; et al. The Eighteenth Data Release of the Sloan Digital Sky Surveys: Targeting and First Spectra from SDSS-V. Astrophys. J. Suppl. Ser. 2023, 267, 44. [Google Scholar] [CrossRef]
- Castro-Ginard, A.; Penoyre, Z.; Casey, A.R.; Brown, A.G.A.; Belokurov, V.; Cantat-Gaudin, T.; Drimmel, R.; Fouesneau, M.; Khanna, S.; Kurbatov, E.P.; et al. Gaia DR3 detectability of unresolved binary systems. arXiv 2024. [Google Scholar] [CrossRef]
- Penoyre, Z.; Belokurov, V.; Evans, N.W. Astrometric identification of nearby binary stars—II. Astrometric binaries in the Gaia Catalogue of Nearby Stars. Mon. Not. RAS 2022, 513, 5270–5289. [Google Scholar] [CrossRef]
- Malofeeva, A.A.; Mikhnevich, V.O.; Carraro, G.; Seleznev, A.F. Unresolved Binaries and Multiples in the Intermediate Mass Range in Open Clusters: Pleiades, Alpha Per, Praesepe, and NGC 1039. Astron. J. 2023, 165, 45. [Google Scholar] [CrossRef]
- Chulkov, D.; Prokhorov, M.; Malkov, O.; Sichevskij, S.; Krussanova, N.; Mironov, A.; Zakharov, A.; Kniazev, A. Detection of unresolved binaries with multicolor photometry. Balt. Astron. 2015, 24, 137–143. [Google Scholar] [CrossRef]
- Wallace, A.L. Photometric determination of main-sequence binaries with Gaia. Mon. Not. RAS 2024, 527, 8718–8726. [Google Scholar] [CrossRef]
- Xiang, M.; Rix, H.W.; Ting, Y.S.; Zari, E.; El-Badry, K.; Yuan, H.B.; Cui, W.Y. Data-driven Spectroscopic Estimates of Absolute Magnitude, Distance, and Binarity: Method and Catalog of 16,002 O- and B-type Stars from LAMOST. Astrophys. J. Suppl. Ser. 2021, 253, 22. [Google Scholar] [CrossRef]
- Kovaleva, D.A.; Malkov, O.Y. On the possible multiplicity of the components of some low-mass systems. Astron. Rep. 1999, 43, 80–88. [Google Scholar]
- Luo, A.L.; Zhao, Y.H.; Zhao, G.; Deng, L.C.; Liu, X.W.; Jing, Y.P.; Wang, G.; Zhang, H.T.; Shi, J.R.; Cui, X.Q.; et al. The first data release (DR1) of the LAMOST regular survey. Res. Astron. Astrophys. 2015, 15, 1095. [Google Scholar] [CrossRef]
- McMillan, P. BDASP Catalogue. 2020. Available online: https://doi.org/10.17876/RAVE/DR.6/008 (accessed on 24 July 2025).
- Buder, S.; Sharma, S.; Kos, J.; Amarsi, A.M.; Nordlander, T.; Lind, K.; Martell, S.L.; Asplund, M.; Bland-Hawthorn, J.; Casey, A.R.; et al. The GALAH+ survey: Third data release. Mon. Not. RAS 2021, 506, 150–201. [Google Scholar] [CrossRef]
- Jönsson, H.; Holtzman, J.A.; Prieto, C.A.; Cunha, K.; García-Hernández, D.A.; Hasselquist, S.; Masseron, T.; Osorio, Y.; Shetrone, M.; Smith, V.; et al. APOGEE Data and Spectral Analysis from SDSS Data Release 16: Seven Years of Observations Including First Results from APOGEE-South. Astron. J. 2020, 160, 120. [Google Scholar] [CrossRef]
- Abdurro’uf; Accetta, K.; Aerts, C.; Silva Aguirre, V.; Ahumada, R.; Ajgaonkar, N.; Filiz Ak, N.; Alam, S.; Allende Prieto, C.; Almeida, A.; et al. The Seventeenth Data Release of the Sloan Digital Sky Surveys: Complete Release of MaNGA, MaStar, and APOGEE-2 Data. Astrophys. J. Suppl. Ser. 2022, 259, 35. [Google Scholar] [CrossRef]
- Gilmore, G.; Randich, S.; Asplund, M.; Binney, J.; Bonifacio, P.; Drew, J.; Feltzing, S.; Ferguson, A.; Jeffries, R.; Micela, G.; et al. The Gaia-ESO Public Spectroscopic Survey. Messenger 2012, 147, 25–31. [Google Scholar]
- Randich, S.; Gilmore, G.; Gaia-ESO Consortium. The Gaia-ESO Large Public Spectroscopic Survey. Messenger 2013, 154, 47–49. [Google Scholar]
- Li, J.; Ting, Y.S.; Rix, H.W.; Green, G.M.; Hogg, D.W.; Ren, J.J.; Müller-Horn, J.; Seeburger, R. Identification of 30,000 White Dwarf-Main Sequence binaries candidates from Gaia DR3 BP/RP(XP) low-resolution spectra. arXiv 2025. [Google Scholar] [CrossRef]
- Seeburger, R.; Rix, H.W.; El-Badry, K.; Xiang, M.; Fouesneau, M. Autonomous disentangling for spectroscopic surveys. Mon. Not. RAS 2024, 530, 1935–1955. [Google Scholar] [CrossRef]
- Birko, D.; Zwitter, T.; Grebel, E.K.; Parker, Q.A.; Kordopatis, G.; Bland-Hawthorn, J.; Freeman, K.; Guiglion, G.; Gibson, B.K.; Navarro, J.; et al. Single-lined Spectroscopic Binary Star Candidates from a Combination of the RAVE and Gaia DR2 Surveys. Astron. J. 2019, 158, 155. [Google Scholar] [CrossRef]
- Price-Whelan, A.M.; Hogg, D.W.; Rix, H.W.; Beaton, R.L.; Lewis, H.M.; Nidever, D.L.; Almeida, A.; Badenes, C.; Barba, R.; Beers, T.C.; et al. Close Binary Companions to APOGEE DR16 Stars: 20,000 Binary-star Systems Across the Color-Magnitude Diagram. Astrophys. J. 2020, 895, 2. [Google Scholar] [CrossRef]
- Traven, G.; Feltzing, S.; Merle, T.; Van der Swaelmen, M.; Čotar, K.; Church, R.; Zwitter, T.; Ting, Y.S.; Sahlholdt, C.; Asplund, M.; et al. The GALAH survey: Multiple stars and our Galaxy. I. A comprehensive method for deriving properties of FGK binary stars. Astron. Astrophys. 2020, 638, A145. [Google Scholar] [CrossRef]
- Merle, T.; Van der Swaelmen, M.; Van Eck, S.; Jorissen, A.; Jackson, R.J.; Traven, G.; Zwitter, T.; Pourbaix, D.; Klutsch, A.; Sacco, G.; et al. The Gaia-ESO Survey: Detection and characterisation of single-line spectroscopic binaries. Astron. Astrophys. 2020, 635, A155. [Google Scholar] [CrossRef]
- Cui, X.Q.; Zhao, Y.H.; Chu, Y.Q.; Li, G.P.; Li, Q.; Zhang, L.P.; Su, H.J.; Yao, Z.Q.; Wang, Y.N.; Xing, X.Z.; et al. The Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST). Res. Astron. Astrophys. 2012, 12, 1197–1242. [Google Scholar] [CrossRef]
- Zhao, G.; Zhao, Y.H.; Chu, Y.Q.; Jing, Y.P.; Deng, L.C. LAMOST spectral survey—An overview. Res. Astron. Astrophys. 2012, 12, 723–734. [Google Scholar] [CrossRef]
- Li, C.q.; Shi, J.r.; Yan, H.l.; Fu, J.N.; Li, J.d.; Hou, Y.H. Double- and Triple-line Spectroscopic Candidates in the LAMOST Medium-Resolution Spectroscopic Survey. Astrophys. J. Suppl. Ser. 2021, 256, 31. [Google Scholar] [CrossRef]
- Guo, Y.; Li, J.; Xiong, J.; Li, J.; Wang, L.; Xiong, H.; Luo, F.; Hou, Y.; Liu, C.; Han, Z.; et al. The Binarity of Early-type Stars from LAMOST medium-resolution Spectroscopic Survey. Res. Astron. Astrophys. 2022, 22, 025009. [Google Scholar] [CrossRef]
- Qian, S.B.; Shi, X.D.; Zhu, L.Y.; Li, L.J.; Zhang, J.; Zhao, E.G.; Han, Z.T.; Zhou, X.; Fang, X.H.; Liao, W.P. More than two hundred and fifty thousand spectroscopic binary or variable star candidates discovered by LAMOST. Res. Astron. Astrophys. 2019, 19, 064. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, F.; Wang, X.; Fu, Y.; Yuan, Y. New SB1s with Spectroscopic Orbits from LAMOST-LRS. Astrophys. J. Suppl. Ser. 2023, 269, 41. [Google Scholar] [CrossRef]
- Liu, C.; Bailer-Jones, C.A.L.; Sordo, R.; Vallenari, A.; Borrachero, R.; Luri, X.; Sartoretti, P. The expected performance of stellar parametrization with Gaia spectrophotometry. Mon. Not. RAS 2012, 426, 2463–2482. [Google Scholar] [CrossRef]
- Ting, Y.S.; Conroy, C.; Rix, H.W.; Cargile, P. Prospects for Measuring Abundances of >20 Elements with Low-resolution Stellar Spectra. Astrophys. J. 2017, 843, 32. [Google Scholar] [CrossRef]
- Li, J.; Wong, K.W.K.; Hogg, D.W.; Rix, H.W.; Chandra, V. AspGap: Augmented Stellar Parameters and Abundances for 37 Million Red Giant Branch Stars from Gaia XP Low-resolution Spectra. Astrophys. J. Suppl. Ser. 2024, 272, 2. [Google Scholar] [CrossRef]
- Luo, A.L.; Zhao, Y.H.; Zhao, G.; Deng, L.-C.; Liu, X.-W.; Jing, Y.-P.; Wang, G.; Zhang, H.-T.; Shi, J.-R.; Cui, X.-Q.; et al. VizieR Online Data Catalog: LAMOST DR5 catalogs (Luo+, 2019). VizieR Online Data Catalog 2019, V/164. [Google Scholar]
- Bai, Z.R.; Zhang, H.T.; Yuan, H.L.; Fan, D.W.; He, B.L.; Lei, Y.J.; Dong, Y.Q.; Yu, S.C.; Zhao, Y.H.; Zhang, Y.; et al. The first data release of LAMOST low-resolution single-epoch spectra. Res. Astron. Astrophys. 2021, 21, 249. [Google Scholar] [CrossRef]
- Pavlovski, K.; Hensberge, H. Reconstruction and Analysis of Component Spectra of Binary and Multiple Stars. In Proceedings of the Binaries—Key to Comprehension of the Universe, Brno, Czech Republic, 8–12 June 2009; Prša, A., Zejda, M., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2010; Volume 435, p. 207. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Tokovinin, A.; Niemczura, E.; Pawłaszek, R.; Yanagisawa, K.; Brahm, R.; Espinoza, N.; Ukita, N.; Kambe, E.; Ratajczak, M.; et al. Orbital and physical parameters of eclipsing binaries from the All-Sky Automated Survey catalogue. X. Three high-contrast systems with secondaries detected with IR spectroscopy. Astron. Astrophys. 2019, 622, A114. [Google Scholar] [CrossRef]
- Furlan, E.; Howell, S.B. Unresolved Binary Exoplanet Host Stars Fit as Single Stars: Effects on the Stellar Parameters. Astrophys. J. 2020, 898, 47. [Google Scholar] [CrossRef]
- Cox, A.N. Allen’s Astrophysical Quantities; Springer: New York, NY, USA, 2000. [Google Scholar]
- Castelli, F.; Kurucz, R.L. New Grids of ATLAS9 Model Atmospheres. In Modelling of Stellar Atmospheres; Piskunov, N., Weiss, W.W., Gray, D.F., Eds.; Uppsala University: Uppsala, Sweden, 2003; Volume 210, p. A20. [Google Scholar] [CrossRef]
- Du, B.; Luo, A.L.; Kong, X.; Zhang, J.N.; Guo, Y.X.; Cook, N.J.; Hou, W.; Yang, H.F.; Li, Y.B.; Song, Y.H.; et al. LAMOST Spectrograph Response Curves: Stability and Application to Flux Calibration. Astrophys. J. Suppl. Ser. 2016, 227, 27. [Google Scholar] [CrossRef]
- Pourbaix, D.; Tokovinin, A.A.; Batten, A.H.; Fekel, F.C.; Hartkopf, W.I.; Levato, H.; Morrell, N.I.; Torres, G.; Udry, S. SB9: The ninth catalogue of spectroscopic binary orbits. Astron. Astrophys. 2004, 424, 727–732. [Google Scholar] [CrossRef]
- Allen, L.E.; Strom, K.M. Moderate-Resolution Spectral Standards From lambda5600 to lambda9000 angstrom. Astron. J. 1995, 109, 1379. [Google Scholar] [CrossRef]
- Prugniel, P.; Soubiran, C.; Koleva, M.; Le Borgne, D. New release of the ELODIE library: Version 3.1. arXiv 2007. [Google Scholar] [CrossRef]
- Valdes, F.; Gupta, R.; Rose, J.A.; Singh, H.P.; Bell, D.J. The Indo-US Library of Coudé Feed Stellar Spectra. Astrophys. J. Suppl. Ser. 2004, 152, 251–259. [Google Scholar] [CrossRef]
- Falcón-Barroso, J.; Sánchez-Blázquez, P.; Vazdekis, A.; Ricciardelli, E.; Cardiel, N.; Cenarro, A.J.; Gorgas, J.; Peletier, R.F. An updated MILES stellar library and stellar population models. Astron. Astrophys. 2011, 532, A95. [Google Scholar] [CrossRef]
- Heap, S.R.; Lindler, D.J. Hubble’s Next Generation Spectral Library (NGSL). In From Stars to Galaxies: Building the Pieces to Build Up the Universe; Vallenari, A., Tantalo, R., Portinari, L., Moretti, A., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2007; Volume 374, p. 409. [Google Scholar]
- Kornilov, V.; Mironov, A.; Zakharov, A. The WBVR Photometry of Bright Northern Stars. Balt. Astron. 1996, 5, 379–390. [Google Scholar] [CrossRef]
- Wielen, R.; Schwan, H.; Dettbarn, C.; Lenhardt, H.; Jahreiß, H.; Jährling, R. Sixth Catalogue of Fundamental Stars (FK6). Part I. Basic fundamental stars with direct solutions. Veroeffentlichungen Astron. Rechen-Instituts Heidelb. 1999, 35, 1. [Google Scholar]
- Fouesneau, M.; Frémat, Y.; Andrae, R.; Korn, A.J.; Soubiran, C.; Kordopatis, G.; Vallenari, A.; Heiter, U.; Creevey, O.L.; Sarro, L.M.; et al. Gaia Data Release 3. Apsis. II. Stellar parameters. Astron. Astrophys. 2023, 674, A28. [Google Scholar] [CrossRef]
- Lindegren, L.; Klioner, S.A.; Hernández, J.; Bombrun, A.; Ramos-Lerate, M.; Steidelmüller, H.; Bastian, U.; Biermann, M.; de Torres, A.; Gerlach, E.; et al. Gaia Early Data Release 3. The astrometric solution. Astron. Astrophys. 2021, 649, A2. [Google Scholar] [CrossRef]
- Riello, M.; De Angeli, F.; Evans, D.W.; Montegriffo, P.; Carrasco, J.M.; Busso, G.; Palaversa, L.; Burgess, P.W.; Diener, C.; Davidson, M.; et al. Gaia Early Data Release 3. Photometric content and validation. Astron. Astrophys. 2021, 649, A3. [Google Scholar] [CrossRef]
- Belokurov, V.; Penoyre, Z.; Oh, S.; Iorio, G.; Hodgkin, S.; Evans, N.W.; Everall, A.; Koposov, S.E.; Tout, C.A.; Izzard, R.; et al. Unresolved stellar companions with Gaia DR2 astrometry. Mon. Not. RAS 2020, 496, 1922–1940. [Google Scholar] [CrossRef]
- Gaia Collaboration; Arenou, F.; Babusiaux, C.; Barstow, M.A.; Faigler, S.; Jorissen, A.; Kervella, P.; Mazeh, T.; Mowlavi, N.; Panuzzo, P.; et al. Gaia Data Release 3. Stellar multiplicity, a teaser for the hidden treasure. Astron. Astrophys. 2023, 674, A34. [Google Scholar] [CrossRef]
- Koleva, M.; Prugniel, P.; Bouchard, A.; Wu, Y. ULySS: A full spectrum fitting package. Astron. Astrophys. 2009, 501, 1269–1279. [Google Scholar] [CrossRef]
- Sharma, K.; Prugniel, P.; Singh, H.P.; Koleva, M. Analysis of stellar spectra using ULySS. In Astronomical Society of India Conference Series; Prugniel, P., Singh, H.P., Eds.; Astronomical Society of India: Hyderabad, India, 2012; Volume 6, p. 257. [Google Scholar]
- Hebb, L.; Cargile, P. SME@XSEDE: An automated spectral synthesis tool for stellar characterization. In American Astronomical Society Meeting Abstracts #225; American Astronomical Society: Washington, DC, USA, 2015; Volume 225, p. 138.13. [Google Scholar]
- Rosario Franco, M.; Cargile, P.; Hebb, L.; Johnson, J.A. vis.SME—Building a Visualization Tool to Analyze and Share Spectral Synthesis Stellar Characterization. In American Astronomical Society Meeting Abstracts #223; American Astronomical Society: Washington, DC, USA, 2014; Volume 223, p. 347.36. [Google Scholar]
- Piskunov, N. Deriving stellar parameters with the SME software package. In Proceedings of the Second BRITE-Constellation Science Conference: Small Satellites—Big Science, Innsbruck, Austria, 22–26 August 2016; Zwintz, K., Poretti, E., Eds.; Polish Astronomical Society: Warsaw, Poland, 2017; Volume 5, pp. 209–213. [Google Scholar]
- Allende-Prieto, C.; Apogee Team. FERRE: A Code for Spectroscopic Analysis. In American Astronomical Society Meeting Abstracts #225; American Astronomical Society: Washington, DC, USA, 2015; Volume 225, p. 422.07. [Google Scholar]
- Ting, Y.S.; Conroy, C.; Rix, H.W.; Cargile, P. The Payne: Self-consistent ab initio Fitting of Stellar Spectra. Astrophys. J. 2019, 879, 69. [Google Scholar] [CrossRef]
- Koposov, S.E. RVSpecFit: Radial velocity and stellar atmospheric parameter fitting. In Astrophysics Source Code Library, Record ascl:1907.013; 2019; Available online: https://ascl.net/1907.013 (accessed on 24 July 2025).
- Cardelli, J.A.; Clayton, G.C.; Mathis, J.S. The Relationship between Infrared, Optical, and Ultraviolet Extinction. Astrophys. J. 1989, 345, 245. [Google Scholar] [CrossRef]
- Gaia Collaboration; Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Evans, D.W.; Eyer, L.; et al. Gaia Early Data Release 3. Summary of the contents and survey properties. Astron. Astrophys. 2021, 649, A1. [Google Scholar] [CrossRef]
- Lallement, R.; Vergely, J.L.; Valette, B.; Puspitarini, L.; Eyer, L.; Casagrande, L. 3D maps of the local ISM from inversion of individual color excess measurements. Astron. Astrophys. 2014, 561, A91. [Google Scholar] [CrossRef]
- Capitanio, L.; Lallement, R.; Vergely, J.L.; Elyajouri, M.; Monreal-Ibero, A. Three-dimensional mapping of the local interstellar medium with composite data. Astron. Astrophys. 2017, 606, A65. [Google Scholar] [CrossRef]
- Lallement, R.; Capitanio, L.; Ruiz-Dern, L.; Danielski, C.; Babusiaux, C.; Vergely, L.; Elyajouri, M.; Arenou, F.; Leclerc, N. Three-dimensional maps of interstellar dust in the Local Arm: Using Gaia, 2MASS, and APOGEE-DR14. Astron. Astrophys. 2018, 616, A132. [Google Scholar] [CrossRef]
- Pogson, N. Magnitudes of Thirty-six of the Minor Planets for the first day of each month of the year 1857. Mon. Not. RAS 1856, 17, 12–15. [Google Scholar] [CrossRef]
- Taylor, M.B. TOPCAT & STIL: Starlink Table/VOTable Processing Software. In Astronomical Data Analysis Software and Systems XIV; Astronomical Society of the Pacific Conference Series; Shopbell, P., Britton, M., Ebert, R., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2005; Volume 347, p. 29. [Google Scholar]
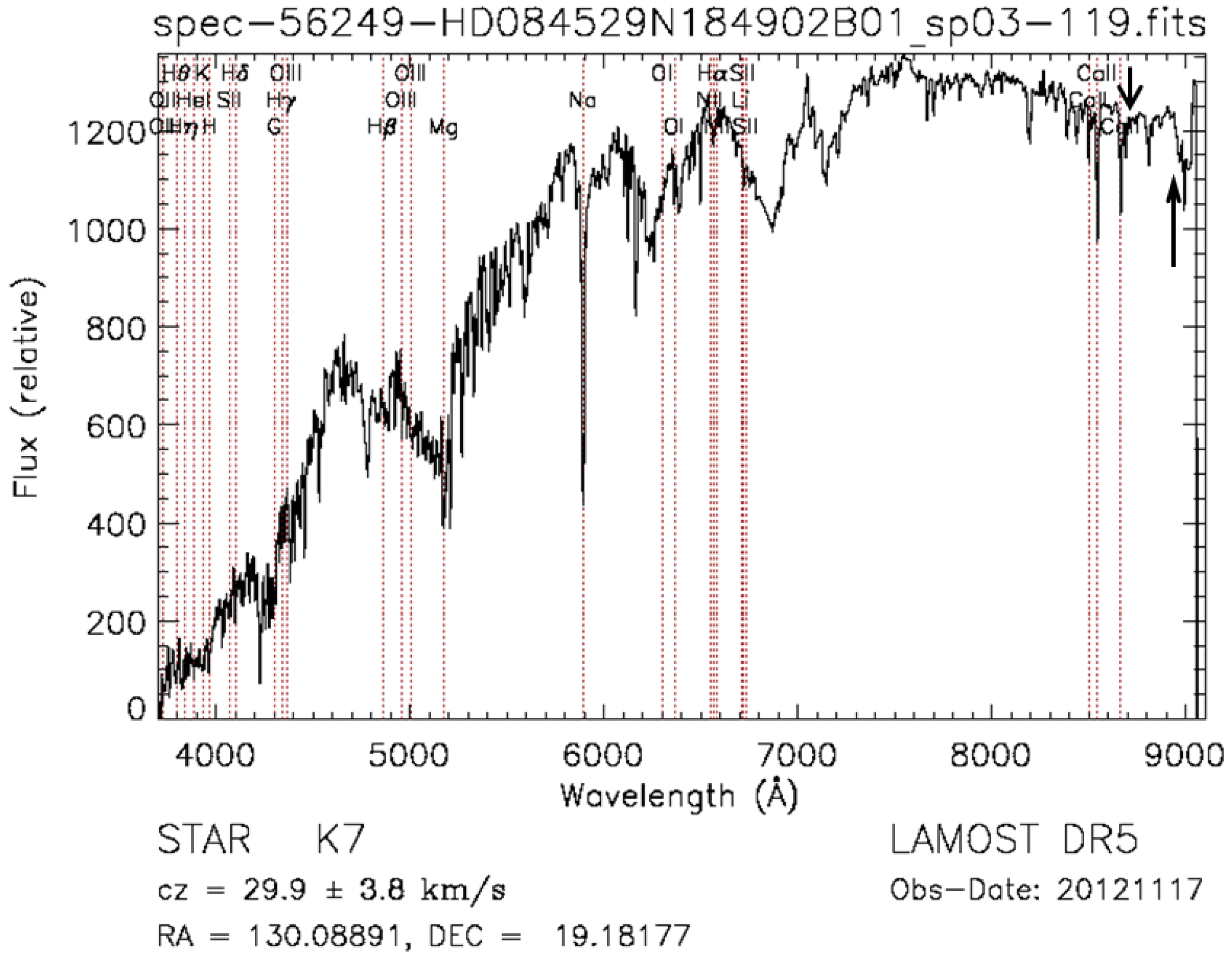
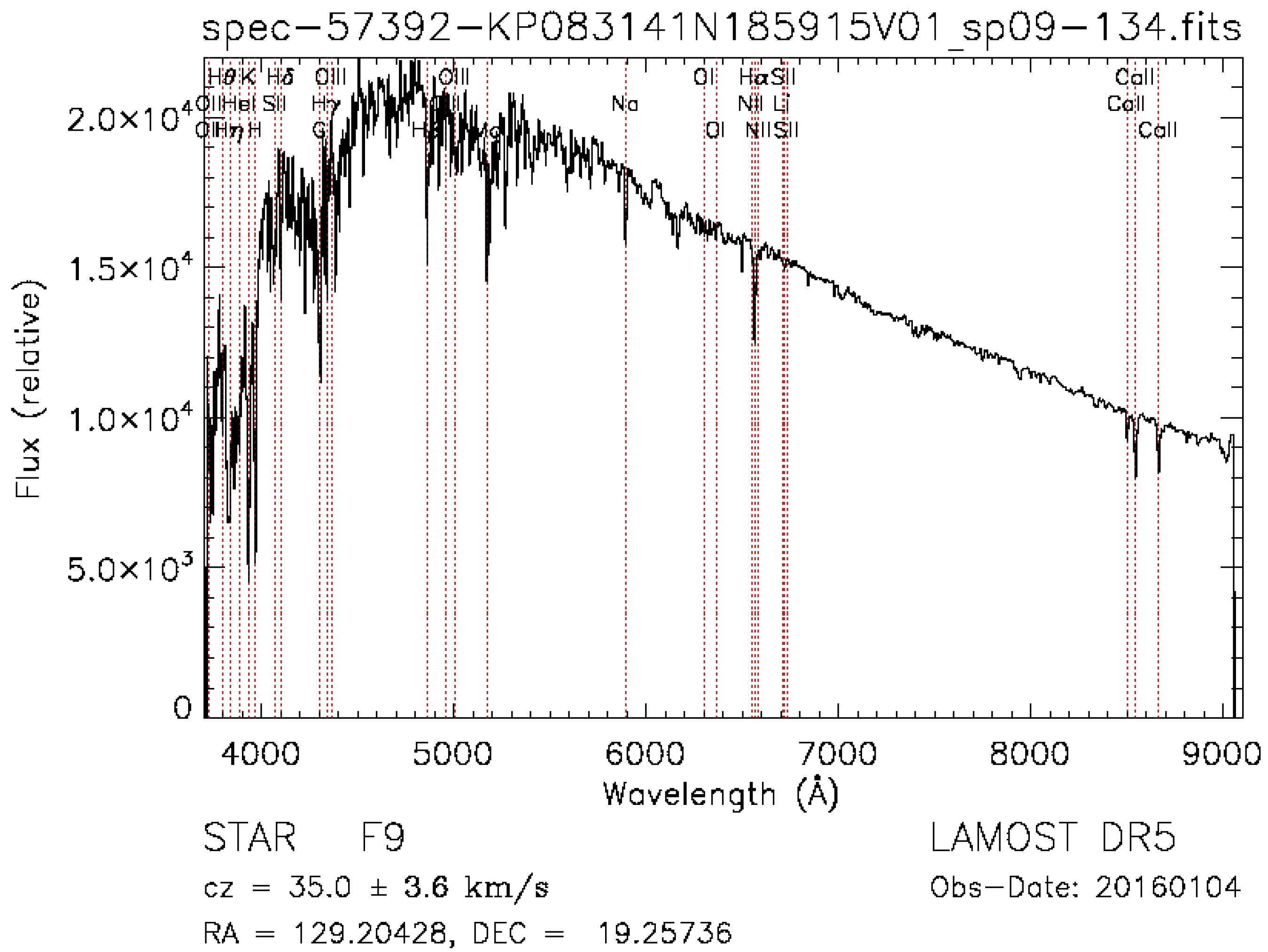
| Obs_ID | Designation | Sp. | ||
|---|---|---|---|---|
| 404058 | J004541.11 + 405100.1 | 11.421 | 40.850 | A1V |
| 113226 | J221422.57 + 005400.8 | 333.594 | 0.900 | M6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prokhorov, M.; Tan, K.; Samus, N.; Luo, A.; Kovaleva, D.; Zhao, J.; Liu, Y.; Kaygorodov, P.; Malkov, O.; Song, Y.; et al. Looking for Signs of Unresolved Binarity in the Continuum of LAMOST Stellar Spectra. Galaxies 2025, 13, 83. https://doi.org/10.3390/galaxies13040083
Prokhorov M, Tan K, Samus N, Luo A, Kovaleva D, Zhao J, Liu Y, Kaygorodov P, Malkov O, Song Y, et al. Looking for Signs of Unresolved Binarity in the Continuum of LAMOST Stellar Spectra. Galaxies. 2025; 13(4):83. https://doi.org/10.3390/galaxies13040083
Chicago/Turabian StyleProkhorov, Mikhail, Kefeng Tan, Nikolay Samus, Ali Luo, Dana Kovaleva, Jingkun Zhao, Yujuan Liu, Pavel Kaygorodov, Oleg Malkov, Yihan Song, and et al. 2025. "Looking for Signs of Unresolved Binarity in the Continuum of LAMOST Stellar Spectra" Galaxies 13, no. 4: 83. https://doi.org/10.3390/galaxies13040083
APA StyleProkhorov, M., Tan, K., Samus, N., Luo, A., Kovaleva, D., Zhao, J., Liu, Y., Kaygorodov, P., Malkov, O., Song, Y., Sichevskij, S., Yungelson, L., & Zhao, G. (2025). Looking for Signs of Unresolved Binarity in the Continuum of LAMOST Stellar Spectra. Galaxies, 13(4), 83. https://doi.org/10.3390/galaxies13040083










