Abstract
In this work, we test the ability of an exact solution, found in the framework of a nonlinear extension of the Israel–Stewart theory, to fit the supernovae Ia, gravitational lensing, and black hole shadow data. This exact solution is a generalization of one previously found for a dissipative unified dark matter model in the context of the near-equilibrium description of dissipative processes, where we do not have the full regime of the nonlinear picture. This generalized solution is restricted to the case where a positive entropy production is guaranteed and is tested under the condition that ensures its causality, local existence, and uniqueness. From the observational constraints, we found that this generalized solution is a good candidate in the description of the observational late-time data used in this work, with best-fit values of , , , , and , at a of confidence level. We show that the nonlinear regime of the Israel–Stewart theory consistently describes the recent accelerated expansion of the universe without the inclusion of some kind of dark energy component and also provides a more realistic description of the fluids that make up the late universe.
1. Introduction
The current picture of the universe is inconceivable without a dark component, which leads to an accelerated cosmic expansion in the framework of general relativity, and it is usually named dark energy (DE). A first attempt to explain this phenomenon motivated the introduction of the cosmological constant in Einstein’s field equations. This simple modification is well known as CDM or the standard cosmological model (where CDM stands for cold dark matter). However, despite its great success in fitting many of the sets of observational data, it does not provide a compelling answer about the actual nature of the DE and it lacks the physical consistency to describe some observational facts: the uniformity of the temperature for the photons coming from the cosmic microwave background (CMB) and the flattening behavior of the universe (in fact, some tensions regarding the actual value of the curvature parameter are well known in modern cosmology; see, for instance, Refs. [1,2]), which are the horizon and flatness problems. A viable explanation for these issues was granted by the inflationary theory [3], a period of over-accelerated expansion after the Big Bang. Another relevant problem is the value of the cosmological constant . In the presence of a cosmological constant, the empty space has an energy density of the form, . Observationally, this vacuum energy density is constrained to be smaller than GeV, and from the elementary theories of particles, it was found that this value must be around GeV [4], representing a discrepancy of 118 orders of magnitude between theory and observations. Furthermore, from some other cosmological results, a very tiny (non-zero) and extremely fine-tuned value for can be found, [5].
On the other hand, assuming that observations are correct, the small value obtained for the density leads to confusing results. From the definition of the vacuum density given above, we can see that such density must remain constant throughout the cosmic evolution and, according to the CDM description, the energy density associated with the matter sector typically has a decreasing behavior, , where a is the scale factor. Therefore, one could expect a difference of several orders of magnitude between both densities along the cosmic expansion. However, the quotient is almost equal to one at present time, i.e., both components aggregate similar amounts to the total energy budget of the universe. This coincidence is not well understood, and it is known as the cosmological coincidence problem [6]. Another well-known problem is the tension, which presents a discrepancy of between the current value of the Hubble parameter inferred from Planck CMB (assuming the CDM cosmology) and the obtained from local (model-independent) measurements of Cepheid [7]. This tension is also supported by the Lenses in COSMOGRAIL’s Wellspring (H0LiCOW) collaboration, with a discrepancy of concerning the value inferred from the Planck CMB [8]. These and some other problems indicate that new alternatives to describe the dark component of the universe are necessary. One possibility is given by dynamical DE models, as stated in Ref. [9], and an interesting proposal can be found in [10]. Within Einstein’s framework, this means that this component can be thought of as a generic dynamical fluid with a given equation of state (EoS) that relates the pressure (p) with the energy density of the fluid. Recent results show that for a barotropic EoS , where is known as a barotropic index, this component could have a parameter situated between the quintessence () and phantom () regimes [11].
Going beyond the standard cosmological model to describe DE can be a difficult task, but an interesting approach to this problem is given by the inclusion of causal dissipative effects (bulk viscosity) in the fluid description [12,13,14,15]. Dissipative processes can characterize important stages of cosmic evolution: reheating of the universe, the decoupling of neutrinos from the cosmic plasma, and nucleosynthesis. Furthermore, viscosity can also be present in several astrophysical mechanisms, such as, for example, the collapse of radiating stars to a neutron star or black hole and in the accretion of matter around neutron stars or black holes [16]. A possible origin for bulk viscosity is attributed to the existence of mixtures. In the single fluid description, the universe as a whole can be characterized by the particle number density, ; therefore the simple assumption of different cooling rates in the expanding mixture can lead to a non-vanishing viscous pressure [17]. As an effect of bulk viscosity, the kinetic energy of particles is converted into heat; thus, a reduction in the effective pressure of the fluid is expected, and the condition for the Hubble parameter is supported by [16], where is the bulk viscous pressure. An interesting alternative to explain the origin of bulk viscosity was explored in [18,19], where it was shown that the decay of dark matter (DM) into relativistic particles naturally allows the emergence of dissipative effects in the cosmic fluid. A scheme such as the aforementioned could help to understand more clearly the role of bulk viscosity in cosmic expansion. Recent results show that a decaying scenario for DM increases the expansion rate relative to CDM, and such behavior provides an alleviation of the and tensions [20]. In the standard description, a cosmological fluid has a constant temperature and cannot generate entropy or frictional heating. Therefore, the cosmological constant as a source of DE has no sense at a thermodynamical level [21]. Also, within the standard description, DE is not allowed to interact with other components of the universe. However, a more realistic (and consistent) picture of the universe should not forbid such interactions [22]. Several works demonstrate that under the description of thermodynamics for reversible processes, dissipative effects play a relevant role during late times of cosmic evolution and, even more, are capable of allowing a phantom cosmology under some assumptions [23,24,25,26,27]. Beyond the bounds of reversible processes, the dissipative effects can be used to solve some problems at the thermodynamic level of the phantom regime, for instance, the simultaneous positivity of entropy and temperature [28].
An interesting work on viscous cosmology can be found in Ref. [29], where the authors show that when dissipative effects are coupled to the gravitational sector, the causal structure of the theory can be maintained without invoking the near-equilibrium condition or a specific EoS; this is also the first work that establishes the initial-value problem in the context of viscous fluids. This formulation represents an important ingredient to perform numerical simulations. This last result could provide a way to assert or discard the findings of Ref. [30], which claimed that bulk viscosity could contribute significantly to the emissions of gravitational waves in neutron star mergers. Some other results can be found in Refs. [31,32], where the role of bulk viscosity is studied in other contexts such as the radial oscillation of relativistic stars and the cosmological implications for universes filled with Quark–Gluon plasma. Recent studies show that bulk viscous cosmologies are not ruled out by the observational data at all. In fact, in Ref. [33], the bulk viscosity effects were tested with the combination of data coming from CMB, type Ia supernovae (SNe Ia), and observational Hubble parameter data (OHD). This complete study shows that the parameter that characterizes the viscosity must be non-zero, and, in addition, the results obtained seem to relieve the current tension. Somehow, this seems to be consistent with the results of Ref. [34], where it was proposed that the tension might be resolved in the context of a new theory and consists in the annexation of an extra form of DE. In the interesting compendium [35], bulk viscous effects are explored as a viable alternative to relieve the tension (see also Ref. [36]).
Our aim in this paper is to study the ability to fit the observational SNe Ia, gravitational lensing, and black hole shadows (BHS) data using an exact solution found in the nonlinear regime of the Israel–Stewart theory in a flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric within the framework of the general relativity. This solution represents a generalization of one previously found in the context of the linear regime for a unified model of dissipative DM [37], a solution that goes beyond the CDM model based on the modification of the energy–momentum tensor for perfect fluids, without modifying general relativity. Since no other fluid was included to obtain this solution, it is suitable only to describe late-time evolution. Furthermore, according to [38], the accelerated expansion in the linear solution can be described within a range of the parameters of the model for a pressureless DM fluid, which is compatible with OHD and SNe Ia data. The main motivation to consider the nonlinear extension of the Israel–Stewart theory comes from the fact that the aforementioned exact solution represents an accelerated universe, which means that the near equilibrium condition is violated, i.e., the viscous stress denoted by is greater than the equilibrium pressure p of the dissipative DM fluid. This violation holds whenever the accelerated expansion is due only to the negative pressure of the viscous fluid [39]. Nevertheless, by relaxing the near-equilibrium condition, it was found that a nonlinear extension of the Israel–Stewart model ensures a bounded value for , as well as the fulfillment of the second law under the upper bound on [40]. Therefore, this approach is more adequate to describe an accelerated cosmic evolution without the inclusion of some DE component. In this description, high values in the nonadiabatic contribution to the speed of sound can be allowed. On the other hand, in this work, we focus on the positive entropy production case within the nonlinear extension. This thermodynamic restriction leads to a simplified version of the full theory. Therefore, the consideration of the full theory could reveal some other different aspects from those obtained here.
This work is organized as follows: In Section 2, we provide a brief description of the Israel–Stewart model and discuss the passage from this scheme to the nonlinear regime of dissipative cosmology in Section 2. The exact solutions emerging from both scenarios are discussed. Section 3 is devoted to briefly explaining the procedure for the observational constraints, whereas in Section 3.1, Section 3.2 and Section 3.3, we describe the construction of the merit function for the SNe Ia, gravitational lensing, and BHS data, respectively. In Section 3.4 we present the prior used in the constraint and the implications of the causality, local existence, and uniqueness condition of the Israel–Stewart theory in the full nonlinear regime. In Section 4, we present the results obtained for the observational analysis of the nonlinear solution. Finally, in Section 5, we give some final comments and remarks. In this work, we will consider units, except in the Section 3.
2. Preliminaries of the Israel–Stewart Theory
In general relativity, within the context of the Israel–Stewart framework for a flat FLRW metric without a cosmological constant, the energy density of the viscous fluid obeys the continuity equation , where we have considered a barotropic EoS of the form . On the other hand, the energy density of the viscous fluid can be written in terms of the Hubble parameter through the Friedmann equation . Also note that if we consider the acceleration equation , then we can obtain the explicit form of the bulk viscous pressure as
Furthermore, in the full Israel–Stewart theory, the bulk viscous pressure obeys the equation [13]
where, in the limit , we have the non-causal Eckart s theory [41]. This latter case is not considered in this work, and we will define later in this section. Therefore, the Hubble parameter for a universe dominated only by a dissipative fluid obeys the following transport equation [26,42]
where the dot denotes derivatives with respect to the cosmic time. Some remarks are in order: is a constant parameter that accounts for the causality of the model, and the bulk viscosity has been chosen proportional to the energy density of the dissipative fluid of the form , where is a positive constant and s is an arbitrary real parameter. An expanding evolution can take place in a scenario for a universe with viscous DM and a cosmological constant; see, for instance, Ref. [43]; de Sitter solutions are allowed by such model for some specific values of the parameter s, including . Although the above election for the bulk viscosity is widely used in the literature, it is still arbitrary. The election also has the important property of simplifying Equation (3) to integrate it, in which we define
where T is the barotropic temperature, which is generally written as , by means of the Gibbs integrability condition and is the value of the temperature when . Therefore, the chosen value for the parameter s represents interesting physical scenarios; see, for instance, Refs. [25,26,42], where some aspects of the observed universe such as phantom regime and/or accelerated cosmic expansion were studied in the framework of viscous cosmology.
It is important to mention that, from the causality condition, we have the restriction , which can be obtained from the definition of the linear relaxation time [16]
where is the non-adiabatic contribution to the speed of sound v (or speed of bulk viscous perturbations). In this sense, the causality condition reads , where is the adiabatic contribution. Therefore, to fulfill the causality condition, we must have , where the parameter was introduced and must satisfy the condition . The previous equation for the relaxation time corrects the relation , which is considered for simplicity in several works.
Taking in Equation (3), this expression becomes
where, for simplicity in the notation, we have defined the constant coefficients
It is worth mentioning that if we consider the limit case in the differential equation written in (6), we obtain the non-relativistic or DM case () explored in Ref. [44].
Exact Solution and Its Extension to a Nonlinear Regime
In the following section, we will provide some generalities of the exact solution found in Ref. [37]. We refer the reader to the aforementioned reference to see the technical details. In this solution, the DM is the only fluid component in the universe’s energy density budget. It also experiences a dissipative process in the form of bulk viscosity during its cosmic evolution. Then, by introducing the change of variable in Equation (6), where is the value for the scale factor at which the Hubble parameter becomes , one obtains
Therefore, solving the previous equation, considering that the scale factor is related with to redshift z through the expression , we can obtain the Hubble parameter as a function of z as follows:
where
The form of the constants defined previously come from the initial conditions for the Hubble parameter and its derivative, and , respectively, where represents the current time, prime denotes derivative with respect to z, and is the deceleration parameter at the current time (the redshift (or scale factor) derivative of the Hubble parameter can be related to the deceleration parameter through the relation ). In this description, the value (CDM) can be considered as the limit case to perform a comparison with the CDM model. In Ref. [38], the solution (9) was tested with the use of the joint SNe Ia+OHD data.
The Israel–Stewart model is based on the assumption that only small deviations from equilibrium are permitted. This implies that we must have a rapid adjustment to the cooling caused by the cosmic expansion, i.e., , which can be seen from Equation (5). However, by using SNe Ia data, some drawbacks in the model were found, according to the analysis performed in [38]. To have late-time cosmic expansion, the best-fit parameters indicate that together with . Therefore, the rapid adjustment condition is lost. Nevertheless, to explore dissipative processes beyond the near-equilibrium condition mentioned before, a nonlinear extension of the Israel–Stewart model was introduced in Ref. [40], in which large deviations from equilibrium are allowed. In this case, the transport equation for the viscous pressure given in (2) transforms into
where characterizes the time scale for the nonlinear effects. The most simple assumption for this time scale is given by . Then, for , we recover the linear Israel–Stewart theory, ensuring the causality of the model.
Using the transport Equation (11), together with an FLRW metric and repeating the procedure, as carried out previously for the linear Israel–Stewart theory, we arrive at the following, more complicated, second-order differential equation for the Hubble parameter [25,40]:
which describes the behavior of the model in the nonlinear regime of Israel–Stewart’s theory for an arbitrary s, in an analogous way to Equation (3) for the linear regime. On the other hand, by considering the special case , Ref. [45] found that for models with barotropic temperature, the term appearing in the differential Equation (12) must be bounded together with to have a positive entropy production. Under these assumptions, the resulting second-order differential equation for H at the first order in takes the same structure as Equation (6), but, in this case, the constant coefficients , and are redefined as follows:
Therefore, the solution for the Hubble parameter in this nonlinear regime will have the same mathematical structure as the solution given in (9) for the linear regime but will describe dissipative processes far from equilibrium. Also note that within the nonlinear regime, the case leads to , which maintains the structure of the differential Equation (8). Then, this limit case can be considered in the context of the solution discussed above. Therefore, in terms of the redshift, the Hubble parameter for the nonlinear regime can be penned as follows:
with
Note that in the previous expressions, the value still represents the model in the linear regime of the Israel–Stewart’s theory, since, for such a case, we have , , , and .
3. Observational Constraints
In this section, we shall constrain the free parameters of the nonlinear solution with SNe Ia, gravitational lensing, and BHS data. For this purpose, we compute the best-fit parameters of the solution at of the confidence level (CL) with the affine-invariant Markov chain Monte Carlo (MCMC) method [46], implemented in the pure-Python code emcee [47]. This code allows us to perform parameter estimation based on Bayes’ theorem of the form
where is the posterior distribution and corresponds to the probability of obtaining the parameter space for the given observational data D, is the likelihood and corresponds to the probability to obtaining the observational data D for a given parameter space , is the prior distribution and corresponds to the previous physical evidence about the parameter space, and is the prior predictive probability, which is estimated by the emcee code. Following this line, for this MCMC analysis, we need to construct the following Gaussian likelihood:
where is a normalization constant, is the merit function, and I stands for each data set, namely SNe Ia, gravitational lensing, BHS, and their joint analysis, where . Therefore, in the following subsections, we will briefly describe the construction of the merit function for each data set.
3.1. Type Ia Supernovae
For the SNe Ia data, we consider the Pantheon+ sample [48], which consists of 1701 data points in the redshift range , whose respective merit function can be conveniently constructed in matrix notation (denoted by bold symbols) as
where and , with the total uncertainty covariance matrix. The matrices and account for the statistical and systematic uncertainties, respectively, and encompasses the free parameters of the model. The quantity corresponds to the observational distance modulus of the Pantheon+ sample, which is obtained by a modified version of Trip’s formula [49] and the BBC (BEAMS with Bias Corrections) approach [50], while is the corrected apparent B-band magnitude of a fiducial SNe Ia at redshift and M is the fiducial magnitude of a SNe Ia, which must be jointly estimated with the free parameters of the model under study.
The theoretical distance modulus for a spatially flat FLRW spacetime is given by
with as the luminosity distance given by
where c is the speed of light given in units of km/s.
In principle, there is a degeneracy between M and . Hence, to constrain using SNe Ia data alone, it is necessary to include the SH0ES (Supernovae and for the Equation of State of the dark energy program) Cepheid host distance anchors, with a merit function of the form
where , with the Cepheid calibrated host–galaxy distance obtained by SH0ES [7]. So we use the Cepheid distances as the “theory model” to calibrate M, considering that the difference is sensitive to M and largely insensitive to other parameters of the cosmological model. Considering that the total uncertainty covariance matrix for Cepheid is contained in the total uncertainty covariance matrix , we can define the merit function for the SNe Ia data as
where
From now on, we will omit the nuisance parameter M, for which we consider the flat prior in our MCMC analysis, and we will focus our analysis only on the free parameters of the cosmological solution. Some models related to bulk viscous cosmologies confronted with the SNe Ia data can be found in Refs. [38,43,51,52,53,54,55].
3.2. Gravitational Lensing
When a background object (the source) is lensed due to the gravitational force of an intervening massive body (the lens), it is obtained as a result of the generation of multiple images. Therefore, the light rays emitted from the source will take different paths through the space-time at the different image positions arriving at the observer at different times. In this sense, the time delay of two different images k and l depends on the mass distribution along the line of sight of the lensing object and can be calculated as
where and are the angular position of the images, is the angular position of the source, and are the lens potential at the image positions, and is the “time-delay distance”, which is theoretically given by the expression [56]
where l, s, and stand for the lens, the source, and the space between the lens and the source, respectively; ; and is the angular diameter distance, which can be written in terms of the luminosity distance (20) as or
In this paper, we consider the gravitational lensing compilation provided by the H0LiCOW collaboration [8], which consists of six lensed quasars: B1608+656 [57], SDSS 1206+4332 [58], WFI2033-4723 [59], RXJ1131-1231, HE 0435-1223, and PG 1115-080 [60], whose respective merit function can be constructed as
where is the observational time-delay distance of the lensed quasar at redshift with an associated error (for more details, see Ref. [8]). It is important to note that, for , the angular diameter distance (26) tends to , and, therefore, the gravitational lensing data of the H0LiCOW collaboration are sensitive to , with a weak dependency on other cosmological parameters. Some models related to bulk viscous cosmologies confronted with the gravitational lensing data can be found in Ref. [61].
3.3. Black Hole Shadows
The BHS data are of interest to study our local universe since their dynamic is quite simple, and they can be seen as standard rulers if the angular size redshift , the relation between the size of the shadow, and the mass of the supermassive black hole that produces it, are established [62]. The first detection of a BHS was made by the Event Horizon Telescope Collaboration for the M87* supermassive black hole [63], which was later complemented with the detection of Sagittarius A* (Sgr A*) [64].
In a black hole (BH), light rays curve around its event horizon, creating a ring with a black spot center, the so-called shadow of the BH. The angular radius of the BHS for a Schwarzschild (SH) BH at redshift is given by
where is given by Equation (26) (note that the sub-index j is not necessary in this case) and is the mass parameter of the BH, with being the mass of the BH in solar masses units and G being the gravitational constant.
It is common to write Equation (28) in terms of the shadow radius , where (the speed of light is given in units of m/s in this case). Therefore, the merit function for the BHS data can be constructed as
where is the observational angular radius of the BHS at redshift with an associated error . According to Ref. [62], we consider for M87* the values , , and , while for Sgr A*, we consider the values , , and . It is important to note that for , the angular radius (28) tends to , and, therefore, in addition to the gravitational lensing data, the BHS data are sensitive to , with a weak dependency on other cosmological parameters. On the other hand, we divide Equation (28) by a factor of to obtain in units of .
3.4. Priors and Causality, Local Existence, and the Uniqueness Condition
The model is contrasted with the cosmological data through the Hubble parameter of the nonlinear solution given in Equation (14), whose respective parameter space is . Since we are interested in the viability of our model to describe the recent accelerated expansion of the universe without the inclusion of a cosmological constant as the CDM model, we assume a pressureless fluid () for the DM and a flat prior on of the form . The Hubble parameter at the current time is written in terms of the reduced Hubble constant , within the flat prior . Considering also that and , we then use a flat prior on k of the form , and we make the change of variable to simplify the sample of the full parameter space, with a flat prior on of the form .
Following Ref. [29], to ensure the causality of the Israel–Stewart theory in the fully nonlinear regime, we need to fulfill the condition
where n is the baryon density. In our case, the universe is dominated only by a dissipative CDM, so we have a negligible baryon density, and the above expression becomes (for illustrative purposes, we will keep )
which is reduced to the standard condition for causality and stability in the linearized regime given by Equation (5) under the near equilibrium condition [65,66,67]. On the other hand, to express the equations of the IS theory as a first-order symmetric hyperbolic system, which implies the local existence and uniqueness of its solutions [68], we need to fulfill the condition
which for a negligible baryon density becomes
Therefore, for (which implies ), we can ensure the causality, local existence, and uniqueness of our solution in the full nonlinear regime of the Israel–Stewart theory by the fulfillment of the conditions (31) and (33), which can be condensed in only one condition of the form
From Equation (5), we can see that the condition (34) only imposes a constraint when of the form , which, after some algebra, can be written as
Thus, the parameter , which was related to the causality in the linearized regime, is now upper-bounded by the deceleration parameter q, which leads to some physical implications: (1) it is not possible that q can take the value of because this implies a solution without dissipation due to Equation (5), and (2) for , there is no new constraint on except for the linearized constraint . In other words, the constraint mainly affects the accelerated solutions. Therefore, for , we consider as a prior the condition (35), which, since the universe must be in a deceleration stage to the past, is enough to fix it at the current time to be valid for all redshifts.
It is important to mention that we also constrain the CDM model as a further comparison, with a Hubble parameter as a function of the redshift given by
whose respective parameter space is and for which we consider the flat priors and .
4. Results and Discussion
In Table 1, we present the best-fit values at CL for the free parameters h and of the CDM model and h, , , , k of the nonlinear solution of the Israel–Stewart theory. We also present the criteria obtained for the SNe Ia, H0LiCOW, BHS, and SNe Ia+H0LiCOW+BHS data. In Figure 1 and Figure 2, we depict the posterior 1D distribution and joint marginalized regions of the free parameters of the CDM model for the SNe Ia data and the joint analysis and for the BHS and H0LiCOW data, respectively. On the other hand, in Figure 3 and Figure 4, we depict the posterior 1D distribution and joint marginalized regions of the free parameters of the nonlinear solution of the Israel–Stewart theory for the SNe Ia data and the joint analysis and for the BHS and H0LiCOW data, respectively. The admissible joint regions presented in the figures correspond to , , and CL, respectively. This division between data sets is made for illustrative purposes considering the BHS and H0LiCOW data are only sensitive to , and, therefore, it is not possible in principle to obtain a best fit for the other parameters. This last fact translates into a plot that covers all the priors considered for those parameters independently of the CL considered.

Table 1.
Best-fit values and criteria of the CDM model and the nonlinear solution of the Israel–Stewart theory for the SNe Ia, H0LiCOW, BHS, and SNe Ia+H0LiCOW+BHS data. The uncertainties presented correspond to CL.
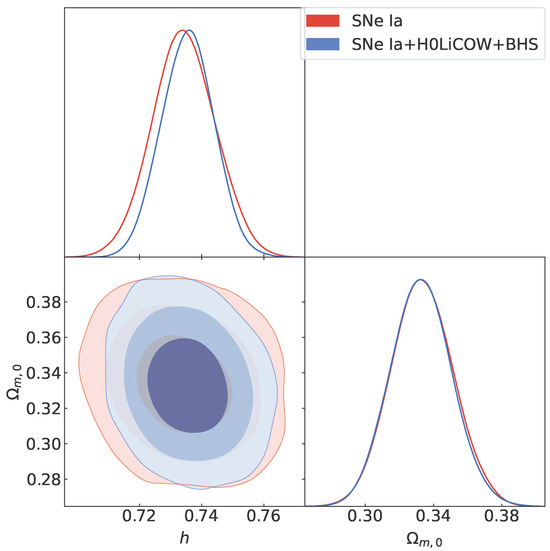
Figure 1.
Posterior 1D distribution and joint marginalized regions of the free parameters space of the CDM model for the SNe Ia and SNe Ia+H0LiCOW+BHS data. The admissible joint regions correspond to , , and CL, respectively. The best-fit values for each model free parameter are shown in Table 1.
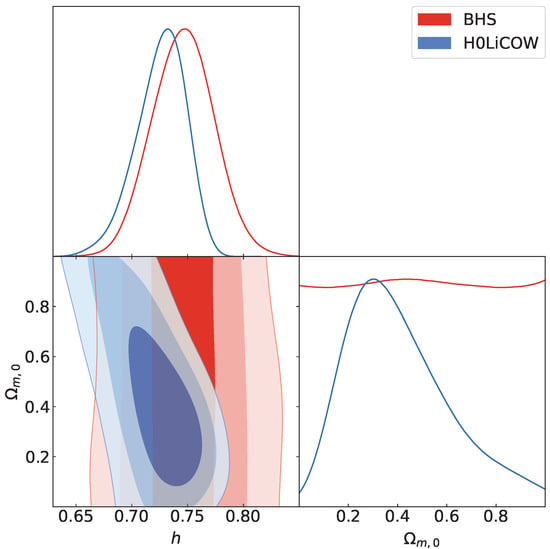
Figure 2.
Posterior 1D distribution and joint marginalized regions of the free parameters space of the CDM model for the BHS and H0LiCOW data. The admissible joint regions correspond to , , and CL, respectively. The best-fit values for each model-free parameter are shown in Table 1.
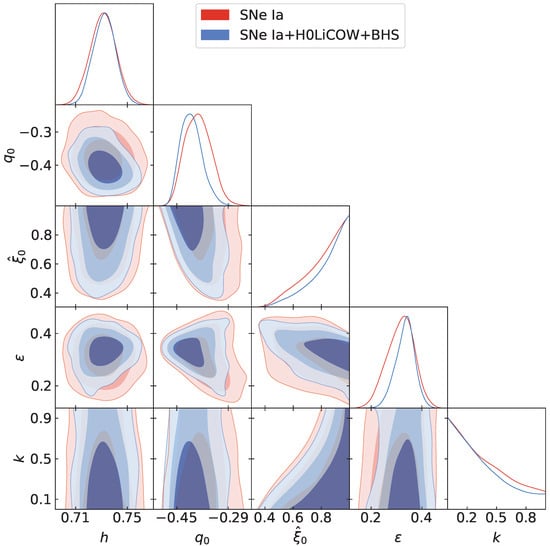
Figure 3.
Posterior 1D distribution and joint marginalized regions of the free parameter space of the nonlinear solution of the Israel–Stewart theory for the SNe Ia and SNe Ia+H0LiCOW+BHS data. The admissible joint regions correspond to , , and CL, respectively. The best-fit values for each model free parameter are shown in Table 1.
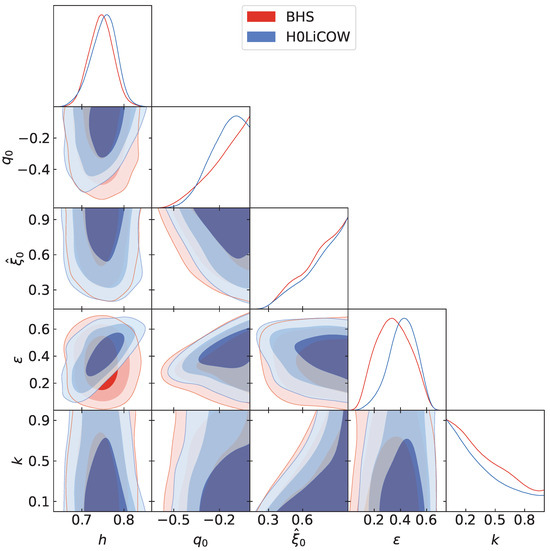
Figure 4.
Posterior 1D distribution and joint marginalized regions of the free-parameter space of the nonlinear solution of the Israel–Stewart theory for the BHS and H0LiCOW data. The admissible joint regions correspond to , , and CL, respectively. The best-fit values for each model’s free parameter are shown in Table 1.
The results presented in Table 1 indicate that the nonlinear solution has slightly lower values of than the CDM model for the H0LiCOW and BHS data, while this last one has slightly lower values that the nonlinear solution for the SNe Ia data and in the joint analysis. Therefore, considering that the difference in the values are practically negligible, we can conclude that both models are competitive in the description of the SNe Ia, H0LiCOW, and BHS data, including their joint analysis. Nevertheless, it is important to emphasize that both BHS and H0LiCOW data are only able to constrain , as they are considered in this paper only to obtain a strong fit on the Hubble parameter at the current time. On physical grounds, the main difference between these models is that in the nonlinear solution, we are describing the recent acceleration expansion of the universe without invoking a cosmological constant, and, at the same time, we are ensuring the causality, local existence, and uniqueness of the solution, where a more realistic description of the cosmic fluids is considered. The price to pay is to add that more free parameters must be added to the solution, which are related to this realistic description of the cosmic medium since the CDM model only considers perfect fluids in the description of the late universe.
Before discussing the best-fit parameters obtained, we need to highlight an important result. From Figure 2, we can see how the BHS and H0LiCOW data are not able to effectively constrain parameters other than (in this case, ). Nevertheless, the H0LiCOW data are capable of weakly constraining other parameters, as can be seen from the same Figure 2 (in other words, we obtain a best fit at CL). This explains why in Table 1 we present the same best-fit value for for the SNe Ia data and the joint analysis, but different best-fit values in the other parameters for the same data. Nevertheless, from Figure 4, we can see that we obtain a constraint on and a lower bound for and for the BHS and H0LiCOW data. This is a consequence of the condition (35) and the restriction imposed in our constraint on Equation (15a) to obtain a real Hubble parameter. These values at CL are , , and for the BHS data and , , and for the H0LiCOW data. Therefore, we can consider these intervals as an approximation of the values that must take the parameters , and to obtain a real solution compatible with the condition of causality, local existence, and uniqueness in the nonlinear Israel–Stewart theory.
Focusing on the best-fit values obtained in the joint analysis presented in Table 1, we can see that the late-time data considered in this paper are not able to strongly constrain the parameter k. This conclusion is supported by the 1D distribution and marginalized joint regions presented in Figure 3 and Figure 4. Nevertheless, we can see through the posterior distribution that a value close to zero is more probable than a value close to 1, which is compatible with the consideration to obtain this nonlinear solution in which . A similar result is obtained for , where we only obtain the lower bound at CL. Considering the change , the lower bound obtained translates into . On the other hand, we obtain a strong best fit on the free parameters , , and , with a value for the first one of , which is compatible with the value obtained by local observations of Cepheids [7]. The best fit obtained for is of interest, which, with a value of at CL, represents a lower value in comparison with the value also obtained by local observations of Cepheids [7]; i.e., the nonlinear solution represents a less accelerated universe than the universe represented by the CDM model. Note that this difference in the value of is expected since the nonlinear solution goes beyond the CDM model by considering viscous fluids in the context of the Israel–Stewart theory for non-perfect fluids. Hence, we do not have a solution whose adiabatic expansion corresponds to the standard cosmological model, since the entropy production of our model is proportional to the bulk viscous pressure , and, therefore, we have deviation from the thermodynamic equilibrium that leads to differences with the standard CDM model. It is important to emphasize that the measures of are model-dependent measures. In fact, following Ref. [69], cannot be directly measured using distance indicators with both accuracy and precision. Also, in Ref. [70], the authors show some anomalies in the deceleration parameter for different redshifts in the context of the standard CDM model. Finally, for the causality parameter, we obtain the best-fit , which is a value strongly incompatible with the condition considered in many works in the relation between and . This highlights the importance of the expression (5) and the conditions (30) and (32) in the Israel–Stewart theory, conditions that ensure the causality of the theory and also lead to unique solutions with local existence.
5. Conclusions and Final Remarks
In this work, we explored the restriction of the cosmological parameters appearing in an exact solution found in the context of a nonlinear regime of the Israel–Stewart theory by using SNe Ia, H0LiCOW, and BHS data. This nonlinear solution represents a generalization of the one found previously by some of the authors in Ref. [37] for the linear version of the Israel–Stewart theory, where the near-equilibrium condition is assumed. It is worth mentioning that the exact nonlinear solution considered in our analysis is not the most general. In fact, the differential equation obeyed by the Hubble parameter was simplified using the thermodynamic condition of positive entropy production, as discussed in Ref. [45]. Throughout this work, we set to compare our results with the CDM model, and we consider the condition (35), which ensures the causality, local existence, and uniqueness of the solution.
From the criteria presented in Table 1, we can conclude that the CDM model and the nonlinear solution of the Israel–Stewart theory are competitive in the description of the SNe Ia, H0LiCOW, BHS, and SNe Ia+H0LiCOW+BHS data. However, we need to highlight that the nonlinear solution describes the recent acceleration in the universe’s expansion without the inclusion of a DE component, contrary to the CDM model. Also, from the best-fit obtained for the BHS and H0LiCOW data, we can obtain approximate validity intervals for the free parameters , and , for which the causality, local existence, and uniqueness of the nonlinear solution (considered to be real) is ensured, according to Equation (35). These intervals can be condensed in only one interval for each free parameter of the form , , and .
Focusing on the best-fit values obtained in the joint analysis, we can see that the parameter k has a posterior 1D distribution that is close to zero, which is compatible with the consideration that we obtain this nonlinear solution where . Also, we obtain the lower bound at CL, which translates into . This last value can lead to some undesirable physical implications that are not of interest of this paper but that we plan to address in the future. For the purposes of this paper, the important fact is that this value is compatible with the causality condition of the nonlinear extension of the Israel–Stewart theory. On the other hand, while we obtain a value of compatible with the model-independent measurements of Cepheid, we obtain a lower value of in comparison with the same measurements. This indicates that the nonlinear solution represents a less accelerated universe than the universe represented by the CDM model. One of the most important results is the best fit obtained for the causality parameter , which highlights the importance of the conditions that ensure the causality, local existence, and uniqueness in the nonlinear extension of the Israel–Stewart theory.
Finally, we need to highlight the significance of the nonlinear extension of the Israel–Stewart theory considered in this paper. In particular, some authors consider the Israel–Stewart framework as a falsifiable theory. For example, the latter is constructed in the vicinity of the near equilibrium, which translates into the fact that the bulk viscous pressure must be lower than the equilibrium pressure p of the fluid. This condition is violated for an expanding universe [39], limiting the range of validity of the theory. Following this line, we extend this range of validity by the consideration of the nonlinear extension of the Israel–Stewart theory, where it is possible to ensure a bound value for [40] and, also, by the consideration of the conditions presented in Ref. [29] to ensure the causality, local existence, and uniqueness of the solutions. Therefore, we can consider the nonlinear regime of the IS theory to be a good theoretical framework to describe the recent accelerated expansion of the universe without the inclusion of a cosmological constant or some type of DE. Nevertheless, it remains as an open question whether the exploration of viscous fluids in a full nonlinear causal thermodynamics, including more general expressions for the bulk viscosity, could lead to cosmological models more consistent than the CDM model. We will consider this in the near future.
Author Contributions
Conceptualization, M.C., N.C., E.G. and S.L.; methodology, M.C. and E.G.; software, E.G.; validation, E.G.; formal analysis, M.C., N.C., E.G. and S.L.; investigation, M.C., N.C., E.G. and S.L.; resources, E.G.; writing—original draft preparation, M.C. and E.G.; writing—review and editing, M.C., N.C., E.G. and S.L.; visualization, E.G.; supervision, M.C. and E.G.; project administration, E.G.; funding acquisition, E.G. All authors have read and agreed to the published version of the manuscript.
Funding
E.G. was funded by Vicerrectoría de Investigación y Desarrollo Tecnológico (VRIDT) at Universidad Católica del Norte (UCN) through Proyecto de Investigación Pro Fondecyt 2023, Resolución VRIDT N°076/2023.
Data Availability Statement
The data underlying this article were cited in Section 3.
Acknowledgments
M.C. acknowledges the hospitality of the Instituto de Física of Pontificia Universidad Católica de Valparaíso and Departamento de Física of Universidad de Santiago de Chile. E.G. acknowledges the scientific support of Núcleo de Investigación No. 7 UCN-VRIDT 076/2020, Núcleo de Modelación y Simulación Científica (NMSC).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DE | Dark energy |
| CDM | Cold dark matter |
| CMB | Cosmic microwave background |
| H0LiCOW | Lenses in COSMOGRAIL’s Wellspring |
| EoS | Equation of state |
| DM | Dark matter |
| SNe Ia | Type Ia supernovae |
| OHD | Observational Hubble parameter data |
| BHS | Black hole shadows |
| FLRW | Friedmann–Lemaître–Robertson–Walker |
| CL | Confidence level |
| MCMC | Markov chain Monte Carlo |
| BBC | Beams with Bias Corrections |
| SH0ES | Supernovae and for the Equation of State of the dark energy program |
| BH | Black hole |
| SH | Schwarzschild |
References
- Di Valentino, E.; Melchiorri, A.; Silk, J. Planck evidence for a closed Universe and a possible crisis for cosmology. Nat. Astron. 2019, 4, 196–203. [Google Scholar] [CrossRef]
- Handley, W. Curvature tension: Evidence for a closed universe. Phys. Rev. D 2021, 103, L041301. [Google Scholar] [CrossRef]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Padmanabhan, T. Cosmological constant: The Weight of the vacuum. Phys. Rept. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Velten, H.E.S.; vom Marttens, R.F.; Zimdahl, W. Aspects of the cosmological “coincidence problem”. Eur. Phys. J. C 2014, 74, 3160. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Yukei, M.; Anand, G.S.; Louise, B. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW – XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. Roy. Astron. Soc. 2020, 498, 1420–1439. [Google Scholar] [CrossRef]
- Jaime, L.G.; Jaber, M.; Escamilla-Rivera, C. New parametrized equation of state for dark energy surveys. Phys. Rev. D 2018, 98, 083530. [Google Scholar] [CrossRef]
- Jaber, M.; Arciniega, G.; Jaime, L.G.; Rodríguez-López, O.A. A single parameterization for dark energy and modified gravity models. Phys. Dark Univ. 2022, 37, 101069. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday Anthony, J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Israel, W. Nonstationary irreversible thermodynamics: A Causal relativistic theory. Ann. Phys. 1976, 100, 310–331. [Google Scholar] [CrossRef]
- Israel, W.; Stewart, J.M. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 1979, 118, 341–372. [Google Scholar] [CrossRef]
- Pavon, D. The Generalized second law and extended thermodynamics. Class. Quant. Grav. 1990, 7, 487–491. [Google Scholar] [CrossRef]
- Chimento, L.; Jakubi, A.S. Cosmological solutions of the Einstein equations with a causal viscous fluid. Class. Quant. Grav. 1993, 10, 2047–2058. [Google Scholar] [CrossRef]
- Maartens, R. Causal thermodynamics in relativity. arXiv 1996, arXiv:astro-ph/9609119. [Google Scholar]
- Zimdahl, W. ’Understanding’ cosmological bulk viscosity. Mon. Not. Roy. Astron. Soc. 1996, 280, 1239. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mathews, G.J.; Fuller, G.M. Bulk Viscosity, Decaying Dark Matter, and the Cosmic Acceleration. Phys. Rev. D 2007, 75, 043521. [Google Scholar] [CrossRef]
- Mathews, G.J.; Lan, N.Q.; Kolda, C. Late Decaying Dark Matter, Bulk Viscosity and the Cosmic Acceleration. Phys. Rev. D 2008, 78, 043525. [Google Scholar] [CrossRef]
- Pandey, K.L.; Karwal, T.; Das, S. Alleviating the H0 and σ8 anomalies with a decaying dark matter model. J. Cosmol. Astropart. Phys. 2020, 07, 026. [Google Scholar] [CrossRef]
- Cárdenas, V.H.; Grandón, D.; Lepe, S. Dark energy and Dark matter interaction in light of the second law of thermodynamics. Eur. Phys. J. C 2019, 79, 357. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavon, D. Dark Matter and Dark Energy Interactions: Theoretical Challenges, Cosmological Implications and Observational Signatures. Rept. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef] [PubMed]
- Cataldo, M.; Cruz, N.; Lepe, S. Viscous dark energy and phantom evolution. Phys. Lett. B 2005, 619, 5–10. [Google Scholar] [CrossRef]
- Disconzi, M.M.; Kephart, T.W.; Scherrer, R.J. New approach to cosmological bulk viscosity. Phys. Rev. D 2015, 91, 043532. [Google Scholar] [CrossRef]
- Cruz, M.; Cruz, N.; Lepe, S. Phantom solution in a non-linear Israel–Stewart theory. Phys. Lett. B 2017, 769, 159–165. [Google Scholar] [CrossRef]
- Cruz, N.; Lepe, S.; Peña, F. Crossing the phantom divide with dissipative normal matter in the Israel–Stewart formalism. Phys. Lett. B 2017, 767, 103–109. [Google Scholar] [CrossRef]
- Cárdenas, V.H.; Cruz, M.; Lepe, S. Cosmic expansion with matter creation and bulk viscosity. Phys. Rev. D 2020, 102, 123543. [Google Scholar] [CrossRef]
- Cruz, M.; Lepe, S.; Odintsov, S.D. Thermodynamically allowed phantom cosmology with viscous fluid. Phys. Rev. D 2018, 98, 083515. [Google Scholar] [CrossRef]
- Bemfica, F.S.; Disconzi, M.M.; Noronha, J. Causality of the Einstein-Israel–Stewart Theory with Bulk Viscosity. Phys. Rev. Lett. 2019, 122, 221602. [Google Scholar] [CrossRef]
- Alford, M.G.; Bovard, L.; Hanauske, M.; Rezzolla, L.; Schwenzer, K. Viscous Dissipation and Heat Conduction in Binary Neutron-Star Mergers. Phys. Rev. Lett. 2018, 120, 041101. [Google Scholar] [CrossRef]
- Barta, D. Effect of viscosity and thermal conductivity on the radial oscillation and relaxation of relativistic stars. Class. Quant. Grav. 2019, 36, 215012. [Google Scholar] [CrossRef]
- Bravo Medina, S.; Nowakowski, M.; Batic, D. Viscous Cosmologies. Class. Quant. Grav. 2019, 36, 215002. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Paliathanasis, A.; Lu, J. Challenging bulk viscous unified scenarios with cosmological observations. Phys. Rev. D 2019, 100, 103518. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy Can Resolve The Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef] [PubMed]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Normann, B.D.; Brevik, I.H. Can the Hubble tension be resolved by bulk viscosity? Mod. Phys. Lett. A 2021, 36, 2150198. [Google Scholar] [CrossRef]
- Cruz, N.; González, E.; Palma, G. Exact analytical solution for an Israel–Stewart cosmology. Gen. Rel. Grav. 2020, 52, 62. [Google Scholar] [CrossRef]
- Cruz, N.; González, E.; Palma, G. Testing dissipative dark matter in causal thermodynamics. Mod. Phys. Lett. A 2021, 36, 2150032. [Google Scholar] [CrossRef]
- Maartens, R. Dissipative cosmology. Class. Quant. Grav. 1995, 12, 1455–1465. [Google Scholar] [CrossRef]
- Maartens, R.; Mendez, V. Nonlinear bulk viscosity and inflation. Phys. Rev. D 1997, 55, 1937–1942. [Google Scholar] [CrossRef]
- Eckart, C. The Thermodynamics of irreversible processes. 3. Relativistic theory of the simple fluid. Phys. Rev. 1940, 58, 919–924. [Google Scholar] [CrossRef]
- Cruz, M.; Cruz, N.; Lepe, S. Accelerated and decelerated expansion in a causal dissipative cosmology. Phys. Rev. D 2017, 96, 124020. [Google Scholar] [CrossRef]
- Cruz, N.; González, E.; Lepe, S.; Sáez-Chillón Gómez, D. Analysing dissipative effects in the ΛCDM model. J. Cosmol. Astropart. Phys. 2018, 12, 017. [Google Scholar] [CrossRef]
- Mohan, N.D.J.; Sasidharan, A.; Mathew, T.K. Bulk viscous matter and recent acceleration of the universe based on causal viscous theory. Eur. Phys. J. C 2017, 77, 849. [Google Scholar] [CrossRef]
- Chimento, L.P.; Jakubi, A.S.; Mendez, V.; Maartens, R. Cosmological solutions with nonlinear bulk viscosity. Class. Quant. Grav. 1997, 14, 3363–3375. [Google Scholar] [CrossRef]
- Goodman, J.; Weare, J. Ensemble samplers with affine invariance. Commun. Appl. Math. Comput. Sci. 2010, 5, 65–80. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306–312. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Tripp, R. A Two-parameter luminosity correction for type Ia supernovae. Astron. Astrophys. 1998, 331, 815–820. [Google Scholar]
- Kessler, R.; Scolnic, D. Correcting Type Ia Supernova Distances for Selection Biases and Contamination in Photometrically Identified Samples. Astrophys. J. 2017, 836, 56. [Google Scholar] [CrossRef]
- Shareef, V.M.; Jerin Mohan, N.D.; Mathew, T.K. Contrasting the bulk viscous model with the standard \LambdaCDM using Bayesian statistics. Astrophys. Space Sci. 2022, 367, 46. [Google Scholar] [CrossRef]
- Sarath, N.; D Jerin Mohan, N.; Mathew, T.K. Running vacuum cosmology with bulk viscous matter. Mod. Phys. Lett. A 2023, 38, 2350099. [Google Scholar] [CrossRef]
- Cruz, N.; González, E.; Jovel, J. Study of a Viscous ΛWDM Model: Near-Equilibrium Condition, Entropy Production, and Cosmological Constraints. Symmetry 2022, 14, 1866. [Google Scholar] [CrossRef]
- Gómez, G.; Palma, G.; González, E.; Rincón, A.; Cruz, N. A new parametrization for bulk viscosity cosmology as extension of the ΛCDM model. Eur. Phys. J. Plus 2023, 138, 738. [Google Scholar] [CrossRef]
- Pai, V.A.; Mathew, T.K. Bulk viscous late acceleration under near equilibrium conditions in f(R, T) gravity with mixed dark matter. Class. Quant. Grav. 2024, 41, 085002. [Google Scholar] [CrossRef]
- Treu, T.; Marshall, P.J. Time Delay Cosmography. Astron. Astrophys. Rev. 2016, 24, 11. [Google Scholar] [CrossRef]
- Jee, I.; Suyu, S.H.; Komatsu, E.; Fassnacht, C.D.; Hilbert, S.; Koopmans, L.V.E. A measurement of the Hubble constant from angular diameter distances to two gravitational lenses. Science 2019, 365, 1134–1138. [Google Scholar] [CrossRef]
- Birrer, S.; Treu, T.; Rusu, C.E.; Bonvin, V.; Fassnacht, C.D.; Chan, J.H.H.; Agnello, A.; Shajib, A.J.; Chen, G.C.; Auger, M.; et al. H0LiCOW–IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant. Mon. Not. Roy. Astron. Soc. 2019, 484, 4726. [Google Scholar] [CrossRef]
- Rusu, C.E.; Wong, K.C.; Bonvin, V.; Sluse, D.; Suyu, S.H.; Fassnacht, C.D.; Chan, J.H.H.; Hilbert, S.; Auger, M.W.; Sonnenfeld, A.; et al. H0LiCOW XII. Lens mass model of WFI2033–4723 and blind measurement of its time-delay distance and H0. Mon. Not. Roy. Astron. Soc. 2020, 498, 1440–1468. [Google Scholar] [CrossRef]
- Chen, G.C.-F.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; Chan, J.H.H.; Wong, K.C.; Auger, M.W.; Hilbert, S.; Bonvin, V.; Birrer, S.; et al. A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging. Mon. Not. Roy. Astron. Soc. 2019, 490, 1743–1773. [Google Scholar] [CrossRef]
- Herrera-Zamorano, L.; García-Aspeitia, M.A.; Hernández-Almada, A. Constraints and cosmography of ΛCDM in presence of viscosity. Eur. Phys. J. C 2020, 80, 637. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C.; Torres Castillejos, R. H0 Tension on the Light of Supermassive Black Hole Shadows Data. Universe 2023, 9, 14. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Denicol, G.S.; Kodama, T.; Koide, T.; Mota, P. Stability and Causality in relativistic dissipative hydrodynamics. J. Phys. G 2008, 35, 115102. [Google Scholar] [CrossRef]
- Pu, S.; Koide, T.; Rischke, D.H. Does stability of relativistic dissipative fluid dynamics imply causality? Phys. Rev. D 2010, 81, 114039. [Google Scholar] [CrossRef]
- Romatschke, P. New Developments in Relativistic Viscous Hydrodynamics. Int. J. Mod. Phys. E 2010, 19, 1–53. [Google Scholar] [CrossRef]
- Reula, O.A.; Nagy, G.B. A Causal statistical family of dissipative divergence type fluids. J. Phys. A 1997, 30, 1695–1709. [Google Scholar] [CrossRef]
- Neben, A.R.; Turner, M.S. Beyond H0 and q0: Cosmology is no longer just two numbers. Astrophys. J. 2013, 769, 133. [Google Scholar] [CrossRef]
- Pastén, E.; Cárdenas, V.H. Testing ΛCDM cosmology in a binned universe: Anomalies in the deceleration parameter. Phys. Dark Univ. 2023, 40, 101224. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).