The Density and Ionization Profiles of Optically Dark and High-Redshift GRBs Probed by X-ray Absorption
Abstract
1. Introduction
2. Data Selection and Analysis Procedure
2.1. Data Selection
| GRB Name | Redshift | Error | Flux | Flux Error | |||
|---|---|---|---|---|---|---|---|
| GRB050315 | 1.95 | 0.95 | 0.46 | 0.63 3 | 9.50 | 0.45 | |
| GRB050401* 3,a | 2.90 | 1.60 | 1.94 | 0.36 3 | 3.98 3,5 | 22.60 | 1.96 |
| GRB050408 | 1.24 | 1.20 | 0.48 | 3.78 | 0.30 | ||
| GRB050416A* | 0.65 | 0.72 | 0.24 | 0.35 6 | 1.56 | 0.09 | |
| GRB050505 | 4.27 | 2.20 | 1.34 | 0.53 3 | 1.26 5 | 3.04 | 0.12 |
| GRB050525A | 0.61 | 0.14 | 0.24 | 0.92 3 | 5.26 | 0.48 | |
| GRB050802 | 1.71 | 0.24 | 0.24 | 0.51 3 | 5.22 | 0.21 | |
| GRB050803* | 4.30 | 7.70 | 3.00 | −0.15 3 | 6.17 | 0.29 | |
| GRB050822 | 1.43 | 0.40 | 0.32 | 3.98 | 0.26 | ||
| GRB050922B | 4.90 | 7.60 | 3.40 | 0.58 3 | 67.00 | 3.70 | |
| GRB051006 | 1.06 | 4.20 | 2.60 | 1.30 3 | 1.02 | 0.13 | |
| GRB051016B | 0.94 | 0.70 | 0.38 | 0.63 3 | 1.53 | 0.12 | |
| GRB051022* | 0.80 | 5.70 | 1.28 | −0.10 2 | 15.90 | 0.82 | |
| GRB051111 | 1.55 | 0.58 | 0.66 | 1.29 | 0.12 | ||
| GRB051221A | 0.55 | 0.18 | 0.18 | 1.70 | 0.13 | ||
| GRB060124 | 2.30 | 0.58 | 0.56 | 0.80 3 | 0.07 5 | 8.55 | 0.32 |
| GRB060202* | 0.79 | 2.10 | 0.52 | 0.20 3 | 1.61 | 0.09 | |
| GRB060204B* | 2.34 | 1.80 | 0.84 | 0.47 3 | 2.32 | 0.14 | |
| GRB060210* | 3.91 | 2.40 | 1.22 | 0.37 3 | 0.35 3,5 | 11.10 | 0.35 |
| GRB060218 | 0.03 | 0.44 | 0.12 | 0.93 | 0.05 | ||
| GRB060306 | 1.55 | 4.00 | 1.20 | 0.54 3 | 1.91 | 0.12 | |
| GRB060502A | 1.51 | 0.42 | 0.44 | 0.53 6 | 8.79 | 0.66 | |
| GRB060522 | 5.11 | 3.30 | 5.80 | 0.74 3 | 0.01 5 | 2.24 | 0.23 |
| GRB060604 | 2.68 | 1.00 | 1.06 | 0.75 3 | 1.32 | 0.09 | |
| GRB060607A | 3.08 | 0.55 | 0.80 | 0.53 3 | 0.10 5 | 17.90 | 0.76 |
| GRB060714 | 2.71 | 0.95 | 1.18 | 0.77 3 | 0.71 5 | 8.40 | 0.57 |
| GRB060719* | 1.53 | 2.90 | 1.04 | −0.13 3 | 2.55 | 0.18 | |
| GRB060729 | 0.54 | 0.07 | 0.04 | 0.80 3 | 10.70 | 0.25 | |
| GRB060814* | 1.92 | 4.40 | 0.98 | −0.06 3 | 5.14 | 0.22 | |
| GRB060904B | 0.70 | 0.28 | 0.32 | 2.43 | 0.20 | ||
| GRB060908* | 1.88 | 0.95 | 0.92 | 0.38 3 | 8.28 | 0.86 | |
| GRB060912A | 0.94 | 0.21 | 0.32 | 0.62 3 | 4.29 | 0.42 | |
| GRB060926 | 3.20 | 3.80 | 5.80 | 3.16 5 | 1.08 | 0.18 | |
| GRB061007 | 1.26 | 0.74 | 0.32 | 0.79 3 | 8.62 | 0.50 | |
| GRB061021 | 0.35 | 0.06 | 0.05 | 0.75 3 | 3.89 | 0.14 | |
| GRB061121 | 1.31 | 0.73 | 0.24 | 0.64 3 | 15.60 | 0.61 | |
| GRB061202 | 2.25 | 15.80 | 4.00 | 15.90 | 0.78 | ||
| GRB061222A* | 2.09 | 5.10 | 1.24 | −0.19 6 | 22.50 | 0.85 | |
| GRB070125 | 1.55 | 0.40 | 0.70 | 2.60 | 0.30 | ||
| GRB070129 | 2.34 | 0.69 | 0.84 | 0.62 3 | 2.75 | 0.17 | |
| GRB070208 | 1.17 | 0.87 | 0.58 | 0.54 6 | 1.47 | 0.16 | |
| GRB070306* | 1.50 | 3.60 | 0.88 | 0.23 3 | 11.60 | 0.54 | |
| GRB070318 | 0.84 | 0.90 | 0.28 | 0.78 3 | 2.72 | 0.16 | |
| GRB070328* | 2.06 | 2.50 | 0.70 | 0.31 3 | 8.51 | 0.37 | |
| GRB070419A | 0.97 | 0.43 | 0.66 | 0.87 6 | 2.33 | 0.43 | |
| GRB070419B* | 1.96 | 0.76 | 0.56 | 0.25 3 | 44.40 | 1.91 | |
| GRB070508* 3,a | 0.82 | 0.82 | 0.46 | 11.20 | 0.72 | ||
| GRB070521* | 2.09 | 15.00 | 4.20 | −0.06 3 | 13.50 | 0.83 | |
| GRB070714B | 0.92 | 0.40 | 0.38 | 0.92 | 0.08 | ||
| GRB070721B | 3.63 | 1.10 | 1.68 | 0.72 3 | 0.32 5 | 21.50 | 1.34 |
| GRB070724A | 0.46 | 0.25 | 0.40 | 0.88 | 0.16 | ||
| GRB070810A | 2.17 | 0.91 | 0.90 | 1.41 5 | 1.93 | 0.17 | |
| GRB071010A | 0.98 | 2.00 | 1.78 | 0.89 6 | 0.82 | 0.13 | |
| GRB071021 | 2.45 | 2.00 | 1.28 | 1.75 | 0.13 | ||
| GRB071025 | 4.80 | 3.80 | 3.00 | 0.50 3 | 3.74 | 0.21 | |
| GRB071117 | 1.33 | 1.60 | 0.90 | 0.58 3 | 1.67 | 0.17 | |
| GRB080205 | 2.72 | 2.30 | 2.60 | 0.79 3 | 1.34 | 0.13 | |
| GRB080207* 2,a | 2.09 | 17.10 | 5.00 | 0.30 2 | 1.97 | 0.15 | |
| GRB080210* 1,b | 2.64 | 2.10 | 2.00 | 0.79 3,5 | 0.90 | 0.09 | |
| GRB080319A* | 2.03 | 1.30 | 1.12 | 0.41 6 | 5.80 | 0.65 | |
| GRB080319B | 0.94 | 0.13 | 0.11 | 0.52 6 | 34.40 | 1.42 | |
| GRB080319C* 3,a | 1.95 | 0.91 | 0.68 | 0.36 6 | 86.80 | 5.99 | |
| GRB080325* 5,a | 1.78 | 1.80 | 1.70 | 0.33 4 | 1.01 | 0.14 | |
| GRB080411 | 1.03 | 0.58 | 0.14 | 20.80 | 0.59 | ||
| GRB080413B | 1.10 | 0.33 | 0.17 | 5.15 | 0.22 | ||
| GRB080430 | 0.77 | 0.49 | 0.16 | 3.60 | 0.18 | ||
| GRB080520 | 1.55 | 2.10 | 2.20 | 1.26 | 0.21 | ||
| GRB080602 | 1.82 | 1.40 | 0.74 | 186.00 | 12.30 | ||
| GRB080603A | 1.69 | 1.00 | 1.00 | 3.26 | 0.38 | ||
| GRB080605* 3,a | 1.64 | 0.68 | 0.74 | 8.07 | 0.63 | ||
| GRB080607* 3,a | 3.04 | 4.00 | 1.50 | 5.01 3,5 | 7.33 | 0.43 | |
| GRB080707 | 1.23 | 0.41 | 0.60 | 1.27 | 0.14 | ||
| GRB080710 | 0.85 | 0.12 | 0.19 | 2.68 | 0.19 | ||
| GRB080721 | 2.60 | 0.83 | 0.62 | 0.20 5 | 12.90 | 0.47 | |
| GRB080805* 1,a,b | 1.51 | 1.80 | 1.52 | 2.16 | 0.29 | ||
| GRB080905A | 0.12 | 0.23 | 0.38 | 12.80 | 2.17 | ||
| GRB080905B | 2.37 | 3.40 | 1.42 | 0.00 5 | 7.80 | 0.48 | |
| GRB080916A | 0.69 | 0.81 | 0.36 | 5.83 | 0.49 | ||
| GRB080928 | 1.69 | 0.34 | 0.42 | 5.62 | 0.34 | ||
| GRB081007 | 0.53 | 0.71 | 0.26 | 5.47 | 0.43 | ||
| GRB081109 | 0.98 | 1.40 | 0.46 | 4.26 | 0.26 | ||
| GRB081203A | 2.10 | 0.85 | 0.60 | 1.00 5 | 5.60 | 0.35 | |
| GRB081221 | 2.26 | 6.90 | 1.64 | 6.00 | 0.31 | ||
| GRB081222 | 2.77 | 0.51 | 0.62 | 0.06 5 | 13.00 | 0.59 | |
| GRB090102* 1,a | 1.55 | 0.75 | 0.42 | 8.33 | 0.47 | ||
| GRB090201 | 2.10 | 10.50 | 2.40 | 5.88 | 0.27 | ||
| GRB090313 | 3.38 | 4.40 | 3.00 | 0.20 5 | 3.67 | 0.35 | |
| GRB090328A | 0.74 | 0.65 | 0.82 | 2.36 | 0.45 | ||
| GRB090404* 2,a | 3.00 | 12.10 | 3.20 | 0.20 2 | 3.21 | 0.18 | |
| GRB090417B* 2,a | 0.34 | 3.30 | 0.64 | −1.90 2 | 32.60 | 1.57 | |
| GRB090418A | 1.61 | 1.50 | 0.56 | 16.20 | 0.90 | ||
| GRB090423 | 8.20 | 9.60 | 15.00 | 3.53 | 0.29 | ||
| GRB090424 | 0.54 | 0.60 | 0.18 | 28.50 | 1.58 | ||
| GRB090516 | 4.11 | 2.10 | 1.58 | 0.54 5 | 2.40 | 0.11 | |
| GRB090530 | 1.27 | 0.39 | 0.34 | 3.54 | 0.28 | ||
| GRB090618 | 0.54 | 0.24 | 0.07 | 24.90 | 0.71 | ||
| GRB090709A | 1.80 | 2.20 | 0.70 | 17.70 | 0.79 | ||
| GRB090715B | 3.00 | 1.30 | 1.22 | 0.45 5 | 1.76 | 0.12 | |
| GRB090726 | 2.71 | 1.50 | 1.58 | 0.63 5 | 0.64 | 0.06 | |
| GRB090809 | 2.74 | 0.96 | 1.24 | 0.50 5 | 7.75 | 0.52 | |
| GRB090812* 1,a | 2.45 | 0.98 | 1.14 | 2.00 5 | 6.54 | 0.59 | |
| GRB090902B | 1.82 | 2.30 | 1.30 | 3.27 | 0.28 | ||
| GRB090926B* 1,a | 1.24 | 2.30 | 1.28 | 23.60 | 2.34 | ||
| GRB091003 | 0.90 | 0.34 | 0.34 | 2.12 | 0.23 | ||
| GRB091018 | 0.97 | 0.25 | 0.16 | 5.51 | 0.27 | ||
| GRB091020 | 1.71 | 0.79 | 0.32 | 5.06 | 0.23 | ||
| GRB091024 | 1.09 | 3.20 | 3.60 | 49.10 | 5.28 | ||
| GRB091029 | 2.75 | 0.53 | 0.64 | 0.05 5 | 5.74 | 0.29 | |
| GRB091109A | 3.08 | 1.30 | 1.98 | 1.93 | 0.20 | ||
| GRB091127 | 0.49 | 0.10 | 0.12 | 80.10 | 5.29 | ||
| GRB091208B | 1.06 | 1.10 | 0.50 | 7.61 | 0.55 | ||
| GRB100424A | 2.46 | 3.40 | 2.60 | 35.50 | 3.77 | ||
| GRB100615A* 2,a | 1.40 | 17.30 | 4.20 | −0.60 2 | 24.90 | 1.49 | |
| GRB100621A | 0.54 | 2.80 | 0.56 | 17.00 | 0.81 | ||
| GRB100728A | 1.57 | 2.60 | 0.78 | 33.30 | 1.31 | ||
| GRB100816A | 0.80 | 0.24 | 0.32 | 2.17 | 0.23 | ||
| GRB100901A | 1.41 | 0.34 | 0.28 | 11.70 | 0.54 | ||
| GRB100906A | 1.73 | 0.60 | 0.92 | 3.11 | 0.16 | ||
| GRB101219A | 0.72 | 0.81 | 0.82 | 5.88 | 0.91 | ||
| GRB101225A | 0.85 | 0.13 | 0.11 | 21.80 | 0.69 | ||
| GRB110205A | 2.22 | 0.39 | 0.44 | 0.28 5 | 4.65 | 0.23 | |
| GRB110422A | 1.77 | 1.70 | 0.52 | 23.30 | 1.00 | ||
| GRB110503A | 1.61 | 0.24 | 0.22 | 6.19 | 0.25 | ||
| GRB110715A | 0.82 | 1.50 | 0.84 | 11.60 | 0.59 | ||
| GRB110818A | 3.36 | 1.40 | 1.46 | 0.79 5 | 3.90 | 0.25 | |
| GRB111008A | 4.99 | 2.50 | 2.20 | 2.51 5 | 8.43 | 0.39 | |
| GRB111117A | 2.21 | 1.50 | 2.40 | 1.18 | 0.19 | ||
| GRB111209A | 0.68 | 0.22 | 0.10 | 10.40 | 0.44 | ||
| GRB111228A | 0.71 | 0.35 | 0.13 | 9.18 | 0.41 | ||
| GRB111229A | 1.38 | 0.57 | 0.78 | 5.64 | 0.50 | ||
| GRB120118B | 2.94 | 5.70 | 3.40 | 3.99 | 0.35 | ||
| GRB120119A | 1.73 | 0.98 | 0.92 | 3.98 5 | 10.30 | 0.71 | |
| GRB120326A | 1.80 | 0.50 | 0.38 | 9.64 | 0.43 | ||
| GRB120404A | 2.87 | 0.75 | 1.22 | 0.05 5 | 7.60 | 0.57 | |
| GRB120711A | 1.41 | 2.00 | 0.56 | 16.80 | 0.67 | ||
| GRB120712A | 4.17 | 1.50 | 2.40 | 0.01 5 | 3.59 | 0.25 | |
| GRB120729A | 0.80 | 0.26 | 0.36 | 2.16 | 0.17 | ||
| GRB120811C | 2.67 | 1.20 | 1.10 | 0.32 5 | 7.24 | 0.53 | |
| GRB120815A | 2.36 | 0.71 | 1.24 | 1.12 5 | 6.29 | 0.48 | |
| GRB120907A | 0.97 | 0.16 | 0.22 | 3.57 | 0.23 | ||
| GRB120909A | 3.93 | 2.00 | 2.00 | 0.50 5 | 9.58 | 0.49 | |
| GRB121024A | 2.30 | 1.10 | 1.02 | 0.71 5 | 6.42 | 0.46 | |
| GRB121027A | 1.77 | 2.00 | 0.62 | 6.31 5 | 11.20 | 0.61 | |
| GRB121209A | 2.10 | 12.10 | 3.40 | 4.34 | 0.26 | ||
| GRB121211A | 1.02 | 0.78 | 0.32 | 3.11 | 0.21 | ||
| GRB130420A | 1.30 | 0.40 | 0.26 | 5.22 | 0.31 | ||
| GRB130427A | 0.34 | 0.11 | 0.08 | 0.95 | 79.30 | 4.02 | |
| GRB130505A | 2.27 | 0.75 | 0.42 | 0.04 5 | 56.60 | 2.03 | |
| GRB130511A | 1.30 | 0.75 | 0.58 | 1.80 | 0.19 | ||
| GRB130603B | 0.36 | 0.44 | 0.18 | 3.94 | 0.30 | ||
| GRB130702A | 0.14 | 0.05 | 0.08 | 11.40 | 0.88 | ||
| GRB130907A | 1.24 | 1.10 | 0.20 | 53.20 | 1.58 | ||
| GRB130925A | 0.35 | 3.10 | 0.58 | 75.30 | 3.64 | ||
| GRB131004A | 0.72 | 0.66 | 0.54 | 4.71 | 0.50 | ||
| GRB131030A | 1.29 | 0.42 | 0.32 | 10.30 | 0.64 | ||
| GRB131103A | 0.60 | 1.40 | 0.54 | 5.76 | 0.45 | ||
| GRB131105A | 1.69 | 2.00 | 0.88 | 3.92 | 0.27 | ||
| GRB131108A | 2.40 | 0.96 | 1.40 | 0.09 5 | 1.10 | 0.12 | |
| GRB131231A | 0.64 | 0.28 | 0.22 | 17.70 | 1.66 | ||
| GRB140206A | 2.73 | 1.80 | 0.76 | 0.32 5 | 21.70 | 0.79 | |
| GRB140213A | 1.21 | 0.14 | 0.24 | 13.20 | 0.52 | ||
| GRB140301A | 1.42 | 0.85 | 0.88 | 1.90 | 0.27 | ||
| GRB140304A | 5.28 | 4.10 | 4.80 | 25.30 | 1.69 | ||
| GRB140419A | 3.96 | 1.20 | 1.04 | 0.00 5 | 11.60 | 0.39 | |
| GRB140423A | 3.26 | 1.10 | 0.92 | 0.03 5 | 8.49 | 0.43 | |
| GRB140430A | 1.60 | 0.74 | 0.94 | 0.63 5 | 1.72 | 0.14 | |
| GRB140506A | 0.89 | 0.88 | 0.32 | 13.10 | 0.61 | ||
| GRB140508A | 1.03 | 0.25 | 0.42 | 6.94 | 0.90 | ||
| GRB140512A | 0.72 | 0.28 | 0.13 | 36.00 | 1.21 | ||
| GRB140515A | 6.32 | 4.30 | 6.60 | 0.00 5 | 4.44 | 0.33 | |
| GRB140518A | 4.71 | 2.90 | 3.20 | 0.45 5 | 6.33 | 0.47 | |
| GRB140629A | 2.27 | 0.80 | 0.52 | 1.00 5 | 3.11 | 0.16 | |
| GRB140703A | 3.14 | 1.00 | 1.60 | 0.79 5 | 10.70 | 0.62 | |
| GRB140903A | 0.35 | 0.18 | 0.16 | 3.70 | 0.32 | ||
| GRB140907A | 1.21 | 0.54 | 0.66 | 2.87 | 0.19 | ||
| GRB141109A | 2.99 | 2.10 | 1.44 | 1.26 5 | 8.30 | 0.56 | |
| GRB141121A | 1.47 | 0.42 | 0.42 | 11.50 | 0.83 | ||
| GRB141220A | 1.32 | 0.38 | 0.54 | 3.09 | 0.35 | ||
| GRB150206A | 2.09 | 1.10 | 0.44 | 0.50 5 | 11.20 | 0.45 | |
| GRB150314A | 1.76 | 1.80 | 0.66 | 55.80 | 3.03 | ||
| GRB150323A | 0.59 | 0.56 | 0.38 | 3.37 | 0.38 | ||
| GRB150403A | 2.06 | 0.81 | 0.32 | 0.63 5 | 28.40 | 0.82 | |
| GRB150821A | 0.76 | 2.20 | 0.70 | 8.24 | 0.60 | ||
| GRB151021A | 2.33 | 2.30 | 0.86 | 1.58 5 | 11.60 | 0.64 | |
| GRB151027A | 0.81 | 0.43 | 0.13 | 34.90 | 1.32 | ||
| GRB151027B | 4.06 | 3.30 | 4.20 | 0.03 5 | 4.00 | 0.35 | |
| GRB151031A | 1.17 | 1.00 | 0.68 | 1.69 | 0.19 | ||
| GRB160131A | 0.97 | 0.40 | 0.17 | 8.04 | 0.28 | ||
| GRB160425A | 0.56 | 1.00 | 0.34 | 4.27 | 0.29 | ||
| GRB160509A | 1.17 | 2.60 | 0.70 | 17.60 | 0.69 | ||
| GRB160623A | 0.37 | 2.40 | 0.96 | 39.70 | 2.25 | ||
| GRB160804A | 0.74 | 0.20 | 0.18 | 2.70 | 0.20 | ||
| GRB161014A | 2.82 | 1.80 | 1.68 | 0.25 5 | 17.10 | 1.17 | |
| GRB161117A | 1.55 | 0.82 | 0.36 | 14.00 | 0.67 | ||
| GRB161219B | 0.15 | 0.20 | 0.05 | 38.90 | 1.34 | ||
| GRB170113A | 1.97 | 0.92 | 0.58 | 16.50 | 0.76 | ||
| GRB170519A | 0.82 | 0.37 | 0.17 | 8.11 | 0.44 | ||
| GRB170705A | 2.01 | 1.20 | 0.40 | 19.20 | 0.74 | ||
| GRB180205A | 1.41 | 0.50 | 0.56 | 8.95 | 0.80 | ||
| GRB180325A | 2.25 | 1.30 | 0.76 | 2.00 5 | 15.70 | 0.93 | |
| GRB180620B | 1.12 | 0.50 | 0.26 | 19.50 | 1.16 | ||
| GRB180624A | 2.85 | 1.00 | 1.54 | 3.16 5 | 2.29 | 0.21 | |
| GRB180720B | 0.65 | 0.34 | 0.11 | 207.00 | 7.86 | ||
| GRB180728A | 0.12 | 0.07 | 0.06 | 41.20 | 1.06 | ||
| GRB181010A | 1.39 | 2.30 | 0.64 | 8.17 | 0.42 | ||
| GRB181020A | 2.94 | 0.75 | 0.62 | 1.58 5 | 26.30 | 1.08 | |
| GRB190114A | 3.38 | 1.50 | 2.00 | 6.52 | 0.36 | ||
| GRB190114C | 0.42 | 8.00 | 1.10 | 37.40 | 1.35 | ||
| GRB190829A | 0.08 | 1.40 | 0.19 | 106.00 | 3.50 | ||
| GRB191011A | 1.72 | 0.67 | 0.68 | 2.17 | 0.21 | ||
| GRB201015A | 0.43 | 0.58 | 1.02 | 1.69 | 0.30 | ||
| GRB201020B | 0.80 | 0.71 | 0.88 | 6.27 | 1.05 | ||
| GRB201221A | 5.70 | 8.30 | 13.20 | 4.68 | 0.49 | ||
| GRB210204A | 0.88 | 0.61 | 0.82 | 4.03 | 0.65 | ||
| GRB210210A | 0.71 | 0.12 | 0.19 | 14.80 | 1.03 | ||
| GRB210321A | 1.49 | 0.88 | 0.90 | 4.28 | 0.44 | ||
| GRB210619B | 1.94 | 0.70 | 0.52 | 76.30 | 2.69 | ||
| GRB210702A | 1.16 | 0.23 | 0.18 | 30.10 | 1.10 | ||
| GRB211024B | 1.11 | 0.30 | 0.13 | 103.00 | 3.90 | ||
| GRB211207A | 2.27 | 1.60 | 1.92 | 1.36 | 0.19 | ||
| GRB221009A | 0.15 | 1.40 | 0.76 | 229.00 | 17.90 | ||
| GRB230325A | 1.66 | 1.70 | 1.22 | 2.71 | 0.34 | ||
| GRB231118A | 0.83 | 0.89 | 0.44 | 45.00 | 4.00 | ||
| GRB240419A | 5.18 | 11.30 | 13.20 | 2.20 | 0.33 |
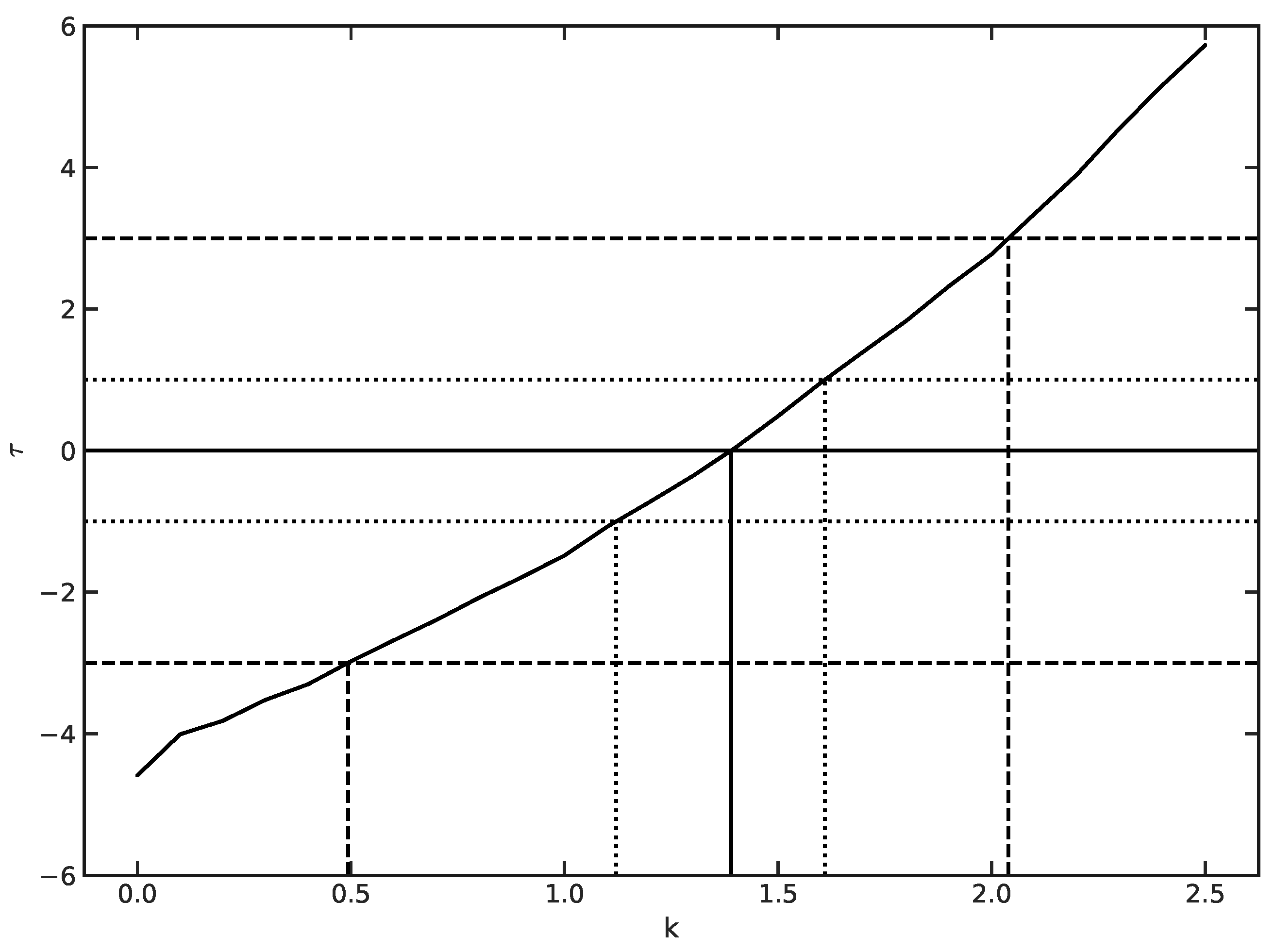
2.2. Analysis Procedure
3. Result
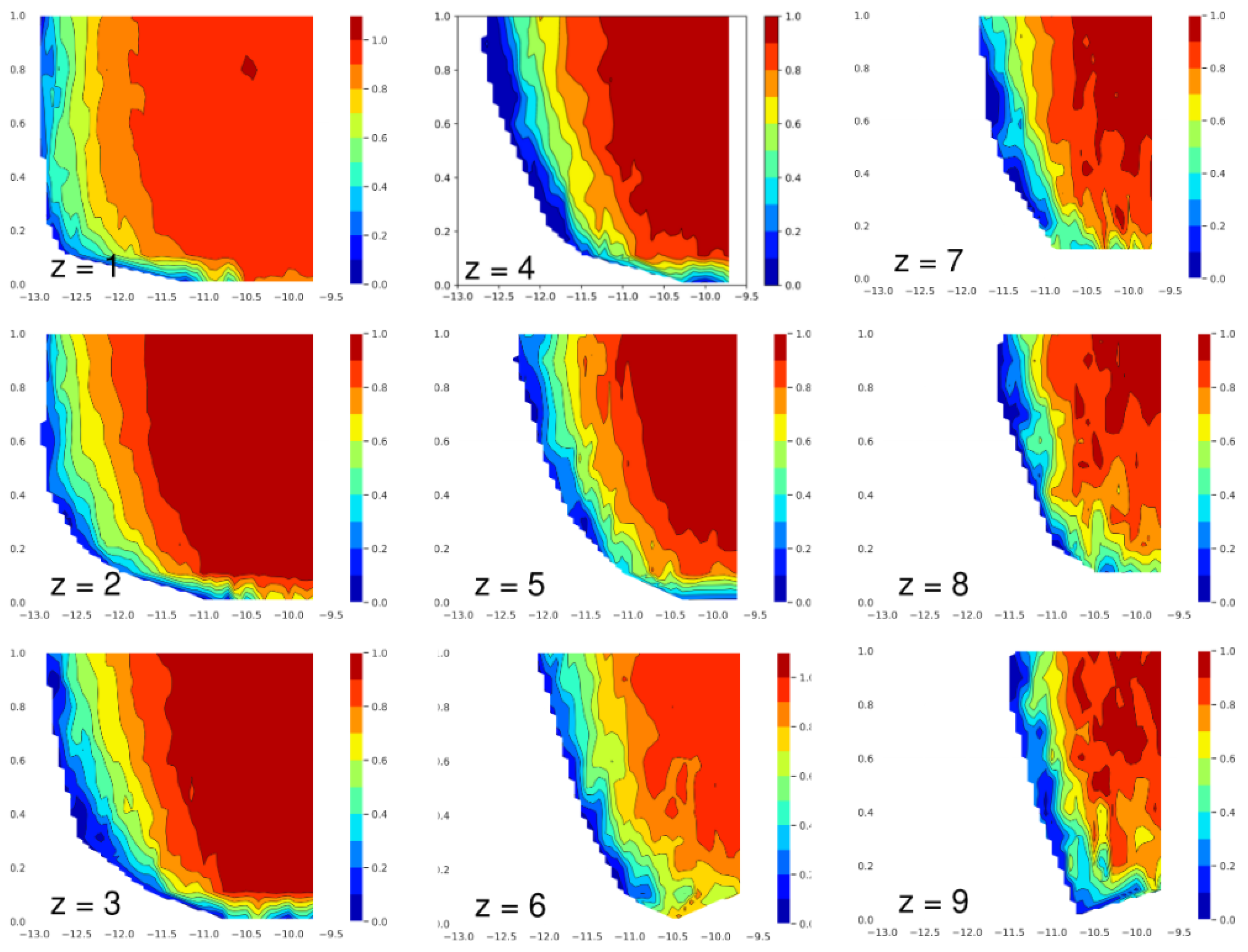
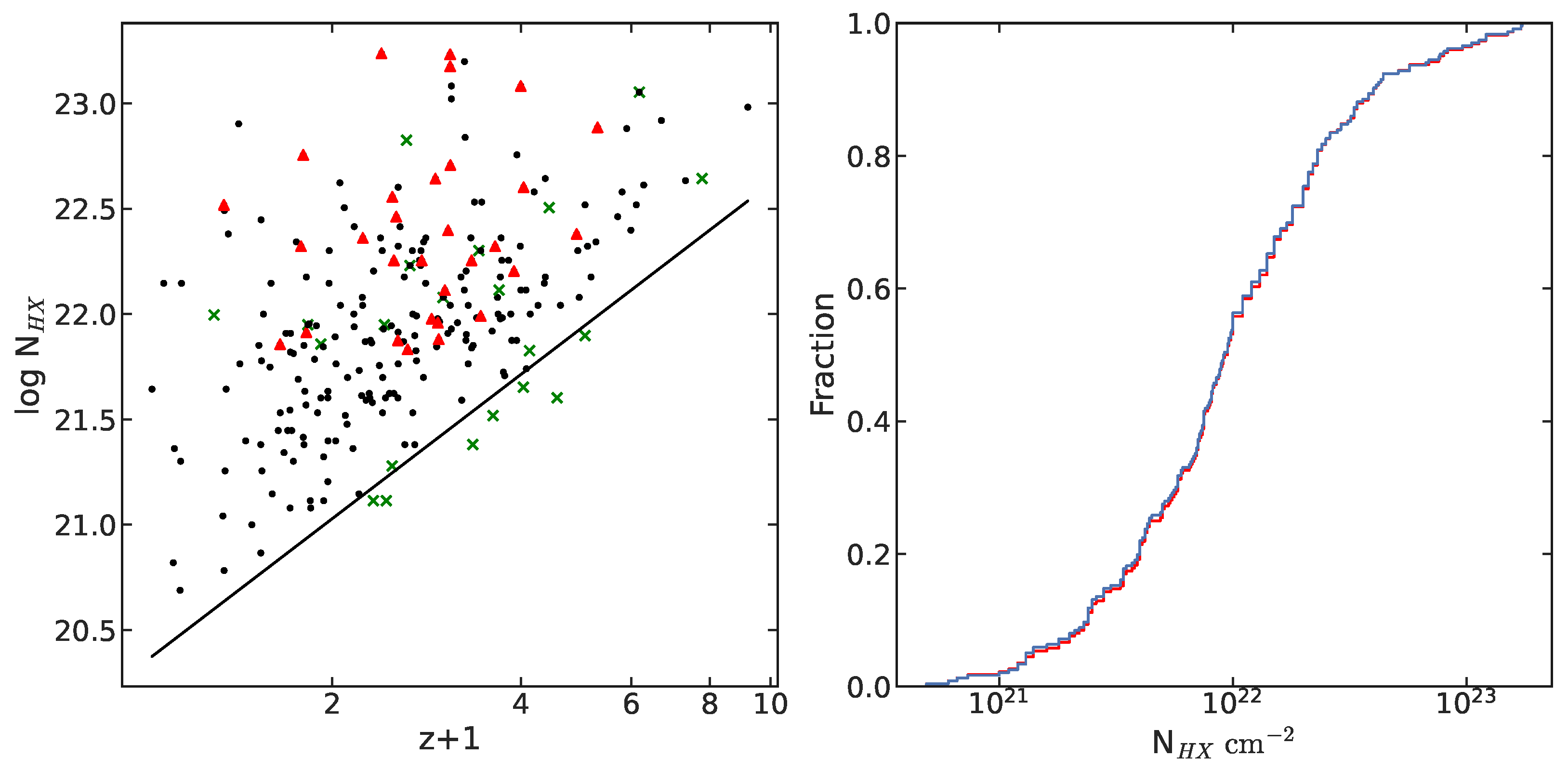
3.1. Evolution of the Redshift of
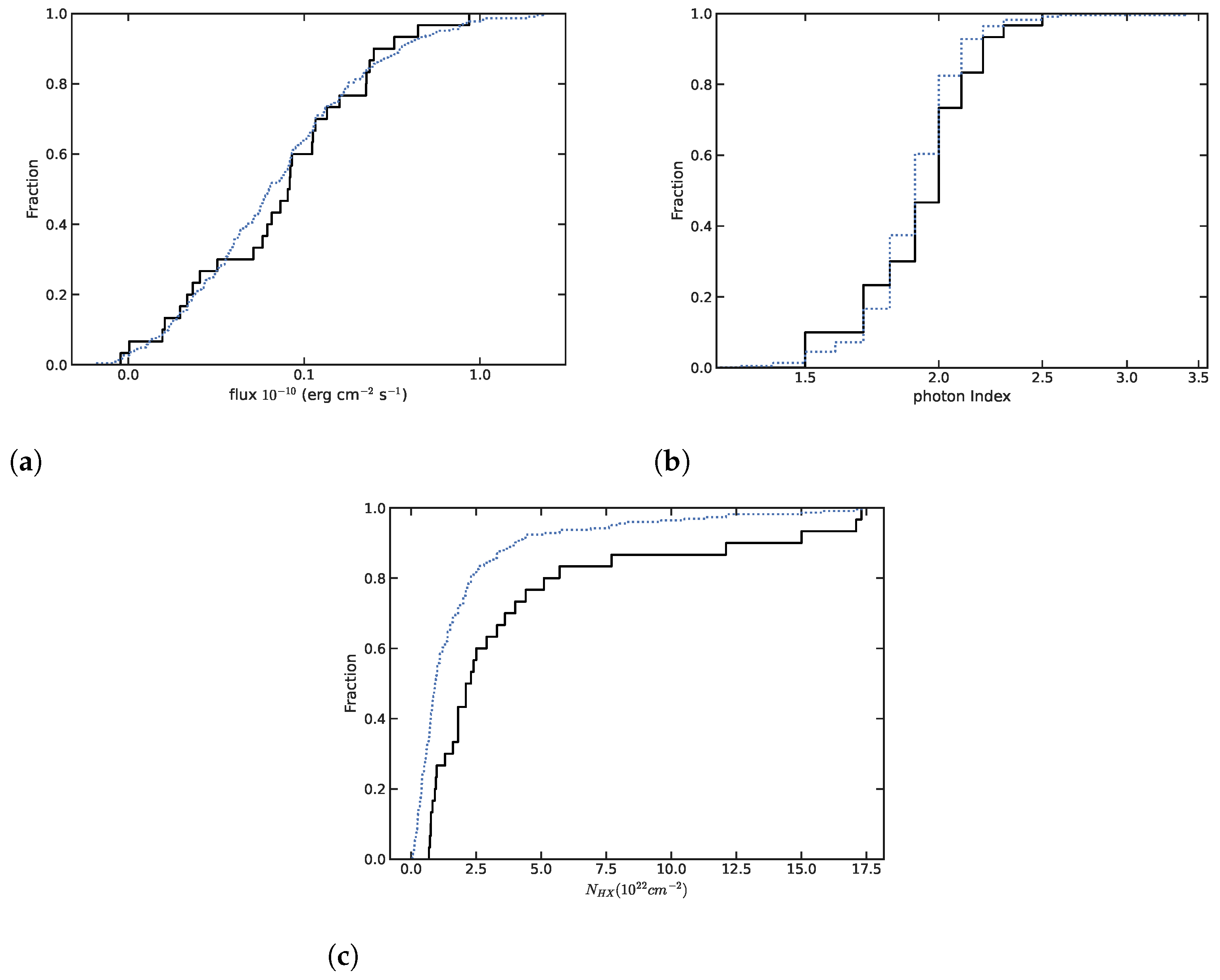
3.2. Properties of Optically Dark GRBs
3.3. The of GRBs with High Redshift
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dainotti, M.G.; Narendra, A.; Pollo, A.; Petrosian, V.; Bogdan, M.; Iwasaki, K.; Prochaska, J.X.; Rinaldi, E.; Zhou, D. Gamma-Ray Bursts as Distance Indicators by a Statistical Learning Approach. Astrophys. J. Lett. 2024, 967, L30. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Taira, E.; Wang, E.; Lehman, E.; Narendra, A.; Pollo, A.; Madejski, G.M.; Petrosian, V.; Bogdan, M.; Dey, A.; et al. Inferring the Redshift of More Than 150 GRBs with a Machine-learning Ensemble Model. Astrophys. J. Suppl. Ser. 2024, 271, 22. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Fynbo, J.P.U.; de Ugarte Postigo, A.; Japelj, J.; Wiersema, K.; Malesani, D.; Perley, D.A.; Levan, A.J.; Selsing, J.; Cenko, S.B.; et al. The Fraction of Ionizing Radiation from Massive Stars That Escapes to the Intergalactic Medium. Mon. Not. R. Astron. Soc. 2019, 483, 5380–5408. [Google Scholar] [CrossRef]
- Jakobsson, P.; Fynbo, J.P.U.; Ledoux, C.; Vreeswijk, P.; Kann, D.A.; Hjorth, J.; Priddey, R.S.; Tanvir, N.R.; Reichart, D.; Gorosabel, J.; et al. H I Column Densities of z > 2 Swift Gamma-Ray Bursts. Astron. Astrophys. 2006, 460, L13–L17. [Google Scholar] [CrossRef][Green Version]
- Rahin, R.; Behar, E. Cosmological Evolution of the Absorption of Υ-ray Burst X-Ray Afterglows. Astrophys. J. 2019, 885, 47. [Google Scholar] [CrossRef]
- Dalton, T.; Morris, S.L. Using Realistic Host Galaxy Metallicities to Improve the GRB X-ray Equivalent Total Hydrogen Column Density and Constrain the Intergalactic Medium Density. Mon. Not. R. Astron. Soc. 2020, 495, 2342–2353. [Google Scholar] [CrossRef]
- Watson, D.; Jakobsson, P. Dust extinction Bias in the Column Density Distribution of Gamma-ray Bursts: High Column Density, Low-Redshift Grbs Are More Heavily Obscured. Astrophys. J. 2012, 754, 89. [Google Scholar] [CrossRef][Green Version]
- Fynbo, J.U.; Gorosabel, J.; Dall, T.H.; Hjorth, J.; Pedersen, H.; Andersen, M.I.; Møller, P.; Holland, S.; Smail, I.; Kobayashi, N.; et al. The Optical Afterglow and Host Galaxy of GRB 000926. Astron. Astrophys. 2001, 373, 796–804. [Google Scholar] [CrossRef]
- Greiner, J.; Krühler, T.; Klose, S.; Afonso, P.; Clemens, C.; Filgas, R.; Hartmann, D.H.; Yoldaş, A.K.; Nardini, M.; Estay, F.O.; et al. The Nature of “Dark” Gamma-Ray Bursts. Astron. Astrophys. 2011, 526, A30. [Google Scholar] [CrossRef]
- Jakobsson, P.; Hjorth, J.; Fynbo, J.P.U.; Watson, D.; Pedersen, K.; Björnsson, G.; Gorosabel, J. Swift Identification of Dark Gamma-Ray Bursts. Astrophys. J. 2004, 617, L21–L24. [Google Scholar] [CrossRef]
- van der Horst, A.J.; Kouveliotou, C.; Gehrels, N.; Rol, E.; Wijers, R.A.M.J.; Cannizzo, J.K.; Racusin, J.; Burrows, D.N. OPTICAL CLASSIFICATION OF GAMMA-RAY BURSTS IN THE SWIFT ERA. Astrophys. J. 2009, 699, 1087–1091. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 497, L17–L20. [Google Scholar] [CrossRef]
- Piran, T. Gamma-Ray Bursts and the Fireball Model. Phys. Rep. 1999, 314, 575–667. [Google Scholar] [CrossRef]
- Lazzati, D.; Covino, S.; Ghisellini, G. On the Role of Extinction in Failed Gamma-Ray Burst optical/IR Afterglows. Mon. Not. R. Astron. Soc. 2002, 330, 583–590. [Google Scholar] [CrossRef][Green Version]
- Tanvir, N.R.; Levan, A.J.; Rol, E.; Starling, R.L.C.; Gorosabel, J.; Priddey, R.S.; Malesani, D.; Jakobsson, P.; O’Brien, P.T.; Jaunsen, A.O.; et al. The Extreme, Red Afterglow of GRB 060923A: Distance or Dust? Mon. Not. R. Astron. Soc. 2008, 388, 1743–1750. [Google Scholar] [CrossRef][Green Version]
- Cucchiara, A.; Levan, A.J.; Fox, D.B.; Tanvir, N.R.; Ukwatta, T.N.; Berger, E.; Krühler, T.; Yoldaş, A.K.; Wu, X.F.; Toma, K.; et al. A Photometric Redshift of z 9.4 for GRB 090429B. Astrophys. J. 2011, 736, 7. [Google Scholar] [CrossRef]
- Perley, D.A.; Cenko, S.B.; Bloom, J.S.; Chen, H.W.; Butler, N.R.; Kocevski, D.; Prochaska, J.X.; Brodwin, M.; Glazebrook, K.; Kasliwal, M.M.; et al. The Host Galaxies of Swift Dark Gamma-Ray Bursts: Observational Constraints on Highly Obscured and Very High-Redshift GRBs. Astron. J. 2009, 138, 1690–1708. [Google Scholar] [CrossRef][Green Version]
- Higgins, A.B.; van der Horst, A.J.; Starling, R.L.C.; Anderson, G.; Perley, D.; van Eerten, H.; Wiersema, K.; Jakobsson, P.; Kouveliotou, C.; Lamb, G.P.; et al. Detailed Multiwavelength Modelling of the Dark GRB 140713A and Its Host Galaxy. Mon. Not. R. Astron. Soc. 2019, 484, 5245–5255. [Google Scholar] [CrossRef]
- Campana, S.; Thone, C.C.; Postigo, A.d.U.; Tagliaferri, G.; Moretti, A.; Covino, S. The X-ray Absorbing Column Densities of Swift Gamma-ray Bursts. Mon. Not. R. Astron. Soc. 2010, 402, 2429–2435. [Google Scholar] [CrossRef]
- Behar, E.; Dado, S.; Dar, A.; Laor, A. CAN The soft X-ray Opacity toward High-Redshift Sources Probe the Missing Baryons? Astrophys. J. 2011, 734, 26. [Google Scholar] [CrossRef]
- Campana, S.; Salvaterra, R.; Melandri, A.; Vergani, S.D.; Covino, S.; D’Avanzo, P.; Fugazza, D.; Ghisellini, G.; Sbarufatti, B.; Tagliaferri, G. The X-ray Absorbing Column Density of a Complete Sample of Bright Swift Gamma-Ray Bursts: Column Densities of Bright Swift GRBs. Mon. Not. R. Astron. Soc. 2012, 421, 1697–1702. [Google Scholar] [CrossRef]
- Starling, R.L.C.; Willingale, R.; Tanvir, N.R.; Scott, A.E.; Wiersema, K.; O’Brien, P.T.; Levan, A.J.; Stewart, G.C. X-Ray Absorption Evolution in Gamma-Ray Bursts: Intergalactic Medium or Evolutionary Signature of Their Host Galaxies? Mon. Not. R. Astron. Soc. 2013, 431, 3159–3176. [Google Scholar] [CrossRef]
- Efron, B.; Petrosian, V. A Simple Test of Independence for Truncated Data with Applications to Redshift Surveys. Astrophys. J. 1992, 399, 345. [Google Scholar] [CrossRef]
- Efron, B.; Petrosian, V. Nonparametric Methods for Doubly Truncated Data. J. Am. Stat. Assoc. 1999, 94, 824–834. [Google Scholar] [CrossRef]
- Kocevski, D.; Liang, E. Quantifying the Luminosity Evolution in Gamma-Ray Bursts. Astrophys. J. 2006, 642, 371–381. [Google Scholar] [CrossRef]
- Yonetoku, D.; Murakami, T.; Nakamura, T.; Yamazaki, R.; Inoue, A.K.; Ioka, K. Gamma-Ray Burst Formation Rate Inferred from the Spectral Peak Energy–Peak Luminosity Relation. Astrophys. J. 2004, 609, 935–951. [Google Scholar] [CrossRef]
- Singal, J.; Petrosian, V.; Lawrence, A.; Stawarz, Ł. On the Radio and Optical Luminosity Evolution of Quasars. Astrophys. J. 2011, 743, 104. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Petrosian, V.; Singal, J.; Ostrowski, M. Determination of the Intrinsic Luminosity Time Correlation in the X-ray afterglows of Gamma-ray bursts. Astrophys. J. 2013, 774, 157. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Vecchio, R.D.; Shigehiro, N.; Capozziello, S. Selection Effects in Gamma-Ray Burst Correlations: Consequences on the Ratio Between Gamma-ray Burst and Star Formation rates. Astrophys. J. 2015, 800, 31. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.; Sarracino, G.; Nagataki, S.; Capozziello, S.; Fraija, N. The X-ray Fundamental Plane of the Platinum Sample, the Kilonovae and the SNe Ib/c Associated with GRBs. Astrophys. J. 2020, 904, 97. [Google Scholar] [CrossRef]
- Yu, H.; Wang, F.Y.; Dai, Z.G.; Cheng, K.S. An Unexpectedly Low-Redshift Excess of swift Gamma-ray Burst Rate. Astrophys. J. Suppl. Ser. 2015, 218, 13. [Google Scholar] [CrossRef]
- Petrosian, V.; Kitanidis, E.; Kocevski, D. Cosmological Evolution of Long Gamma-ray Bursts and Star Formation Rate. Astrophys. J. 2015, 806, 44. [Google Scholar] [CrossRef]
- Pescalli, A.; Ghirlanda, G.; Salvaterra, R.; Ghisellini, G.; Vergani, S.D.; Nappo, F.; Salafia, O.S.; Melandri, A.; Covino, S.; Götz, D. The Rate and Luminosity Function of Long Gamma Ray Bursts. Astron. Astrophys. 2016, 587, A40. [Google Scholar] [CrossRef]
- Lloyd-Ronning, N.M.; Aykutalp, A.; Johnson, J.L. On the Cosmological Evolution of Long Gamma-Ray Burst Properties. Mon. Not. R. Astron. Soc. 2019, 488, 5823–5832. [Google Scholar] [CrossRef]
- Evans, P.A.; Beardmore, A.P.; Page, K.L.; Osborne, J.P.; O’Brien, P.T.; Willingale, R.; Starling, R.L.C.; Burrows, D.N.; Godet, O.; Vetere, L.; et al. Methods and Results of an Automatic Analysis of a Complete Sample of Swift-XRT Observations of GRBs. Mon. Not. R. Astron. Soc. 2009, 397, 1177–1201. [Google Scholar] [CrossRef]
- Chrimes, A.A.; Levan, A.J.; Stanway, E.R.; Lyman, J.D.; Fruchter, A.S.; Jakobsson, P.; O’Brien, P.; Perley, D.A.; Tanvir, N.R.; Wheatley, P.J.; et al. Chandra and Hubble Space Telescope Observations of Dark Gamma-Ray Bursts and Their Host Galaxies. Mon. Not. R. Astron. Soc. 2019, 486, 3105–3117. [Google Scholar] [CrossRef]
- Fynbo, J.P.U.; Jakobsson, P.; Prochaska, J.X.; Malesani, D.; Ledoux, C.; de Ugarte Postigo, A.; Nardini, M.; Vreeswijk, P.M.; Wiersema, K.; Hjorth, J.; et al. Low-Resolution Spectroscopy of Gamma-ray Burst Optical Afterglows: Biases in the Swift Sample and Characterization of the Absorbers. Astrophys. J. Suppl. Ser. 2009, 185, 526–573. [Google Scholar] [CrossRef]
- Hashimoto, T.; Ohta, K.; Aoki, K.; Tanaka, I.; Yabe, K.; Kawai, N.; Aoki, W.; Furusawa, H.; Hattori, T.; Iye, M.; et al. “DARK” GRB 080325 in a Dusty Massive Galaxy at z 2. Astrophys. J. 2010, 719, 378–384. [Google Scholar] [CrossRef]
- Burrows, D.N.; Hill, J.E.; Nousek, J.A.; Kennea, J.A.; Wells, A.; Osborne, J.P.; Abbey, A.F.; Beardmore, A.; Mukerjee, K.; Short, A.D.T.; et al. The Swift X-ray Telescope. Space Sci. Rev. 2005, 120, 165–195. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Petrosian, V.; Bowden, L. Cosmological Evolution of the Formation Rate of Short Gamma-Ray Bursts with and Without Extended Emission. Astrophys. J. Lett. 2021, 914, L40. [Google Scholar] [CrossRef]
- Hjorth, J.; Malesani, D.; Jakobsson, P.; Jaunsen, A.O.; Fynbo, J.P.U.; Gorosabel, J.; Krühler, T.; Levan, A.J.; Michałowski, M.J.; Milvang-Jensen, B.; et al. The Optically Unbiased Gamma-ray Burst Host (Tough) Survey. I. Survey Design and Catalogs. Astrophys. J. 2012, 756, 187. [Google Scholar] [CrossRef][Green Version]
- Perley, D.A.; Levan, A.J.; Tanvir, N.R.; Cenko, S.B.; Bloom, J.S.; Hjorth, J.; Krühler, T.; Filippenko, A.V.; Fruchter, A.; Fynbo, J.P.U.; et al. A Population of Massive, Luminous Galaxies Hosting Heavily Dust-Obscured Gamma-ray bursts: Implications for the Use of Grbs As Tracers of Cosmic Star Formation. Astrophys. J. 2013, 778, 128. [Google Scholar] [CrossRef]
- Levesque, E.M.; Kewley, L.J.; Graham, J.F.; Fruchter, A.S. A high-metallicity host environment for the long-duration GRB 020819. Astrophys. J. 2010, 712, L26–L30. [Google Scholar] [CrossRef]
- Castro-Tirado, A.J.; Bremer, M.; McBreen, S.; Gorosabel, J.; Guziy, S.; Fakthullin, T.A.; Sokolov, V.V.; González Delgado, R.M.; Bihain, G.; Pandey, S.B.; et al. The Dark Nature of GRB 051022 and Its Host Galaxy. Astron. Astrophys. 2007, 475, 101–107. [Google Scholar] [CrossRef]
- Trani, A.A.; Mapelli, M.; Bressan, A. The Impact of Metallicity-Dependent Mass Loss Versus Dynamical Heating on the Early Evolution of Star Clusters. Mon. Not. R. Astron. Soc. 2014, 445, 1967–1976. [Google Scholar] [CrossRef][Green Version]
- Haislip, J.; Nysewander, M.; Reichart, D.; Levan, A.; Tanvir, N.; Cenko, S.B.; Fox, D.B.; Price, P.A.; Castro-Tirado, A.J.; Gorosabel, J.; et al. AuthA photometric redshift of z = 6.39 ± 0.12 for GRB 050904. Nature 2005, 440, 181–183. [Google Scholar] [CrossRef] [PubMed]
- Niino, Y.; Aoki, K.; Hashimoto, T.; Hattori, T.; Ishikawa, S.; Kashikawa, N.; Kosugi, G.; Onoue, M.; Toshikawa, J.; Yabe, K. The Redshift-Selected Sample of Long Gamma-Ray Burst Host Galaxies: The Overall Metallicity Distribution at z ≪ 0.4. Publ. Astron. Soc. Jpn. 2017, 69, 27. [Google Scholar]
- Cucchiara, A.; Fumagalli, M.; Rafelski, M.; Kocevski, D.; Prochaska, J.X.; Cooke, R.J.; Becker, G.D. Unveiling the Secrets of Metallicity and Massive Star Formation using Dlas along Gamma-ray Bursts. Astrophys. J. 2015, 804, 51. [Google Scholar] [CrossRef]
- Graham, J.F.; Schady, P.; Fruchter, A.S. A Surprising Lack of Metallicity Evolution with Redshift in the Long Gamma-Ray Burst Host Galaxy Population. Astrophys. J. 2023, 954, 13. [Google Scholar] [CrossRef]
- Petrosian, V.; Dainotti, M.G. Progenitors of Low-redshift Gamma-Ray Bursts. Astrophys. J. Lett. 2024, 963, L12. [Google Scholar] [CrossRef]
- Dong, X.F.; Li, X.J.; Zhang, Z.B.; Zhang, X.L. A Comparative Study of Luminosity Functions and Event Rate Densities of Long GRBs with Non-Parametric Method. Mon. Not. R. Astron. Soc. 2022, 513, 1078–1087. [Google Scholar] [CrossRef]
- Bolmer, J.; Greiner, J.; Krühler, T.; Schady, P.; Ledoux, C.; Tanvir, N.R.; Levan, A.J. Dust Reddening and Extinction Curves Toward Gamma-Ray Bursts at z > 4. Astron. Astrophys. 2018, 609, A62. [Google Scholar] [CrossRef]
- Cen, R.; Kimm, T. Diverse Properties of Interstellar Medium Embedding Gamma-ray Bursts at the Epoch of Reionization. Astrophys. J. 2014, 794, 50. [Google Scholar] [CrossRef]
- Corre, D.; Buat, V.; Basa, S.; Boissier, S.; Japelj, J.; Palmerio, J.; Salvaterra, R.; Vergani, S.D.; Zafar, T. Investigation of Dust Attenuation and Star Formation Activity in Galaxies Hosting GRBs. Astron. Astrophys. 2018, 617, A141. [Google Scholar] [CrossRef]
- Wilkins, S.M.; Trentham, N.; Hopkins, A.M. The Evolution of Stellar Mass and the Implied Star Formation History. Mon. Not. R. Astron. Soc. 2008, 385, 687–694. [Google Scholar] [CrossRef]
- Nanayakkara, T.; Glazebrook, K.; Kacprzak, G.G.; Yuan, T.; Fisher, D.; Tran, K.V.; Kewley, L.J.; Spitler, L.; Alcorn, L.; Cowley, M.; et al. ZFIRE: Using Hα Equivalent Widths to Investigate the in Situ Initial Mass Function at z 2. Mon. Not. R. Astron. Soc. 2017, 468, 3071–3108. [Google Scholar] [CrossRef]
- Stacy, A.; Greif, T.H.; Bromm, V. The First Stars: Formation of Binaries and Small Multiple Systems. Mon. Not. R. Astron. Soc. 2010, 403, 45–60. [Google Scholar] [CrossRef]
- Toma, K.; Sakamoto, T.; Mészáros, P. Population III Gamma-ray Burst Afterglows: Constraints on Stellar Masses and External Medium Densities. Astrophys. J. 2011, 731, 127. [Google Scholar] [CrossRef]
- Bromm, V.; Loeb, A. High-Redshift Gamma-Ray Bursts from Population III Progenitors. Astrophys. J. 2006, 642, 382–388. [Google Scholar] [CrossRef]
- Campisi, M.A.; Maio, U.; Salvaterra, R.; Ciardi, B. Population III Stars and the Long Gamma-Ray Burst Rate: Population III Stars and LGRBs. Mon. Not. R. Astron. Soc. 2011, 416, 2760–2767. [Google Scholar] [CrossRef]
- Lamb, D.Q.; Reichart, D.E. Gamma-Ray Bursts as a Probe of the Very High Redshift Universe. Astrophys. J. 2000, 536, 1. [Google Scholar] [CrossRef]
- Collaboration, P.; Adam, R.; Aghanim, N.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck Intermediate Results: XLVII. Planck Constraints on Reionization History. Astron. Astrophys. 2016, 596, A108. [Google Scholar]
- Chen, H.W.; Prochaska, J.X.; Gnedin, N.Y. A New Constraint on the Escape Fraction in Distant Galaxies Using γ-Ray Burst Afterglow Spectroscopy. Astrophys. J. 2007, 667, L125. [Google Scholar] [CrossRef]
- Phillips, G.D.; Oey, M.S.; Cuevas, M.; Castro, N.; Kothari, R. Runaway OB Stars in the Small Magellanic Cloud. III. Updated Kinematics and Insights into Dynamical Versus Supernova Ejections. Astrophys. J. 2024, 966, 243. [Google Scholar] [CrossRef]
- Le Floc’h, E.; Charmandaris, V.; Gordon, K.; Forrest, W.J.; Brandl, B.; Schaerer, D.; Dessauges-Zavadsky, M.; Armus, L. THE FIRST INFRARED STUDY OF THE CLOSE ENVIRONMENT OF A LONG GAMMA-RAY BURST. Astrophys. J. 2012, 746, 7. [Google Scholar] [CrossRef][Green Version]
- Tanvir, N.R.; Le Floc’h, E.; Christensen, L.; Caruana, J.; Salvaterra, R.; Ghirlanda, G.; Ciardi, B.; Maio, U.; D’Odorico, V.; Piedipalumbo, E.; et al. Exploration of the High-Redshift Universe Enabled by THESEUS. Exp. Astron. 2021, 52, 219–244. [Google Scholar] [CrossRef]
- Yonetoku, D.; Mihara, T.; Doi, A.; Sakamoto, T.; Tsumura, K.; Ioka, K.; Amaya, Y.; Arimoto, M.; Enoto, T.; Fujii, T.; et al. High-z Gamma-Ray Bursts Unraveling the Dark Ages and Extreme Space-Time Mission: HiZ-GUNDAM. In Proceedings of the Space Telescopes and Instrumentation 2020: Ultraviolet to Gamma Ray, Online, 14–18 December 2020; p. 318. [Google Scholar]
- Lanza, M.L.; Godet, O.; Arcier, B.; Yassine, M.; Atteia, J.L.; Bouchet, L. High-z Gamma-Ray Burst Detection by SVOM/ECLAIRs: Impact of Instrumental Biases on the Bursts’ Measured Properties. Astron. Astrophys. 2024, 685, A163. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arumaningtyas, E.P.; Al Rasyid, H.; Dainotti, M.G.; Yonetoku, D. The Density and Ionization Profiles of Optically Dark and High-Redshift GRBs Probed by X-ray Absorption. Galaxies 2024, 12, 51. https://doi.org/10.3390/galaxies12050051
Arumaningtyas EP, Al Rasyid H, Dainotti MG, Yonetoku D. The Density and Ionization Profiles of Optically Dark and High-Redshift GRBs Probed by X-ray Absorption. Galaxies. 2024; 12(5):51. https://doi.org/10.3390/galaxies12050051
Chicago/Turabian StyleArumaningtyas, Eka Puspita, Hasan Al Rasyid, Maria Giovanna Dainotti, and Daisuke Yonetoku. 2024. "The Density and Ionization Profiles of Optically Dark and High-Redshift GRBs Probed by X-ray Absorption" Galaxies 12, no. 5: 51. https://doi.org/10.3390/galaxies12050051
APA StyleArumaningtyas, E. P., Al Rasyid, H., Dainotti, M. G., & Yonetoku, D. (2024). The Density and Ionization Profiles of Optically Dark and High-Redshift GRBs Probed by X-ray Absorption. Galaxies, 12(5), 51. https://doi.org/10.3390/galaxies12050051






