Abstract
The dynamical interaction between binary systems is crucial in understanding the nature of orbital motion under the influence of gravitational potential. In our study, we focused on investigating the effects of dynamical forces on the regularity of binary pulsar orbits, which represent a pure two-body system. To incorporate the necessary time dependence and have a regular 3-D axisymmetric potential, we utilized the Rebound package as a numerical integrator. This package integrates the motion of particles under the influence of gravity, allowing for changing orbital parameters at a given instant, and providing a variety of integrators to be used. By analyzing the regularity properties of binaries and their sensitivity to initial conditions, we gained insight into the importance of considering even small perturbations to the system, as they can lead to significant changes in its dynamics.
1. Introduction
Binary systems have two types of orbits: internal orbits, which are primarily governed by the interaction between the two objects (see, e.g., [1] and references therein), and external orbits within the potential of the galaxy, which can significantly affect their dynamics and evolution [2]. The study of binary pulsars in known gravitational potential can be used to constrain galaxies’ initial masses and thin and thick disk parameters. Thus, the various dynamical characteristics for the orbital evolution of neutron stars can be obtained under a certain gravitational potential (see, e.g., [3,4,5,6,7,8,9,10,11,12,13,14]). As a result, it would be possible to determine whether neutron stars have ordered or chaotic orbits, classify ordered orbits, and understand the evolutionary nature of the galactic disk itself. Ordered orbits are found by calculating a third integral of motion in the form of a series [3,15] while the Hamiltonians can be described as the motion in a meridian plane with respect to the radius of a circular orbit (see [16,17]).
The kick velocity resulting from supernovae is a crucial factor in determining the dynamical effect on the orbital parameters of a binary system. This kick can cause significant changes to the velocity and trajectory of the compact object resulting from the collapse, which in turn can have a major impact on the overall dynamics of the binary system [18].
The magnitude and direction of the kick velocity are subject to a number of constraints, such as conservation of momentum and energy, and are highly dependent on the specific physical conditions of the supernova event [19,20,21]. As a result, accurate modeling of kicks requires a detailed understanding of the physical mechanisms that underlie these events, as well as careful consideration of the various constraints that govern the kick velocity [22].
To examine the regular nature of the orbits, we can use tools such as Lyapunov exponents and Poincar maps. The concept of Lyapunov exponents measures the rate at which nearby orbits diverge from each other over time [17,23,24]. However, if the Lyapunov exponent of a binary pulsar system is positive, this indicates that the orbits of the pulsars are chaotic and sensitive to initial conditions. If the Lyapunov exponent is zero or negative, the orbits are considered to be regular and not sensitive to initial conditions. On the other hand, the Poincaré maps provide a graphical representation of the long-term behavior of the orbits if they show regular patterns [25].
The axisymmetric gravitational potential (which is composed of a spheroid, halo, and disk components) can be used to constrain the initial parameters of mass, thin and thick disks, as well as gain a variety of information on the formation and evolution history of a galaxy, and effect of a dark-matter halo on a large scale. We studied the interaction and orbital dynamics of binary pulsars in known gravitational potentials, including the Galactic bulge by Miyamoto–Nagai potential [26] for the perturbation force, using the Paczyński gravitational potential [27].
The purpose of this work is to discuss how the orbits in the axisymmetric galactic gravitational potential of Paczyński potential can be simulated and how such simulations help studies of the dynamical evolution of binary pulsar orbits within our numerical data-sets. The problem to be solved is to study the regular or chaotic character of binary pulsar orbits, which may have certain initial conditions (i.e., mass, orbital period, eccentricity, velocity distributions), and then apply them under a set of galactic potentials.
2. Numerical Simulations for Regular Processes
The Hamiltonian for binary pulsars can be described as a mathematical function that describes the dynamics of the system. It can be expressed as a combination of regular equations of motion and a potential (see [10] and references therein).
where = , = , and = , while x, y, and z are Cartesian coordinates and , , are the conjugate velocities in cartesian coordinates. The preserved Hamiltonian has a value of , which is conserved.
The associated Hamiltonian for the system can be obtained by numerically integrating the motion equations (at z = 0 and = 0).
where the energy’s numerical value is h. The motion equations for pulsars (10 Gyr) under an axisymmetric potential were numerically solved. The potential term represents the interaction between the two bodies in the binary system, while the equations of motion describe how the system evolves over time. To obtain the Hamiltonian for a specific binary pulsar system, numerical integration of the equations of motion with initial conditions of z = 0 and = 0 would be required. This would give the corresponding Hamiltonian, which can then be used to analyze and predict the behavior of the binary pulsar system.
To study and describe a wide range of shapes, from a spherical system to an infinitely thin disk, we have adopted the Miyamoto–Nagai potential [26]. However, this potential can be calculated analytically (see [10] and references therein).
where R is the perpendicular radial distance to the galactic central axis and z is the vertical distance from the galactic plane. The scale length of the disk is represented by , and the scale height in the z direction is represented by . The subscripts I in the equation represent a spheroid and a disk, respectively. The potential parameters are as follows: (for the spheroid component) kpc, kpc, and M⊙; kpc, kpc, and M⊙.
The galactic gravitational potential’s halo component is:
where kpc and . For further information, see [5,10].
To study the reduced-mass of the binary pulsars effectively, the standard two-body problem can be used. As a result, the regular motions can be seen due to the Poincaré–Bendixson theorem (i.e., [28,29]). This theorem can be used to prove that the system will remain in regular motion as long as the dynamical interactions between the two bodies are confined to a closed and bounded region and the flow of the system is smooth.
3. Rebound Package
We used the standard N-body solver, called the Rebound package (see [30]), which could help us make an integration for the N-particle’s motion in the presence of gravity as well as changes in orbital parameters at certain intervals. By following this method, we first need to set up the initial conditions for the system, including the masses, positions, and velocities of the pulsars. We would then use the Rebound package to numerically integrate the equations of motion for the system and track the evolution of the orbits over time. We consider the two-body problem with the following setup: eccentricity , semi-major axis au, , and . As a result, the initial period is yr. The kick is defined to occur one year after the simulation begins ( yr). Energy and angular momentum should be conserved.
However, the initial velocity and the position of the two bodies are given by
It is worth noting that there is a simple linear formula that is sometimes used to describe the magnitude of the kick velocity resulting from supernovae, in which the magnitude of the kick velocity is related to the amount of fallback that occurs during a supernova event. This formula has been used in a number of studies, including [31,32,33].
The formula takes the following form:
where is the final kick velocity, is the maximum velocity drawn from a Maxwellian distribution, and is the fallback factor. The value of ranges between 0, which corresponds to no fallback and a full kick, and 1, which corresponds to total fallback and no kick [34].
The fallback process during a supernova event can introduce additional correlations between different properties of pulsars and can also lead to a larger kick velocity [35]. By incorporating the effects of fallback into models of supernovae, we can gain a more complete understanding of the physical mechanisms that underlie these events and improve our ability to predict the properties and behavior of pulsars and other compact objects [36].
Numerical simulations show a tendency towards periodic behavior in both 2-D and 3-D models, as illustrated in Figure 1 and Figure 2. This provides a broad view of the dynamics of the phase space for a given gravitational potential.
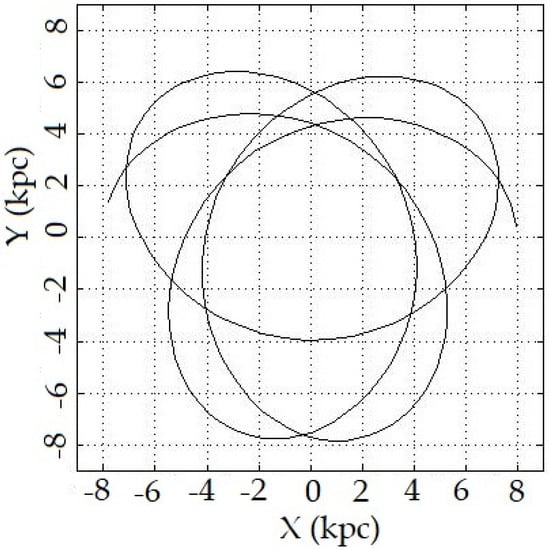
Figure 1.
The consequence of a projection for the 2-D star orbit around a galaxy in the Galactic plane. When projecting the 2-D star orbit onto the Galactic plane, the resulting figure depends on the gravitational potential used to model the galaxy. In our study, we used the Paczyński gravitational potential, which includes the Galactic bulge, and the Miyamoto–Nagai potential to represent the gravitational field of the galaxy.
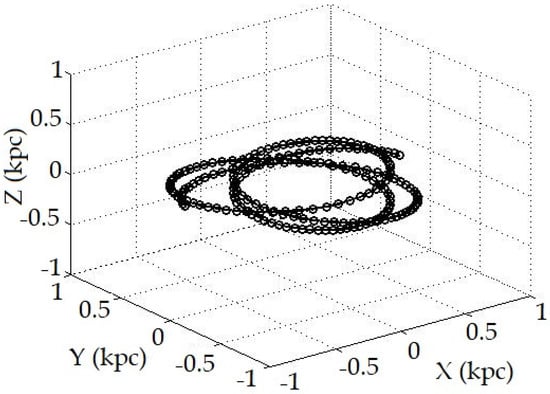
Figure 2.
We modeled the 3−D orbit of the star in the Galactic plane using the Paczyński gravitational potential, which includes the Galactic bulge, and the Miyamoto–Nagai potential to represent the gravitational field of the galaxy.
These figures represent the projection of a star’s orbit around a galaxy in the Galactic plane. However, they depend on the specific gravitational potential used to model the galaxy, such as the Paczyński and Miyamoto–Nagai potentials, in order to describe the gravitational field. As we can see, the 2-D and 3-D projections of the star’s orbit in the galactic plane depend on the shape and strength of the potential and have a disk-like shape. This projection would be influenced by the gravitational force of the disk. To extend our current work, we plan to utilize the Rebound package to numerically integrate the equations of motion for the binary pulsars and track the evolution of the orbits over time.
Figure 3 and Figure 4 demonstrate that the some initial orbital conditions for the binary pulsar system can produce different resulting orbits depending on the timing of the kick during orbit integration. For Figure 3, we consider the two-body problem with an eccentricity of and a semi-major axis of AU. The masses of the white dwarf and the companion star are and , respectively. The initial period in this setup is years. In Figure 4, we use a semi-major axis of AU and the masses of the white dwarf and the companion star are and , respectively. The initial period for this configuration is years. By integrating the orbits of the binary pulsar system and implementing a small kick velocity, we were able to model the resulting orbits in the x-y plane, as depicted in Panel A.
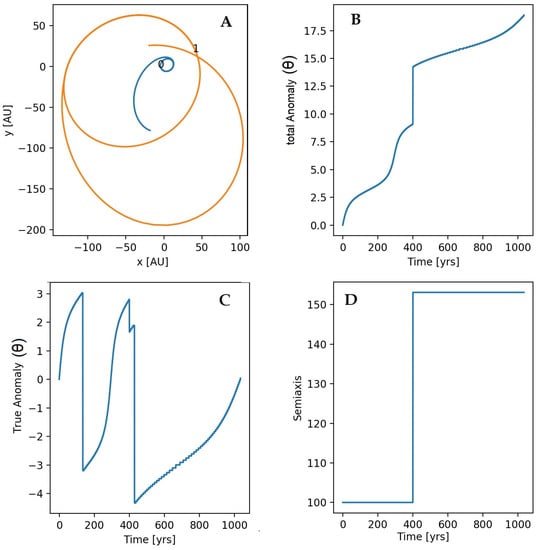
Figure 3.
We modeled the binary pulsar system and integrated the orbits while implementing a small kick velocity. The red color represents the companion star, while the blue color represents the pulsar. The resulting orbits in the x–y plane are shown in Panel A. Panels B and C illustrate the variation of total and true anomalies, respectively, over time periods. To capture the complex behavior of the system, we created a delay plot in Panel D, which shows the effect of the kick velocity modulus of = 15 km/s on the semi-major axis and orbital period. Although the kick velocity is relatively small, we can still observe changes in the orbital parameters of the binary pulsar system.
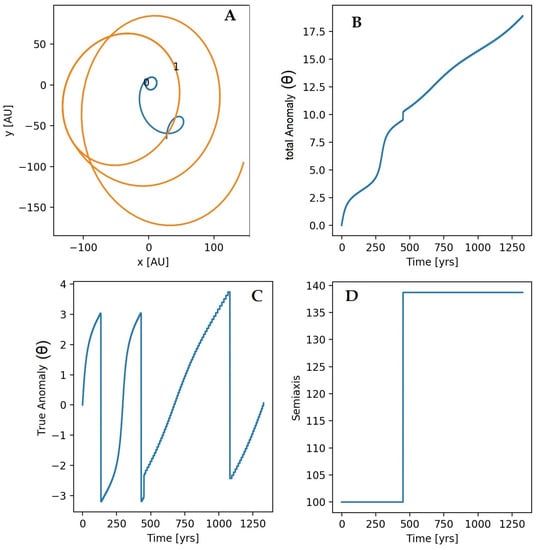
Figure 4.
The same as in Figure 3, but with different initial conditions. The red color represents the companion star, while the blue color represents the pulsar. The explanations for panels A, B, C and D on this figure are the same as in Figure 3, but with different initial conditions, see the text.
In Panel B, we plotted the total anomaly, which is the angle between the line of axis and the reference direction, to show the effect of a small kick velocity on the orbit. As mentioned, this plot demonstrates that the kick velocity can significantly affect the orbit even at small velocities. Therefore, it would be informative to investigate the effect of different kick velocities on the system’s dynamics and understand how the magnitude of the kick affects the orbit. While Panel C in Figure 3 displays a complex pattern of true anomalies, which represents the angle between the position of the pulsar and the line of apsides, the spikes in this plot reflect a variety of changes in the final orbital parameters when the same explosion is applied to initial systems with different companion star masses (M). This means that the explosion of the white dwarf (WD) occurs at the same instant in all cases, and the kick to the companion star is applied at the same time in all modeled binaries. It is interesting to note that by changing the mass of the companion star, we observe different variations in the final orbital parameters, indicating the importance of the companion star’s mass in the system dynamics. In Panel D of Figure 3, a delay plot visualizes the time delay between the pulsars over time, revealing the complex behavior of the binary pulsar system. This plot can provide valuable insights into the system’s long-term behavior, including identifying patterns or regularities in the pulsar orbits, as well as any chaotic behavior that may be present. The delay plot is a crucial tool for identifying changes in the pulsar orbits and linking them to the kick velocity, = 15 km/s (in Figure 3) and = 25 km/s (in Figure 4) applied in the simulation.
4. Conclusions
This work focuses on understanding the dynamics of binary pulsars in 3-D Hamiltonian systems with axisymmetric potential. We keep our attention on the role of initial orbital parameters and binary component masses. On the other hand, the effect of this process can be parameterized analytically and numerically by the parameters of accretion mass and kick velocity imparted to the newborn (younger) pulsar. We identify the correlation of these parameters with the dynamics of binaries. We have also found that the dynamical interaction of binary pulsars with the gravitational potential exhibits stable periodic orbits in the direction of their positions in phase space. Our numerical simulations of these events have described the outcome as regular, resulting in sudden and short-lived changes in their orbits over time. This provides valuable insights into the dynamics of these systems and helps improve our understanding of the gravitational forces at play. The application of numerical simulations in this work can provide a great deal of information that can help to clarify many of the physical processes and could help to identify new trends in the behavior of these systems. Future research will use the Rebound package to apply it to different galactic gravitational potentials, as well as the effect of dark matter.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We are grateful to Juan Carlos Vallejo and Diomar Laobao for helping the simulations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hurley, J.R.; Tout, C.A.; Pols, O.R. Evolution of binary stars and the effect of tides on binary populations. Mon. Not. R. Astron. Soc. 2002, 329, 897. [Google Scholar] [CrossRef]
- Horch, E. Binaries and Multiple Stellar Systems. In Planets, Stars and Stellar Systems; Oswalt, T.D., Barstow, M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Contopoulos, G. Order and Chaos in Dynamical Astronomy; Springer: New York, NY, USA, 2004. [Google Scholar]
- Patsis, P.A.; Kaufmann, D.A.; Gottesman, S.T.; Boonyasait, V. Stellar and gas dynamics of late-type barred-spiral galaxies: NGC 3359, a test case. Mon. Not. R. Astron. Soc. 2009, 394, 142. [Google Scholar] [CrossRef]
- Wei, Y.C.; Taani, A.; Pan, Y.; Wang, J. Neutron star motion in the disk galaxy. Chin. Phys. Lett. 2010, 27, 9801. [Google Scholar]
- Harsoula, M.; Kalapotharako, C.; Contopoulos, G. Diffusion of Chaotic Orbits in Barred Spiral Galaxies. Int. J. Bifurc. Chaos 2011, 21, 2221. [Google Scholar] [CrossRef]
- Zotos, E.E.; Carpintero, D.D. Orbit classification in the meridional plane of a disk galaxy model with a spherical nucleus. Celest. Mech. Dyn. Astron. 2013, 116, 417. [Google Scholar] [CrossRef]
- Patsis, P.A.; Katsanikas, M. The phase space of boxy-peanut and X-shaped bulges in galaxies - I. Properties of non-periodic orbits. Mon. Not. R. Astron. Soc. 2014, 445, 3525. [Google Scholar] [CrossRef]
- Zotos, E.E. How does the mass transport in disk galaxy models influence the character of orbits? BaltA 2014, 23, 37. [Google Scholar] [CrossRef]
- Taani, A.; Vallejo, J.C. Dynamical Monte Carlo simulations of 3-D galactic systems in axisymmetric and triaxial potentials. Publ. Astron. Soc. Aust. 2017, 34, 24. [Google Scholar] [CrossRef]
- Dai, Z.B.; Szkody, P.; Taani, A.; Garnavich, P.M.; Kennedy, M. Quiescent photometric modulations of two low-inclination cataclysmic variables KZ Geminorum and TW Virginis. Astron. Astrophys. 2017, 606, 45. [Google Scholar] [CrossRef]
- Mardini, M.K.; Placco, V.M.; Meiron, Y.; Ishchenko, M.; Avramov, B.; Mazzarini, M.; Berczik, P.; Sedda, M.A.; Beers, T.; Frebel, A. Cosmological Insights into the Early Accretion of r-process-enhanced Stars. I. A Comprehensive Chemodynamical Analysis of LAMOST J1109+ 0754. Astrophys. J. 2020, 903, 88. [Google Scholar] [CrossRef]
- Taani, A.; Vallejo, J.C.; Abu-Saleem, M. Assessing the complexity of orbital parameters after asymmetric kick in binary pulsars. J. High Energy Astrophys. 2022, 35, 83. [Google Scholar] [CrossRef]
- Taani, A.; Karino, S.; Song, L.; Zhang, C.M.; Chaty, S. Determination of wind-fed model parameters of neutron stars in high-mass X-ray binaries. Publ. Astron. Soc. Aust. 2022, 39, e040. [Google Scholar] [CrossRef]
- Cai, Y.; Taani, A.; Zhao, Y.H.; Zhang, C.M. Statistics and evolution of pulsars’ parameters. Chin. Astron. Astrophys. 2012, 36, 137. [Google Scholar] [CrossRef]
- Cincotta, P.M.; Simó, C. Simple tools to study global dynamics in non-axisymmetric galactic potentials-I. Astron. Astrophys. Suppl. Ser. 2000, 147, 2. [Google Scholar] [CrossRef]
- Taani, A.; Abushattal, A.; Mardini, M. The regular dynamics through the finite-time Lyapunov exponent distributions in 3D Hamiltonian systems. Astron. Nachr. 2019, 1, 5. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, C.M.; Taani, A.; Zhao, Y.H. Characteristic age and true age of pulsars. Int. J. Mod. Phys. Conf. Ser. 2013, 23, 95. [Google Scholar] [CrossRef]
- Janka, H.-T. Neutron Star Kicks by the Gravitational Tug-boat Mechanism in Asymmetric Supernova Explosions: Progenitor and Explosion Dependence. Astrophys. J. 2017, 837, 84. [Google Scholar] [CrossRef]
- Mardini, M.K.; Placco, V.M.; Taani, A.; Li, H.; Zhao, G. Metal-poor Stars Observed with the Automated Planet Finder Telescope. II. Chemodynamical Analysis of Six Low-metallicity Stars in the Halo System of the Milky Way. Astrophys. J. 2019, 882, 27. [Google Scholar] [CrossRef]
- Mardini, M.K.; Li, H.; Placco, V.M.; Alexeeva, S.; Carollo, D.; Taani, A.; Ablimit, I.; Wang, L.; Zhao, G. Metal-poor stars observed with the automated planet finder telescope. I. Discovery of five carbon-enhanced metal-poor stars from LAMOST. Astrophys. J. 2019, 875, 89. [Google Scholar] [CrossRef]
- Tauris, T.M.; Kramer, M.; Freire, P.C.C.; Wex, N.; Janka, H.-T.; Langer, N.; Podsiadlowski, P.; Bozzo, E.; Chaty, S.; Kruckow, M. Formation of Double Neutron Star Systems. Astrophys. J. 2017, 846, 170. [Google Scholar] [CrossRef]
- Vallejo, J.C.; Aguirre, J.; Sanjuán, M.A.F. Characterization of the local instability in the Hénon-Heiles Hamiltonian. Phys. Lett. A 2003, 311, 26. [Google Scholar] [CrossRef]
- Ott, W.; Yorke, J.A. When Lyapunov exponents fail to exist. Phys. Rev. E 2008, 78, 056203. [Google Scholar] [CrossRef] [PubMed]
- Vallejo, J.C.; Sanjuan, M.A.F. Predictability of Chaotic Dynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2019; p. 11. [Google Scholar]
- Miyamoto, M.; Nagai, R. Three-dimensional models for the distribution of mass in galaxies. Astron. Soc. Jpn. Publ. 1975, 27, 533. [Google Scholar]
- Paczyński, B. A test of the galactic origin of gamma-ray bursts. Astrophys. J. 1990, 348, 485. [Google Scholar] [CrossRef]
- Arrowsmith, D.K.; Place, C.M. Ordinary Differential Equations, Chapman and Hall Math. Ser.; Chapman & Hall: London, UK, 1982. [Google Scholar]
- Perko, L. Differential Equations and Dynamical Systems, 3rd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Rein, H.; Liu, S.F. REBOUND: An open-source multi-purpose N-body code for collisional dynamics. Astron. Astrophys. 2012, 537, 128. [Google Scholar] [CrossRef]
- Popov, S.B.; Prokhorov, M.E.; Colpi, M.; Treves, A.; Turolla, R. Young compact objects in the Solar vicinity. arXiv 2002, arXiv:0210688. [Google Scholar]
- Bombaci, I.; Popov, S.B. On the nature of the bimodal initial velocity distribution of neutron stars. Astron. Astrophys. 2004, 424, 627. [Google Scholar] [CrossRef]
- Dominik, M.; Belczynski, K.; Fryer, C.; Christopher, H.; Daniel, E.; Berti, E.; Bulik, T.; Mandel, I.; O’Shaughnessy, R. Double Compact Objects. II. Cosmological Merger Rates. Astrophys. J. 2013, 779, 72. [Google Scholar] [CrossRef]
- Abu-Saleem, M.; Taani, A. Retraction and folding on the hyperbolic black hole. Aip Adv. 2021, 11, 015309. [Google Scholar] [CrossRef]
- Janka, H.-T. Natal kicks of stellar mass black holes by asymmetric mass ejection in fallback supernovae. Mon. Not. R. Astron. Soc. 2013, 434, 1355. [Google Scholar] [CrossRef]
- Abu-Saleem, M.; Taani, A. Geometric transformations on a topological black hole and their applications. Chin. J. Phys. 2021, 74, 53. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).