Explaining the Hardening Structures of Helium Spectrum and Boron to Carbon Ratio through Different Propagation Models
Abstract
1. Introduction
2. Models
2.1. Traditional Propagation Model
2.2. Spatially Dependent Propagation
2.3. SDP+Fresh
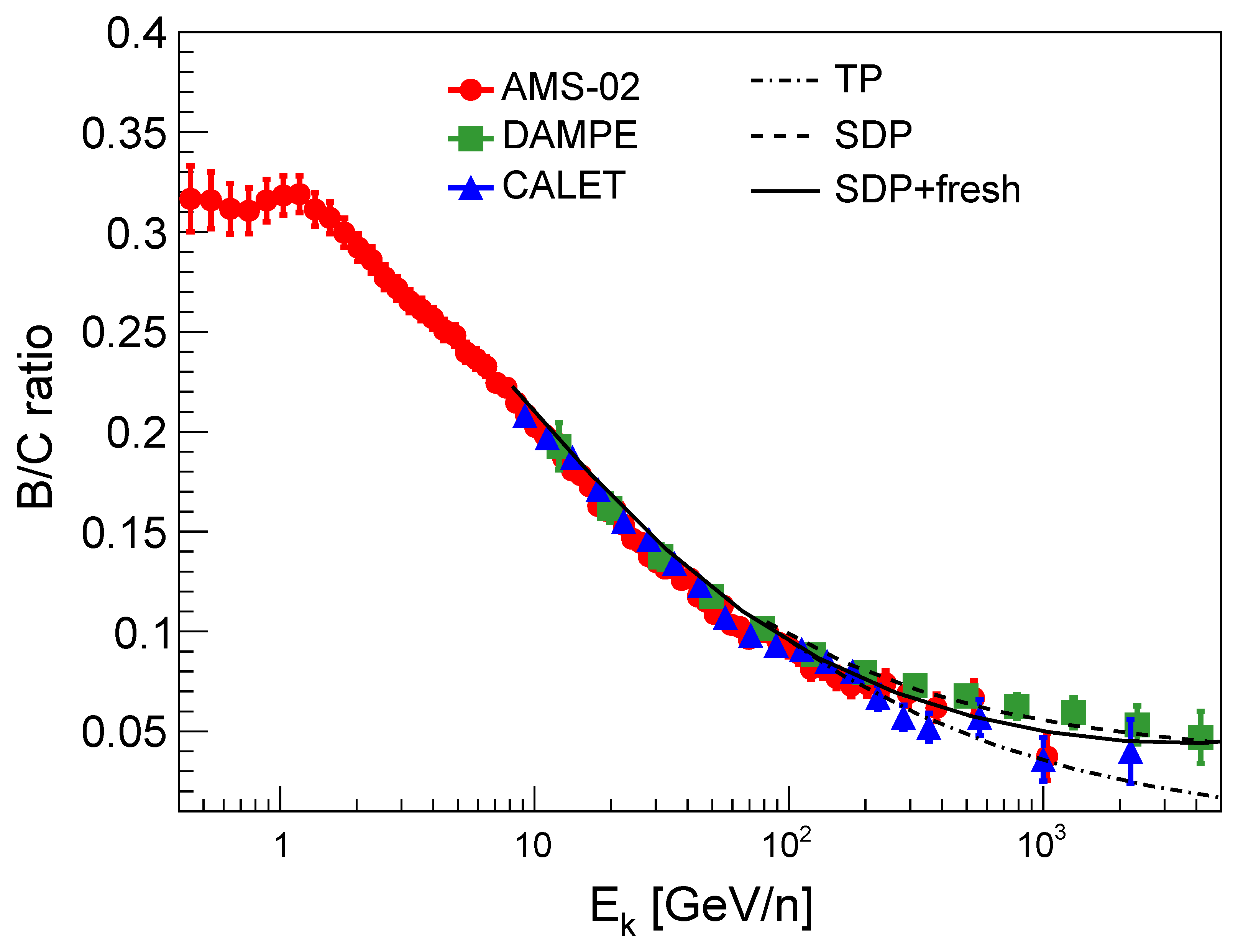
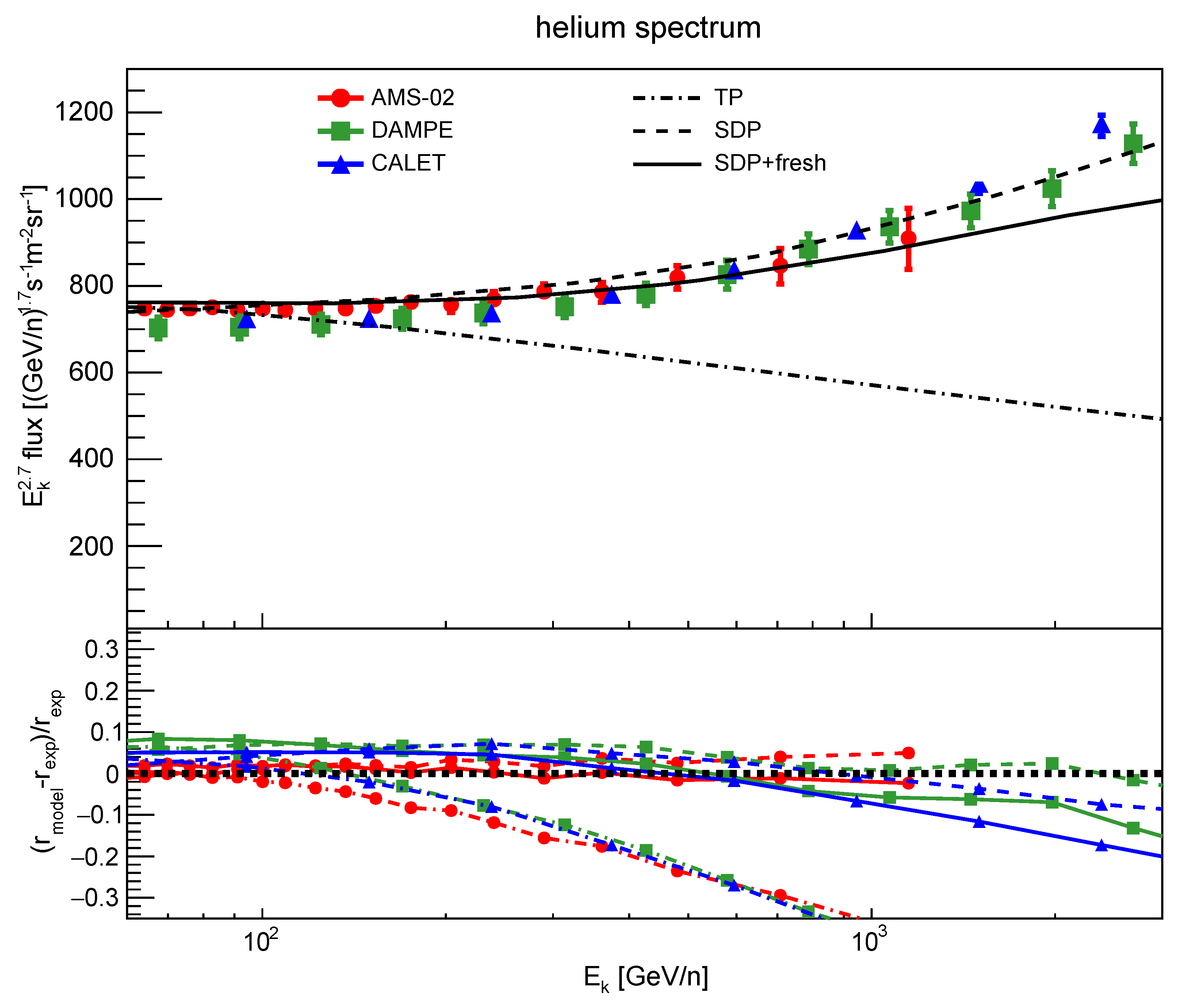
3. Results
3.1. B/C Ratio
3.2. Helium Spectra
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AMS-02 | Alpha Magnetic Spectrometer |
| ATIC-2 | Advanced Thin Ionization Calorimeter |
| B/C | Boron-to-carbon |
| CALET | Calorimetric Electron Telescope |
| CR | Cosmic ray |
| CREAM | Cosmic Ray Energetics and Mass |
| DAMPE | Dark Matter Particle Explorer |
| ECR | Extragalactic cosmic ray |
| GCR | Galactic cosmic ray |
| HAWC | High-Altitude Water Cherenkov Observator |
| IH | Inner halo |
| ISM | Interstellar Medium |
| LHAASO | Large High Altitude Air Shower Observatory |
| OH | Outer halo |
| PAMELA | Payload for Antimatter Matter Exploration and Light-nuclei Astrophysic |
| SDP | Spatially dependent propagation |
| SNR | Supernova remnant |
| THM | Two-halo model |
| TP | Traditional propagation |
Appendix A
Appendix A.1
Appendix A.2
References
- Biermann, P.L.; de Souza, V. Centaurus A: The Extragalactic Source of Cosmic Rays with Energies above the Knee. Astrophys. J. 2012, 746, 72. [Google Scholar] [CrossRef]
- Boulares, A. The Nature of the Cosmic-Ray Electron Spectrum, and Supernova Remnant Contributions. Astrophys. J. 1989, 342, 807. [Google Scholar] [CrossRef]
- Blasi, P. The origin of galactic cosmic rays. Astron. Astrophys. Rev. 2013, 21, 70. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Detection of the Characteristic Pion-Decay Signature in Supernova Remnants. Science 2013, 339, 807–811. [Google Scholar] [CrossRef]
- Panov, A.D.; Adams, J.H., Jr.; Ahn, H.S.; Batkov, K.E.; Bashindzhagyan, G.L.; Watts, J.W.; Wefel, J.P.; Wu, J.; Ganel, O.; Guzik, T.G.; et al. Elemental energy spectra of cosmic rays from the data of the ATIC-2 experiment. Bull. Russ. Acad. Sci. Phys. 2007, 71, 494–497. [Google Scholar] [CrossRef]
- Panov, A.D.; Adams, J.H.; Ahn, H.S.; Bashinzhagyan, G.L.; Watts, J.W.; Wefel, J.P.; Wu, J.; Ganel, O.; Guzik, T.G.; Zatsepin, V.I.; et al. Energy spectra of abundant nuclei of primary cosmic rays from the data of ATIC-2 experiment: Final results. Bull. Russ. Acad. Sci. Phys. 2009, 73, 564–567. [Google Scholar] [CrossRef]
- Ahn, H.S.; Allison, P.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Childers, J.T.; Conklin, N.B.; Coutu, S.; DuVernois, M.A.; Ganel, O.; et al. Discrepant Hardening Observed in Cosmic-ray Elemental Spectra. Astrophys. J. Lett. 2010, 714, L89–L93. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Anderson, T.; Barrau, A.; Conklin, N.B.; Coutu, S.; Derome, L.; Han, J.H.; Jeon, J.A.; Kim, K.C.; Kim, M.H.; et al. Proton and Helium Spectra from the CREAM-III Flight. Astrophys. J. 2017, 839, 5. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Borisov, S.; et al. PAMELA Measurements of Cosmic-Ray Proton and Helium Spectra. Science 2011, 332, 69–72. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Alpat, B.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; et al. Observation of the Identical Rigidity Dependence of He, C, and O Cosmic Rays at High Rigidities by the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2017, 119, 251101. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; et al. Observation of New Properties of Secondary Cosmic Rays Lithium, Beryllium, and Boron by the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2018, 120, 021101. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Barao, F.; Barrin, L.; Bartoloni, A.; Başeğmez-du Pree, S.; Bates, J.; et al. The Alpha Magnetic Spectrometer (AMS) on the international space station: Part II—Results from the first seven years. Phys. Rept. 2021, 894, 1–116. [Google Scholar] [CrossRef]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Bagliesi, M.G.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bonechi, S.; Bongi, M.; et al. Direct Measurement of the Cosmic-Ray Proton Spectrum from 50 GeV to 10 TeV with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2019, 122, 181102. [Google Scholar] [CrossRef]
- Atkin, E.; Bulatov, V.; Dorokhov, V.; Gorbunov, N.; Filippov, S.; Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; et al. First results of the cosmic ray NUCLEON experiment. J. Cosmol. Astropart. Phys. 2017, 7, 020. [Google Scholar] [CrossRef]
- Atkin, E.; Bulatov, V.; Dorokhov, V.; Gorbunov, N.; Filippov, S.; Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; et al. New Universal Cosmic-Ray Knee near a Magnetic Rigidity of 10 TV with the NUCLEON Space Observatory. Sov. J. Exp. Theor. Phys. Lett. 2018, 108, 5–12. [Google Scholar] [CrossRef]
- An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; Chen, J.L.; et al. Measurement of the cosmic ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Sci. Adv. 2019, 5, eaax3793. [Google Scholar] [CrossRef]
- Alemanno, F.; An, Q.; Azzarello, P.; Barbato, F.C.T.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Catanzani, E.; Chang, J.; Chen, D.Y.; et al. Measurement of the Cosmic Ray Helium Energy Spectrum from 70 GeV to 80 TeV with the DAMPE Space Mission. Phys. Rev. Lett. 2021, 126, 201102. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Syrovatskii, S.I. The Origin of Cosmic Rays; Macmillan: New York, NY, USA, 1964. [Google Scholar]
- Gaisser, T.K. Cosmic Rays and Particle Physics; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1990. [Google Scholar]
- Berezinskii, V.S.; Bulanov, S.V.; Dogiel, V.A.; Ptuskin, V.S. Astrophysics of Cosmic Rays; North-Holland: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Engelmann, J.J.; Ferrando, P.; Soutoul, A.; Goret, P.; Juliusson, E.; Koch-Miramond, L.; Lund, N.; Masse, P.; Peters, B.; Petrou, N.; et al. Charge composition and energy spectra of cosmic-ray nuclei for elements from Be to Ni - Results from HEAO-3-C2. Astron. Astrophys. 1990, 233, 96–111. [Google Scholar]
- Swordy, S.P.; Mueller, D.; Meyer, P.; L’Heureux, J.; Grunsfeld, J.M. Relative Abundances of Secondary and Primary Cosmic Rays at High Energies. Astrophys. J. 1990, 349, 625. [Google Scholar] [CrossRef]
- Ferrando, P.; Lal, N.; McDonald, F.B.; Webber, W.R. Studies of low-energy Galactic cosmic-ray composition at 22 AU. I-Secondary/primary ratios. Astron. Astrophys. 1991, 247, 163–172. [Google Scholar]
- Panov, A.D.; Sokolskaya, N.V.; Adams, J.H.; Ahn, H.S.; Bashindzhagyan, G.L.; Batkov, K.E.; Chang, J.; Christl, M.; Fazely, A.R.; Ganel, O.; et al. Relative abundances of cosmic ray nuclei B-C-N-O in the energy region from 10 GeV/n to 300 GeV/n. Results from ATIC-2 (the science flight of ATIC). In Proceedings of the International Cosmic Ray Conference, Mexico City, Mexico, 3–11 July 2008; International Cosmic Ray Conference. Volume 2, pp. 3–6. [Google Scholar] [CrossRef]
- Ahn, H.S.; Allison, P.S.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Boyle, P.J.; Brandt, T.J.; Childers, J.T.; Conklin, N.B.; Coutu, S.; et al. Measurements of cosmic-ray secondary nuclei at high energies with the first flight of the CREAM balloon-borne experiment. Astropart. Phys. 2008, 30, 133–141. [Google Scholar] [CrossRef]
- George, J.S.; Lave, K.A.; Wiedenbeck, M.E.; Binns, W.R.; Cummings, A.C.; Davis, A.J.; de Nolfo, G.A.; Hink, P.L.; Israel, M.H.; Leske, R.A.; et al. Elemental Composition and Energy Spectra of Galactic Cosmic Rays During Solar Cycle 23. Astrophys. J. 2009, 698, 1666–1681. [Google Scholar] [CrossRef]
- Aguilar, M.; Alcaraz, J.; Allaby, J.; Alpat, B.; Ambrosi, G.; Anderhub, H.; Ao, L.; Arefiev, A.; Arruda, L.; Azzarello, P.; et al. Relative Composition and Energy Spectra of Light Nuclei in Cosmic Rays: Results from AMS-01. Astrophys. J. 2010, 724, 329–340. [Google Scholar] [CrossRef]
- Obermeier, A.; Ave, M.; Boyle, P.; Höppner, C.; Hörandel, J.; Müller, D. Energy Spectra of Primary and Secondary Cosmic-Ray Nuclei Measured with TRACER. Astrophys. J. 2011, 742, 14. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bongi, M.; Bonvicini, V.; Bottai, S.; Bruno, A.; et al. Measurement of Boron and Carbon Fluxes in Cosmic Rays with the PAMELA Experiment. Astrophys. J. 2014, 791, 93. [Google Scholar] [CrossRef]
- Cummings, A.C.; Stone, E.C.; Heikkila, B.C.; Lal, N.; Webber, W.R.; Jóhannesson, G.; Moskalenko, I.V.; Orlando, E.; Porter, T.A. Galactic Cosmic Rays in the Local Interstellar Medium: Voyager 1 Observations and Model Results. Astrophys. J. 2016, 831, 18. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; et al. Precision Measurement of the Boron to Carbon Flux Ratio in Cosmic Rays from 1.9 GV to 2.6 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2016, 117, 231102. [Google Scholar] [CrossRef] [PubMed]
- Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; Panov, A.; Podorozhny, D.; Tkachenko, A.; Tkachev, L.; Turundaevskiy, A.; et al. Secondary cosmic rays in the NUCLEON space experiment. Adv. Space Res. 2019, 64, 2559–2563. [Google Scholar] [CrossRef]
- Collaboration, D. Detection of spectral hardenings in cosmic-ray boron-to-carbon and boron-to-oxygen flux ratios with DAMPE. Sci. Bull. 2022, 67, 2162–2166. [Google Scholar] [CrossRef]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Bagliesi, M.G.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bongi, M.; Brogi, P.; et al. Direct Measurement of the Cosmic-Ray Carbon and Oxygen Spectra from 10 GeV /n to 2.2 TeV /n with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2020, 125, 251102. [Google Scholar] [CrossRef]
- Vladimirov, A.E.; Jóhannesson, G.; Moskalenko, I.V.; Porter, T.A. Testing the Origin of High-energy Cosmic Rays. Astrophys. J. 2012, 752, 68. [Google Scholar] [CrossRef]
- Sveshnikova, L.G.; Strelnikova, O.N.; Ptuskin, V.S. Spectrum and anisotropy of cosmic rays at TeV-PeV-energies and contribution of nearby sources. Astropart. Phys. 2013, 50, 33–46. [Google Scholar] [CrossRef]
- Liu, W.; Bi, X.J.; Lin, S.J.; Wang, B.B.; Yin, P.F. Excesses of cosmic ray spectra from a single nearby source. Phys. Rev. D 2017, 96, 023006. [Google Scholar] [CrossRef]
- Liu, W.; Guo, Y.Q.; Yuan, Q. Indication of nearby source signatures of cosmic rays from energy spectra and anisotropies. J. Cosmol. Astropart. Phys. 2019, 2019, 010. [Google Scholar] [CrossRef]
- Malkov, M.A.; Moskalenko, I.V. The TeV Cosmic-Ray Bump: A Message from the Epsilon Indi or Epsilon Eridani Star? Astrophys. J. 2021, 911, 151. [Google Scholar] [CrossRef]
- Guo, Y.Q.; Tian, Z.; Jin, C. Spatial-dependent Propagation of Cosmic Rays Results in the Spectrum of Proton, Ratios of P/P, and B/C, and Anisotropy of Nuclei. Astrophys. J. 2016, 819, 54. [Google Scholar] [CrossRef]
- Jin, C.; Guo, Y.Q.; Hu, H.B. Spatial dependent diffusion of cosmic rays and the excess of primary electrons derived from high precision measurements by AMS-02. Chin. Phys. C 2016, 40, 015101. [Google Scholar] [CrossRef]
- Guo, Y.Q.; Yuan, Q. Understanding the spectral hardenings and radial distribution of Galactic cosmic rays and Fermi diffuse γ rays with spatially-dependent propagation. Phys. Rev. D 2018, 97, 063008. [Google Scholar] [CrossRef]
- Liu, W.; Yao, Y.h.; Guo, Y.Q. Revisiting the Spatially Dependent Propagation Model with the Latest Observations of Cosmic-Ray Nuclei. Astrophys. J. 2018, 869, 176. [Google Scholar] [CrossRef]
- Parker, E.N. The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 1965, 13, 9–49. [Google Scholar] [CrossRef]
- Grenier, I.A.; Black, J.H.; Strong, A.W. The Nine Lives of Cosmic Rays in Galaxies. Annu. Rev. Astron. Astrophys. 2015, 53, 199–246. [Google Scholar] [CrossRef]
- Ptuskin, V.S.; Soutoul, A. Cosmic rays in the cloudy interstellar medium - Production of secondary nuclei. Astron. Astrophys. 1990, 237, 445–453. [Google Scholar]
- Tsao, C.H.; Silberberg, R.; Barghouty, A.F.; Sihver, L. Energy Degradation in Cosmic-Ray Nuclear Spallation Reactions: Relaxing the Straight-ahead Approximation. Astrophys. J. 1995, 451, 275. [Google Scholar] [CrossRef]
- Feng, J.; Tomassetti, N.; Oliva, A. Bayesian analysis of spatial-dependent cosmic-ray propagation: Astrophysical background of antiprotons and positrons. Phys. Rev. D 2016, 94, 123007. [Google Scholar] [CrossRef]
- Seo, E.S.; Ptuskin, V.S. Stochastic Reacceleration of Cosmic Rays in the Interstellar Medium. Astrophys. J. 1994, 431, 705. [Google Scholar] [CrossRef]
- Case, G.; Bhattacharya, D. Revisiting the galactic supernova remnant distribution. Astron. Astrophys. Suppl. 1996, 120, 437–440. [Google Scholar]
- Gleeson, L.J.; Axford, W.I. Solar Modulation of Galactic Cosmic Rays. Astrophys. J. 1968, 154, 1011. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Barber, A.S.; et al. Extended gamma-ray sources around pulsars constrain the origin of the positron flux at Earth. Science 2017, 358, 911–914. [Google Scholar] [CrossRef]
- Aharonian, F.; An, Q.; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Bi, Y.J.; Cai, H.; Cai, J.T.; et al. Extended Very-High-Energy Gamma-Ray Emission Surrounding PSR J 0622 +3749 Observed by LHAASO-KM2A. Phys. Rev. Lett. 2021, 126, 241103. [Google Scholar] [CrossRef]
- Hooper, D.; Cholis, I.; Linden, T.; Fang, K. HAWC observations strongly favor pulsar interpretations of the cosmic-ray positron excess. Phys. Rev. D 2017, 96, 103013. [Google Scholar] [CrossRef]
- Fang, K.; Bi, X.J.; Yin, P.F.; Yuan, Q. Two-zone Diffusion of Electrons and Positrons from Geminga Explains the Positron Anomaly. Astrophys. J. 2018, 863, 30. [Google Scholar] [CrossRef]
- Tomassetti, N. Origin of the Cosmic-Ray Spectral Hardening. Astrophys. J. Lett. 2012, 752, L13. [Google Scholar] [CrossRef]
- Tomassetti, N. Cosmic-ray protons, nuclei, electrons, and antiparticles under a two-halo scenario of diffusive propagation. Phys. Rev. D 2015, 92, 081301. [Google Scholar] [CrossRef]
- Strong, A.W.; Moskalenko, I.V.; Ptuskin, V.S. Cosmic-Ray Propagation and Interactions in the Galaxy. Annu. Rev. Nucl. Part. Sci. 2007, 57, 285–327. [Google Scholar] [CrossRef]
- Yang, R.; Aharonian, F. Interpretation of the excess of antiparticles within a modified paradigm of galactic cosmic rays. Phys. Rev. D 2019, 100, 063020. [Google Scholar] [CrossRef]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bongi, M.; Brogi, P.; Bruno, A.; et al. Cosmic-Ray Boron Flux Measured from 8.4 GeV /n to 3.8 TeV /n with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2022, 129, 251103. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Ambrosi, G.; Arruda, L.; Attig, N.; Barao, F.; Barrin, L.; Bartoloni, A.; Başeğmez-du Pree, S.; Battiston, R.; et al. Properties of Daily Helium Fluxes. Phys. Rev. Lett. 2022, 128, 231102. [Google Scholar] [CrossRef]
- Marrocchesi, P.S. New Results from the first 5 years of CALET observations on the International Space Station. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 10. [Google Scholar] [CrossRef]
- Strong, A.W.; Moskalenko, I.V. Propagation of Cosmic-Ray Nucleons in the Galaxy. Astrophys. J. 1998, 509, 212–228. [Google Scholar] [CrossRef]
- Moskalenko, I.V.; Strong, A.W. Production and Propagation of Cosmic-Ray Positrons and Electrons. Astrophys. J. 1998, 493, 694–707. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Grasso, D.; Maccione, L. Cosmic ray nuclei, antiprotons and gamma rays in the galaxy: A new diffusion model. J. Cosmol. Astropart. Phys. 2008, 2008, 018. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Vittino, A.; Di Bernardo, G.; Di Mauro, M.; Ligorini, A.; Ullio, P.; Grasso, D. Cosmic-ray propagation with DRAGON2: I. numerical solver and astrophysical ingredients. J. Cosmol. Astropart. Phys. 2017, 2017, 015. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Vittino, A.; Di Mauro, M.; Grasso, D.; Mazziotta, M.N. Cosmic-ray propagation with DRAGON2: II. Nuclear interactions with the interstellar gas. J. Cosmol. Astropart. Phys. 2018, 2018, 006. [Google Scholar] [CrossRef]
- Atoyan, A.M.; Aharonian, F.A.; Völk, H.J. Electrons and positrons in the galactic cosmic rays. Phys. Rev. D 1995, 52, 3265–3275. [Google Scholar] [CrossRef] [PubMed]
| Model | n | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| [] | [] | [] | |||||||
| TP | 0.49 | 5 | 6 | 4 | 0.05 | 4 | |||
| SDP | 0.63 | 0.33 | 5 | 0.1 | 6 | 4 | 0.05 | 4 | |
| SDP+Fresh | 0.64 | 0.58 | 5 | 0.1 | 6 | 4 | 0.05 | 4 |
| Background | Local | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | ||||||||
| [GV] | [TV] | [TV] | ||||||
| TP | 4.75 | 2.3 | 2.42 | 6.8 | 150 | |||
| SDP | 4.62 | 2 | 2.54 | 6 | 200 | |||
| SDP+Fresh | 4.02 | 2 | 2.39 | 6 | 4 | 7000 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Feng, J.; Tam, P.-H.T. Explaining the Hardening Structures of Helium Spectrum and Boron to Carbon Ratio through Different Propagation Models. Galaxies 2023, 11, 43. https://doi.org/10.3390/galaxies11020043
Luo Q, Feng J, Tam P-HT. Explaining the Hardening Structures of Helium Spectrum and Boron to Carbon Ratio through Different Propagation Models. Galaxies. 2023; 11(2):43. https://doi.org/10.3390/galaxies11020043
Chicago/Turabian StyleLuo, Qing, Jie Feng, and Pak-Hin Thomas Tam. 2023. "Explaining the Hardening Structures of Helium Spectrum and Boron to Carbon Ratio through Different Propagation Models" Galaxies 11, no. 2: 43. https://doi.org/10.3390/galaxies11020043
APA StyleLuo, Q., Feng, J., & Tam, P.-H. T. (2023). Explaining the Hardening Structures of Helium Spectrum and Boron to Carbon Ratio through Different Propagation Models. Galaxies, 11(2), 43. https://doi.org/10.3390/galaxies11020043






