Abstract
We aim to establish a rough first prospect on the potential of certain biorelevant solvents (water, ammonia, and methane) being present in liquid form inside the uppermost few meters of several modeled rocky and icy surfaces of hypothetical bodies orbiting active galactic nuclei (AGNs) and investigate under which constraints this might occur. For this, we adjust and average X-ray spectra from a sample of 20 Type-1 Seyfert galaxies to calculate the mean snowline of the sample used. We then vary the hypothetical body’s orbit between 10% and 100% of the snowline radius and calculate a sub-surface attenuation within four different model surface compositions for each. We then use this as a continuous source term for a thermal model. Example bodies are systematically investigated with sizes between 1/30 and 20 earth radii, with further variations also considered (such as possible bound rotation), to end up with a perspective of solvent phases under a wide slew of different conditions. We find that liquid solvents are possible under a multitude of parameters, with temperature being the main constraint to liquid water whereas body size and pressure are the main constraint to liquid methane and ammonia.
1. Introduction
We aim to investigate some of the factors that play into the potential of (and the process of detecting) life outside of earth’s own biosphere. To this end we take a rudimentary first look into the constraints of the habitability regarding one of the most bizarre astrophysical environments imaginable: the circumnuclear regions of active galactic nuclei.
The pre-existing variety of research pertaining to energy sources and the formation of liquid environments is the result of important steps in astrophysics, astrochemistry, and astrobiology. However, the respective research of uncommon energy sources has so far not thoroughly touched upon the possibilities that the combination of sub-surface environments and high-energy radiation offer.
Considerations on habitability become exceedingly complex, encompassing a wealth of topics such as energy supply, mechanisms to gather, store, transport, and process said energy in biochemical form, or the way in which extraterrestrial organisms might shield themselves from harmful influences such as radiation or temperature extremes. As such, a comprehensive look at the habitability of the environments discussed here would go far beyond any reasonable scope. We focus on only one aspect of habitability that seems to be the most prevalent in both standard and proposed exotic biologies and is expected to exist in great abundance in the universe: liquid solvents.
The solvents were chosen based on the following considerations. Water goes almost without saying, as it is the key solvent for most life on earth and fulfills many important roles, such as providing a transportation medium to distribute molecules throughout the organism. Methane and ammonia are also important solvents for complex life on earth and are furthermore proposed in some models for exotic biochemistries [1,2,3], with liquid methane proven to exist on Saturn’s moon titan [4] and liquid ammonia also being suspected [5]. These promising findings, as well as the beneficial thermochemical impact of salt-mixtures on water (with being the most common salt in water on earth and showing the most beneficial impact), lead us to choose these five solvents for our investigation.
Regarding the active galactic nuclei (AGNs), this work will focus mainly on radio-quiet ones as external energy sources with X-ray emissions strong enough for their radiation to mostly penetrate both otherwise optically thick circumnuclear material1 and the upper regions of regolith on bodies in their vicinity (which encompasses several parsec for objects such as these). This coincides with a recent proposal of planetary formation in the snowline around Seyfert-type AGNs [6], but despite this overlap, we want to avoid strict adherence to the planetary properties considered in that work to keep a broad perspective on this uncommon field and check a reasonably wide slew of possibilities. A graphic overview of the model is given in Figure 1.
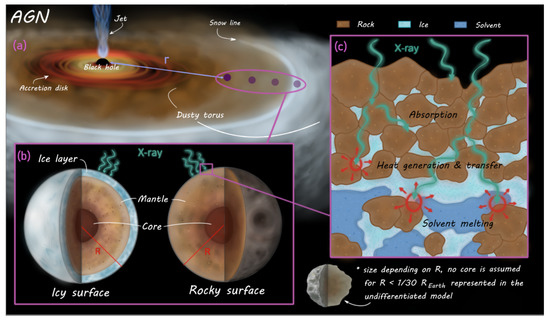
Figure 1.
Schematic outline of modelling process and considered variations: (a) We investigate a sample of 20 Seyfert 1 active galactic nuclei (AGNs), taking an average X-ray spectrum as input “source” for simulations. Simulated bodies orbit this source at distances between 10% and 100% of the snowline distance within the toroidal plane, at an angle of 68°. (b) Attenuation of the X-ray radiation is calculated for two proposed crusts of the model bodies: One of an initially frozen fresh water, methane, and ammonia mixture, and one crust consisting of 50% rocky compounds combined with 50% frozen solvents. The solvent mixture on the rocky model features three variations between fresh water, –, and –saltwater respectively. (c) Attenuated energy is used as a continuous source term for a 1D-heat transfer model. Each timestep of the model, solvent phase states are determined and thermochemical properties are adjusted in turn. After a timeframe determined to reach sufficient thermal equilibrium, results are read out and displayed. Further variabilities beyond this core process include how the results were impacted by different model body radii, changes to the radiation source, impact of different model body densities (allowing concrete relations to known and relevant solar system bodies) and determining a smallest viable body size.
2. Materials and Methods
2.1. Obtaining a Mean Energy Spectrum
We sample 20 Type-1 Seyfert galaxies taken from a multi-wavelength catalog of such objects [8].
Erroneous short dips into negative flux values observed in the data were interpreted as errors, likely of the detector, and were replaced with the value of the longer wavelength point adjacent to the sudden dip. Given that so-replaced values lie well within the bulk of the dataset and that this was only necessary for a single spectrum, this solution was deemed satisfactory.
To obtain appropriate liquid layers in the subsurface, X-rays need to penetrate a non-negligible depth. We therefore focus on X-ray photon energies in the dataset between 1 and 120 keV for the thermal simulation, as photons below 1 keV do not penetrate very deep and the respective integrated flux does not generate enough heat to be of significance for the overall result of deeper liquid subsurface layers. They will, however, contribute to direct surface temperatures, and therefore, calculations regarding both the snowline radius and the surface equilibrium temperature have been made with a dataset between 1.24 eV (more precisely, λ = 1001.8 μm) and 120 keV to include a significant IR-tail present in half of the dataset (while the other half terminates at this point).
After having obtained such a spectrum, the calculated absorbed energy is used as the continuous source term for a thermal model calculating heat generation, transfer, and transport down to a depth of 10 m, at the end of which a temperature profile is generated. This is checked against the thermochemical properties of five model solvents (in combination with a value of pressure at different depths, calculated from 9 different body configurations) to determine where a given solvent could exist in the liquid phase.
2.1.1. Adjusting Measurements for Distance and Angle
Using the distances (their calculation is outlined in Appendix A) for the observed targets from the point of observation (earth) , which were obtained using the astroquery python package [9], as well as the flux received at this point of observation , we can determine the flux received at a model planet at an orbit of radius using the inverse square law to:
However, this is first carried out for a distance of 10 pc from the central source to establish a point at which we can calculate the mean of the taken sample.
The viewing angle is a more delicate issue. We can expect that most AGNs show an incredibly large energy emission in the pole-on direction (viewing the accretion disk from above) and only marginal energy emission in the disk-on direction [10]; however, we are unable to fully verify this as we are unable to observe a single such object from multiple angles. This is further complicated by a lack of precise information about the viewing angle at which we see these objects, as AGNs are both too bright and too far away to resolve them sufficiently to make geometric assumptions about viewing angle; instead, we have to resort to using kinematics [11] or similar derivation techniques. To combat these problems here, we use the assumption of a simple unified model of AGNs, which poses that different types of active galactic nuclei are all similar objects viewed at different angles and at different stages of a similar evolutionary process [12]. According to this assumption then, Seyfert 1 (Sy1) galaxies are viewed as pole-on, derived from the existence of broad emission lines imbued in the spectrum by the region of high-velocity dust and gas surrounding the accretion disk close to the equatorial plane (that are obscured when viewed at lower angles, constituting Seyfert 2 (Sy2) AGNs).
However, a planet forming in the circumnuclear disk would not exist this high above the disk’s equatorial plane; it would be much more likely to form at a lower angle close to the denser regions of dust surrounding the AGNs. To adjust for this in a sufficiently concise way, we utilize a formula expressing the reduction in observed apparent luminosity for a unified luminosity function for AGNs from [13] by a factor of:
which then leads to a formula for the observed luminosity :
where is the inclination angle of the accreation disk relative to the observer, with for an edge-on view of the disk.
As the same work classifies Type-2 AGNs at a viewing angle of 68° or greater, this angle corresponds to a position on the edge of the broad line region of the circumnuclear disk and will therefore be used as an example value to set the model in to not add another parameter to variate over. This, Equation (2), and Equation (3) are explained visually in Appendix A. Further work on the chemical makeup as well as the dynamics of circumnuclear regions can help constrain this value.
2.1.2. Interpolating and Averaging
To effectively calculate a mean of the sample luminosities, which all exhibit uneven datapoints, a universal grid is defined for the energy axis that runs from the first to the last photon energy value that is in at least one of the spectral grids used. In this case, this is between 1 and 120 keV, defined with 5205 logarithmically equidistant steps. (The exact number arose from the construction of the framework.) This universal grid is then sliced corresponding to each of the contributing spectra, and each spectrum is in turn interpolated onto its respective slice. Interpolation is conducted using the “interp1d”-function of python’s “numpy”-package [14] and is set to also extrapolate missing values to circumvent conflicts at the boundaries. Values outside these boundaries (above and below a certain spectrum’s recorded range) are set to NaN. The result of this is an array of 20 spectra along a single x-axis.
After transposing, the mean can be calculated per energy value (in a kind of cross-section of the spectra) using numpy’s “nanmean”-function, which automatically disregards any NaN values. This outputs a mean Seyfert 1 spectrum as it would be observed at a distance of 10 pc.
The distance at which this mean spectrum would exhibit a snowline is defined as the distance from the source where the equilibrium temperature of a body:
where I denotes the energy flux, the surface albedo, and is the Stefan–Boltzmann constant as obtained using python’s scipy package [15], becomes a set temperature (conventionally ). In this case, the X-ray albedo is almost zero and can be neglected, and we are interested in the flux at a certain distance .
This snowline is calculated from the integrated flux of the mean spectrum (carried out using numpy’s trapezoid integration function integrate.trapz) to be at a distance of pc. Individual spectra as well as the averaged spectrum at 10 pc and at the snowline of pc can be seen in Figure 2.
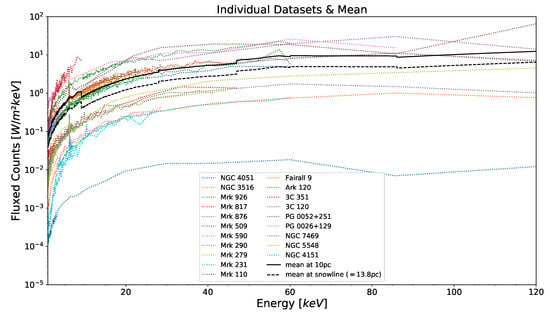
Figure 2.
Data of individual X-ray spectra based on a catalog of AGNs [8] (between 1 and 120 keV) of 20 Seyfert 1 AGNs used in this work (colored and dotted) as they would be observed at a distance of 10 pc, as well as the mean of their spectra as it would be observed a distance of 10 pc (black, solid line) and at a snowline distance of 13.8 pc (black, dashed line), with the snowline distance determined cutting off at 1.24 eV instead of 1 keV. (CC BY 4.0).
Distance variation is introduced here with all of the following computations being conducted for a set of ten fractions (from 10% to 100%) of the snowline distance.
2.2. Obtaining Surface Properties for Model Bodies
With the radiation environment figured out, we construct models for potential bodies as well as their uppermost few meters of crust. We choose a series of body sizes between 20 and here2 to systematically cover an array of possibilities, with two main achor points: the factor 20 (although originally attributed to earth masses, not radii) stems from the planetary models proposed in [7], and radii down to act as attempts to reach sizes at which accretion energy and radioactive heating become less important, equivalent to asteroids or tiny moons in the solar system.
2.2.1. Proposing Surface Models
We lack chemical data about the circumnuclear disks (CNDs) of any Seyfert-type galaxy, and information about exoplanetary surfaces is extremely scarce as well.
To compensate for this and build a reasonable initial model, we work with a chemical composition and morphology similar to lunar soil, as reported by [16], to emulate rocky bodies and a pure solvent ice regolith to emulate icy bodies without many minerals in the upper layers, similar to icy moons found in the solar system. The former was based on multiple points of reasoning: the moon is the best-researched body without a significant atmosphere, we have extensive geological data about its surface regolith, and the few exoplanetary surfaces with available data have shown to be similar to the moon’s composition [17].
To introduce solvents to the originally dry lunar model, we propose the regolith porosity of 50% to be filled with (initially) solvent ices of water, methane, and ammonia. The ratio of these solvents, both when introduced to the lunar model and as part of the icy model, was determined—as a loose guideline—by the chemical abundances obtained from spectroscopic observations and models of the milky way’s own central region [18]. Saltwater concentrations were chosen to yield the maximum reduction in melting points. The end results of the rocky crust filled with freshwater will be displayed in Section 3, while the results for the other models will be elaborated upon in Appendix B.
In the interest of the scope of this work—and because minute details in the composition ultimately do not impact the mass attenuation coefficient a lot—we focus on the abundances of the relevant solvents, ignoring other volatiles with generally lower abundances such as or . The abundances of all molecules involved in our four models are shown in Table 1.

Table 1.
Surface compositions.
Another important factor (more important than even the input energy, as shown in Figure 3) is the surface density. We approximate the overall complicated geometry of regolith by utilizing a calculated density from the density of compounds involved3 (and the porosity assumed), which can be seen in Table 2.
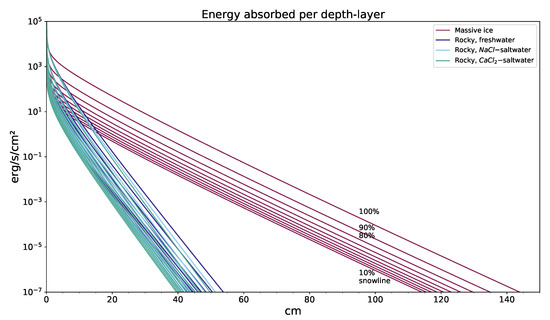
Figure 3.
Energy flux absorbed at a certain depth in 4 surface models, with a family of graphs from 10% to 100% snowline distances (descriptions of which are only shown for pure ice models for improved legibility in the graph), with different water-mixtures being very close to each other in the rocky model. What can be clearly seen is that saltwater compositions have a small but noticeable impact on absorption, although the main determining factor of the absorption is material density.

Table 2.
Surface densities.
2.2.2. Calculating Attenuated Energy Using Lambert–Beer’s Law
Attenuation in matter was calculated using Lambert–Beer’s law in the form:
where and denote intensity before and after traversing a depth d inside the matter of density and with a mass attenuation coefficient of . For the photon energies considered, the mass attenuation coefficient will vary. To account for this, the mass attenuation coefficients of the investigated surface compositions have been obtained in an energy range between 1 keV and 120 keV using the national institute of standards and technology (NIST) [20] database’s online mass attenuation coefficient calculator for mixtures of molecules. This was then interpolated to fit onto the generalized energy grid constructed earlier. The result is shown in Appendix C.
This creates a family of spectral attenuation curves over both the energy and the depth grid. Integrating over the entire spectrum at each depth-point n allows us to obtain the bolometric intensity per depth, which, when subtracted from the intensity at a point , leads to information about the energy deposited inside the layer between n and and thus what amount of energy is available for heat generation4. This is shown in Figure 3.
2.2.3. Preparing Thermal Properties: Triple Point Depth
To determine whether a solvent is present in its liquid phase, the two key factors are temperature and pressure. Both of which are complex matters that will need to be approximated to a certain degree, starting with pressure here. We obtained these pressures from the NIST Chemistry WebBook, NIST Standard Reference Database Number 69 [19], and used them to calculate, for each model body, the depth at which the triple point would be reached using:
whereas and denote the properties of the model body, that being a radius between 1/30 and 20 times earth’s radius and a density equal to the overall average density of the earth (), describes the density of the surface model as built in Section 2.2.1. A detailed derivation of Equation (6) is given in Appendix D.2.
2.2.4. Vapor Pressure Curve
The last step in determining the phase of a solvent, as mentioned in the previous section, is temperature, namely where a solvent reaches melting and boiling points. The melting point can be handled with relative ease, as most solvents show a constant melting point equal to the temperature at their triple point (anomalies notwithstanding). Triple point temperatures are discussed in detail in Appendix D.
To deal with the boiling point however, we have access to multiple equations approximating part of the phase profile of certain substances, with a particularly simple and effective one being the Antoine equation:
which relates the vapor pressure with the respective boiling temperature and a set of empirically determined coefficients and C. This can be easily rearranged to determine the temperature instead of pressure with: . Coefficients for freshwater, ammonia, and methane were obtained from the NIST Chemistry WebBook, where we chose the sets with the widest temperature coverage, and can be seen in Table 3. The saltwater saw adjustments in the form of shifting the equation by about four Kelvin along the T-axis for both mixtures5.

Table 3.
Antoine coefficients of utilized solvents.
2.3. Simulating Thermal Profile within the Surface
2.3.1. Calculating Specific Heat Capacities Using Polynomial Equations
The goal is to arrive at a continuous temperature source term that can be fed to a numerical thermal model. For this purpose, we can compute temperature from the input energy derived earlier by using the specific heat capacity
which allows us to obtain the temperature change per timestep of a mass element m hit by a change in heat energy or, in this case, an amount of radiative energy I per timestep. We also introduce the conservative approximation that only roughly 90% of radiation hitting an average substance will be converted into heat, with the other 10% leading to secondary radiation effects not further discussed in this work. A detailed breakdown of the reasoning behind this can be found in Appendix E. Thus, to calculate the source term, we use:
splitting the mass element into volume V and density . Density is carried over from the surface model constructed earlier, the radiation flux from the adjusted, meaned, and integrated photometric data. The volume is chosen as a column of the height of one depth grid cell (0.1 cm) over a unit area 1 m2. This leaves the specific heat capacity to be determined.
A popular way to account for the temperature dependency of the specific heat capacity is the usage of the “Shomate equation”, a polynomial equation that uses empirically determined coefficients to approximate a –T curve. We used a slightly modified polynomial equation taken from the Chemical Engineering and Materials Research Information Center (CHERIC) [21] database in the form of:
with the result being in units of . Of note is that kg-mol is a distinct unit equivalent to one kilomole and thus . This library, however, only encompasses values for liquids and gases, so solids need to be treated with exceptions:
(a) Rocky solids: For most monoatomic solid materials of heavier atoms, the specific heat capacity is relatively constant, following the Dulong–Petit law [22]:
(b) Ammonia ice and methane ice: In these cases, tables containing experimental information about the specific heat capacity can be found. For ammonia, this is Table IV in [23], which is used here up until 191 Kelvin, the melting point. For methane, Table 2 from [24] is used. In both cases, the obtained data are fitted to Equation (10) using python’s SciPy package and a least square fit. The polynomial coefficients obtained are given over to the function calculating the overall specific heat capacity.
(c) Water ice: Here the specific heat is approximated using a different formula specific to it, as obtained from [25] in Equation (1) of that work. It should be noted that this work outlines more precise ways to approximate ice’s specific heat (that is the main purpose of said paper), but for the scope of this work here, the lower precision formula given at the start is wholly sufficient:
With the specific heat capacities obtained, a function was written to calculate the overall heat capacity of the mixture, depending on the current temperature and pressure of the simulation, using the known abundances as a sum over all involved substances:
2.3.2. Setting Up a Solver for the 1-D Heat Equation
The core of this thermal solver is the 1-D heat equation with advection and an additional continuous source term. A finite difference method to solve this problem numerically was described in [26], based on a Forward Time Centered Space (FTCS) scheme used to solve the 1-D heat equation with no source term. This method utilized the algorithm used to solve a 1-D heat equation with diffusivity and decay:
Here, T describes the temperature, k is the decay coefficient, which will be set to 06, and is the width of steps within the discrete time grid used. In accordance with this, describes the spacing of the space grid. Subscript indices (i) denote steps over the space grid, while superscript indices (n) denote time. is the thermal diffusivity coefficient adjusted onto the space and time grid used as:
with thermal diffusivity coefficient . Given the simplicity of this scheme, we set .
To now implement continuous emission, a source term is added flat to all spatial grid points , where the external heating applies:
In our case, the source term is applied to all spatial grid points but varies over them. Within the code, this is expressed using Numpy arrays along the spatial grid for both T and .
Furthermore, to implement a day-and-night cycle relatively easily, the source term was only applied every other time step. Compared to a simple one-half multiplier on the source term, this implementation allows for the model to cool down during the simulated night steps.
Boundary conditions are modeled at the initial spatial grid point (the exact surface layer) by setting the temperature to be equal to the equilibrium temperature given the radiation input at that point.
The equilibrium temperature is an accurate measure for surface temperatures of atmosphere-less bodies; hence, we deemed this boundary condition a sound assumption. Otherwise, heat conducted upwards within the model and reaching the surface would either build up indefinitely (due to the lack of any further conduction and decay) or decay too fast (were the decay term kept for this purpose).
At the initial time grid point (time 0), we set the temperature at a depth layer i to be the equilibrium temperature based on the energy deposition of the X-rays absorbed within that layer i.
This alone would not be an accurate thermal model, but it provides a sufficient starting point. As the simulation progresses, conductive effects will correct this initial outset to a more realistic profile.
2.3.3. Forming a Frame for the Simulation with Continuous Input
The full function takes arguments for the surface model, body size, grid spacing and , as well as the full simulation timeframe . With a given profile of absorbed energy calculated in Section 2.2.2, the boundary conditions for the thermal solver are calculated and then applied to that solver recursively, meaning each timestep provides the basis for the next timestep . A “while”-loop repeats this over timesteps counting a variable t until it reaches the full time . A day-and-night cycle is simulated by setting up a boolean variable before initializing the loop and then using each loop step to flip the value using . The source term is only applied when —thus, only every other step.
The results are given to a dictionary. Said dictionary is plotted directly7 and, using temperature and pressure criteria discussed in Section 2.2.3 and Appendix D, used to evaluate the phase of contributing solvents.
2.4. Notes about IPython Multiprocessing for the Simulation
The character of this work, with several simulations running over multiple, independent parameters, lends itself to multiprocessing, i.e., having multiple simulations run simultaneously on different CPU threads. For this purpose, computations have been carried out in the IPython environment [27], and its built-in multiprocessing package IPython parallel (ipyparallel) has been used. This allows us to execute certain cells of IPython notebooks on different clusters, using a multicore processor to its full extent while shortening the overall computation time if multiple simulations are run simultaneously.
With this arise some quirks: We ran all computations, with the exception of the final simulation, on all clusters to ensure all necessary variables were available in all clusters. The final plots were conducted in the general IPython environment (using the matplotlib python package [28]), and for this purpose, results from the simulation as well as necessary variables from earlier parts of the code were transported from specific clusters to the general environment using .push and .pull commands of the ipyparallel package.
3. Results
The results displayed in Figure 4 are a detailed breakdown of where and under what conditions, the discussed solvents would be liquid given the rocky, “lunar soil” model with freshwater ices. (Results for the other surface models as well as some further conditions considered can be found in Appendix B.) The four sub-plots seen show the sizes of model bodies considered in this work, from largest at 20 earth radii to smallest at earth radii. Smaller sizes are discussed in Appendix F.3 and Appendix F.4. Overall, the simulation was carried out over nine different size models (); however, only four representatives are shown in this paper to keep the sub-plots legible. The y-axes display model depth beneath the surface, with the surface itself (depth 0) placed at the top of each sub-plot. As previously mentioned, the simulation was carried out up to a depth of 10 m. The x-axes display groupings of the ten considered orbital distances between 10% and 100% . Within each of these groupings, the five different solvents considered are displayed with different colors/patterns. As such, the bars display where solvents would be liquid and are labeled with the respective bar’s length (representing the thickness of the liquid layer), taking both the subterranean pressure and temperature into account. We can then make some key observations based on these results as well as the ones explained in detail in the Appendices mentioned above:
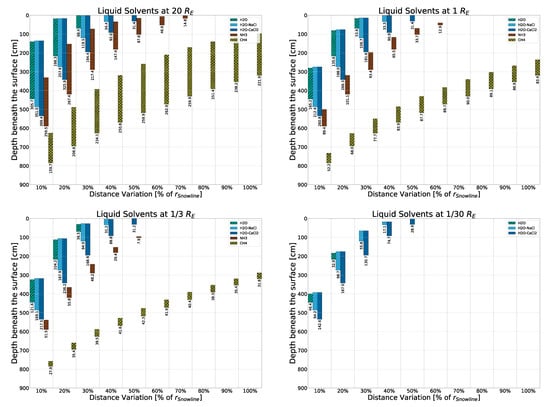
Figure 4.
Liquid solvent layers within 10 m of the surface of four model bodies of rocky, freshwater surface composition around a modeled X-ray source. From top left to bottom right, the four bodies are of the sizes , respectively. The surface density of the rocky, freshwater model involved is , with the composition shown in Table 1. Numbers labeling the columns show the thickness of the liquid layers in centimeters.
- It is possible for solvents to be liquid in bodies orbiting an AGN at a few parsecs of distance, fueled mainly by the X-ray emission of that AGN. This can happen in a somewhat wide variety of environments, with the AGN’s own energy output having much less of an impact compared to the density of a surface regolith (which greatly influences attenuation) or the size of the body itself (which greatly influences phase changes). The body’s inner density (beneath the regolith) plays a vital role as well, as seen in Appendix F.3. The influences are stronger for and .
- The salt content of the optimal concentration can have a tremendously beneficial effect on the thermal properties of water in extreme environments (with this effect being more prominent for than ), and one can easily imagine that even away from the optimal concentration saltwater could beget liquidity on otherwise frozen worlds. However, in warmer environments, these effects can be slightly detrimental as compared to fresh water.
- Unsurprisingly, different solvents are constrained by different variables in this simulation, depending on the respective thermal properties. Water’s main constraint is temperature: Freezing points determine if and at what distance from the central source liquid layers can form, while boiling points mainly determine how deep within the crust this has to happen. On bodies too close to the central source, water close to the surface evaporates (the consequences of which would lead to stark alterations in the model itself that have not been considered here, as it would be beyond the scope of this paper), while water too far below would not be warm enough to melt. Methane and ammonia are constrained mainly by pressure, which allows these substances to be liquid even close to the snowline if the pressure is sufficient—so, if the body is large (and dense) enough.
To illustrate these key observations, we can determine that layers of liquid fresh water inside a rocky, lunar-like model can be found as far away from the central source as at , at around 50 cm below the surface, with layers ranging from 70 cm to 40 cm on bodies between and radius. Saltwater behaves similarly but can also form thick (down to roughly 28.9 cm) liquid layers on bodies as small as and as far away as thanks to the low triple point pressure (1 mbar and 0.2 mbar for optimal concentrations of - and -saltwater, respectively, as opposed to 6.1 mbar for freshwater).
The liquid layers may also be formed within bodies of lower densities (as shown in Figure A9) or much smaller radii (as shown in Figure A10) under certain conditions, especially for -saltwater.
Opposite behavior is seen within methane and ammonia. For those, triple point pressures are high, making them unable to exist in liquid form on bodies without a large radius in this model (and a high mass in general). However, on large-enough bodies, methane and ammonia exhibit great versatility thanks to their temperature indifference. As such, methane can persist in liquid form within the upper meters on bodies at or above , with layers between 160 and 260 cm being pushed deeper below the surface closer to the central source the model is placed due to methane’s low boiling point. Ammonia covers the middle ground, can be liquid between and , and is able to form a slim layer at on bodies as small as (data not shown).
Further variations of parameters and their influence on the stability of the liquid systems were investigated by considering both the daylight side of a possibly tidally locked body and limited the input to the two extremes of the AGN sample (the strongest and weakest non-outlier AGNs), with results displayed in Appendix F. It can be seen that within the investigated group of AGNs, there is barely any difference between strongest, weakest, and averaged spectra, and the overall impact of the spectrum used as input is overshadowed by the greater impact of the chosen surface and body models. The same goes for the tidally locked simulation with barely any noticeable difference due to the overall small impact of the source term influx.
4. Discussion
Given the wide slew of parameters tested (different model body sizes, surface compositions, and solvents), we consider it to be fairly certain that liquid solvents are possible on bodies in such an exotic environment as in an orbit around an active galactic nucleus. In the same vein, this wide slew of parameters together with the current lack of research on the topic does not allow a clear statement on the probabilities involved, which was, however, not the point of this work to begin with. It thus serves as a good base for further, even more complex models.
One aspect to investigate in such future models may be the matter of crust stability. Several factors impact the stability of a celestial body’s crust (present liquids, the presence and—if so—nature of an atmosphere, and the overall climate situation) and can do so in a drastic manner. Just in the solar system, we know the moon’s regolith is stable enough for humans to comfortably walk on, while some research has suggested the regolith of some icy moons such as Europa is so loose that it would be more akin to light, fresh snow than actual solid ground [29]. It would not be far from reason to also expect a complex interplay of solid, gas, and liquid phase to result in unstable crusts in the form of cryovolcanism, as expected on Titan [30], especially in the models showing shallow water layers where eruption or refreezing events might lead to significant pressure buildup (while such a risk seems less significant for the often deeper layers of methane and ammonia). As a result of this, despite what the wider liquid layers found on larger model bodies might suggest, smaller model bodies are actually advantageous for the existence of liquid ammonia and methane. These volatiles would greatly destabilize the crust if too close to the surface. However, smaller bodies with less gravity at play to generate pressure would force liquid ammonia and methane layers deeper beneath the surface, in turn stabilizing the crust indirectly. Furthermore, while the greater depth would require a stronger external heat source to be viable, it would also increase the chance of these solvents benefiting from potential internal heat sources; however, such smaller bodies have access to an overall smaller array of internal heat generation methods. So this thought ends up a delicate balancing act that is going to benefit from future research on the interior of comets, asteroids, and small moons. Even greater risks for crust stability arise for models very close to the central source (at ), as sub-surface temperatures in these cases can be destructive (approaching the melting points of rocky compounds), endangering the stability of even rocky crusts at shallow depths and necessarily needing the evaporative effects of involved volatiles to be taken into account for a full assessment of the situation. As such, any results from to have to be investigated cautiously and should be reconsidered in new, more refined models. Similar considerations may be true for shallow depths on icy crusts even close to the snowline.
These outliers would thus be perfect candidates for exogeological and exoplanetary investigations of the expected surface composition and structure of a circumnuclear body. This would also allow for more precise considerations on body size—a topic that has only been generally outlined in this work. While we find liquid ammonia on bodies roughly equivalent to the Jovian moon Ganymede and Europa, liquid saltwater layers (and thin fresh water layers) can effectively be found in bodies as small as (equivalent to the range of large asteroids such as Vesta), with both as well as proving beneficial to a liquid phase. -saltwater alone may even be found in liquid layers on bodies well below sizes of (equivalent to the realm of comets under special conditions), as shown in Figure A10, although we expect some simulational artifacts to be at play here. On the other end of the scale, large bodies would pose their own set of challenges and interesting aspects that might influence these results, such as an accumulation of radioactive material and stored accretion energy begetting internal heating (similar to processes inside earth) or perhaps even the formation of gas giants under certain conditions.
A further point deserving mention, focusing on the character of the simulation itself, is that after adjustments, the continuous thermal source of absorbed X-rays is a negligible component in rocky models and a minor component in icy models. In both cases, the temperature profile will approach the solution of a one-dimensional rod with a fixed temperature on each end. In our case, these fixed temperatures are the equilibrium temperature at the surface and 0K at the bottom of the model due to the thermal model allowing heat transfer away from that point outside of the model itself. Icy models (such as the standard icy simulation or the approximated Europa and Ganymede environments) experience a slight bump or flattening of the temperature in the uppermost few centimeters, stemming from the continuous source. The results thus depend on the chosen depth of the simulation. However, higher model depths (approaching that of a potential planet radius) result in flatter and higher temperature profiles in this simulation; the 10-m simulation is thus deemed a conservative view given the tools available. (Other internal or radiative heat sources were not considered but would only further raise probabilities for deeper and thicker liquid layers of solvents given our results thus far.) Still, it is clear that the thermal model employed here has very apparent limits. Better theoretical modeling of sub-surface temperature environments on extraterrestrial bodies (especially with future missions on the surface of Europa and Titan) will enable these issues to be solved with better precision. Two-dimensional heat transfer effects and, most notably, the tremendous impact of an atmosphere are also topics for further research. All of these open up the possibility for an improved thermal model in future works.
These prospects about liquid solvents of course serve the greater purpose of enabling us to make educated considerations about the possibility of life in such exotic environments as seen here. Liquid layers of thicknesses between half a meter and a few millimeters seem unconventionally small biospheres, but comparable microhabitats have already been considered on earth for microscopic [31,32], as well as macroscopic lifeforms, especially within arctic and antarctic regions [33,34,35]. The wide range of possibilities here on earth illustrates why microhabitation continues to grow in relevancy for astrobiology. This then warrants thoughts about the usability (and hostility) of the energy not just for the potential habitat itself, but the organisms within it as well. Models for the conversion of gamma-ray energy into biomass have already been proposed [36,37] before. However, these models were developed for or from low-energy environments, which makes it questionable if or how they may be applied to high-energy environments, and applications of these models here would lead one to expect high, probably unrealistic amounts of potential biomass. Especially given the new restrictions on growth and homeostasis by the amount of gamma-radiation, the emergence and amount of secondary and tertiary particles or the potential new mechanisms for converting energy into usable units for living entities may play bigger roles within the upper meters. We believe that a thoughtful analysis of the possibilities of gamma-ray-driven life in this environment may deserve much deeper investigation and, as such, consider that beyond the scope of this paper.
5. Conclusions
Our aim with this work was testing the waters (quite literally so) of a rather exotic, high-energy environment to add to the increasing awareness of the potential that circumnuclear clouds around active galactic nuclei hold. Our results show that solvents in such a model can exist in liquid phase even over a wide set of parameters. We thus point to a number of new research fields, especially in geology and astrobiology, for both in-depth theoretical work surrounding this and similar topics, as well as experimental investigations (such as remote sensing of appropriate sources or laboratory models of such environments) and deem our initial goal as successfully reached.
Author Contributions
Conceptualization, D.R. and G.H.; methodology, D.R.; software, D.R.; validation, G.H. and M.H.; writing—original draft preparation, D.R.; writing—review and editing, G.H. and D.R.; visualization, M.S. and D.R.; supervision, M.H. and G.H.; project administration, M.H. and G.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. These datasets can be found here: https://archive.stsci.edu/hlsp/agnsedatlas, accessed on 23 September 2020.
Acknowledgments
For the publication fee we acknowledge financial support by Deutsche Forschungsgemeinschaft within the funding programme „Open Access Publikationskosten“ as well as by Heidelberg University. We would like to thank Malice Rudolph for their help in optimizing the accessibility of the core figures in this work, as well as continued support concerning the English language.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGN | Active galactic nucleus |
| Sy1 | Seyfert Type 1 |
| Sy2 | Seyfert Type 2 |
| CND | Circumnuclear disk |
| NIST | National Institute Of Standards Furthermore, Technology |
| CHERIC | Chemical Engineering and Materials Research Information Center |
| FTCS | Forward Time Centered Space |
| SIMBAD | Set of Identifications, Measurements and Bibliography for Astronomical Data |
Appendix A. Handling Distances and Viewing Angle of Investigated AGNs
To determine the flux arriving at a model planet located a certain distance from the central object, we first need to correct measurements taken for distance and viewing angle from both the measurements and the model planet in relation to the object’s geometry.
To apply the former using the inverse square law, as shown in Equation (1), we need the distances from the earth to the different galaxies of the sample.
Where possible for each of these objects, a direct luminosity distance was obtained from the Set of Identifications, Measurements and Bibliography for Astronomical Data (SIMBAD) online library. Where this was not possible, a redshift z was still available from SIMBAD, and as a consequence, the estimated distance D was approximated using Hubble’s law:
with c being the velocity of light in vacuum, and using a hubble parameter of [38].
Accessing SIMBAD was conducted via the astroquery python package [9], specifically astroquery.simbad, and setting up a custom query using object denominators taken from the filenames of [8] data.
The viewing angle can be regarded properly when assuming a unified model of AGNs, under which condition Equations (2) and (3) make assertions about the luminosity of AGNs based on viewing angle. Figure A1 visually explains the concept behind it.
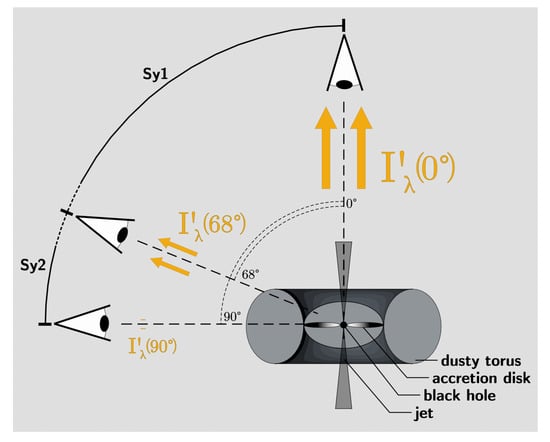
Figure A1.
Visually explaining Equations (2) and (3): the unified model of AGNs proposes that the difference between Type-1 and Type-2 AGNs, in our case Seyfert (Sy) galaxies, which is nominally determined by spectral features, is due to the viewing angle relative to the AGN plane with its accretion disk. In this case, the luminosity received along a certain viewing angle also changes, with [13] proposing the equations above to calculate the luminosity as a function of luminosity along the pole-on direction, which sees the maximum area of the luminous accretion disk. They also propose 68° as the separating angle between Sy1 and Sy2 systems. As such, we deem 68° a sufficient angle for the approximate extent of the dusty torus over the equatorial plane and, as such, an adequate limit angle for potential planetary formation.
Appendix B. Exhaustive Model Simulations
To keep the main part of this work focused, we show variations in the core simulation (rocky crust with freshwater) here, namely the deviation of both liquid layer thickness and liquid layer upper boundaries from that of the rocky-crust, freshwater model. Deviation in the icy-crust model is shown in Figure A2, that in the rocky-crust model that features -saltwater instead of freshwater in its solvent inclusions is shown in Figure A3, and that in the rocky-crust model with -saltwater inclusions is shown in Figure A4.
We note small deviations across the board, the smallest of which occur within the -saltwater model, which shows nearly identical results to the freshwater version. The icy model exhibits deviations of only up to 10% from the rocky, freshwater result, with only eight datapoints above a deviation of 5%. Surprisingly, -saltwater is the most deviant result, with 11 points between 5% and 10% deviation and 2 points for the thickness of liquid ammonia layers deviating up to about 20% from the rocky, freshwater result.
Therefore, while the crust model does impact the results to a noticeable degree, model body size and distance from the central source are the two main parameters influencing the formation of liquid layers within this slew of models.
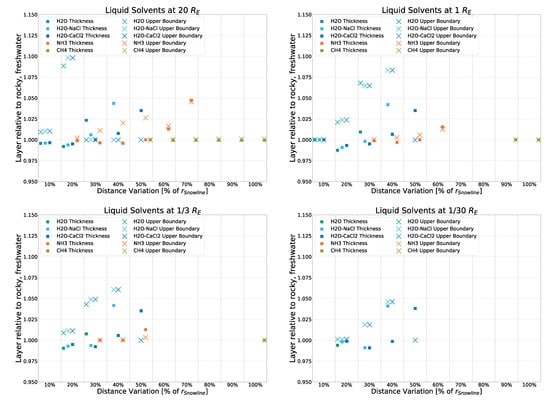
Figure A2.
Deviation from the rocky, freshwater model for liquid layer thickness and upper boundary for an icy crust.
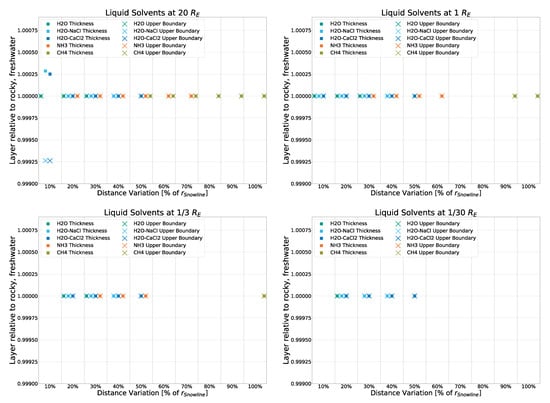
Figure A3.
Deviation from the rocky, freshwater model for liquid layer thickness and upper boundary for a rocky crust with -saltwater inclusions.
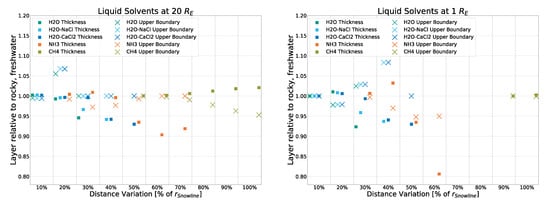
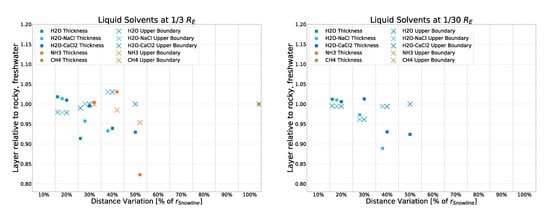
Figure A4.
Deviation from the rocky, freshwater model for liquid layer thickness and upper boundary for a rocky crust with -saltwater inclusions.
Appendix C. Mass Attenuation Coefficient
The mass attenuation coefficients for the considered surface compositions, interpolated from data obtained from the NIST XCOM database [20], as explained in Section 2.2.2, is shown in Figure A5.
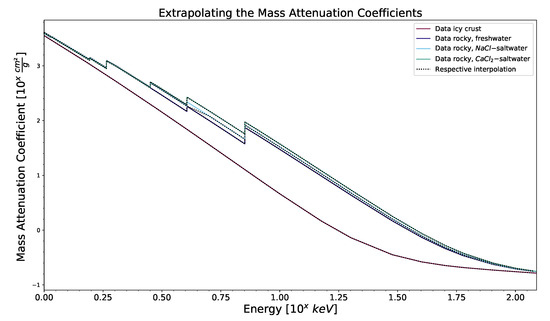
Figure A5.
A plot of mass attenuation coefficients across a photon energy range, with data obtained from [20] (in colored, solid lines) and respective interpolated data (as black, dotted line) for four surface compositions.
Appendix D. About the Triple Point (Equivalent)
Appendix D.1. Triple Point (Equivalent) Properties
The properties for fresh water, methane, and ammonia have been obtained from a NIST database. The matter gets more complicated when dealing with saltwater. However, it can be shown [39] that the triple point equivalent8 of saltwater solutions at their eutectic points can be approximated by the vapor pressure of pure water ice at that temperature. Thus, using the known temperatures of the eutectic points of -saltwater at and -saltwater at [40], we can determine the respective equivalent for the triple point pressure from the behavior of fresh water. All resulting triple points (equivalents) are shown in Table A1.

Table A1.
Triple point (equivalent) properties.
Table A1.
Triple point (equivalent) properties.
| Formula | Properties | |
|---|---|---|
| ptriple[bar] | Ttriple[Kelvin] | |
| a | 273 a | |
| a | 91 a | |
| a | 195 a | |
| b | b | |
| b | b | |
a NIST Chemistry WebBook, NIST Standard Reference Database Number 69 [19]. b [40].
Appendix D.2. Derivation of Triple Point Depth
In Equation (6) the depth at which the triple point pressure, that is the pressure necessary for the relevant solvents to melt (instead of just sublimate), is calculated. The process of arriving at this equation is outlined here:
The triple point pressure is a material constant and can be obtained from databases or literature and expressed as the gravitative force of (on an atmosphere-less body: just) the ground above an observed area A, which here lies at the desired depth :
The force can then be broken down, where, in this case, denotes the mass of the planet below the area at and denotes the mass of the crust weighing down from above:
Since we later want to vary the object radius of hypothetical bodies but not their density , which we set to [41], to simplify the model, it is a good choice to further break down:
As our model in general only considers depths of up to 10 m, it isnegligible when compared to the radius of all the considered models (between 20 and ), so the radius in Equation (A3) can be assumed to be equal to . As such, we can insert Equations (A5) and (A4) into Equation (A3) and this then into Equation (A2) and simplify:
which we can rearrange to reach our desired Equation (6) for the triple depth.
Appendix E. About Heat Conversion
As mentioned, when radiation hits a material, not all of the energy is converted purely into heat, with some energy resulting in secondary radiation or the chemical “upgrade” (breaking and reformation of chemical bonds, resulting in new compounds with the potential to store more energy than before) of the matter hit by radiation. While these secondary processes lie beyond the scope of this work, we wish to make a conservative estimation on the amount of photon energy that actually gets converted into heat to adjust the thermal model therewith.
This estimation is based on evaluating the amount of “pure” kinetic energy released in the medium as minimum input for heating (secondary and tertiary particles will also still render part of their energy into heat). This was carried out utilizing the mass energy-absorption coefficient , which expresses the amount of energy from the incident photon that is transferred as kinetic energy to charged particles in the interaction minus the energy from photons resulting from the movement of these charged particles. When compared to the mass attenuation coefficient , this lets us estimate the portion of attenuated energy “lost” to heating.
For a variety of substances (comparable to the compounds involved in our model, as no exact data for those could be obtained), in the energy range with the most impact from the analyzed AGN spectra (50 keV to 150 keV) and for densities , more than 80% and less than 90% of energy is absorbed via the mechanisms considered under (see Table A2). At higher densities, as they would be seen in the rocky compositions, absorption reaches more than 90% across the board.
This further encourages us to choose 0.9 as a very conservative factor, posing a general minimum of energy available to the thermal model.

Table A2.
Mass energy absorption and mass attenuation coefficients.
Table A2.
Mass energy absorption and mass attenuation coefficients.
| Substance | |||||
|---|---|---|---|---|---|
| 50 | 60 | 80 | 100 | 150 | |
| for | |||||
| water, liquid | 83.14 | 84.03 | 85.41 | 86.48 | 88.44 |
| glass | 83.64 | 84.77 | 86.36 | 87.49 | 89.44 |
| concrete | 83.12 | 84.33 | 85.99 | 87.17 | 89.17 |
| for | |||||
| water, liquid | 91.18 | 91.67 | 92.42 | 93.00 | 94.04 |
| glass | 91.45 | 92.07 | 92.93 | 93.54 | 94.57 |
| concrete | 91.17 | 91.83 | 92.73 | 93.36 | 94.43 |
| for | |||||
| water, liquid | 94.03 | 94.36 | 94.88 | 95.27 | 95.99 |
| glass | 94.22 | 94.64 | 95.23 | 95.64 | 96.35 |
| concrete | 94.02 | 94.48 | 95.09 | 95.53 | 96.25 |
A list of mass energy absorption coefficient values, mass attenuation coefficient values, both from [42], and
the portion of attenuated energy NOT lost in secondary processes exp.
Appendix F. Further Variabilities Investigated
As a final step, we consider four points of variability not touched upon before: the impact of AGN-flux and, by extension, the mean conducted to simplify calculations here on the temperature curve and liquidity of solvents, the impact of the implemented day-and-night-cycle, concrete comparisons to solar system bodies and the lower boundary regarding viable body size in our model.
Appendix F.3. Simulation on a Tidally Locked Body
For this, we disable the part of the code that ensures the continuous source term is added only every other timestep, simulating the lit side of a body tidally locked to the AGNs. (Terminator results are not simulated; rotation is generally half the stepping.) While it should be noted that tidal locking seems unlikely for bodies orbiting several parsecs away from the source (even if said source is supermassive), it allows us to investigate an extreme case. This will be especially interesting in potential follow-up work considering atmospheric bodies. The results, as can be seen in Figure A6, show only very small deviations (<0.8%) from the standard simulation, further showing that, in the case of rocky models, the continuous source term has a marginal impact on the thermal profile.
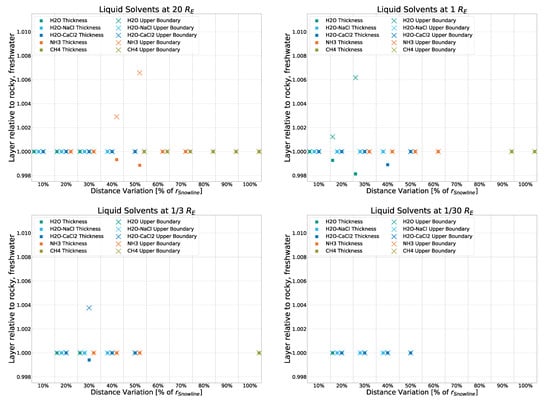
Figure A6.
Deviation from the rocky, freshwater model (with a day and night cycle) for a simulation of the rocky, freshwater model with a continuous “day” as if tidally locked.
Appendix F.4. Simulation with Individual Galaxies
To compare the different impacts that strong and weak sources have on the eventual results, two runs of the simulation were performed without using the input of the averaged spectrum of all 20 AGNs but the spectra of two non-averaged, individual AGNs instead. Specifically, Mrk 876 and NGC 3516, which were identified as the strongest and weakest non-outlier sources of the dataset, respectively. As can be seen in Figure A7 and Figure A8, small to no deviation from that of the averaged spectrum used forNGC 3516) the main simulation is found. The simulation using the “weak” NGC 3516 as input exhibits a maximum deviation of 10% in a single datapoint, with all others staying below 2.5%. The simulation using the “strong” Mrk 876 as input shows no discernible deviation. This further confirms that in this simulation, the strength of the source (as long as said source is of the same object class: Seyfert Type 1) has marginal to no impact on the temperature profile and thus the liquid layers resulting from them.
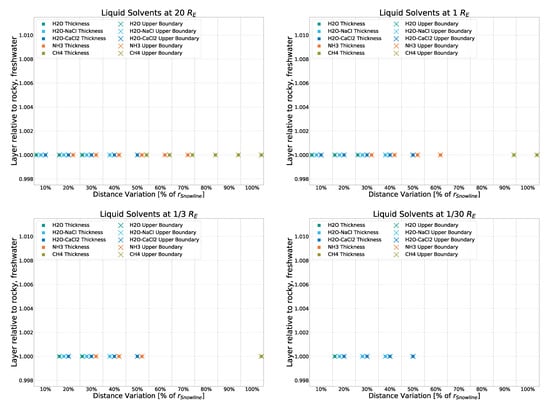
Figure A7.
Deviation from the rocky, freshwater model (with input being the average spectrum of 20 AGNs) for a simulation with input coming from a single, strong source (Mrk 876).
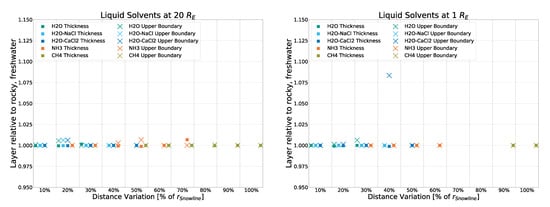
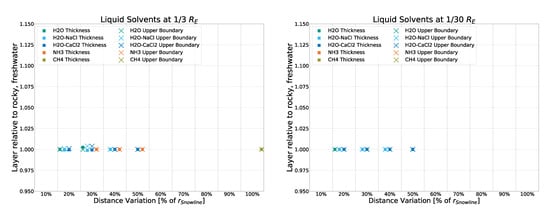
Figure A8.
Deviation from the rocky, freshwater model (with input being the average spectrum of 20 AGNs) for a simulation with input coming from a single, weak source (NGC 3516).
Appendix F.5. Simulations of Small Moons and Asteroids
We then conducted rough approximations of four small, real bodies in the solar system to show the results of a more constraint but realistic approach to density and size. Simulations were ran after adjusting (as mentioned in Appendix D.2) to the density of Ganymede (), 511 Davida (), Europa (), and 4 Vesta () [43,44], respectively. We further modified the crust density to be equal the body density for the asteroid 511 Davida, as it is non-differentiated. Results are shown in Figure A9, with the very notable result of liquid ammonia and methane being possible on bodies roughly equivalent to the Galilean moons Ganymede and Europa.
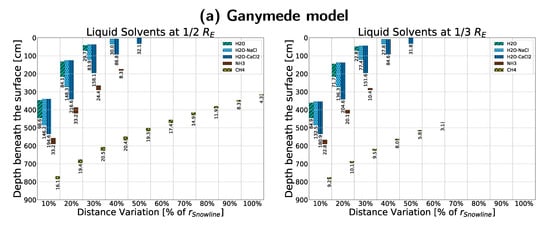
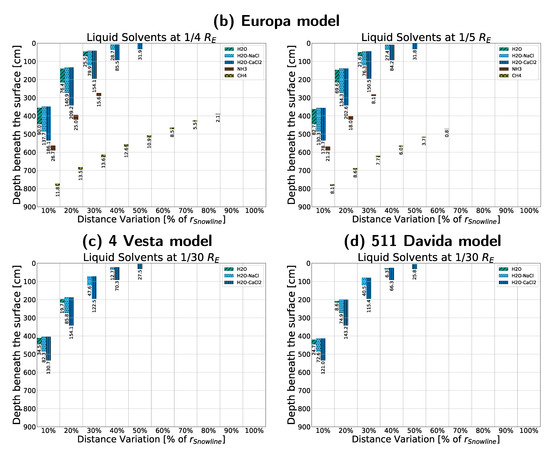
Figure A9.
Comparisons between different approximations of smaller bodies with sizes and densities close to their real-life counterparts and crust densities , as seen in Table 2: (a) Jupiter’s moon Ganymede ()shown for sizes , using an icy crust; (b) Jupiter’s moon Europa () shown for sizes of , using an icy crust; (c) Asteroid 4 Vesta () shown for a size of , using a rocky, freshwater crust; (d) Asteroid 511 Davida () shown for a size of , using a rocky, freshwater crust with modified density .
Appendix F.6. Determining the Minimum Valid Model Body Size
As a last point of this appendix, we attempt to determine a rough measure of how small a body within a certain subset of parameters must be in order to support any form of liquid layers. This has been carried out by manually adjusting the model body sizes within the final calculations of where liquid layers are present using the thermal profile of the rocky-crust model as an input, meaning that these different sizes were not taken into account during the simulation of said thermal profiles, again to stay within a certain realistic scope. The results can be seen in Figure A10. One can see that, in accordance with our previous assessments, saltwater is able to persist with only marginal limitations from a body’s size (and therefore the pressure environment beneath the surface). This results in -saltwater’s ability to, in our simulations, stay liquid even on bodies smaller than 4.3 km. Fresh water can still persist on bodies between and , which is of particular interest as this range (radii of of 60 to 85 km and thus diameters of 120 to 170 km) roughly coincides with the size ranges of the largest known icy comet nuclei (for example, , also known as Bernardinelli–Bernstein, which is estimated to measure between 120 and 137 km [45,46]), which itself opens a number of interesting possibilities for follow-ups.
It should be noted that at this size, many other factors may support or hamper the persistence of liquid solvents that we did not take into account here, but this serves as a fitting proof-of-concept that, in environments such as the ones considered here, even bodies as small as this are worth investigating more closely.
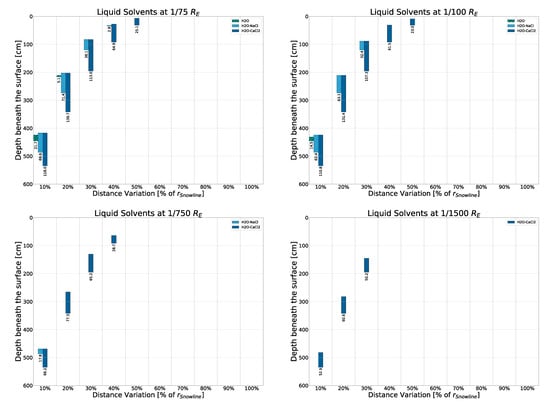
Figure A10.
Liquid layers on very small bodies using the standard rocky, freshwater model (). On distances close to the source, fresh water can be liquid on bodies as small as , while both forms of saltwater can be liquid on bodies as small as . -saltwater can be liquid even on bodies smaller than .
Notes
| 1 | Similar to the reasoning behind using X-ray luminosity for snowline calculations [6,7]. |
| 2 | For the bulk of the simulations. Special calculations with systems as small as were carried out as well. |
| 3 | With data taken from the NIST WebBook [19]. |
| 4 | Only 90% of which will be used to generate the heat in this model however, with 10% being “reserved” for effects not inspected closer here such as secondary radiation and the modification of bonds of chemical compounds. This is discussed in detail in Appendix E. |
| 5 | Corresponding to the boiling point shift of these mixtures at these concentrations. |
| 6 | We do not account for lateral thermal decay as we are building a 1-D model, and horizontal thermal decay only occurs at the surface, which is controlled here using the equilibrium temperature. |
| 7 | Calculations were carried out in separate clusters, but plotting was carried out in the general IPython environment. This necessitates extra steps at this point that are laid out in more detail in Section 2.4. |
| 8 | Triple points are strictly speaking only defined for pure substances; we here use the critical point equivalent of a triple point as we are not interested in the exact phase behavior, merely the minimum pressure and temperature necessary for liquids to occur. |
References
- Stevenson, J.; Lunine, J.; Clancy, P. Membrane alternatives in worlds without oxygen: Creation of an azotosome. Sci. Adv. 2015, 1, e1400067. [Google Scholar] [CrossRef] [PubMed]
- Palmer, M.Y.; Cordiner, M.A.; Nixon, C.A.; Charnley, S.B.; Teanby, N.A.; Kisiel, Z.; Irwin, P.G.J.; Mumma, M.J. ALMA detection and astrobiological potential of vinyl cyanide on Titan. Sci. Adv. 2017, 3, e1700022. [Google Scholar] [CrossRef]
- Rampelotto, H.P. The search for life on other planets: Sulfur-based, silicon-based, ammonia-based life. J. Cosmol. 2010, 5, 818–827. [Google Scholar]
- Stofan, E.R.; Elachi, C.; Lunine, J.I.; Lorenz, R.D.; Stiles, B.; Mitchell, K.L.; Ostro, S.; Soderblom, L.; Wood, C.; Zebker, H.; et al. The lakes of Titan. Nature 2007, 445, 61–64. [Google Scholar] [CrossRef]
- Grasset, O.; Sotin, C.; Deschamps, F. On the internal structure and dynamics of Titan. Planet. Space Sci. 2000, 48, 617–636. [Google Scholar] [CrossRef]
- Wada, K.; Tsukamoto, Y.; Kokubo, E. Planet Formation around Supermassive Black Holes in the Active Galactic Nuclei. Astrophys. J. 2019, 886, 107. [Google Scholar] [CrossRef]
- Wada, K.; Tsukamoto, Y.; Kokubo, E. Formation of “Blanets” from Dust Grains around the Supermassive Black Holes in Galaxies. Astrophys. J. 2021, 909, 96. [Google Scholar] [CrossRef]
- Brown, M. An Atlas of Active Galactic Nuclei Spectral Energy Distributions (“AGNSEDATLAS”). Mon. Not. R. Astron. Soc. 2019, 489, 3351–3367. [Google Scholar] [CrossRef]
- Ginsburg, A.; Sipöcz, B.M.; Brasseur, C.E.; Cowperthwaite, P.S.; Craig, M.W.; Deil, C.; Guillochon, J.; Guzman, G.; Liedtke, S.; Lim, P.L.; et al. astroquery: An Astronomical Web-querying Package in Python. Astron. J. 2019, 157, 98. [Google Scholar] [CrossRef]
- Padovani, P. Active Galactic Nuclei at All Wavelengths and from All Angles. Front. Astron. Space Sci. 2017, 4, 35. [Google Scholar] [CrossRef]
- Fischer, T.C.; Crenshaw, D.M.; Kraemer, S.B.; Schmitt, H.R. Determining inclinations of active galactic nuclei via their narrow-line region kinematics. i. observational results. Astrophys. J. Suppl. Ser. 2013, 209, 1. [Google Scholar] [CrossRef]
- Antonucci, R. Unified Models for Active Galactic Nuclei and Quasars. Annu. Rev. Astron. Astrophys. 1993, 31, 473–521. [Google Scholar] [CrossRef]
- Zhang, S.N. A Single Intrinsic Luminosity Function for Both Type I and Type II Active Galactic Nuclei. Astrophys. J. 2004, 618, L79–L82. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Alexander, L.; Snape, J.; Joy, K.; Downes, H.; Crawford, I. An analysis of Apollo lunar soil samples 12070,889, 12030,187, and 12070,891: Basaltic diversity at the Apollo 12 landing site and implications for classification of small-sized lunar samples. Meteorit. Planet. Sci. 2016, 51, 1654–1677. [Google Scholar] [CrossRef]
- Kreidberg, L.; Koll, D.D.B.; Morley, C.; Hu, R.; Schaefer, L.; Deming, D.; Stevenson, K.B.; Dittmann, J.; Vanderburg, A.; Berardo, D.; et al. Absence of a thick atmosphere on the terrestrial exoplanet LHS 3844b. Nature 2019, 573, 87–90. [Google Scholar] [CrossRef] [PubMed]
- Harada, N.; Riquelme, D.; Viti, S.; Jiménez-Serra, I.; Requena-Torres, M.A.; Menten, K.M.; Martín, S.; Aladro, R.; Martin-Pintado, J.; Hochgürtel, S. Chemical features in the circumnuclear disk of the Galactic center. Astron. Astrophys. 2015, 584, A102. [Google Scholar] [CrossRef]
- Thermodynamics Research Center; NIST Boulder Lab.; Muzny, C. Thermodynamics Source Database. In NIST Chemistry WebBook, NIST Standard Reference Database 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1997. [Google Scholar] [CrossRef]
- XCOM. NIST XCOM Selection. 2010. Available online: https://physics.nist.gov/PhysRefData/Xcom/html/xcom1.html (accessed on 25 October 2021).
- CHERIC. CHERIC Pure Component Properties. 2011. Available online: https://www.cheric.org/research/kdb/hcprop/cmpsrch.php (accessed on 23 October 2021).
- Landau, L.D.; Lifshitz, E.M. Statistical Physics Part 1; Pergamon Press: Oxford, UK, 1980; pp. 193–196. [Google Scholar]
- Overstreet, R.; Giauque, W.F. Ammonia. The Heat Capacity and Vapor Pressure of Solid and Liquid. Heat of Vaporization. The Entropy Values from Thermal and Spectroscopic Data. J. Am. Chem. Soc. 1937, 59, 254–259. [Google Scholar] [CrossRef]
- Yakub, L.; Bodiul, O. Low-temperature equation of state of solid methane. Refrig. Eng. Technol. 2016, 52, 80–85. [Google Scholar] [CrossRef]
- Shulman, L.M. The heat capacity of water ice in interstellar or interplanetary conditions. Astron. Astrophys. 2004, 416, 187–190. [Google Scholar] [CrossRef]
- Riflet, G. 1D Heat Equation and a Finite-Difference Solver. 2010. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/3779573658038/HeatEquation.pdf (accessed on 3 January 2020).
- Perez, F.; Granger, B.E. IPython: A System for Interactive Scientific Computing. Comput. Sci. Eng. 2007, 9, 21–29. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Nelson, R.M.; Boryta, M.D.; Hapke, B.W.; Shkuratov, Y.; Vandervoort, K.; Vides, C.L. Understanding Europa’s Surface Texture from Remote Sensing Photopolarimetry. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 12–16 December 2016. abstract id. P11C–1870. [Google Scholar]
- Mitri, G.; Showman, A.; Lunine, J.; Lopes, R. Cryovolcanism on Titan. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2008. [Google Scholar]
- Fritsen, C.H.; Coale, S.L.; Neenan, D.R.; Gibson, A.H.; Garrison, D.L. Biomass, production and microhabitat characteristics near the freeboard of ice floes in the Ross Sea, Antarctica, during the austral summer. Ann. Glaciol. 2001, 33, 280–286. [Google Scholar] [CrossRef]
- Meckenstock, R.U.; von Netzer, F.; Stumpp, C.; Lueders, T.; Himmelberg, A.M.; Hertkorn, N.; Schmitt-Kopplin, P.; Harir, M.; Hosein, R.; Haque, S.; et al. Water droplets in oil are microhabitats for microbial life. Science 2014, 345, 673–676. [Google Scholar] [CrossRef]
- da Silva, T.H.; Silva, D.A.S.; Thomazini, A.; Schaefer, C.E.G.R.; Rosa, L.H. Antarctic Permafrost: An Unexplored Fungal Microhabitat at the Edge of Life. In Fungi of Antarctica: Diversity, Ecology and Biotechnological Applications; Rosa, L.H., Ed.; Springer International Publishing: Cham, Switzerland, 2019; Volume 345, pp. 147–164. [Google Scholar] [CrossRef]
- Kennedy, A. Antarctic Permafrost: An Unexplored Fungal Microhabitat at the Edge of Life. Antarct. Sci. 1999, 11, 27–37. [Google Scholar] [CrossRef]
- Glass, T.W.; Breed, G.A.; Iwahana, G.; Kynoch, M.C.; Robards, M.D.; Williams, C.T.; Kielland, K. Permafrost ice caves: An unrecognized microhabitat for Arctic wildlife. Ecology 2021, 102, e03276. [Google Scholar] [CrossRef]
- Altair, T.; de Avellar, M.G.B.; Rodrigues, F.; Galante, D. Microbial habitability of Europa sustained by radioactive sources. Sci. Rep. 2018, 8, 260. [Google Scholar] [CrossRef]
- Braun, S.; Morono, Y.; Littmann, S.; Kuypers, M.; Aslan, H.; Dong, M.; Jørgensen, B.B.; Lomstein, B.A. Size and Carbon Content of Sub-seafloor Microbial Cells at Landsort Deep, Baltic Sea. Front. Microbiol. 2016, 7, 1375. [Google Scholar] [CrossRef]
- Khetan, N.; Izzo, L.; Branchesi, M.; Wojtak, R.; Cantiello, M.; Murugeshan, C.; Agnello, A.; Cappellaro, E.; Della Valle, M.; Gall, C.; et al. A new measurement of the Hubble constant using Type Ia supernovae calibrated with surface brightness fluctuations. Astron. Astrophys. 2021, 647, A72. [Google Scholar] [CrossRef]
- Bodnar, R.J. PTX Phase Equilibria in the H2O-CO2-Salt System at Mars Near-Surface Conditions. In Proceedings of the Lunar and Planetary Science Conference, Houston, TX, USA, 12–16 March 2001; p. 1689. [Google Scholar]
- Ketcham, S.A.; Minsk, L.D.; Blackburn, R.R.; Fleege, E.J. Manual of Practice for an Effective Anti-Icing Program; Turner-Fairbank Highway Research Center: McLean, VA, USA, 1996; Publication Number: FHWA-RD-95-202. [Google Scholar]
- Williams, D. Earth Fact Sheet. 2020. Available online: https://nssdc.gsfc.nasa.gov/planetary/factsheet/earthfact.html (accessed on 12 April 2021).
- Hubbell, J.H.; Seltzer, S.M. Tables of X-Ray Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients (Version 1.4); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2004. Available online: http://physics.nist.gov/xaamdi (accessed on 5 January 2020). [CrossRef]
- Showman, A.P.; Malhotra, R. The Galilean Satellites. Science 1999, 286, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Carry, B. Density of asteroids. Planet. Space Sci. 2012, 73, 98–118. [Google Scholar] [CrossRef]
- Hui, M.T.; Jewitt, D.; Yu, L.L.; Mutchler, M.J. Hubble Space Telescope Detection of the Nucleus of Comet C/2014 UN271 (Bernardinelli-Bernstein). Astrophys. J. Lett. 2022, 929, L12. [Google Scholar] [CrossRef]
- Lellouch, E.; Moreno, R.; Bockelée-Morvan, D.; Biver, N.; Santos-Sanz, P. Size and albedo of the largest detected Oort-cloud object: Comet C/2014 UN271 (Bernardinelli-Bernstein). Astron. Astrophys. 2022, 659, L1. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).