Spirality: A Novel Way to Measure Spiral Arm Pitch Angle
Abstract
1. Introduction
1.1. Current Work
1.2. Motivation
2. Materials and Methods
2.1. Spiral Coordinate System
2.2. Computation Method
2.2.1. Error Bars
2.2.2. Measuring a Symmetric Component
2.2.3. Measuring a Combination of Symmetric Components
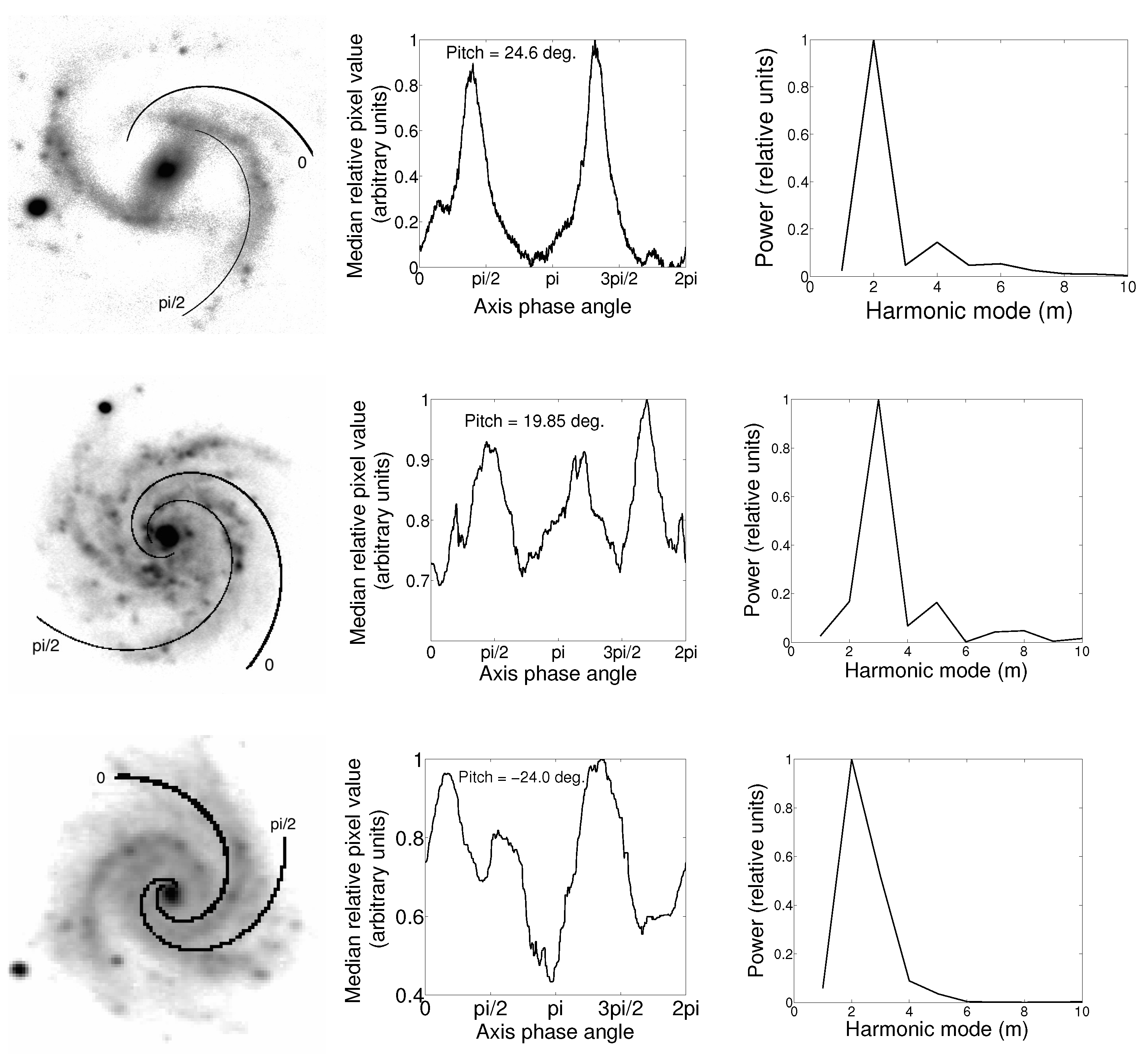
2.2.4. Counting the Spiral Arms
3. Results
3.1. Pitch Angle Measurement Examples
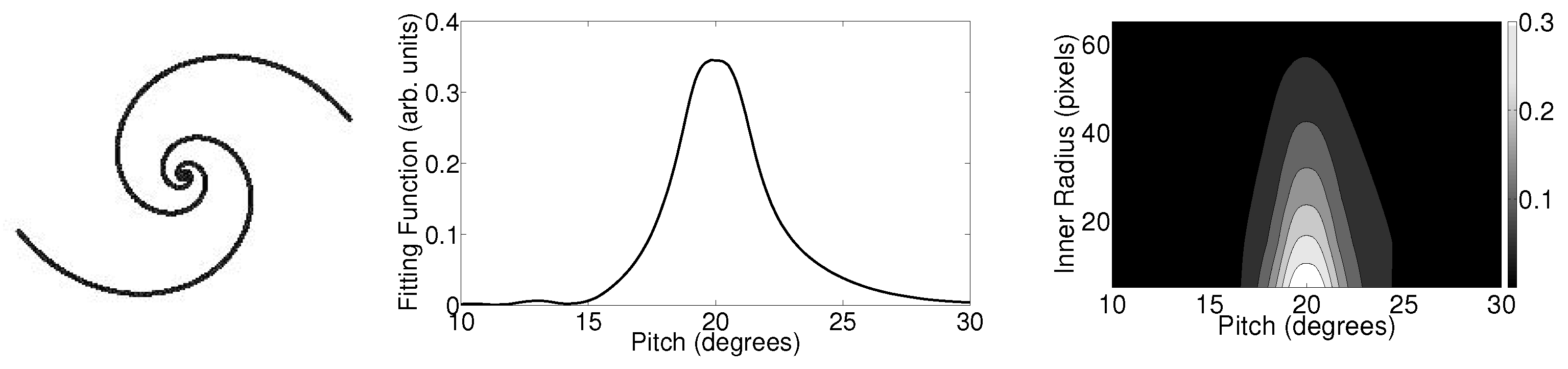
3.1.1. Synthetic Spiral
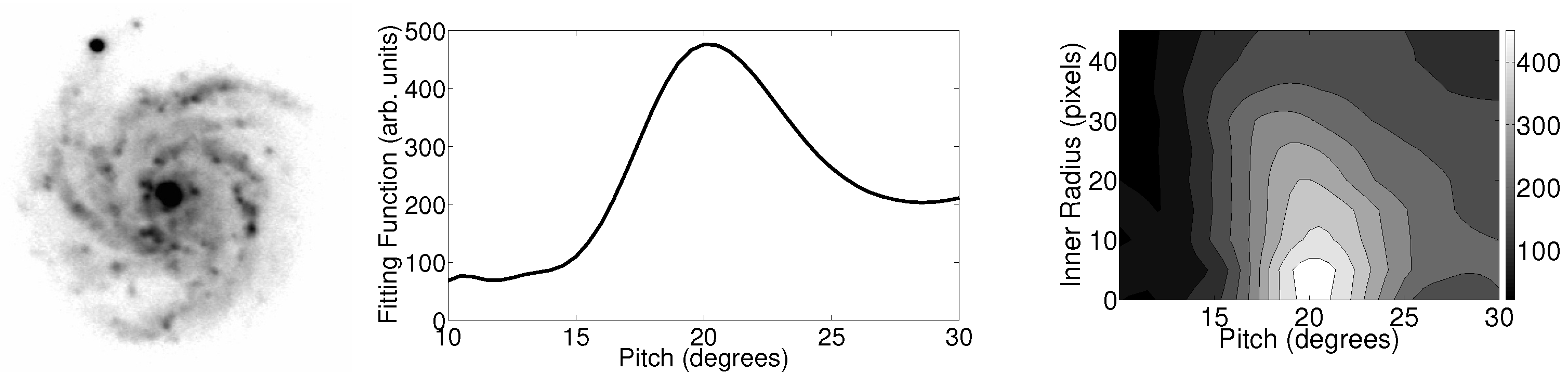
3.1.2. Simple Galaxy: UGC 463
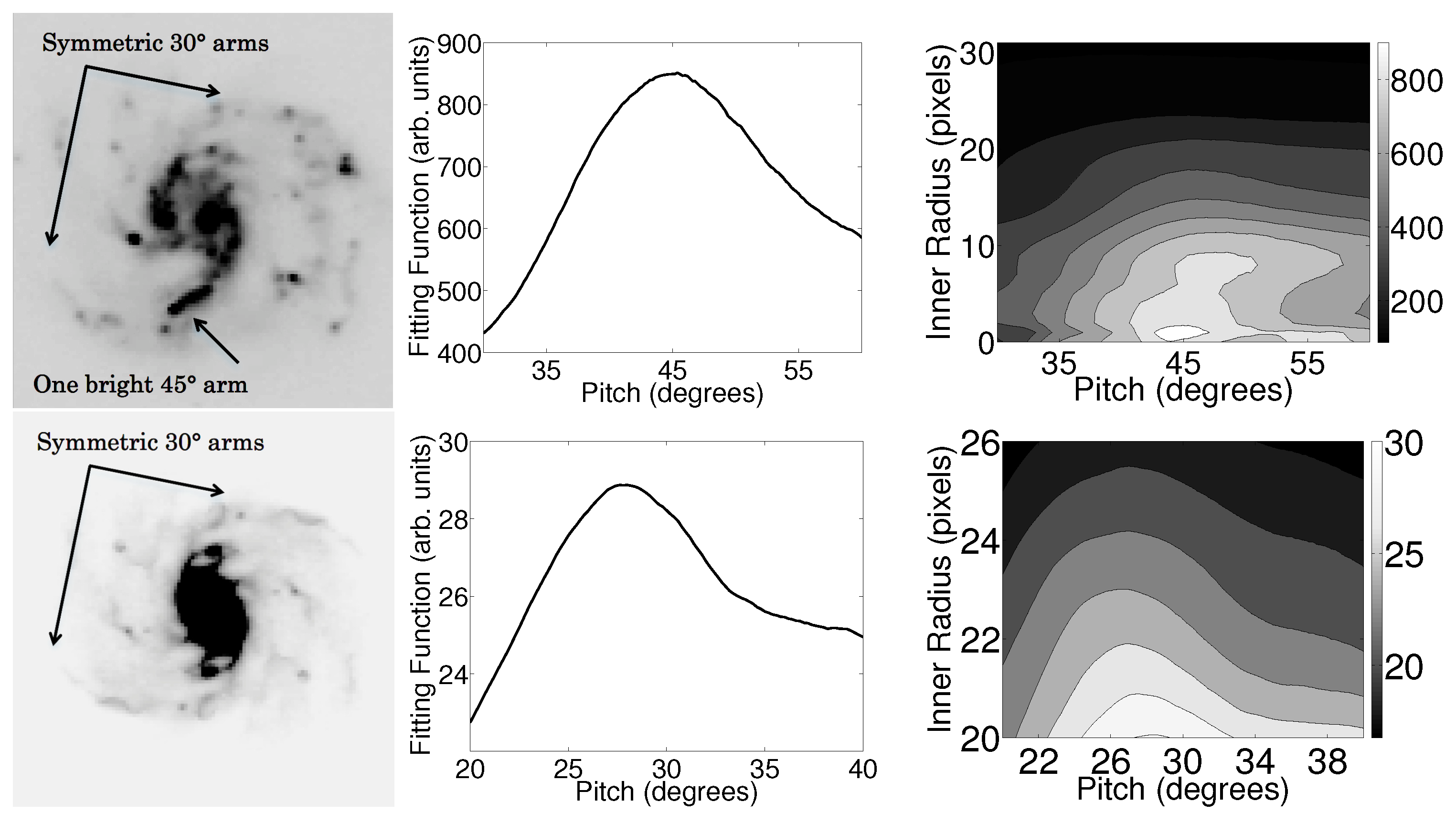
3.1.3. Interesting Galaxy: UGC 4256
3.2. Tests on Synthetic Spirals
3.2.1. Varying Spiral Properties
Number of Spiral Arms
Pitch
Non-Logarithmicity
Radius
Arm Thickness
SNR
Inclination
Bar Half-Length
Bulge Radius
3.2.2. Varying Inputs
Center Offset (Input Variables X0 and Y0)
Inner Radius Spacing (Input Variable Inner Radius Spacing)
Number of Spiral Axes (Input Variable NAXIS)
Pitch Angle Spacing (Input Variable PSTEP)
Axis Point Spacing (Input Variable Axis Point Spacing)
3.3. Tests on Galaxy Samples
3.3.1. Nearby Galaxies: DMS PPak
UGC 1635
UGC 3091
UGC 3997
UGC 4256
3.3.2. Measurement Quality of Low-Resolution Images
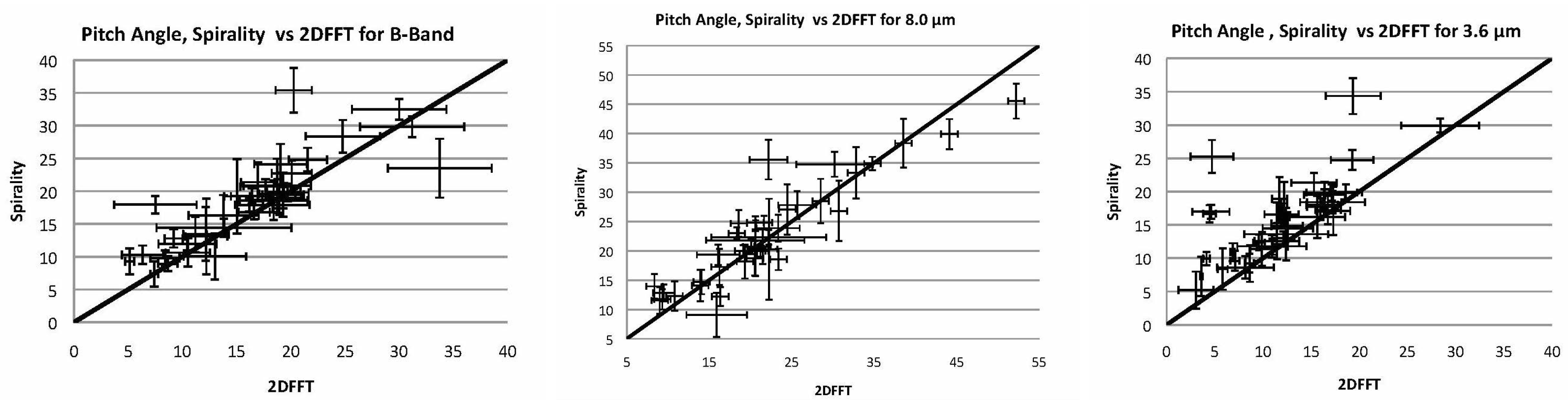
3.3.3. More Nearby Galaxies: Pitch Angle vs. Wavelength
3.3.4. High Redshift, Low Resolution Galaxies
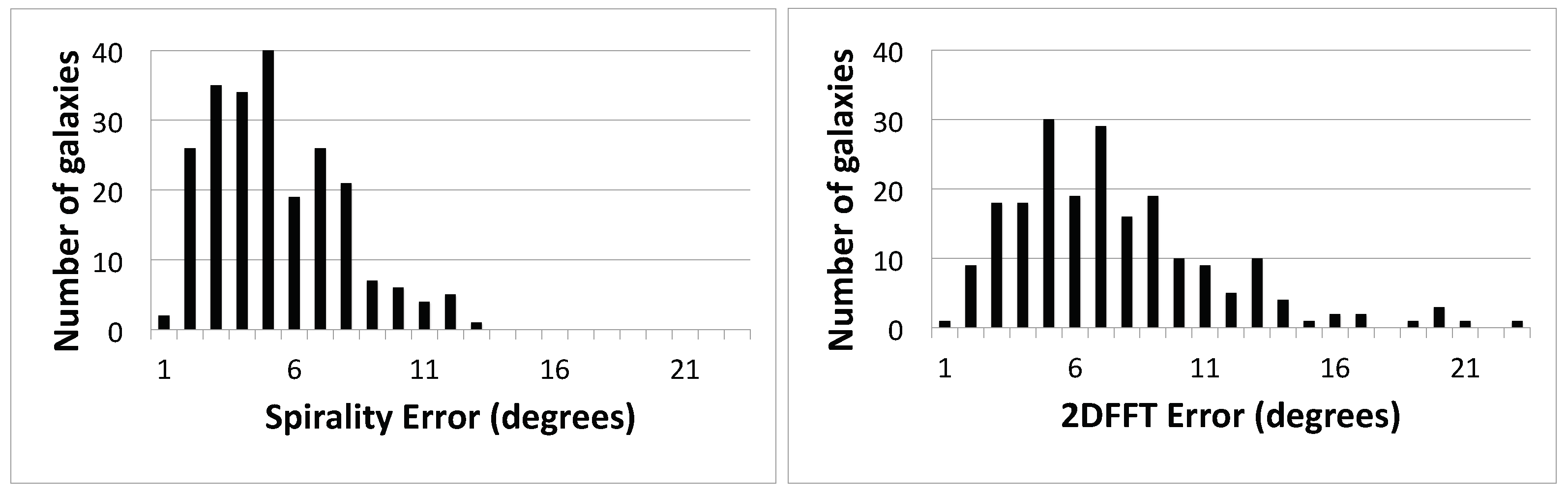
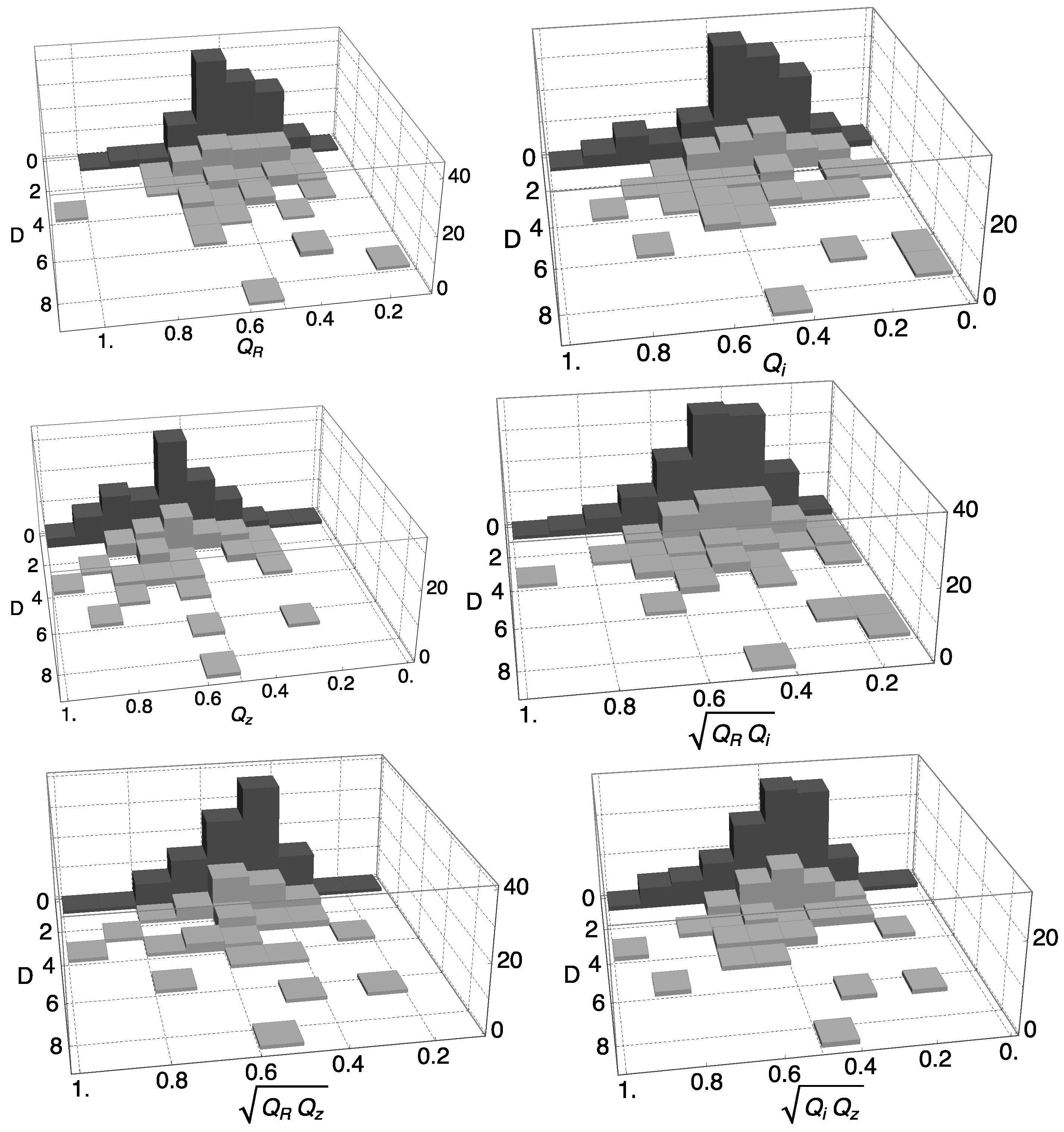
3.3.5. Testing the Error Bars
4. Discussion
Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Spirality Code
Appendix A.1. File: Spirality.m
- PITCHvsINNER (Double)—A two-column array showing the galaxy’s best-fit pitch angle, in degrees, as a function of inner measurement radius.
- BESTFITPITCH (Double)—The answer, i.e., the mean pitch angle in the PITCHvsINNER array, or the best-fit pitch angle of the galaxy.
- ERR (Double)—The total error in the BESTFITPITCH measurement. It is the standard deviation of the pitch angles in the PITCHvsINNER array, scaled by the range of visible spiral radii divided by the range of inner measurement radii, then added in quadrature with the input parameter InnerRadiusSpacing.
- FILE (String)—The filename of the galaxy image. The file must be in *.FITS format, and the galaxy must be oriented face-on or deprojected to circular.
- X0, Y0 (Positive doubles)—The center of the galaxy in Cartesian pixel coordinates.
- VIS_INNER, VIS_OUTER (Positive doubles, VIS_INNER < VIS_OUTER)—Visually estimated inner and outer radii, in pixels, of the galaxy’s spirals. These inputs are used to compute the error bar, not to compute pitch angle itself.
- MSMT_INNER1, MSMT_INNER2, MSMT_OUTER (Positive doubles, MSMT_INNER1 < MSMT_INNER2 < MSMT_OUTER)—The code first measures the galaxy on an annulus with inner radius MSMT_INNER1, in pixels, and outer radius MSMT_OUTER, in pixels. It then repeats the process, increasing the inner radius incrementally to MSMT_INNER2. The outer radius is held constant at MSMT_OUTER. The best-fit pitch is the mean of pitch angles measured on all such annuli.
- InnerRadiusSpacing (Positive double)—Spacing, in pixels, between successive inner radii. As a starting point, we recommend measuring around 11 inner radii, meaning InnerRadiusSpacing ∼ (MSMT_INNER2—MSMT_INNER1)/10.
- NAXIS (Positive integer)—Number of spiral axes in each spiral template. We recommend between 2 and 4, where R is the outer radius of the galaxy in pixels. Insufficient values of NAXIS will result in high-frequency, periodic variations in the fitting function, particularly in the loose end of pitch angle domain (that is, near ±90°).
- MINP, MAXP (Doubles, −90 ≤ MINP ≤ MAXP ≤ 0 or 0 ≤ MINP ≤ MAXP ≤ 90)—Minimum and maximum pitch angles, respectively, in degrees, of the pitch angle measurement domain. Computation time diverges if zero is included in the domain.
- PSTEP (Positive double) Spacing, in degrees, between pitch angles of successive measurement templates. For coarse measurements, we recommend PSTEP = 1. For fine measurements, we recommend PSTEP = 0.2. Note that PSTEP is the minimum possible error in the pitch angle measurement.
- AxisPointSpacing (Positive double) The spacing, in pixels, between computation points on each spiral axis of each pitch angle template. As a starting point, we recommend AxisPointSpacing = 0.2. Computation time varies inversely with this quantity.
- SMOOTH (0 or 1)—A toggle for applying a 5-point moving average to the fitting function. If SMOOTH is 1, the moving average is applied; otherwise it is not. This feature is useful in smoothing high-frequency variations caused by an insufficient value of NAXIS. However, it can also affect the location of the peaks, so use with caution.
- Save2D, Save3D (0 or 1)—Toggles for saving the output files. If Save2D is 1, a 2-D graph of the fitting function vs. pitch angle will be generated for each inner radius. If Save3D is 1, a 3-D graph of the fitting function vs. pitch angle and inner radius will be generated. If either variable is set to 1, then a text file summarizing the results will be generated.
Appendix A.2. File: SpiralArmCount.m
- Median pixel value vs. phase angle (.fig, .eps)—A graph showing one local max for each spiral arm.
- FFT (Counting function vs. Mode) (.fig, .eps)—A graph showing the strength of the counting function for each symmetric mode.
- M (Double array, 1 × 10)—The symmetry mode domain of the counting function.
- Power (Double array, 1 × 10)—The counting function.
- Count (Double)—The mode with the maximum value of the counting function, i.e., the number of spiral arms.
- FILE (String)—The filename of the galaxy image. The file must be in *.FITS format, and the galaxy must be oriented face-on or deprojected to circular.
- X0, Y0 (Positive doubles)—The center of the galaxy in Cartesian pixel coordinates.
- INNER (Positive double)—The inner radius, in pixels, of the spiral annulus. In other words, the radius of the bulge or bar.
- OUTER (Positive double)—The outer radius, in pixels, of the spiral annulus. In other words, radius of the galaxy.
- PITCH (Double, −90 ≤ PITCH < 0, or 0 < PITCH ≤ 90)—The pitch angle, in degrees, of the galaxy. For S-windings, the pitch is positive. For Z-windings, the pitch is negative. Computation time diverges as PITCH approaches zero.
Appendix A.3. File: GenSpiral.m
- M (Integer)—The number of arms in the output spiral.
- PCONST (Double, −90 ≤ PCONST ≤ 90)—The pitch angle, in degrees, at the center of the spiral. If the spiral is logarithmic (specified by the input PSLOPE = 0), then PCONST is the pitch angle of the spiral.
- PSLOPE (Double)—Linear change in pitch angle, in degrees, from the spiral’s center to the edge. In other words, the pitch angle at the center is PCONST, while the pitch angle at the edge is PCONST + PSLOPE.
- RADIUS (Positive integer)—Radius, in pixels, of the output spiral.
- THICK (Positive integer)—Thickness, in pixels, of the spiral arms.
- INVSNR (Positive double)—The reciprocal of the signal-to-noise ratio of the output image. If INVSNR = 0, no noise is added to the image. Otherwise, Gaussian noise is added such that the SNR is equal to 1/INVSNR.
- GRADIENT (0, 1, or 2)—Determines whether the spiral will have a galaxy-like luminosity profile or whether the spiral arms will have the same intensity throughout:
- -
- If GRADIENT = 0, then every pixel on the spiral has the same pixel value before the Gaussian noise is added.
- -
- If GRADIENT = 1, then the spiral’s luminosity is modeled after UGC 463, and the Gaussian noise has the same luminosity profile as the spiral.
- -
- If GRADIENT = 2, then the spiral’s luminosity is modeled after UGC 463, but the Gaussian noise distribution remains constant throughout the image.
- FILESAVE (0 or 1)—Toggle that determines whether the output files will be saved. If FILESAVE = 1, a FITS file and a JPEG file are output. If FILESAVE = 0, no files are output.
- BULGERADIUS—Radius, in pixels, of the circular bulge in the output spiral. If BULGERADIUS = 0, no bulge is added.
Appendix A.4. File: SymPart.m
- SYM (Double array)—The symmetric component of the input image.
- RESID (Double array)—The residual from the symmetric component of the input image. Adding RESID to SYM yields the original image array.
- IMAGE (Double array)—The array containing the pixel values of the input image.
- M (Integer)—The harmonic mode to be extracted. For example, if M = 2, the code will compute the 2-arm (180°) symmetric component.
- C0, R0 (Double)—The column and row, respectively, of the center of the spiral in the input image array. This is equivalent to the Cartesian X and Y in a FITS image.
Appendix A.5. File: MultiSymPart.m
- MULTI_SYM (Double array)—The sum of the specified symmetric components of the input image.
- MULTI_RESID (Double array)—The residual from the symmetric components. Adding MULTI_RESID to MULTI_SYM yields the original image array.
Appendix A.6. File: Functions Called by Other Functions
- Extract_Filename.m
- fitsread.m
- fitsheader.m
- fitswrite.m
- PeriodToDash.m
- RotateTheta.m
References
- Seigar, M.S.; Kennefick, D.; Kennefick, J.; Lacy, C.H.S. Discovery of a Relationship between Spiral Arm Morphology and Supermassive Black Hole Mass in Disk Galaxies. Astrophys. J. Lett. 2008, 678, L93–L96. [Google Scholar] [CrossRef]
- Berrier, J.C.; Davis, B.L.; Kennefick, D.; Kennefick, J.D.; Seigar, M.S.; Barrows, R.S.; Hartley, M.; Shields, D.; Bentz, M.C.; Lacy, C.H.S. Further Evidence for a Supermassive Black Hole Mass-Pitch Angle Relation. Astrophys. J. 2013, 769, 132. [Google Scholar] [CrossRef]
- Davis, B.L.; Graham, A.W.; Seigar, M.S. Updating the (supermassive black hole mass)-(spiral arm pitch angle) relation: A strong correlation for galaxies with pseudobulges. Mon. Not. R. Astron. Soc. 2017, 471, 2187. [Google Scholar] [CrossRef]
- Davis, B.L.; Graham, A.W.; Combes, F. A Consistent Set of Empirical Scaling Relations for Spiral Galaxies: The (vmax, MoM)-(σ0, MBH, ϕ) Relations. Astrophys. J. 2019, 877, 64. [Google Scholar] [CrossRef]
- Ma, J. A Method of Obtaining the Pitch Angle of Spiral Arms and the Inclination of Galactic Discs. Chin. J. Astron. Astrophys. 2001, 1, 395. [Google Scholar] [CrossRef]
- Kennicutt, R.C., Jr. The shapes of spiral arms along the Hubble sequence. Astron. J. 1981, 86, 1847–1858. [Google Scholar] [CrossRef]
- Grosbol, P.J.; Patsis, P.A. Stellar disks of optically flocculent and grand design spirals. Decoupling of stellar and gaseous disks. Astron. Astrophys. 1998, 336, 840–854. [Google Scholar]
- Kendall, S.; Kennicutt, R.C.; Clarke, C. Spiral structure in nearby galaxies—I. Sample, data analysis and overview of results. Mon. Not. R. Astron. Soc. 2011, 414, 538–564. [Google Scholar] [CrossRef]
- Saraiva Schroeder, M.F.; Pastoriza, M.G.; Kepler, S.O.; Puerari, I. The distribution of light in the spiral galaxy NGC 7412. Astron. Astrophys. 1994, 108, 41–54. [Google Scholar]
- Davis, B.L.; Berrier, J.C.; Shields, D.W.; Kennefick, J.; Kennefick, D.; Seigar, M.S.; Lacy, C.H.S.; Puerari, I. Measurement of Galactic Logarithmic Spiral Arm Pitch Angle Using Two-dimensional Fast Fourier Transform Decomposition. Astrophys. J. Suppl. Ser. 2012, 199, 33. [Google Scholar] [CrossRef]
- Gonzalez, R.A.; Graham, J.R. Tracing the Dynamics of Disk Galaxies with Optical and Infrared Surface Photometry: Color Gradients in M99. Astrophys. J. 1996, 460, 651. [Google Scholar] [CrossRef]
- Martínez-García, E.E.; Puerari, I.; Rosales-Ortega, F.F.; González-Lópezlira, R.A.; Fuentes-Carrera, I.; Luna, A. The Behavior of the Pitch Angle of Spiral Arms Depending on Optical Wavelength. Astrophys. J. Lett. 2014, 793, L19. [Google Scholar] [CrossRef]
- Davis, D.R.; Hayes, W.B. SpArcFiRe: Scalable Automated Detection of Spiral Galaxy Arm Segments. Astrophys. J. 2014, 790, 87. [Google Scholar] [CrossRef]
- Puerari, I.; Elmegreen, B.G.; Block, D.L. A New Method to Estimate Local Pitch Angles in Spiral Galaxies: Application to Spiral Arms and Feathers in M81 and M51. Astron. J. 2014, 148, 133. [Google Scholar] [CrossRef]
- Hewitt, I.B.; Treuthardt, P. Comparison of galaxy spiral arm pitch angle measurements using manual and automated techniques. Mon. Not. R. Astron. Soc. 2020, 493, 3854. [Google Scholar] [CrossRef]
- Lindblad, B. On the possibility of a quasi-stationary spiral structure in galaxies. Stock. Obs. Ann. 1963, 5, 5. [Google Scholar]
- Lin, C.C.; Shu, F.H. On the Spiral Structure of Disk Galaxies. Astrophys. J. 1964, 140, 646. [Google Scholar] [CrossRef]
- Goldreich, P.; Lynden-Bell, D. II. Spiral arms as sheared gravitational instabilities. Mon. Not. R. Astron. Soc. 1965, 130, 125. [Google Scholar] [CrossRef]
- Julian, W.H.; Toomre, A. Non-Axisymmetric Responses of Differentially Rotating Disks of Stars. Astrophys. J. 1966, 146, 810. [Google Scholar] [CrossRef]
- Athanassoula, E.; Romero-Gómez, M.; Bosma, A.; Masdemont, J.J. Rings and spirals in barred galaxies—III. Further comparisons and links to observations. Mon. Not. R. Astron. Soc. 2010, 407, 1433–1448. [Google Scholar] [CrossRef]
- Pour-Imani, H.; Kennefick, D.; Kennefick, J.; Davis, B.L.; Shields, D.W.; Abdeen, M.S. Strong Evidence for the Density-wave Theory of Spiral Structure in Disk Galaxies. Astrophys. J. 2016, 827, L2. [Google Scholar] [CrossRef]
- Miller, R.; Kennefick, D.; Kennefick, J.; Abdeen, M.S.; Monson, E.; Eufrasio, R.T.; Shields, D.W.; Davis, B.L. Investigating the Origins of Spiral Structure in Disk Galaxies through a Multiwavelength Study. Astrophys. J. 2019, 874, 177. [Google Scholar] [CrossRef]
- Berrier, J.C.; Sellwood, J.A. Smoothing Rotation Curves and Mass Profiles. Astrophys. J. 2015, 799, 213. [Google Scholar] [CrossRef]
- D’Onghia, E. Disk-stability Constraints on the Number of Arms in Spiral Galaxies. Astrophys. J. Lett. 2015, 808, L8. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G. The Onset of Spiral Structure in the Universe. Astrophys. J. 2014, 781, 11. [Google Scholar] [CrossRef]
- Martinsson, T.P.K.; Verheijen, M.A.W.; Westfall, K.B.; Bershady, M.A.; Andersen, D.R.; Swaters, R.A. The DiskMass Survey. VII. The distribution of luminous and dark matter in spiral galaxies. Astron. Astrophys. 2013, 557, A131. [Google Scholar] [CrossRef]
- Giavalisco, M.; Ferguson, H.C.; Koekemoer, A.M.; Dickinson, M.; Alexander, D.M.; Bauer, F.E.; Bergeron, J.; Biagetti, C.; Brandt, W.N.; Casertano, S.; et al. The Great Observatories Origins Deep Survey: Initial Results from Optical and Near-Infrared Imaging. Astrophys. J. Lett. 2004, 600, L93–L98. [Google Scholar] [CrossRef]
- Davis, B.L.; Berrier, J.C.; Shields, D.W.; Kennefick, J.; Kennefick, D.; Seigar, M.S.; Puerari, I. 2DFFT: Measuring Galactic Spiral Arm Pitch Angle; Astrophysics Source Code Library. Available online: https://ui.adsabs.harvard.edu/abs/2016ascl.soft08015D/exportcitation (accessed on 1 September 2022).
- Nilson, P. Uppsala General Catalogue of Galaxies. 1973. Available online: http://ned.ipac.caltech.edu/level5/March02/Nilson/Nilson_contents.html (accessed on 9 October 2022).
- de Vaucouleurs, G.; de Vaucouleurs, A.; Corwin, H.G., Jr.; Buta, R.J.; Paturel, G.; Fouqué, P. Third Reference Catalogue of Bright Galaxies. Volume I: Explanations and references. Volume II: Data for galaxies between 0h and 12h. Volume III: Data for galaxies between 12h and 24h; Springer: New York, NY, USA, 1991; ISBN 3-540-97552-7; 0-387-97552-7. [Google Scholar]
- Davis, B.L.; Kennefick, D.; Kennefick, J.; Westfall, K.B.; Shields, D.W.; Flatman, R.; Hartley, M.T.; Berrier, J.C.; Martinsson, T.P.K.; Swaters, R.A. A Fundamental Plane of Spiral Structure in Disk Galaxies. Astrophys. J. Lett. 2015, 802, L13. [Google Scholar] [CrossRef]
- Guo, Y.; Ferguson, H.C.; Bell, E.F.; Koo, D.C.; Conselice, C.J.; Giavalisco, M.; Kassin, S.; Lu, Y.; Lucas, R.; Mandelker, N.; et al. Clumpy Galaxies in CANDELS. I. The Definition of UV Clumps and the Fraction of Clumpy Galaxies at 0.5 < z < 3. Astrophys. J. 2015, 800, 39. [Google Scholar] [CrossRef]
- Kermack, K.A.; Haldane, J.B.S. Organic Correlation and Allometry. Biometrika 1950, 37, 30–41. [Google Scholar] [CrossRef]
- York, D. Least-squares fitting of a straight line. Can. J. Phys. 1966, 44, 1079. [Google Scholar] [CrossRef]


| No. of spiral arms | 1 | 2 | 3 | 4 | 5 | 6 | 8 |
| P | 20.01 | 20.01 | 20.00 | 20.01 | 20.00 | 20.00 | 20.01 |
| ± | 0.12 | 0.12 | 0.10 | 0.11 | 0.10 | 0.10 | 0.11 |
| True pitch (°) | 5 | 10 | 15 | 25 | 30 | 40 | 50 |
| P | 5.02 | 10.03 | 14.96 | 24.87 | 30.23 | 40.05 | 49.62 |
| ± | 0.12 | 0.14 | 0.12 | 0.48 | 0.29 | 0.76 | 0.72 |
| Non-logarithmicity 2 (°) | −19 | −15 | −10 | −5 | 5 | 10 | 15 |
| P | 8.41 | 10.20 | 13.26 | 16.25 | 23.43 | 26.75 | 29.99 |
| ± | 5.06 | 3.54 | 2.04 | 0.82 | 0.79 | 1.86 | 3.21 |
| Spiral radius (px) | 15 | 20 | 25 | 35 | 50 | 75 | 200 |
| P | 20.73 | 20.04 | 19.66 | 19.75 | 20.02 | 20.03 | 20.00 |
| ± | 1.69 | 0.82 | 0.64 | 0.29 | 0.12 | 0.12 | 0.10 |
| Arm thickness (px) | 1 | 3 | 6 | 10 | 15 | 20 | 25 |
| P | 19.99 | 19.97 | 20.00 | 20.03 | 19.72 | 20.60 | 19.48 |
| ± | 0.12 | 0.13 | 0.10 | 0.45 | 0.66 | 1.38 | 0.79 |
| 3 | 16 | 8 | 4 | 2 | 1 | 0.5 | 0.25 |
| P | 20.10 | 20.02 | 19.96 | 20.10 | 20.05 | 20.23 | 20.86 |
| ± | 0.10 | 0.18 | 0.20 | 0.20 | 0.64 | 0.50 | 0.73 |
| Inclination (°) | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| P | 20.17 | 20.30 | 20.46 | 20.74 | 20.68 | 20.63 | 21.59 |
| ± | 0.34 | 0.56 | 1.26 | 2.27 | 3.54 | 5.15 | 7.61 |
| Bar half-length (px) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 4 | 20.11 | 20.15 | 20.18 | 20.21 | 20.27 | 33.19 | 40.18 |
| ± | 0.18 | 0.18 | 0.18 | 0.18 | 0.21 | 14.32 | 15.70 |
| 5 | 20.02 | 20.02 | 20.03 | 20.00 | 20.11 | 20.02 | 20.13 |
| ± | 0.14 | 0.12 | 0.13 | 0.10 | 0.15 | 0.14 | 0.19 |
| Bulge radius (px) | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 4 | 20.06 | 20.05 | 20.04 | 20.04 | 20.09 | 20.10 | 20.10 |
| ± | 0.11 | 0.11 | 0.11 | 0.11 | 0.10 | 0.10 | 0.10 |
| 5 | 20.00 | 20.02 | 20.01 | 20.00 | 20.11 | 20.02 | 20.13 |
| ± | 0.10 | 0.11 | 0.11 | 0.10 | 0.15 | 0.13 | 0.20 |
| Center offset 2 (px) | 0 | 2 | 4 | 6 | 8 | 10 |
| P | 20.01 | 20.01 | 19.95 | 20.12 | 19.96 | 22.03 |
| ± | 0.12 | 0.31 | 4.04 | 6.95 | 10.15 | 13.41 |
| Inner radius spacing 3 (px) | 2 | 5 | 10 | 15 | 20 | 25 |
| P | 20.02 | 20.02 | 20.01 | 20.02 | 20.03 | 20.00 |
| ± | 0.11 | 0.12 | 0.12 | 0.12 | 0.13 | 0.10 |
| Number of spiral axes 4 | 10 | 50 | 100 | 500 | 1000 | 4000 |
| P | 20.70 | 19.00 | 19.20 | 19.81 | 19.82 | 19.83 |
| ± | 0.10 | 0.10 | 0.21 | 0.24 | 0.16 | 0.16 |
| Pitch angle spacing 5 (°) | 0.1 | 0.3 | 0.5 | 1 | 3 | 5 |
| P | 20.00 | 19.86 | 20.00 | 20.00 | 19.00 | 20.00 |
| ± | 0.10 | 0.44 | 0.50 | 1.00 | 3.00 | 5.00 |
| Axis point spacing 6 (px) | 0.25 | 0.5 | 0.75 | 1 | 1.5 | 2 |
| P | 19.91 | 19.91 | 19.93 | 19.87 | 19.84 | 19.96 |
| ± | 0.12 | 0.25 | 0.15 | 0.18 | 0.20 | 0.18 |
| Galaxy Name | Type 1 | Band | Source 2 | Spirality Pitch (°) | 2DFFT Pitch 3 (°) | D 4 |
|---|---|---|---|---|---|---|
| UGC 448 | SABc | r | a | −15.1 ± 4.9 | −18.1 ± 1.7 | 0.46 |
| UGC 463 | SABc | B | d | 19.9 ± 1.6 | 22.4 ± 3.2 | 0.52 |
| UGC 1081 | SBc | r | a | 24.6 ± 2.0 | 24.3 ± 3.1 | 0.06 |
| UGC 1087 | Sc | r | a | 9.7 ± 5.1 | 10.6 ± 2.2 | 0.13 |
| UGC 1529 | Sc | B | d | −28.3 ± 3.3 | −26.1 ± 4.4 | 0.28 |
| UGC 1635 | Sbc | r | a | 9.3 ± 1.5 | 11.8 ± 0.8 | 1.09 |
| UGC 1862 | SABcd | r | a | 27.4 ± 8.1 | 23.9 ± 3.5 | 0.30 |
| UGC 1908 | SBc | B | d | 22.4 ± 1.1 | 20.6 ± 3.5 | 0.39 |
| UGC 3091 | SABd | i | a | −14.6 ± 5.9 | −29.5 ± 4.0 | 1.50 |
| UGC 3140 | Sc | r | a | −19.7 ± 1.8 | −16.2 ± 4.8 | 0.54 |
| UGC 3701 | Scd | r | a | −14.8 ± 4.7 | −15.4 ± 4.8 | 0.07 |
| UGC 3997 | Im | g | b | −16.2 ± 2.5 | −10.5 ± 2.6 | 1.12 |
| UGC 4036 | SABbc | B | d | −16.9 ± 4.1 | −15.0 ± 1.1 | 0.36 |
| UGC 4107 | Sc | g | b | −24.3 ± 3.1 | −20.4 ± 2.1 | 0.76 |
| UGC 4256 | SABc | g | b | 45.1 ± 3.8 | 29.1 ± 4.3 | 1.97 |
| UGC 4368 | Scd | g | b | 34.3 ± 6.2 | 23.7 ± 2.1 | 1.28 |
| UGC 4380 | Scd | g | b | −15.4 ± 4.3 | −23.3 ± 4.6 | 0.89 |
| UGC 4458 | Sa | g | b | −9.7 ± 4.0 | −13.6 ± 3.0 | 0.56 |
| UGC 4555 | SABbc | g | b | 12.6 ± 0.5 | 12.1 ± 1.0 | 0.38 |
| UGC 4622 | Scd | g | b | −15.1 ± 3.3 | −21.8 ± 4.9 | 0.83 |
| UGC 6903 | SBcd | g | b | −14.8 ± 2.1 | −15.8 ± 2.2 | 0.23 |
| UGC 6918 | SABb | F606W | c | −15.2 ± 1.2 | −17.0 ± 2.3 | 0.53 |
| UGC 7244 | SBcd | g | b | 25.7 ± 11.6 | 32.1 ± 4.3 | 0.40 |
| UGC 7917 | SBbc | g | b | −14.2 ± 4.9 | −15.5 ± 1.4 | 0.21 |
| UGC 8196 | Sb | g | b | −7.3 ± 1.6 | −8.2 ± 0.5 | 0.42 |
| UGC 9177 | Scd | g | b | −12.7 ± 2.9 | −14.4 ± 1.9 | 0.35 |
| UGC 9837 | SABc | g | b | 28.6 ± 4.6 | 25.7 ± 2.8 | 0.39 |
| UGC 9965 | Sc | g | b | −12.7 ± 2.2 | −13.3 ± 2.0 | 0.15 |
| UGC 11,318 | SBbc | B | d | −34.7 ± 2.9 | −29.7 ± 4.4 | 0.70 |
| UGC 12,391 | SABc | r | a | −11.3 ± 0.8 | −13.2 ± 5.0 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shields, D.; Boe, B.; Pfountz, C.; Davis, B.L.; Hartley, M.; Miller, R.; Slade, Z.; Abdeen, M.S.; Kennefick, D.; Kennefick, J. Spirality: A Novel Way to Measure Spiral Arm Pitch Angle. Galaxies 2022, 10, 100. https://doi.org/10.3390/galaxies10050100
Shields D, Boe B, Pfountz C, Davis BL, Hartley M, Miller R, Slade Z, Abdeen MS, Kennefick D, Kennefick J. Spirality: A Novel Way to Measure Spiral Arm Pitch Angle. Galaxies. 2022; 10(5):100. https://doi.org/10.3390/galaxies10050100
Chicago/Turabian StyleShields, Deanna, Benjamin Boe, Casey Pfountz, Benjamin L. Davis, Matthew Hartley, Ryan Miller, Zac Slade, M. Shameer Abdeen, Daniel Kennefick, and Julia Kennefick. 2022. "Spirality: A Novel Way to Measure Spiral Arm Pitch Angle" Galaxies 10, no. 5: 100. https://doi.org/10.3390/galaxies10050100
APA StyleShields, D., Boe, B., Pfountz, C., Davis, B. L., Hartley, M., Miller, R., Slade, Z., Abdeen, M. S., Kennefick, D., & Kennefick, J. (2022). Spirality: A Novel Way to Measure Spiral Arm Pitch Angle. Galaxies, 10(5), 100. https://doi.org/10.3390/galaxies10050100






