On the VHE Spectrum and Formation of the Teraelectronvolt Pulsed Emission of the Crab Pulsar

Abstract

In the present paper, a model for the pulsed $\gamma$-ray emission of the Crab pulsar from $0.01$ GeV to 1 TeV in the context of synchrotron emission generated in the vicinity of a light cylinder is developed. The generation of such high energies through the synchrotron process requires the existence of very energetic plasma particles in pulsar magnetospheres. It is assumed that the emitting particles are ultra-relativistic primary beam electrons re-accelerated to very high energies due to the Landau damping process of a special type of parametrically driven Langmuir waves. This type of Langmuir wave carries energy released through the rotational slow-down of a pulsar and is very effective in supplying the resonant particles with energy from a natural reservoir. The model provides simultaneous generation of energetic $\gamma$-ray and low-frequency radio (0.1–1 GHz) emission in the same location of the pulsar magnetosphere. These two radiations processes are triggered by a single plasma process, namely excitation of the cyclotron instability. This provides a natural explanation for the observed coincidence of radio and $\gamma$-ray signals observed from the Crab pulsar.

1. Introduction

The young Crab pulsar (PSR J0534+220) is one of the most powerful pulsars in our Galaxy. Due to its proximity of ∼2 kpc [1] and to its high spin-down luminosity of $4.6\times {10}^{38}$ erg s⁻¹, it is one of the best studied non-thermal astrophysical sources. The Crab pulsar and its nebula are products of the supernova explosion SN1054. The pulsar emits radiation with a period $P=33.6$ ms and slows down by $\dot{P}=4.2\times {10}^{-13}$ ss⁻¹ [2], giving the characteristic value for the magnetic field at the poles $B_0\simeq 7.6\times {10}^{12}$ G [3]. It is one of the few pulsars that radiates pulsed emission across the electromagnetic spectrum from radio (${10}^{-6}$ eV) to VHE $\gamma$-rays (reaching up to 1.5 TeV). This object is also exceptional among other pulsars in the context of emitting pulsed $\gamma$-rays above 100 GeV [4,5] and recently, the pulsed emission has been detected even up to TeV energies [6]. This further underlines the importance of understanding the plasma processes developed in the source.

The relevant mechanisms for the generation of high-energy $\gamma$-rays in pulsar magnetosphere are still under investigation. The recent discovery puts the $\gamma$-ray emission generation region far out in the magnetosphere, close to the light cylinder (LC) that excludes the so-called polar-cap models from consideration. The polar-cap models also predict sharp superexponential cut-off at several GeV, contrary to recent observations [7]. In the outer gap models, the generation region of the VHE radiation is located at high altitudes in the outer area of the magnetosphere and extends to the edge of the LC [8,9,10]. Another important observational feature that should be taken into account when searching for the radiation generation mechanisms in the Crab pulsar is the phase-alignment of the two-peaked pulse profiles at all wavelengths [4,6,11,12]. This observational fact indicates that the emission at different energy bands is generated in the same region of the pulsar magnetosphere, which gives reason to question the validity of outer gap models. To our knowledge, there is no mechanism defined for the generation of low-frequency radio emission in the outer gap region.

The pulsed emission of the Crab pulsar at high energies has been gradually measured for many years, presently reaching up to ∼2 TeV, and it can not be ruled out that through farther searches, even higher-energy pulsed $\gamma$-rays could be detected from this source. In 2008, the pulsed emission was first detected above 25 GeV by the MAGIC telescope, and the measured spectrum was well-explained with a power law (the spectral index $\Gamma \approx 2$) that required an exponential cut-off somewhere between 5 and 25 GeV, as the measured flux at 25 GeV appeared to be several times smaller than that at lower energies [13]. A few years later, VERITAS and MAGIC revealed pulsed $\gamma$-rays above 100 GeV, and the measured energy spectrum was harder than expected for an exponential cut-off at ∼10 GeV, ruling out the models predicting exponential cut-off [4,5]. New data points above 100 GeV enabled better understand the spectral shape of pulsed emission in the VHE domain. The combined fit of older Fermi-LAT data in the energy range from 0.1 to 20 GeV [14] together with the MAGIC and VERITAS measurements revealed a clear favor of a broken power law (with the indices ${\Gamma }_1\approx 1.96$ and ${\Gamma }_2\approx 3.52$, and the turnover point approximately at 4 GeV) as a parametrization of the spectral shape [4,5]. Recently, MAGIC reported the detection of the Crab pulsar’s pulsed emission up to ∼2 TeV, which is the most energetic pulsed emission ever detected from pulsars [6]. The pulse profile shows two narrow peaks that are synchronized with the ones measured in the GeV energy range. The joint fit of the Fermi-LAT and MAGIC data above 10 GeV is well-described by a simple power law. Since one of the peaks cannot be measured above 600 GeV, the fitting is achieved for each emission peak separately. The resultant photon indices of the two power-law functions are 3.5 and 3.0, respectively, showing slightly different spectral slopes. Interestingly, the photon index correspondent to the first peak does not differ much from the one obtained through the analysis of previous measurements of pulsed radiation above 100 GeV. Moreover, the phase-averaged differential energy spectrum obtained by VERITAS observations in the interval 100 GeV extending up to 1 TeV is described by photon index 3.5 [15]. Consequently, in the present work, it is assumed that the Crab pulsar spectral energy distribution can be represented by two power-law functions with different spectral slopes in the HE ($E\le 10$ GeV) and the VHE (up to ∼2 TeV) domains, with corresponding spectral indices of ${\Gamma }_1\approx 1.96$ and ${\Gamma }_2\approx 3.5$ [6,15].

Although the recent discovery of pulsed VHE emission challenges commonly accepted HE emission generation mechanisms, it is more or less agreed that the Crab must be a very powerful particle accelerator. Additionally, the acceleration region where it is believed that the observed VHE $\gamma$-rays are produced must be located somewhere in the outer part of the magnetosphere. In order to develop a self-consistent theory, one needs to define the basic properties of pulsar magnetosphere and the nature of plasma that generates radiation. According to observational data of typical pulsars and general energetic considerations, it seems consequential to assume that a high-density electron–positron ($e^{-}{e}^{+}$) plasma is created in the polar regions of the magnetosphere. A spinning magnetized neutron star generates an electric field directed along the open magnetic field lines, extracting electrons from the star’s surface [16]. The particles moving along the weakly curved magnetic field lines generate $\gamma$-quanta, which in turn produce $e^{-}{e}^{+}$ pairs [17]. The produced particles again generate radiation that produces more pairs. The process takes place near the star surface in the so-called ‘vacuum-gap’ region, which is at the same time the particle acceleration area. The longitudinal electrostatic field must provide particle acceleration along the open magnetic field lines. However, the gap appears to have a limited height, while the plasma produced through the cascade process becomes at some stage sufficiently dense to be able to screen the original electric field. This naturally stops the acceleration process as well and puts limitations on the energy obtained by electrons and positrons in the vicinity of the vacuum-gap acceleration region. The cascade processes developing near the star surface in the pulsar magnetospheres has been thoroughly investigated [18,19,20], and despite different attempts to increase the gap size [21], the maximum attainable Lorentz factors can not exceed ∼10${}^7$. Such particles are not energetic enough to explain the recently detected VHE emission from the Crab pulsar.

It is well-known that the plasma particles produced and accelerated in the vacuum-gap region at the polar cap of the star flow along the open magnetic field lines in their ground Landau states. This happens due to very efficient synchrotron losses in the strong magnetic field near the star surface, that in turn leads to transversal energy loss. It is obvious that the pulsar magnetosphere is characterized by rotation, and correspondingly the plasma particles that move along the magnetic field lines inevitably co-rotate, leading to the centrifugal acceleration becoming extremely efficient in the LC area. In a series of works [22,23,24], it has been shown that the centrifugal force can induce certain kinds of plasma instabilities, which in turn might contribute to particle re-acceleration. Considering Crab-like millisecond pulsars, it has been shown that the electrons might reach energies of the order of ${10}^2$ TeV [24], which appears promising in the context of VHE photon generation. We consider the possibility of obtaining such energetic electrons in the vicinity of the LC in Section 3 of the present work.

In order to explain the recent detection of pulsed emission at the VHE, we refer to the emission model that has been developed in a series of works [25,26,27], following the progress in observations of the Crab pulsar’s $\gamma$-ray emission. The magnetosphere is filled by a dense, relativistic $e^{-}{e}^{+}$ plasma with an anisotropic one-dimensional distribution function, which makes it unstable [28]. The detailed investigations have shown that for such magnetospheric $e^{-}{e}^{+}$ plasma, the conditions for the development of the cyclotron instability can be satisfied at the LC-length scales [29]. The cyclotron instability generates low-frequency radiation, invoking simultaneous diffusion of resonant particles along and across the magnetic field lines, violating the one-dimensionality. Particles acquire perpendicular momenta followed by the sequential synchrotron emission process, which generates high-frequency radiation. The interesting feature of this scenario is the simultaneous generation of low- and high-frequency radiation in the same spacial area as the pulsar magnetosphere. It is assumed that the aforementioned particle re-acceleration process in the outer parts of the magnetosphere continues until cyclotron resonance appears, which involves accelerated beam electrons in a diffusion enabling activation of the synchrotron emission process. In the case of the Crab pulsar, we show that the originally excited cyclotron modes come in the radio domain, while the emission of resonant beam electrons provides an explanation of the VHE observations. The generation of radio and high-energy gamma-ray emission in the same area of the magnetosphere inevitably explains the observed pulse phase coincidence.

The paper is organized as follows. In Section 2, we describe the emission model. In Section 3, the possibility of particle re-acceleration in the outer parts of pulsar magnetosphere is considered. In Section 4, we derive the theoretical spectrum for high and VHE $\gamma$-ray pulsed emission of the Crab pulsar in the framework of our model, and in Section 5 we make conclusions.

2. Emission Model

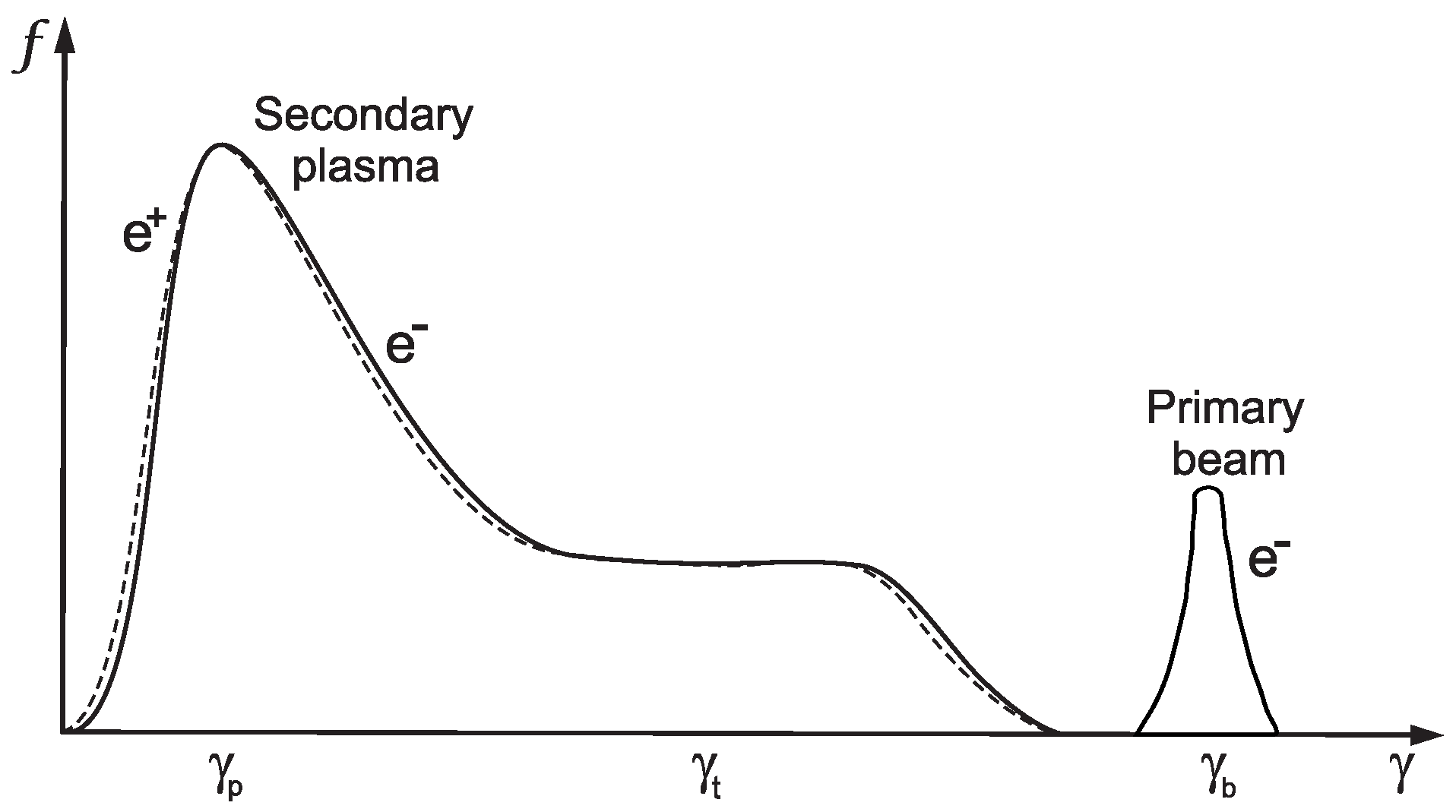
It is assumed that the pulsar magnetosphere is filled with $e^{-}{e}^{+}$ plasma flowing along open magnetic field lines with the one-dimensional distribution function shown in Figure 1 [28]. For typical pulsars, the multicomponent plasma consists of the following components: the bulk of plasma with an average Lorentz factor ${\gamma }_p\simeq {10}^2$ and the number density at the star surface $n_{p_0}\simeq {10}^{18}$ cm⁻³; a tail on the distribution function with ${\gamma }_t\simeq {10}^4÷{10}^5$ ($n_{t_0}\simeq {10}^{14}÷{10}^{15}$ cm⁻³); and the most energetic primary electrons’ beam with the Lorentz factor ${\gamma }_b\simeq {10}^6$ and the characteristic Goldreich–Julian density $n_{b_0}=n_{GJ}=B_0/\left(Pce\right)\simeq {10}^{13}$ cm⁻³ (here, c is the speed of light and e is the electron’s charge) [16]. We assume the equipartition of energy between the plasma components $n_{p_0}{\gamma }_p\approx n_{t_0}{\gamma }_t\approx n_{b_0}{\gamma }_b/2$. The multicomponent plasma with one-dimensional anisotropic distribution appears to be unstable, which might cause excitation of the electromagnetic oscillations. The properties of $e^{-}{e}^{+}$ plasma in pulsar magnetospheres have been studied in high detail [30,31,32], and according to Machabeli & Usov [29] and Lominadze et al. [33], in the magnetospheres of young pulsars such as Crab, purely transversal, low-frequency t-waves can be excited with the corresponding spectrum.

$${\omega }_t=kc(1-\delta ),$$

(1)

where

$$\delta =\frac{{\omega }_p^2}{4{\gamma }_p^3{\omega }_B^2}\mathrm{and}{\omega }_p^2=\frac{4\pi n_p{e}^2}{m}.$$

(2)

Here, ${\omega }_p$ is plasma frequency, m is the rest mass of the electron, ${\omega }_B=eB/mc$ is the cyclotron frequency. The magnetic field is assumed to be dipole, decreasing with the distance from the star’s center according to the following law $B=B_0{(r_0/r)}^3$. The plasma number density also decreases with the cubic law $n_p=n_{p_0}{(r_0/r)}^3$, where $r_0\approx {10}^6$ cm is the neutron star radius.

The generation of t-waves occurs in the outflowing plasma on the open field lines due to instabilities developing in the outer regions of the pulsar magnetosphere. The strongest instabilities that can develop in the pulsar magnetosphere are the electromagnetic cyclotron and Cherenkov-drift instabilities. The low-frequency radio emission detected from the Crab pulsar is a core-type emission that can be excited only through the anomalous cyclotron resonance process. The resonance condition for the cyclotron instability is [31]

$${\omega }_c-k_{\Vert }{\upsilon }_{\Vert }+\frac{{\omega }_B}{{\gamma }_{res}}=0,$$

(3)

where ${\omega }_c$ is the resonance frequency of the excited cyclotron modes, ${\gamma }_{res}$ is the Lorentz factor of the resonant particles, $k_{\Vert }$ and ${\upsilon }_{\Vert }$ are the components of the wave vector and the particle velocity along the magnetic field, respectively. During the wave generation process by resonant particles, one also has a simultaneous back reaction of t-waves on the particles [34]. This mechanism is described by quasi-linear diffusion (QLD), leading to the diffusion of particles along and across the magnetic field lines. Therefore, resonant electrons acquire the transverse momenta (pitch angles), and as a result, start to radiate through the synchrotron regime. Consequently, the development of QLD violates the one-dimensionality of the plasma distribution, incorporating the sequential activation of a high-frequency-emission generation process. It is worth noting that the cyclotron waves are vacuum-like electromagnetic waves, which can leave the pulsar magnetosphere freely, reaching an observer as pulsar-pulsed emission. As a very precise feature of this mechanism, the low- and high-frequency waves are generated almost simultaneously in the same location of the pulsar magnetosphere, ensuring the phase-coincidence of emission impulses in these domains.

The equation that describes the diffusion of particles during the resonance interaction of excited waves back on resonant particles can be written as [29,35]

$$\frac{\partial f^0}{\partial t}+\frac{\partial }{\partial p_{\Vert }}\left[F_{\Vert }{f}^0\right]+\frac{1}{p_{\perp }}\frac{\partial }{\partial p_{\perp }}\left[p_{\perp }{F}_{\perp }{f}^0\right]=S_{QL},$$

(4)

where for the Crab pulsar case

$$S_{QL}\simeq \frac{1}{p_{\perp }}\frac{\partial }{\partial p_{\perp }}\left[p_{\perp }{D}_{\perp \perp }\frac{\partial f^0}{\partial p_{\perp }}\right]+\frac{\partial }{\partial p_{\Vert }}\left[D_{\Vert \perp }\frac{\partial f^0}{\partial p_{\perp }}\right].$$

(5)

$S_{QL}$ is the diffusion term that describes the quasi-linear relaxation of the cyclotron instability [25]. Here, $D_{\perp \perp }$ and $D_{\Vert \perp }$ are the diffusion coefficients and can be defined as follows

$$D_{\perp \perp }\simeq \frac{e^2}{8c}\delta |E_k{|}_{k=k_{res}}^2,D_{\Vert \perp }\simeq -\frac{e^2}{8c}\psi {\left|E_k\right|}_{k=k_{res}}^2,$$

(6)

and the resonance value for the wave vector $k_{res}$ is easily obtained from the resonance condition (3) [26]

$$k_{res}\approx \frac{{\omega }_B}{c\delta {\gamma }_{res}}.$$

(7)

Supposing that the pitch angles acquired through the QLD are very small, $\psi \ll 1$, hereafter it is assumed that $sin\psi \approx \psi$.

When emitting in the synchrotron regime, the resonant particles undergo the radiation reaction force, with longitudinal and transversal components [36]

$$F_{\Vert }=-{\alpha }_s{\gamma }^2{\psi }^2,F_{\perp }=-{\alpha }_s\psi (1+{\gamma }^2{\psi }^2),$$

(8)

where ${\alpha }_s=2e^2{\omega }_B^2/3c^2$.

The Equation (4) is given in the plasma rest frame and $f^0\left(\mathbf{p}\right)$ is the distribution function of the resonant particles (hereafter we omit the upper index ’0’ by the distribution function). Taking into account that $\psi \simeq p_{\perp }/p_{\Vert }\ll 1$, one can consider the case when $\partial /\partial p_{\perp }\gg \partial /\partial p_{\Vert }$ and rewrite Equation (4) in the following form

$$\frac{\partial f}{\partial t}=\frac{1}{p_{\perp }}\frac{\partial }{\partial p_{\perp }}\left[p_{\perp }{D}_{\perp \perp }\frac{\partial f}{\partial p_{\perp }}-p_{\perp }{F}_{\perp }f\right].$$

(9)

The transversal diffusion leads to the isotropization of the one-dimensional distribution function, whereas the force $F_{\perp }$ acts against the diffusion. The dynamical process saturates when these effects balance each other. Considering the quasi-stationary state ($\delta f/\delta t=0$) and assuming that for the parameters of the Crab pulsar the case ${\gamma }_{res}\psi \ll 1$ will be realized, the expression for the transverse reaction force writes as $F_{\perp }\approx -{\alpha }_s\psi$ and from Equation (9) one can find

$$f\left(p_{\perp }\right)=Cexp\left(\int \frac{F_{\perp }}{D_{\perp \perp }}d{p}_{\perp }\right)=C{e}^{-p_{\perp }^2/p_{{\perp }_0}^2},$$

(10)

where $p_{{\perp }_0}^2=2p_{\Vert }{D}_{\perp \perp }/{\alpha }_s$. Taking into account Equations (6) and (7) and assuming that half of the resonant particles’ energy density, $m{c}^2{n}_{res}{\gamma }_{res}/2$, converts to the energy density of the cyclotron waves $|E_k{|}^{2}k$, which gives an approximate expression for $|E_k{|}^2\approx m{c}^3{n}_{res}{\gamma }_{res}/2{\omega }_{res}$, one can estimate the mean value of the pitch-angles (${\psi }_0\approx p_{{\perp }_0}/p_{\Vert }$) acquired by resonant particles

$${\psi }_0\simeq \frac{\pi }{B^2{\gamma }_p^2}{\left(\frac{3}{32}\frac{m^5{c}^7{\gamma }_{res}^3}{e^6{P}^3}\right)}^{1/2}.$$

(11)

Now we can estimate the mean energy of the emitting particles that could provide radiation at TeV energies through the synchrotron mechanism. The characteristic photon energy emitted by the relativistic electrons through the synchrotron radiation process is ${\epsilon }_{syn}\simeq 5\times {10}^{-21}B\psi {\gamma }^2$ TeV [37]. Taking into account that the process takes place at the LC-length scales, the value of the magnetic field induction is assumed to be $B\approx 3.8\times {10}^6$ G. Using expression (11) for the mean value of the pitch-angles, we obtain

$${\epsilon }_{syn}\left(\mathrm{TeV}\right)\simeq 5\times {10}^{-21}\frac{\pi }{B{\gamma }_p^2}{\left(\frac{3m^5{c}^7{\gamma }_{res}^7}{32e^6{P}^3}\right)}^{1/2}.$$

(12)

Consequently, for the particles to be able to emit photons at TeV energies, the Lorentz factors should be of the order of ${\gamma }_{res}\simeq {10}^8$. The maximum achievable value of the Lorentz factor of the most energetic beam electrons in the framework of the standard polar cap and outer gap models is of the order of ${10}^6÷{10}^7$ [8,19,38]. Therefore, to explain the observed VHE pulsed emission of the Crab pulsar via the synchrotron mechanism, an additional particle acceleration that can accelerate the fastest beam electrons to even higher energies should be invoked. Expression (12) also gives us the possibility to estimate the minimum value of the Lorentz factor of resonant particles contributing to the pulsed Gamma-ray emission in the domain $0.01$ GeV to 2 TeV, which accordingly is ${\gamma }_{min}\simeq 4\times {10}^6$. As expected, the only particles taking part in the process of generation of energetic pulsed emission in the Crab magnetosphere are the most energetic primary beam electrons.

As the resonant particles are defined, one can estimate the frequency of the original waves that cause activation of the synchrotron mechanism. From expressions (1–3), it is easy to define the frequency of the excited cyclotron-modes ${\omega }_c^t\approx {\omega }_B/\delta {\gamma }_{res}$. Taking into account that the magnetic field and the particle density change by distance with the cubic law ${(r_0/r)}^3$, one can write

$${\omega }_c\simeq \frac{4{\gamma }_p^3}{{\gamma }_{res}}\frac{{\omega }_{B_0}^3}{{\omega }_{p_0}^2}{\left(\frac{r_0}{r}\right)}^6.$$

(13)

For the LC-length scales $r\sim r_{LC}\simeq 1.5\times {10}^8$ cm and the particles with Lorentz factors from the interval ${\gamma }_{res}\simeq 4\times {10}^6÷{10}^8$ at the distances $r/r_{LC}\simeq 0.5÷1$, the frequency of the excited waves ${\nu }_c={\omega }_c/\left(2\pi \right)\sim 0.1÷1$ GHz comes in the radio domain. Consequently, the described scenario naturally explains coincidence of radio and $\gamma$-ray signals detected from the Crab pulsar.

3. Re-Acceleration of Primary Beam Electrons

It is generally believed that the pulsar magnetospheric plasma energy supply is star rotation energy. This enormous energy reservoir must be the only source for processes taking place in the pulsar magnetospheres. On the other hand, the exact mechanism for the energy transfer from pulsar rotation into particle kinetic energy is one of the most important unsolved problems in pulsar physics. It is clear that existing models for particle acceleration scenarios can not provide sufficiently effective transfer of the rotational energy into the particles. Regardless of locating the acceleration region near the star surface [7,17] or in outer parts of the magnetosphere [8,9,10], the attainable energies are small compared to the energy losses of the source. Finding a better possibility for energy pumping into the plasma particles obtained even more importance after the pulsed radiation at TeV energies from the Crab pulsar was detected.

In Osmanov et al. [24], it was shown that near the LC, the electrons might reach energies of the order of ${10}^2$ TeV in Crab-like pulsars. In the aforementioned work and the preceding ones (see for example Machabeli et al. [22], Mahajan et al. [23], Osmanov et al. [39]), the innovative particle acceleration scenario is considered, providing very effective pumping of pulsar rotation energy into the plasma particles. This mechanism converts the pulsar spin-down energy into the kinetic energy of magnetospheric particles through a two-step process. First, parametrically driven two-stream instability generates electrostatic Langmuir waves (L-waves) in the bulk $e^{-}{e}^{+}$ plasma. The role of the parameter in this process plays the time-dependent centrifugal force, creating the so-called parametric instability that efficiently converts the pulsar rotational energy into L-waves. This mechanism differs from the standard two-stream instability developed on the account of particles’ kinetic energy, and drives energy from a much bigger reservoir, the neutron star rotation. As a second step of the process, the unstable L-waves damp on the most energetic beam electrons via Landau damping, accelerating them to ultra-high energies. In Osmanov et al. [24], it was shown that the energy gained through this process by resonant beam particles can be estimated with the following formula

$$ϵ\approx \frac{n_p}{n_{GJ}}F\ell ,$$

(14)

where $F\approx$ 2 mc$\Omega {\xi }^{-3}$ is the centrifugal force, $\xi ={(1-{\Omega }^2{r}^2/c^2)}^{1/2}$, $\Omega =2\pi /P$ and ℓ is the characteristic length of the Landau damping-process area. As was shown in Osmanov et al. [24], depending on the plasma particles that participate in the two-stream instability and the size of the area where this processes take place, the energy accumulated by resonant beam particles can vary. We assume that the energy accumulation process in beam particles is interrupted by the development of the electromagnetic cyclotron instability that takes place in the same spacial area near the LC. Therefore, taking $\ell \sim {10}^6$ cm and assuming that the secondary plasma particles, which invoke the parametric process of the L-wave generation, are ${\gamma }_t\sim {10}^5$ (this corresponds to the tail particles that have been shown to be dominant in the wave generation process), one can obtain the Lorentz factor of the re-accelerated beam particles as ${\gamma }_b^{\prime }\sim {10}^8$. Such particles can easily provide generation of TeV photons through the synchrotron emission process. It should be mentioned that gaining of even more energies by beam particles, which depends on the selection of certain parameters, is not excluded in the framework of the model. Consequently, the detection of even more energetic pulsed emission from the Crab could be expected. It is important to note that in spite of the extremely efficient energy transfer to particles, the process is maintained as the L-waves are continuously generated.

The re-accelerated particles are, at the same time, redistributed through the acceleration process, and the distribution function of resonant electrons that contribute to the pulsed synchrotron emission of the Crab should be redefined. Initially, the distribution function of primary beam electrons is formed near the star surface when the particles are ejected from the polar cap region. The beam electrons are farther accelerated via the electric field induced by rotation of the magnetized star [16]. As no exact calculations are available, at this stage one can only assume the shape of the initial distribution function that depends on surface properties. Therefore, let us assume that the beam electrons’ distribution function is a power law with an index equal to n (for the right slope satisfying $\partial f_{b_0}/\partial p_{\Vert }<0$, see Figure 1). 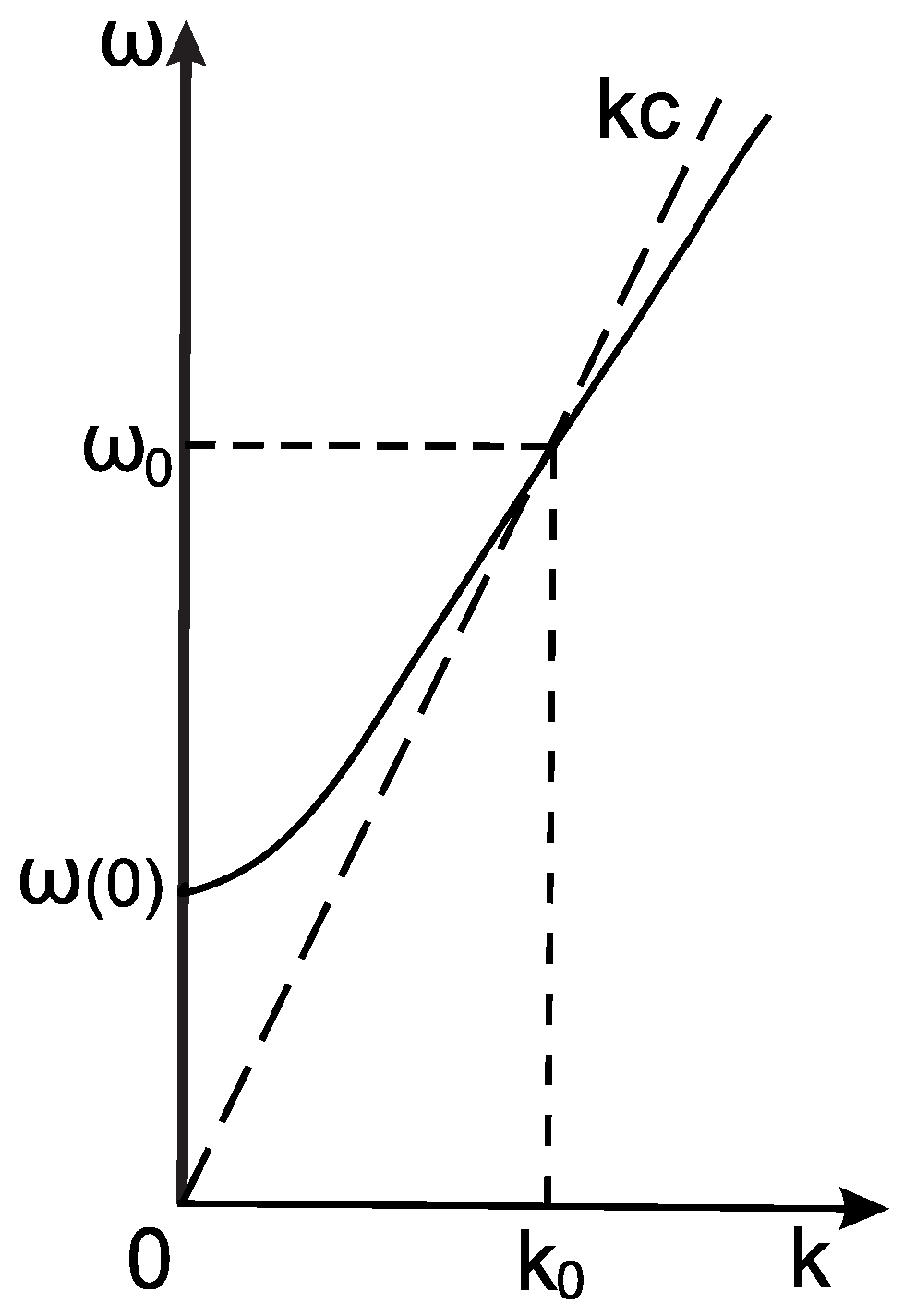As soon as the particles flowing along the field lines reach the L-wave generation region, the Landau damping process is activated for electrons with velocities that equal the phase-speed of the L-waves. In magnetospheric $e^{-}{e}^{+}$ plasma, the dispersion relation has two simple solutions for L-waves, when $\omega /k\gg c$, that can not be damped on particles, and $\omega /k\approx c$ (see Figure 2). For the second case, the dispersion has the following form [40]

$${\omega }_L\approx c[k-\beta (k-k_0)],$$

(15)

where $k_0={\left(2\langle \gamma \rangle \right)}^{1/2}{\omega }_p/c$ is the value for k at which the phase velocity equals the speed of light, $\beta =\langle \gamma \rangle /2\langle {\gamma }^3\rangle$ is a very small parameter and the angular brackets denote averaging over the distribution function. As the phase-speed of Langmuir waves is very close to c, only the fastest particles can participate in the damping process. One can estimate the minimum Lorentz factor of the beam electron that can damp the L-waves with the dispersion relation given by expression (15), if defining the Lorentz factor of the resonant particles in the following way:

$${\gamma }_L={\left(1-\frac{{\upsilon }_{ph}^2}{c^2}\right)}^{-\frac{1}{2}}\approx {\left(2\beta \frac{\Delta k}{k}\right)}^{-1},$$

(16)

where $\Delta k=k_{max}-k_0$ denotes the difference between the maximum possible values of the wave number and $k_0$, corresponding to waves with phase speed equal to c. For the parameter values of the Crab pulsar, $\Delta k\simeq (\langle \gamma \rangle /{\gamma }_{res})\approx {10}^{-6}$ [40], and correspondingly, ${\gamma }_L\simeq {10}^7$, which defines the minimum Lorentz factor of the particles which are able to participate in the Landau damping process. As a result the distribution function of the beam, electrons will be elongated in the direction of higher energies. This happens as only a small fraction of the particles with the highest energies can take part in the Landau damping process. 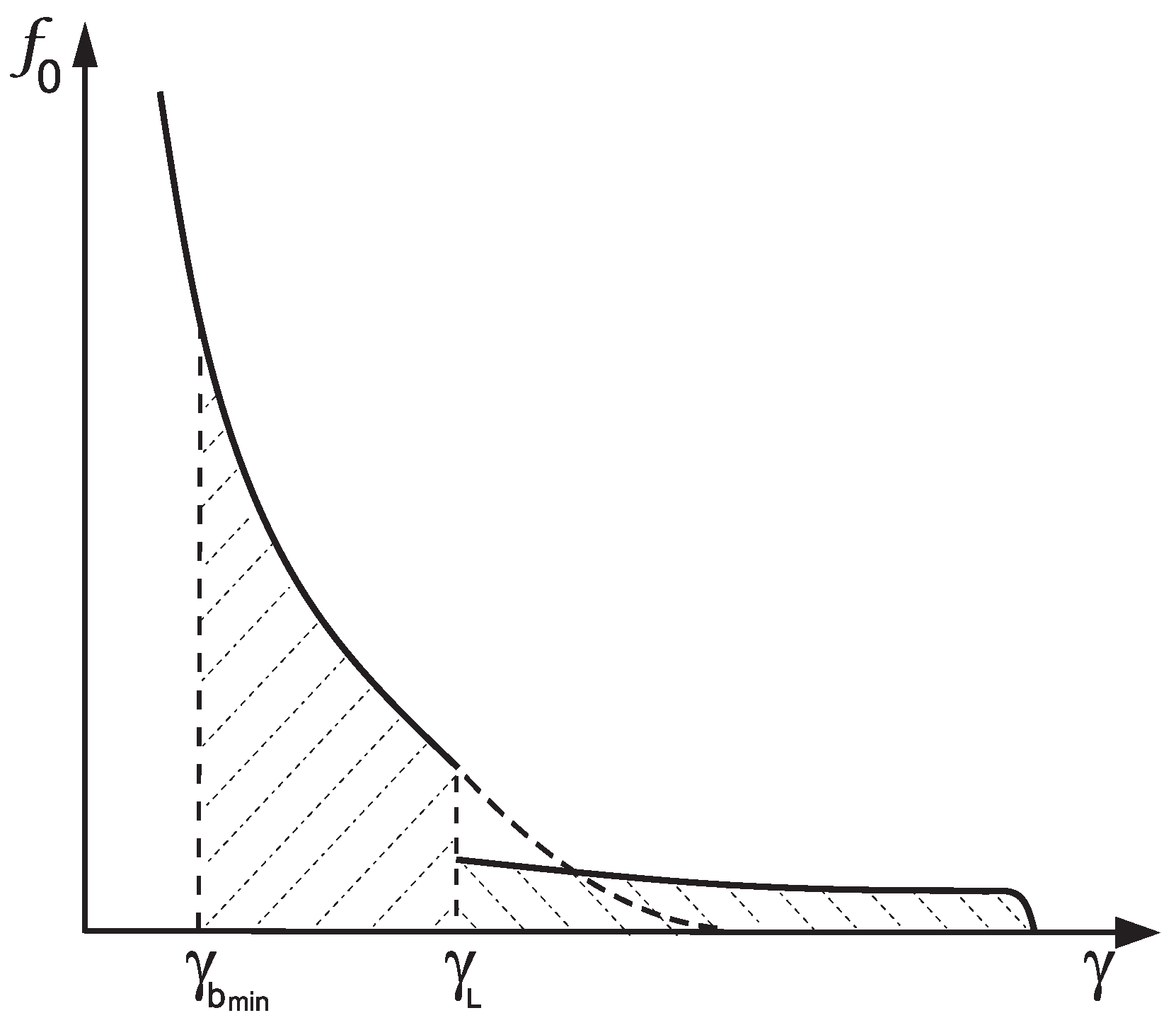Consequently, beginning from ${\gamma }_L$, the distribution function of the beam electrons will acquire a high-energy “tail”, which might be described by a power-law function as well, but with a different index m. It is obvious that $m<n$, as the Landau damping tries to flatten the slope of the distribution of the resonant particles. The only reason that the final distribution will not form a plateau is that the stationary state cannot be reached, since a cyclotron instability develops in the same region of the magnetosphere, ending the Landau damping process. Therefore, the final distribution of the beam particles will be a broken power law with indices n and m and a breaking point at ${\gamma }_L$. Consequently, at the moment of excitement of the cyclotron instability, the distribution of the beam particles can be presented as (Chkheidze et a. [26]; see Figure 3)

$$\begin{array}{c}\hfill f_0\propto \left\{\begin{array}{cc}{p}_{\Vert }^{-n},& p_{{\Vert }_{min}}\le p_{\Vert }\le p_{{\Vert }_L}\\ p_{\Vert }^{-m},& p_{{\Vert }_L}\le p_{\Vert }\le p_{{\Vert }_{max}}\end{array}\right\}.\end{array}$$

(17)

Here, $p_{{\Vert }_{min}}=m{c}^2{\gamma }_{b_{min}}$, $p_{{\Vert }_L}=m{c}^2{\gamma }_L$ and consequently, $p_{{\Vert }_{max}}=m{c}^2{\gamma }_{b_{max}}$.

4. Synchrotron Emission Spectrum

Now let us define the theoretical spectrum of the synchrotron radiation generated in the vicinity of the LC zone in the magnetosphere of the Crab pulsar, which is assumed to be observed as the high-energy pulsed Gamma-ray emission. The synchrotron power spectrum of a single electron can be written as [37]

$$P_{\epsilon }={\displaystyle \frac{\sqrt{3}{e}^{3}B\psi }{m{c}^2}}{\displaystyle \frac{\epsilon }{{\epsilon }_{syn}}}\left[{\int }_{\epsilon /{\epsilon }_{syn}}^{\infty }{K}_{5/3}\left(\mu \right)d\mu \right],$$

(18)

where $K_{5/3}\left(\mu \right)$ is the MacDonald function. Now, considering the emission of a bunch of particles, the spectral density of synchrotron emission photon flux can be written as

$$F_{\epsilon }=\int P_{\epsilon }N\left(\epsilon \right)d\epsilon ,$$

(19)

where $N\left(\epsilon \right)$ is the number of emitting particles with energies from the interval ($\epsilon ,\epsilon +d\epsilon$). We are considering the problem in terms of parallel and perpendicular impulses and also taking into account that the distribution function is given by f. One can rewrite expression (19) in the following form

$$F_{\epsilon }\propto {\int }_{p_{{\Vert }_{min}}}^{p_{{\Vert }_{max}}}{f}_{\Vert }\left(p_{\Vert }\right)B{\psi }_0{\displaystyle \frac{\epsilon }{{\epsilon }_{syn}}}\left[{\int }_{\epsilon /{\epsilon }_{syn}}^{\infty }{K}_{5/3}\left(\mu \right)d\mu \right]d{p}_{\Vert },$$

(20)

where we have taken into account the following definition of the longitudinal distribution function ${\int }_0^{\infty }{p}_{\perp }f(p_{\Vert },p_{\perp })d{p}_{\perp }=f_{\Vert }\left(p_{\Vert }\right)$. This function can be found from Equation (4), by multiplying both sides of the equation on and integrating the expression over $p_{\perp }$. The terms with $\partial /\partial p_{\perp }$ turn to zero, and in place of (4) one obtains

$$\frac{\partial f_{\Vert }}{\partial t}=\frac{\partial }{\partial p_{\Vert }}\left[{\int }_0^{\infty }{p}_{\perp }\left(D_{\Vert \perp }\frac{\partial }{\partial p_{\perp }}-F_{\Vert }\right)fd{p}_{\perp }\right].$$

(21)

After performing some basic calculations and taking into account that the term of the parallel reaction force is much greater than the diffusion term, Equation (21) reduces to

$$\frac{\partial f_{\Vert }}{\partial t}=\frac{\partial }{\partial p_{\Vert }}\left[{\displaystyle \frac{{\alpha }_s}{m^2{c}^2}}{\displaystyle \frac{1}{{\omega }_B^4}}{\displaystyle \frac{3c{\omega }_p^2}{32{\gamma }_p^3}}{p}_{\Vert }{\left|E_k\right|}^2{f}_{\Vert }\right].$$

(22)

Considering the quasi-stationary case ($\partial f_{\Vert }/\partial t=0$), we find

$$f_{\Vert }\propto {\left(p_{\Vert }{\left|E_k\right|}^2\right)}^{-1}.$$

(23)

The density of the electric energy of cyclotron waves satisfies the following equation [33]

$${\displaystyle \frac{\partial |E_k{|}^2}{\partial t}}=2{\Gamma }_c{\left|E_k\right|}^2,$$

(24)

where ${\Gamma }_c={\pi }^2{e}^2{f}_{\Vert }/k_{res}$ is the growth rate of the cyclotron instability and $k_{res}$ can be found from expression (7).

Combining Equations (22) and (24), and taking into account that the initial distribution function of the emitting particles at the beginning of the development of cyclotron instability is given by the broken power-law function (expression (17)), we obtain

$$\begin{array}{c}\hfill |E_k{|}^2\propto \left\{\begin{array}{cc}{p}_{\Vert }^{1-n},& p_{{\Vert }_{min}}\le p_{\Vert }\le p_{{\Vert }_L}\\ \\ p_{\Vert }^{1-m},& p_{{\Vert }_L}\le p_{\Vert }\le p_{{\Vert }_{max}}\end{array}\right\}.\end{array}$$

(25)

Now we can obtain the theoretical expression for the emission spectral density defined by Equation (20). By using expressions (23) and (25) and replacing the integration variable $p_{\Vert }$ by $\eta =\epsilon /{\epsilon }_{syn}$, we find

$$\begin{array}{c}\hfill F_{\epsilon }\propto \left\{\begin{array}{cc}{\epsilon }^{-{\displaystyle \frac{n-2}{n-4}}}\times G_n\left(\epsilon \right),& {\gamma }_{b_{min}}\le \gamma \le {\gamma }_L\\ \\ {\epsilon }^{-{\displaystyle \frac{m-2}{m-4}}}\times G_m\left(\epsilon \right),& {\gamma }_L\le \gamma \le {\gamma }_{b_{max}}\end{array}\right\}.\end{array}$$

(26)

Here

$$\begin{array}{c}\hfill G_n\left(\epsilon \right)={\int }_{{\eta }^{\prime }}^{{\eta }^{″}}{\eta }^{{\displaystyle \frac{n-2}{n-4}}}\left[{\int }_{\eta }^{\infty }{K}_{5/3}\left(\mu \right)d\mu \right]d\eta ,\\ \hfill G_m\left(\epsilon \right)={\int }_{{\eta }^{‴}}^{{\eta }^{\prime }}{\eta }^{{\displaystyle \frac{m-2}{m-4}}}\left[{\int }_{\eta }^{\infty }{K}_{5/3}\left(\mu \right)d\mu \right]d\eta ,\end{array}$$

(27)

where, ${\eta }^{\prime }\simeq {10}^{28}\epsilon {\gamma }_L^{-7/2}$, ${\eta }^{″}\simeq {10}^{28}\epsilon {\gamma }_{b_{min}}^{-7/2}$ and ${\eta }^{‴}\simeq {10}^{28}\epsilon {\gamma }_{b_{max}}^{-7/2}$ are the integration intervals for the new variable $\eta$ (here ${\gamma }_{b_{min}}\simeq 4\times {10}^6$, ${\gamma }_L\simeq {10}^7$ and ${\gamma }_{b_{max}}\simeq {10}^8$). Taking into account the parameter values for the Crab pulsar and the photon energy range of the observed emission, the functions defined by Equation (27) satisfy $G_n\left(\epsilon \right)\approx G_m\left(\epsilon \right)\approx G\left(0\right)$. According to the observations, the spectral energy distribution of the Crab pulsar emission can be represented by two power-law functions with different spectral slopes in the HE ($E\le 10$ GeV) and the VHE (up to ∼2 TeV) domains, with corresponding spectal indices ${\Gamma }_1\approx 1.96$ and ${\Gamma }_2\approx 3.5$ [15]. Consequently, we can assume that $(n-2)/(n-4)\approx 1.96$ and $(m-2)/(m-4)\approx 3.5$, defining the values $n\approx 6$ and $m\approx 4.7$. The more exact numerical calculations also give the possibility to define the breaking point that depends on the value of ${\gamma }_L$, obtaining ${\epsilon }_b\simeq 4$ GeV. Finally, we represent the theoretical emission spectrum in the following form

$$F_{\epsilon }\propto {\left[{\left({\displaystyle \frac{\epsilon }{{\epsilon }_b}}\right)}^{1.96}+{\left({\displaystyle \frac{\epsilon }{{\epsilon }_b}}\right)}^{3.5}\right]}^{-1},$$

(28)

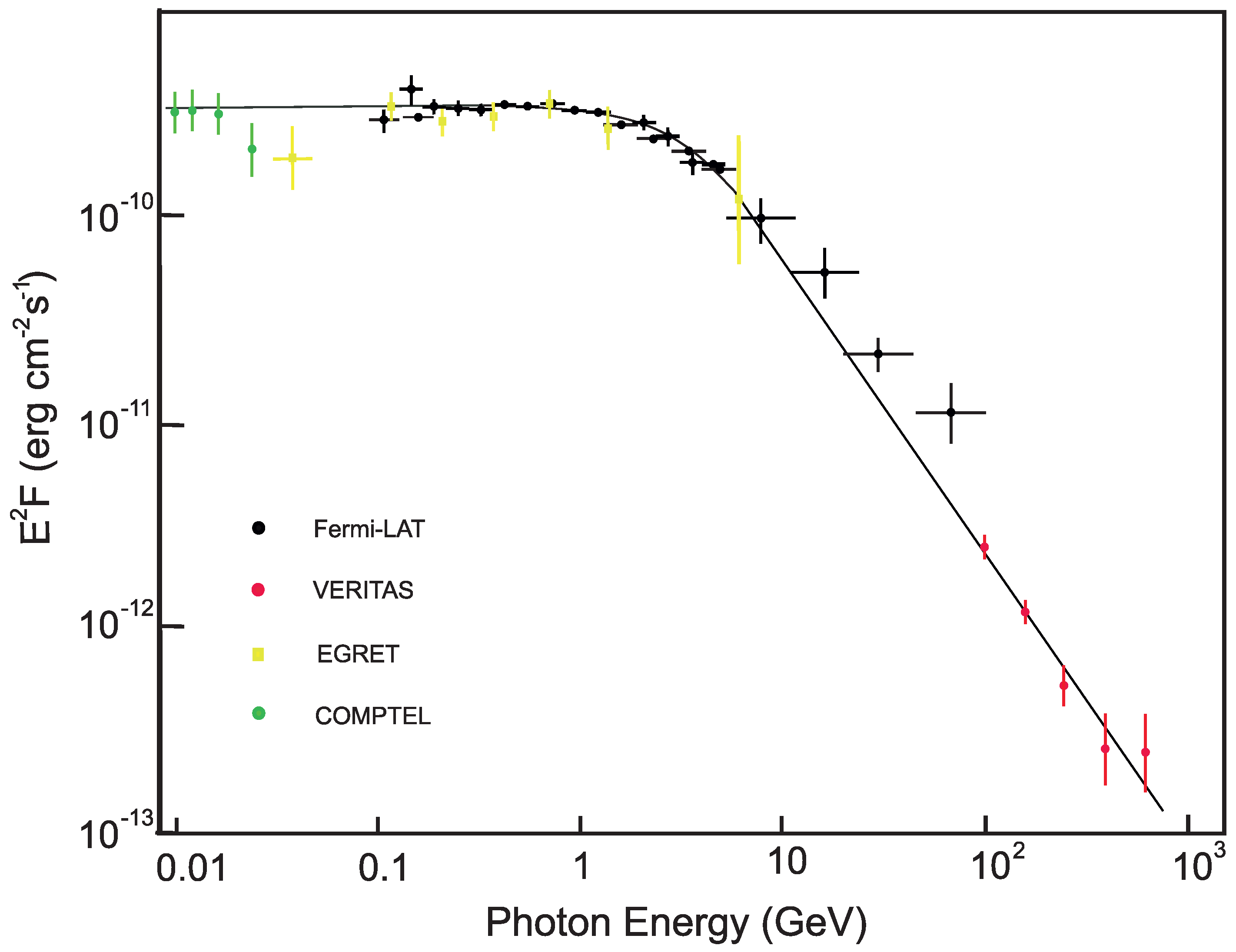
and the corresponding fit to the observations is shown in Figure 4.

5. Conclusions

The remarkable detection of pulsed emission from the Crab pulsar, reaching almost teraelectronvolts, revealed by VERITAS [15] and later by MAGIC at even higher energies, up to 2 TeV [6], imposed constraints on the energy of emitting electrons and on the location of the radiation generation area in the magnetosphere. Particularly, only emission scenarios that predict generation far out in the magnetosphere should be considered. As stated in Bogovalov [41], the electron population responsible for the emission at such high energies should have Lorentz factors greater than $5\times {10}^6$, which can provide the generation of VHE emission only when accelerated near the LC. In this scenario, the curvature radiation mechanism is mostly excluded for explaining the production of VHE photons in the pulsar magnetospheres, requiring a curvature radius of the magnetic field lines one order of magnitude larger than the usually adopted one [42]. The most generally accepted emission mechanism for explaining pulsed emission above 100 GeV is Inverse-Compton (IC) scattering. In this view, several scenarios have been put forward: synchrotron-self-Compton (SSC) scattering model [43] and IC scattering off the synchrotron pulsed optical/X-ray photons by relativistic wind electrons and positrons [44]. In Mochol & Petri [45], the spectrum up to VHE is reproduced as a sum of two components, the synchrotron component providing the power-law spectrum up to few hundred GeV and the SSC extending up to TeV energies. The SSC model assumes the existence of acceleration gaps in the outer magnetosphere, where the magnetospheric infrared (IR) photons are up-scattered by primary positrons propagating along the field lines. As a result, the primary IR photons reach energies of TeV orders and are efficiently absorbed by the same IR field, finally materialized as secondary $e^{-}{e}^{+}$ pairs reaching the energies of several TeV [46]. These secondary plasma particles are created near the LC and can up-scatter IR/UV photons up to 5 TeV, some of them escaping from the magnetosphere and reaching the Earth as pulsar VHE emission. However, the pulse profile in GeV and TeV suggests the same region of generation, limiting this interpretation. The pulsar wind scenario was first proposed to explain the emission up to few hundred GeV, and could well reproduce the pulse profile through assuming anisotropic wind. However, in order to obtain TeV photons in the framework of this model, one requires an electron population with a Lorentz factor larger than $5\times {10}^6$. Consequently, the region of acceleration has to extend up to ∼100 LC radii. The model also fails to reproduce the spectral shape below 100 GeV [44]. So far, the existing models providing the generation of VHE in pulsar magnetospheres face difficulties in explaining broadband spectra in high to very-high energies and their pulse-phase coincidence.

As mentioned above, the pulse profile in TeV shows two peaks synchronized with those measured in the GeV energy range, which at the same time are phase-aligned with the broadband emission signals including the radio pulses. This observational fact should indicate the same spacial origin of the generation of pulsed multi-wavelength emission of the Crab pulsar, automatically excluding one of the generally accepted mechanisms for high-energy emission generation in pulsars, the curvature radiation mechanism, which can not provide restriction of the spatial location of radiation. This particular problem has been studied in more detail in previous works (see e.g., Osmanov et al. [47,48]). It has been shown that near the LC, where the emission generation processes are taking place, the so-called curvature drift instability is developed, efficiently rectifying the magnetic field lines and making the role of the curvature emission process negligible [25]. The emission model presented in the present work explains the generation of radio and $\gamma$-ray emission up to TeV energies through the plasma processes naturally developing near the LC, which ensures the same generation region, and consequently, pulse-peak coincidence. At the length-scale of the LC the conditions for the development of cyclotron instability are fulfilled, which causes diffusion of the particles taking place in this process in both directions, along and across the local magnetic field lines [29,31]. Due to perpendicular diffusion, the pitch angles re-appear, causing the resonant particles to start radiating through the synchrotron mechanism. Taking into account the energies of the resonant primary beam electrons (${\gamma }_{res}\simeq 4\times {10}^6÷{10}^8$, see Section 3 for more details), the resultant synchrotron photons comprises a 0.01 GeV to TeV energy range (Equation (12)). The waves excited on the cyclotron resonance itself come in the radio domain (${\nu }_c={\omega }_c/\left(2\pi \right)\sim 0.1÷1$ GHz, see Equation (13)). This particular issue was studied in more detail in Machabeli & Chkheidze [49], where we showed that the radio emission generated through the cyclotron resonance via the energetic beam particles reveals a power-law spectral shape with an index equal to 3.7, which is in good agreement with the observations. Both emission processes, radio-wave production and generation of very energetic $\gamma$-ray photons, are part of one plasma process taking place simultaneously in the same location of the magnetosphere, inevitably causing the production of pulses peaking at the same phases. The availability of electrons in the vicinity of the LC with Lorentz factors as high as ${10}^8$ is essential for the model. We assume that such re-acceleration of particles far from the star surface is provided due to the existence of magnetocentrifugally excited electrostatic L-waves that extract the pulsar spin energy and transfer it to the fastest magnetospheric particles through the Landau damping process [24]. The most energetic primary beam electrons obtain even more kinetic energy and their distribution function obtains the high-energy “tail” (see Figure 3). This scenario provides not only a possibility for the generation of TeV photons through the simple synchrotron emission process, but also ensures the explanation of two different spectral indices for the HE ($E\le 10$ GeV) and VHE (up to ∼2 TeV) domains, ${\Gamma }_1\approx 1.96$ and ${\Gamma }_2\approx 3.5$, simply caused by the shape of the distribution function of emitting particles [6,15]. The slight difference in spectral slopes of first and second pulses measured by MAGIC (particularly spectral indices of 3.5 and 3.0) could be related to measurement issues. Or, the emission of different pulses could originate from two different poles of the star, which has long been discussed, but not yet proven.