What Is Needed of a Scalar Field If It Is to Unify Inflation and Late Time Acceleration?
Abstract
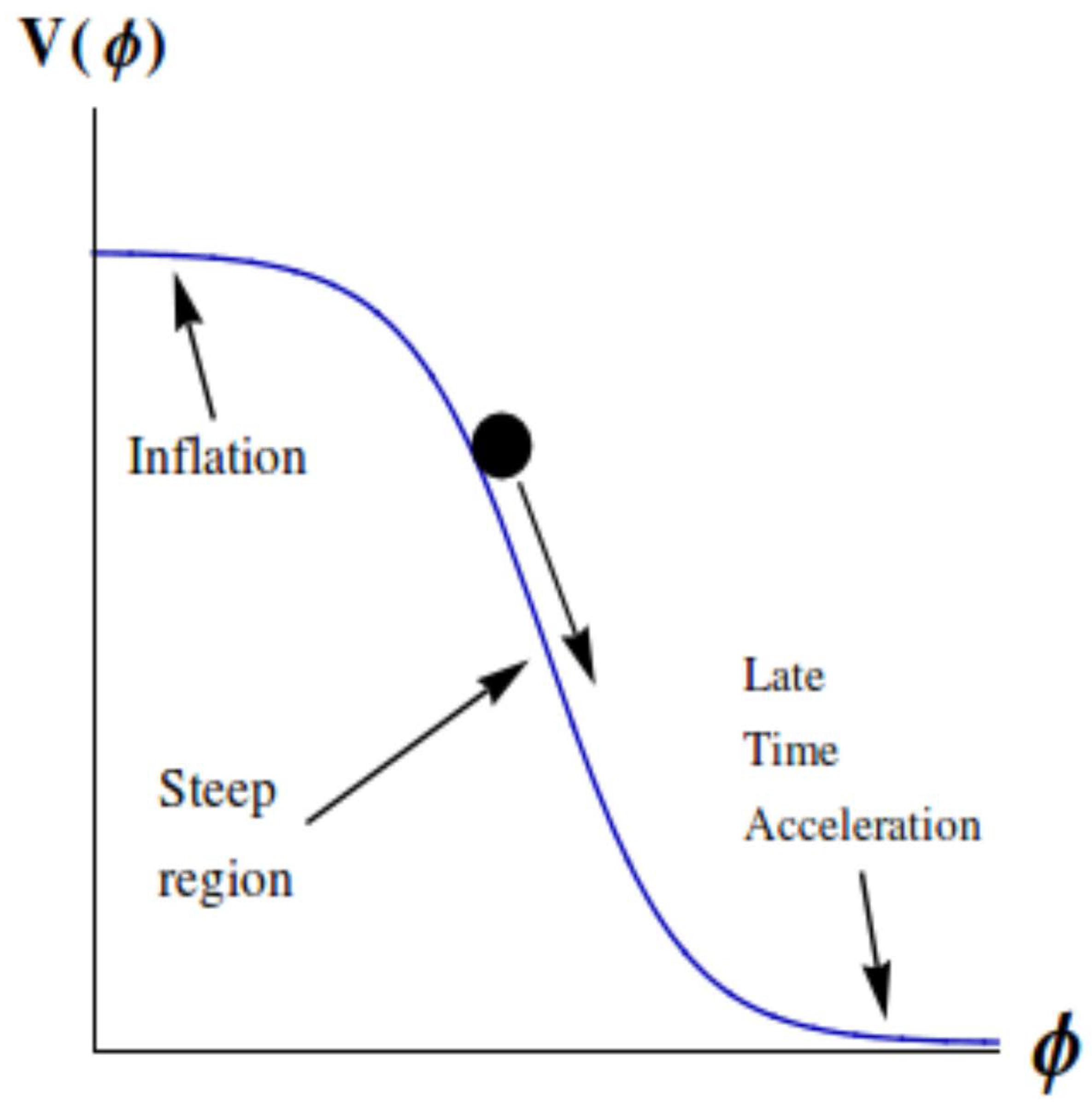
1. Introduction
2. Quintessential Inflation: Building Blocks
2.1. Reheating through Gravitational Particle Production
2.2. Instant Preheating
2.3. Curvaton Reheating
2.4. Ricci Reheating
2.5. Independence of Late Time Dynamics from Initial Conditions
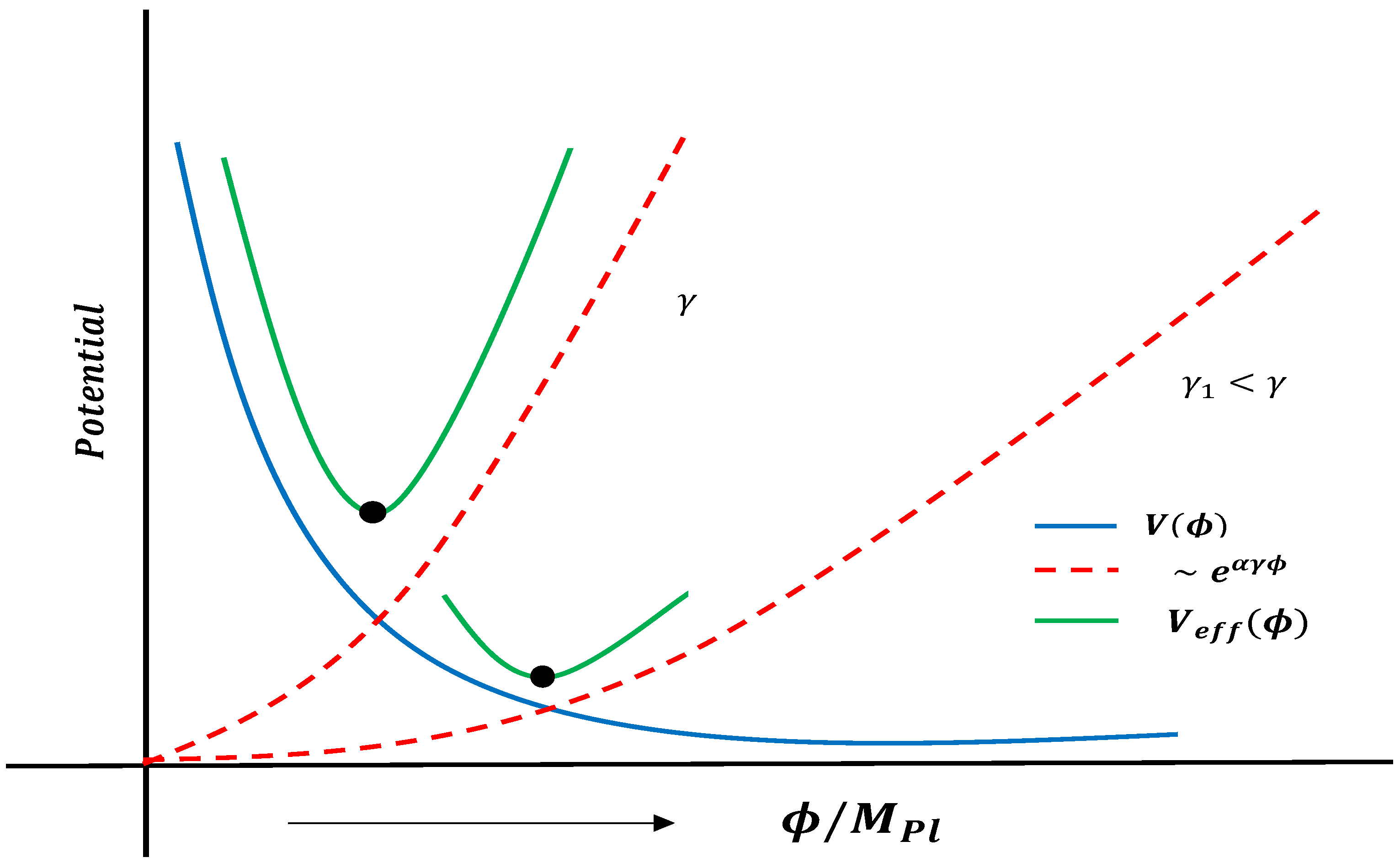
2.6. Exit Mechanisms
2.7. Suitable Class of Scalar Field Potentials
3. Cosmological Dynamics of Scalar Field in a Nut Shell
3.1. Field Evolution in Absence of Background Matter: Slow Roll versus Fast Roll
3.2. Inflation: Model-Independent Features
3.3. Evolution in Presence of Background Matter: Scaling Solution
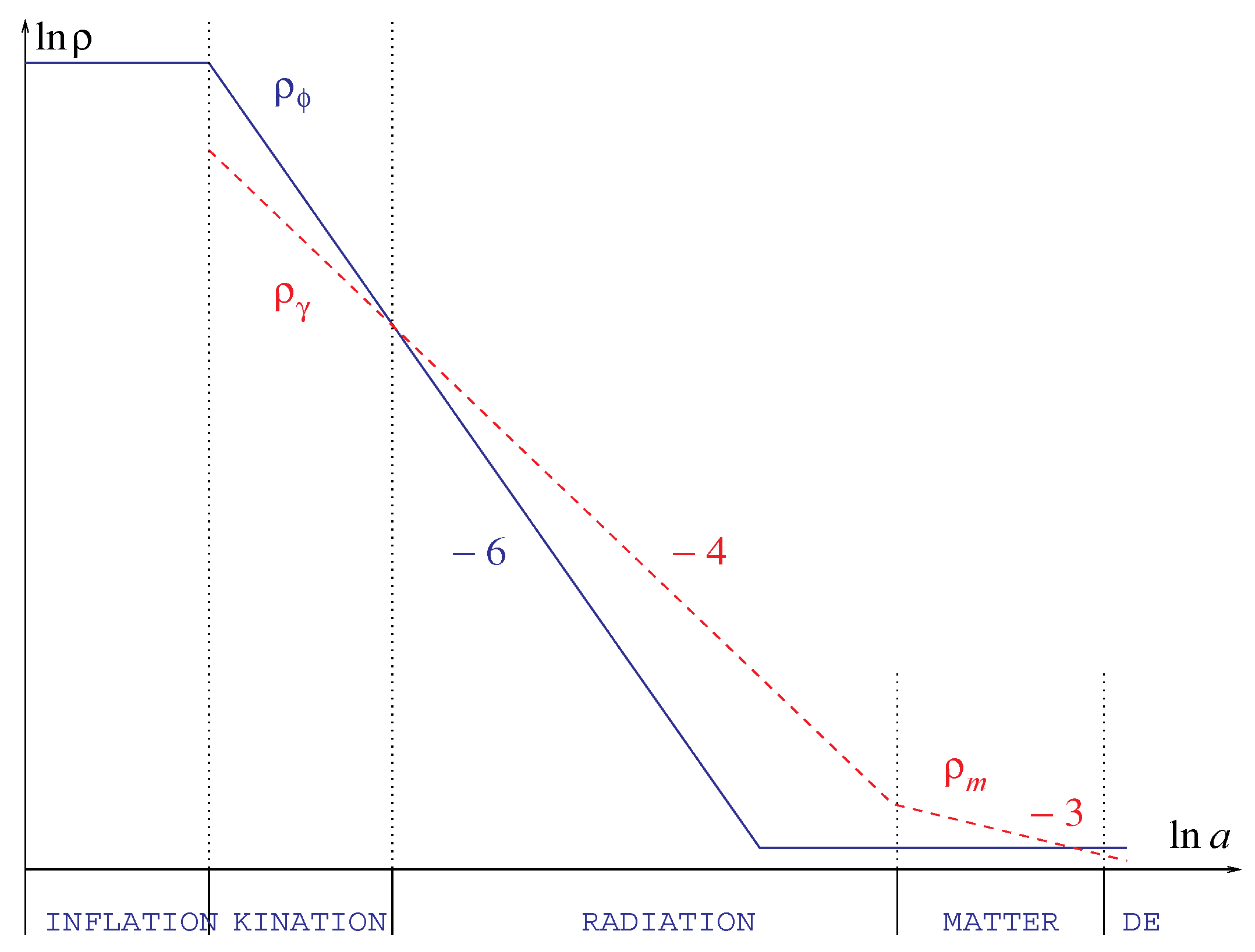
3.4. Nucleosynthesis Constraint on Extra Species
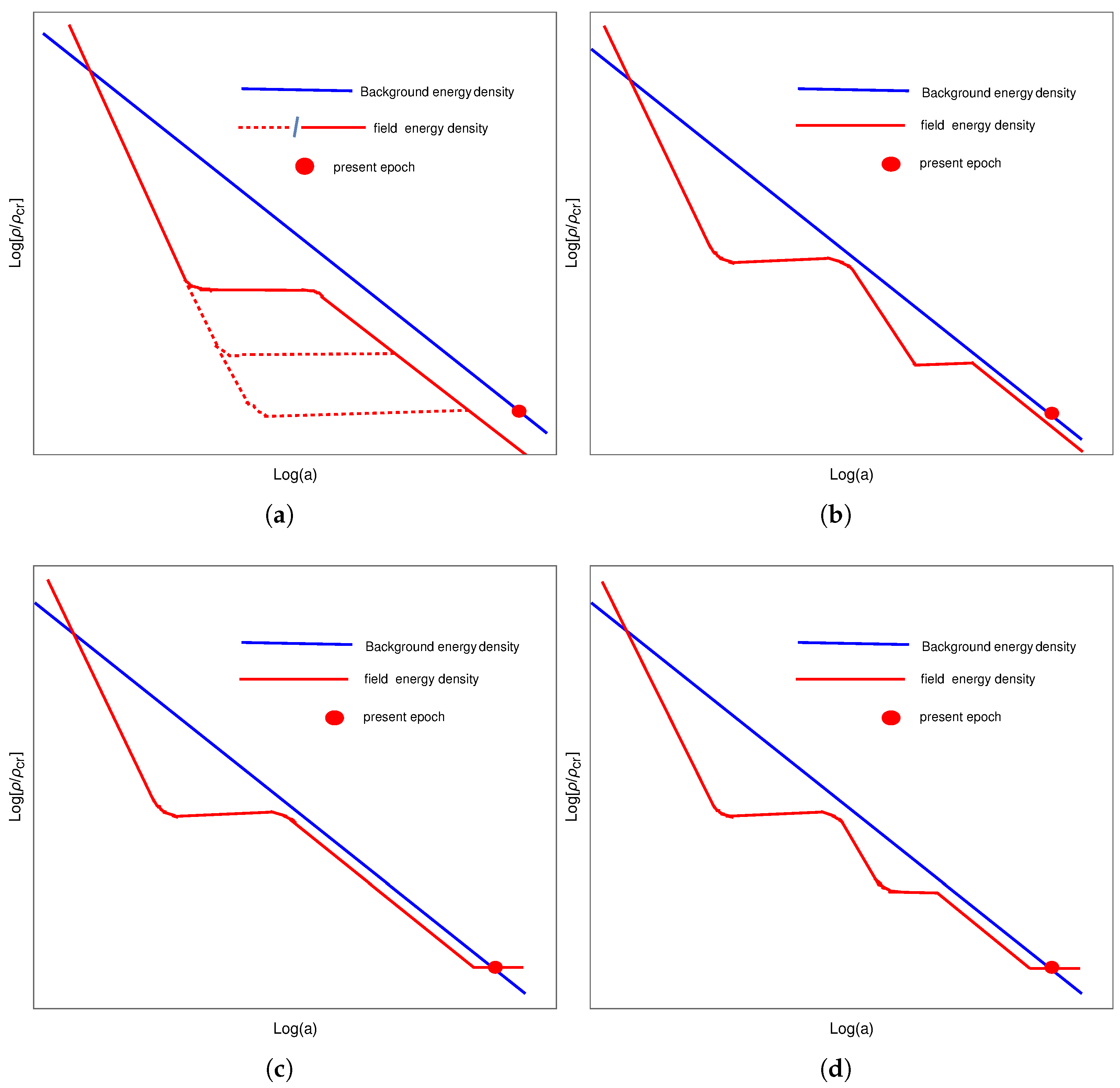
3.5. Dynamics with General Class of Potentials and Emergence of Scaling Behaviour in the Asymptotic Regime
Making a Perfect Tracker from Scaling Solutions:
3.6. Slow Roll in Presence of Background Matter: Freezing Regime
3.6.1. Recovery from Freezing Regime
3.6.2. Slowly Rolling Quintessence
3.6.3. The Asymptotic Scaling Solution
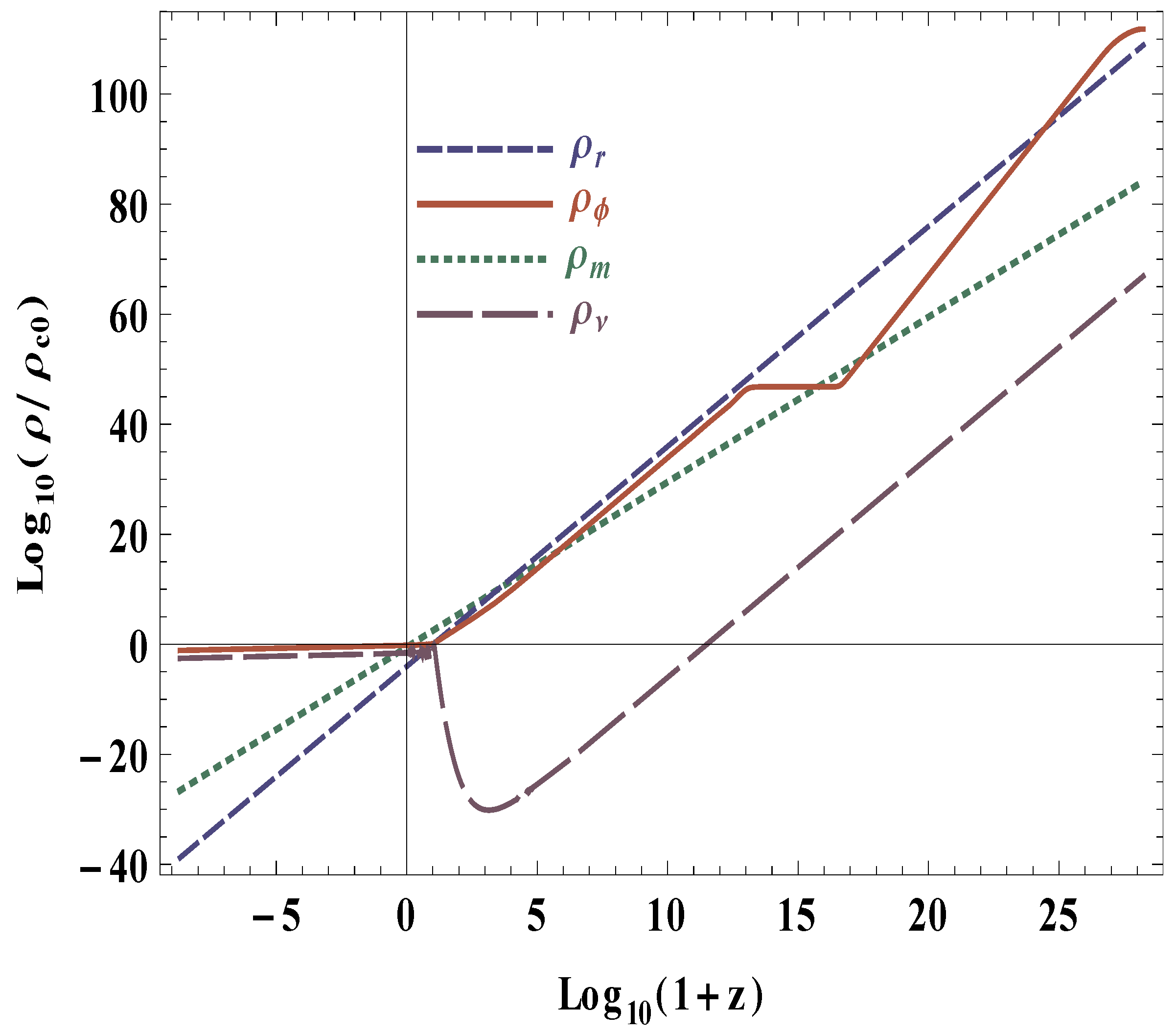
4. Post-Inflationary Dynamics: The Exit Mechanism via Coupling with Massive Neutrino
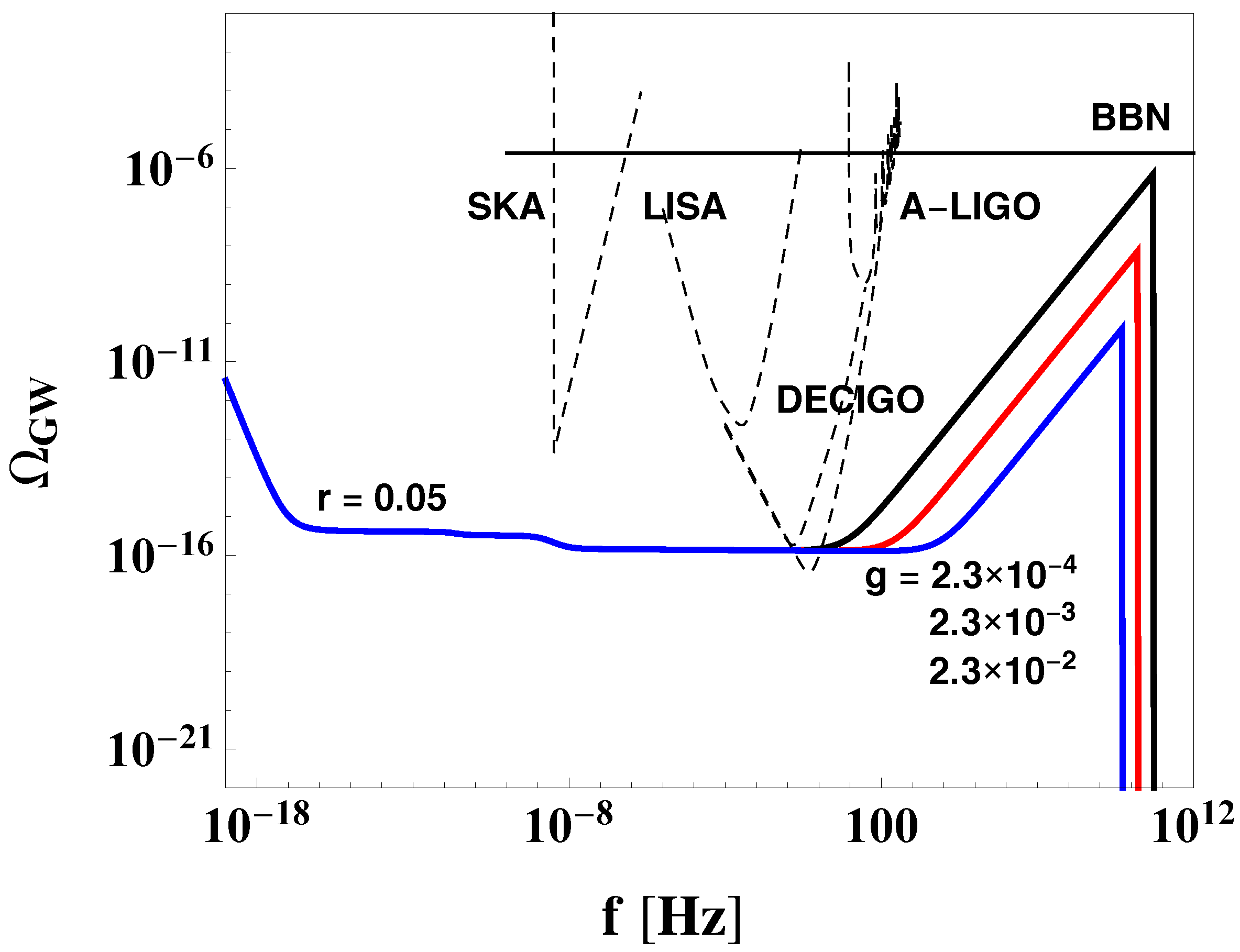
5. The Distinguished Features of Quintessential Inflation: Relic Gravity Waves
Nucleosynthesis Constraint on Reheating Temperature
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | In this framework, field is coupled to another scalar field , which in turn couples to matter fields: . In this case, does not bear mass; its effective mass depends upon , . After inflation, as runs down its potential rapidly, changes in a non-adiabatic fashion, giving rise to the production of particles, which might instantaneously decay into matter fields. Assuming that the energy of the produced particles is instantaneously thermalised (denoted by ), one finds at the end of inflation that . |
| 2 | Expansion has character of acceleration ( for ); see Equation (5). |
| 3 | The acceleration term, in (8), can no longer be be dropped in the case of a steep potential. |
| 4 | It might look more natural to use the variable as we know their values for the scaling solution. However, in this case, one requires one more variable, A, which is directly linked to the field . However, the equation for this variable decouples from the system and we can analyse equations for without bothering about the third equation for the variable A. These variables are useful in the analysis of asymptotic scaling solutions that occur in the case of steep potentials of variable slope, where we have a system of three coupled equations for and A. |
| 5 | Given that is constrained using primordial abundances and other data, bound (45) is referred to as a “nucleosynthesis” constraint or “BBN” bound. |
| 6 | Notice that for , which is not surprising as the power law corresponds to exponential in this limit. |
| 7 | We skip details here and refer the reader to [130] for the same. |
| 8 | It should be noted that, in the present situation, is not related to the slow roll parameter due to the presence of background matter. In the case of slowly rolling quintessence, the friction term need not to be large and may not be negligible. For tracker models, ; however, for thawing quintessence, , and is nearly constant, . Unlike the thawing case, the consistency of slow roll gives rise to in the case of the trackers. |
| 9 | Let us note that this feature is central to thawing models where the field is frozen on a shallow potential such that the field begins slow roll after it recovers from Hubble damping and accounts for late time acceleration. Initial conditions are set specially or tuned, allowing it to happen around the present epoch, and model parameters are chosen to comply with observation |
| 10 | for radiation and matter domination, respectively. |
| 11 | One should be careful here with regard to , which is one for exponential potential, irrespective of its being steep or shallow. |
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Sato, K. First Order Phase Transition of a Vacuum and Expansion of the Universe. Mon. Not. R. Astron. Soc. 1981, 195, 467–479. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220–1223. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of phase transition in the new inflationary universe scenario and generation of perturbations. Phys. Lett. B 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Liddle, A.R. An Introduction to cosmological inflation. arXiv 1999, arXiv:astro-ph/9901124. [Google Scholar]
- Tsujikawa, S. Introductory review of cosmic inflation. arXiv 2003, arXiv:hep-ph/0304257. [Google Scholar]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia Inflationaris. Phys. Dark Univ. 2014, 5–6, 75–235. [Google Scholar] [CrossRef]
- Vázquez, J.A.; Padilla, L.E.; Matos, T. Inflationary Cosmology: From Theory to Observations. Rev. Mex. Física E 2020, 17, 73–91. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Hawking, S.W. The Development of Irregularities in a Single Bubble Inflationary Universe. Phys. Lett. B 1982, 115, 295. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Steinhardt, P.J.; Turner, M.S. Spontaneous Creation of Almost Scale—Free Density Perturbations in an Inflationary Universe. Phys. Rev. D 1983, 28, 679. [Google Scholar] [CrossRef]
- Krauss, L.M.; Turner, M.S. The Cosmological constant is back. Gen. Relativ. Gravit. 1995, 27, 1137–1144. [Google Scholar] [CrossRef]
- Turner, M.S. The Case for ΛCDM. arXiv 1997, arXiv:astro-ph/9703161. [Google Scholar]
- Netterfield, C.B.; Ade, P.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Contaldi, C.; Crill, B.; de Bernardis, P.; et al. A measurement by Boomerang of multiple peaks in the angular power spectrum of the cosmic microwave background. Astrophys. J. 2002, 571, 604–614. [Google Scholar] [CrossRef]
- Halverson, N.W. DASI first results: A Measurement of the cosmic microwave background angular power spectrum. Astrophys. J. 2002, 568, 38–45. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Vilenkin, A. Quintessential inflation. Phys. Rev. D 1999, 59, 063505. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. Cosmology with a Time Variable Cosmological Constant. Astrophys. J. Lett. 1988, 325, L17. [Google Scholar] [CrossRef]
- Sahni, V.; Sami, M.; Souradeep, T. Relic gravity waves from brane world inflation. Phys. Rev. D 2002, 65, 023518. [Google Scholar] [CrossRef]
- Huey, G.; Lidsey, J.E. Inflation, braneworlds and quintessence. Phys. Lett. B 2001, 514, 217–225. [Google Scholar] [CrossRef]
- Majumdar, A.S. From brane assisted inflation to quintessence through a single scalar field. Phys. Rev. D 2001, 64, 083503. [Google Scholar] [CrossRef]
- Dimopoulos, K. Towards a model of quintessential inflation. Nucl. Phys. B Proc. Suppl. 2001, 95, 70–73. [Google Scholar] [CrossRef]
- Sami, M.; Dadhich, N.; Shiromizu, T. Steep inflation followed by Born–Infeld reheating. Phys. Lett. B 2003, 568, 118–126. [Google Scholar] [CrossRef]
- Dimopoulos, K. Curvaton hypothesis and the η problem of quintessential inflation, with and without branes. Phys. Rev. D 2003, 68, 123506. [Google Scholar] [CrossRef]
- Dias, M.; Liddle, A.R. On the possibility of braneworld quintessential inflation. Phys. Rev. D 2010, 81, 83515. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Berera, A.; Jackson, B.M.; Taylor, A. Hybrid quintessential inflation. Phys. Lett. B 2009, 678, 157. [Google Scholar] [CrossRef][Green Version]
- Chun, E.J.; Scopel, S.; Zaballa, I. Gravitational reheating in quintessential inflation. JCAP 2009, 22, 907. [Google Scholar] [CrossRef]
- Bento, M.C.; Felipe, R.G.; Santos, N.M.C. Brane assisted quintessential inflation with transient acceleration. Phys. Rev. D 2008, 77, 123512. [Google Scholar] [CrossRef]
- Matsuda, T. NO curvatons or hybrid quintessential inflation. JCAP 2007, 8, 3. [Google Scholar] [CrossRef][Green Version]
- Neupane, I.P. Reconstructing a model of quintessential inflation. Class. Quantum Gravity 2008, 25, 125013. [Google Scholar] [CrossRef]
- Dimopoulos, K. Trapped quintessential inflation from flux compactifications. arXiv 2007, arXiv:hep-ph/0702018. [Google Scholar]
- Gardner, C.L. Braneworld quintessential inflation and sum of exponentials potentials. arXiv 2007, arXiv:hep-ph/0701036. [Google Scholar]
- Sami, M.; Dadhich, N. World inflation with quintessence. arXiv 2004, arXiv:hep-th/0405016. [Google Scholar]
- Rosenfeld, R.; Frieman, J.A. Cosmic microwave background and large-scale structure constraints on a simple quintessential inflation model. Phys. Rev. D 2007, 75, 043513. [Google Scholar] [CrossRef]
- Sanchez, J.C.B.; Dimopoulos, K. Trapped quintessential inflation in the context of flux compactifications. JCAP 2007, 10, 2. [Google Scholar] [CrossRef][Green Version]
- Membiela, A.; Bellini, M. Quintessential inflation from a variable cosmological constant in a 5D vacuum. Phys. Lett. B 2006, 641, 125. [Google Scholar] [CrossRef][Green Version]
- Cardenas, V.H. Tachyonic quintessential inflation. Phys. Rev. D 2006, 73, 103512. [Google Scholar] [CrossRef]
- Zhai, X.-h.; Zhao, Y.-b. Dynamics of quintessential inflation. Chin. Phys. 2006, 15, 2465. [Google Scholar] [CrossRef]
- Rosenfeld, R.; Frieman, J.A. A simple model for quintessential inflation. CAP 2005, 9, 3. [Google Scholar] [CrossRef]
- Giovannini, M. Low-scale quintessential inflation. Phys. Rev. D 2003, 67, 123512. [Google Scholar] [CrossRef]
- Dimopoulos, K. Models of Quintessential Inflation. arXiv 2001, arXiv:astro-ph/0111500. [Google Scholar]
- Dimopoulos, K.; Valle, J.W.F. Modeling quintessential inflation. Astropart. Phys. 2002, 18, 287. [Google Scholar] [CrossRef]
- Yahiro, M.; Mathews, G.J.; Ichiki, K.; Kajino, T.; Orito, M. Constraints on cosmic quintessence and quintessential inflation. Phys. Rev. D 2002, 65, 63502. [Google Scholar] [CrossRef]
- Kaganovich, A.B. Field theory model giving rise to “quintessential inflation” without the cosmological constant and other fine-tuning problems. Phys. Rev. D 2000, 63, 25022. [Google Scholar] [CrossRef]
- Baccigalupi, C.; Perrotta, F. Perturbations in quintessential inflation. arXiv 1998, arXiv:astro-ph/9811385. [Google Scholar]
- Lee, J.; Lee, T.H.; Oh, P.; Overduin, J. Cosmological coincidence without fine tuning. Phys. Rev. D 2014, 90, 123003. [Google Scholar] [CrossRef]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D. Unified phantom cosmology: Inflation, dark energy and dark matter under the same standard. Phys. Lett. B 2006, 632, 597–604. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying phantom inflation with late-time acceleration: Scalar phantom–non-phantom transition model and generalized holographic dark energy. Gen. Relativ. Grav. 2006, 38, 1285. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D.; Faraoni, V. Reconstructing the universe history, from inflation to acceleration, with phantom and canonical scalar fields. Phys. Rev. D 2008, 77, 106005. [Google Scholar] [CrossRef]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Class of quintessential inflation models with parameter space consistent with BICEP2. Phys. Rev. D 2014, 89, 123513. [Google Scholar] [CrossRef]
- Guendelman, E.I.; Katz, O. Inflation and transition to a slowly accelerating phase from SSB of scale invariance. Class. Quantum Grav. 2003, 20, 1715. [Google Scholar] [CrossRef]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Unification of inflation and dark energy à la quintessential inflation. Int. J. Mod. Phys. D 2015, 24, 1530014. [Google Scholar] [CrossRef]
- Ahmad, S.; Myrzakulov, R.; Sami, M. Relic gravitational waves from Quintessential Inflation. Phys. Rev. D 2017, 96, 63515. [Google Scholar] [CrossRef]
- de Haro, J.; Saló, L.A. A Review of Quintessential Inflation. Galaxies 2021, 9, 73. [Google Scholar] [CrossRef]
- Dimopoulos, K.; López, S.S. Quintessential inflation in Palatini f(R) gravity. Phys. Rev. D 2021, 103, 43533. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I. Lorentzian Quintessential Inflation. Int. J. Mod. Phys. D 2020, 29, 2042002. [Google Scholar] [CrossRef]
- Karčiauskas, M.; Rusak, S.; Saez, A. Quintessential Inflation and the Non-Linear Effects of the Tachyonic Trapping Mechanism. arXiv 2021, arXiv:2112.11536. [Google Scholar]
- Capozziello, S.; Carloni, S.; Troisi, A. Quintessence without scalar fields. Recent Res. Dev. Astron. Astrophys. 2003, 1, 625. [Google Scholar]
- Sami, M.; Sahni, V. Quintessential inflation on the brane and the relic gravity wave background. Phys. Rev. D 2004, 70, 083513. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Owen, C. Quintessential Inflation with α-attractors. JCAP 2017, 6, 27. [Google Scholar] [CrossRef]
- Bettoni, D.; Rubio, J. Quintessential inflation: A tale of emergent and broken symmetries. Galaxies 2022, 10, 22. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Wood, L.D.; Owen, C. Instant preheating in quintessential inflation with α-attractors. Phys. Rev. D 2018, 97, 63525. [Google Scholar] [CrossRef]
- Wetterich, C. The quantum gravity connection between inflation and quintessence. Galaxies 2022, 10, 50. [Google Scholar] [CrossRef]
- Jaman, N.; Myrzakulov, K. Braneworld inflation with an effective α-attractor potential. Phys. Rev. D 2019, 99, 103523. [Google Scholar] [CrossRef]
- Rosati, F. Quintessential enhancement of dark matter abundance. Phys. Lett. B 2003, 570, 5–10. [Google Scholar] [CrossRef][Green Version]
- Salati, P. Quintessence and the relic density of neutralinos. Phys. Lett. B 2003, 571, 121–131. [Google Scholar] [CrossRef]
- Akrami, Y.; Kallosh, R.; Linde, A.; Vardanyan, V. Dark energy, α-attractors, and large-scale structure surveys. JCAP 2018, 6, 41. [Google Scholar] [CrossRef]
- Akrami, Y.; Casas, S.; Deng, S.; Vardanyan, V. Quintessential α-attractor inflation: Forecasts for Stage IV galaxy surveys. JCAP 2021, 4, 6. [Google Scholar] [CrossRef]
- Saba, N.; Farhoudi, M. Chameleon Field Dynamics During Inflation. Int. J. Mod. Phys. D 2017, 27, 1850041. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J.; Turner, M.S.; Wilczek, F. Reheating an Inflationary Universe. Phys. Rev. Lett. 1982, 48, 1437. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Linde, A.D. Baryon Asymmetry in Inflationary Universe. Phys. Lett. B 1982, 116, 329. [Google Scholar] [CrossRef]
- Abbott, L.F.; Farhi, E.; Wise, M.B. Particle Production in the New Inflationary Cosmology. Phys. Lett. B 1982, 117, 29. [Google Scholar] [CrossRef]
- Ford, L.H. Gravitational Particle Creation and Inflation. Phys. Rev. D 1987, 35, 2955. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Kirilova, D.P. On particle creation by a time dependent scalar field. Sov. J. Nucl. Phys. 1990, 51, 172–177. [Google Scholar]
- Traschen, J.H.; Brandenberger, R.H. Particle Production During Out-of-equilibrium Phase Transitions. Phys. Rev. D 1990, 42, 2491–2504. [Google Scholar] [CrossRef]
- Spokoiny, B. Deflationary universe scenario. Phys. Lett. B 1993, 315, 40–45. [Google Scholar] [CrossRef]
- Shtanov, Y.; Traschen, J.H.; Brandenberger, R.H. Universe reheating after inflation. Phys. Rev. D 1995, 51, 5438–5455. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Reheating after inflation. Phys. Rev. Lett. 1994, 73, 3195–3198. [Google Scholar] [CrossRef] [PubMed]
- Kofman, L.; Linde, A.D.; Starobinsky, A.A. Towards the theory of reheating after inflation. Phys. Rev. D 1997, 56, 3258–3295. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Linde, A.D. Preheating in hybrid inflation. Phys. Rev. D 1998, 57, 6075–6088. [Google Scholar] [CrossRef]
- Felder, G.N.; Kofman, L.; Linde, A.D. Instant preheating. Phys. Rev. D 1999, 59, 123523. [Google Scholar] [CrossRef]
- Lyth, D.H.; Wands, D. Generating the curvature perturbation without an inflaton. Phys. Lett. B 2002, 524, 5–14. [Google Scholar] [CrossRef]
- Feng, B.; Li, M.Z. Curvaton reheating in nonoscillatory inflationary models. Phys. Lett. B 2003, 564, 169–174. [Google Scholar] [CrossRef]
- del Campo, S.; Herrera, R.; Saavedra, J.; Campuzano, C.; Rojas, E. Curvaton reheating in logamediate inflationary model. Phys. Rev. D 2009, 80, 123531. [Google Scholar] [CrossRef]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation dynamics and reheating. Rev. Mod. Phys. 2006, 78, 537–589. [Google Scholar] [CrossRef]
- Hardwick, R.J.; Vennin, V.; Koyama, K.; Wands, D. Constraining Curvatonic Reheating. JCAP 2016, 8, 42. [Google Scholar] [CrossRef][Green Version]
- Campos, A.H.; Reis, H.C.; Rosenfeld, R. Preheating in quintessential inflation. Phys. Lett. B 2003, 575, 151–156. [Google Scholar] [CrossRef][Green Version]
- Allahverdi, R.; Brandenberger, R.; Cyr-Racine, F.Y.; Mazumdar, A. Reheating in Inflationary Cosmology: Theory and Applications. Ann. Rev. Nucl. Part. Sci. 2010, 60, 27–51. [Google Scholar] [CrossRef]
- Amin, M.A.; Hertzberg, M.P.; Kaiser, D.I.; Karouby, J. Nonperturbative Dynamics Of Reheating After Inflation: A Review. Int. J. Mod. Phys. D 2014, 24, 1530003. [Google Scholar] [CrossRef]
- Garcia, M.A.G.; Kaneta, K.; Mambrini, Y.; Olive, K.A. Reheating and Post-inflationary Production of Dark Matter. Phys. Rev. D 2020, 101, 123507. [Google Scholar] [CrossRef]
- Tambalo, G.; Rinaldi, M. Inflation and reheating in scale-invariant scalar-tensor gravity. Gen. Relativ. Gravit. 2017, 49, 52. [Google Scholar] [CrossRef]
- López, M.; Otalora, G.; Videla, N. Chaotic inflation and reheating in generalized scalar-tensor gravity. JCAP 2021, 10, 21. [Google Scholar] [CrossRef]
- Saha, P. Model-independent constraints on inflation and reheating. arXiv 2021, arXiv:2108.06612. [Google Scholar]
- Pareek, P.; Nautiyal, A. Reheating constraints on k-inflation. Phys. Rev. D 2021, 104, 83526. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Das, K.; Gangopadhyay, M.R. Probing the era of reheating for reconstructed inflationary potential in the RS II braneworld. Class. Quantum Gravity 2020, 37, 215009. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Donaldson-Wood, L. Warm quintessential inflation. Phys. Lett. B 2019, 796, 26–31. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef] [PubMed]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Gannouji, R.; Sami, M.; Thongkool, I. Generic f(R) theories and classicality of their scalarons. Phys. Lett. B 2012, 716, 255–259. [Google Scholar] [CrossRef]
- Cosmai, L.; Fanizza, G.; Tedesco, L. Cosmic Acceleration and f (R) Theory: Perturbed Solution in a Matter FLRW Model. Int. J. Theor. Phys. 2016, 55, 754–765. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified non-local-F(R) gravity as the key for the inflation and dark energy. Phys. Lett. B 2008, 659, 821–826. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Markkanen, T. Non-minimal gravitational reheating during kination. JCAP 2018, 6, 21. [Google Scholar] [CrossRef]
- Bettoni, D.; Lopez-Eiguren, A.; Rubio, J. Hubble-induced phase transitions on the lattice with applications to Ricci reheating. JCAP 2022, 1, 2. [Google Scholar] [CrossRef]
- Opferkuch, T.; Schwaller, P.; Stefanek, B.A. Ricci Reheating. JCAP 2019, 7, 16. [Google Scholar] [CrossRef]
- Tashiro, H.; Chiba, T.; Sasaki, M. Reheating after quintessential inflation and gravitational waves. Class. Quantum Gravity 2004, 21, 1761–1772. [Google Scholar] [CrossRef]
- Chun, E.J.; Scopel, S. Quintessential Kination and Leptogenesis. JCAP 2007, 10, 11. [Google Scholar] [CrossRef]
- Kamada, K.; Kume, J.; Yamada, Y.; Yokoyama, J. Gravitational leptogenesis with kination and gravitational reheating. JCAP 2020, 1, 16. [Google Scholar] [CrossRef]
- Berera, A.; Fang, L.Z. Thermally induced density perturbations in the inflation era. Phys. Rev. Lett. 1995, 74, 1912–1915. [Google Scholar] [CrossRef] [PubMed]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar] [CrossRef]
- Lima, G.B.F.; Ramos, R.O. Unified early and late Universe cosmology through dissipative effects in steep quintessential inflation potential models. Phys. Rev. D 2019, 100, 123529. [Google Scholar] [CrossRef]
- Basak, S.; Bhattacharya, S.; Gangopadhyay, M.R.; Jaman, N.; Rangarajan, R.; Sami, M. The paradigm of warm quintessential inflation and spontaneous baryogenesis. arXiv 2021, arXiv:2110.00607. [Google Scholar]
- Levy, M.; Rosa, J.G.; Ventura, L.B. Warm inflation, neutrinos and dark matter: A minimal extension of the Standard Model. JHEP 2021, 12, 176. [Google Scholar] [CrossRef]
- Gangopadhyay, M.R.; Myrzakul, S.; Sami, M.; Sharma, M.K. Paradigm of warm quintessential inflation and production of relic gravity waves. Phys. Rev. D 2021, 103, 43505. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Joyce, M. Structure formation with a selftuning scalar field. Phys. Rev. Lett. 1997, 79, 4740–4743. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Joyce, M. Cosmology with a primordial scaling field. Phys. Rev. D 1998, 58, 23503. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Wands, D. Exponential potentials and cosmological scaling solutions. Phys. Rev. D 1998, 57, 4686–4690. [Google Scholar] [CrossRef]
- Tsujikawa, S.; Sami, M. A unified approach to scaling solutions in a general cosmological background. Phys. Lett. B 2004, 603, 113–123. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Wang, L.M.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef]
- Chiba, T. The Equation of State of Tracker Fields. Phys. Rev. D 2010, 81, 23515. [Google Scholar] [CrossRef]
- Barreiro, T.; Copeland, E.J.; Nunes, N.J. Quintessence arising from exponential potentials. Phys. Rev. D 2000, 61, 127301. [Google Scholar] [CrossRef]
- Haro, J.; Amorós, J.; Pan, S. Scaling solutions in quintessential inflation. Eur. Phys. J. C 2020, 80, 404. [Google Scholar] [CrossRef]
- Tsujikawa, S.; Sami, M. String-inspired cosmology: A late time transition from a scaling matter era to a dark energy universe caused by a Gauss–Bonnet coupling. JCAP 2007, 701, 6. [Google Scholar] [CrossRef]
- Gumjudpai, B.; Naskar, T.; Sami, M.; Tsujikawa, S. Coupled dark energy: Towards a general description of the dynamics. JCAP 2005, 6, 7. [Google Scholar] [CrossRef]
- Adhikari, R.; Gangopadhyay, M.R.; Yogesh. Power Law Plateau Inflation Potential In The RS II Braneworld Evading Swampland Conjecture. Eur. Phys. J. C 2020, 80, 899. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Lidsey, J.E. Steep inflation: Ending brane world inflation by gravitational particle production. Phys. Rev. D 2001, 64, 23509. [Google Scholar] [CrossRef]
- Geng, C.Q.; Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Quintessential inflation with canonical and noncanonical scalar fields and Planck 2015 results. Phys. Rev. D 2015, 92, 23522. [Google Scholar] [CrossRef]
- Carroll, S.M. Why is the universe accelerating? In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2004; Volume 743, pp. 16–32. [Google Scholar] [CrossRef]
- Sahni, V. Dark matter and dark energy. In The Physics of the Early Universe; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2004; Volume 653, pp. 141–180. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A. Reconstructing Dark Energy. Int. J. Mod. Phys. D 2006, 15, 2105–2132. [Google Scholar] [CrossRef]
- Mortonson, M.J.; Weinberg, D.H.; White, M. Dark Energy: A Short Review. arXiv 2013, arXiv:1401.0046. [Google Scholar]
- Sami, M.; Myrzakulov, R. Late time cosmic acceleration: ABCD of dark energy and modified theories of gravity. Int. J. Mod. Phys. D 2016, 25, 1630031. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Li, M.; Li, X.D.; Wang, S.; Wang, Y. Dark Energy: A Brief Review. Front. Phys. 2013, 8, 828–846. [Google Scholar] [CrossRef]
- Brax, P. What makes the Universe accelerate? A review on what dark energy could be and how to test it. Rept. Prog. Phys. 2018, 81, 16902. [Google Scholar] [CrossRef]
- Zhang, Z. Geometrization of light bending and its application to SdSw spacetime. Class. Quantum Gravity 2022, 39, 15003. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J.E. Cosmological Consequences of a Rolling Homogeneous Scalar Field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef]
- Sami, M. Models of dark energy. In The Invisible Universe: Dark Matter and Dark Energy; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2007; Volume 720, pp. 219–256. [Google Scholar]
- Sami, M. A primer on problems and prospects of dark energy. Curr. Sci. 2009, 97, 887. [Google Scholar]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Tristram, M.; Banday, A.J.; Górski, K.M.; Keskitalo, R.; Lawrence, C.R.; Andersen, K.J.; Barreiro, R.B.; Borrill, J.; Colombo, L.P.L.; Eriksen, H.K.; et al. Improved limits on the tensor-to-scalar ratio using BICEP and Planck. arXiv 2021, arXiv:2112.07961. [Google Scholar]
- Liddle, A.R.; Scherrer, R.J. A Classification of scalar field potentials with cosmological scaling solutions. Phys. Rev. D 1999, 59, 23509. [Google Scholar] [CrossRef]
- Skugoreva, M.A.; Sami, M.; Jaman, N. Emergence of cosmological scaling behavior in the asymptotic regime. Phys. Rev. D 2019, 100, 43512. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe. Front. Phys. 1990, 69, 1–547. [Google Scholar] [CrossRef]
- Husdal, L. On Effective Degrees of Freedom in the Early Universe. Galaxies 2016, 4, 78. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.H. Big Bang Nucleosynthesis: 2015. Rev. Mod. Phys. 2016, 88, 15004. [Google Scholar] [CrossRef]
- Caprini, C.; Figueroa, D.G. Cosmological Backgrounds of Gravitational Waves. Class. Quantum Gravity 2018, 35, 163001. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Skillman, E. New BBN limits on physics beyond the standard model from 4He. Astropart. Phys. 2005, 23, 313–323. [Google Scholar] [CrossRef]
- de la Macorra, A.; Piccinelli, G. Cosmological evolution of general scalar fields and quintessence. Phys. Rev. D 2000, 61, 123503. [Google Scholar] [CrossRef]
- Nunes, A.; Mimoso, J.P. On the potentials yielding cosmological scaling solutions. Phys. Lett. B 2000, 488, 423–427. [Google Scholar] [CrossRef]
- Ng, S.C.C.; Nunes, N.J.; Rosati, F. Applications of scalar attractor solutions to cosmology. Phys. Rev. D 2001, 64, 83510. [Google Scholar] [CrossRef]
- Wetterich, C. Variable gravity Universe. Phys. Rev. D 2014, 89, 24005. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Linder, E.V. The Limits of quintessence. Phys. Rev. Lett. 2005, 95, 141301. [Google Scholar] [CrossRef] [PubMed]
- Linder, E.V. The paths of quintessence. Phys. Rev. D 2006, 73, 63010. [Google Scholar] [CrossRef]
- Scherrer, R.J.; Sen, A.A. Thawing quintessence with a nearly flat potential. Phys. Rev. D 2008, 77, 083515. [Google Scholar] [CrossRef]
- Linder, E.V. Quintessence’s last stand? Phys. Rev. D 2015, 91, 63006. [Google Scholar] [CrossRef]
- Urena-López, L.A.U.; Roy, N. Generalized tracker quintessence models for dark energy. Phys. Rev. D 2020, 102, 063510. [Google Scholar] [CrossRef]
- Chiba, T. Slow-roll thawing quintessence. Phys. Rev. D 2009, 79, 083517, Erratum in Phys. Rev. D 2009, 80, 109902. [Google Scholar] [CrossRef]
- Geng, C.; Lee, C.; Sami, M.; Saridakis, E.N.; Starobinsky, A.A. Observational constraints on successful model of quintessential Inflation. JCAP 2017, 6, 11. [Google Scholar] [CrossRef]
- Scherrer, R.J. Exact general solutions for cosmological scalar field evolution in a background-dominated expansion. arXiv 2022, arXiv:2202.01132. [Google Scholar]
- Bartolo, N.; Pietroni, M. Scalar tensor gravity and quintessence. Phys. Rev. D 2000, 61, 23518. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Sushkov, S.V. Quintessence and phantom cosmology with non-minimal derivative coupling. Phys. Rev. D 2010, 81, 083510. [Google Scholar] [CrossRef]
- Wetterich, C. Cosmon inflation. Phys. Lett. B 2013, 726, 15–22. [Google Scholar] [CrossRef][Green Version]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Variable gravity: A suitable framework for quintessential inflation. Phys. Rev. D 2014, 90, 23512. [Google Scholar] [CrossRef]
- Sami, M.; Gannouji, R. Spontaneous symmetry breaking in the late Universe and glimpses of the early Universe phase transitions à la baryogenesis. Int. J. Mod. Phys. D 2021, 30, 2130005. [Google Scholar] [CrossRef]
- Sahni, V. The Energy Density of Relic Gravity Waves From Inflation. Phys. Rev. D 1990, 42, 453–463. [Google Scholar] [CrossRef]
- Boyle, L.A.; Steinhardt, P.J. Probing the early universe with inflationary gravitational waves. Phys. Rev. D 2008, 77, 63504. [Google Scholar] [CrossRef]
- Watanabe, Y.; Komatsu, E. Improved Calculation of the Primordial Gravitational Wave Spectrum in the Standard Model. Phys. Rev. D 2006, 73, 123515. [Google Scholar] [CrossRef]
- Kuroyanagi, S.; Chiba, T.; Sugiyama, N. Precision calculations of the gravitational wave background spectrum from inflation. Phys. Rev. D 2009, 79, 103501. [Google Scholar] [CrossRef]
- Ahmad, S.; Felice, A.D.; Jaman, N.; Kuroyanagi, S.; Sami, M. Baryogenesis in the paradigm of quintessential inflation. Phys. Rev. D 2019, 100, 103525. [Google Scholar] [CrossRef]
- Figueroa, D.G.; Tanin, E.H. Inconsistency of an inflationary sector coupled only to Einstein gravity. JCAP 2019, 10, 50. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaman, N.; Sami, M. What Is Needed of a Scalar Field If It Is to Unify Inflation and Late Time Acceleration? Galaxies 2022, 10, 51. https://doi.org/10.3390/galaxies10020051
Jaman N, Sami M. What Is Needed of a Scalar Field If It Is to Unify Inflation and Late Time Acceleration? Galaxies. 2022; 10(2):51. https://doi.org/10.3390/galaxies10020051
Chicago/Turabian StyleJaman, Nur, and Mohammad Sami. 2022. "What Is Needed of a Scalar Field If It Is to Unify Inflation and Late Time Acceleration?" Galaxies 10, no. 2: 51. https://doi.org/10.3390/galaxies10020051
APA StyleJaman, N., & Sami, M. (2022). What Is Needed of a Scalar Field If It Is to Unify Inflation and Late Time Acceleration? Galaxies, 10(2), 51. https://doi.org/10.3390/galaxies10020051






