Lessons from the Ionised and Molecular Mass of Post-CE PNe
Abstract
1. Introduction
2. Sample and Observations
3. The Mass of Post-CE PNe
3.1. Ionised Masses
3.2. Molecular Masses
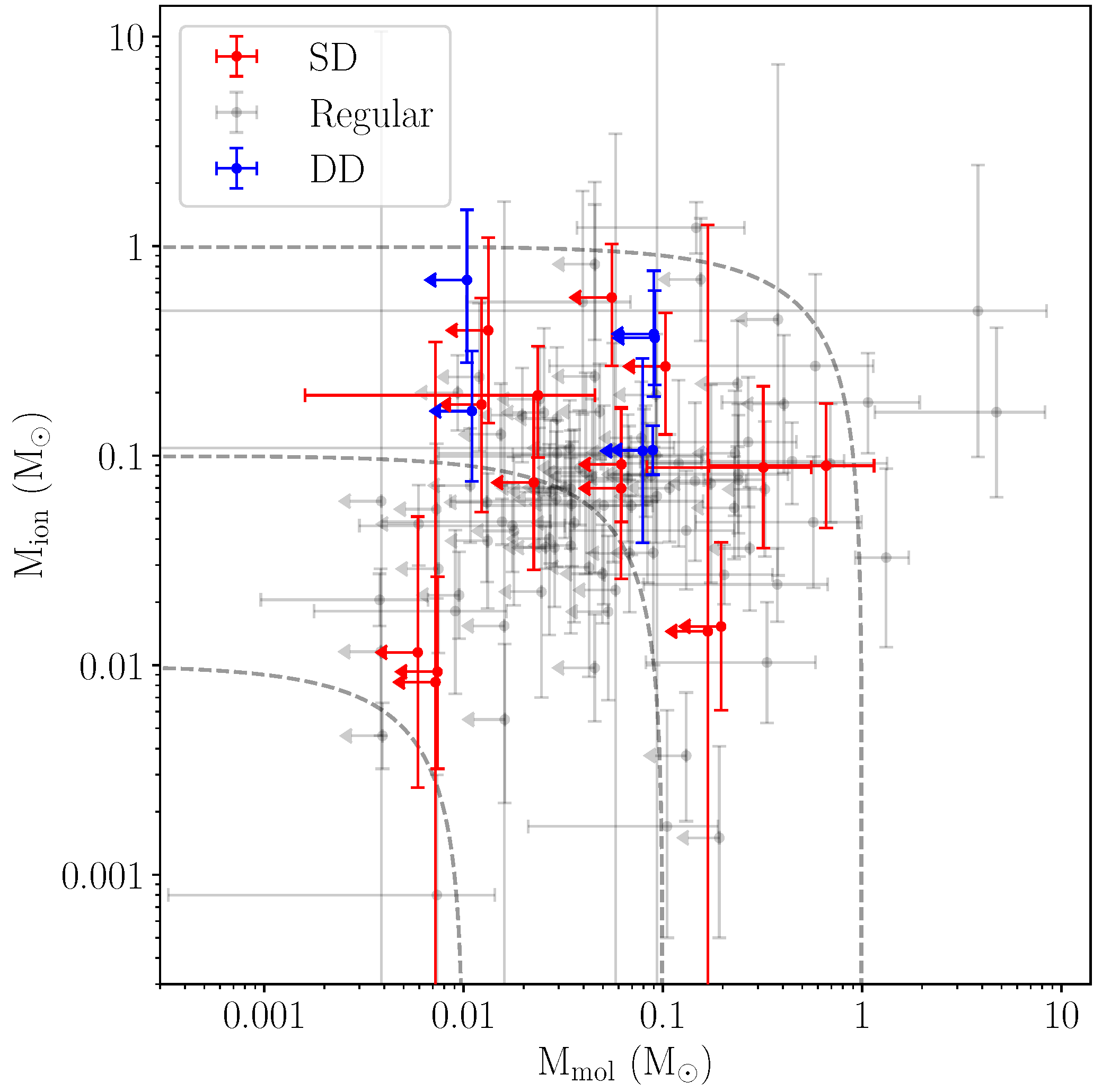
3.3. Results
3.4. Comparison with Regular PNe
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Balick, B.; Frank, A. Shapes and Shaping of Planetary Nebulae. Annu. Rev. Astron. Astrophys. 2002, 40, 439–486. [Google Scholar] [CrossRef]
- Jones, D.; Boffin, H.M.J. Binary stars as the key to understanding planetary nebulae. Nat. Astron. 2017, 1, 0117. [Google Scholar] [CrossRef]
- Decin, L.; Montargès, M.; Richards, A.M.S.; Gottlieb, C.A.; Homan, W.; Mcdonald, I.; El Mellah, I.; Danilovich, T.; Wallström, S.H.J.; Zijlstra, A.; et al. (Sub)stellar companions shape the winds of evolved stars. Science 2020, 369, 1497–1500. [Google Scholar] [CrossRef] [PubMed]
- Paczynski, B. Structure and Evolution of Close Binary Systems. In Proceedings of the IAU Symposium 73, Cambridge, UK, 28 June–1 October 1975; p. 75. [Google Scholar]
- Ricker, P.M.; Taam, R.E. An AMR Study of the Common-envelope Phase of Binary Evolution. Astrophys. J. 2012, 746, 74. [Google Scholar] [CrossRef]
- Jones, D. Observational Constraints on the Common Envelope Phase. In Reviews in Frontiers of Modern Astrophysics; From Space Debris to Cosmology; Springer: Berlin/Heidelberg, Germany, 2020; pp. 123–153. [Google Scholar]
- Ohlmann, S.T.; Röpke, F.K.; Pakmor, R.; Springel, V. Hydrodynamic Moving-mesh Simulations of the Common Envelope Phase in Binary Stellar Systems. Astrophys. J. Lett. 2016, 816, 90. [Google Scholar] [CrossRef]
- Ivanova, N. On the Use of Hydrogen Recombination Energy during Common Envelope Events. Astrophys. J. Lett. 2018, 858, 24. [Google Scholar] [CrossRef]
- Chamandy, L.; Blackman, E.G.; Frank, A.; Carroll-Nellenback, J.; Tu, Y. Common envelope evolution on the asymptotic giant branch: Unbinding within a decade? Mon. Not. R. Astron. Soc. 2020, 495, 4028–4039. [Google Scholar] [CrossRef]
- Kwok, S. Conference Summary. In Proceedings of the IAU Symp. 323, Planetary Nebulae: Multi-Wavelength Probes of Stellar and Galactic Evolution, Beijing, China, 10–14 October 2016; pp. 317–324. [Google Scholar]
- Frew, D.J.; Parker, Q.A. Do post-common envelope objects form a distinct subset of PNe? In Proceedings of the Asymmetrical Planetary Nebulae IV Conference, La Palma, Spain, 19–22 June 2007; pp. 475–482. [Google Scholar]
- Santander-García, M.; Jones, D.; Alcolea, J.; Bujarrabal, V.; Wesson, R. The ionised and molecular mass of post-common-envelope planetary nebulae. The missing mass problem. Astron. Astrophys. 2022; in press. [Google Scholar] [CrossRef]
- Guerrero, M.A.; Miranda, L.F. NGC 6778: A disrupted planetary nebula around a binary central star. Astron. Astrophys. 2012, 539, 47. [Google Scholar] [CrossRef]
- Huggins, P.J.; Healy, A.P. CO in planetary nebulae. Astrophys. J. 1989, 346, 201–211. [Google Scholar] [CrossRef]
- Huggins, P.J.; Bachiller, R.; Cox, P.; Forveille, T. The molecular envelopes of planetary nebulae. Astron. Astrophys. 1996, 315, 284–302. [Google Scholar]
- Huggins, P.J.; Bachiller, R.; Planesas, P.; Forveille, T.; Cox, P. A CO Survey of Young Planetary Nebulae. Astrophys. J. 2005, 160, 272–285. [Google Scholar] [CrossRef][Green Version]
- Guzman-Ramirez, L.; Gómez-Ruíz, A.I.; Boffin, H.M.J.; Jones, D.; Wesson, R.; Zijlstra, A.A.; Smith, C.L.; Nyman, L.A. Opening PANDORA’s box: APEX observations of CO in PNe. Astron. Astrophys. 2018, 618, 91. [Google Scholar] [CrossRef]
- Frew, D.J.; Parker, Q.A.; Bojičić, I.S. The Hα surface brightness-radius relation: A robust statistical distance indicator for planetary nebulae. Mon. Not. R. Astron. Soc. 2016, 455, 1459–1488. [Google Scholar] [CrossRef]
- Corradi, R.L.; García-Rojas, J.; Jones, D.; Rodríguez-Gil, P. Binarity and the Abundance Discrepancy Problem in Planetary Nebulae. Astrophys. J. 2015, 803, 99. [Google Scholar] [CrossRef]
- Brown, A.G.; Vallenari, A.; Prusti, T.; De Bruijne, J.H.J.; Babusiaux, C.; Biermann, M.; Creevey, O.L.; Evans, D.W.; Eyer, L.; Hutton, A.; et al. Gaia Early Data Release 3. Summary of the contents and survey properties. Astron. Astrophys. 2020, 649, 1. [Google Scholar]
- Weinberger, R. A catalogue of expansion velocities of galactic planetary nebulae. Astron. Astrophys. Suppl. Ser. 1989, 78, 301–324. [Google Scholar]
- Scholz, F.W.; Stephens, M.A. K-Sample Anderson-Darling Tests. J. Am. Stat. Assoc. 1987, 399, 918–924. [Google Scholar]
- Iaconi, R.; De Marco, O. Speaking with one voice: Simulations and observations discuss the common envelope α parameter. Mon. Not. R. Astron. Soc. 2019, 450, 2550–2566. [Google Scholar] [CrossRef]
- De Marco, O.; Passy, J.C.; Moe, M.; Herwig, F.; Mac Low, M.M.; Paxton, B. On the α formalism for the common envelope interaction. Mon. Not. R. Astron. Soc. 2011, 411, 2277–2292. [Google Scholar] [CrossRef]
- Wesson, R.; Jones, D.; García-Rojas, J.; Boffin, H.M.J.; Corradi, R.L.M. Confirmation of the link between central star binarity and extreme abundance discrepancy factors in planetary nebulae. Mon. Not. R. Astron. Soc. 2018, 480, 4589–4613. [Google Scholar] [CrossRef]
- Soker, N. Close Stellar Binary Systems by Grazing Envelope Evolution. Astrophys. J. 2015, 800, 114. [Google Scholar] [CrossRef]
- Shiber, S.; Kashi, A.; Soker, N. Simulating the onset of grazing envelope evolution of binary stars. Mon. Not. R. Astron. Soc. Lett. 2017, 465, L54–L58. [Google Scholar] [CrossRef]
- Santander-García, M.; Jones, D.; Alcolea, J.; Bujarrabal, V.; Gómez-Garrido, M.; Aladro, R.; Verbena, J.L. The neutral atomic mass of post-common-envelope planetary nebulae. 2022; in preparation. [Google Scholar]
- Castro-Carrizo, A.; Bujarrabal, V.; Fong, D.; Meixner, M.; Tielens, A.G.G.M.; Latter, W.B.; Barlow, M.J. Low-excitation atomic gas around evolved stars. II. ISO observations of O-rich nebulae. Astron. Astrophys. 2001, 367, 674. [Google Scholar] [CrossRef][Green Version]
- Fong, D.; Meixner, M.; Castro-Carrizo, A.; Bujarrabal, V.; Latter, W.B.; Tielens, A.G.G.M.; Kelly, D.M.; Sutton, E.C. Low-excitation atomic gas around evolved stars. I. ISO observations of C-rich nebulae. Astron. Astrophys. 2001, 367, 652. [Google Scholar] [CrossRef][Green Version]
| PN G | Common Name | D | ||
|---|---|---|---|---|
| (kpc) | (M) | (M) | ||
| Single-Degenerate post-CE PNe | ||||
| G034.5-06.7 | NGC 6778 | 2.79 ± 0.79 | 0.19 | 0.02 ± 0.02 |
| G036.1-57.1 | NGC 7293 | 0.200 ± 0.002 | 0.09 | 0.3 ± 0.2 |
| G053.8-03.0 | Abell 63 | 2.703 ± 0.219 | 0.012 | <0.006 |
| G054.2-03.4 | Necklace | 4.6 ± 1.1 | 0.009 | <0.007 |
| G068.1+11.1 | ETHOS 1 | 4.2 ± 0.0 | 0.008 | <0.007 |
| G086.9-03.4 | Ou 5 | 5.0 ± 1.0 | 0.18 | <0.012 |
| G118.8-74.7 | NGC 246 | 0.556 ± 0.025 | 0.07 | <0.02 |
| G208.5+33.2 | Abell 30 | 2.222 ± 0.148 | 0.015 | <0.20 |
| G215.6+03.6 | NGC 2346 | 1.389 ± 0.039 | 0.09 | 0.7 ± 0.5 |
| G221.8-04.2 | PM 1-23 | 5.2 ± 2.0 | 0.015 | <0.17 |
| G307.5-04.9 | MyCn 18 | 4.000 ± 1.280 | 0.07 | <0.06 |
| G338.1-08.3 | NGC 6326 | 5.000 ± 1.500 | 0.6 | <0.06 |
| G338.8+05.6 | Hen 2-155 | 4.348 ± 1.323 | 0.3 | <0.10 |
| G342.5-14.3 | Sp 3 | 2.22 | 0.09 | <0.06 |
| G349.3-04.2 | Lo 16 | 1.818 ± 0.132 | 0.4 | <0.013 |
| Double-Degenerate post-CE PNe | ||||
| G009.6+10.5 | Abell 41 | 4.89 ± 1.4 | 0.16 | <0.011 |
| G049.4+02.4 | Hen 2-428 | 4.545 ± 1.446 | 0.7 | <0.010 |
| G058.6-03.6 | V458 Vul | 12.5 ± 2.0 | 0.11 | <0.08 |
| G197.8+17.3 | NGC 2392 | 1.818 ± 0.165 | 0.4 | <0.09 |
| G290.5+07.9 | Fg 1 | 2.564 ± 0.197 | 0.4 | <0.09 |
| G307.2-03.4 | NGC 5189 | 1.471 ± 0.043 | 0.11 | <0.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santander-García, M.; Jones, D.; Alcolea, J.; Bujarrabal, V.; Wesson, R. Lessons from the Ionised and Molecular Mass of Post-CE PNe. Galaxies 2022, 10, 26. https://doi.org/10.3390/galaxies10010026
Santander-García M, Jones D, Alcolea J, Bujarrabal V, Wesson R. Lessons from the Ionised and Molecular Mass of Post-CE PNe. Galaxies. 2022; 10(1):26. https://doi.org/10.3390/galaxies10010026
Chicago/Turabian StyleSantander-García, Miguel, David Jones, Javier Alcolea, Valentín Bujarrabal, and Roger Wesson. 2022. "Lessons from the Ionised and Molecular Mass of Post-CE PNe" Galaxies 10, no. 1: 26. https://doi.org/10.3390/galaxies10010026
APA StyleSantander-García, M., Jones, D., Alcolea, J., Bujarrabal, V., & Wesson, R. (2022). Lessons from the Ionised and Molecular Mass of Post-CE PNe. Galaxies, 10(1), 26. https://doi.org/10.3390/galaxies10010026







